1. Introduction
When modeling complex systems, statistical physicists often posit that the interacting entities they consider have simple individual properties, and that the possibly more complex behavior observed at a collective level, when considering many such simple entities, is simply the result of interactions between entities [
1,
2,
3,
4]. The emergence of macroscopically different properties from simpler interacting entities, often through a collective symmetry breaking mechanism, has been emphasized long ago by P. W. Anderson in his seminal paper “More is Different” [
5] as one of the key mechanisms at play to account for the wealth of different objects or behaviors found in the real world. In this paper, Anderson actually presents the statistical physics approach as a generic and somewhat iterative method, to deal with the emerging complexity in a multilevel way, the outcome of a given level of analysis being the building blocks (i.e., the interacting entities) of the next level. The key role played by symmetry breaking phenomena in the emerging complexity at collective scale has been widely acknowledged in many different contexts (see, e.g., [
2,
6,
7,
8] among many others). Interestingly, a perhaps less explicit suggestion of Anderson’s paper is also to consider statistical physics models where the interacting entities are not simple objects with a handful of characteristics, but are already rather complex objects with many internal degrees of freedom. Although it has been formulated almost 50 years ago, this suggestion looks very timely by now.
In recent decades, statistical physics has gone beyond the equilibrium paradigm based on molecular entities, and has indeed started to consider assemblies of macroscopic and potentially complex objects like grains of sand [
9,
10], or active particles modeling for instance some types of bacteria, or self-phoretic colloids [
8]. However, in these examples, macroscopic particles may in practice still be considered to be simple particles, as their many internal degrees of freedom can be subsumed into a small number of effective parameters encoding their macroscopic, non-equilibrium character, like dissipation coefficients [
9,
10] or self-propulsion forces [
8]. To find genuine examples of assemblies of complex entities in a theoretical context, one may rather turn to the field of population dynamics and evolution in theoretical biology, where for instance large populations of individuals characterized by a complicated genome evolve under some evolutionary rules [
11,
12].
When considering models of social systems, it would be necessary at first sight to take into account the intrinsic complexity of human beings [
1]. However, this complexity is too extreme to be captured by any type of statistical physics models, so that statistical physicists have often considered very simple models of social agents, retaining a small number of characteristics, for instance a binary [
13] or continuous [
14] opinion. A natural question is then to understand how more complex agents could in some situations reduce their intrinsic complexity to effectively appear as simple. This question can already be addressed within the framework of statistical physics, because there is no need to model the full complexity of human beings to address at least some aspects of this issue. A simple tentative answer has been given in [
15], by illustrating on a toy model how the simplification of agents with many internal degrees of freedom may result from interactions among agents. This point of view is qualitatively consistent with the idea advocated by some sociologists that ‘the whole is less than the parts’ [
16,
17], in the sense that, roughly speaking, human beings may leave aside part of their complexity to build a group. It has been argued in [
15] that this point of view can be reconciled with the seemingly antagonist viewpoint of statistical physicists according to which ‘the whole is more than the sum of the part’, due to collective phenomena and symmetry breakings.
Yet, the model introduced in [
15] considered an assembly of identical agents, while agent heterogeneity may be expected to be an important characteristic of human beings. In this note, we extend the model of [
15] by including heterogeneity between agents. We show, using methods inspired by the physics of glasses, that two different types of agents simplification can occur in this model, one driven by interactions as in [
15], and the other one driven by heterogeneity.
2. Model
We introduce a model of complex agents generalizing the one introduced in [
15] by now considering heterogeneous agents. The model is composed of
N interacting agents with an internal state described by a configuration
, with
and where the number
H of configurations is large. We write for later convenience
H in the form
, where
is a fixed integer number, and
M is assumed to be large. This is typically the case if the configuration
is composed of
M degrees of freedom, each of which taking
possible values. Each agent is endowed with a characteristic that can be either present or absent depending on the configuration
. Intuitively, this characteristic could be a preference for a specific kind of music or tempo for the members of a vocal ensemble [
17] for instance, or more generally be related to a binary opinion [
13]. This feature is conveniently encoded by a variable
: the characteristic is present when
, and absent when
. The general idea is that the characteristic would be present only in a small number of internal states, so that it would typically remain unobserved except if there is a strong probability bias towards the few configurations for which
. To implement this idea in practice in the model, we assume that the characteristic is present in a single configuration, which we label
.
We now need to define the dynamics of agents. Following standard practice in the modeling of social agents [
18,
19], we assume that the dynamics is driven by an individual utility function
that accounts both for individual preferences and for interactions with other agents. An agent
i stochastically changes configurations according to the following rule. Given the current configuration
, the new configuration
is randomly chosen with a probability rate given by the logit rule, a standard rule in the field of social agents modeling [
18,
19],
with
the variation of utility generated by the change of configuration (note that configurations
of the other agents
are kept fixed). The parameter
T plays a role similar to temperature in statistical physics, and characterizes the degree of stochasticity in the decision rule.
Our goal is to model heterogeneous agents that interact through their characteristic
(their internal state is otherwise invisible to other agents). Such an interaction between characteristics was already introduced in Ref. [
15] for the homogeneous case, by considering a mean-field (or fully connected) coupling. We keep here the same mean-field expression of the interaction contribution to the utility. To model heterogeneity in a minimal way, we include an additive contribution
to the utility of agent
i, which corresponds to the agent’s intrinsic (or idiosyncratic) utility associated with configuration
. Under these assumptions, we end up with the following form of the utility function of agent
i,
where
K is the coupling constant characterizing the interaction with the other agents. Note the
scaling of the interaction term, typical of fully connected models where all particles or agents interact with each other in a similar way. Another, and possibly interesting way to introduce heterogeneity would be to have heterogeneous couplings among agents, by replacing the single coupling constant
J by different coupling constants
that would depend on the pair of agents
. However, this would make the analysis of the model much more involved. In the present work, we restrict ourselves to the simplest case when heterogeneity is introduced only in the idiosyncratic utility.
To fully define the model, we need to specify the heterogeneous intrinsic utilities
. Inspired by spin-glass physics, and more precisely by the Random Energy Model for spin-glasses [
20,
21], we model the heterogeneous intrinsic utilities
as a quenched randomness. To be specific, for all
and
, the intrinsic utility
is randomly drawn from a Gaussian distribution
,
where we recall that
M is defined by
. The utilities
do not change in time. The Gaussian form of the intrinsic utility distribution, as well as the scaling of the variance with
M, is guided by similar assumptions made on the energy distribution in the original version of the Random Energy Model [
20,
21]. However, the results obtained are not expected to depend on this Gaussian assumption at a qualitative level, because the analysis conducted here is similar to the one performed in the Random Energy Model, whose phenomenology is the same for a broad class of energy distributions [
22,
23].
Now that the dynamics of the model has been defined, we would like to determine the steady-state probability distribution
of the model. Although the transition rate (
1) looks similar to the Glauber or Kawasaki rates used in statistical physics for spin models or lattice gas models, it is actually different because the utility
is a function attached to each agent
i, and not a unique global function like the energy in physics models (see, e.g., [
24] for a more detailed discussion of this issue). Yet, it is possible in some cases to find a global function
that thus does not depend on the agent
i, such that the variation
during a transition from one configuration to another is equal to the variation
of the utility of agent
i. The global observable
E plays a role similar to the energy in physics (up to a change of sign). The main difference is that in physics models, the energy (or Hamiltonian) is given by the definition of the model, whereas in socioeconomic models the function
E has to be determined (if it exists) from the dynamical rules defined in terms of the utility. Here, due to the simple enough form of the utility function, such a global function
E exists and can be determined explicitly as
Please note that the quantity E is thus different from the total utility , due to the factor in the interaction term.
Given the property
, it can now be easily checked that the dynamics defined by the transition rate Equation (
1) obeys the detailed balance property in terms of the equilibrium distribution
with
, and where
Z is a normalization constant. In this form, it becomes clear that the present model shares similarities with the Random Energy Model [
20,
21,
22] as mentioned above, as well as with the Ising model [
7], the Potts model [
25] or the Blume-Emery-Griffiths spin-1 model [
26]. However, it also exhibits important differences with each of these models.
Now that we determined the equilibrium distribution of the model, our goal is to investigate its phase diagram to assess the effect of the competition between agents heterogeneity (due to their quenched intrinsic utility) and collective effects that could arise from interactions. As recalled in the introduction, the homogeneous version of the model, studied in [
15], exhibits a transition driven by interactions between a phase where agents essentially visit all their internal states and thus have no strongly preferred configurations, and an ordered state where all agents ‘standardize’ in the same configuration
such that
(i.e., the characteristic of the agent becomes visible). In the present generalization of the model, we wish to explore whether the standardized state survives the heterogeneity of agent intrinsic utility. Indeed, the internal state
such that
may have a lower intrinsic utility
than other more favored configurations of agent
i, and this may prevent a common standardization of all agents in the same state.
To investigate this issue, we introduce the order parameter
q defined as
If the number
N of agents is large, the pseudo-energy
E can be expressed in terms of the order parameter
q as
We now wish to determine the distribution
of the order parameter
q. This distribution is obtained by summing the joint distribution
over all configurations
with a given value of
q, namely
with
a generalized Kronecker delta such that
and
otherwise. For a given value of
q, there are
agents in configuration
and
agents in any of the other
configurations. To evaluate
according to its definition given in Equation (
8), we thus need to sum over all possible ways to choose the
agents in configuration
and the
agents in other configurations. Technically, we need to sum over all possible unordered subsets with
elements of the integer set
. To write reasonably compact equations, we denote by
a generic unordered subset with
elements of the set
, and we sum over all possible such subsets
. With these notations,
can be written as
where in the second product, the index
i is implicitly restricted to the interval
. The distribution
defined in Equation (
8) actually depends on the specific realization of the random utilities
, so that
should in principle be eventually averaged over these random utilities. However, to make calculations easier, we do not compute explicitly the average over
, but rather use heuristic arguments to evaluate the typical values of the random quantities appearing in Equation (
9). Such an estimate is expected to be sufficient to determine the leading exponential behavior
of the distribution
. The first product between brackets in Equation (
9) can be rewritten as the exponential of
. The latter sum is (up to the factor
) a sum of independent and identically distributed Gaussian random variables drawn from the distribution Equation (
3). The sum is thus also Gaussian distributed, with zero mean and variance
. It follows that
and this product can thus be neglected (i.e., replaced by 1) when looking for the behavior of
at exponential order in
N.
The key point to determine
explicitly is now to evaluate the typical value
of the sum
where we recall that each
is an independent random variable drawn from the distribution
given in Equation (
3). Once this estimate is known, the distribution
can be approximated as
The quantity
has the same form as the partition function of the Random Energy Model (REM) [
20,
21], and we can thus borrow some methods from the REM to evaluate it. A standard approach to study the REM is to evaluate the density of states of a typical realization of the disorder. It is convenient at this stage to define the rescaled variable
. Denoting as
the density of state of a given realization, the average
over the disorder is given by
to exponential order in
M, with the definition
. Hence if
, corresponding to
, the average density of state
is exponentially large with
M, and for a typical sample
. By contrast, when
, the average density of state is exponentially small with
M, meaning that in most realizations there are actually no states with
(the exponentially small value of the average density of states comes from very rare and atypical realizations with a few states in this range). Therefore, to describe a typical realization, one can in practice consider that the density of state is equal to zero for
, and equal to
for
. We can thus evaluate
as
The integral in Equation (
14) can be evaluated by a saddle-point calculation in the large
M limit. Defining
,
is given for large
M by
, where
is the maximum value of
over the interval
. Let us first look for the maximum of
over the whole real axis. Defining
such that
, we find
. Recalling that
, and defining
we find that
for
, whereas
for
. Hence
for
, and
for
, taking into account the fact that
is monotonously increasing for
. We thus obtain
Using Equations (
12) and (
16), we obtain after expanding the factorials thanks to the Stirling formula that
takes a large deviation form
. In physical terms,
may be thought of as (the opposite of) a free energy. The explicit expression of
depends on the temperature range. For
,
reads
whereas for
,
Please note that we did not take into account in
the contribution coming from the normalization factor
Z, as this would simply add a constant to
. Inspired by Ref. [
15], where interesting results were obtained for a coupling constant
, we assume in what follows that
and take the reduced constant
k as the relevant control parameter in the model (on top of temperature
T). For large
M, the expression of
then simplifies to
We first observe that in this large-
M approximation,
is a convex function of
q for all values of temperature
T, so that the maximum of
over the interval
is either
or
. The most probable state is found to be
for
and
for
, where the critical line
is defined as (with
)
The curve
thus separates the
phase diagram into two regions, a region with
at low coupling and a region with
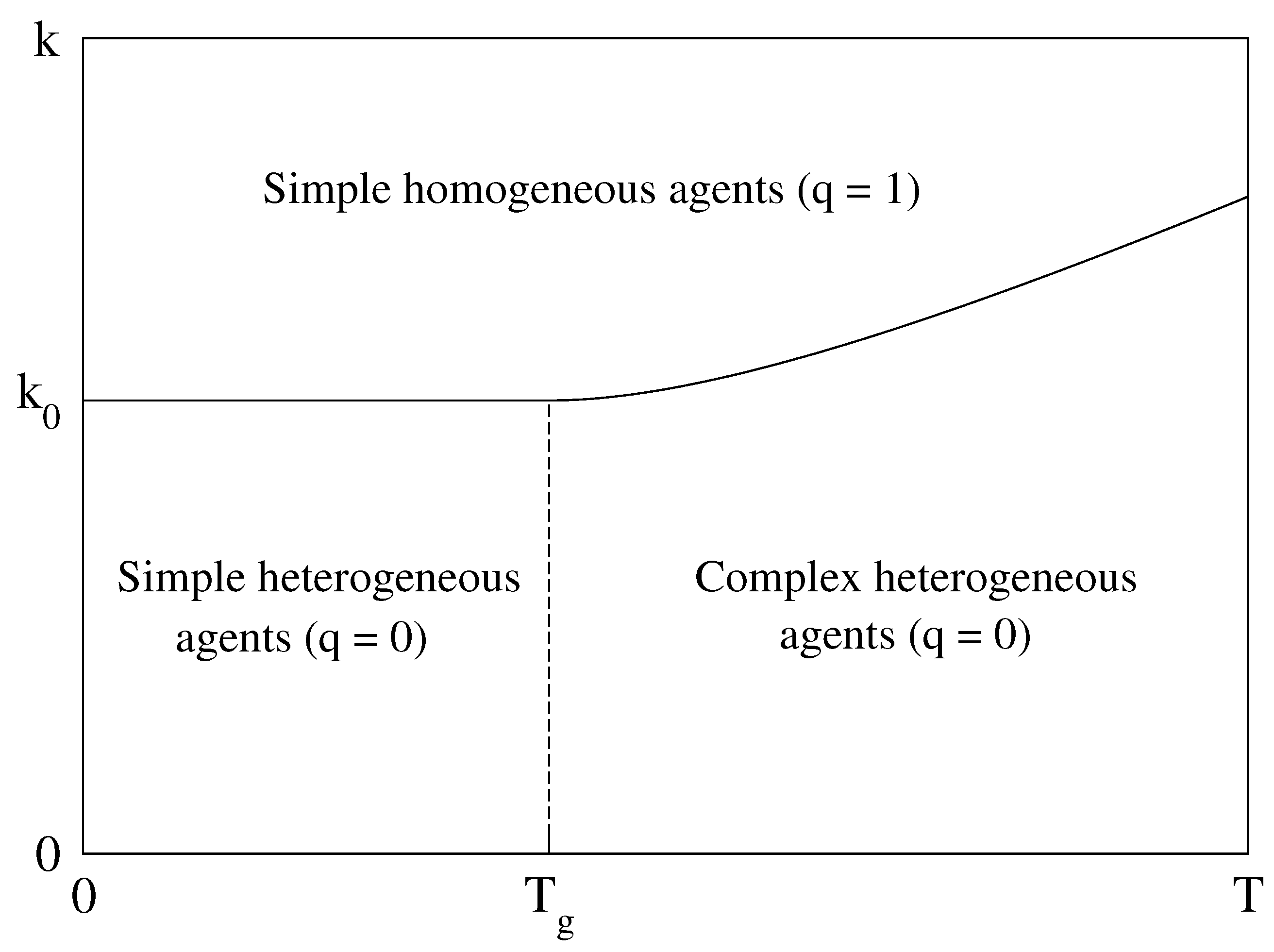
at high coupling. The corresponding phase diagram is plotted in
Figure 1. Please note that for
(i.e., in the absence of disorder), the glassy region in the phase diagram disappears, and one recovers the phase transition at
between a high-temperature phase with
and a low-temperature phase with
found in the homogeneous model [
15].
Moreover, we have also seen that a change of behavior occurs at . For , the agents dynamically visit a large number of configurations, while for their dynamics becomes essentially frozen, and only a few configurations have a significant probability to be visited. In other words, for agents become ‘stuck’ in a small number of configurations with the highest utility. In the context of the Random Energy Model for glasses, the temperature corresponds to the glass transition.
Hence there are actually three different regions in the phase diagram shown in
Figure 1. For
and
, agents have no preferred configurations and visit many different configurations over time. For
and
, each agent spends a lot of time in a small set of preferred configurations. In other words, agents look simple, but they remain different one from the other. This regime is dominated by agent heterogeneity, and there is on average no macroscopic overlap between agent configurations (
). In the last region
, the coupling between agents dominates over agents heterogeneity, and all agents are essentially in the same configuration, leading to a strong overlap (
) and to the emergence of a common characteristic, a phenomenon that has been called standardization in [
15].