A New Objective Function for the Recovery of Gielis Curves
Abstract
1. Introduction
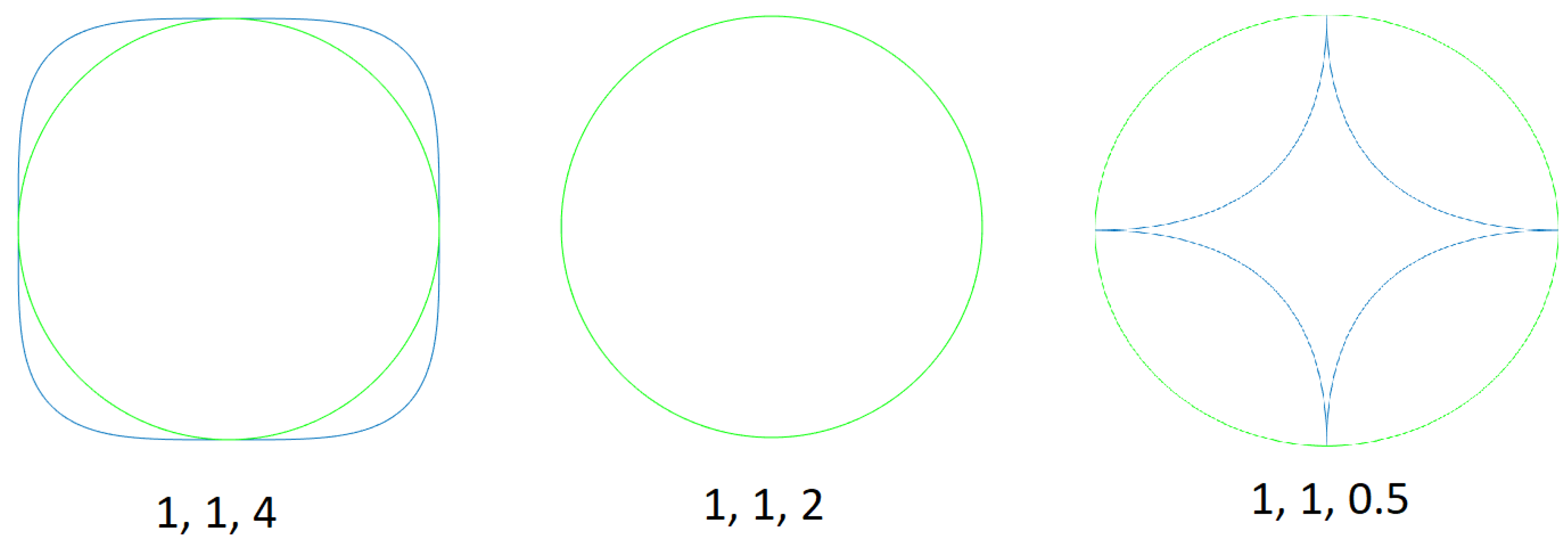
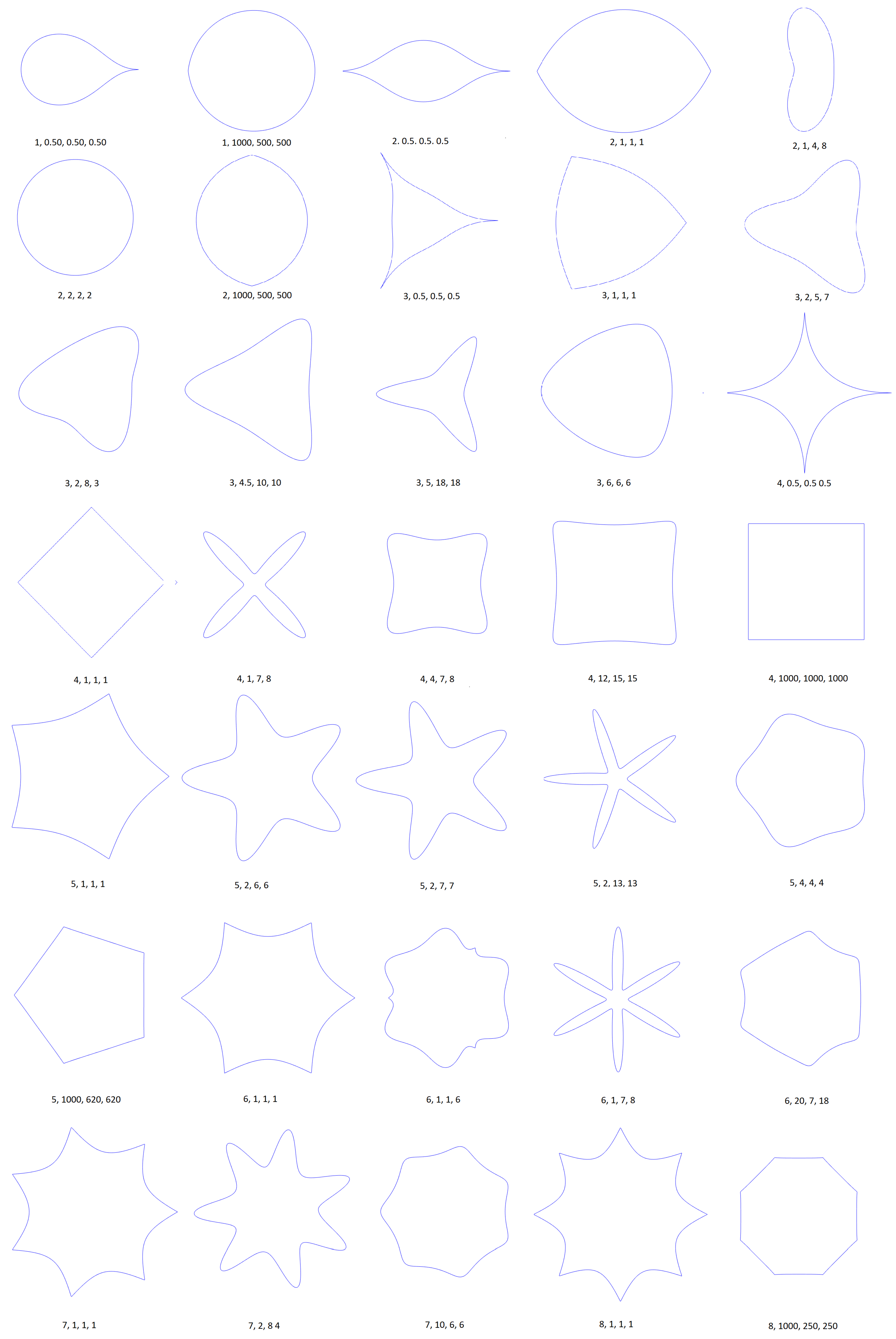
2. Gielis Curves
3. Background
- Each gene represents a parameter from the superformula, i.e., each gene may be represented by a real number, except p and q, which are restricted to integer numbers.
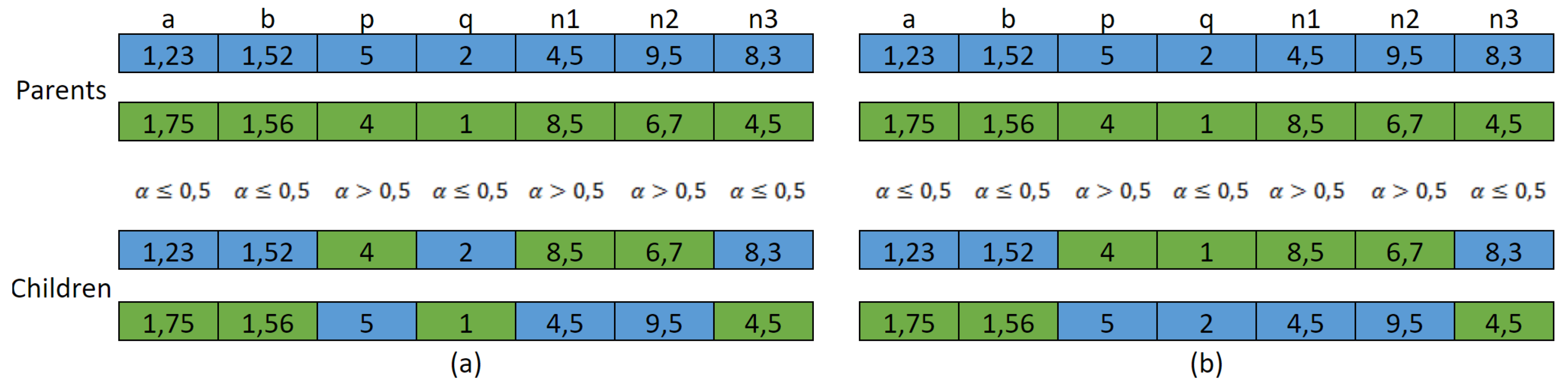
- Crossover is performed as follows: given two parent solutions, two children solutions are obtained, where each child inherits each gene from one of the parents with a probability of 0.5, using a value between 0 and 1. Since p and q must be relative primes, in case they are taken from different parents, the fulfillment of this condition is verified. If it is not fulfilled, both genes are taken from the same parent, in order for this condition to be fulfilled. Figure 3 shows crossover method: in Figure 3a an example in which the crossover produces a child in which p and q are not relative primes (4 and 2, respectively), and in Figure 3b the correction applied in order for the condition to be fulfilled.
- In order to perform mutation on continuous variables (a, b, , , ), a normal distribution is used as follows:where N is the normal distribution, is gene i, is the interval length of the variable represented by gene and k is a user defined parameter, the suggested value is (0.1). Then, mutation is performed with a normal distribution with a standard deviation of a tenth of the interval length of the variable.
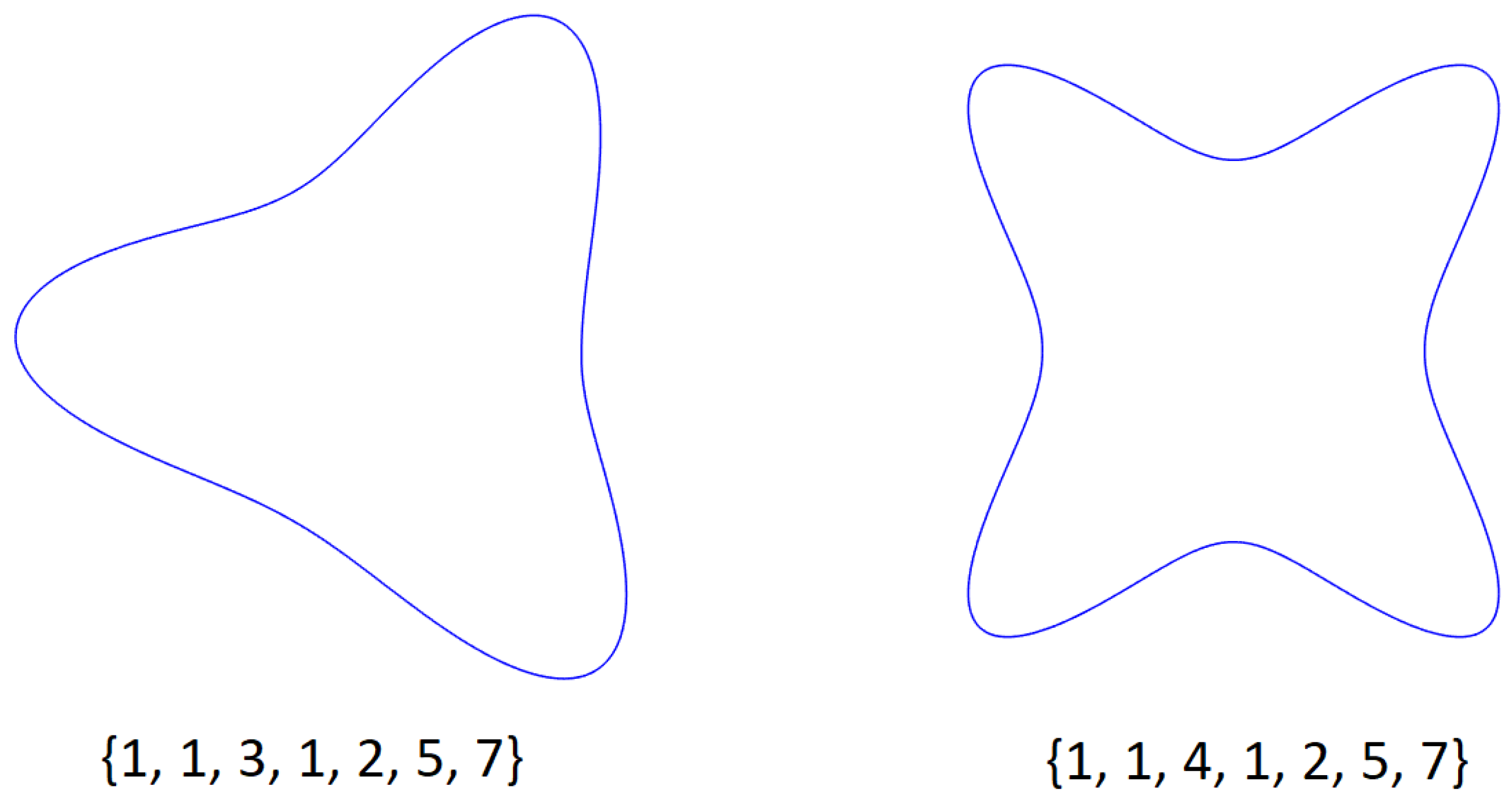
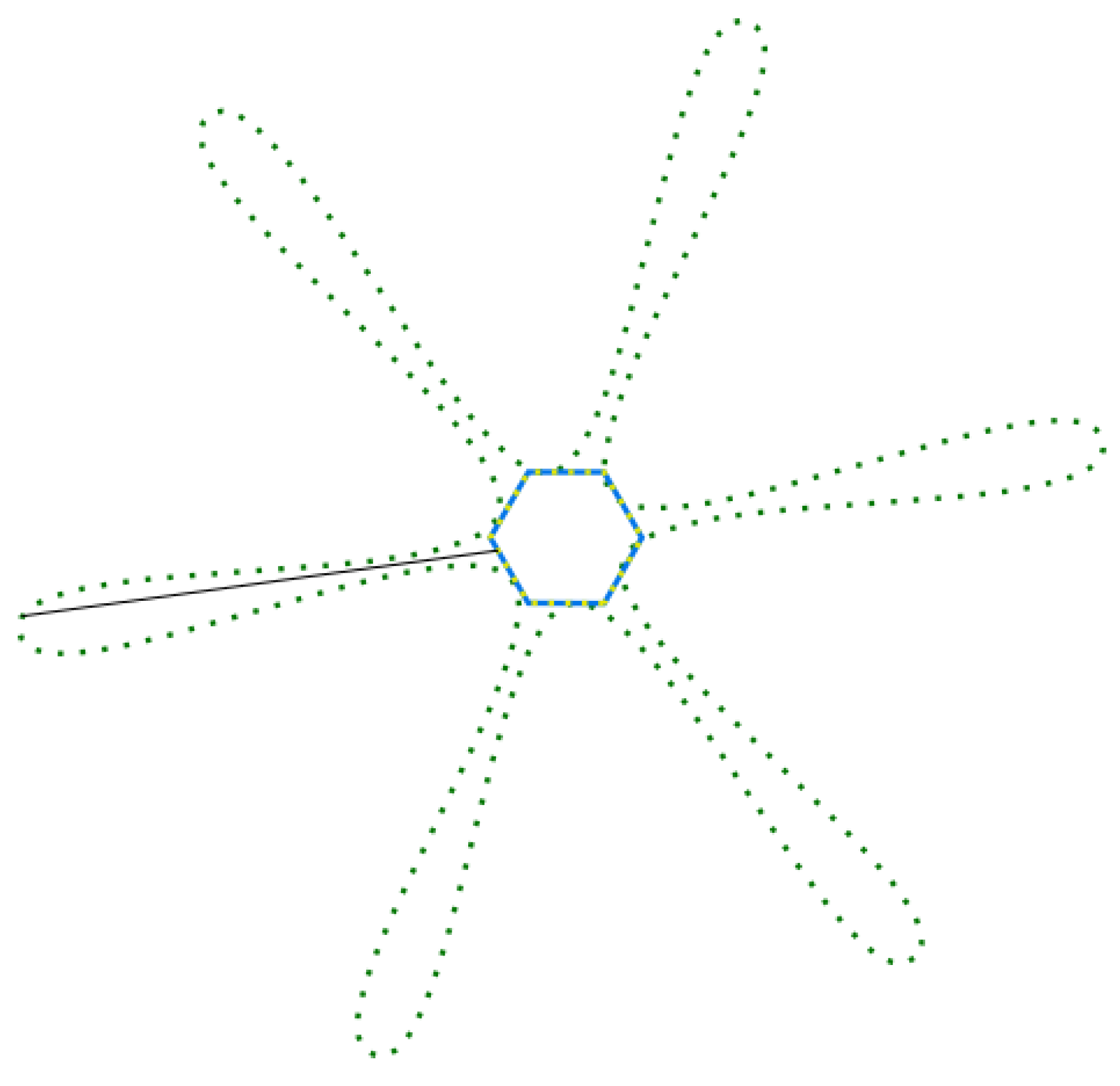
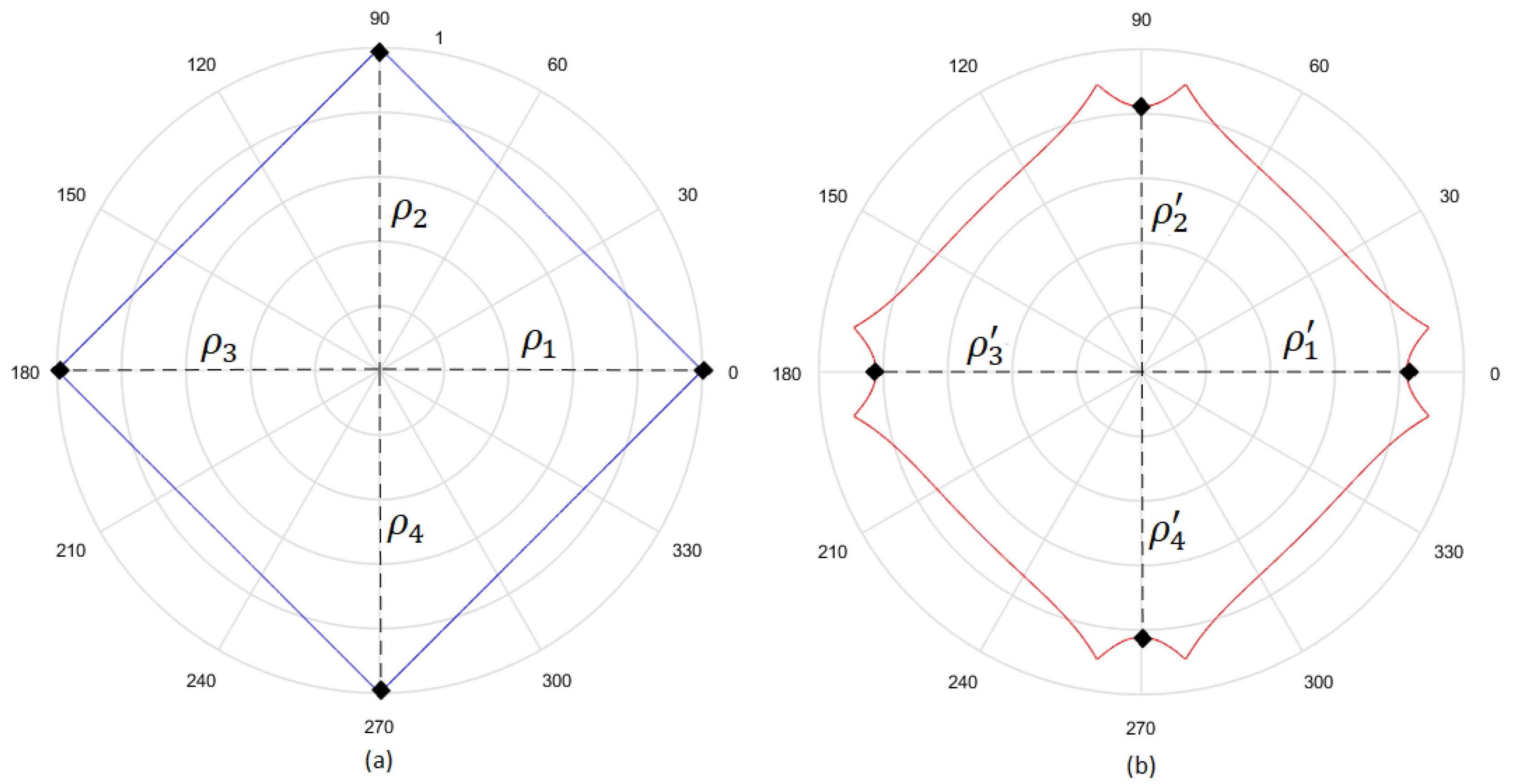
- Discrete variables (p and q in this case) indicate the number of sectors of the Gielis curve and the maximum number of self-intersections, respectively. When performing mutation, small variations of these variables have no reason for being, since they produce big changes in the adaptation to the sample points. This can be observed in Figure 4, where both Gielis curves have the same parameters, except p, but they have completely different shapes. For this reason, it is suggested to simply generate random values, with the condition that p and q must be relative prime.
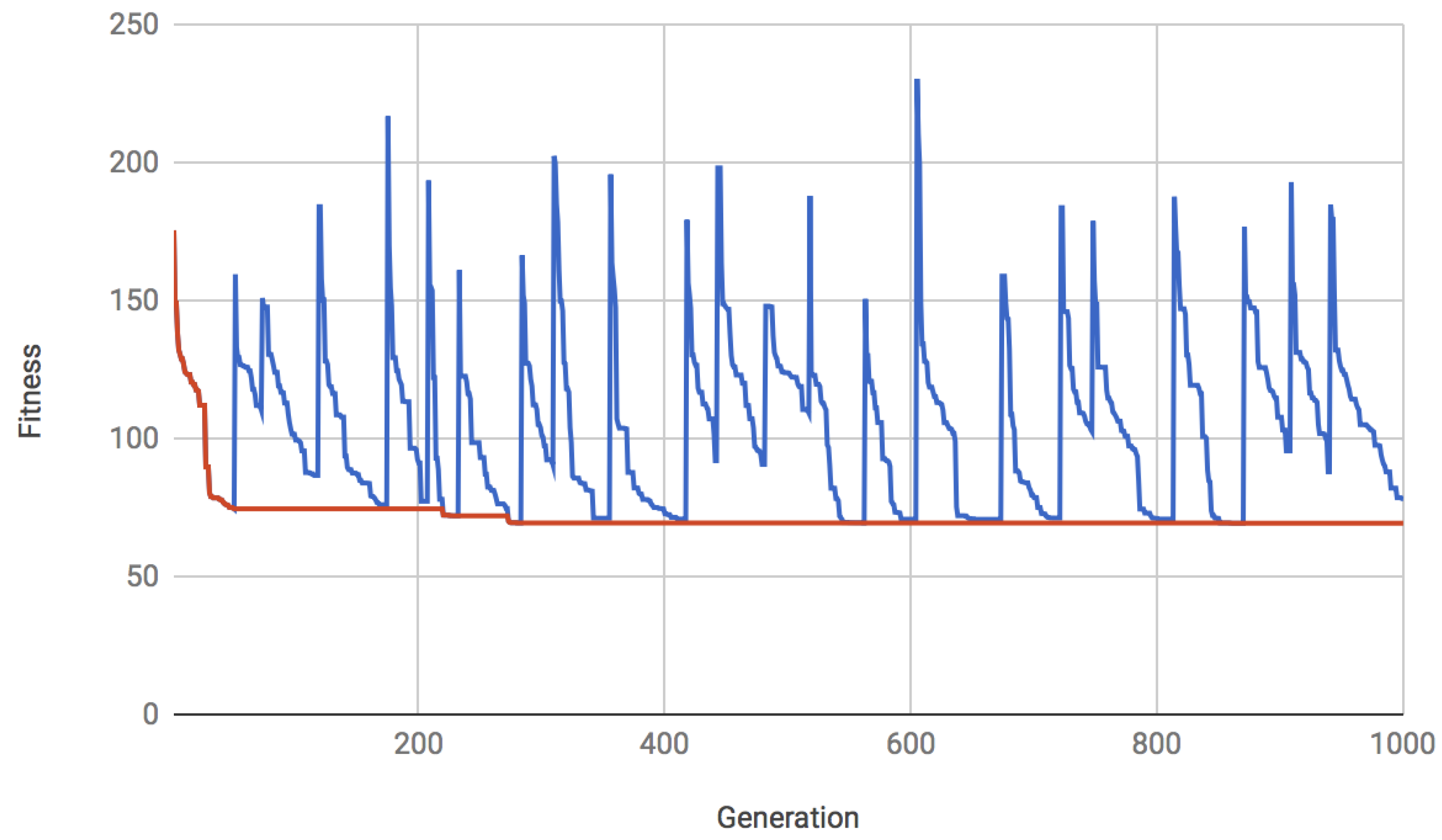
- The selection process is performed as follows: the size of the population is kept constant and individuals with best adaptive value remain. In order to face local convergence and premature convergence issues, Fougerolle et al. [11] suggested to measure the standard deviation of the population after each iteration, and if it is less than a user defined threshold, , the population is re-initialized randomly. This is computed with normalized values. The norm used is defined according to Equation (4), denoted aswhere c F is the value of the variable to be normalized, F = {a, b, p, q, , , } is the set of parameters from the superformula, is the lower limit of the interval of the variable, is the upper limit of the interval of the variable and v is the normalized value.
- If the standard deviation of all variables is less than the defined threshold, population is re-initialized randomly.
4. Proposal
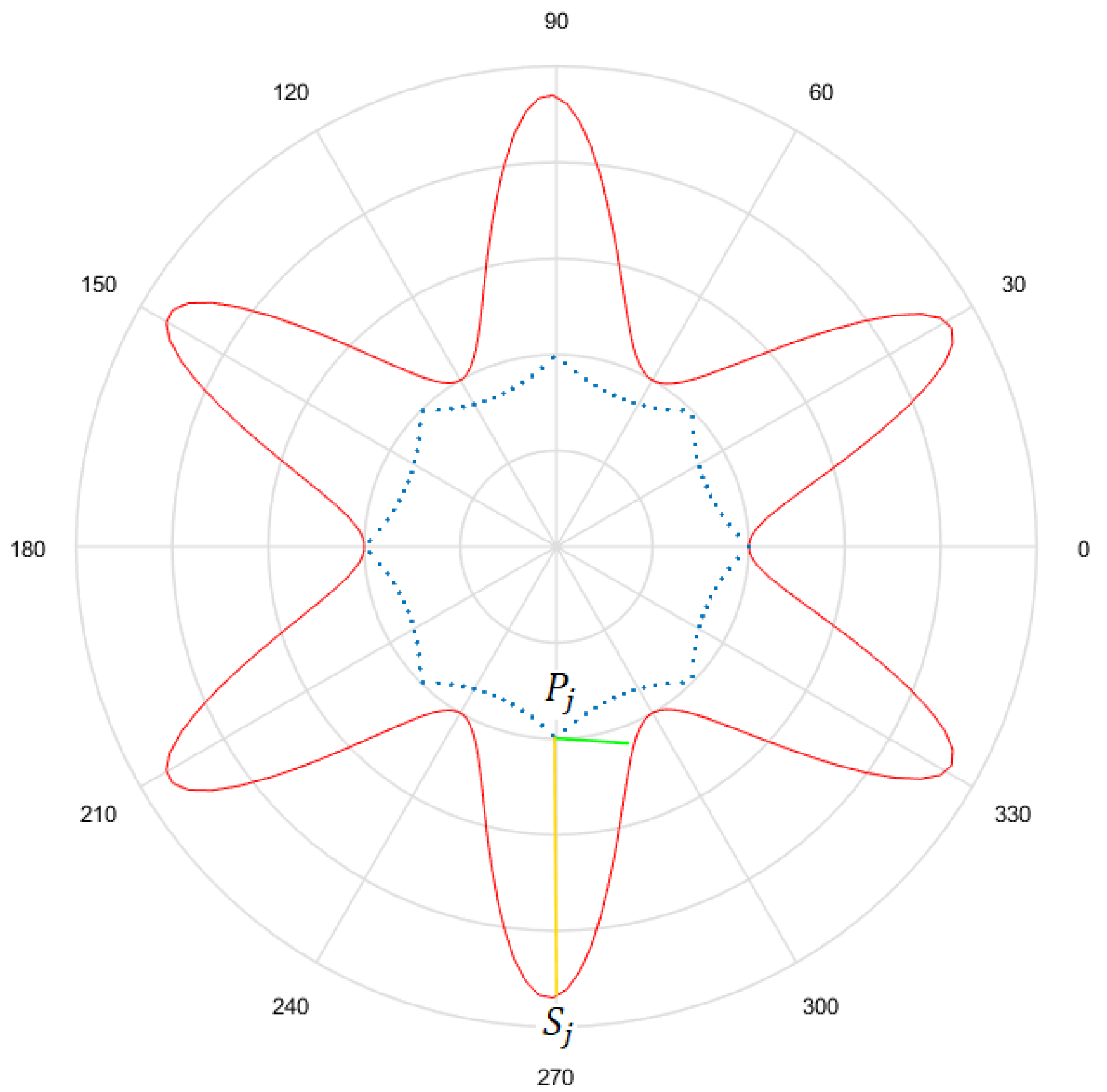
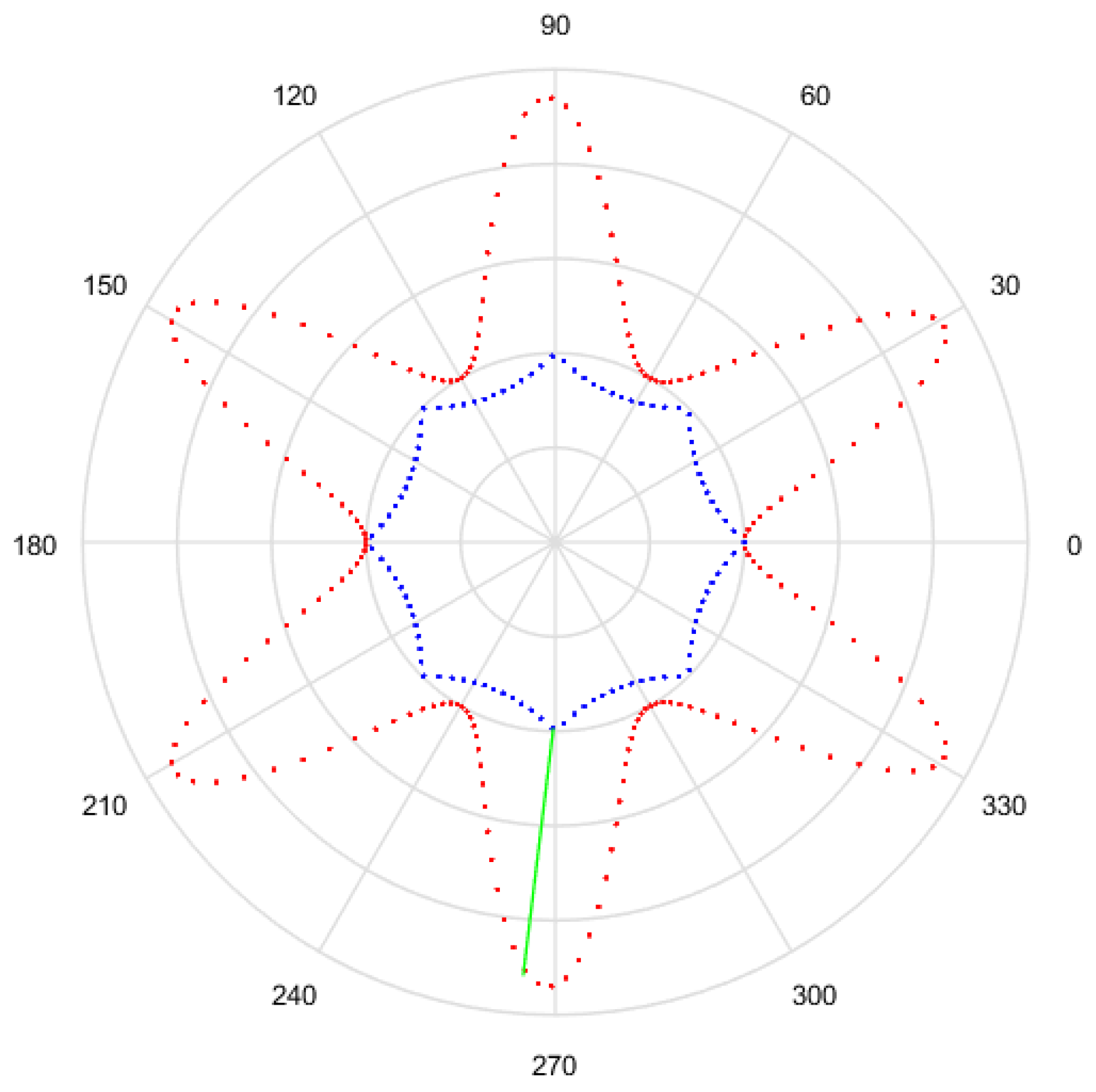
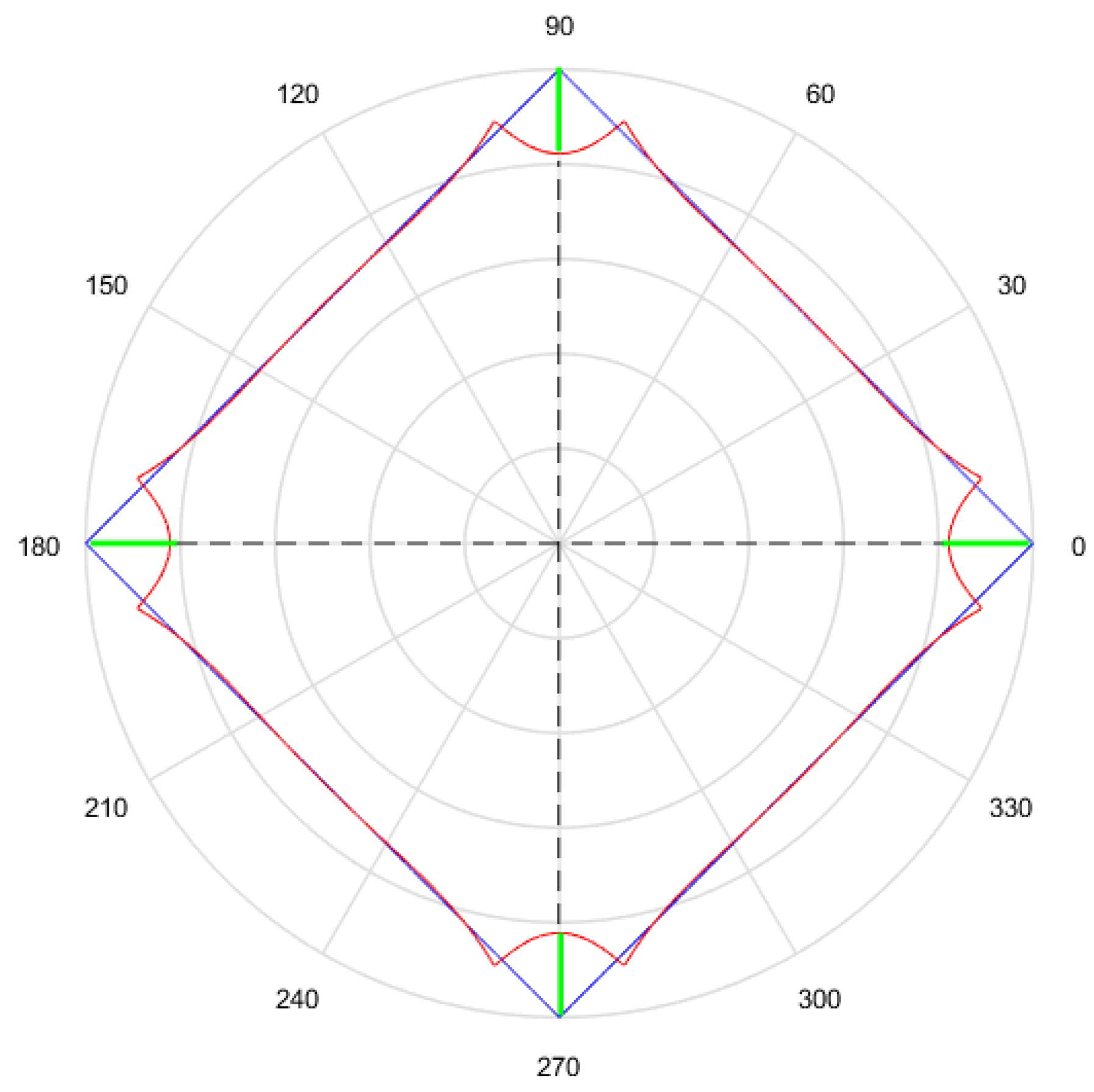
- Obtain a finite amount of points from the generated Gielis curve, to equals intervals of , with a sampling. An example of this is observed in Figure 9, with the points in red.
- For each point = find the sample point that is closest and compute its Euclidean distance. This distance is observed in green in Figure 9.
5. Experimental Tests
5.1. Evaluation Metrics
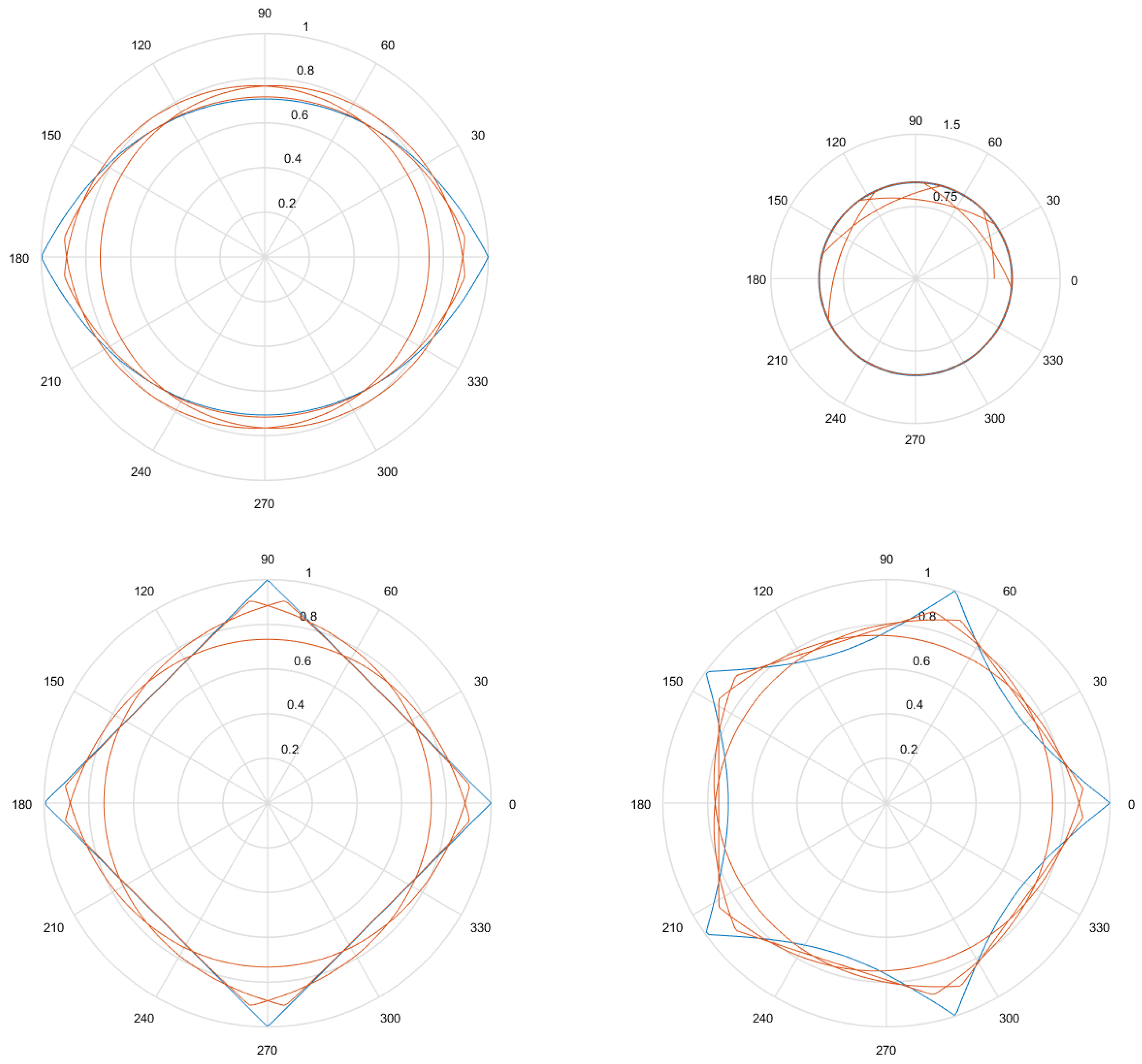
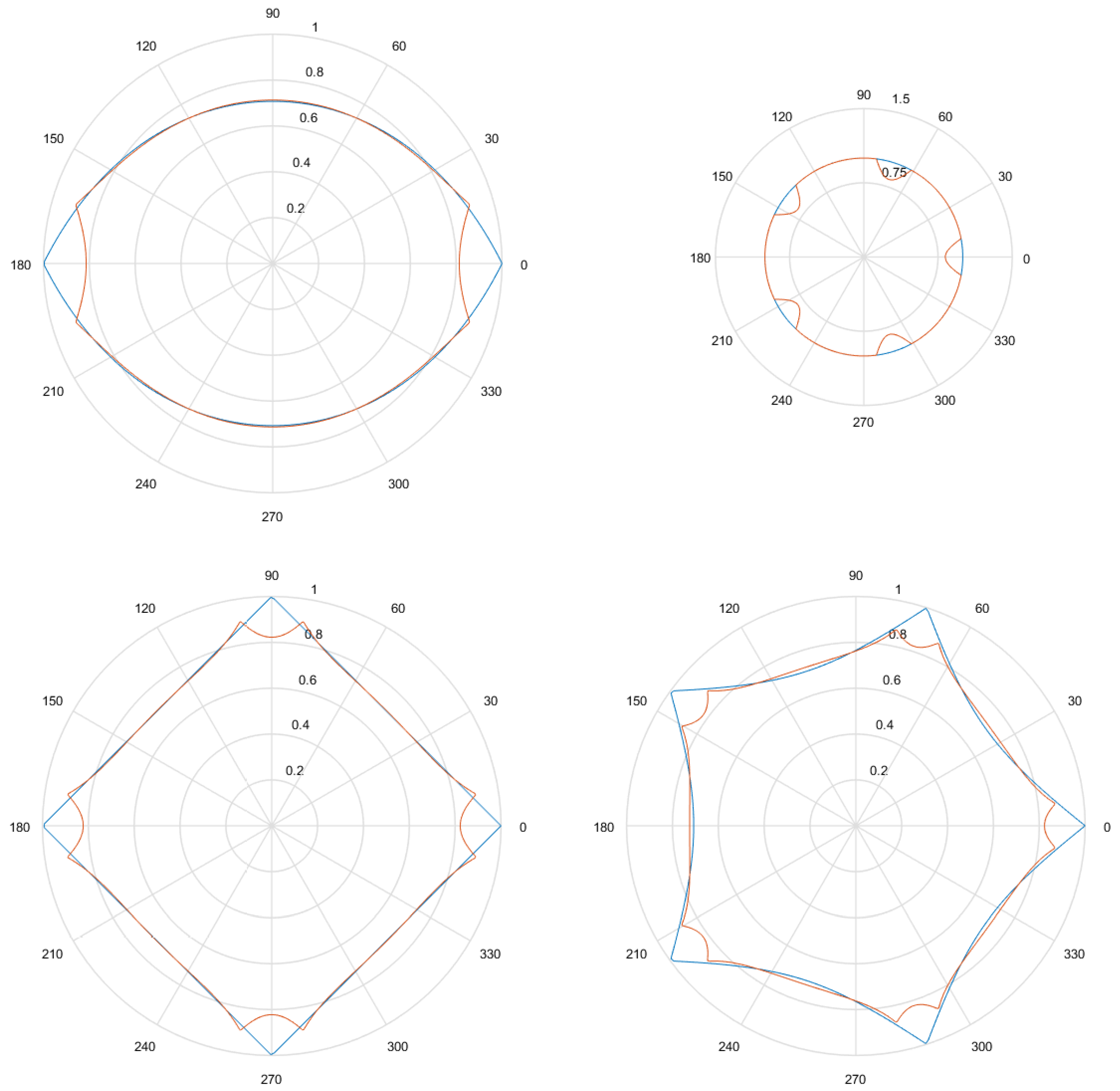
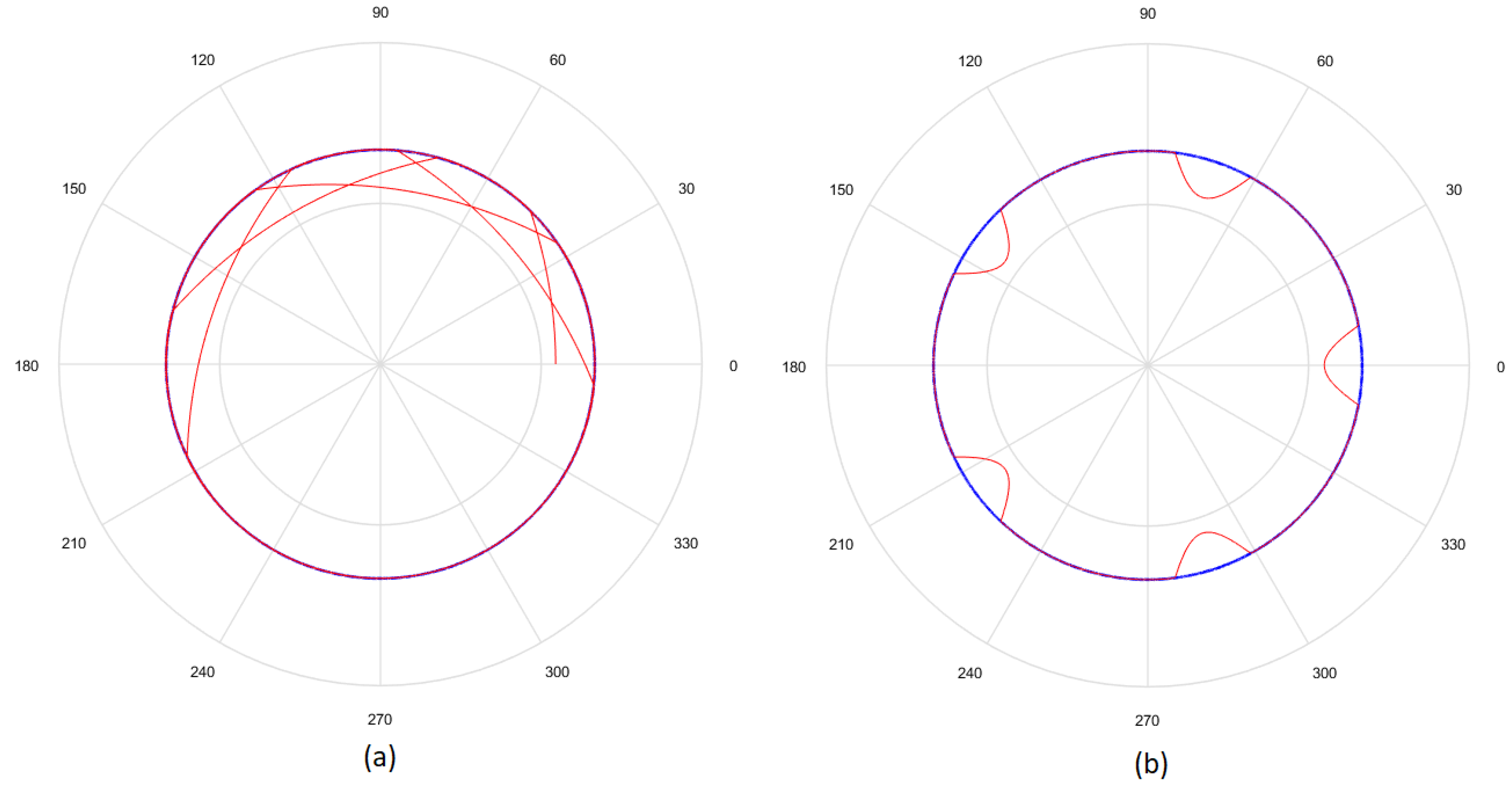
- Considering that the tests were performed using Gielis curves with known parameters, an amount h of sample points in the original curve is obtained, to equal intervals of . These sample points are obtained by dividing the interval in h equal parts. Figure 13a shows an example where , and since , the values of are . There is in blue the original curve and in black the points obtained.
- For each solution (one for each method), an amount h of sample points is obtained, where values of are the same used for the original curve. Figure 13b shows an example, corresponding to the Gielis curve obtained using objective function in Equation (14). The Gielis curve is in red and the sample points are in black.
- Considering a h-dimensional space, finite representation of the original curve and the solutions obtained with each method are built, with polar distances (, ,..., ) for each of them. We denote as the original curve, as the Gielis curve from the method proposed by Fougerolle et al., as the curve from the method that uses objective function from Equation (13) and for the method that uses our contribution, the objective function from Equation (14). In the example from Figure 13, there are and .
- Finally, the Euclidean distance between and each h-dimensional point corresponding to each solution is calculated. The distance between and will be called ; between and , ; and between and , . The lower the value of the distance, the better the quality of the solution. Continuing with the example given in Figure 13, Figure 14 shows , that is equal to the root square of the sum of squares of the length of the segments in green.
5.2. Parameters Used
- Mutation parameter k = 0.1.
- Mutation probability is 0.15.
- Minimum limit for population standard deviation = 0.05.
- The size of the population is 100 individuals.
- The number of generations is 1000.
- The intervals of the parameters of the superformula are a, b∈ [0.01, 100]; , , ∈ [0.01, 1000]; p, q∈ [1, 11].
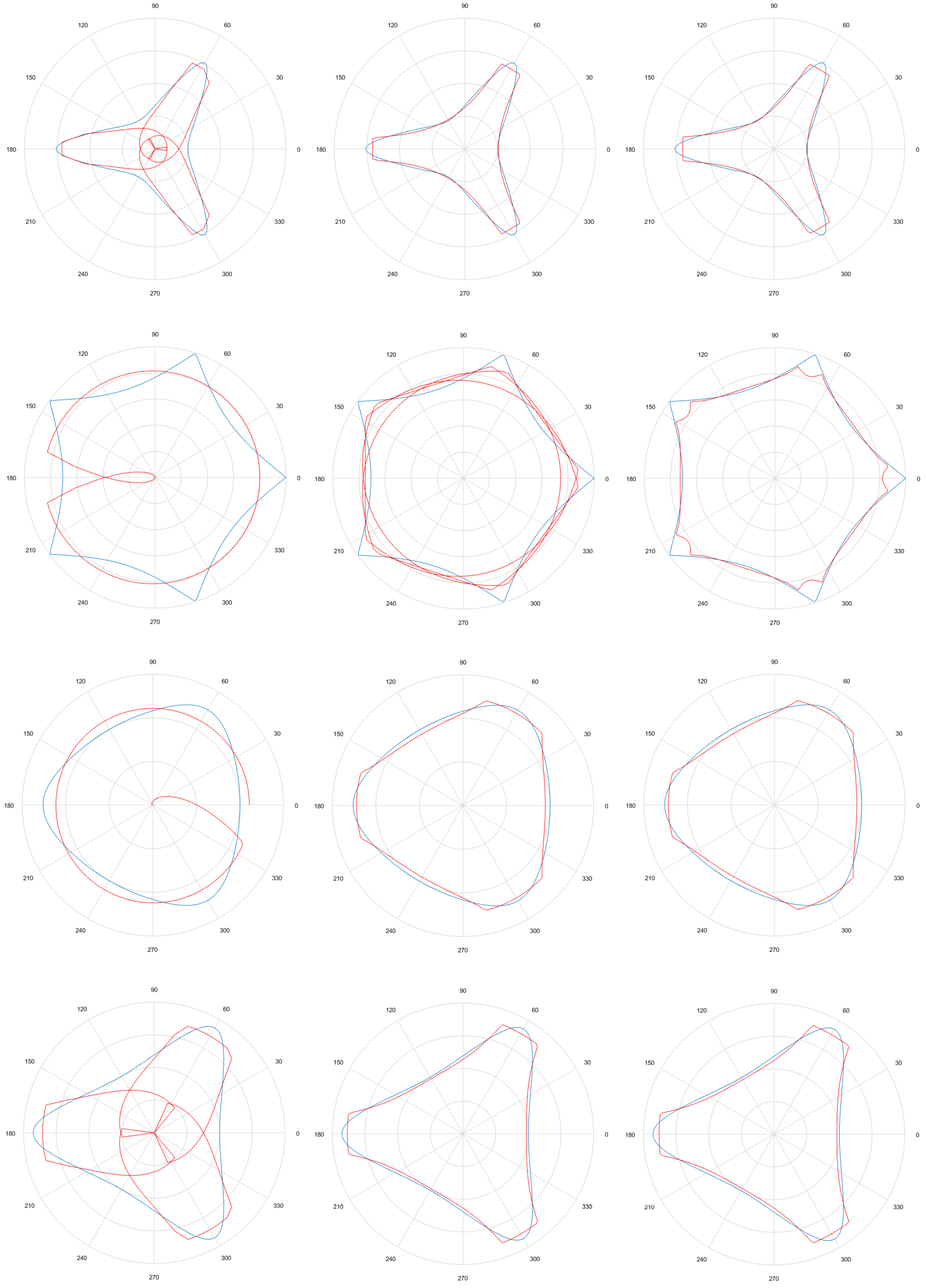
5.3. Results
6. Conclusions and Future Work
Author Contributions
Funding
Conflicts of Interest
Appendix A
| N | ■ | F1 | F2 | F3 |
|---|---|---|---|---|
| 1 | 1, 1, 2, 1, 1, 1, 1 | 0.484, 0.791, 4, 3, 98.105, 975.495, 129.099 | 0.319, 0.832, 4, 3, 424.050, 114.101, 770.828 | 0.914, 0.159, 4, 1, 325.238, 742.188, 59.849 |
| 2 | 1, 1, 2, 1, 1, 4, 8 | 4.588, 0.414, 4, 7, 191.792, 144.745, 383.061 | 1.042, 93.605, 4, 1, 279.456, 290.473, 67.824 | 1.079, 75.865, 4, 1, 498.795, 499.327, 127.463 |
| 3 | 1, 1, 2, 1, 2, 2, 2 | 0.696, 0.714, 1, 2, 6.293, 960.253, 0.142 | 0.936, 0.704, 9, 5, 304.509, 938.779, 1.222 | 0.893, 0.686, 10, 1, 438.576, 755.576, 0.190 |
| 4 | 1, 1, 3, 1, 1, 1, 1 | 0.297, 0.937, 6, 5, 61.612, 979.904, 316.092 | 0.297, 0.812, 2, 1, 449.637, 118.878, 703.362 | 0.334, 0.786, 2, 1, 607.431, 176.358, 733.708 |
| 5 | 1, 1, 3, 1, 2, 5, 7 | 0.224, 2.645, 6, 5, 906.527, 578.865, 557.219 | 0.950, 61.136, 6, 1, 381.374, 232.292, 56.792 | 0.978, 44.759, 6, 1, 639.679, 364.542, 103.393 |
| 6 | 1, 1, 3, 1, 2, 8, 3 | 0.228, 99.150, 6, 5, 985.876, 704.128, 83.234 | 0.906, 91.677, 6, 1, 696.133, 434.260, 61.787 | 0.921, 41.385, 6, 1, 145.878, 87.718, 15.638 |
| 7 | 1, 1, 3, 1, 4.5, 10, 10 | 0.193, 60.239, 6, 5, 992.387, 599.391, 129.943 | 0.939, 63.322, 6, 1, 170.368, 77.200, 23.420 | 0.921, 52.455, 6, 1, 261.234, 121.281, 37.254 |
| 8 | 1, 1, 3, 1, 6, 6, 6 | 5.496, 0.677, 1, 2, 62.279, 3.720, 970.215 | 0.838, 46.878, 6, 1, 388.904, 127.007, 20.249 | 0.837, 45.008, 6, 1, 667.043, 213.335, 34.701 |
| 9 | 1, 1, 4, 1, 1, 1, 1 | 0.394, 0.903, 1, 5, 32.366, 888.396, 93.668 | 0.315, 0.856, 8, 3, 431.634, 116.629, 972.433 | 0.905, 0.180, 8, 1, 395.665, 775.248, 79.420 |
| 10 | 1, 1, 4, 1, 1, 7, 8 | 0.410, 81.424, 8, 3, 164.276, 183.371, 68.693 | 1.433, 42.658, 8, 1, 207.048, 193.665, 100.481 | 1.367, 86.056, 8, 1, 148.692, 142.402, 60.464 |
| 11 | 1, 1, 4, 1, 4, 7, 7 | 0.191, 53.318, 8, 5, 998.697, 696.744, 92.477 | 0.898, 52.965, 8, 1, 316.163, 129.131, 31.248 | 0.906, 63.402, 8, 1, 362.938, 143.311, 34.214 |
| 12 | 1, 1, 4, 1, 12, 15, 15 | 1.099, 0.864, 1, 3, 34.511, 19.664, 987.355 | 0.872, 43.314, 8, 1, 797.762, 238.308, 70.626 | 0.889, 81.139, 8, 1, 403.617, 114.207, 30.281 |
| 13 | 1, 1, 5, 1, 1, 1, 1 | 0.848, 0.284, 2, 5, 51.066, 68.858, 585.738 | 0.248, 0.821, 10, 3, 563.117, 119.934, 821.261 | 0.887, 0.109, 10, 1, 236.899, 385.290, 34.413 |
| 14 | 1, 1, 5, 1, 2, 6, 6 | 0.324, 89.303, 10, 3, 963.528, 737.523, 133.673 | 0.952, 97.590, 10, 1, 910.599, 540.286, 127.384 | 0.934, 95.054, 10, 1, 689.156, 424.957, 95.793 |
| 15 | 1, 1, 5, 1, 2, 7, 7 | 0.330, 64.725, 10, 3, 917.122, 780.768, 174.389 | 0.981, 70.353, 10, 1, 643.578, 427.705, 119.979 | 0.971, 74.536, 10, 1, 560.602, 374.459, 103.183 |
| 16 | 1, 1, 5, 1, 2, 13, 13 | 0.640, 33.693, 10, 1, 319.418, 528.108, 168.248 | 1.167, 49.765, 10, 1, 192.044, 187.902, 87.704 | 1.162, 86.827, 10, 1, 397.561, 393.287, 159.129 |
| 17 | 1, 1, 5, 1, 4, 4, 4 | 6.275, 0.698, 1, 2, 41.642, 1.731, 932.093 | 0.864, 51.242, 10, 1, 726.014, 316.870, 25.547 | 0.855, 76.795, 10, 1, 397.161, 142.118, 13.019 |
| 18 | 1, 1, 6, 1, 1, 1, 1 | 0.546, 0.313, 1, 5, 59.006, 20.648, 974.668 | 0.392, 0.755, 4, 1, 421.788, 147.881, 404.971 | 0.442, 0.848, 4, 1, 259.665, 110.289, 515.247 |
| 19 | 1, 1, 6, 1, 1, 1, 6 | 0.698, 1.688, 1, 2, 27.366, 853.319, 2.926 | 0.962, 2.174, 4, 1, 198.741, 953.943, 14.875 | 0.962, 5.971, 4, 1, 227.450, 982.408, 9.511 |
| 20 | 1, 1, 6, 1, 1, 7, 8 | 2.374, 0.963, 6, 1, 81.518, 115.277, 655.809 | 8.294, 1.447, 6, 1, 414.832, 234.199, 919.898 | 1.202, 62.511, 6, 1, 188.828, 636.551, 61.603 |
| 21 | 1, 1, 7, 1, 1, 1, 1 | 0.228, 0.796, 1, 7, 56.159, 966.942, 51.085 | 0.018, 0.298, 7, 1, 660.991, 48.570, 7.766 | 0.018, 0.059, 7, 1, 466.989, 34.758, 10.356 |
| 22 | 1, 1, 7, 1, 2, 8, 4 | 1.182, 0.861, 7, 1, 195.049, 229.272, 994.438 | 2.160, 54.319, 7, 1, 752.321, 261.122, 58.741 | 48.455, 1.099, 7, 1, 423.512, 36.542, 497.736 |
| 23 | 1, 1, 7, 1, 10, 6, 6 | 0.489, 2.846, 1, 3, 68.889, 990.144, 3.635 | 0.979, 44.029, 7, 1, 528.443, 177.371, 9.506 | 0.951, 3.575, 7, 1, 420.321, 944.751, 19.205 |
| 24 | 1, 1, 2, 1, 1000, 500, 500 | 1.608, 0.478, 1, 3, 111.856, 12.889, 893.247 | 0.775, 82.087, 4, 1, 306.454, 58.462, 8.942 | 0.777, 70.782, 4, 1, 366.679, 70.328, 10.946 |
| 25 | 1, 1, 4, 1, 1000, 1000, 1000 | 1.264, 0.774, 1, 3, 60.161, 24.313, 976.459 | 0.859, 60.688, 8, 1, 656.404, 149.167, 46.354 | 0.849, 65.430, 8, 1, 479.034, 116.408, 32.591 |
| 26 | 1, 1, 8, 1, 1, 1, 1 | 0.712, 0.554, 1, 3, 22.621, 16.037, 967.899 | 0.018, 0.144, 8, 1, 874.896, 65.141, 6.006 | 0.016, 0.524, 8, 1, 767.258, 54.812, 71.630 |
| 27 | 1, 1, 1, 1, 1000, 500, 500 | 0.679, 2.652, 1, 2, 41.237, 996.966, 2.147 | 0.794, 79.753, 2, 1, 559.873, 97.563, 16.814 | 0.773, 17.350, 2, 1, 117.0166, 20.657, 5.439 |
| 28 | 1, 1, 5, 1, 1000, 620, 620 | 0.682, 2.357, 1, 2, 43.564, 901.749, 3.277 | 0.769, 26.136, 10, 1, 111.150, 25.130, 5.558 | 0.786, 35.709, 10, 1, 262.462, 59.409, 11.482 |
| 29 | 1, 1, 8, 1, 1000, 250, 250 | 2.634, 0.685, 1, 2, 24.175, 0.511, 979.266 | 0.945, 8.361, 8, 1, 341.364, 853.906, 4.977 | 0.979, 4.642, 4, 1, 135.842, 860.048, 2.014 |
| 30 | 1, 1, 1, 1, 0.5, 0.5, 0.5 | 0.340, 0.025, 2, 3, 568.301, 107.696, 241.609 | 0.210, 0.0387, 2, 1, 551.615, 166.097, 173.486 | 0.0516, 0.045842, 2, 1, 576.631, 91.610, 188.738 |
| 31 | 1, 1, 2, 1, 0.5, 0.5, 0.5 | 0.071, 0.042, 4, 1, 696.523, 25.619, 225.346 | 0.269, 0.523, 4, 3, 306.789, 239.774, 332.319 | 0.011, 0.375, 2, 1, 655.324, 137.798, 114.037 |
| 32 | 1, 1, 3, 1, 0.5, 0.5, 0.5 | 0.441, 0.033, 6, 1, 663.516, 127.949, 210.569 | 0.014, 0.310, 3, 1, 686.319, 148.248, 105.755 | 0.322, 0.780, 2, 1, 161.041, 139.607, 615.988 |
| 33 | 1, 1, 4, 1, 0.5, 0.5, 0.5 | 0.080, 0.027, 8, 1, 692.735, 50.256, 205.811 | 0.271, 0.803, 8, 3, 231.396, 162.512, 997.629 | 0.339, 0.794, 8, 3, 208.952, 182.210, 898.340 |
| 34 | 1, 1, 3, 1, 5, 18, 18 | 0.139, 47.910, 6, 7, 662.0582, 458.929, 179.941 | 1.054, 22.793, 6, 1, 317.024, 185.602, 105.142 | 1.024, 75.162, 6, 1, 403.783, 250.648, 96.175 |
| 35 | 1, 1, 6, 1, 20, 7, 18 | 2.072, 0.691, 1, 2, 43.927, 3.034, 999.968 | 0.934, 25.758, 4, 1, 171.253, 336.431, 2.883 | 0.957, 4.325, 6, 1, 328.796, 890.099, 14.078 |
| N | F | M1 | M2 | M3 | Visual |
|---|---|---|---|---|---|
| 1 | 1, 1, 2, 1, 1, 1, 1 | 377.053 | 43.293 | 34.294 | F3 |
| 2 | 1, 1, 2, 1, 1, 4, 8 | 1009.591 | 218.157 | 217.863 | F2, F3 |
| 3 | 1, 1, 2, 1, 2, 2, 2 | 706.607 | 34.252 | 50.560 | F3 |
| 4 | 1, 1, 3, 1, 1, 1, 1 | 455.757 | 50.816 | 51.171 | F2, F3 |
| 5 | 1, 1, 3, 1, 2, 5, 7 | 686.339 | 57.359 | 53.733 | F2, F3 |
| 6 | 1, 1, 3, 1, 2, 8, 3 | 648.761 | 70.691 | 68.729 | F2, F3 |
| 7 | 1, 1, 3, 1, 4.5, 10, 10 | 681.300 | 35.201 | 38.909 | F2, F3 |
| 8 | 1, 1, 3, 1, 6, 6, 6 | 80.002 | 28.249 | 28.169 | F2, F3 |
| 9 | 1, 1, 4, 1, 1, 1, 1 | 564.189 | 51.252 | 32.550 | F3 |
| 10 | 1, 1, 4, 1, 1, 7, 8 | 1749.448 | 247.471 | 238.497 | F2, F3 |
| 11 | 1, 1, 4, 1, 4, 7, 7 | 683.150 | 31.546 | 29.996 | F2, F3 |
| 12 | 1, 1, 4, 1, 12, 15, 15 | 114.992 | 27.884 | 25.087 | F2, F3 |
| 13 | 1, 1, 5, 1, 1, 1, 1 | 385.339 | 48.252 | 33.713 | F3 |
| 14 | 1, 1, 5, 1, 2, 6, 6 | 665.170 | 43.641 | 47.987 | F2, F3 |
| 15 | 1, 1, 5, 1, 2, 7, 7 | 767.114 | 52.248 | 54.319 | F2, F3 |
| 16 | 1, 1, 5, 1, 2, 13, 13 | 523.584 | 176.658 | 174.971 | F2, F3 |
| 17 | 1, 1, 5, 1, 4, 4, 4 | 48.117 | 28.069 | 25.447 | F2, F3 |
| 18 | 1, 1, 6, 1, 1, 1, 1 | 60.797 | 53.942 | 52.437 | F3 |
| 19 | 1, 1, 6, 1, 1, 1, 6 | 735.628 | 63.434 | 63.769 | F2, F3 |
| 20 | 1, 1, 6, 1, 1, 7, 8 | 966.208 | 1112.325 | 1170.644 | F1 |
| 21 | 1, 1, 7, 1, 1, 1, 1 | 564.189 | 52.983 | 53.652 | F3 |
| 22 | 1, 1, 7, 1, 2, 8, 4 | 227.429 | 193.666 | 166.163 | F1 |
| 23 | 1, 1, 7, 1, 10, 6, 6 | 750.658 | 31.693 | 38.823 | F3 |
| 24 | 1, 1, 2, 1, 1000, 500, 500 | 46.976 | 23.665 | 23.606 | F2, F3 |
| 25 | 1, 1, 4, 1, 1000, 1000, 1000 | 84.709 | 24.656 | 26.681 | F2, F3 |
| 26 | 1, 1, 8, 1, 1, 1, 1 | 63.033 | 53.164 | 53.052 | F2 |
| 27 | 1, 1, 1, 1, 1000, 500, 500 | 735.506 | 20.497 | 22.454 | F2, F3 |
| 28 | 1, 1, 5, 1, 1000, 620, 620 | 739.203 | 29.093 | 27.489 | F2, F3 |
| 29 | 1, 1, 8, 1, 1000, 50, 250 | 71.043 | 35.788 | 29.789 | F2, F3 |
| 30 | 1, 1, 1, 1, 0.5, 0.5, 0.5 | 235.733 | 28.127 | 29.374 | F2 |
| 31 | 1, 1, 2, 1, 0.5, 0.5, 0.5 | 102.927 | 82.178 | 73.118 | F1 |
| 32 | 1, 1, 3, 1, 0.5, 0.5, 0.5 | 106.666 | 76.119 | 69.748 | F1 |
| 33 | 1, 1, 4, 1, 0.5, 0.5, 0.5 | 148.707 | 72.191 | 75.124 | F2, F3 |
| 34 | 1, 1, 3, 1, 5, 18, 18 | 1103.138 | 62.807 | 63.799 | F2, F3 |
| 35 | 1, 1, 6, 1, 20, 7, 18 | 48.787 | 54.227 | 42.373 | F3 |
References
- Forestiere, C.; He, Y.; Wang, R.; Kirby, R.M.; Negro, L.D. Inverse Design of Metal Nanoparticles’ Morphology. ACS Photonics 2016, 3, 68–78. [Google Scholar] [CrossRef]
- Tzarouchis, D.; Ylä-Oijala, P.; Ala-Nissilä, T.; Sihvola, A. Plasmonic properties and energy flow in rounded hexahedral and octahedral nanoparticles. J. Opt. Soc. Am. 2016, 33, 2626–2633. [Google Scholar] [CrossRef]
- Leonardis, A.; Jaklic, A.; Solina, F. Superquadrics for segmenting and modeling range data. IEEE Trans. Pattern Anal. Mach. Intell. 1997, 19, 1289–1295. [Google Scholar] [CrossRef]
- Gielis, J. A generic geometric transformation that unifies a wide range of natural and abstract shapes. Am. J. Bot. 2003, 90, 333–338. [Google Scholar] [CrossRef] [PubMed]
- Vega, V.; Sidibé, D.; Fougerolle, Y. Road signs detection and reconstruction using gielis curves. In Proceedings of the International Conference on Computer Vision Theory and Applications, Rome, Italy, 24–26 February 2012; pp. 393–396. [Google Scholar]
- Tassadit, A.; Macías, D.; Sanchez-Gil, J.A.; Adam, P.-M.; Rodríguez-Oliveros, R. Metal nanostars: Stochastic optimization of resonant scattering properties. Superlattices Microstruct. 2011, 49, 288–293. [Google Scholar] [CrossRef][Green Version]
- Macías, D.; Adam, P.-M.; Ruíz-Cortes, V.; Rodríguez-Oliveros, R.; Sanchez-Gil, J.A. Heuristic optimization for the design of plasmonic nanowires with specific resonant and scattering properties. Opt. Express 2012, 20, 13146–13163. [Google Scholar] [CrossRef] [PubMed]
- Duda, R.O.; Hart, P.E. Pattern Classification and Scene Analysis; Wiley: New York, NY, USA, 1973. [Google Scholar]
- Fougerolle, Y.D.; Gribok, A.; Foufou, S.; Truchetet, F.; Abidi, M.A. Boolean operations with implicit and para- metric representation of primitives using R-functions. IEEE Trans. Vis. Comput. Graph. 2005, 11, 529–539. [Google Scholar] [CrossRef] [PubMed]
- Barr, A.H. Superquadrics and angle-preserving transformations. IEEE Comput. Graph. Appl. 1981, 1, 11–23. [Google Scholar] [CrossRef]
- Fougerolle, Y.D.; Gielis, J.; Truchetet, F. A robust evolutionary algorithm for the recovery of rational Gielis curves. Pattern Recognit. 2013, 46, 2078–2091. [Google Scholar] [CrossRef]
- Gielis, J.; Caratelli, D.; Fougerolle, Y.; Ricci, P.E.; Tavkelidze, I.; Gerats, T. Universal Natural Shapes: From Unifying Shape Description to Simple Methods for Shape Analysis and Boundary Value Problems. PLoS ONE 2012, 7, e29324. [Google Scholar] [CrossRef]
- Mishra, S.K. Some Experiments on Fitting of Gielis Curves by Simulated Annealing and Particle Swarm Methods of Global Optimization. IUP J. Comput. Math. 2011, 4, 50–59. Available online: https://ssrn.com/abstract=2141745 (accessed on 3 June 2020). [CrossRef]
- Von Seggern, D.H. Practical Handbook of Curve Design and Generation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Frome, UK, 2010. [Google Scholar]
- Blum, C.; Roli, A. Metaheuristics in combinatorial optimization: Overview and conceptual comparison. ACM Comput. Surv. (CSUR) 2003, 35, 268–308. [Google Scholar] [CrossRef]
- Falkenauer, E. Genetic Algorithms and Grouping Problems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1998. [Google Scholar]
- Jäntschi, L.; Bălan, M.C.; Sestraş, R.E. Results of evolution supervised by genetic algorithms. arXiv 2010, arXiv:1009.091. [Google Scholar] [CrossRef]
- Janežič, D.; Jäntschi, L.; Bolboacă, S.D. Sugars and sweeteners: Structure, properties and in silico modeling. Curr. Med. Chem. 2020, 27, 5–22. [Google Scholar] [CrossRef]
- Bokhabrine, Y.; Fougerolle, Y.; Foufou, S.; Truchetet, F. Genetic algorithms for Gielis surface recovery from 3D data sets. In Proceedings of the 2007 IEEE International Conference on Image Processing, San Antonio, TX, USA, 16 September–19 October 2007; IEEE: Piscataway, NJ, USA, 2007. [Google Scholar]
- Wang, X.; Wang, H. Classification by evolutionary ensembles. Pattern Recognit. 2006, 39, 595–607. [Google Scholar] [CrossRef]
- Maulik, U.; Bandyopadhyay, S. Genetic algorithm-based clustering technique. Pattern Recognit. 2000, 33, 1455–1465. [Google Scholar] [CrossRef]
- Cross, A.D.; Myers, R.; Hancock, E.R. Convergence of a hill-climbing genetic algorithm for graph matching. Pattern Recognit. 2000, 33, 1863–1880. [Google Scholar] [CrossRef]
- Rvachev, V.L. Theory of R-Functions and Some Applications; Naukova Dumka: Kiev, Ukraine, 1982. [Google Scholar]
- Shapiro, V. Theory of R-Functions and Applications: A Primer; Cornell University: Ithaca, NY, USA, 1991. [Google Scholar]
- Shapiro, V. Semi-analytic geometry with R-functions. ACTA Numer. 2007, 16, 239–303. [Google Scholar] [CrossRef]

| x | y | |
|---|---|---|
| + | + | + |
| + | − | + |
| − | + | + |
| − | − | − |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arce, A.M.; Caroni, G.G.; Vázquez Noguera, J.L.; Pinto-Roa, D.P.; Legal-Ayala, H.; Grillo, S.A. A New Objective Function for the Recovery of Gielis Curves. Symmetry 2020, 12, 1016. https://doi.org/10.3390/sym12061016
Arce AM, Caroni GG, Vázquez Noguera JL, Pinto-Roa DP, Legal-Ayala H, Grillo SA. A New Objective Function for the Recovery of Gielis Curves. Symmetry. 2020; 12(6):1016. https://doi.org/10.3390/sym12061016
Chicago/Turabian StyleArce, Alejandro Marcelo, Gabriel Giovanni Caroni, José Luis Vázquez Noguera, Diego P. Pinto-Roa, Horacio Legal-Ayala, and Sebastián A. Grillo. 2020. "A New Objective Function for the Recovery of Gielis Curves" Symmetry 12, no. 6: 1016. https://doi.org/10.3390/sym12061016
APA StyleArce, A. M., Caroni, G. G., Vázquez Noguera, J. L., Pinto-Roa, D. P., Legal-Ayala, H., & Grillo, S. A. (2020). A New Objective Function for the Recovery of Gielis Curves. Symmetry, 12(6), 1016. https://doi.org/10.3390/sym12061016







