Abstract
The relativistic coupled-cluster (RCC) theory has been applied recently to a number of heavy molecules to determine their properties very accurately. Since it demands large computational resources, the method is often approximated to single and double excitations (RCCSD method). The effective electric fields () and molecular permanent electric dipole moments (PDMs) of SrF, BaF, and mercury monohalides (HgX with X = F, Cl, Br, and I) molecules are of immense interest for probing fundamental physics. In our earlier calculations of and PDMs for the above molecules, we neglected the non-linear terms in the property evaluation expression of the RCCSD method. In this work, we demonstrate the roles of these terms in determining the above quantities and their computational time scalability with the number of processors of a computer. We also compare our results with previous calculations that employed variants of RCC theory, as well as other many-body methods and available experimental values.
1. Introduction
The coupled-cluster (CC) theory is considered to be the gold standard of electronic structure calculations in atoms and molecules [1,2]. It owes the title to its ability to capture electron correlation effects to a much better extent than other well-known many-body approaches such as configuration interaction (CI) [3], at a given level of truncation. This feature has led to accurate calculations of many properties in both the atomic and molecular systems (for example, see [4,5]). We shall focus on the application of this method to evaluate molecular properties that are useful to probe fundamental physics, specifically the permanent electric dipole moment (PDM) and parity and time-reversal violating electric dipole moment of the electron (eEDM) [6,7]. The molecular PDM is a very interesting property, and it plays a role in the sensitivity of an eEDM experiment through the polarizing factor [8,9]. The PDM is also an extremely relevant property in the ultracold sector, and molecules with large PDMs find innumerable applications in that domain. For example, the SrF molecule possesses a fairly large PDM and hence gives rise to long-range, tunable, and anisotropic dipole-dipole interactions. This aspect, in combination with the fact that SrF is laser-coolable, makes the molecule important for applications such as exploring new quantum phases and quantum computing [10].
The extremely tiny eEDM is yet to be detected. The upper bounds to it are extracted by a combination of relativistic many-body theory and experiment [11]. These bounds, in turn, help to constrain several theories that lie beyond the Standard Model of particle physics, for example supersymmetric theories [12]. The knowledge of the eEDM also aids in understanding the underlying physics that describes the matter-antimatter asymmetry in the universe [13]. The theoretical molecular property of interest to eEDM is the effective electric field, . It is the internal electric field that is experienced by an electron due to other electrons and nuclei in a molecule. An accurate estimate of this quantity is used in setting or improving an upper bound to eEDM (for example, [5]), or to propose a new candidate for molecular eEDM experiments (for example, [8]). This quantity can only be obtained using a relativistic many-body theory [14]. Calculating the PDM provides information on the polarizing factor for molecules that are proposed for eEDM searches, where the property has not been measured.
There have been several calculations of for various molecules using the single and double excitations approximation in the relativistic CC theory (RCCSD method), for example [15,16]. In our earlier RCCSD calculations [5,8,17,18,19,20], the expectation value evaluating the expression was approximated to only the linear terms (referred to as LERCCSDmethod). Later, the calculations performed for HgX (X = F, Cl, Br, and I), SrF, and BaF besides other molecules were verified by using the finite-field energy derivative approach of the RCCSD theory (FFRCCSD method) [9], by adding the interaction Hamiltonians along with the residual Coulomb interaction operator. The LERCCSD and the FFRCCSD approaches showed excellent agreements (within one percent) in the values of . The results for the PDMs obtained in these methods were comparable for SrF and BaF and also overestimated the property with respect to their experimental values, but they differed substantially for HgX (with as much as 20 percent for HgI). The shortcomings of the above FFRCCSD method were that the accuracy of the results depended on numerical differentiation. Moreover, orbital relaxation effects were neglected by not including the perturbation in the Dirac–Fock (DF) level itself, in order to avoid breaking of Kramer’s symmetry in the presence of a time-reversal symmetry violating eEDM interaction, which has to be compensated for eventually with further iterations.
Here, we intend to calculate the values of and PDM by including the non-linear terms in the expectation value evaluation expression of the RCCSD method (nLERCCSD method). We adopt the intermediate-diagram approach as discussed in [21,22] to implement these non-linear RCC terms. For this purpose, we undertook molecules that were very relevant for eEDM studies. HgX molecules were identified as promising candidates for future eEDM searches, owing to their extremely large effective electric fields, as well as experimental advantages [8]. A recent work that proposed to laser-cool HgF opened new avenues for an upcoming eEDM experiment with the molecule [23]. Another very important molecule in this regard is BaF, and two eEDM experiments are simultaneously underway for this system [24,25]. Experimental values of the PDMs are available only for BaF among the systems that we mentioned above. We also present results for the PDM of SrF, as it was the first molecule to be laser-cooled [10], and a very precise measurement of this quantity has been reported [26].
2. Theory and Implementation
In the RCC theory, the wave function of a molecular state is expressed as [27]:
where T is the cluster operator and is the reference state obtained by mean-field theory. We used the Dirac–Coulomb Hamiltonian in our calculations, and was obtained using the DF method. In the RCCSD method, we approximated with subscripts 1 and 2 indicating single and double excitations, respectively, and they are given using the second-quantization operators as:
where the notation is used to denote holes, refer to particles, is the one hole-one particle excitation amplitude, and is the two-hole two-particle excitation amplitude.
We employed the UTChem [28,29,30] program for the DF calculations, the atomic orbital to molecular orbital integral transformations, as well as generating the property integrals and the Dirac08 [31] code to obtain the RCCSD excitation operator amplitudes. It is important to reiterate that all the non-linear terms were included in the equations of the RCCSD method to determine the excitation amplitudes.
The expectation value of an operator, O, in the (R)CC method, can be written as follows:
where the subscript, “c”, means that each term is fully contracted [32], or in the diagrammatic terminology, connected [22].
The PDM of a molecule is determined as [33]:
where D is the electric dipole operator, the index A runs over the number of nuclei, is the atomic number of the Ath nucleus, and is the position vector from the origin to the site of the Ath nucleus. The first term in the above expression is the electronic term, while the second term is the nuclear contribution.
Similarly, is evaluated as:
where the summation is over the number of electrons, , is one of the Dirac matrices (also known as in the literature), is the (4 × 4) version of Pauli matrices, and is the internal electric field that is experienced by the ith electron, and is given by the negative of the gradient of the sum of electron-nucleus and electron-electron interaction potentials. Since the expression given above involves evaluating integrals over a two-body Coulomb operator, , and is complicated, we resorted to employing an effective eEDM Hamiltonian instead of the one introduced above [14]. It follows that:
where is the product of the gamma matrices (given by ), while is the momentum of the ith electron.
In the LERCCSD method, the following expression has been used in the evaluation of the expectation values:
These terms are represented using Goldstone diagrams and are shown in Figure 1. Note that and its Hermitian conjugate are zero, due to Slater–Condon rules [34,35]. Diagrammatically, such a diagram will have at least two open lines, that is it is not fully connected. The evaluation of the properties using the LERCCSD approximation misses the contributions corresponding to many correlation effects that will arise from the relativistic third-order many-body perturbation theory (RMBPT method). On the other hand, it is not possible to evaluate exactly Equation (3) even in the RCCSD method as it contains a non-terminating expression. However, it is possible to demonstrate the importance of contributions from the leading-order non-linear terms corresponding to the third- and fourth-order effects of the RMBPT method. It is still extremely challenging to perform direct calculations by incorporating the non-linear terms of Equation (3) in heavier molecules, due to the amount of computations involved in it. In order to tackle this issue, we adopted an additional computational step by breaking the non-linear terms into intermediate parts as described more elaborately below. Further, we parallelized the program using Message Passing Interface (MPI) and show the scalability of their calculations with the number of processors of a computer.
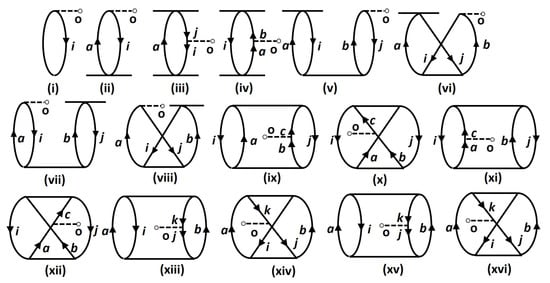
Figure 1.
Depictions of Goldstone diagrams representing the linear terms of the expectation value evaluation expression using the LERCCSDmethod. The notations denote the hole lines, while denote the particle lines. Diagram (i) corresponds to contribution from the DF method; (ii) is from the term; (iii,iv) are from ; (v–viii) are diagrams for , with (v,vii) corresponding to direct terms and (vi,viii) corresponding to exchange terms. Sub-figures (ix–xvi) include direct and exchange diagrams from . We also note that the Hermitian conjugate diagrams of those given above are not explicitly sketched here.
The approach can be understood by revisiting the diagrams in Figure 1, and relating each of them to Figure 2, Figure 3, and Figure 4. As an example, we consider Sub-figure (ii). The property vertex has one incoming particle line and an outgoing hole line. We define it as a particle-hole vertex. Such particle-hole vertices can be found in Sub-figures (v) to (viii) as well. In the intermediate-diagram formalism, the vertex O is removed and replaced successively by each of the particle-hole (p-h) diagrams (more precisely, their Hermitian conjugates) of Figure 4. We assign the notation for such a vertex. This sequence of operations already generates 28 diagrams from and includes terms that occur in the RMBPT method. We note that in the case of the Hermitian conjugate of Sub-figure (i) of Figure 4 gives back the LERCCSD diagram for . Similar to , we also construct the analogous and diagrams (as given in Figure 2 and Figure 3, respectively), and generate more terms. We note that the property vertex from the DF diagram in Figure 1 is not replaced with any intermediate diagram, as otherwise there would be repetition of diagrams in the calculations. Further, one has to be careful to avoid repetition of diagrams while contracting effective O operators with the T RCC operators. For example, it can be shown that diagrams can appear twice through and terms. Such diagrams are identified by careful analysis, and their double counting is removed manually.
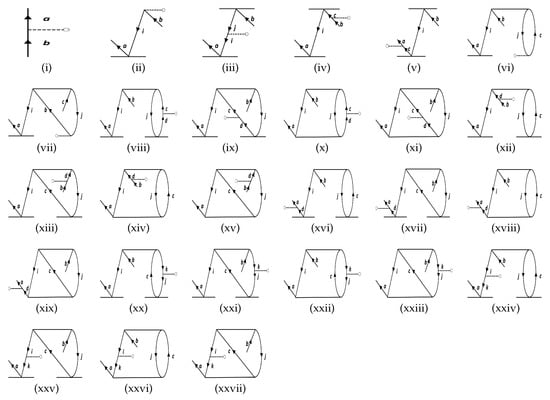
Figure 2.
The effective one-body terms representing particle-particle (p-p) diagrams considered in this work. and refer to holes and particles, respectively. The symbol of the operator, , is not mentioned explicitly in the diagrams, and the property vertex is the dashed line ending with an “o” in each diagram.
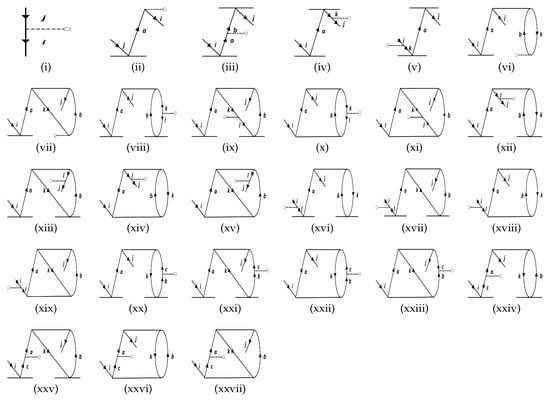
Figure 3.
The effective one-body terms representing the hole-hole (h-h) diagrams that are included in this work. The notations are the same as in the figure for the particle-particle diagrams. The property operator, , is not explicitly mentioned in each of the diagrams, just as in Figure 2.
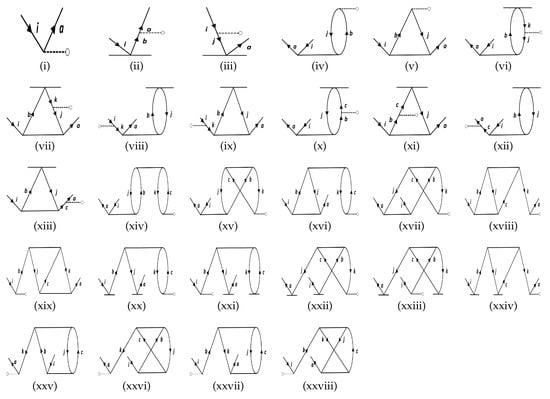
Figure 4.
The list of the effective one-body terms representing the particle-hole (p-h) diagrams in this work. The notations are the same as in the particle-particle and the hole-hole diagrams.
As can be seen from the above discussions, some of the diagrams that were undertaken in this procedure demanded up to the order of in computational cost for number of holes and number of particles. Therefore, the intermediate diagram approach systematically took into account non-linear terms while simultaneously cutting down drastically on the computational cost as compared to a direct brute-force evaluation of a non-linear expectation value expression. This could be understood by choosing an example as follows. Replacing O of Figure 1v by the property vertex with Sub-figure (xxv) from Figure 4 entailed a computational cost for the direct evaluation of such a diagram. However, the intermediate-diagram approach led to a cost of . This became especially relevant when we performed computations on heavy systems and with high-quality basis sets, such as those that we chose for this work. For instance, the RCC calculations on HgF involved and , and therefore, the computational cost with an intermediate-diagram approach was a full five orders of magnitude smaller than a brute-force approach to computing the same diagram (without considering any molecular point group symmetries). A similar level of reduction in computational cost could be seen from the heaviest HgI as well. We add at this point that we exploited the double point group symmetry in our nLERCCSD code, as we had done for the earlier LERCCSD program [5,36]. This aspect also substantially lessened the computational cost, as it restricted the number of matrix elements to be evaluated based on group theoretic considerations. For example, involves computing matrix elements of the form . Given that we had 89 holes and 429 particles, the number of possible matrix elements was ∼. However, since we imposed the restriction that both i and a should belong to the same irreducible representation, we needed to evaluate only ∼ matrix elements. Similar considerations for the more complicated terms involving led to evaluating much fewer matrix elements.
3. Results and Discussions
To carry out the calculations in the considered molecules, we chose values for the bond lengths as 2.00686 , 2.42 , 2.62 , 2.81 , 2.075 , and 2.16 for HgF, HgCl, HgBr, HgI, SrF, and BaF, respectively [37,38,39,40,41,42]. It is to be noted that the chosen values for the HgX molecules were from theory, while those for SrF and BaF were from experiment. Furthermore, we opted for Dyall’s quadruple zeta (QZ) basis for Hg and I [43], Dunning’s correlation consistent polarized valence quadruple zeta (cc-pVQZ) basis for the halide atoms (F, Cl, and Br) [44], and Dyall’s QZ functions augmented with Sapporo’s diffuse functions [45] for Sr and Ba. We chose Dyall’s basis for Hg and I as it was among the most reliable and widely used basis functions for heavy atoms. We did not add diffuse functions as it increased the computational cost drastically for QZ quality basis sets. Moreover, it was found that the inclusion of diffuse functions changed the effective electric field by around 2.5 percent for HgF, and it was expected to lead to a similar difference for the heavier HgX systems [9]. However, in the foreseeable future, such computations could be performed to improve the calculated values of the PDMs. To minimize steep computational costs that we incurred due to our choice of QZ basis sets, as well as performing all-electron calculations, we cut-off the high-lying virtuals above 1000 atomic units (a.u.) for HgX and BaF. At such a high cut-off value, we could expect that the missing contributions would be minimal, and possibly even negligible.
In Table 1, we present our results for HgX, SrF, and BaF, all using QZ basis sets. We discuss the trends in the PDMs and s across HgX in the three different approaches, namely the LERCCSD and nLERCCSD methods, while briefly making a comparison with the FFRCCSD method from [9] wherever relevant, and we also examined the correlation effects in the property from lower to all-order methods. SrF and BaF molecules were treated as stand-alone systems. Firstly, we observed that the effect of non-linear corrections was to increase the PDM and decrease the effective electric field (except in the case of SrF, where the difference was still within 0.5 percent). We find from Table 1 that for SrF and BaF, the nLERCCSD method yielded PDMs that were very close to their LERCCSD counterparts (within 1.5 percent of each other for both the molecules), but were not in better agreement with experiments than their LERCCSD counterparts. However, the nLERCCSD values agreed well with the results from the earlier work that used the FFRCCSD approach (within 1.2 percent of each other) that also employed a QZ quality basis with diffuse functions. Such a comparison could not be made with the HgX molecules, as available FFRCCSD data used a double zeta (DZ) quality basis. For HgX systems, we observed that unlike in the cases of SrF and BaF, the difference between the LERCCSD and the nLERCCSD results widened from about six percent for HgF and HgCl, to about 25 percent for HgI. The values for for SrF and BaF showed that the LERCCSD, nLERCCSD, and FFRCCSD methods all agreed to within one percent. In the case of HgX molecules, the LERCCSD and nLERCCSD results were found to differ by at most 2.5 percent. We chose HgF as a representative molecule and performed FFRCCSD calculations with a QZ basis, and we found that its effective electric field was 110.87 GV/cm, which was lesser than the nLERCCSD value by 2.5 percent.

Table 1.
Contributions from the Dirac–Fock (DF), LERCCSD, and nLERCCSDmethods to the s (in GV/cm) and permanent electric dipole moments (PDMs) (in Debye) of HgX, SrF, and BaF molecules from the present work (denoted as “This work” in the table). Comparison of the two properties from various works with our results are also presented. CASSCF, complete active space self-consistent field; RSPT2, second-order Rayleigh–Schrodinger perturbation theory; X2C-FSCC, exact two-component Hamiltonian–Fock space coupled-cluster.
The individual contributions that arose from the diagrams given in Figure 1 to the effective electric fields and PDMs of HgX, SrF, and BaF molecules are given in Table 2 and Table 3. The tables give the LERCCSD contributions, where the property vertex is O, as well as the nLERCCSD values, where the property vertex could be of the , , or the type, depending on the diagram. For example, the contribution from Sub-figure (ii) of Figure 1, for the nLERCCSD case, involved a p-h vertex, that is , and therefore included in it the contributions from the 26 diagrams in Figure 4. In general, O or (where “x” and “y” could be p or h) was the eEDM Hamiltonian for (which is given in Table 2), while it was the dipole operator for the PDM (which is presented in Table 3).

Table 2.
Individual correlation contributions to the effective electric fields (in GV/cm) of mercury monohalides (HgX; X = F, Cl, Br, and I), SrF, and BaF, from the LERCCSD (abbreviated as “L”) and nLERCCSD (denoted by “nL”) methods. In the first column, A could be O (which corresponds to LERCCSD diagrams) or (which is associated with nLERCCSD diagrams), where “x” and “y” could stand for the corresponding particle or hole line for a given term. The values are all rounded-off to two decimal places for HgX, while numbers that are extremely small in the case of SrF and BaF are denoted in the scientific notation instead.

Table 3.
Correlation contributions to the PDMs (in Debye) of mercury monohalides (HgX; X = F, Cl, Br, and I), SrF, and BaF. The notation is the same as in Table 2. The entry “NC” stands for nuclear contribution to the PDM.
Table 2 shows that for all the systems, the term always dominated among the correlation terms, where A could correspond to either or for LERCCSD or nLERCCSD, respectively. For the effective electric fields of the HgX molecules, in the LERCCSD case, there were strong cancellations among the positive and the negative and terms. However, the final values of nLERCCSD and the LERCCSD calculations matched within 2.5 percent, since in the former case, the values were significantly lower than the latter, and the sector provided a far smaller contribution. In the case of SrF, the terms were comparable for LERCCSD and the nLERCCSD scenarios, and therefore, inclusion of non-linear terms did not change its effective electric field, while for BaF, we observed a mechanism that was similar to that for the HgX systems. We observed a different trend for the PDMs, in Table 3. As the DF value and the nuclear contribution were the same for a given molecule, whether it be LERCCSD or an nLERCCSD calculation, the interplay between and terms decided the importance of non-linear terms. For HgX, the term in nLERCCSD calculations was always slightly larger in magnitude than the LERCCSD ones, while the net contributions from the terms, which were less significant, were the other way round. The resulting non-linear effects were not so important for SrF and BaF, as seen in the earlier paragraph, while for HgX molecules, it became significant, with their effects changing the PDM by up to about 25 percent for HgI.
We now conduct a survey of previous works on the effective electric fields and PDMs of the molecules that we considered, in Table 1. For the effective electric fields of BaF, we observed that the effective core potential-restricted active space SCF(ECP-RASSCF) [51] and restricted active space CI(RASCI) [52] methods gave larger values, while the result from the MRCIapproach in [54] estimated the values as being slightly lower, with respect to our nLERCCSD value. A discussion of the previous works on the effective electric fields of HgX and our improved estimate of the quantity using LERCCSD approach was already presented in [8], and hence, we re-direct the reader to the earlier work. Our nLERCCSD results improved over the earlier LERCCSD and FFRCCSD results, as both of those were calculated using a DZ quality basis. Most of the works that calculated PDMs and that were not mentioned in the table, including [39,41,59,60,61], were expounded in our earlier works in detail [9,33], and therefore, we only discuss in this paragraph the more recent works. The differences in the PDMs between the LERCCSD results in our earlier work and those in the present work for HgX were due to the choice of basis (DZ basis functions [8,57] in the former, as against a QZ basis in the current work). We observed that the values of PDM for SrF that were obtained by using the complete active space self-consistent field (CASSCF) approach to multi-reference CI (MRCI) and second-order Rayleigh–Schrodinger perturbation theory (RSPT2) [46] (which agreed with our nLERCCSD, as well as FFRCCSD results) underestimated and overestimated the results with respect to the experiment, respectively. The results for PDMs of SrF and BaF from Hao et al. [48] using the exact two-component Hamiltonian–Fock space coupled-cluster (X2C-FSCC) formalism and the PDM of SrF from Sasmal et al. [47] using a relativistic Z-vector coupled-cluster approach (with both works employing a QZ basis) agreed closely with the experimental values. However, we also note that while the Z-vector approach predicted the PDM of SrF very accurately, it underestimated that of BaF [50]. This existing difference in the PDMs of SrF and BaF between the nLERCCSD and the FFRCCSD approaches on one side and the Z-vector RCCSD approach on the other could possibly be resolved in future works that employ methods that are even more refined.
We now check for the scalability of our code that was parallelized using MPI. We did so by testing it with the SrF molecule, using a DZ basis. The code was to calculate both the effective electric field and PDM of the molecule for this test. As the code was structured in a way that the extent of parallelization was limited by the number of virtuals, which was 208 in this case, we chose to study scaling up to 192 processors (across eight nodes, and with 24 processors employed per node). The details of the computer (VIKRAM-100 super-computing facility at Physical Research Laboratory, Ahmedabad, India) that we used are: a 100-teraflop IBM nx360 M5 machine with 1848 processors. Each node had 24 processors (two Intel Xeon E5-2670 v3, each with 12 cores) and a memory of 256 GB RAM. The inter-process communication was via a 100% non-blocking FAT Tree Topology FDR (56 Gbits/s) Infiniband network. We used an Intel 15.2 compiler and impi5.0 and mkl libraries. As Figure 5 shows, our calculations indicated that the code was scalable up to this mark. In the figure, we plot the speedup against the number of processors, where the former was defined as , with referring to the time taken for a computation with p processors. Performing the computations in serial mode took about 6.5 days, while calculations with four processors consumed around two days. The code took only 2.17 h to finish with 192 processors. The wall time approached saturation after 96 processors (2.51 h to 2.17 h from 96 to 192 processors), and hence, the optimal number of processors to use was around 96, where we still obtained a speed-up from 6.5 days to 2.51 h. The wall times were reliable as estimates, but not extremely accurate, as the computations were performed on a common cluster, and the speeds depended on other factors such as the number of users, the computer’s specifications, and type of jobs during the time interval across which our computations were done, although we took utmost care to ensure that no other application ran on the same node(s) as ours. However, our analysis was sufficient for the purposes of broadly demonstrating that our code was scalable to a reasonably large number of processors.
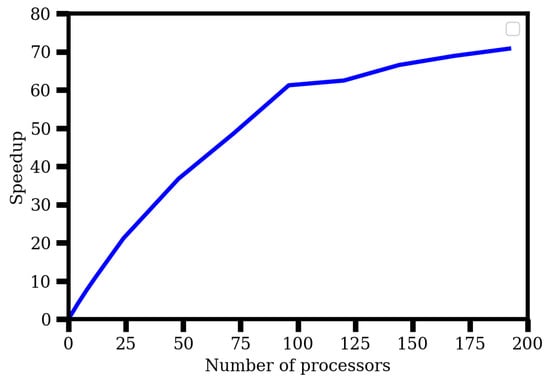
Figure 5.
Plot showing the scaling behavior of the program in the property evaluating expression for a representative system, SrF, with the number of processors of our computer. The X-axis gives the number of processors, while the Y-axis is the speedup, , where t is the time taken and the subscript denotes the number of processors. We used a double-zeta quality basis for this purpose and tested up to 192 processors, as the parallelism in our code was limited by the number of virtual orbitals, which was 208 in this case.
We also estimated the errors in our calculations. We first examined the error due to the choice of basis. We used QZ quality basis sets for our calculations, and as there was no five-zeta basis that was available for us to carry out any kind of estimate, we calculated the effective electric fields and the PDMs at the DZ level of the basis with our nLERCCSD code. We found that the percentage fraction difference between the DZ and QZ basis for was around 3, 4, 5, and 7 percent for HgF, HgCl, HgBr, and HgI, respectively. We did not anticipate the difference between the DZ and QZ estimates to be over 10 percent for SrF and BaF either. Therefore, we did not expect that the difference between results from a higher quality basis set than QZ and those from a QZ basis should exceed 10 percent. Based on similar considerations, we estimated the error due to the choice of basis for the PDM to be at most 15 percent. Next, we shall look at the errors due to the ignored non-linear terms. They were expected to be negligible, and we ascribed a conservative estimate of two percent, which was the percentage fraction difference between the DF values and the current nLERCCSD values for the HgX molecules. Lastly, we comment on the importance of triple and other higher excitations. Based on our previous works and error estimates in them, we expected that these excitations would be around three percent for the purposes of calculating [9], but could become important for PDMs. In conclusion, we linearly added the uncertainties and set an optimistic error estimate for the effective electric fields at about 15 percent. However, it was not so straightforward to set an error estimate for PDMs, as seen above, but we did not anticipate it to exceed 20 percent.
4. Conclusions
We investigated the contributions from the non-linear terms of the property evaluating the expression of the relativistic coupled-cluster theory in the determination of permanent electric dipole moments and effective electric field due to the electron electric dipole moment of SrF, BaF, and mercury monohalide (HgX with X = F, Cl, Br, and I) molecules. We found that the inclusion of these terms at the single and double excitation approximation brought the permanent electric dipole moments (PDMs) of SrF and BaF closer to the previously calculated finite-field relativistic coupled-cluster values, which were found to have overestimated the PDMs of the two molecules with respect to available measurements. The non-linear terms considerably changed the PDMs of HgX systems. For all of the chosen molecules, the non-linear terms were found not to change significantly the values of effective electric fields with respect to the results from the linear expectation value approach. However, such a result was a consequence of several cancellations at work. Since accurate estimation of these quantities are of immense interest to probe new physics from the electron electric dipole moment studies using molecules, our analysis demonstrated the importance of considering non-linear terms in relativistic coupled-cluster theory for their evaluations. We also presented the scaling behavior of our code with a representative SrF molecule and discussed the error estimates.
Author Contributions
Conceptualization, B.K.S.; Formal analysis, V.S.P.; Investigation, V.S.P.; Project administration, B.K.S.; Resources, B.K.S.; Software, V.S.P., B.K.S. and M.A.; Supervision, B.K.S. and B.P.D.; Writing—original draft, V.S.P.; Writing—review and editing, V.S.P., B.K.S., M.A. and B.P.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
All the computations were performed on the VIKRAM-100 cluster at Physical Research Laboratory, Ahmedabad.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eliav, E.; Kaldor, U.; Ishikawa, Y. Relativistic coupled cluster theory based on the no-pair dirac–coulomb–breit hamiltonian: Relativistic pair correlation energies of the xe atom. Int. J. Quantum Chem. 1994, 52, 205–214. [Google Scholar] [CrossRef]
- Nataraj, H.S.; Sahoo, B.K.; Das, B.P.; Mukherjee, D. Intrinsic Electric Dipole Moments of Paramagnetic Atoms: Rubidium and Cesium. Phys. Rev. Lett. 2008, 101, 033002. [Google Scholar] [CrossRef] [PubMed]
- Bishop, R.F. Microscopic Quantum Many-Body Theories and Their Applications; Springer: Berlin/Heidelberg, Germany, 1998; Chapter 1. [Google Scholar]
- Sahoo, B.K.; Kumar, P. Relativistic coupled-cluster-theory analysis of unusually large correlation effects in the determination of gj factors in Ca+. Phys. Rev. A 2017, 96, 012511. [Google Scholar] [CrossRef]
- Abe, M.; Gopakumar, G.; Hada, M.; Das, B.P.; Tatewaki, H.; Mukherjee, D. Application of relativistic coupled-cluster theory to the effective electric field in YbF. Phys. Rev. A 2014, 90, 022501. [Google Scholar] [CrossRef]
- Landau, L. On the conservation laws for weak interactions. Nucl. Phys. 1957, 3, 127. [Google Scholar] [CrossRef]
- Luders, G. Proof of the TCP theorem. Ann. Phys. 2000, 281, 1004. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Vutha, A.C.; Abe, M.; Das, B.P. Mercury Monohalides: Suitability for Electron Electric Dipole Moment Searches. Phys. Rev. Lett. 2015, 114, 183001. [Google Scholar] [CrossRef] [PubMed]
- Abe, M.; Prasannaa, V.S.; Das, B.P. Application of the finite-field coupled-cluster method to calculate molecular properties relevant to electron electric-dipole-moment searches. Phys. Rev. A 2018, 97, 032515. [Google Scholar] [CrossRef]
- Shuman, E.S.; Barry, J.F.; DeMille, D. Laser cooling of a diatomic molecule. Nature 2010, 467, 820. [Google Scholar] [CrossRef]
- Andreev, V.; Ang, D.G.; DeMille, D.; Doyle, J.M.; Gabrielse, G.; Haefner, J.; Hutzler, N.R.; Lasner, Z.; Meisenhelder, C.; Leary, B.R.; et al. Improved limit on the electric dipole moment of the electron. Nature 2018, 562, 355. [Google Scholar]
- Cesarotti, C.; Lu, Q.; Nakai, Y.; Parikh, A.; Reece, M. Interpreting the electron EDM constraint. J. High Energy Phys. 2019, 59, 2019. [Google Scholar] [CrossRef]
- Fuyuto, K.; Hisano, J.; Senaha, E. Toward verification of electroweak baryogenesis by electric dipole moments. Phys. Lett. B 2016, 755, 491. [Google Scholar] [CrossRef]
- Das, B.P. Aspects of Many-Body Effects in Molecules and Extended Systems; Mukherjee, D., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; p. 411. [Google Scholar]
- Sasmal, S.; Pathak, H.; Nayak, M.K.; Vaval, N.; Pal, S. Calculation of P,T-odd interaction constant of PbF using Z-vector method in the relativistic coupled-cluster framework. J. Chem. Phys. 2015, 143, 084119. [Google Scholar] [CrossRef] [PubMed]
- Sasmal, S.; Pathak, H.; Nayak, M.K.; Vaval, N.; Pal, S. Relativistic coupled-cluster study of RaF as a candidate for the parity- and time-reversal-violating interaction. Phys. Rev. A 2016, 93, 062506. [Google Scholar] [CrossRef]
- Sunaga, A.; Prasannaa, V.S.; Abe, M.; Hada, M.; Das, B.P. Enhancement factors of parity- and time-reversal-violating effects for monofluorides. Phys. Rev. A 2018, 98, 042511. [Google Scholar] [CrossRef]
- Sunaga, A.; Prasannaa, V.S.; Abe, M.; Hada, M.; Das, B.P. Ultracold mercury alkali-metal molecules for electron-electric-dipole-moment searches. Phys. Rev. A 2019, 99, 040501(R). [Google Scholar] [CrossRef]
- Fazil, N.M.; Prasannaa, V.S.; Latha, K.V.P.; Abe, M.; Das, B.P. RaH as a potential candidate for electron electric-dipole-moment searches. Phys. Rev. A 2019, 99, 052502. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Shitara, N.; Sakurai, A.; Abe, M.; Das, B.P. Enhanced sensitivity of the electron electric dipole moment from YbOH: The role of theory. Phys. Rev. A 2019, 99, 062502. [Google Scholar] [CrossRef]
- Singh, Y.; Sahoo, B.K.; Das, B.P. Correlation trends in the ground-state static electric dipole polarizabilities of closed-shell atoms and ions. Phys. Rev. A 2013, 88, 062504. [Google Scholar] [CrossRef]
- Shavitt, I.; Bartlett, R.J. Many Body Methods in Chemistry and Physics; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Yang, Z.; Li, J.; Lin, Q.; Xu, L.; Wang, H.; Yang, T.; Yin, J. Laser-cooled HgF as a promising candidate to measure the electric dipole moment of the electron. Phys. Rev. A 2019, 99, 032502. [Google Scholar] [CrossRef]
- Aggarwal, P.; Bethlem, H.L.; Borschevsky, A.; Denis, M.; Esajas, K.; Haase, P.A.B.; Hao, Y.; Hoekstra, S.; Jungmann, K.; Meijknecht, T.B.; et al. The NL-eEDM collaboration. Measuring the electric dipole moment of the electron in BaF. Eur. Phys. J. D 2018, 72, 197. [Google Scholar] [CrossRef]
- Vutha, A.C.; Horbatsch, M.; Hessels, E.A. Oriented Polar Molecules in a Solid Inert-Gas Matrix: A Proposed Method for Measuring the Electric Dipole Moment of the Electron. Atoms 2018, 6, 3. [Google Scholar] [CrossRef]
- Ernst, W.E.; Kandler, J.; Kindt, S.; Torring, T. Electric dipole moment of SrF X2Σ+ from high-precision stark effect measurements. Chem. Phys. Lett. 1985, 113, 351. [Google Scholar] [CrossRef]
- Cizek, J. Advances in Chemical Physics, Volume XIV: Correlation Effects in Atoms and Molecules; Lefebvre, W.C., Moser, C., Eds.; Interscience Publishers: New York, NY, USA, 1969. [Google Scholar]
- Yanai, T.; Nakano, H.; Nakajima, T.; Tsuneda, T.; Hirata, S.; Kawashima, Y.; Nakao, Y.; Kamiya, M.; Sekino, H.; Hirao, K. UTCHEM: A Program for ab initio Quantum Chemistry; Lecture Notes in Computer Science; Goos, G., Hartmanis, J., van Leeuwen, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2660, p. 84. [Google Scholar]
- Yanai, T.; Nakajima, T.; Ishikawa, Y.; Hirao, K. A new computational scheme for the Dirac Hartree Fock method employing an efficient integral algorithm. J. Chem. Phys. 2001, 114, 6526. [Google Scholar] [CrossRef]
- Abe, M.; Yanai, T.; Nakajima, T.; Hirao, K. A four-index transformation in Dirac’s four-component relativistic theory. Chem. Phys. Lett. 2004, 388, 68. [Google Scholar] [CrossRef]
- Visscher, L.; Jensen, H.J.A.; Saue, T.; Bast, R.; Dubillard, S.; Dyall, K.G.; Ekstrom, U.; Eliav, E.; Fleig, T.; Gomes, A.S.P.; et al. DIRAC: A Relativistic ab initio Electronic Structure Program. Release DIRAC08 2008. [Google Scholar]
- Kvasnicka, V.; Laurinc, V.; Biskupic, S. Coupled-cluster approach in electronic structure theory of molecules. Phys. Rep. 1982, 90, 159. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Sreerekha, S.; Abe, M.; Bannur, V.M.; Das, B.P. Permanent electric dipole moments of alkaline-earth-metal monofluorides: Interplay of relativistic and correlation effects. Phys. Rev. A 2016, 93, 042504. [Google Scholar] [CrossRef]
- Slater, J.C. The Theory of Complex Spectra. Phys. Rev. 1929, 34, 1293. [Google Scholar] [CrossRef]
- Condon, E.U. The Theory of Complex Spectra. Phys. Rev. 1930, 36, 1121. [Google Scholar] [CrossRef]
- Yanai, T.; Harrison, R.J.; Nakajima, T.; Ishikawa, Y.; Hirao, K. New implementation of molecular double point group symmetry in four component relativistic Gaussian type spinors. Int. J. Quantum Chem. 2007, 107, 1382. [Google Scholar] [CrossRef]
- Knecht, S.; Fux, S.; van Meer, R.; Visscher, L.; Reiher, M.; Saue, T. Mossbauer spectroscopy for heavy elements: A relativistic benchmark study of mercury. Theor. Chem. Acc. 2011, 129, 631. [Google Scholar] [CrossRef]
- Cheung, N.-H.; Cool, T.A. Franck-Condon Factors and r-Centroids for the B2ΣX2Σ Systems of HgCl, HgBr, and MgI. J. Quant. Spectrosc. Radiat. Transf. 1979, 21, 397. [Google Scholar] [CrossRef]
- Langhoff, S.R.; Bauschlicher, C.W., Jr.; Partridge, H.; Ahlrichs, R. Theoretical study of the dipole moments of selected alkaline earth halides. J. Chem. Phys. 1986, 84, 5025. [Google Scholar] [CrossRef]
- Huber, K.P.; Herzberg, G. (Eds.) Molecular Spectra and Molecular Structure, IV. Constants of Diatomic Molecules; Reinhold: New York, NY, USA, 1979. [Google Scholar]
- Mestdagh, J.M.; Visticot, J.P. Semiempirical electrostatic polarization model of the ionic bonding in alkali and alkaline earth hydroxides and halides. Chem. Phys. 1991, 155, 79. [Google Scholar] [CrossRef]
- Ryzlewicz, C.; Torring, T. Formation and microwave spectrum of the 2Σ-radical barium-monofluoride. Chem. Phys. 1980, 51, 329. [Google Scholar] [CrossRef]
- Dyall, K.G. Relativistic Quadruple-Zeta and Revised Triple-Zeta and Double-Zeta Basis Sets for the 4p, 5p, and 6p Elements. Theor. Chem. Acc. 2006, 115, 441. [Google Scholar] [CrossRef]
- Schuchardt, K.L.; Didier, B.T.; Elsethagen, T.; Sun, L.; Gurumoorthi, V.; Chase, J.; Li, J.; Windus, T.L. Basis Set Exchange: A Community Database for Computational Sciences. J. Chem. Inf. Model 2007, 47, 1045. [Google Scholar] [CrossRef]
- Noro, T.; Sekiya, M.; Koga, T. Segmented contracted basis sets for atoms H through Xe: Sapporo-(DK)-nZP sets (n = D, T, Q). Theor. Chem. Acc. 2012, 131, 1124. [Google Scholar] [CrossRef]
- Jardali, F.; Korek, M.; Younes, G. Theoretical calculation of the low-lying doublet electronic states of the SrF molecule. Canad. J. Phys. 2014, 92, 1223. [Google Scholar] [CrossRef]
- Sasmal, S.; Pathak, H.; Nayak, M.K.; Vaval, N.; Pal, S. Implementation of the Z-vector method in the relativistic-coupled-cluster framework to calculate first-order energy derivatives: Application to the SrF molecule. Phys. Rev. A 2015, 91, 030503(R). [Google Scholar] [CrossRef]
- Hao, Y.; Pasteka, L.F.; Visscher, L.; Aggarwal, P.; Bethlem, H.L.; Boeschoten, A.; Borschevsky, A.; Denis, M.; Esajas, K.; Hoekstra, S.; et al. High accuracy theoretical investigations of CaF, SrF, and BaF and implications for laser-cooling. J. Chem. Phys. 2019, 151, 034302. [Google Scholar] [CrossRef] [PubMed]
- Tohme, S.N.; Korek, M. Theoretical study of the electronic structure with dipole moment calculations of barium monofluoride. J. Quant. Spectrosc. Radiat. Transf. 2015, 167, 82. [Google Scholar] [CrossRef]
- Talukdar, K.; Nayak, M.K.; Vaval, N.; Pal, S. Relativistic coupled-cluster study of BaF in search of CP violation. arXiv 2020, arXiv:2002.02505. [Google Scholar] [CrossRef]
- Kozlov, M.G.; Titov, A.V.; Mosyagin, N.S.; Souchko, P.V. Enhancement of the electric dipole moment of the electron in the BaF molecule. Phys. Rev. A 1997, 56, R3326(R). [Google Scholar] [CrossRef]
- Nayak, M.K.; Chaudhuri, R.K. Ab initio calculation of P, T-odd interaction constant in BaF: A restricted active space configuration interaction approach. J. Phys. B At. Mol. Opt. Phys. 2006, 39, 1231. [Google Scholar] [CrossRef]
- Meyer, E.R.; Bohn, J.L.; Deskevich, M.P. Candidate molecular ions for an electron electric dipole moment experiment. Phys. Rev. A 2006, 73, 062108. [Google Scholar] [CrossRef]
- Meyer, E.R.; Bohn, J.L. Prospects for an electron electric-dipole moment search in metastable ThO and ThF+. Phys. Rev. A 2008, 78, 010502(R). [Google Scholar] [CrossRef]
- Ernst, W.E.; Kandler, J.; Torring, T. Hyperfine structure and electric dipole moment of BaF X2Σ+. J. Chem. Phys. 1986, 84, 4769. [Google Scholar] [CrossRef]
- Dmitriev, Y.Y.; Khait, Y.G.; Kozlov, M.G.; Labzovsky, L.N.; Mitrushenkov, A.O.; Shtoff, A.V.; Titov, A.V. Calculation of the spin-rotational Hamiltonian including P- and P, T-odd weak interaction terms for HgF and PbF molecules. Phys. Lett. A 1992, 167, 280. [Google Scholar] [CrossRef]
- Prasannaa, V.S.; Abe, M.; Das, B.P. The role of molecular electric dipole moments of mercury monohalides in the search for the electron electric dipole moment. Asian J. Phys. 2016, 25, 1259. [Google Scholar]
- Wadt, W.R. The electronic structure of HgCl and HgBr. Appl. Phys. Lett. 1979, 34, 658. [Google Scholar] [CrossRef]
- Torring, T.; Ernst, W.E.; Kindt, S. Dipole moments and potential energies of the alkaline earth monohalides from an ionic model. J. Chem. Phys. 1984, 81, 4614. [Google Scholar] [CrossRef]
- Allouche, A.R.; Wannous, G.; Aubert-Frecon, M. A ligand-field approach for the low-lying states of Ca, Sr and Ba monohalides. Chem. Phys. 1993, 170, 11. [Google Scholar] [CrossRef]
- Kobus, J.; Moncrieff, D.; Wilson, S. Comparison of the electric moments obtained from finite basis set and finite-difference Hartree-Fock calculations for diatomic. Phys. Rev. A 2000, 62, 062503. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).