1. Introduction
Gamma distribution is one family of continuous probability distributions and generalizations of exponential distributions [
1]. Nagar, Correa, and Gupta [
2] mentioned that the gamma distribution function was first introduced by Swiss mathematician Leonhard Euler (1729). Because this function is considered important, many researchers have studied and developed it. Bhattacharya [
3], among others, conducted a study on testing the homogeneity of the parameters (shape and scale) of the gamma distribution. Chen and Kotz [
4] conducted a study on the probability density function (pdf) of gamma distribution with three parameters (shape, scale, and location). Many researchers also study and develop bivariate gamma distribution; among others are Schickedanz and Krause [
5], who conducted a study on testing scale parameters from two gamma-distributed data using the generalized likelihood ratio (GLR). Nadarajah [
6] studied the types of bivariate gamma distribution. Next, Nadarajah and Gupta [
7] developed two new bivariate gamma distributions based on gamma and beta random variables. In addition, Mathai and Moschopoulos [
8] discussed joint densities, product moments, conditional densities, and conditional moments that were developed from two bivariate gamma distributions.
One statistical method that can be applied to analyze the data that follow gamma distribution and its predictor variables is gamma regression. Gamma regression is a type of non-linear regression. A non-linear regression contains at least one parameter with a non-linear form [
9,
10]. The gamma regression with multiple responses is the so-called multivariate gamma regression (MGR).
The MGR model proposed in this article is the extension of the trivariate gamma regression (TGR) proposed by Rahayu, Purhadi, Sutikno, and Prastyo [
11], which describes the theory of parameter estimation and its hypothesis testing. The MGR is developed based on multivariate gamma distribution with three parameters (shape, scale, and location). The supporting references about multivariate gamma distribution were written by Mathai and Moschopoulos [
12], and Vaidyanathan and Lakshmi [
13]. The parameter estimation method for MGR in this study uses maximum likelihood estimation (MLE). However, the solution cannot be obtained in the closed form. Therefore, a numerical method is needed to achieve the parameter estimator value. The numerical optimization used in this study is the Berndt–Hall–Hall–Hausman (BHHH).
Based on the previously mentioned background, the aims of this study are: (i) how to construct the MGR model, (ii) how to estimate the parameters, and (iii) how to test the significance of the model as well as the significance of the individual parameter. The last objective of this work is how to apply the proposed MGR model to real data. The case study used in this study includes the factors that affect the life expectancy index (first response), education index (second response), and expenditure index (third response), the three indexes that compose the human development dimensions. The unit of observation is the regency/municipality in Java, Indonesia, in 2018. The predictor variables include the percentage of households that have a private toilet, net enrollment rate of schooling, population density, the percentage of poor people, and the unemployment rate.
The rest of the article is organized as follows.
Section 2 introduces the detail of the proposed MGR model.
Section 3 and
Section 4 explore the data and application, respectively. The last section contains conclusions and further research.
2. Multivariate Gamma Regression Model
Suppose is the response variables data that follows multivariate gamma distribution and is the corresponding predictor variables , with sample size as n observations In this section, we discuss the construction of the MGR model, its parameter estimation, and hypothesis testing. A short explanation about univariate gamma regression is introduced to make a smooth transition into the MGR model.
According to Balakrishnan and Wang [
14], a random variable
follows univariate gamma distribution with three parameters
denoted by
with pdf formulated in Equation (1).
If
, then the statistics are as follows [
15,
16].
, , and the skewness is
Mathai and Moschopoulos (1992) defined the pdf as in Equation (2) for a pair of random variables
that follows bivariate gamma distribution as:
with
for otherwise.
The mean for and are and , while the variances are
Suppose there are
k response variables; the pdf for random variables
that follow multivariate gamma distribution (Mathai and Moschopoulos, 1992) is:
with
otherwise
.
The mean and variance for
are
and
with
and
The MGR model can be stated in Equation (4).
with
The pdf for the
lth observation is formulated in Equation (5) which will be used to compose the likelihood function in Equation (6).
with
otherwise .
Later, we discuss parameter estimation on MGR using MLE. The likelihood function constructed from Equation (5) is:
with values
based on Equation (5).
The log-likelihood function from Equation (6) is:
By substituting the values of
according to Equation (5), the log-likelihood function is:
In this article, the log value is based on
e or natural logarithm. The first derivatives of the log-likelihood function for each parameter are as follows.
with
= digamma function, which is the first derivative of gamma function, formulated with
A maximum likelihood (ML) can be found by setting all the derivatives above to zero and solving the system. No closed-form solution to that system can be found. A numerical method is needed to obtain the solution, i.e., parameter estimate One of the numerical techniques that can be employed is the BHHH algorithm as follows.
Step 1. Determine the initial value for
where satisfies the constraints in Equation (5), and are obtained from the estimate of univariate gamma regression. The Hessian in BHHH is approximated as the negative of the sum of the outer products of the gradients of individual observations. The gradient vector is a vector with each element consisting of the first derivative of the log-likelihood function for each of the estimated parameters.
Step 2. Determine the tolerance limit so that the BHHH iteration process stops. In this study, the tolerance value used is
Step 3. Start the BHHH iteration using the following formula.
with
Step 4. The iteration stops at the
iteration if it satisfies . When converging, the last iteration produces an estimator value for each parameter.
The null hypothesis on the MGR model is
and alternative hypothesis
H1. At least one
with
is the set of parameters under the population. The
is the set of parameters under the null hypothesis. The first derivatives of the log-likelihood function for each parameter under the null hypothesis are provided in
Appendix A.
Proposition 1. If
is a set of parameters under the population,
is a set of parameters under the null hypothesis, and the hypothesis
being used is the simultaneous test of MGR model, then the test statistic is
A Corollary of Proposition 1: The hypothesis being used in the simultaneous test of the MGR model in
Section 2 can be stated in the following form: the null hypothesis is
and the alternative hypothesis is
with
and
for
.
It is noted that
and
are estimators that maximize the likelihood and the log-likelihood functions under the population and under the null hypothesis. The principle of the MLE method is to maximize the likelihood functions [
17]. The following are test statistics for the hypothesis being used in the simultaneous test of the MGR model in
Section 2.
where
is a constant value between
.
and
in Equation (16) are:
and
with
Based on Equation (17),
is difficult to simplify. To simplify the calculation, the test statistics in Equation (16) are expressed in a form equivalent to:
The application of natural logarithms in Equation (18) obtains the following test statistics.
with
Proposition 2. Based on Proposition 1, the distribution of test statistics
is Chi-square with sk degrees of freedom, which can be written as follows. A Corollary of Proposition 2: If is an estimator that maximizes the likelihood and the log-likelihood functions under the population, is an estimator that maximizes the likelihood and the log-likelihood functions under the null hypothesis, based on Equation (19), so:
function can be approached by Taylor’s second-degree expansion around
as follows.
with
and
Because
then Equation (21) becomes:
function can be approached by Taylor’s second-degree expansion around
as follows.
Because
then Equation (23) becomes:
Based on Equations (22) and (24), the test statistics on Equation (20) can be stated as follows.
Equation (25) can be simplified by outlining the quadratic form of
, so we obtained:
From Equation (26), this can be obtained:
Based on Equation (28), the quadratic form given by Equation (26) distributed Chi-square with sk degrees of freedom is:
with
sk is a vector dimension or the difference between the number of parameter sets under the population with the number of parameter sets under the null hypothesis, symbolized by
Proposition 3. The critical area for testing the hypothesis of the MGR model regression parameters simultaneously with regard to Equation (16) is:
Based on Proposition 2 and Proposition 3, the decision to reject the null hypothesis is made if , with is the number of parameters under the population, and is the number of parameters under the null hypothesis.
The null hypothesis for the partial test is
, whereas the alternative is
, with
. According to Pawitan [
18], the test statistic is stated in Equation (31).
with
. The
is diagonal elements that correspond to the
matrix. The null hypothesis is rejected if
3. Data and Method
The parameter estimation and hypothesis testing on MGR were done based on the following steps. The MGR model was specified based on the pdf in Equation (5) for n observations, l = 1, 2, …, n, to construct the likelihood and the log-likelihood functions. The first derivative of the log-likelihood function for each parameter was computed, then equalized to zero. If the solutions were closed-form, then the parameter estimators were obtained. Otherwise, numerical optimization was needed. As shown in the previous section, the solution for parameter optimization was not closed-form, such that the BHHH algorithm was employed in this work.
The overall test for MGR’s significance was done using the maximum likelihood ratio test (MLRT). The test statistic was formulated in Equation (19). Meanwhile, the partial test for individual parameter significance in MGR was done using the Wald test [
18]. Its test statistics are provided in Equation (31). The proposed MGR model, along with its parameter estimation and hypothesis testing, was applied on real data as an application of this study.
This study used secondary data obtained from Statistics Indonesia. The data used were three response variables, i.e., the life expectancy index, education index, and expenditure index, with six predictor variables: percentage of households that have a private toilet, net enrollment rate of schooling, population density, percentage of poor people, and unemployment rate. The data were observed for 119 regencies/municipalities in Java, Indonesia, in the year 2018.
4. Application on Human Development Dimensions Data
First, testing the gamma distribution was done using the Kolmogorov–Smirnov (KS) test. The null hypothesis is the data that follows the gamma distribution against the alternative hypothesis that data does not follow the gamma distribution. The test statistic value of the KS test for each response variable is presented in
Table 1. In this paper, the goodness of fit is done univariately as the test for multivariate gamma distribution is not available yet. The test for that is another extensive work that is not covered in this paper. Once each response follows gamma distribution, we assume the multiresponses data follow a multivariate gamma distribution. This assumption is the limitation of this work, such that the proposed model can be applied to real data without delay.
Each response variable has and p-value > α. The test concludes not to reject the null hypothesis, meaning that the data of life expectancy index (Y1), the education index (Y2), and the expenditure index (Y3) follow the gamma distribution. Therefore, as our research limitation, as mentioned previously, the three response variables are assumed to follow MG distribution.
To support our assumption, we calculated the correlation between the pair of the response variables to show there are dependencies among responses. The correlation coefficients for each pair are as follows: (i) Y1 and Y2 is 0.398 with p-value close to zero, (ii) Y1 and Y3 is 0.324 with p-value close to zero, (iii) Y2 and Y3 is 0.818 with p-value close to zero. The correlation coefficient between education index (Y2) and expenditure index (Y3) is stronger than the other pairs. To find out whether there is dependency among the response variables, one can use Bartlett’s test of sphericity so that the data are feasible for multivariate analysis. This test has statistic value and p-value = 2.22 × 10−16. The (or 7.815) and p-value < α, and alpha is 0.05. The decision is to reject the null hypothesis (Pearson correlation matrix not equal to an identity matrix), which means the correlation between the response variables is significant in the multivariate sense. Therefore, the data analysis needs to be done in a multivariate way using the MGR model.
We also tested the multicollinearity among the predictor variables. The variance inflation factor (VIF) value for each predictor variable is 1.358 (for X1), 1.350 (X2), 1.560 (X3), 1.849 (X4), and 1.211 (X5). The VIF value for each of the predictor variables is less than ten which shows there is no multicollinearity among the predictor variables.
In
Table 2, the mean values for response variables
Y1,
Y2, and
Y3 are 0.806, 0.632, and 0.735. Although
Y1,
Y2, and
Y3 have mean values that do not differ greatly, they are not necessarily of the same quality; it depends on the size of the spread of the data. One measure of data distribution that can be used is the coefficient of variation (CoV). The CoV for
Y1,
Y2, and
Y3 are 5.200, 12.210, and 9.140, respectively. The CoV for education index (
Y2) is the highest among others, which means that the variable is more heterogeneous. The CoV for predictor variables
X1,
X2,
X3,
X4, and
X5 are, respectively, 12.100, 16.750, 136.250, 43.750, and 45.530. The CoV for population density (
X3) is the highest among other predictor variables as its range is also the biggest one.
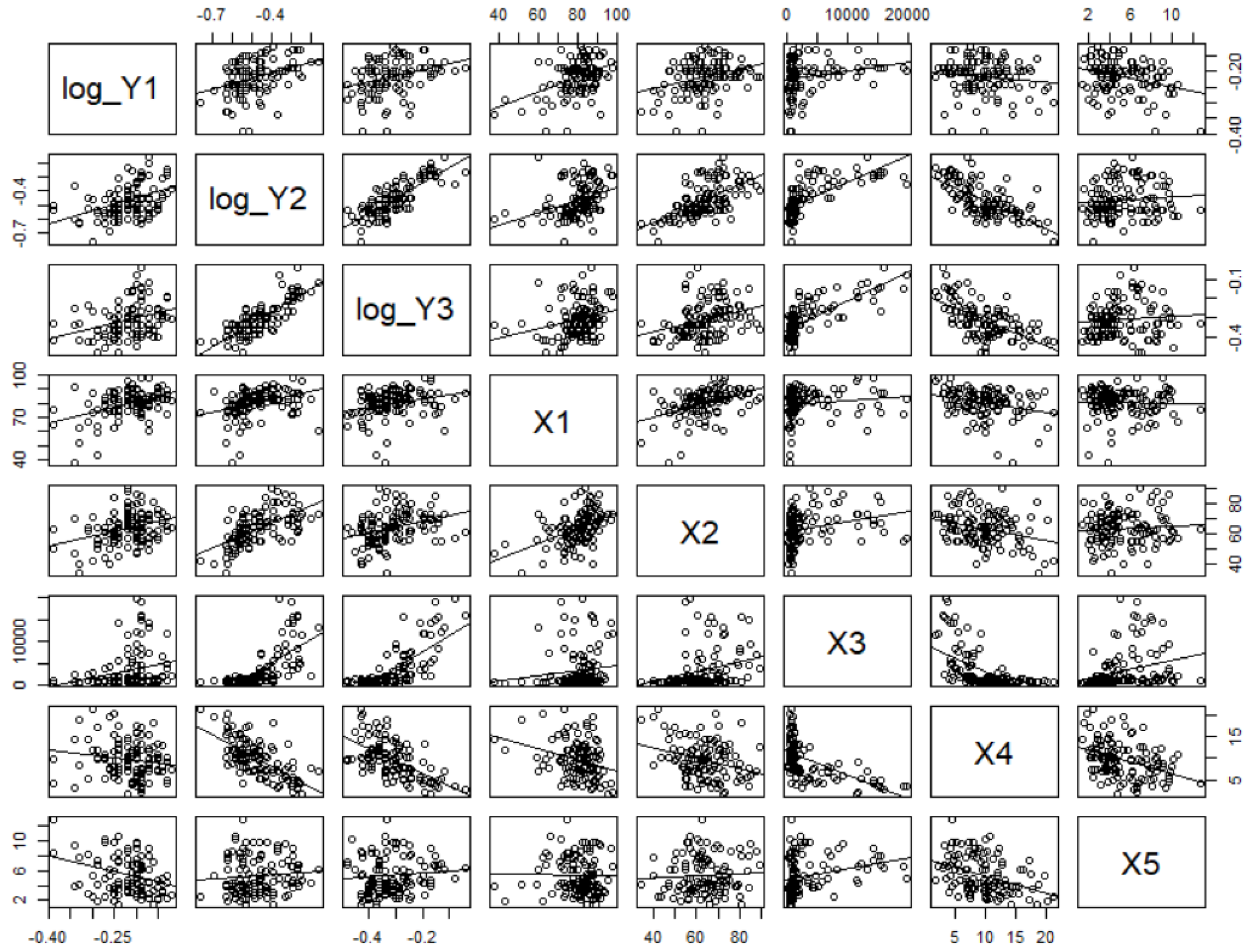
The dependency between response and predictor variables can be shown visually by the matrix plot, as exhibited in
Figure 1. The correlation between
X3 and
X4 (−0.585) is stronger than the correlation between
X4 and the other predictor variables, even stronger than other pairs. The correlation between
X1 and
X5 (−0.017) is weakest compared to the correlation of other couples. There are indications that the relationship is non-linear between
X3 with the response variable and the other predictor variables. For the correlation between response and predictor variables, log(
Y1) has the strongest correlation with
X1 (0.434) compared to other predictors. The log(
Y2) and
X3 have the strongest correlation (0.705) compared with other predictors, while the correlation of log(
Y3) and
X3 is the strongest one (0.744). This value shows that log expenditure index and population density has the strongest relationship among other pairs.
To find out which predictor variables significantly predicted response variables, we employed the MGR model.
Table 3 presents the ML estimates of the MGR model with a single predictor and their corresponding standard errors, z score, and
p-value. Every single predictor does not affect any response variables. Only the intercepts when the MGR model employs
X3 as a single predictor are significant.
The MGR model with a single predictor (for example, the
X5) for the life expectancy index, education index, and expenditure index is obtained as follows.
As summarized in
Table 3, it is shown that all predictor variables are not significant. For comparison, we also did MGR modeling with multiple predictors.
Table 4 presents the ML estimates of the MGR model with multiple predictors along with their corresponding standard errors, z score, and
p-value.
The estimate of the scale parameter is 0.649423, with its standard error 0.000028. The estimate of
, the location parameter for
Y1, is 0.670845 (standard error 0.006884); meanwhile, the estimate for
is −0.309362, with standard error 0.006507, and for
is 0.000468 (standard error 0.006530). The significant parameters are the scale parameter
, the location parameter for
Y1 and
Y2, respectively, and
and
, as their
p-values are less than
The estimate of each parameter corresponding to each predictor is summarized in
Table 4. Therefore, the MGR model for the life expectancy index, education index, and expenditure index is obtained as follows.
The Akaike information criterion (AIC) value is −63.903, and the corrected Akaike information criterion (AICc) value is −53.361. To know the average squared difference between the estimated and the actual values, one can use the mean square error (MSE). The MSEs for the life expectancy index, education index, and expenditure index are 0.001, 0.002, and 0.003, respectively. As the MSE is an unbiased estimator of variance, the MSE value is expected to be not much different from the variance of each response variable, i.e., 0.002 (expectancy index), 0.006 (education index), and 0.004 (expenditure index).
We can perform the simultaneous test for the model’s significance using Wilk’s likelihood ratio statistics derived based on the MLRT. The test statistic value is 46.682, and the value of the Chi-square table with 15 degrees of freedom and
is 22.307. The test statistical value is larger than the value of the Chi-square table; therefore, the decision is to reject the null hypothesis. It means that the five predictor variables have a significant effect on the response variables simultaneously. To find out the predictor variables that partially affect the response variable, one can use test statistics in Equation (31). From
Table 4, it can be seen that the significant predictor variable that influences the life expectancy index is the unemployment rate (
X5); meanwhile the education index and expenditure index are significantly affected by the percentage of poor people (
X4) and unemployment rate (
X5).
Based on the results of MGR modeling with a single predictor (
Table 3) and multiple predictors (
Table 4), it can be determined the differences in the coefficient signs only happen for
X5 in response to
Y2 and
Y3, as shown in
Table 5. We can also find the supports of this evidence from the matrix plot in
Figure 1, that individually,
X5 has a negative relationship with
Y1, while it has positive dependencies with
Y2 and
Y3. On the other side, the
X4 has a stronger negative individual relationship with all responses. Therefore, when
X4 and
X5 are used as predictors together in the MGR model, the sign of
X5 changes as there is a significant correlation (−0.391 with
p-value < 0.05) between
X4 and
X5, where
X4 affects the response of
Y2 and
Y3 is stronger than
X5.
.
Recall the VIF value for X5 is 1.211, which is small. This value means that there is a weak relationship between X5 and (X1, X2, X3, and X4). However, there is a significant correlation between X4 alone and X5. In the MGR with multiple predictors, the positive sign for X5 will not change if X4 also has a positive sign for responses X2 and X3. Unfortunately, that is not the case. The correlation between X4 and X2 has a different sign compared with the correlation between X5 and X2. The sign of X4 and X5 in MGR with multiple predictors can change depending on its correlation with the response variable. The same explanation pertains to response X3.
Life expectancy index (Y1) has a negative association with the percentage of poor people (X4), even though it is not significant for regency/municipality in Java. This finding means that an increase in life expectancy index is not affected by the percentage of poor people in Java. The education index (Y2) and expenditure index (Y3) have a significant negative dependency on the percentage of poor people in Java.
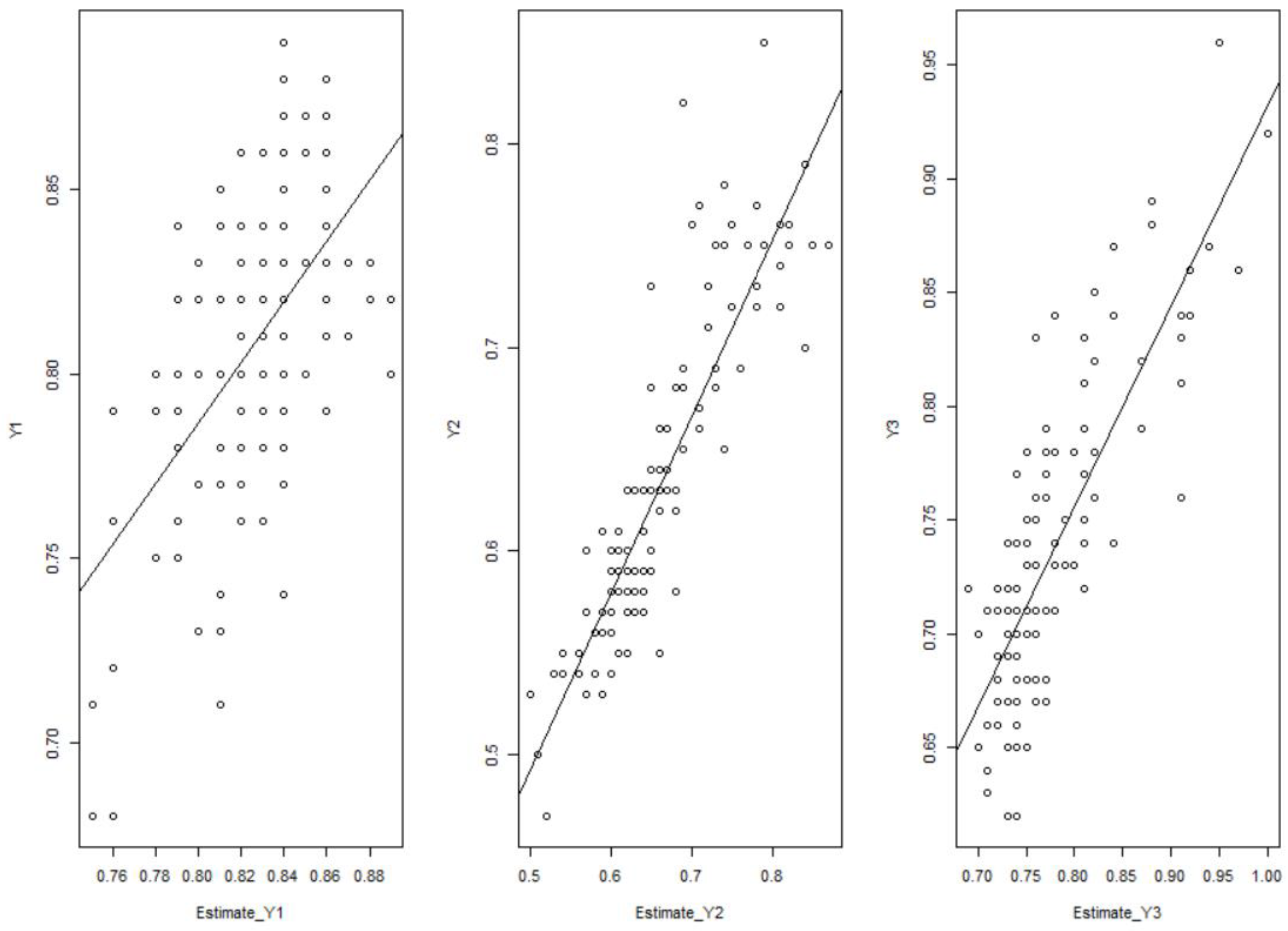
The predictions resulting from the MGR model are expected to be close to the actual values. The closer those two values, the narrower the spread, as displayed in
Figure 2. It can be seen that fitting values for
Y2 and
Y3 are better than those of
Y1. This result is also supported by significant predictors, as reported in
Table 4. The life expectancy index has one significant predictor, while the other two responses have two significant predictors that increase their coefficients of determination.