Representing Measurement as a Thermodynamic Symmetry Breaking
Abstract
1. Introduction
- We formulate the distinction between system identification and pointer-state measurement as a collection of equivalence relations on cocones, and showing that: (1) transitions between cocone equivalence classes can be represented more generally as groupoid operations; and (2) these groupoid operations correspond to entanglement swaps that result in O-relative decoherence [27].
- We show that free-energy acquisition and waste-heat dissipation into the “environment” component of W can generically have non-negligible effects on observational outcomes due to entanglement swapping/contextuality.
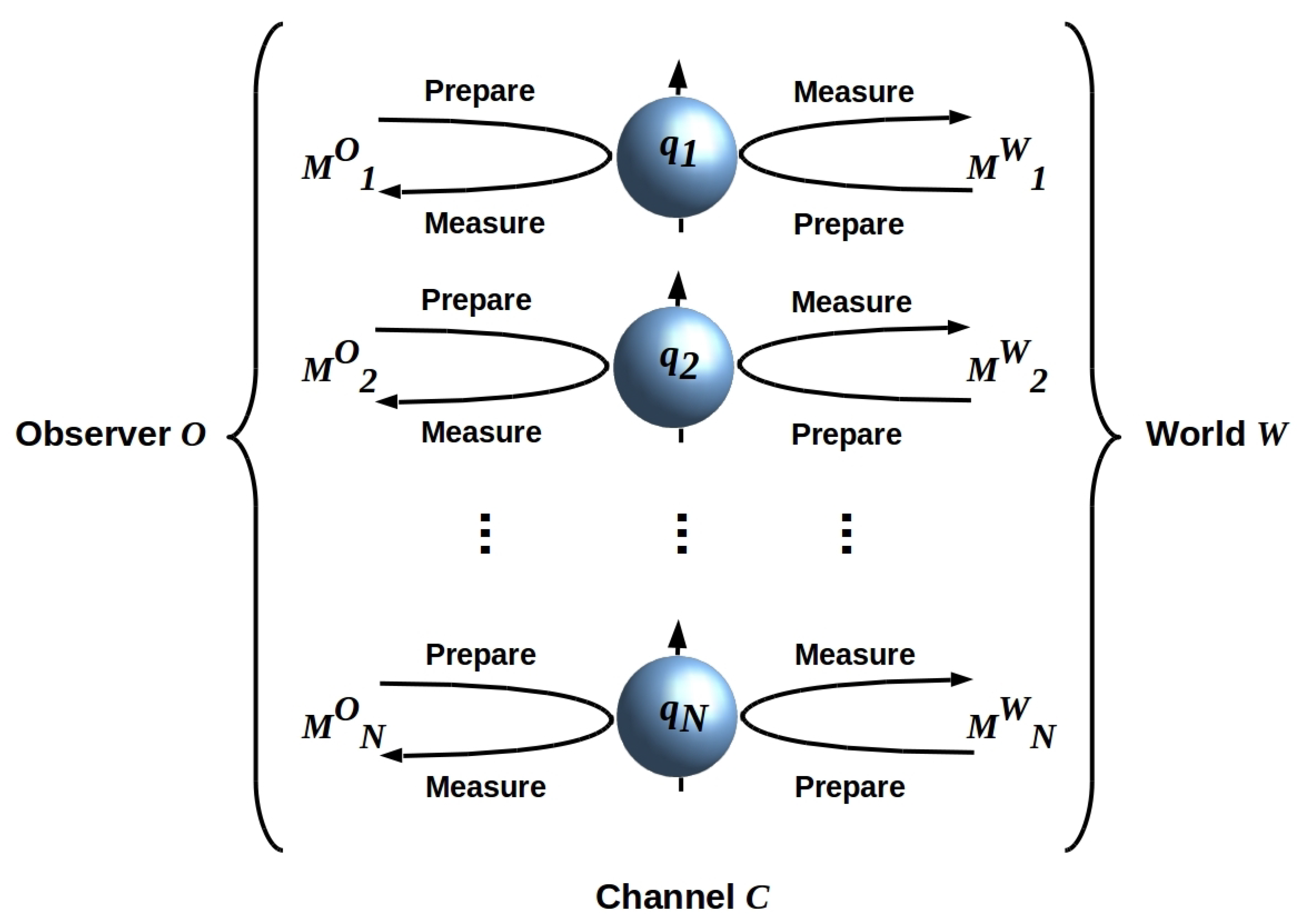
2. Interaction as Mutual Measurement by and
2.1. Sequential Measurements
2.2. Mutual Measurement Is Classical Communication
3. System Identification and Measurement by
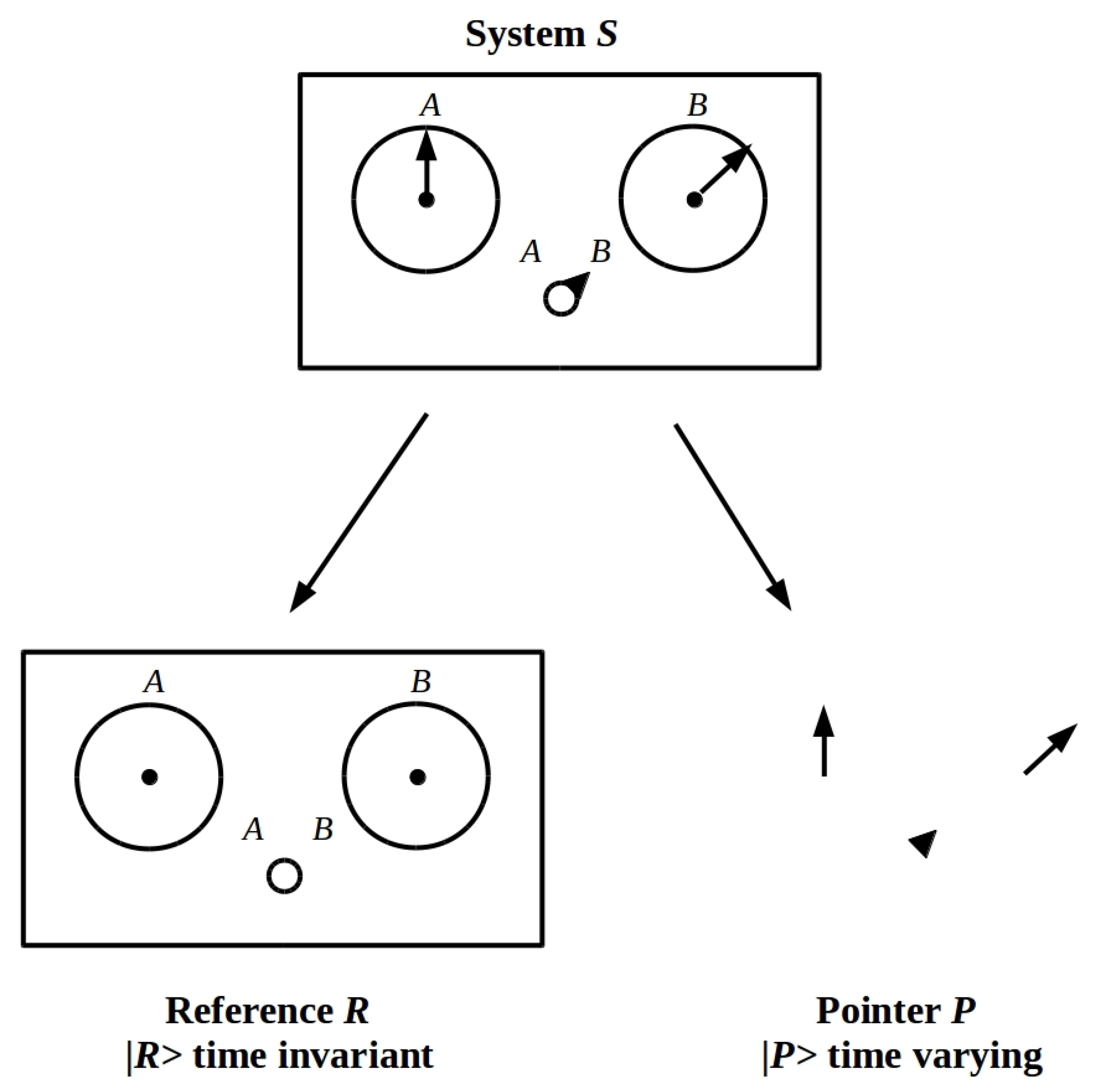
3.1. Systems Require Reference Components with Invariant States
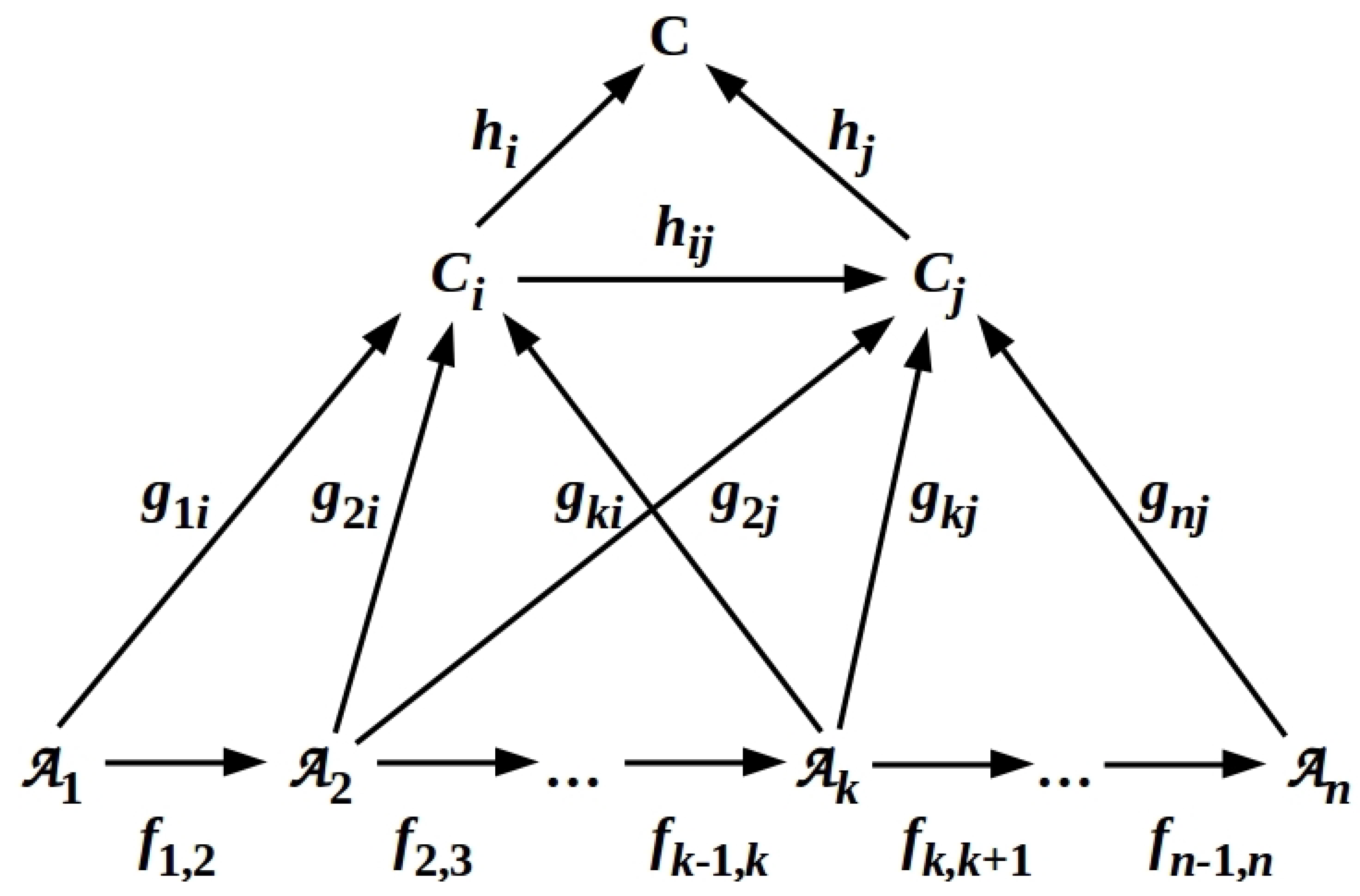
3.2. Reference Components Can Be Represented as Cocones over One-Bit Classifiers
- The must be representable as a finite nonredundant set with infomorphisms .
- There exist infomorphisms and .
- All compositions of infomorphisms with codomain commute.
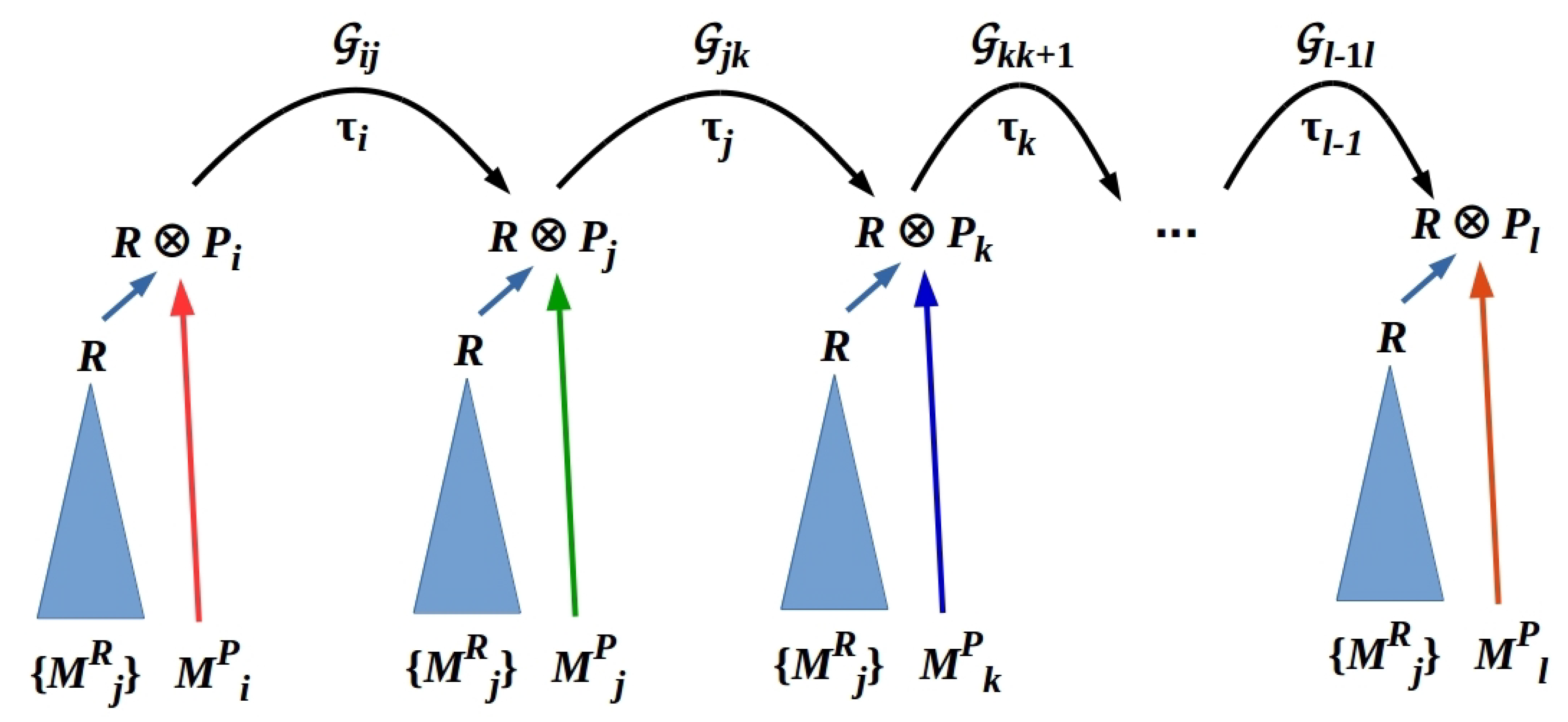
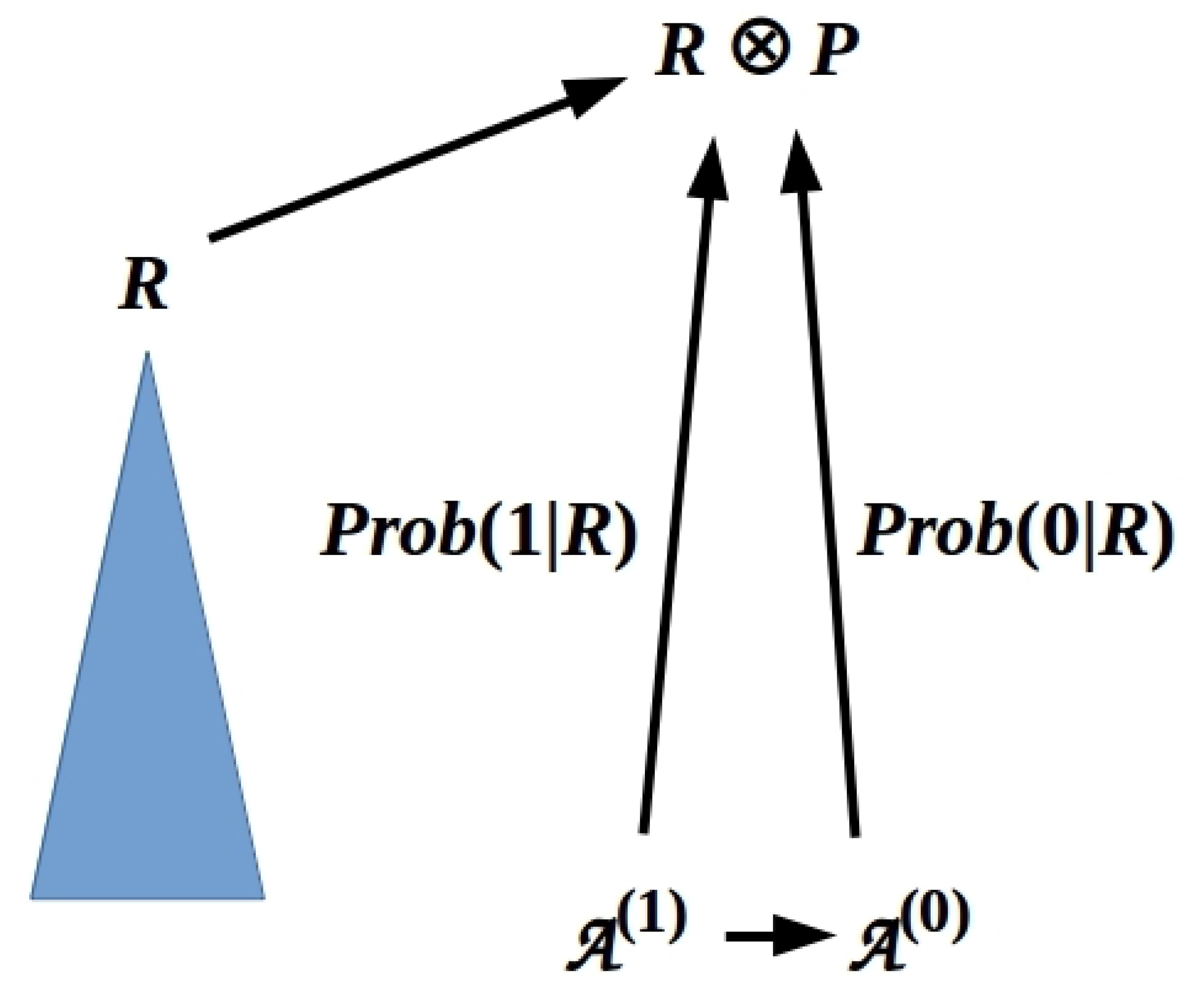
3.3. Measuring the Pointer State of an Identified System S
3.4. Sequential Measurements Induce Decoherence
3.5. Entanglement Swapping Induces Contextuality
3.6. CCD Commutativity Enforces Bayesian Coherence
- that only the shortest paths between objects in a diagram (such as a CCD) are labeled, and that the probability of a such a path is the product of the probabilities of its component arrows; and
- that the probabilities of all paths sum to unity.
4. Thermodynamic Asymmetries and Their Effects
4.1. Information Processing Demands Are Asymmetrical between R, P and E
4.2. Thermodynamic Interactions with E Generically Disturb
5. Discussion
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EPR | Einstein–Podolsky–Rosen |
| IGUS | Information Gathering and Using System |
| CCD | Cocone Diagram |
| CCCD | Cone–Cocone Diagram |
| CbD | Contextuality by Default |
References
- Landsman, N.P. Between classical and quantum. In Handbook of the Philosophy of Science: Philosophy of Physics; Butterfield, J., Earman, J., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 417–553. [Google Scholar]
- Schlosshauer, M. Decoherence and the Quantum to Classical Transition; Springer: Berlin, Germany, 2007. [Google Scholar]
- Bohr, N. The quantum postulate and the recent development of atomic theory. Nature 1928, 121, 580–590. [Google Scholar] [CrossRef]
- Fröwis, F.; Sekatski, P.; Dür, W.; Gisin, N.; Sangouard, N. Macroscopic quantum states: Measures, fragility, and implementations. Rev. Mod. Phys. 2018, 90, 025004. [Google Scholar] [CrossRef]
- Schrödinger, E. The present situation in quantum mechanics. Naturwissenschaften 1980, 23, 807–812. (In German) (English translation by Trimmer, J. D. Proc. Am. Phil. Soc. 1980, 124, 323–328) [Google Scholar] [CrossRef]
- Wigner, E.P. Remarks on the mind-body question. In The Scientist Speculates; Good, I.J., Ed.; Heinemann: London, UK, 1961; pp. 284–302. [Google Scholar]
- Mermin, D. Hidden variables and the two theorems of John Bell. Rev. Mod. Phys. 1993, 65, 803–815. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection and the existential interpretation (the rough guide). Philos. Trans. R. Soc. A 1998, 356, 1793–1821. [Google Scholar] [CrossRef]
- Zurek, W.H. Decoherence, einselection, and the quantum origins of the classical. Rev. Mod. Phys. 2003, 75, 715–775. [Google Scholar] [CrossRef]
- Schlosshauer, M. Quantum decoherence. Phys. Rep. 2019, 831, 1–57. [Google Scholar] [CrossRef]
- Ollivier, H.; Poulin, D.; Zurek, W.H. Environment as a witness: Selective proliferation of information and emergence of objectivity in a quantum universe. Phys. Rev. A 2005, 72, 042113. [Google Scholar] [CrossRef]
- Chiribella, G.; D’Ariano, G.M. Quantum information becomes classical when distributed to many users. Phys. Rev. Lett. 2006, 97, 250503. [Google Scholar] [CrossRef]
- Zurek, W.H. Quantum Darwinism. Nat. Phys. 2009, 5, 181–188. [Google Scholar] [CrossRef]
- Korbicz, J.K.; Horodecki, P.; Horodecki, R. Objectivity in a noisy photonic environment through quantum state information broadcasting. Phys. Rev. Lett. 2014, 112, 120402. [Google Scholar] [CrossRef] [PubMed]
- Fields, C. Quantum Darwinism requires an extra-theoretical assumption of encoding redundancy. Int. J. Theor. Phys. 2010, 49, 2523–2527. [Google Scholar] [CrossRef]
- Kastner, R.E. ‘Einselection’ of pointer observables: The new H-theorem? Stud. Hist. Phil. Mod. Phys. 2014, 48, 56–58. [Google Scholar] [CrossRef]
- Fields, C. Some consequences of the thermodynamic cost of system identification. Entropy 2018, 20, 797. [Google Scholar] [CrossRef]
- Ghirardi, G.C.; Rimini, A.; Weber, T. Unified dynamics for microscopic and macroscopic systems. Phys. Rev. D 1986, 34, 470–491. [Google Scholar] [CrossRef]
- Penrose, R. On gravity’s role in quantum state reduction. Gen. Relativ. Gravit. 1996, 28, 581–600. [Google Scholar] [CrossRef]
- Weinberg, S. Collapse of the state vector. Phys. Rev. A 2012, 85, 062116. [Google Scholar] [CrossRef]
- Wheeler, J.A. Law without law. In Quantum Theory and Measurement; Wheeler, J.A., Zurek, W.H., Eds.; Princeton University Press: Princeton, NJ, USA, 1983; pp. 182–213. [Google Scholar]
- Emary, C.; Lambert, N.; Nori, F. Leggett-Garg inequalities. Rep. Prog. Phys. 2013, 77, 016001. [Google Scholar] [CrossRef]
- Kochen, S.; Specker, E.P. The problem of hidden variables in quantum mechanics. J. Math. Mech. 1967, 17, 59–87. [Google Scholar] [CrossRef]
- Landauer, R. Irreversibility and heat generation in the computing process. IBM J. Res. Dev. 1961, 5, 183–195. [Google Scholar] [CrossRef]
- Barwise, J.; Seligman, J. Information Flow: The Logic of Distributed Systems; Cambridge Tracts in Theoretical Computer Science 44; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Fields, C.; Glazebrook, J.F. A mosaic of Chu spaces and Channel Theory I: Category-theoretic concepts and tools. J. Expt. Theor. Artif. intell. 2019, 31, 177–213. [Google Scholar] [CrossRef]
- Fields, C. Decoherence as a sequence of entanglement swaps. Results Phys. 2019, 12, 1888–1892. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Kujala, J.V.; Cervantes, V.H. Contextuality-by-default: A brief overview of concepts and terminology. In Lecture Notes in Computer Science 9525; Atmanspacher, H., Filik, T., Pothos, E., Eds.; Springer: Heidelberg, Germany, 2016; pp. 12–23. [Google Scholar]
- Dzhafarov, E.N.; Kujala, J.V. Contextuality-by-Default 2.0: Systems with binary random variables. In Lecture Notes in Computer Science 10106; Barros, J.A., Coecke, B., Pothos, E., Eds.; Springer: Berlin, Germany, 2017; pp. 16–32. [Google Scholar]
- Dzharfarov, E.N.; Kon, M. On universality of classical probability with contextually labeled random variables. J. Math. Psych. 2018, 85, 17–24. [Google Scholar] [CrossRef]
- Bartlett, S.D.; Rudolph, T.; Spekkens, R.W. Reference frames, superselection rules, and quantum information. Rev. Mod. Phys. 2007, 79, 555–609. [Google Scholar] [CrossRef]
- Gell-Mann, M.; Hartle, J.B. Quantum mechanics in the light of quantum cosmology. In Foundations of Quantum Mechanics in the Light of New Technology; Nakajima, S., Murayama, Y., Tonomura, A., Eds.; World Scientific: Singapore, 1997; pp. 347–369. [Google Scholar]
- Fields, C.; Marcianò, A. Sharing nonfungible information requires shared nonfungible information. Quant. Rep. 2019, 1, 252–259. [Google Scholar] [CrossRef]
- Zanardi, P. Virtual quantum subsystems. Phys. Rev. Lett. 2001, 87, 077901. [Google Scholar] [CrossRef]
- Zanardi, P.; Lidar, D.A.; Lloyd, S. Quantum tensor product structures are observable-induced. Phys. Rev. Lett. 2004, 92, 060402. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić, J. What is “system”: Some decoherence-theory arguments. Int. J. Theor. Phys. 2006, 45, 2215–2225. [Google Scholar] [CrossRef]
- Dugić, M.; Jeknić, J. What is “system”: The information-theoretic arguments. Int. J. Theor. Phys. 2008, 47, 805–813. [Google Scholar] [CrossRef]
- Fuchs, C.A.; Schack, R. Quantum-bayesian coherence. Rev. Mod. Phys. 2013, 85, 1693–1715. [Google Scholar] [CrossRef]
- Leifer, M.S.; Spekkens, R.W. Towards a formulation of quantum theory as a causally neutral theory of Bayesian inference. Phys. Rev. A 2013, 88, 052130. [Google Scholar] [CrossRef]
- Fields, C. If physics is an information science, what is an observer? Information 2012, 3, 92–123. [Google Scholar] [CrossRef]
- Mueller, M.P. Law without law: From observer states to physics via algorithmic information theory. arXiv 2019, arXiv:1712.01826v4. [Google Scholar]
- Realpe-Gómez, J. Modeling observers as physical systems representing the world from within: Quantum theory as a physical and self-referential theory of inference. arXiv 2019, arXiv:1705.04307v4. [Google Scholar]
- Smith, J.E.; Nair, R. The architecture of virtual machines. IEEE Comput. 2005, 38, 32–38. [Google Scholar] [CrossRef]
- Nielsen, M.A.; Chuang, I.L. Quantum Computation and Quantum Information; Cambridge University Press: New York, NY, USA, 2000. [Google Scholar]
- Fields, C.; Glazebrook, J.F. A mosaic of Chu spaces and Channel Theory II: Applications to object identification and mereological complexity. J. Expt. Theor. Artif. Intell. 2019, 31, 237–265. [Google Scholar] [CrossRef]
- Roederer, J. Information and Its Role in Nature; Springer: Berlin, Germany, 2005. [Google Scholar]
- Weinstein, A. Groupoids: Unifying internal and external symmetry. Notices AMS 1996, 43, 744–752. [Google Scholar]
- Brown, R. Topology and Groupoids; Ronald Brown: Deganwy, UK, 2006. [Google Scholar]
- Cervantes, V.H.; Dzhafarov, E.N. Snow Queen is evil and beautiful: Experimental evidence for probabilistic contextuality in human choices. Decision 2018, 5, 193–204. [Google Scholar] [CrossRef]
- Dzhafarov, E.N.; Zhang, R.; Kujala, J. Is there contextuality in behavioural and social systems? Philos. Trans. R. Soc. A 2016, 374, 20150099. [Google Scholar] [CrossRef]
- De Finetti, B. Theory of Probability, Vol. I; Wiley: New York, NY, USA, 1974. [Google Scholar]
- Allwein, G.; Moskowitz, I.S.; Chang, L.-W. A New Framework for Shannon Information Theory; Technical Report A801024; Naval Research Laboratory: Washington, DC, USA, 2004.
- Seligman, J. Channels: From logic to probability. In Formal Theories of Information; Sommaruga, G., Ed.; Lecture Notes in Computer Science, 5363; Springer: Berlin, Geramny, 2009; pp. 193–233. [Google Scholar]
- Adams, E.W. A Primer of Probabilistic Logic; University of Chicago Press: Chicago, IL, USA, 1998. [Google Scholar]
- Nielsen, M.A.; Chuang, I.L. Quantum Information and Quantum Computation; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Tegmark, M. How unitary cosmology generalizes thermodynamics and solves the inflationary entropy problem. Phys. Rev. D 2012, 85, 123517. [Google Scholar] [CrossRef]
- Pegg, D.; Barnett, S.; Jeffers, J. Quantum theory of preparation and measurement. J. Mod. Opt. 2002, 49, 913–924. [Google Scholar] [CrossRef]
- Walter, M.; Gross, D.; Eisert, J. Multi-partite entanglement. In Lectures on Quantum Information; Bruss, D., Leuchs, D., Eds.; Wiley-VCH: Weinheimm, Germany, 2006. [Google Scholar]
- Arkani-Hamed, N.; Trnka, J. The amplituhedron. J. High Energy Phys. 2014, 10, 030. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fields, C.; Glazebrook, J.F. Representing Measurement as a Thermodynamic Symmetry Breaking. Symmetry 2020, 12, 810. https://doi.org/10.3390/sym12050810
Fields C, Glazebrook JF. Representing Measurement as a Thermodynamic Symmetry Breaking. Symmetry. 2020; 12(5):810. https://doi.org/10.3390/sym12050810
Chicago/Turabian StyleFields, Chris, and James F. Glazebrook. 2020. "Representing Measurement as a Thermodynamic Symmetry Breaking" Symmetry 12, no. 5: 810. https://doi.org/10.3390/sym12050810
APA StyleFields, C., & Glazebrook, J. F. (2020). Representing Measurement as a Thermodynamic Symmetry Breaking. Symmetry, 12(5), 810. https://doi.org/10.3390/sym12050810




