Abstract
This study mainly concerns with the examination of heat transfer rate, mass and motile micro-organisms for convective second grade nanofluid flow. The considered model comprises of both nanoparticles as well as gyrotactic micro-organisms. Microorganisms stabilize the suspension of nanoparticles by bio-convective flow which is generated by the combined effects of nanoparticles and buoyancy forces. The Brownian motion and thermophoretic mechanisms along with Newtonian heating are also considered. Appropriately modified transformations are invoked to get a non-linear system of differential equations. The resulting problems are solved using a numerical scheme. Velocity field, thermal and solute distributions and motile micro-organism density are discussed graphically. Wall-drag (skin-friction) coefficient, Nusselt, Sherwood and motile micro-organisms are numerically examined for various parameters. The outcomes indicate that for a larger Rayleigh number, the bio-convection restricts the upward movement of nanoparticles that are involved in nanofluid for the given buoyancy effect. Furthermore, larger buoyancy is instigated which certainly opposes the fluid flow and affects the concentration. For a larger values of fluid parameter, the fluid viscosity faces a decline and certainly less restriction is faced by the fluid. In both assisting and opposing cases, we notice a certain rise in fluid motion. Thermal layer receives enhancement for larger values of Brownian diffusion parameter. The random motion for stronger Brownian impact suddenly raises which improves the heat convection and consequently thermal distribution receives enhancement. Thermal distribution receives enhancement for a larger Lewis number whereas the decline is noticed in concentration distribution. The larger Rayleigh number results in a strong buoyancy force that effectively increases the fluid temperature. This also increases the concentration difference, thus more nanoparticles transport between surface and micro-organisms. Furthermore, for larger (Nb), the thermal state of fluid receives enhancement while a decline in motile density is observed. Numerical results show that mass flux is an enhancing function of both the (Le) and (Nb).
1. Introduction
Bio convection is a fluid dynamic mechanism that occurs in the movement of micro-organisms. In this type of motion, the micro-organisms are way denser than water and swim upwardly. Gyrotactic micro-organisms like algae, which swim upward tend to penetrate the upper part of the fluid layer and as a result the most upper layer of fluid becomes denser than the layer below, thus causing unstable density stratification. Although nanofluid bio-convection narrates the density stratification and spontaneous pattern formation generated by the simultaneously interactive nanoparticles, denser micro-organisms are self-propelled and the buoyancy is affected. These micro-organisms sufficiently include the gravitaxis, gyrotaxis or other oxytaxis type organisms. In a study, Wang and Fan [1] discussed the involvement of four scales including the typical molecular level, the macroscale, the microscale, and the larger/mega scale in nanofluid flow. Bio-convection is a macroscale phenomenon wherein the motion of so-called motile micro-organisms introduces a macroscopic movement (convection) in the fluid. Despite motile micro-organisms, the nano-particles are generally not self-impelled, and their movement is solely due to the Brownian diffusion as well as thermophoresis that take place within the nanofluid. In contrast, the up-swimming of motile micro-organisms is mainly a reaction of an external force field including gravitaxis or geotaxis, biochemical inducement such as increasing or decreasing concentration of oxygen (chemotaxis), response to light (phototaxis) either towards the source of light ( positive photo taxis ) or away from it ( negative phototaxis ) and torques in a flow (gyro taxis). Addition of motile micro-organisms to the suspensions made a significant contribution to the convective bio-microsystems (for instance, biotechnology and enzyme biosensors) such that an enhancement can be achieved in mass transport microfluidic instruments and devices like bacteria-powered micromixers, particularly in micro volumes. This improves the instability of nanofluids. Recently, Kuznetsov [2] examined the onset of bio-convection because of nanofluid particles containing micro-organisms (gyrotactic). He [3] also observed the nanofluid bio-thermal convection containing gyrotactic and oxytocic micro-organisms simultaneously. In a study, Aziz et al. [4] disclosed the free movement nanofluid through motile micro-organisms over a horizontal flat plate. Mixed convection flow of a nanofluid containing the so-called gyrotactic micro level organisms towards a rigid sphere was assumed to be embedded in a permeable/porous medium as discussed by Tham et al. [5]. Xu and Pop [6] analyzed the fully grown mixed-convective flow of nanofluid in a plane (horizontal) channel which comprises gyrotactic micro-organisms and nanoparticles. Khan et al. [7] reported a free convective flow of non-Newtonian fluid assumed to be embedded in a porous/permeable cavity containing the typical gyrotactic type micro-organisms together with nanoparticles. Mutuku and Makinde [8] observed the hydro magnetic bio-convective type of nanofluid bounded by a permeable/porous plate and saturated with gyrotactic micro-organisms. Akbar [9] investigated the bio-convection peristaltic convection of nanofluid in a given asymmetric channel saturated with gyrotactic micro-organisms. Mabood et al. [10] reported a free convective flow of non-Newtonian-type nanofluids (see for example [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26] to understand the term non-Newtonian nanofluids) in permeable medium saturated with gyrotactic-type micro-organisms.
It has been pointed out by Merkin [27] that in wall temperature towards the ambient temperature, we encounter four common heating procedures; namely, (i) constant temperature (at surface) (ii) constant heat flux (at surface) (iii) conjugate conditions (at boundary) and (iv) Newtonian heating. In particular, Newtonian heating involves the rate of heat transfer within the range of finite heat capacity from a bounding surface. This attribute is proportional to the local temperature (at surface). This is also termed as conjugate convective flow. Newtonian heating is widely utilized by various researchers and scientists due to its practical and physical applications i.e., conjugate heat flux around fins and design heating exchanger, as well as in convection flows where due to solar radiation the bounding surfaces absorb heat. Recently, Hayat et al. [28] analyzed the boundary layer convection in a Walters-B fluid subject to Newtonian heating. Awais et al. [29] disclosed the features of thermal diffusivity and Newtonian heating in a given axis-symmetrical Jeffrey liquid flow bounded by a stretching flat/surface. Farooq et al. [30] analyzed the MHD convective flow of Jeffrey fluid with Newtonian heating. Ramzan et al. [31] examined the 3-dimensional convection of an Oldroyd-B-type fluid over a stretching sheet with Newtonian heating. The characteristics and influences of Newtonian heating in stagnation flow and free stream velocity of a Burgers fluid is reported by Hayat et al. [32].
The properties of nanofluids especially low resistivity and effective thermophysical characteristics are very much important in research. To maintain, sustain and develop technological products such as laptop, computers, power electronics, high-powered rays and motor engines are highly effective in various industrial procedures. For the said reason, nanofluids have promisingly increased the productivity and outcomes of the industry. Prior to their properties and the dilution of nanoparticles in base fluids, the suspension becomes highly effective in the presence of micro-organisms especially gyrotactic-type organisms. These features have received attention by the research community especially of those working in the field of bio-convection, bio-technology, bio-microsystems and bio-medical devices. Many industrial procedures involve convection based on motile density and bio-convection. Some recent studies include Kuznetsov and Avramenko [33] who used tiny-sized solid nanoparticles for the stability of dilution and motile density via fluid layers in lieu of pharmaceutical applications. Geng and Kuznetsov [34] reported the impact of small nanoparticles on the development of bio-convection due to plums. Another important study reported by Kuznetsov et al. [35] disclosed the features of nanoparticles and their impact on bio-convective flow induced by gyrotactic micro-organisms. Moreover, Uddin et al. [36] disclosed the importance and application of such fluids in nano-biofuel and bio-convection flow. Kuznetsov [37] used motile gyrotactic micro-organisms to enhance the mass flux, microscale mixing and stability of the nanofluid.
The prime objective here is to interpret the consequent influence of buoyancy and chemical reaction on heat flux, mass and motile micro-organism flux, for the convective flow of grade-II nanofluids saturated with both tiny nanoparticles and tiny gyrotactic-type micro-organisms. The heat (thermal state) transfer rate, mass and motile micro-organisms for convective second grade nanofluid flow are examined. The considered model comprises both the tiny nanoparticles along with tiny gyrotactic micro-organisms. Micro-organisms stabilize the suspension of nanoparticles by bio-convective flow which is generated via the combined effects of nanoparticles and buoyancy forces. The Brownian motion and thermophoretic mechanisms along with Newtonian heating are also considered. Appropriately modified transformations are invoked to get a non-linear system of non-linear differential equations. The resulting system is treated using numerical schemes. Velocity field, thermal and solute distributions and motile micro-organism density are discussed graphically. Wall-drag (skin-friction) parameter, Nusselt, Sherwood and motile micro-organisms are numerically examined for various parameters.
2. Mathematical Modeling
The considered model comprises both nanoparticles along with gyrotactic micro-organisms. Microorganisms stabilize the suspension of nanoparticles by bio-convective flow which is generated by the combined simultaneous effects of nanoparticles and buoyancy. The Brownian type diffusion and thermophoretic mechanisms along with Newtonian heating are also considered. Without introduction of the external factor, the in-stability creates the agglomeration of nanoparticles on the basis of highly inconsistent thermal conductivity although the concentration of the nanoparticles might be as low as possible. Using some experimental methodologies, one can prepare a nanoparticle suspension that may remain stable for weeks. The imposition of micro-organisms into the nanofluid is solely required to stabilize the tiny nanoparticles because of the phenomenon best known as bio-convection. It is further assumed that the nanoparticles carry no effect in the way of swimming as well as the velocity of micro-organisms. Furthermore, in order to refrain from the instability of bio-convection, there is a reasonably appropriate assumption that nanoparticle dilution (suspension) is prepared with very small amounts (i.e., ≤1%), otherwise, the higher amount of concentration distribution of nanoparticles leads to the highly effective saturation (suspension) viscosity that ultimately results in suppression of the given bio-convective flow. Geometry of the problem can be seen in Figure 1.
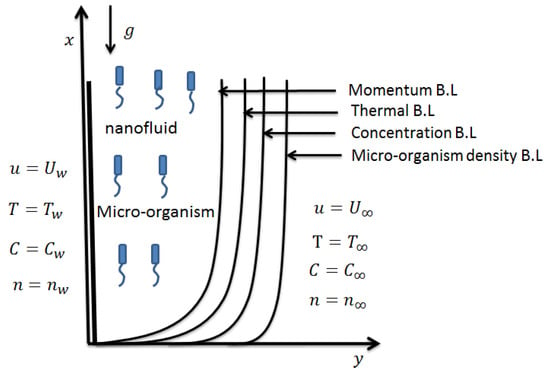
Figure 1.
Geometry of the problem.
Following Waqas et al. [38], the governing equations are,
The suitable boundary conditions are prescribed in the form
Here, represents the horizontal fluid movement component and is the vertical fluid movement component, is the given density of nanofluid, is the given nanoparticles density, is the given micro-organisms density, is a given ratio (of the given heat capacity of nanoparticles versus the given heat capacity of the given nanofluid), is the given viscosity nanofluid to micro-organisms, the symbol is the given thermal diffusivity, is used for the given kinematic viscosity, is the given grade-II fluid parameter, is the given volume expansion fluid coefficient, g is the symbol used for gravity, is the given micro-organisms volume, is used for the given heat (specific), b a constant and is used for the given maximum swimming velocity, is given thermophoresis (diffusion), is symbol used for the given Brownian diffusion, is the given diffusivity for micro-organisms, C is used as symbol of the given concentration distribution, is used for the given wall concentration (of nanoparticles), n is the given motile density, T is the given temperature, is fixed for the given stretching rate (velocity), is used as the given suction velocity, is given heat transport (coefficient), is the given mass transport (coefficient), is used for the given heat transfer rate, is used for ambient temperature, is used for ambient concentration and is used for ambient concentration of micro-organisms. is used for chemical reaction. Define,
Now incompressibility condition is trivially satisfied while the Equations (2)–(6) become
Here denotes the dimensionless second grade fluid parameter, the mixed convection parameter, the buoyancy influence parameter, is used as bioconvection Rayleigh number, the Brownian motion, the thermophoresis diffusion parameter, Lewis number is given by , the bioconvection Lewis number, the bioconvection Pecelt number, the Prandtl number and A the dimensionless suction/injection parameter. These quantities are defined as follows:
The Skin friction coefficient (at surface), Nusselt number (at surface), Sherwood number (at surface) and local density number of the motile micro-organisms are
Such that,
where is the given local Reynolds number.
3. Methodology
The system of governing equations given in (8)–(12) and Equations (17)–(19) are solved numerically for various graphical outputs and numerical data for wall-drag and other relevant flux rates. The mathematical-based RK45 scheme is used with the help of the shooting technique to obtain initial values first from the given non-linear boundary value problems and to solve them numerically. A critical choice of initial guesses is mandatory in these numerical simulations such that the initial conditions must satisfy the solutions. The iterations have been performed repeatedly to get the final convergent result. An upper limit of difference upto is fixed as a general criteria of convergence. The results are efficient as compared to analytical methods. The specified values assigned to the given parameters are typically selected on the basis of the above convergence criteria. Each iteration is performed on the basis of a new assigned parameter value.
4. Analysis
In this section, we have arranged the effective impact of various non-dimensional parameters on the flow velocity, thermal and solute distributions, density of motile gyrotactic micro-organisms and other physical quantities such as wall-drag, heat and mass flux rates etc. The important parameters are Rayleigh number , the buoyancy force factor , fluid parameter , Brownian diffusion factor , Thermophoresis represented by , Lewis number represented by , Pecelt number in the context of bio-convection, Lewis number in the perspective of bio-convection given by , Mixed convection given by are very important for the present model. Figure 2, Figure 3, Figure 4 and Figure 5 are managed to discuss the impact of important fluid parameters on flow velocity/horizontal movement. In particular Figure 2 portrays the combined impact of Rayleigh factor and buoyancy number on fluid velocity. The dashed lines represent the impact of Rayleigh number whereas the solid lines are given for buoyancy force. Physically, for larger Rayleigh numbers, the bio-convection restricts the upward movement of nanoparticles that are involved in a nanofluid for the given buoyancy effect. Furthermore, larger buoyancy is instigated which certainly opposes the fluid flow and affects the concentration. Thus, a sufficient decline in flow movement is noticed for both the parameters. The influence of grade-II fluid parameter is quite obvious on flow movement. Physically, there exists an inverse relation in the fluid parameter and fluid viscosity. For larger values of fluid parameter, the fluid viscosity faces a decline and certainly less restriction is faced by the fluid. As a result, fluid velocity increases as shown in Figure 3. In the context of mixed convection, the mixed convection parameter is responsible for the variations noticed in the velocity field. This phenomenon is discussed in lieu of (a) assisting and (b) opposing flows. In both assisting and opposing cases (Figure 4 and Figure 5), we notice a certain rise in fluid motion. Physically, we see the relation of buoyancy force with inertial force. Both are inversely proportional to each other. In mixed convection, both these factors are directly affected. Clearly, the dominance of buoyancy force over inertial force enhances the fluid flow for augmented values of the mixed convection parameter.
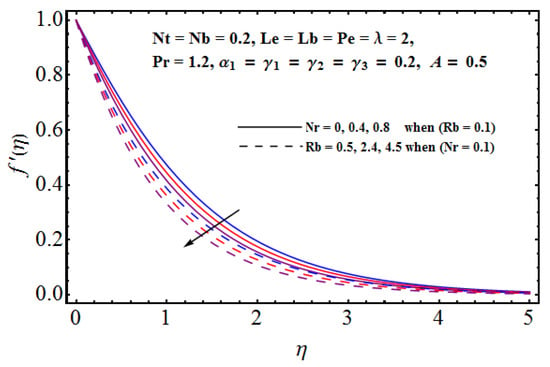
Figure 2.
Effect of and on .
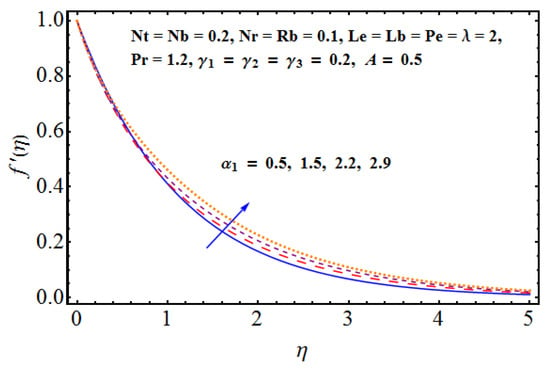
Figure 3.
Effect of on .
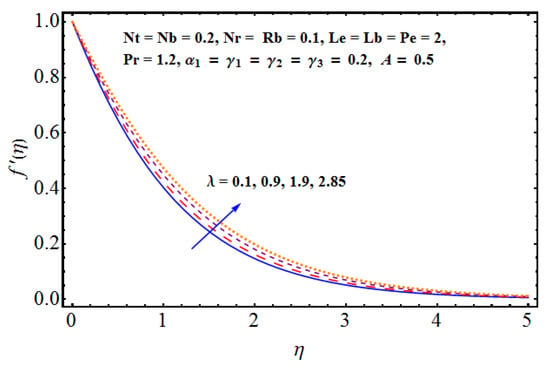
Figure 4.
Effect of (assisting flow) on .
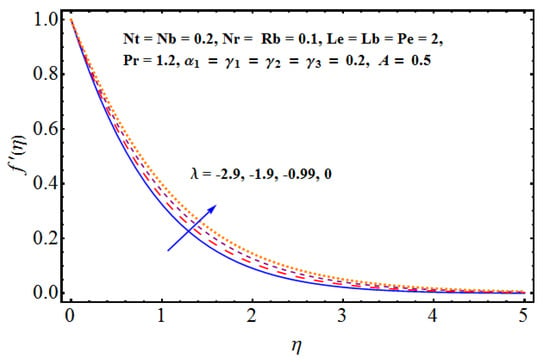
Figure 5.
Effect of (opposing flow) on .
Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 are prepared on the basis of numerical data achieved in lieu of the various parameters and their impact on thermal and solute distributions. In particular, the combined impact of Brownian motion factors on thermal and solute distributions can be seen in Figure 6. Solid lines are related to thermal distribution, whereas dashed lines are linked to solute distribution. The thermal layer receives enhancement for larger values of Brownian diffusion parameters. Physically, we notice that the random motion for a stronger Brownian impact suddenly rises, which abruptly enhances the heat production and consequently, thermal distribution receives enhancement. On the other hand, the away movement and diffusion results in certain decline in concentration of the nanoparticles and solute profile declines. Figure 7 shows the combined effect of thermophoresis on thermal and solute distributions. An assistance is offered by the thermophoresis parameter for both the thermal and solute/nanoparticles diffusion. Physically, for positive and intensive thermophoresis, the plate is cold enough and subsequently, the nanoparticles are transported from hot to colder regions which augments nanoparticle concentration. The impact of both Lewis numbers is given on both the thermal and solute distributions in Figure 8. Thermal distribution receives enhancement whereas the decline is noticed in concentration distribution. Physically, the inverse relation between Brownian diffusion and Lewis factor is responsible for these variations. Figure 9 gives the impact of Rayleigh number on both the thermal and solute distributions. Both the profiles receive enhancement for a larger Rayleigh number in lieu of bio-convection. Physically, the larger Rayleigh number results in strong buoyancy force that effectively increases the fluid temperature. This also increases the concentration difference, thus, more nanoparticles are transported between surface and micro-organisms. Thus, the concentration profile increases. Figure 10 and Figure 11 are given in the context of impact of buoyancy on thermal and solute distributions. For stronger buoyancy, the volumetric fraction of nanoparticles increases and, consequently, we notice an enhancement in both the thermal and solute distributions.
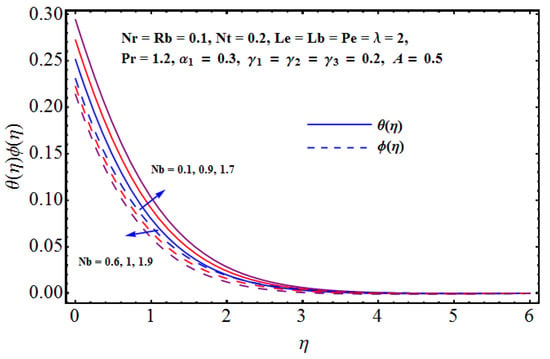
Figure 6.
Effect of on and .
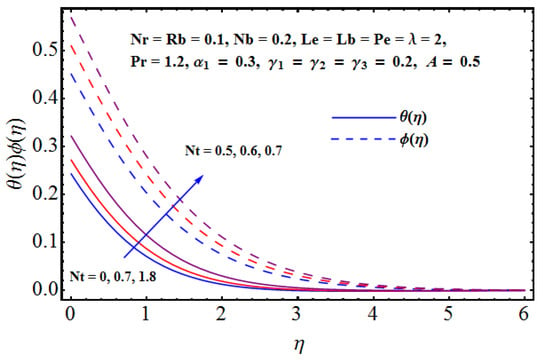
Figure 7.
Effect of on and .
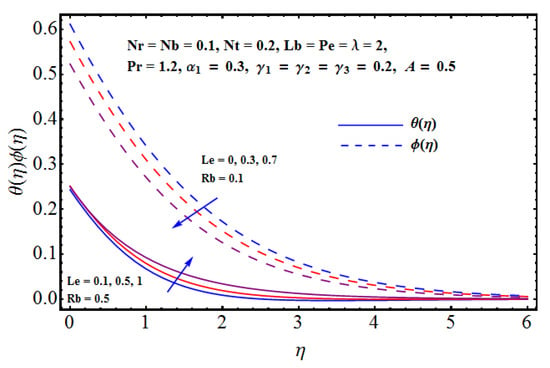
Figure 8.
Effect of and on and .
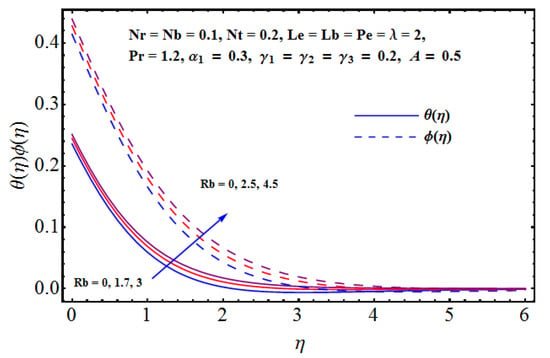
Figure 9.
Effect of on and .
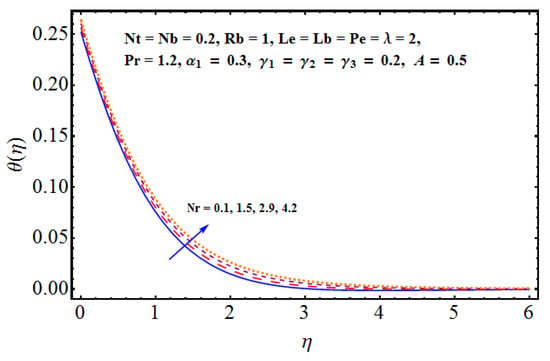
Figure 10.
Effect of on .
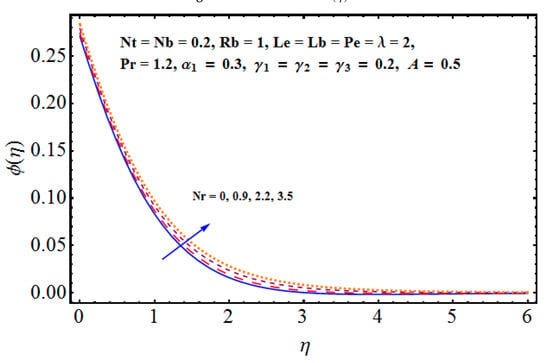
Figure 11.
Effect of on .
Figure 12 pointed out the impact of buoyancy force parameter and Rayleigh number in lieu of bioconvection on the motile density profile. Physically, the larger buoyancy force parameter augments the solute buoyancy force and, therefore, the density increases. Further greater values of ) increase the buoyancy force because of the bio-convection process. This fact gives rise to the density of fluid. Influence of Brownian diffusion and intensive thermophoretic force given by on density (motile) profile are given in Figure 13. It is noticed that larger leads to more random movements of fluid particles. Ultimately, the thermal state of fluid receives enhancement while a decline in motile density is observed. On the other hand, the motile density profile increases for larger . In fact, higher and intensive thermophoresis leads larger micro-organisms to jump away from the heated region to the colder region. As a result motile density increases. Characteristics of Lewis number in lieu of bioconvection and Pecelt number are sketched in Figure 14. Motile density profile declines with the enhanced and . Physically, the higher values of and decrease the diffusivity of micro-organisms and, hence, motile density of micro-organisms decreases. Influences of the Brownian diffusion parameter () and the given Lewis number () on Sherwood (mass flux) number are displayed in Figure 15 and Figure 16. These Figures show that the Sherwood number is an enhancing function of () and (). Figure 17 and Figure 18 predict the effects of Pecelt number () and bioconvective Lewis number () on local density number of motile tiny(micro) organisms. Here, motile density increases for the higher values of () and (). Interesting results are given in contour graphs in Figure 19 and Figure 20.
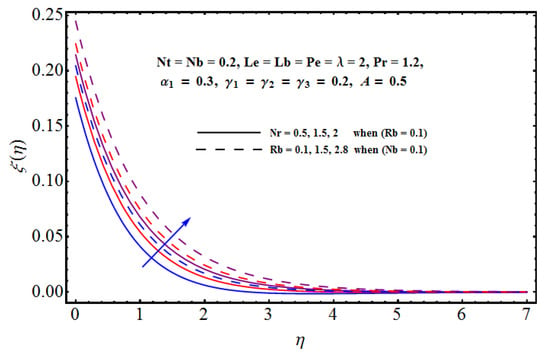
Figure 12.
Effect of and on .
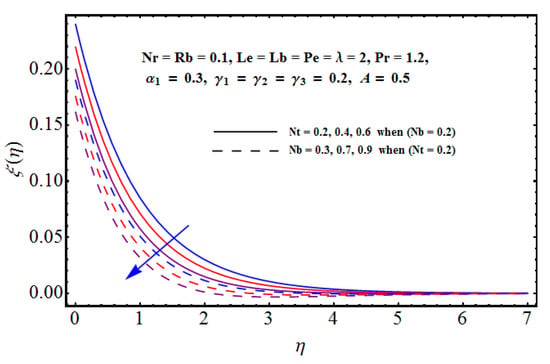
Figure 13.
Effect of and on .
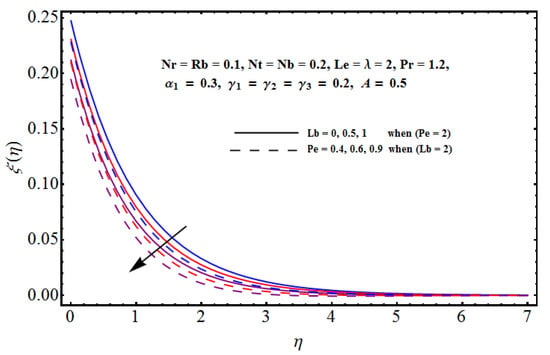
Figure 14.
Effect of and on .
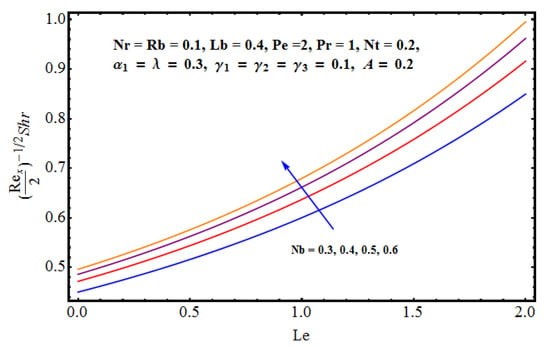
Figure 15.
Effect of on Sherwood number.
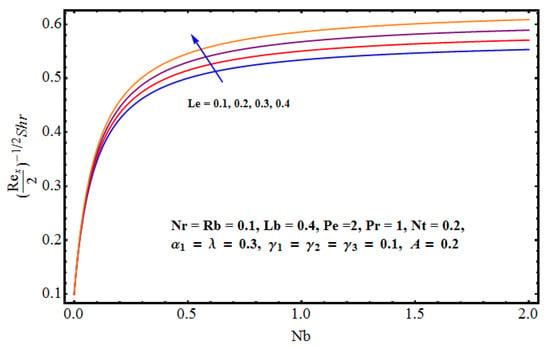
Figure 16.
Effect of on Sherwood number.
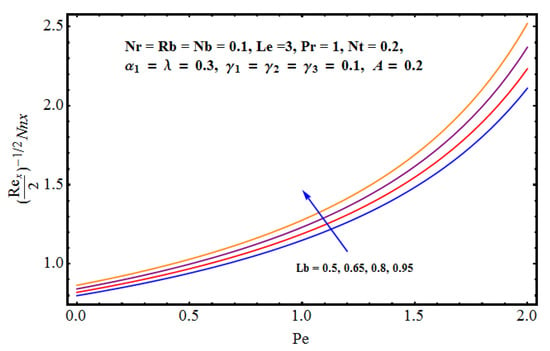
Figure 17.
Effect of on motile density.
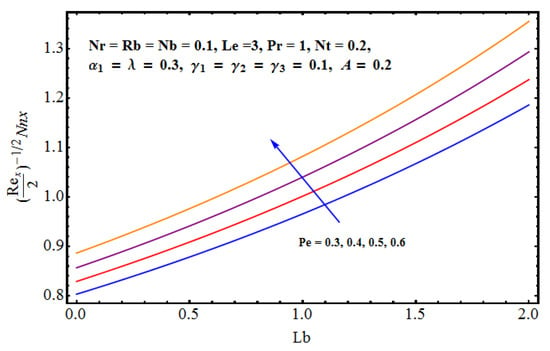
Figure 18.
Effect of on motile density.
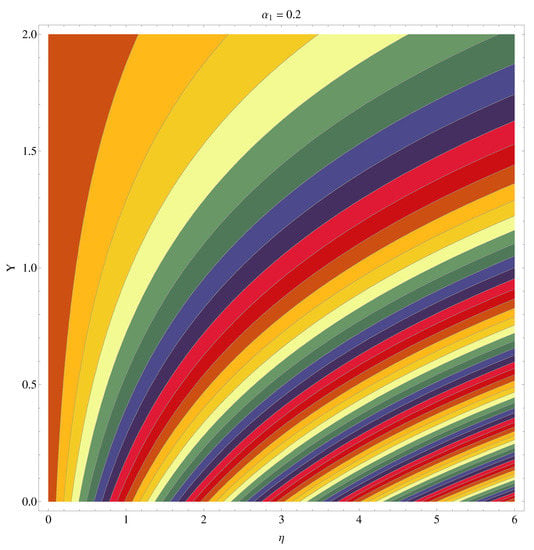
Figure 19.
Contour graph at .
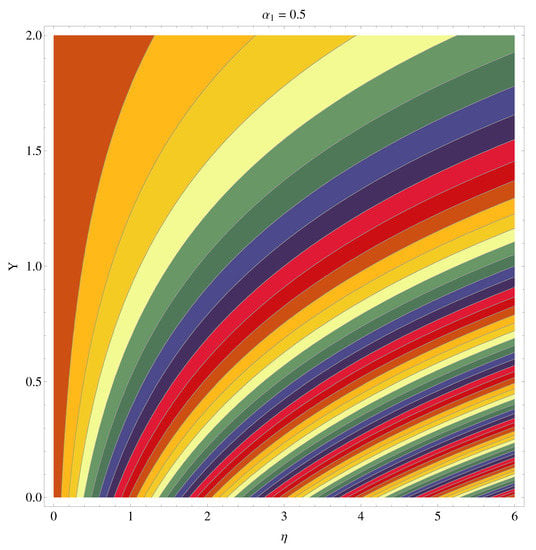
Figure 20.
Contour graph at .
Table 1 is prepared on the basis of numerical outcomes obtained for skin-friction for various fluid parameters. Table 2 is given on the basis of data obtained for Nusselt number. One can see that the given values of parameters are varied one by one while keeping all the other parameters fixed at one value. The table remains unfilled for those parameters whose values are not repeated for the specific iteration(s). The results fully support the formulation and previous literature.

Table 1.
Numerical outcomes of skin friction coefficient for different values of parameters when

Table 2.
Numerical outcomes of Nusselt number for different values of parameters when
5. Conclusions
Here, we have analyzed the consequences of buoyancy and chemical reaction on heat flux, mass and motile micro-organism flux for the convective flow of grade second nanofluid saturated with both the tiny nanoparticles and gyrotactic micro-organisms. The heat transfer rate, mass and motile micro-organisms for convective second grade nanofluid flow is examined. The considered model comprises of both nanoparticles alongwith gyrotactic micro-organisms. Micro-organisms stabilize the suspension of nanoparticles by bio-convective flow which is generated by the combined effects of nanoparticles and buoyancy forces. The Brownian motion and thermophoretic mechanisms along with Newtonian heating are also considered. Appropriately modified transformations are invoked to get a non-linear system of differential problems. The resulting system is dealt with using a numerical technique. The salient features are listed below:
- For larger Rayleigh numbers, the bio-convection restricts the upward movement of nanoparticles that are involved in nanofluids for the given buoyancy effect. Furthermore, larger buoyancy is instigated which certainly opposes the fluid flow and affects the concentration. Thus, a sufficient decline in flow movement is noticed for both parameters.
- The influence of grade-II fluid parameter is quite obvious on flow movement. There is an inverse relation in fluid parameter and fluid viscosity. For larger values of fluid parameters, the fluid viscosity faces a decline and certainly less restriction is faced by the fluid. As a result, fluid velocity increases.
- The mixed convection parameter is responsible for the variations noticed in the velocity field. This phenomenon is discussed in lieu of (a) assisting and (b) opposing flows. In both assisting and opposing cases, we notice a certain rise in fluid motion.
- The thermal layer receives enhancement for larger values of Brownian diffusion parameters. The random motion for stronger Brownian impact suddenly rises which abruptly enhances the heat production and consequently thermal distribution receives enhancement.
- An assistance is offered by the thermophoresis parameter for both the thermal and solute/nanoparticles diffusion. For positive and intensive thermophoresis, the plate is cold enough and, subsequently, the nanoparticles are transported from hot to colder regions which augments nanoparticle concentration.
- Thermal distribution receives enhancement, whereas the decline is noticed in concentration distribution. Physically, the inverse relation between Brownian diffusion and Lewis factor is responsible for these variations.
- The larger buoyancy force parameter augments the solute buoyancy force, therefore, the density increases. Further greater values of ) increase the buoyancy force because of the bio-convection process. This fact gives rise to the density of fluid.
- The motile density profile increases for larger for higher and intensive thermophoresis
- The motile density profile declines with the enhanced and . Higher values of and decrease the diffusivity of micro-organisms and, hence, the motile density of micro-organisms decreases.
Author Contributions
A.S.: Conceptualization, Software, validation. G.R.: Software, Conceptualization, Validation. C.M.K.: Mathodology, concept. S.A.: Formal Analysis, Funding, Review and Revision. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
Authors are highly obliged and thankful to the unanimous reviewers for their time and valuable suggestions. This has really helped us in shaping the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, L.; Fan, J. Nanofluids Research: Key Issue. Nanoscale Res. Lett. 2010, 5, 1241–1252. [Google Scholar] [CrossRef] [PubMed]
- Kuznetsov, A.V. The onset of nanofluid bioconvection in a suspension containing both nanoparticles and gyrotactic micro-organisms. Int. Commun. Heat Mass Trans. 2010, 37, 1421–1425. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluid bio-thermal convection: Simultaneous effects of gyrotactic and oxytactic micro-organisms. Fluid Dyn. Res. 2011, 43, 055505. [Google Scholar] [CrossRef]
- Aziz, A.; Khan, W.A.; Pop, I. Free convection boundary layer flow past a horizontal flat plate embedded in porous medium filled by nanofluid containing gyrotactic micro-organisms. Int. J. Therm. Sci. 2012, 56, 48–57. [Google Scholar] [CrossRef]
- Tham, L.; Nazar, R.; Pop, I. Mixed convection flow over a solid sphere embedded in a porous medium filled by a nanofluid containing gyrotactic micro-organisms. Int. J. Heat Mass Transf. 2013, 62, 647–660. [Google Scholar] [CrossRef]
- Xu, H.; Pop, I. Fully developed mixed convection flow in a horizontal channel filled by a nanofluid containing both nanoparticles and gyrotactic micro-organisms. Eur. J. Mech. B Fluids 2014, 46, 37–45. [Google Scholar] [CrossRef]
- Khan, W.A.; Uddin, M.J.; Ismail, A.I.M. Free convection of Non-Newtonian nanofluids in porous media with gyrotactic micro-organisms. Transp. Porous Med. 2013, 97, 241–252. [Google Scholar] [CrossRef]
- Mutuku, W.N.; Makinde, O.D. Hydromagnetic bioconvection of nanofluid over a permeable vertical plate due to gyrotactic micro-organisms. Comput. Fluids 2014, 95, 88–97. [Google Scholar] [CrossRef]
- Akbar, N.S. Bioconvection peristaltic flow in an asymmetric channel filled by nanofluid containing gyrotactic micro-organism: Bio nano engineering model. Int. J. Numer. Meth. Heat Fluid Flow 2015, 25, 214–224. [Google Scholar] [CrossRef]
- Mabood, F.; Khan, W.A.; Ismail, A.I.M. Analytical modelling of free convection of non-Newtonian nanofluids flow in porous media with gyrotactic micro-organisms using OHAM. AIP Conf. Proc. 2014, 1635, 131–137. [Google Scholar]
- Rasool, G.; Shafiq, A.; Khalique, C.M.; Zhang, T. Magnetohydrodynamic Darcy Forchheimer nanofluid flow over non-linear stretching sheet. Phys. Scr. 2019, 94, 105221. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T.; Shafiq, A. Second grade nanofluidic flow past a convectively heated vertical Riga plate. Phys. Scr. 2019, 94, 125212. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Raza, J.; Bakouri, M.; Tlili, I. Stability analysis of Darcy-Forchheimer flow of Casson type Nanofluid over an exponential sheet: Investigation of critical points. Symmetry 2019, 11, 412. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Darcy-Forchheimer nanofluidic flow manifested with Cattaneo-Christov theory of heat and mass flux over non-linearly stretching surface. PLoS ONE 2019, 14, e0221302. [Google Scholar] [CrossRef]
- Lund, L.A.; Omar, Z.; Khan, I.; Dero, S. Multiple solutions of Cu-C6 H9 NaO7 and Ag-C6 H9 NaO7 nanofluids flow over non-linear shrinking surface. J. Centr. South Univ. 2019, 26, 1283–1293. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Tlili, I. Marangoni convective nano-fluid flow over an electromagnetic actuator in the presence of first order chemical reaction. Heat Transf.-Asian Res. 2019, 49, 274–289. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Durur, H. Darcy-Forchheimer relation in Magnetohydrodynamic Jeffrey nanofluid flow over stretching surface. Discr. Contin. Dyn. Syst.-Ser. S 2019. accepted. [Google Scholar]
- Sohail, M.; Naz, R.; Abdelsalam, S.I. On the onset of entropy generation for a nanofluid with thermal radiation and gyrotactic micro-organisms through 3D flows. Phys. Scr. 2019. accepted. [Google Scholar]
- Shafiq, A.; Rasool, G.; Khalique, C.M. Significance of thermal slip and convective boundary conditions in three dimensional rotating Darcy-Forchheimer nanofluid flow. Symmetry 2020. accepted. [Google Scholar]
- Sohail, M.; Naz, R. Modified heat and mass transmission models in the magnetohydrodynamic flow of Sutterby nanofluid in stretching cylinder. Phys. A Stat. Mech. Its Appl. 2020, 124088. [Google Scholar] [CrossRef]
- Rasool, G.; Zhang, T. Characteristics of chemical reaction and convective boundary conditions in Powell-Eyring nanofluid flow along a radiative Riga plate. Heliyon 2019, 5, e01479. [Google Scholar] [CrossRef] [PubMed]
- Rasool, G.; Zhang, T.; Chamkha, A.J.; Shafiq, A.; Tlili, I.; Shahzadi, G. Entropy Generation and Consequences of Binary Chemical Reaction on MHD Darcy—Forchheimer Williamson Nanofluid Flow Over Non-Linearly Stretching Surface. Entropy 2020, 22, 18. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Ismael, M.; Kasaeipoor, A.; Armaghani, T. Entropy Generation and Natural Convection of CuO-Water Nanofluid in C-Shaped Cavity under Magnetic Field. Entropy 2016, 18, 50. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Khaled, A.-R.A. Similarity Solutions for Hydromagnetic Mixed Convection Heat and Mass Transfer for Hiemenz Flow Through Porous Media. Int. J. Numer. Methods Heat Fluid Flow 2000, 10, 94–115. [Google Scholar] [CrossRef]
- Rasool, G.; Shafiq, A.; Khan, I.; Baleanu, D.; Nisar, K.S.; Shahzadi, G. Entropy generation and consequences of MHD in Darcy-Forchheimer nanofluid flow bounded by non-linearly stretching surface. Symmetry 2020. accepted. [Google Scholar]
- Choi, S.U.S.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. ASME Publ.-Fed. 1995, 231, 99–106. [Google Scholar]
- Merkin, J.H. Natural convection boundary-layer flow on a vertical surface with Newtonian heating. Int. J. Heat Fluid Flow 1992, 15, 392–398. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiq, A.; Mustafa, M.; Alsaedi, A. Boundary-layer flow of Walters’B fluid with Newtonian heating. Zeitschrift für Naturforschung A 2015, 70, 333–341. [Google Scholar] [CrossRef]
- Awais, M.; Hayat, T.; Nawaz, M.; Alsaedi, A. Newtonian heating, thermal diffusion and duffsion thermo effects in an axisymmetric flow of Jeffrey fluid over a stretching surface. Braz. J. Chem. Eng. 2015, 32, 555–561. [Google Scholar] [CrossRef]
- Farooq, M.; Gull, N.; Alsaedi, A.; Hayat, T. MHD flow of a Jeffrey fluid with Newtonian heating. J. Mech. 2015, 31, 319–329. [Google Scholar] [CrossRef]
- Ramzan, M.; Farooq, M.; Alhothuali, M.S.; Malaikh, H.M.; Hayat, W.C.T. Three dimensional flow of an Oldroyd-B fluid with Newtonian Heating. Int. J. Numer. Meth. Heat Fluid Flow 2015, 25, 68–85. [Google Scholar] [CrossRef]
- Hayat, T.; Ali, S.; Awais, M.; Alhothuali, M.S. Newtonian heating in stagnation point flow of Burgers fluid. Appl. Math. Mech. 2015, 36, 61–68. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Avramenko, A.A. Effect of small particles on the stability of bioconvection in a suspension of gyrotactic micro-organisms in a layer of finite depth. Int. Commun. Heat Mass Transf. 2014, 31, 1–10. [Google Scholar] [CrossRef]
- Geng, P.; Kuznetsov, A.V. Effect of small solid particles on the development of bioconvection plumes. Int. Commun. Heat Mass Transf. 2004, 31, 629–638. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Geng, P. The interaction of bioconvection caused by gyrotactic micro-organisms and settling of small solid particles. Int. J. Numer. Methods Heat Fluid Flow 2005, 15, 328–347. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.A.; Qureshi, S.R.; Beg, O.A. Bioconvection nanofluid slip flow past a wavy surface with applications in nano-biofuel cells. Chin. J. Phys. 2017, 55, 2048–2063. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic micro-organisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 100. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.U.; Hassan, M.; Bhatti, M.M.; Imran, M. Analysis on the bioconvection flow of modified second-grade nanofluid containing gyrotactic micro-organisms and nanoparticles. J. Mol. Liq. 2019, 291, 111231. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).