Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction
Abstract
1. Introduction
2. Maximum Prediction Steps Based on Lyapunov Exponent
3. Fractional Levy Stable Motion
3.1. Parameter Meaning of Levy Stable Motion
3.2. Long-Range Dependence and Self-Similarity Fractional Levy Stable Motion
4. Iterative Forecasting Model Based on Fractional Levy Stable Motion
4.1. Iterative Forecasting Model
4.2. Parameter Estimation with the Characteristic Function
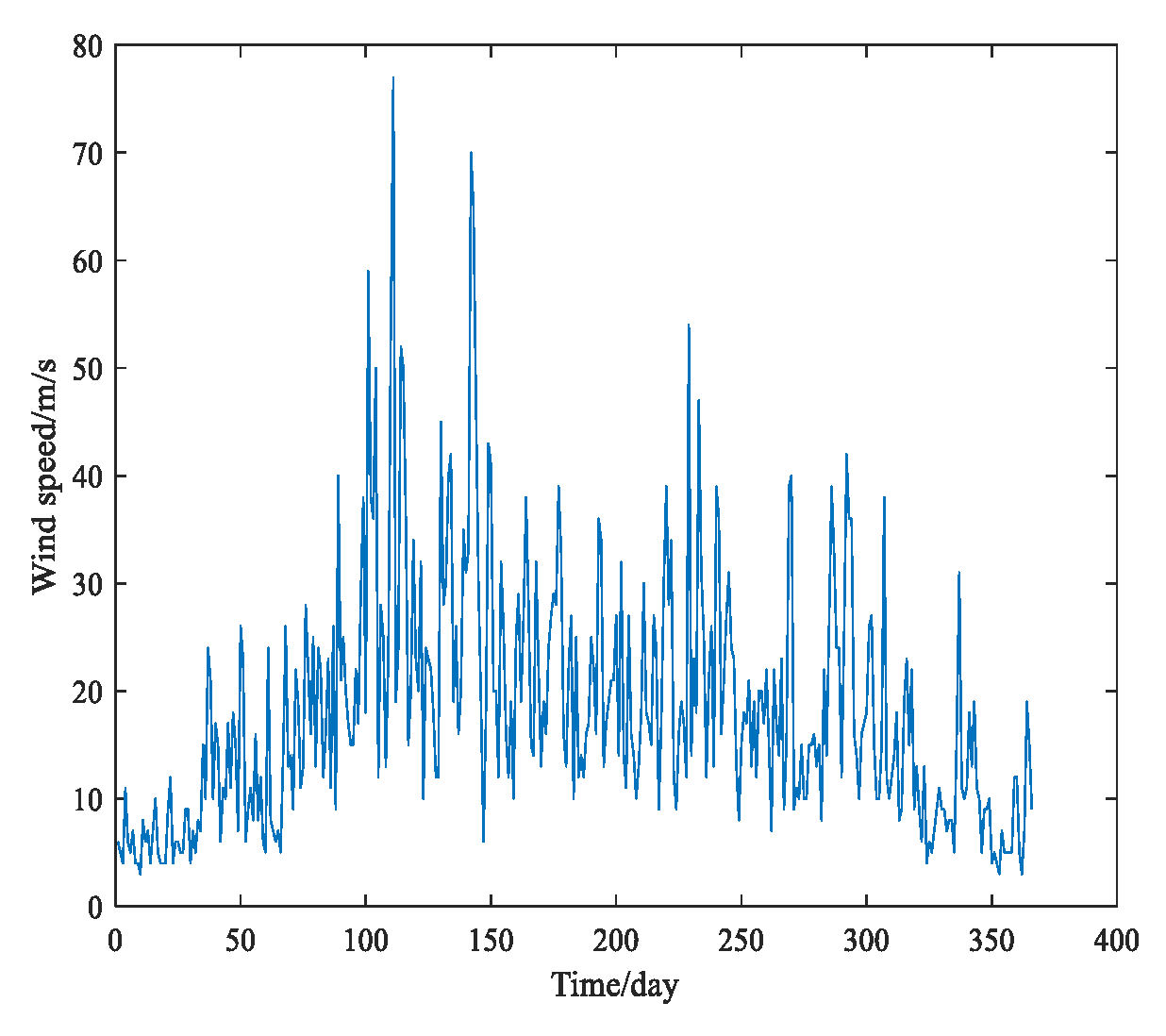
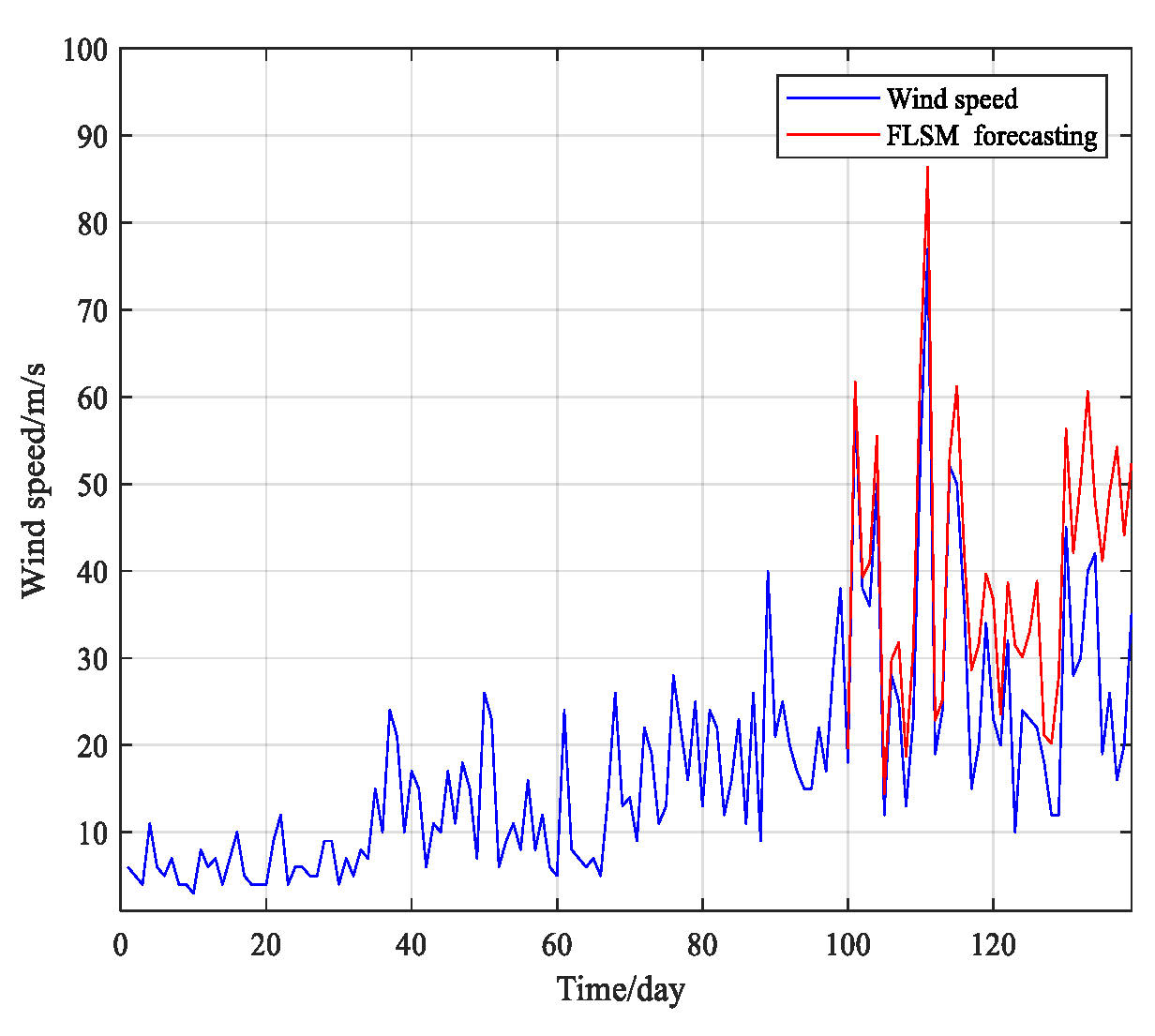
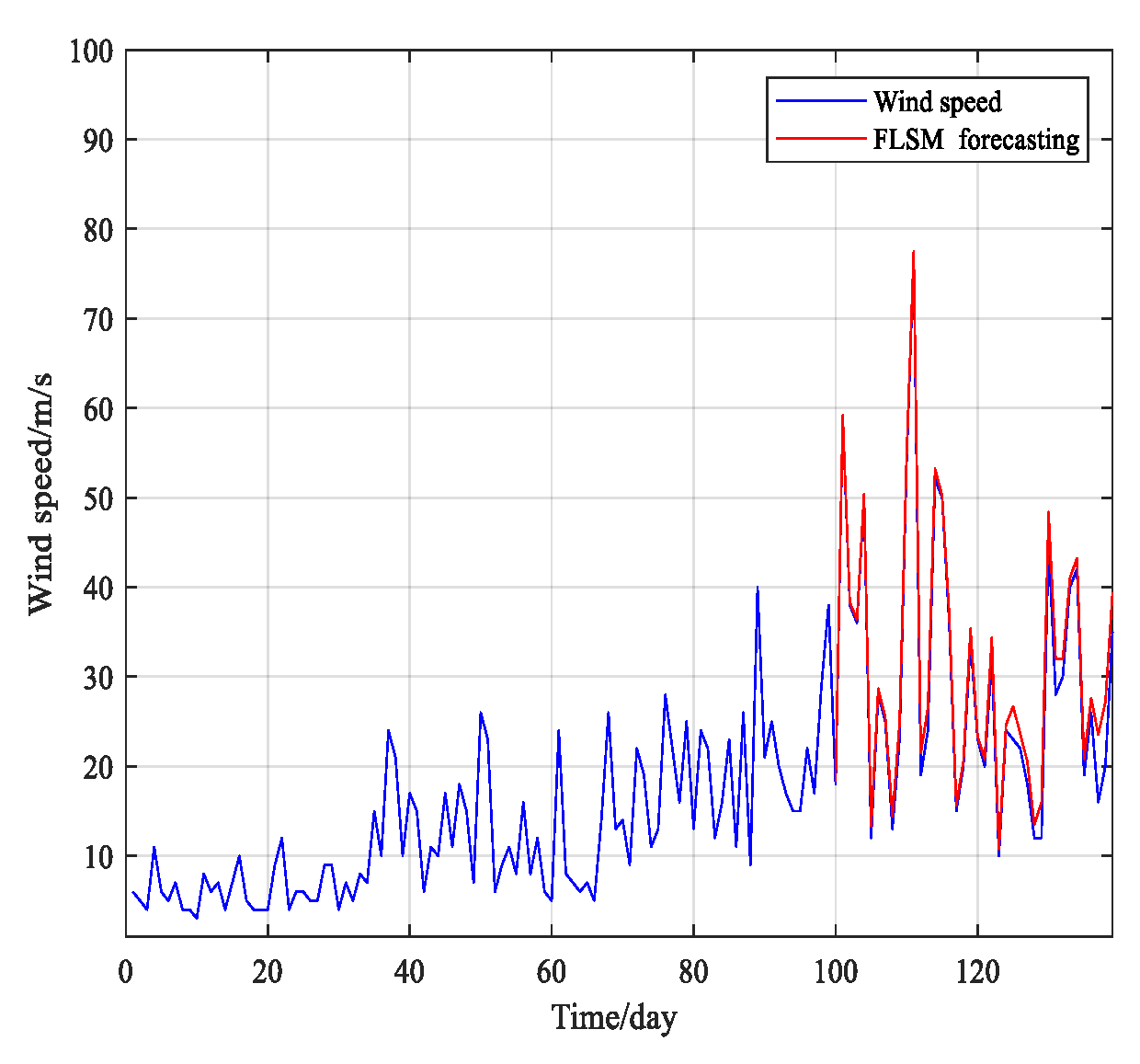
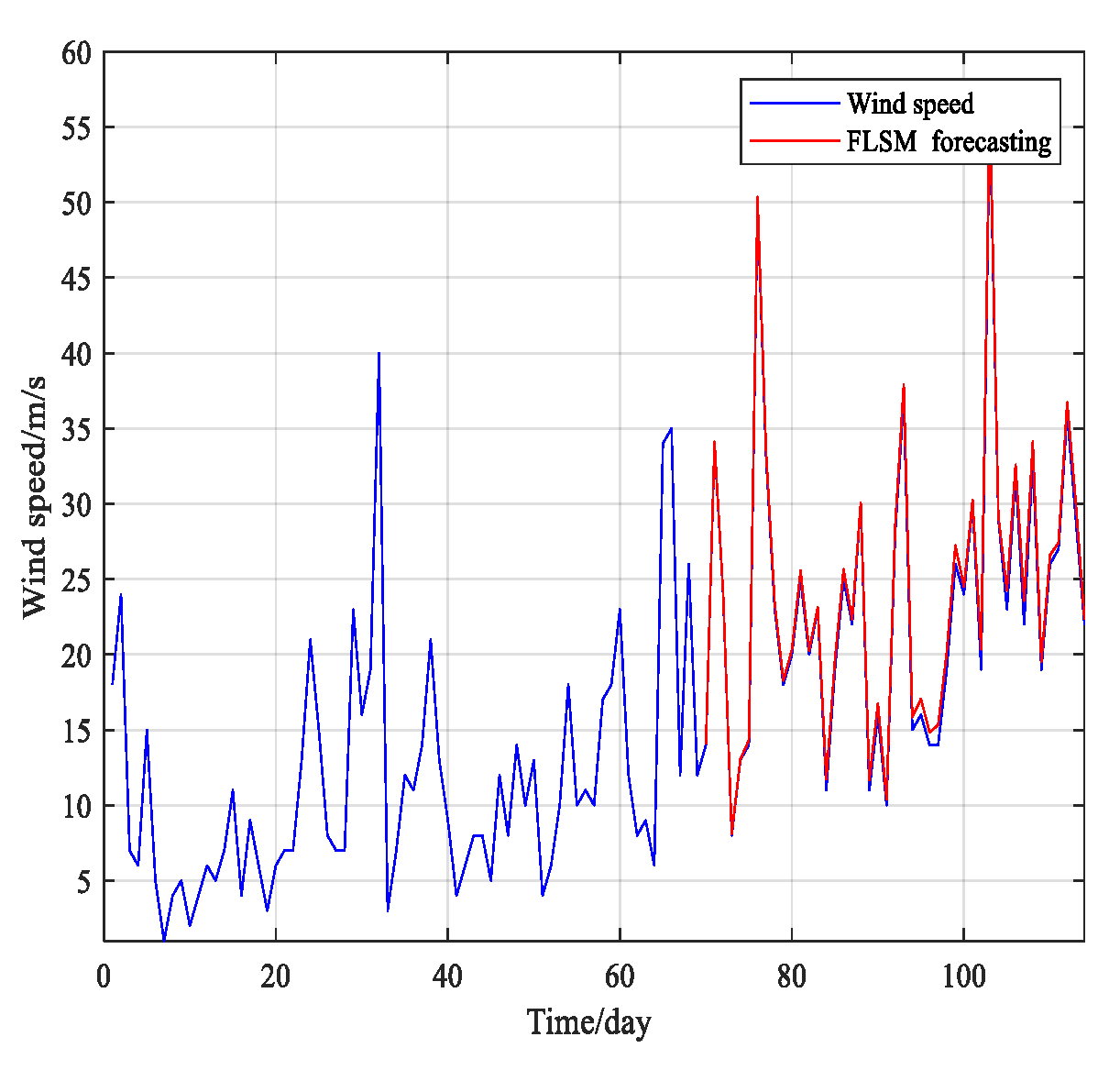
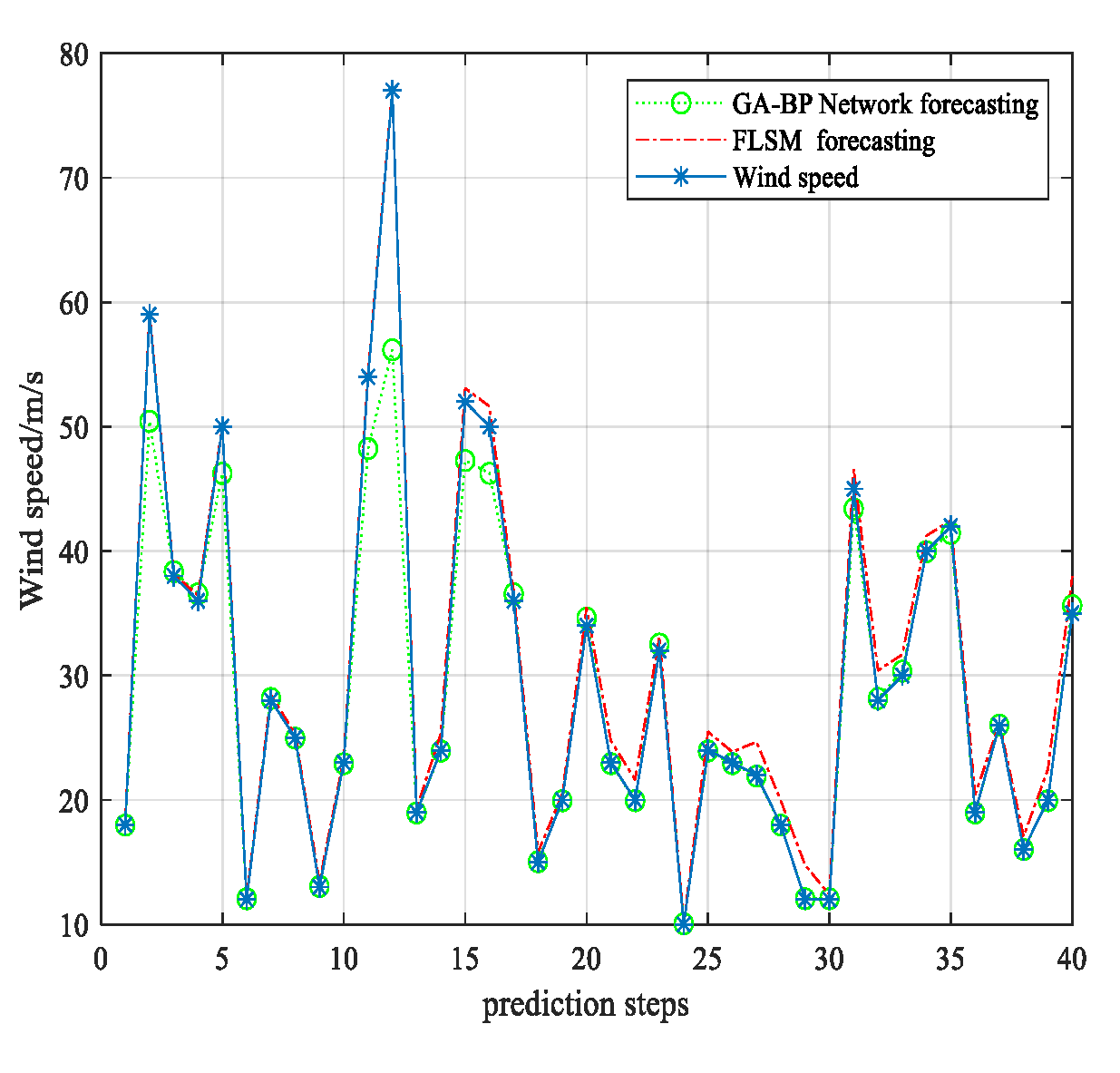
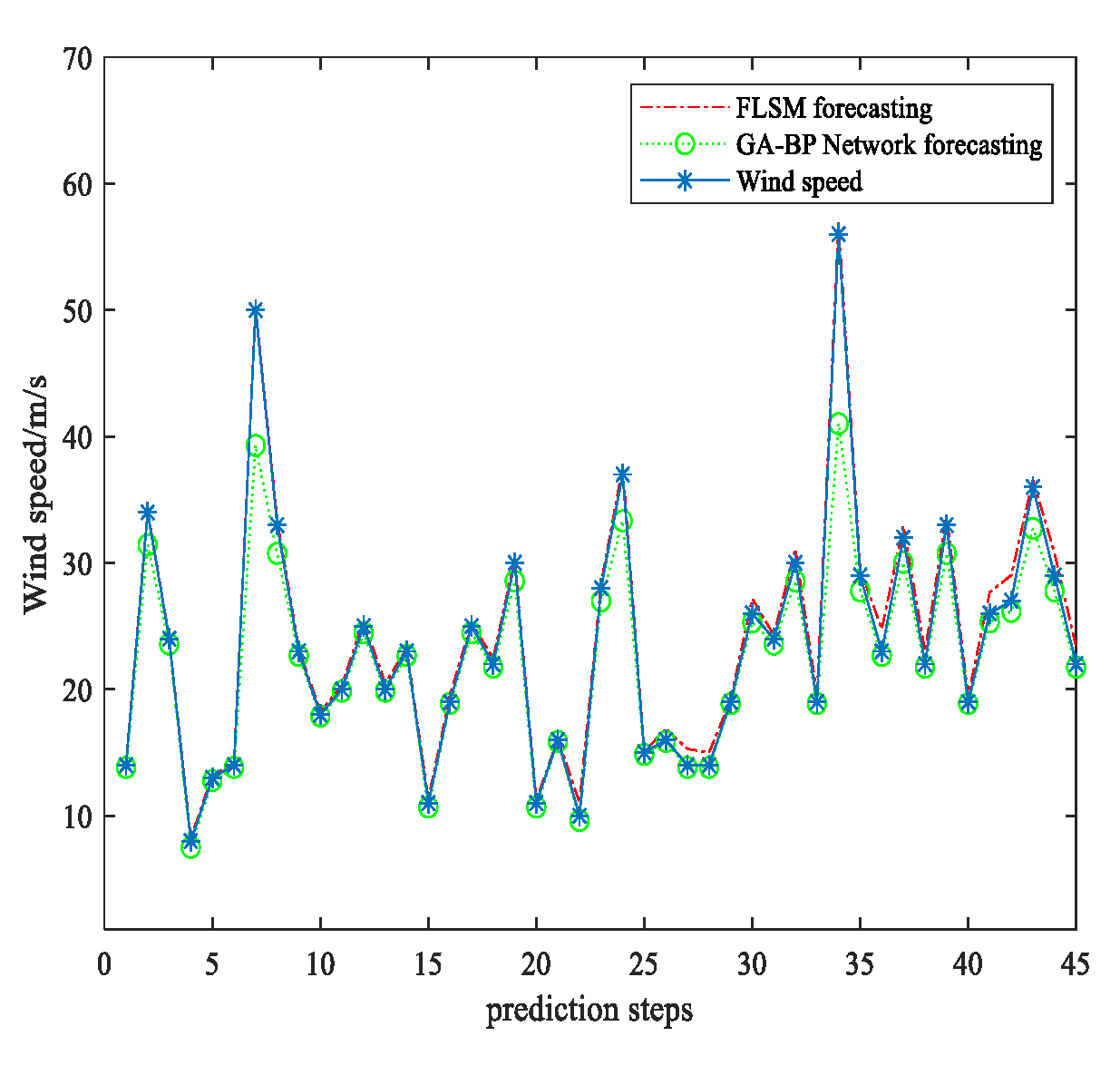
5. Wind Speed Forecasting
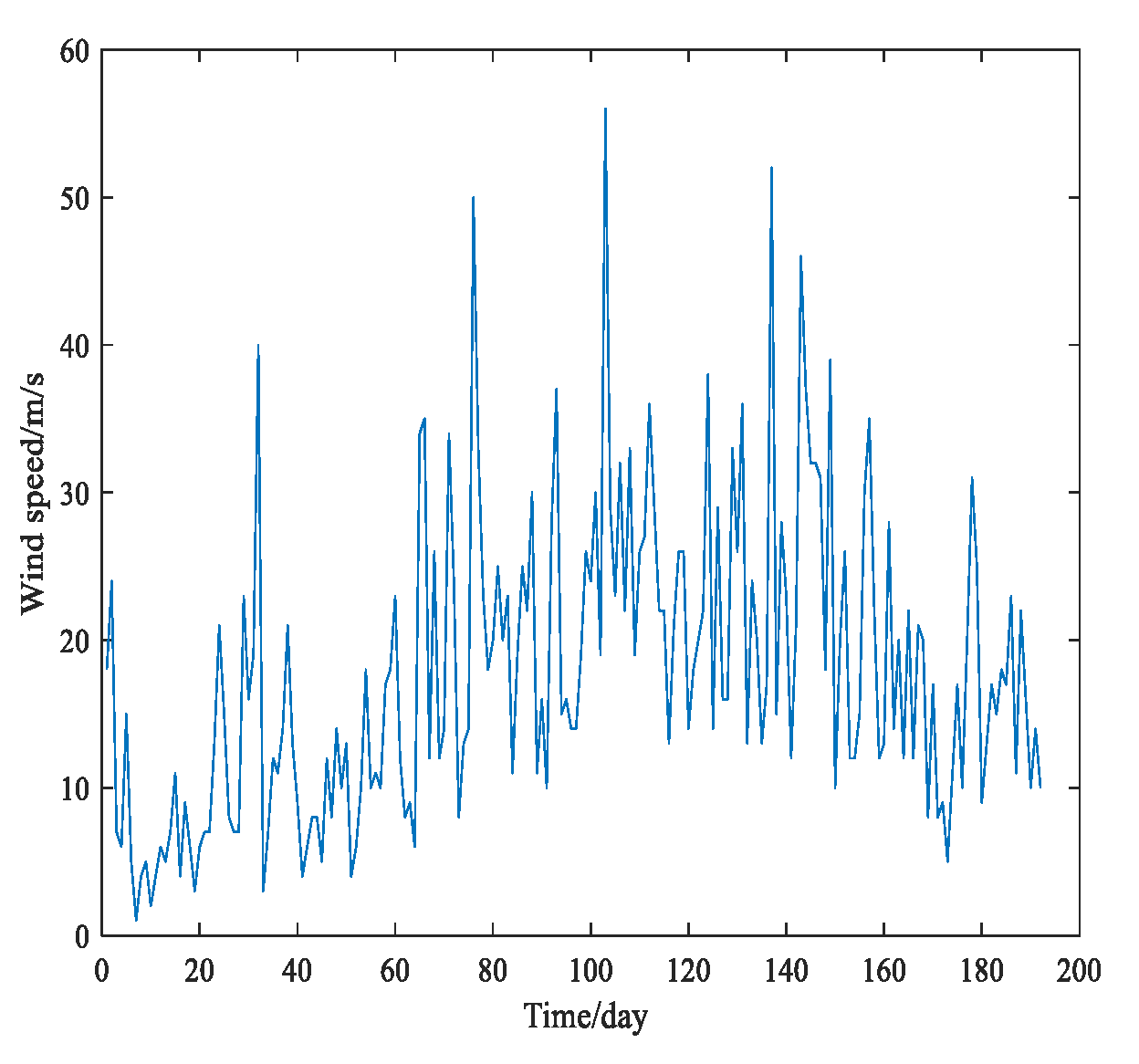
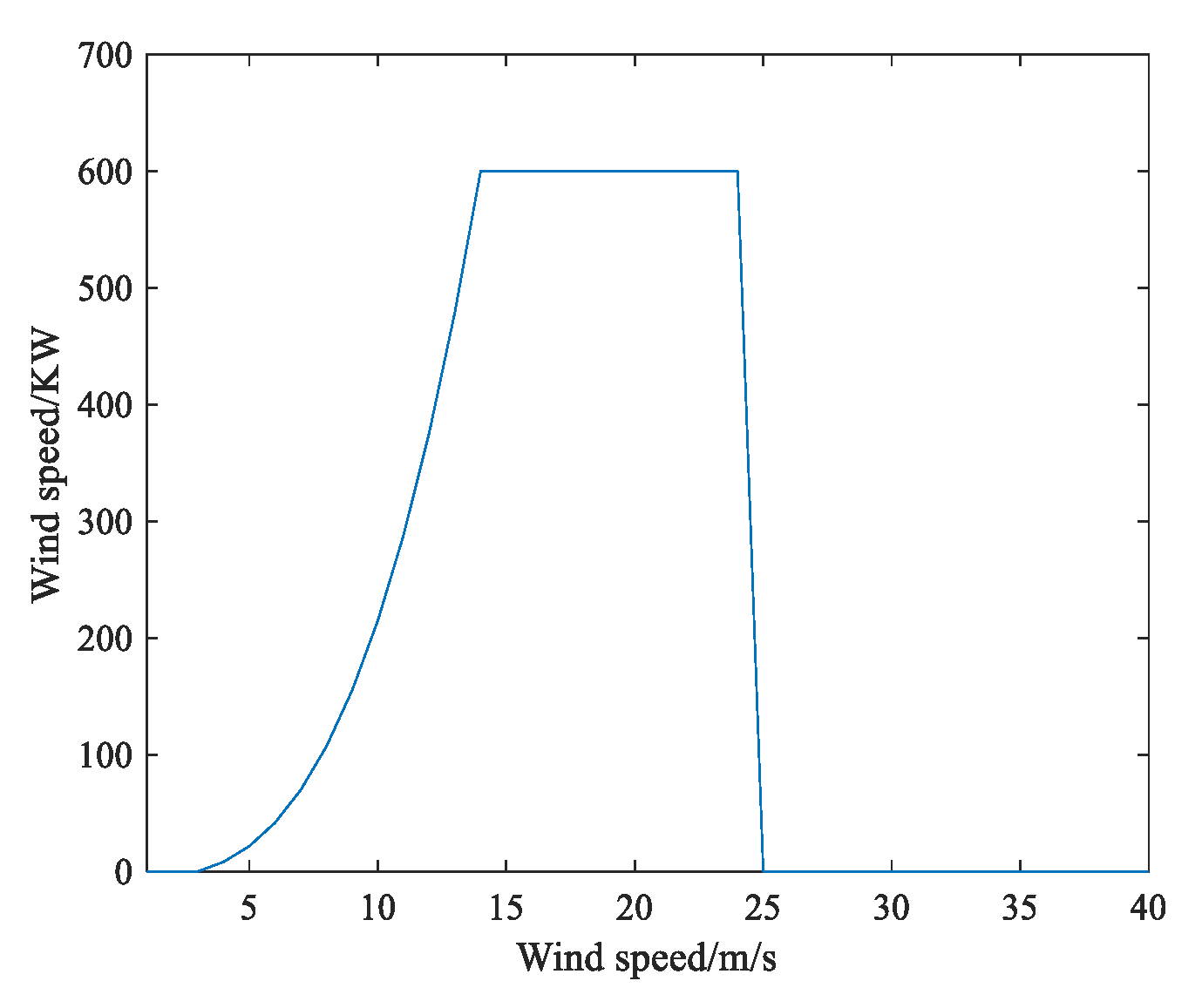
6. Relationship between Wind Speed and Wind Power
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lei, Y.Z.; Wang, W.S.; Yin, Y.H.; Dai, H.Z. Analysis of wind power value to power system operation. Power Syst. Technol. 2002, 5, 62–66. [Google Scholar]
- Shu-Yong, C.H.E.N.; Hui-Zhu, D.A.I.; Xiao-Min, B.A.I.; Xiao-Xin, Z.H.O.U. Reliability model of wind power plants and its application. Proc. -Chin. Soc. Electr. Eng. 2000, 20, 26–29. [Google Scholar]
- Ya-Zhou, L.; Wei-Sheng, W.; Yong-Hua, Y. An optimization method for determining wind power penetration limit in power system under static security constraints. Proc. -Chin. Soc. Electr. Eng. 2001, 21, 25–28. [Google Scholar]
- Lei, Y.Z.; Wang, W.S.; Yin, Y.H.; Dai, H.Z. Wind power penetration limit calculation based on chance constrained programming. Proc. CSEE 2002, 22, 32–35. [Google Scholar]
- Alexiadis, M.C.; Dokopoulos, P.S.; Sahsamanoglou, H.S.; Manousaridis, I.M. Short term forecasting of wind speed and related electrical power. Sol. Energy. 1998, 63, 61–68. [Google Scholar] [CrossRef]
- Bossanyi, E.A. Short-term wind prediction using Kalman filters. Wind Eng. 1985, 9, 1–8. [Google Scholar]
- Kamal, L.; Jafri, Y.Z. Time series models to simulate and forecast hourly averaged wind speed in Wuetta, Pakistan. Sol. Energy 1997, 61, 23–32. [Google Scholar] [CrossRef]
- Kariniotakis, G.N.; Stavrakakis, G.S.; Nogaret, E.F. Wind power forecasting using advanced neural network models. IEEE Trans Energy Convers. 1996, 11, 762–767. [Google Scholar] [CrossRef]
- Bayraktar, E.; Poor, H.V.; Rao, R. Prediction and tracking of long-range dependent sequences. Syst. Control Lett. 2005, 34, 1083–1090. [Google Scholar] [CrossRef]
- Gao, Y.; Villecco, F.; Li, M.; Song, W. Multi-Scale Permutation Entropy Based on Improved LMD and HMM for Rolling Bearing Diagnosis. Entropy 2017, 19, 176. [Google Scholar] [CrossRef]
- Song, W.; Cattani, C.; Chi, C.H. Multifractional Brownian Motion and Quantum-Behaved Particle Swarm Optimization for Short Term Power Load Forecasting: An Integrated Approach. Energy 2020, 194, 116847. [Google Scholar] [CrossRef]
- Wanqing, S.; Chen, X.; Cattani, C.; Zio, E. Multifractional Brownian Motion and Quantum-Behaved Partial Swarm Optimization for Bearing Degradation Forecasting. Complexity 2020. [Google Scholar] [CrossRef]
- Li, Y.; Song, W.; Wu, F.; Zio, E.; Zhang, Y. Spectral Kurtosis of Choi–Williams Distribution and Hidden Markov Model for Gearbox Fault Diagnosis. Symmetry 2020, 12, 285. [Google Scholar] [CrossRef]
- Li, M. Fractal Time Series—A Tutorial Review. Math. Probl. Eng. 2010. [Google Scholar] [CrossRef]
- Liu, H.; Song, W.; Li, M.; Kudreyko, A.; Zio, E. Fractional Lévy stable motion: Finite difference iterative Forecasting model. Chaos Solitons Fractals 2020, 133, 109632. [Google Scholar] [CrossRef]
- Rosenstein, M.T.; Collins, J.J.; De Luca, C.J. A practical method for calculating largest Lyapunov exponents from small data sets. Phys. D: Nonlinear Phenom. 1993, 65, 117–134. [Google Scholar] [CrossRef]
- Kim, H.; Eykholt, R.; Salas, J.D. Nonlinear dynamics, delay time and embedding windows. Phys. D: Nonlinear Phenom. 1999, 127, 48–60. [Google Scholar] [CrossRef]
- Tao, H.Y.C. Phase-space reconstruction technology of chaotic attractor based on c-c method. J. Electron. Meas. Instrum. 2012, 26, 425–430. [Google Scholar]
- Weron, A.; Burnecki, K.; Mercik, S.; Weron, K. Complete description of all self-similar models driven by Levy stable noise. Phys. Rev. E 2005. [Google Scholar] [CrossRef]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Jumarie, G. Merton’s model of optimal portfolio in a Black-Scholes market driven by a fractional Brownian motion with short-range dependence. Insur. Math. Econ. 2005, 37, 585–598. [Google Scholar] [CrossRef]
- Jumarie, G. On the representation of fractional Brownian motion as an integral with respect to (dt)a. Appl. Math. Lett. 2005, 18, 739–748. [Google Scholar] [CrossRef]
- Qin, Y.; Xiang, S.; Chai, Y.; Chen, H. Macroscopic-microscopic attention in LSTM networks based on fusion features for gear remaining life prediction. IEEE Trans. Ind. Electron. 2020. [Google Scholar] [CrossRef]
- Wang, X.; Li, K.; Gao, P.; Meng, S. Research on parameter estimation methods for alpha stable noise in a laser gyroscope’s random error. Sensors 2015, 15, 18550–18564. [Google Scholar] [CrossRef] [PubMed]
- Ding, Z.; Sun, G.; Guo, M.; Jiang, X.; Li, B.; Liang, S.Y. Effect of phase transition on micro-grinding-induced residual stress. J. Mater. Process. Technol. 2020, 281, 116647. [Google Scholar] [CrossRef]
- Zou, H.L.; Yu, Z.G.; Anh, V.; Ma, Y.L. From standard alpha-stable levy motions to horizontal visibility networks: Dependence of multifractal and Laplacian spectrum. J. Stat. Mech. Theory Exp. 2018, 053403. [Google Scholar] [CrossRef]
- Song, W.; Li, M.; Li, Y.; Cattani, C.; Chi, C.H. Fractional Brownian motion: Difference iterative forecasting models. Chaos Solitons Fractals 2019, 123, 347–355. [Google Scholar] [CrossRef]
- Kogon, S.M.; Manolakis, D.G. Signal modeling with self-similar stable processes: The fractional levy stable motion model. IEEE Trans. Signal Process. 1996, 44, 1006–1010. [Google Scholar] [CrossRef]
- Laskin, N.; Lambadaris, I.; Harmantzis, F.C.; Devetsikiotis, M. Fractional levy motion and its application to network traffic modeling. Comput. Netw. 2002, 40, 363–375. [Google Scholar] [CrossRef]
- Karasaridis, A.; Hatzinakos, D. Network heavy traffic modeling using stable self-similar processes. Ieee Trans. Commun. 2001, 49, 1203–1214. [Google Scholar] [CrossRef]
- Dai, W.; Heyde, C.C. It’s formula with respect to fractional brownian motion and its application. J. Appl. Math. Stoch. Anal. 1996, 9. [Google Scholar] [CrossRef]
- Wang, X.T.; Qiu, W.Y.; Ren, F.Y. Option pricing of fractional version of the black-scholes model with hurst exponent h being in (1/3,1/2). Chaos Solitons Fractals 2001, 12, 599–608. [Google Scholar] [CrossRef]



| Parameter Name | Parameter Value |
|---|---|
| Average period | 12 |
| Embedding Dim | 5 |
| Time delay | 2 |
| Lyapunov exponent | 0.0238 |
| Max. prediction steps | 43 |
| Name | Unweighted | 5 Weighted | 10 Weighted |
|---|---|---|---|
| Max error percentage | 3.7319 | 0.4425 | 0.1419 |
| H | 0.7595 | 0.7595 | 0.7595 |
| α | 1.7959 | 1.8280 | 1.6305 |
| var | 173.7598 | 4344 | 17376 |
| Years | Name | GA-BP Network | FLSM Forecasting |
|---|---|---|---|
| 2011 | Max error percentage | 0.2706 | 0.1419 |
| 2011 | Mean error percentage | 0.0350 | 0.0304 |
| 2012 | Max error percentage | 0.2676 | 0.1022 |
| 2012 | Mean error percentage | 0.0378 | 0.0282 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, S.; Song, W.; Cattani, C.; Yasen, Y.; Liu, H. Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction. Symmetry 2020, 12, 605. https://doi.org/10.3390/sym12040605
Duan S, Song W, Cattani C, Yasen Y, Liu H. Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction. Symmetry. 2020; 12(4):605. https://doi.org/10.3390/sym12040605
Chicago/Turabian StyleDuan, Shouwu, Wanqing Song, Carlo Cattani, Yakufu Yasen, and He Liu. 2020. "Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction" Symmetry 12, no. 4: 605. https://doi.org/10.3390/sym12040605
APA StyleDuan, S., Song, W., Cattani, C., Yasen, Y., & Liu, H. (2020). Fractional Levy Stable and Maximum Lyapunov Exponent for Wind Speed Prediction. Symmetry, 12(4), 605. https://doi.org/10.3390/sym12040605







