Dynamical Properties of Fractional-Order Memristor
Abstract
1. Introduction
2. The Fractional Derivative
- (1)
- (2)
- ,
- (3)
- ,
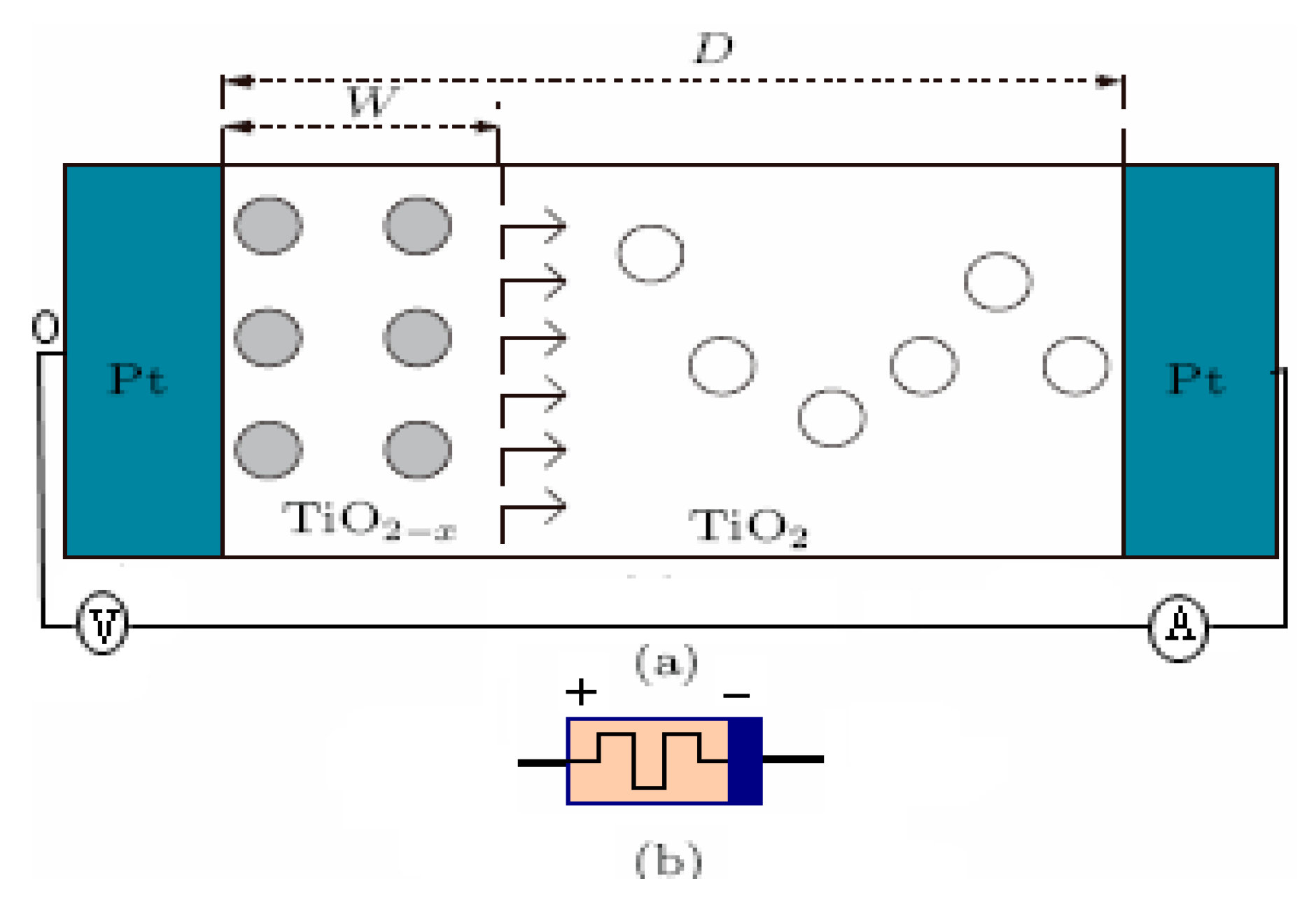
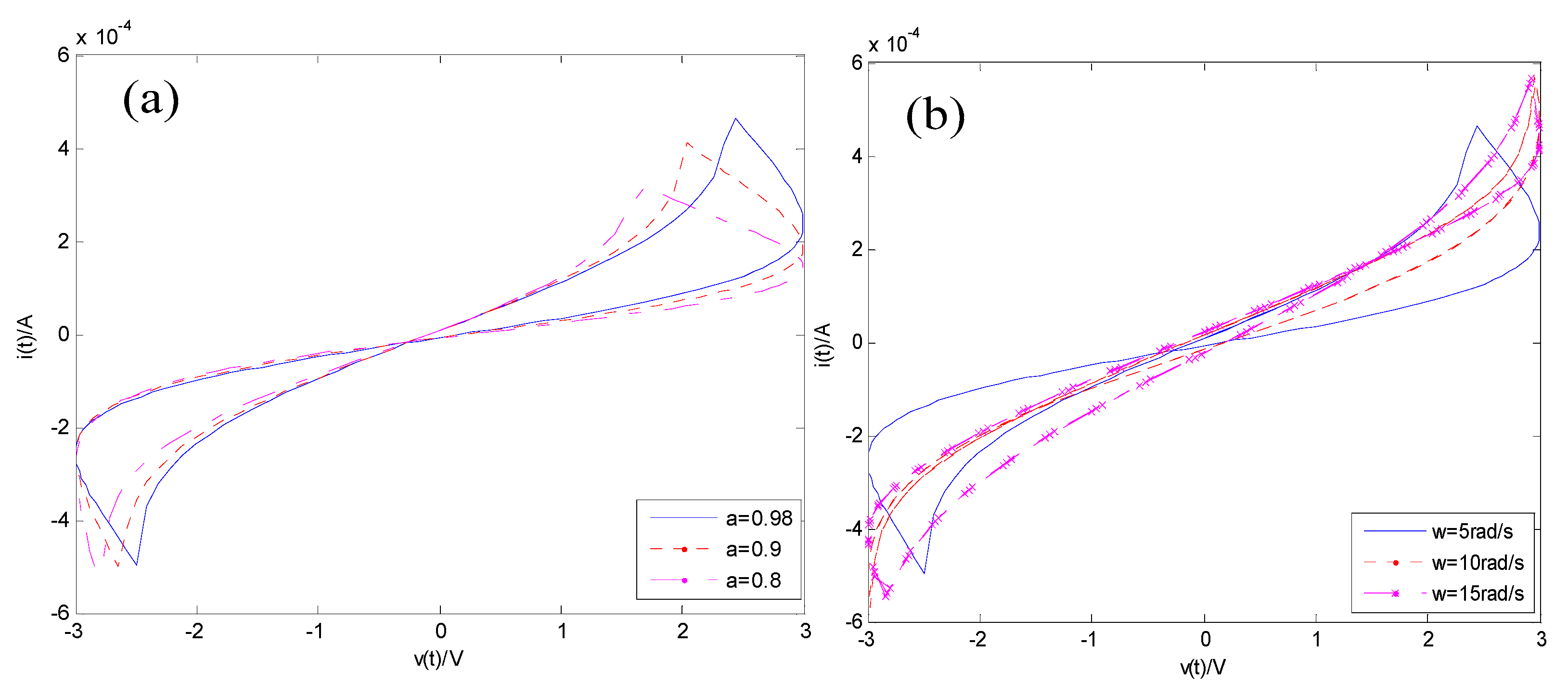
3. The Model of Fractional-Order Memristor
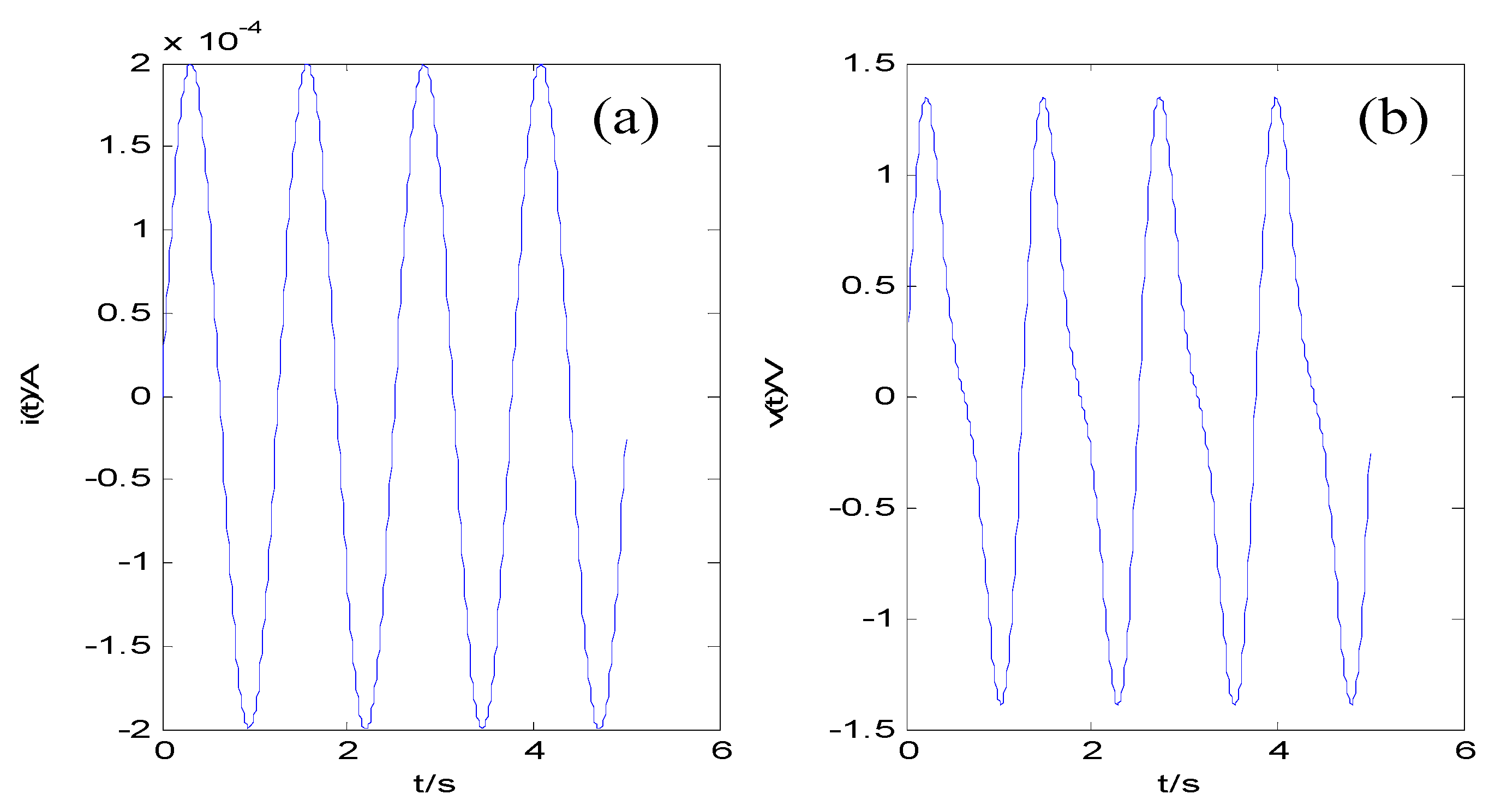
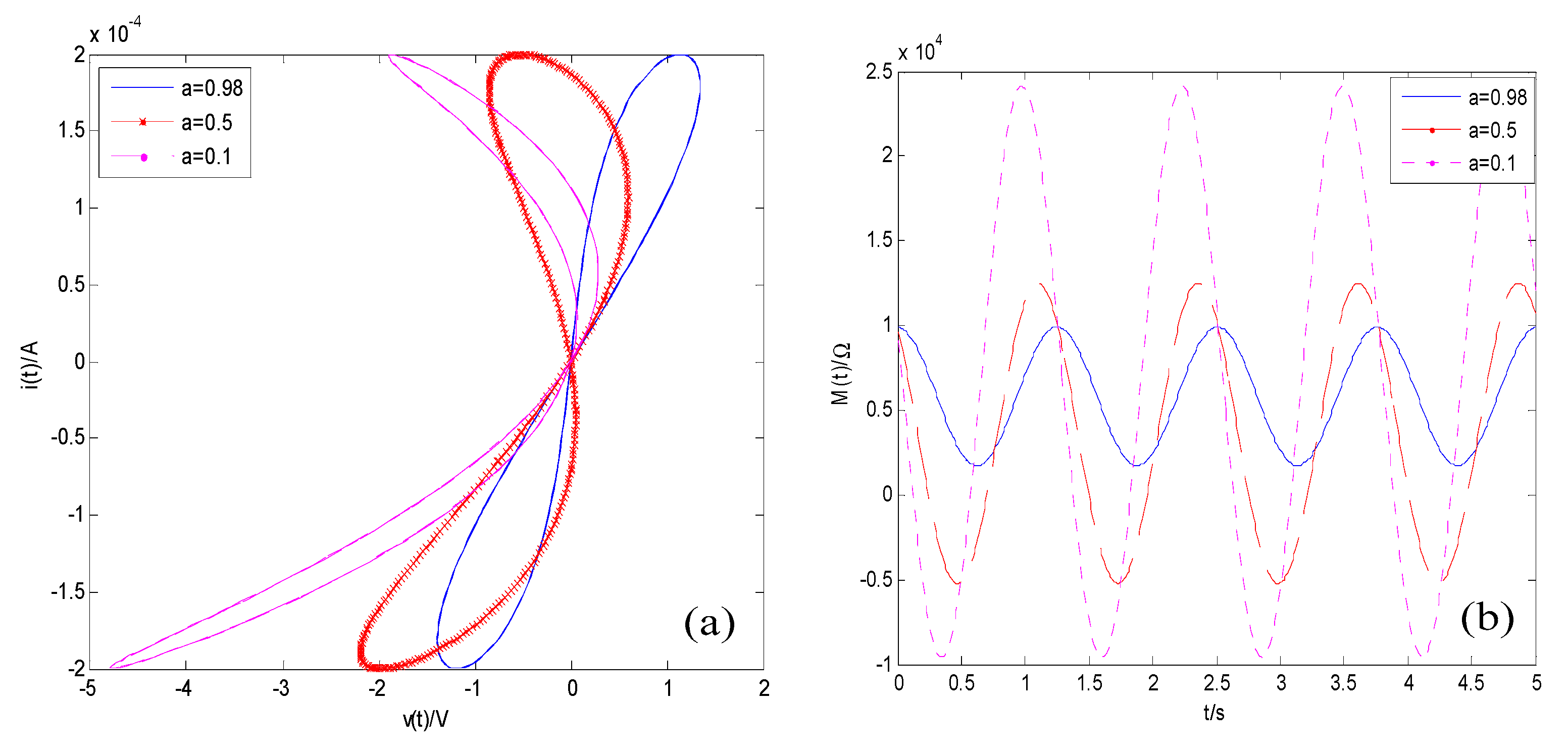
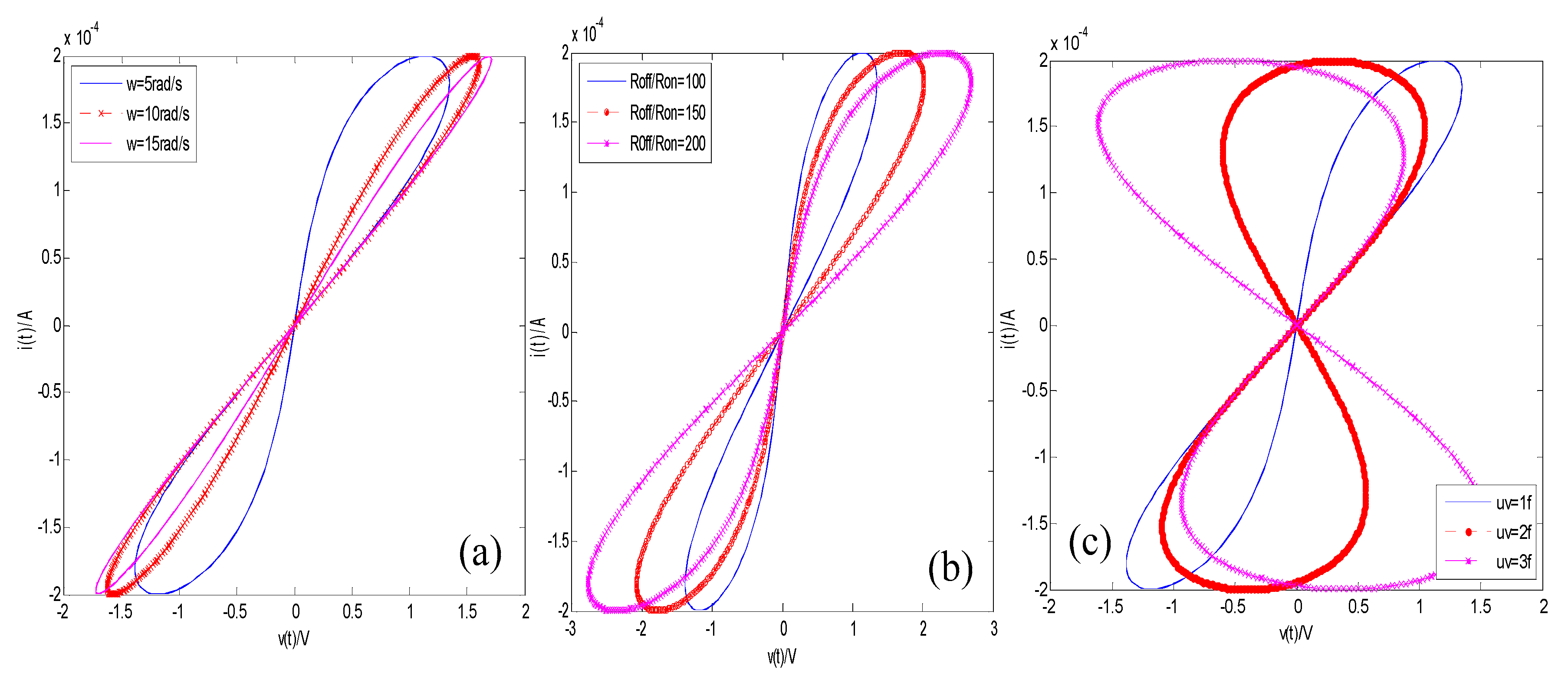
4. The Properties of Fractional-Order Memristor
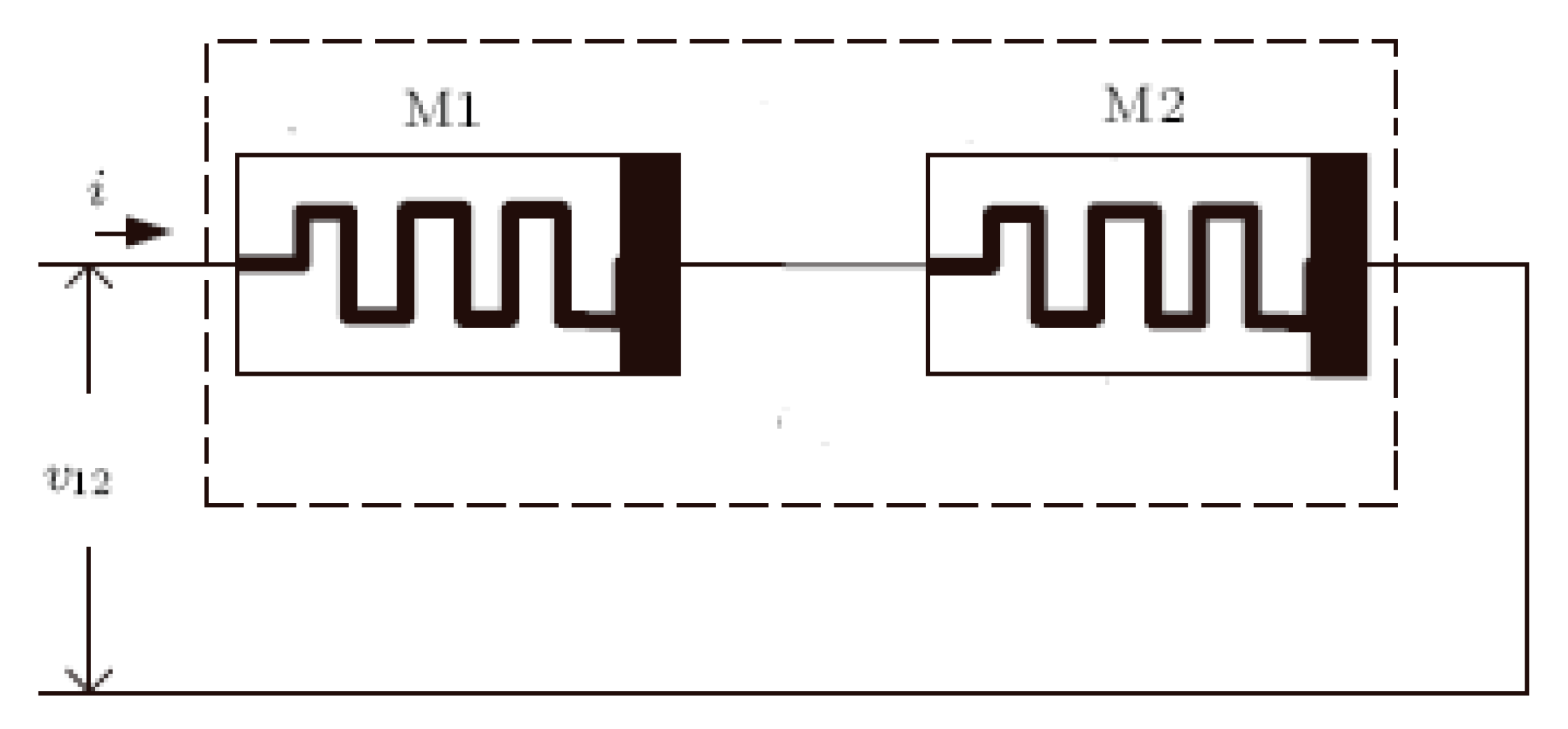
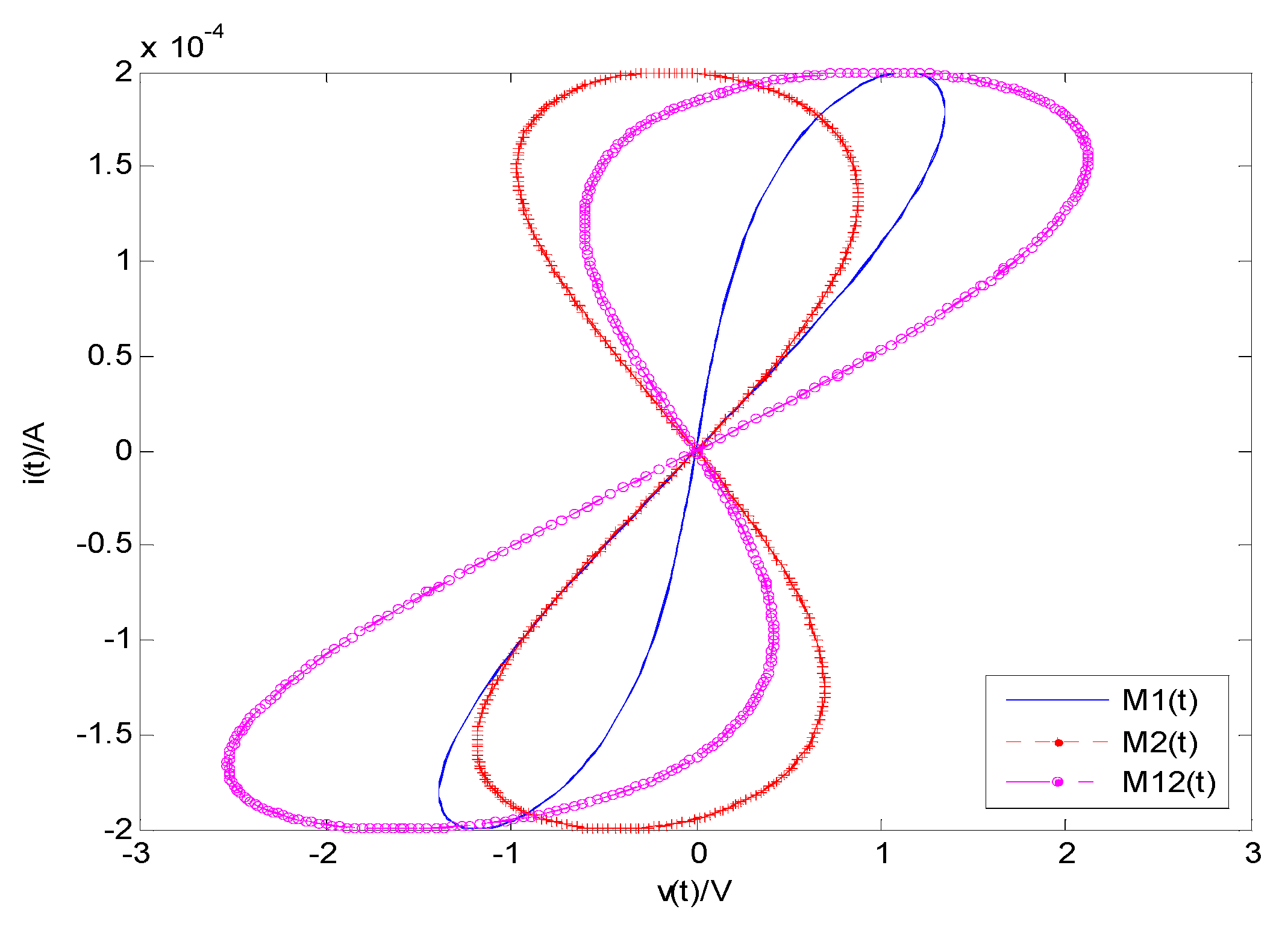
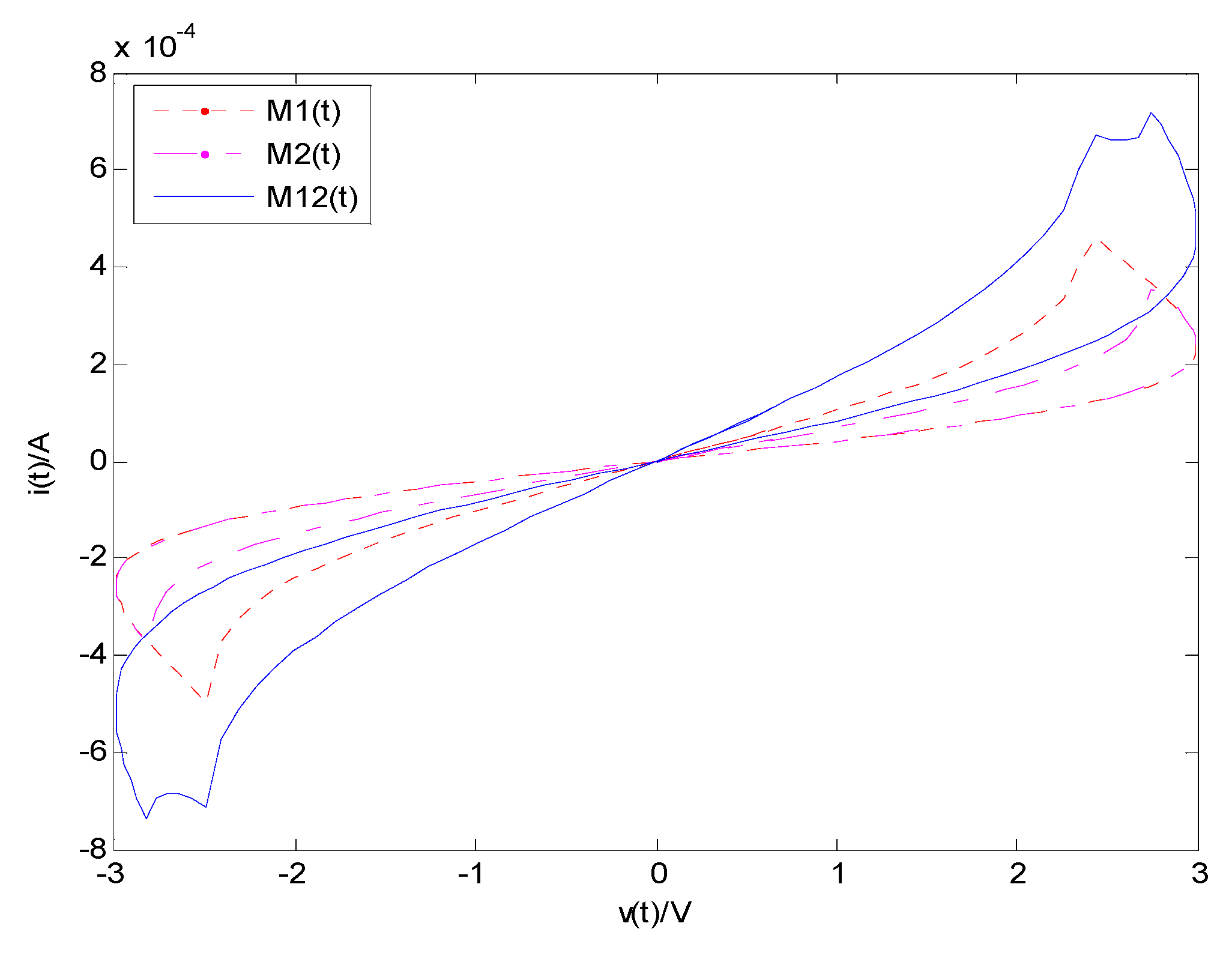
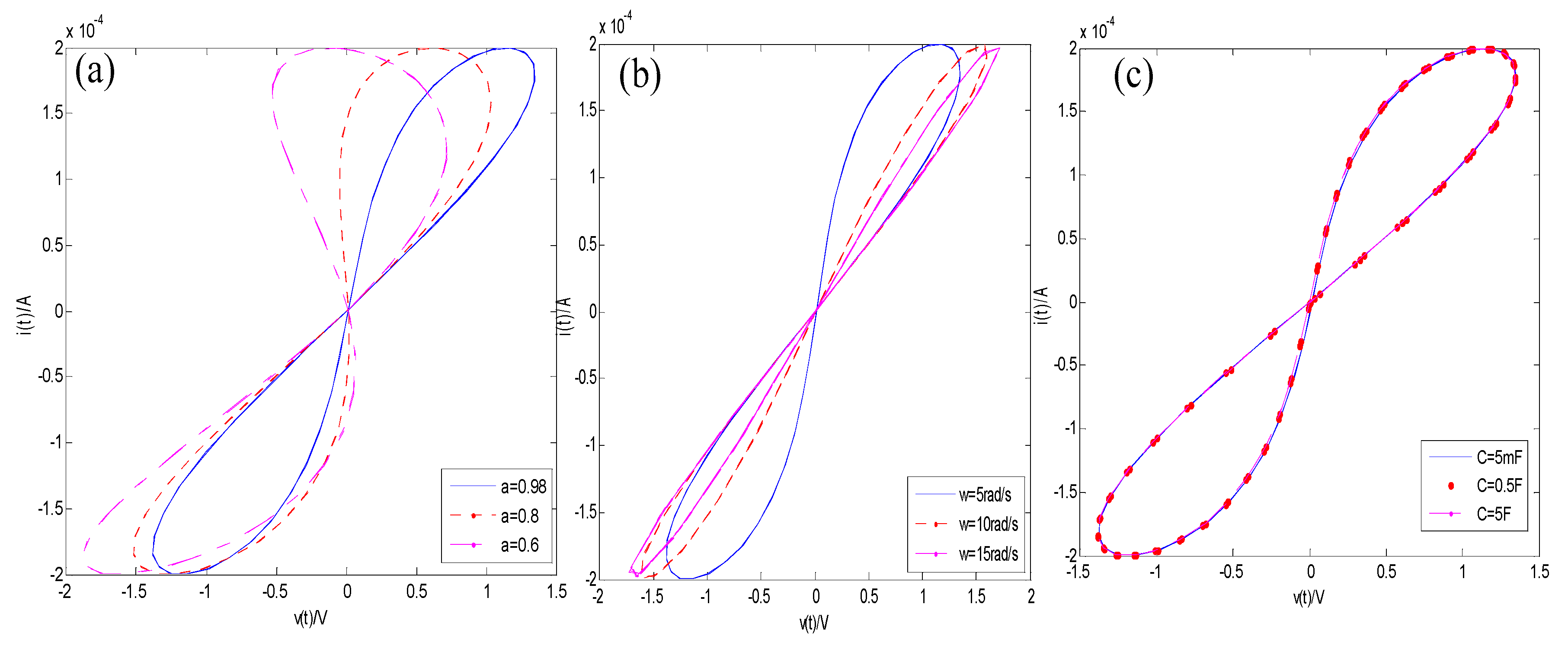
4.1. The Two Fractional-Order Memristors in Serial
4.2. The Circuit of Fractional-Order MR in Parallel
4.3. The Circuit of Fractal-Order Memristor and Capacitor That Are Serially Connected
4.4. The Circuit of Fractal-Order Memristor and Capacitor That Were Connected in Parallel
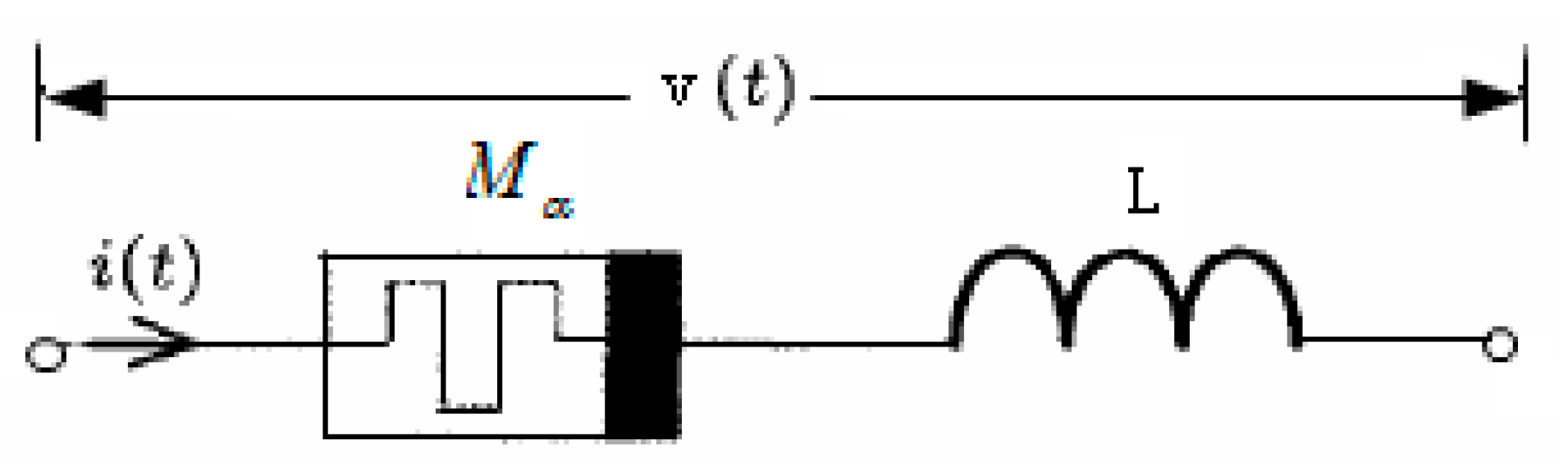
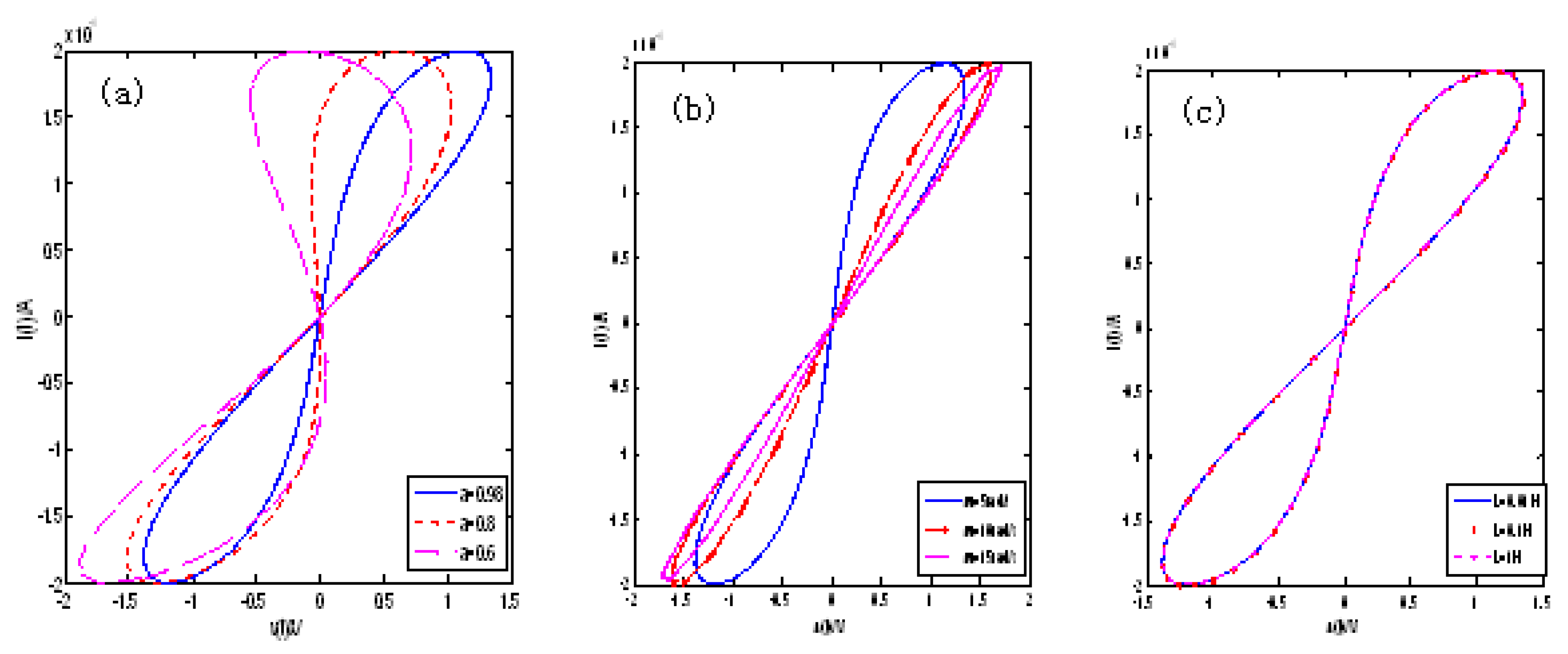
4.5. The Circuit of Fractal-Order Memristor and Inductor That Are Serially Connected
4.6. The Circuit of Fractal-Order Memristor and Inductor Connected in Parallel
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chua, L.O. Memristor—The missing circuit element. IEEE Trans. Circuit Theory 1971, CT-18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.B.; Snider, G.S.; Stewart, D.R.; Williams, R.S. The missing memristor found. Nature 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Yu, D.; Iu HH, C.; Liang, Y.; Fernando, T.; Chua, L.O. Dynamic Behavior of Coupled Memristor Circuits. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1607–1615. [Google Scholar] [CrossRef]
- Kim, H.; Sah, M.P.; Yang, C.; Roska, T.; Chua, L.O. Neural synaptic weighting with a pulse-based memristor circuit. IEEE Trans. Circuit Syst. I Reg. Pap. 2012, 59, 148–158. [Google Scholar] [CrossRef]
- Papandroulidakis, G.; Vourkas, I.; Vasileiadis, N.; Sirakoulis, G.C. Boolean logic operations and computing circuits based on memristors. IEEE Trans. Circuits Syst. II Exp. Briefs. 2014, 61, 972–976. [Google Scholar] [CrossRef]
- Bao, B.-C.; Zou, X. Voltage-Current Relationship of Active Memristor and Frequency Characteristic of Active Memristive Circuit. Acta Electron. Sin. 2013, 41, 593–596. [Google Scholar]
- Ascoli, A.; Corinto, F.; Tetzlaff, R. Generalized boundary condition memristor model. Int. J. Circuit Theor. Appl. 2015, 44, 60–84. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, J. Research of coupling behavior based series-parallel flux-controlled memristor. Acta Phys. Sin. 2015, 64, 237303. [Google Scholar]
- Sozen, H. First-order memristor–capacitor filter circuits employing hp memristor. J. Circuits Syst. Comput. 2014, 23, 1450116. [Google Scholar] [CrossRef]
- Song, D.-H.; Lü, M.-F.; Ren, X.; Li, M.-M.; Zu, Y.-X. Basic properties and applications of the memristor circuit. Acta Phys. Sin. 2012, 61, 118101. [Google Scholar]
- Dong, Z.-K.; Duan, S.-K. Two types of nanoscale nonlinear memristor models and their series-parallel circuit. Acta Phys. Sin. 2014, 63, 128502. [Google Scholar]
- Wang, Q.-H.; Song, W.-P. Characteristics of memristor and it’s application in the circuit design. Electron. Compon. Mater. 2014, 33, 5–7. [Google Scholar]
- Frasca, M.; Gambuzza, L.V. Implementation of adaptive coupling through memristor. Phys. Status Solidi 2015, 12, 206–210. [Google Scholar] [CrossRef]
- Gambuzza, L.-V.; Buscarino, A. Memristor-Based Adaptive Coupling for Consensus and Synchronization. IEEE Trans. Circuits Syst. I Regul. Pap. 2015, 62, 1175–1184. [Google Scholar] [CrossRef]
- Wang, T.-S.; Zhang, R.-D. Properties of memristor in RLC circuit and diode circuit. Acta Phys. Sin. 2014, 63, 178101. [Google Scholar]
- Duan, S.-K.; Hu, X.-F. Memristor-based RRAM with applications. Sci. China 2012, 42, 754–768. [Google Scholar] [CrossRef]
- Yu, Y.J.; Wang, Z.H. A fractional-order memristor model and the fingerprint of the simple series circuits including a fractional-order memristor. Acta Phys. Sin. 2015, 64, 238401. [Google Scholar]
- Riaza, R. First Order Mem-Circuits: Modeling, Nonlinear Oscillations and Bifurcations. IEEE Trans. Circuits Syst. I Regul. Pap. 2013, 60, 1570–1582. [Google Scholar] [CrossRef]
- He, B.-X.; Bao, B.-C. Research on the Equivalent Analysis Circuit of Memristors Network and Its Characteristics. J. Electron. Inf. Technol. 2012, 34, 1252–1256. [Google Scholar]
- Yuan, F.; Wang, G.-Y. Study on dynamical characteristics of a meminductor model and its meminductor-based oscillator. Acta Phys. Sin. 2015, 64, 210504. [Google Scholar]
- Xu, H.; Tian, X.B. Influence of temperature change on conductive characteristics of titanium oxide memristor. Acta Phys. Sin. 2014, 63, 098402. [Google Scholar]
- Papoutsidkis, M.; Kalovrektis, K.; Drosos, C. Design of an Autonomous Robotic vehicle for area mapping and remote monitroing. Int. J. Comput. Appl. 2017, 12, 36–41. [Google Scholar]
- Cai, W.; Tetzlaff, R. Beyond series and parallel: Coupling as a third relation in memristive systems. In Proceedings of the 2014 IEEE International Symposium on Circuits and Systems (ISCAS), Melbourne, VIC, Australia, 1–5 June 2014; pp. 1259–1262. [Google Scholar]
- Long, Z.X.; Zhang, Y. Noether’s theorem for fractional variational problem from El-Nabulsi extended exponentially fractional integral in phase space. Acta Mech. 2014, 225, 77–90. [Google Scholar] [CrossRef]
- El-Nabulsi, A.R. Fractional derivatives generalization of Einstein’s field equations. Indian J. Phys. 2013, 87, 195–200. [Google Scholar] [CrossRef]
- Fellah, Z.; Depollier, C.; Fellah, M. Application of fractional calculus to the sound waves propagation in rigid porus materials:validation via ultrasonic measurements. Acta Acust. United Acust. 2002, 88, 34–39. [Google Scholar]
- Magin, R.; Ortigueira, M.D.; Podlubny, I.; Trujillo, J. On the fractional signals and systems. Signal. Process. 2011, 91, 350–371. [Google Scholar] [CrossRef]
- Ostalczyk, P. Discrete Fractional Calculus: Applications in Control and Image Processing; World Scientific: Singapore, 2015. [Google Scholar]
- Das, S. Functional Fractional Calculus; Springer Science & Business Media: Berlin, Germany, 2011. [Google Scholar]
- Kilbas, A.A.; Marichev, O.I.; Samko, S.G. Fractional Integrals and Derivatives, Theory and Applications; Gordon and Breach: Yverdon, Switzerland, 1993. [Google Scholar]





© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.F.; Ye, A. Dynamical Properties of Fractional-Order Memristor. Symmetry 2020, 12, 437. https://doi.org/10.3390/sym12030437
Wang SF, Ye A. Dynamical Properties of Fractional-Order Memristor. Symmetry. 2020; 12(3):437. https://doi.org/10.3390/sym12030437
Chicago/Turabian StyleWang, Shao Fu, and Aiqin Ye. 2020. "Dynamical Properties of Fractional-Order Memristor" Symmetry 12, no. 3: 437. https://doi.org/10.3390/sym12030437
APA StyleWang, S. F., & Ye, A. (2020). Dynamical Properties of Fractional-Order Memristor. Symmetry, 12(3), 437. https://doi.org/10.3390/sym12030437




