A Symmetric Controllable Hyperchaotic Hidden Attractor
Abstract
1. Introduction
- I)
- There exists a parameter to control amplitude and frequency of signals in a small range.
- II)
- Amplitude of x and y can be controlled simultaneously.
- III)
- There is an offset boosting controller.
- IV)
- A special parameter can realize both amplitude and offset control of one system variable.
2. Model Description
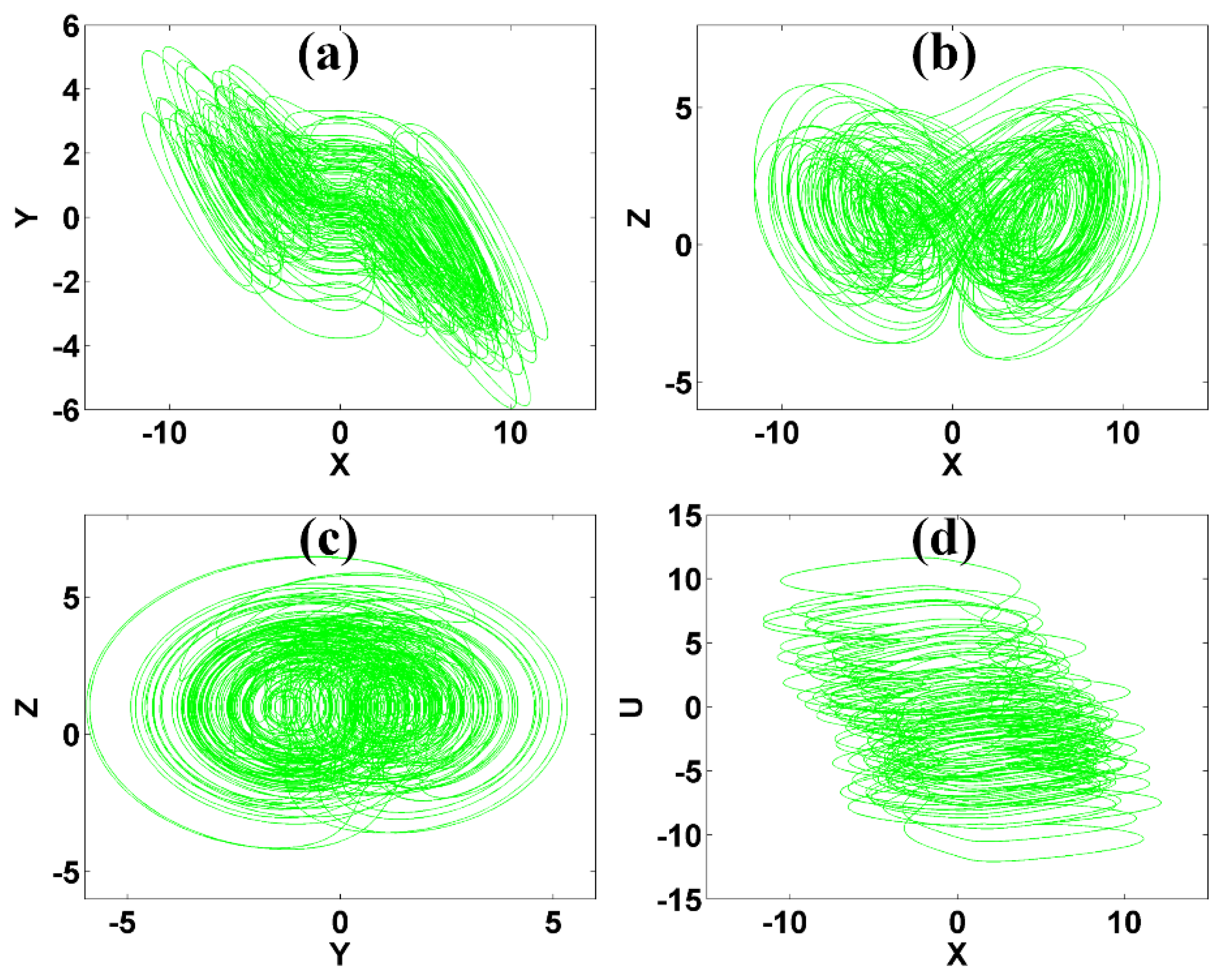
3. Basic Dynamic Analysis
3.1. Anylis of Equilibria
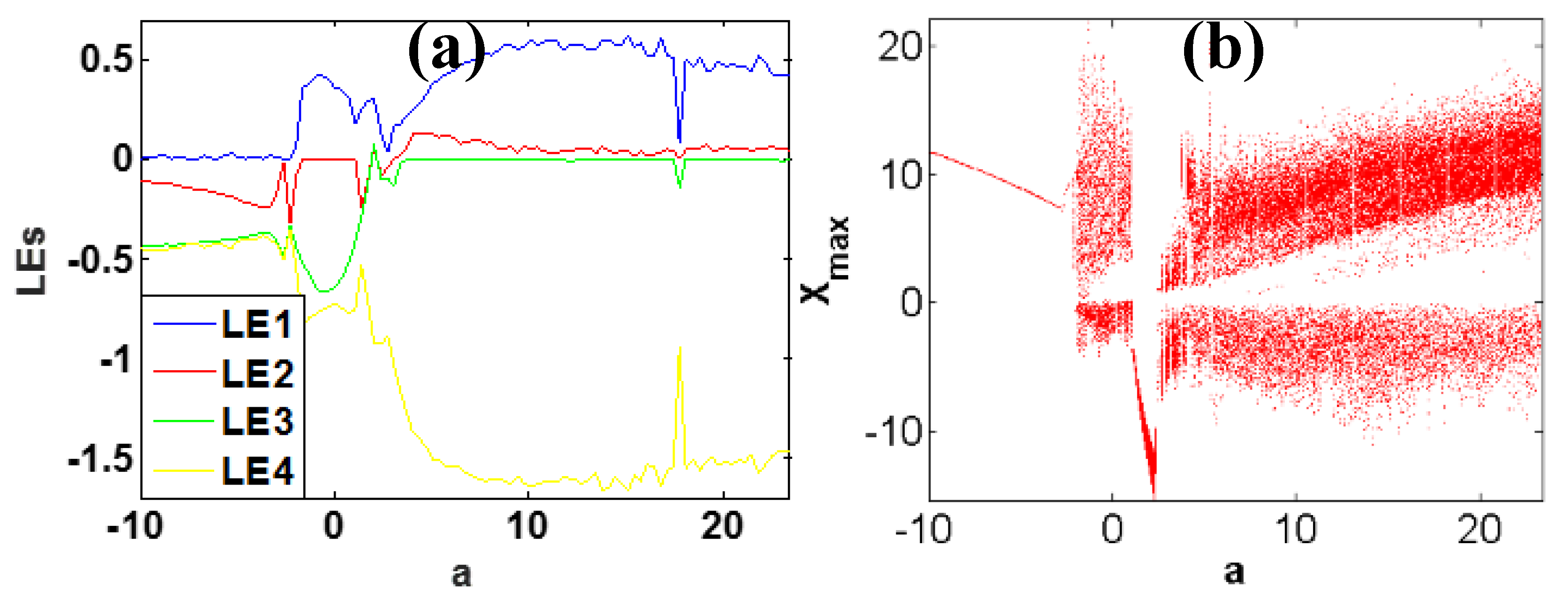
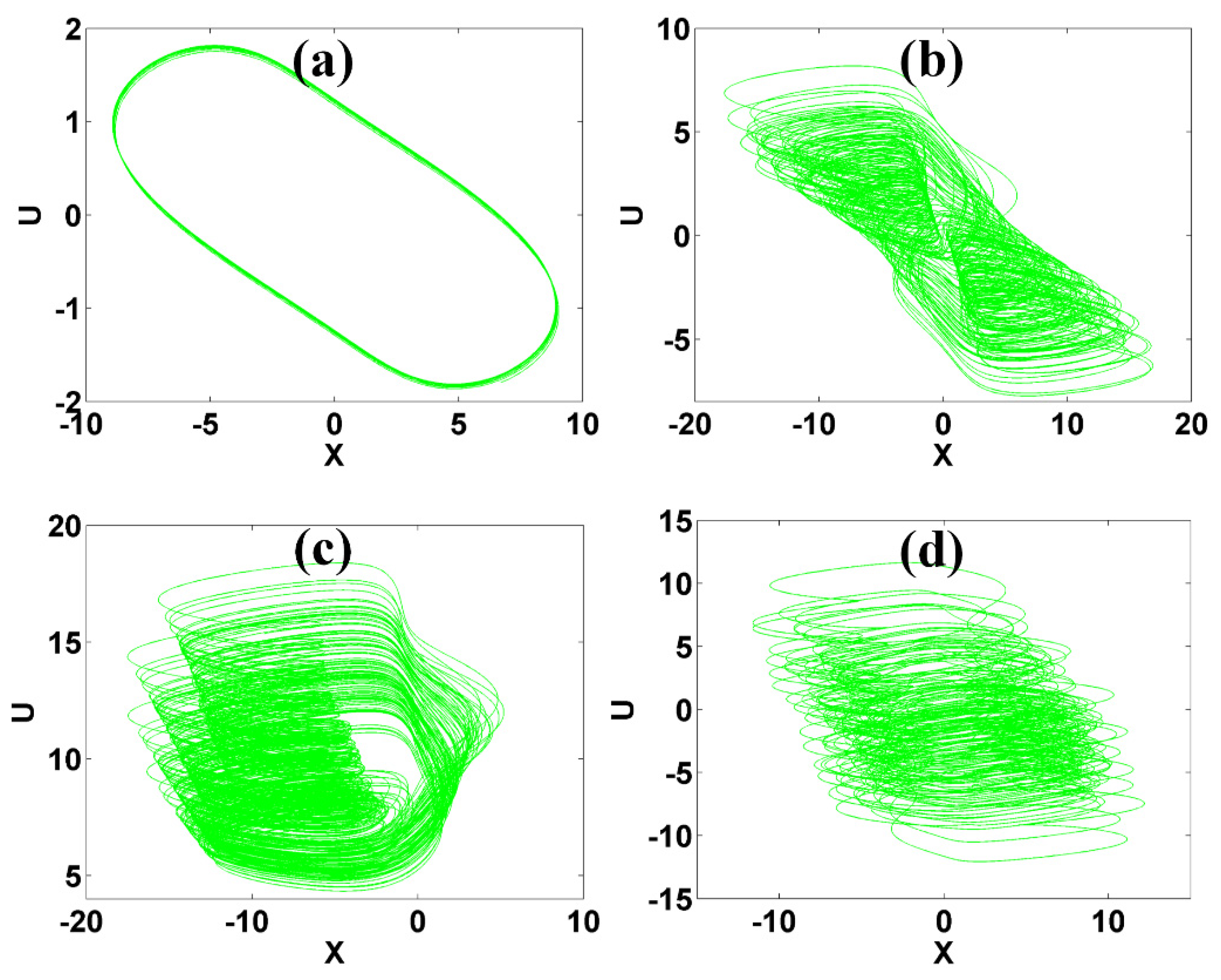
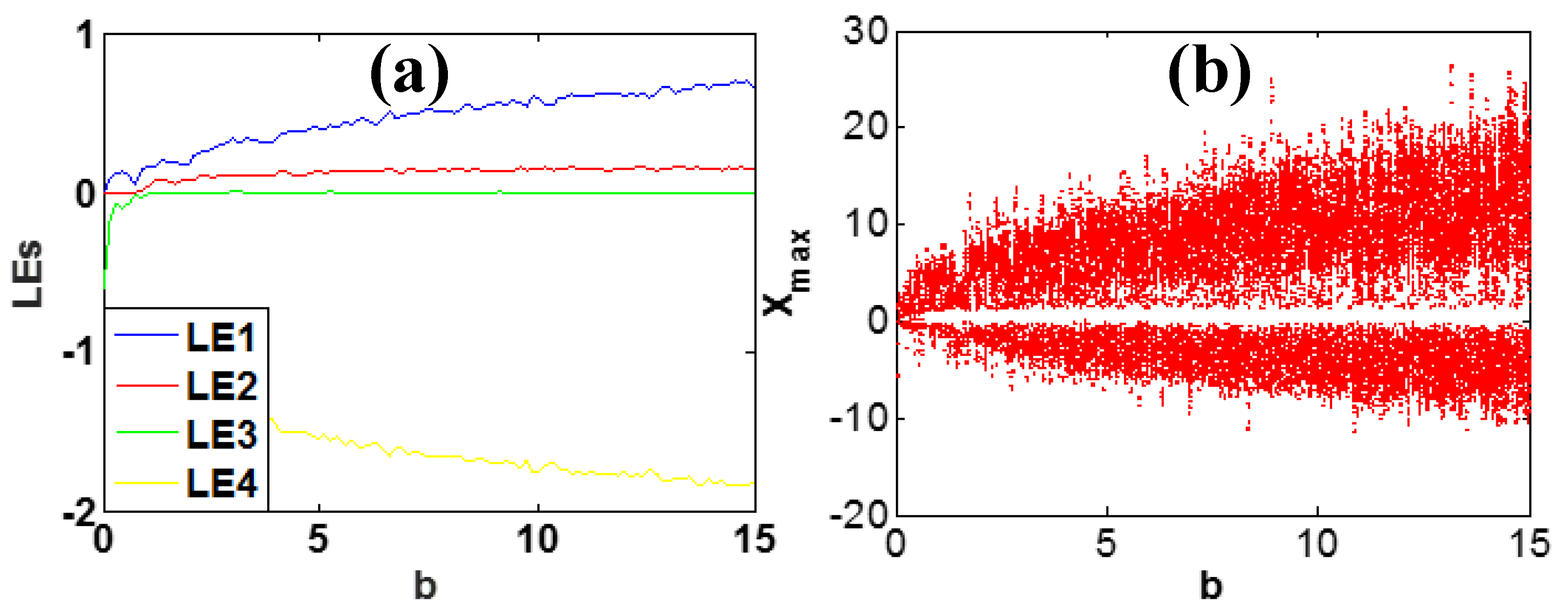
3.2. Bifurcation Analysis
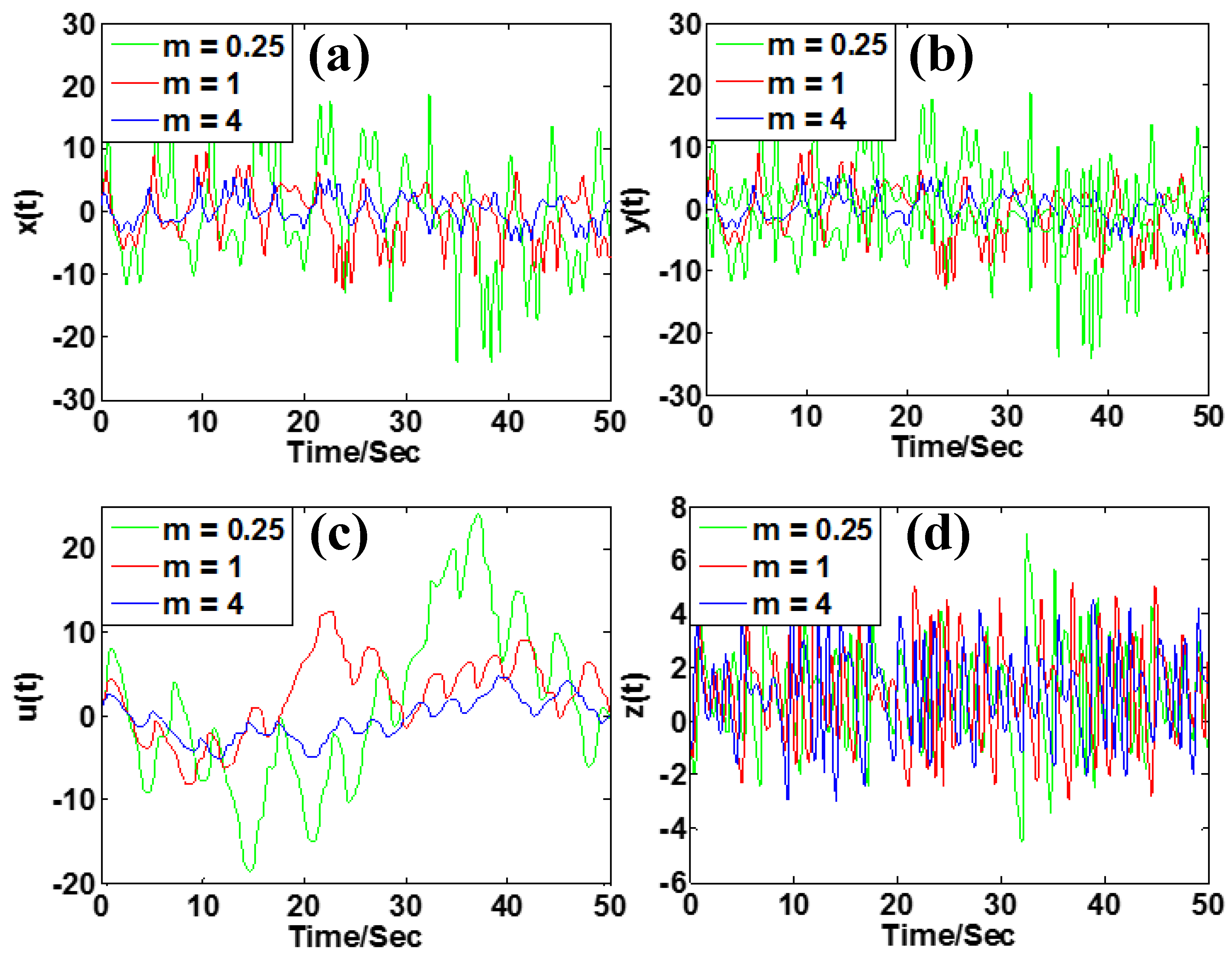
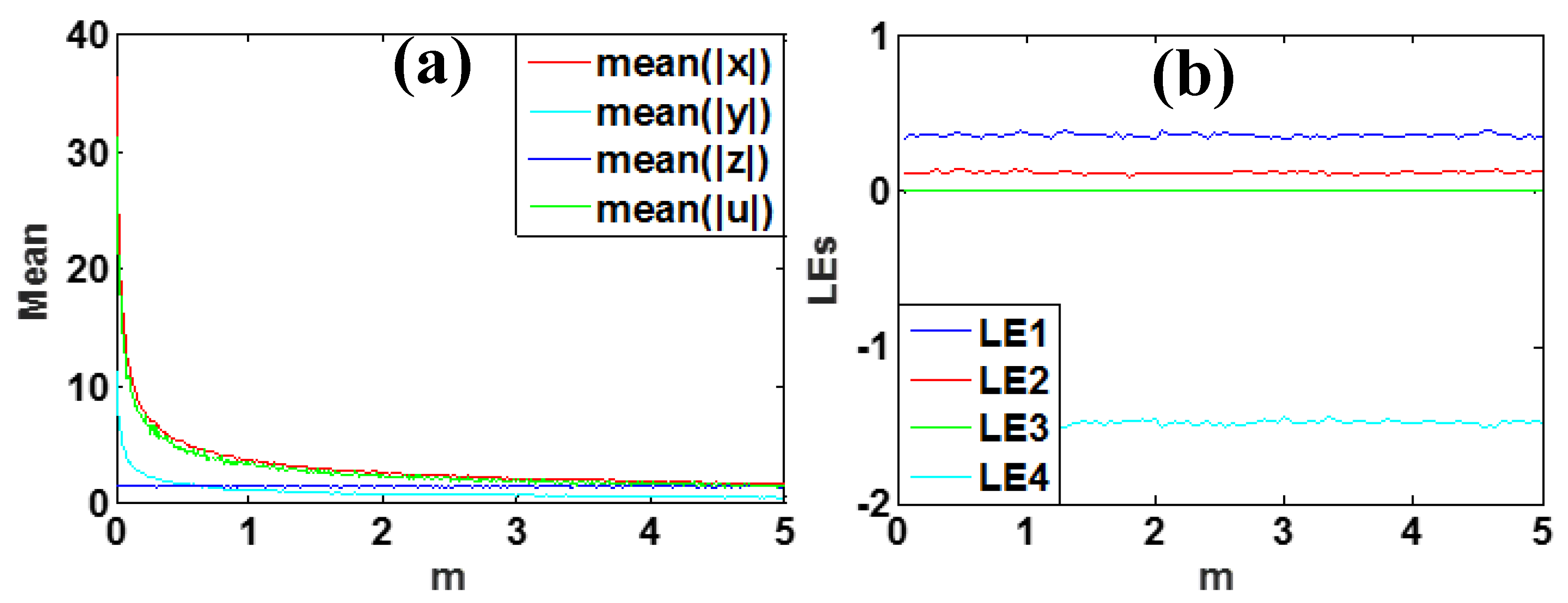
3.3. Amplitude Control
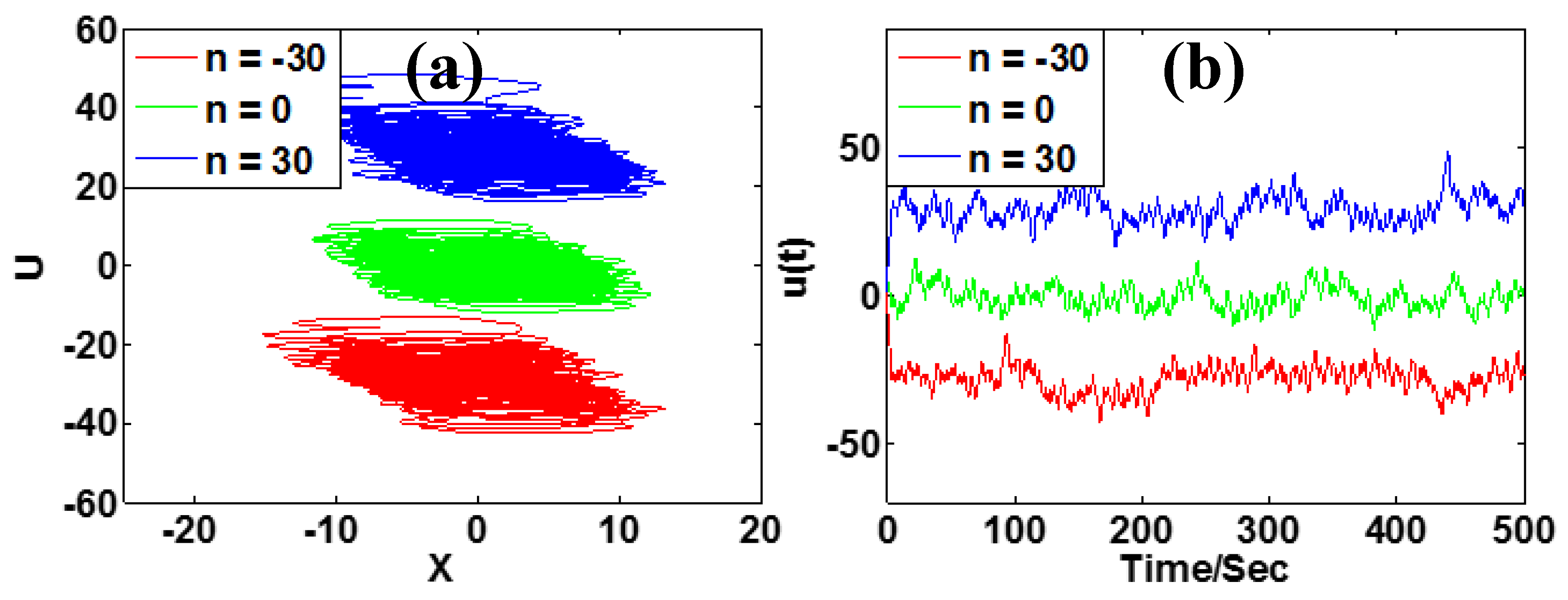
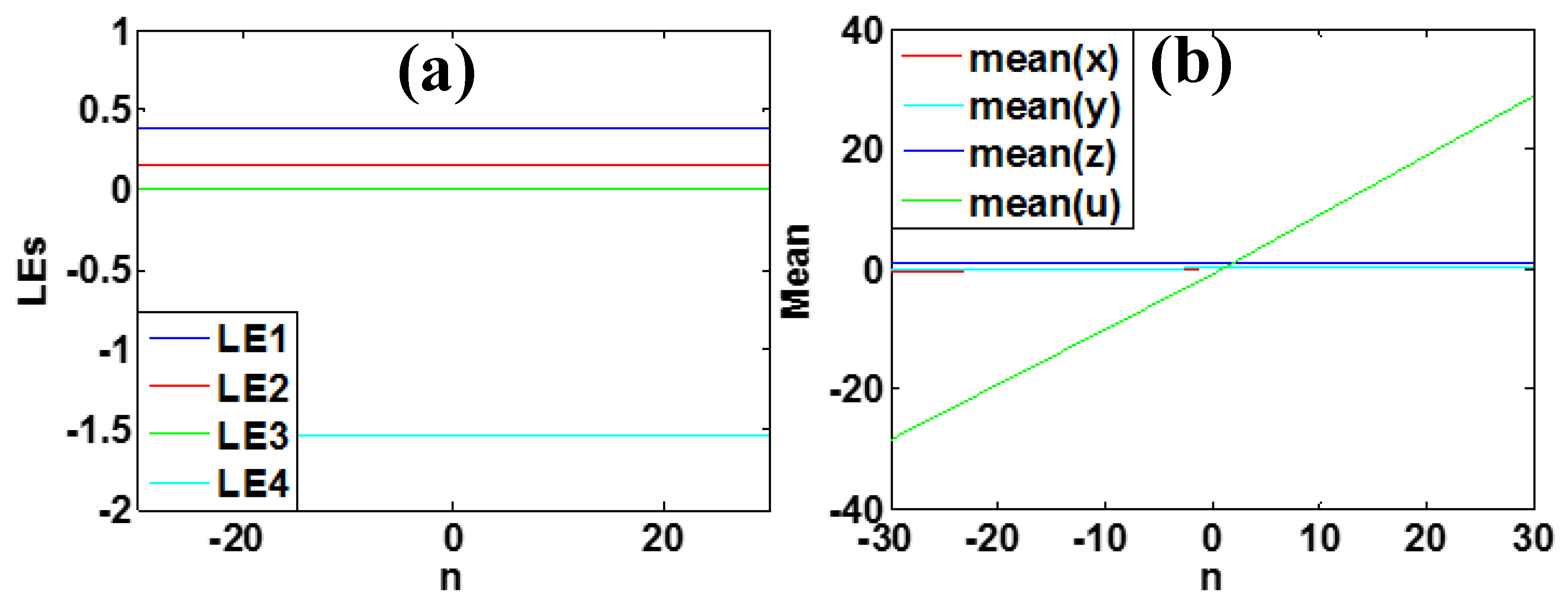
3.4. Offset Boosting
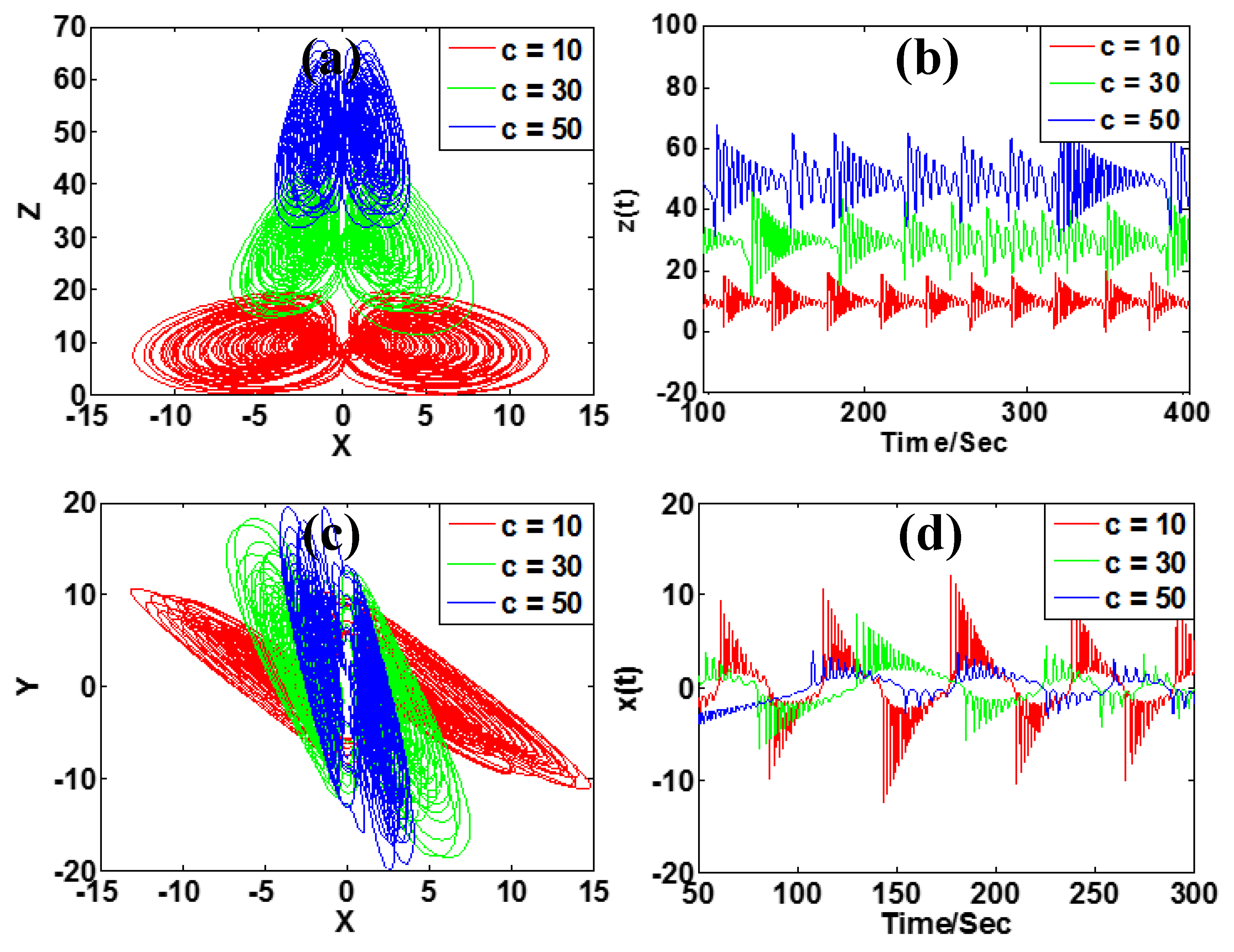
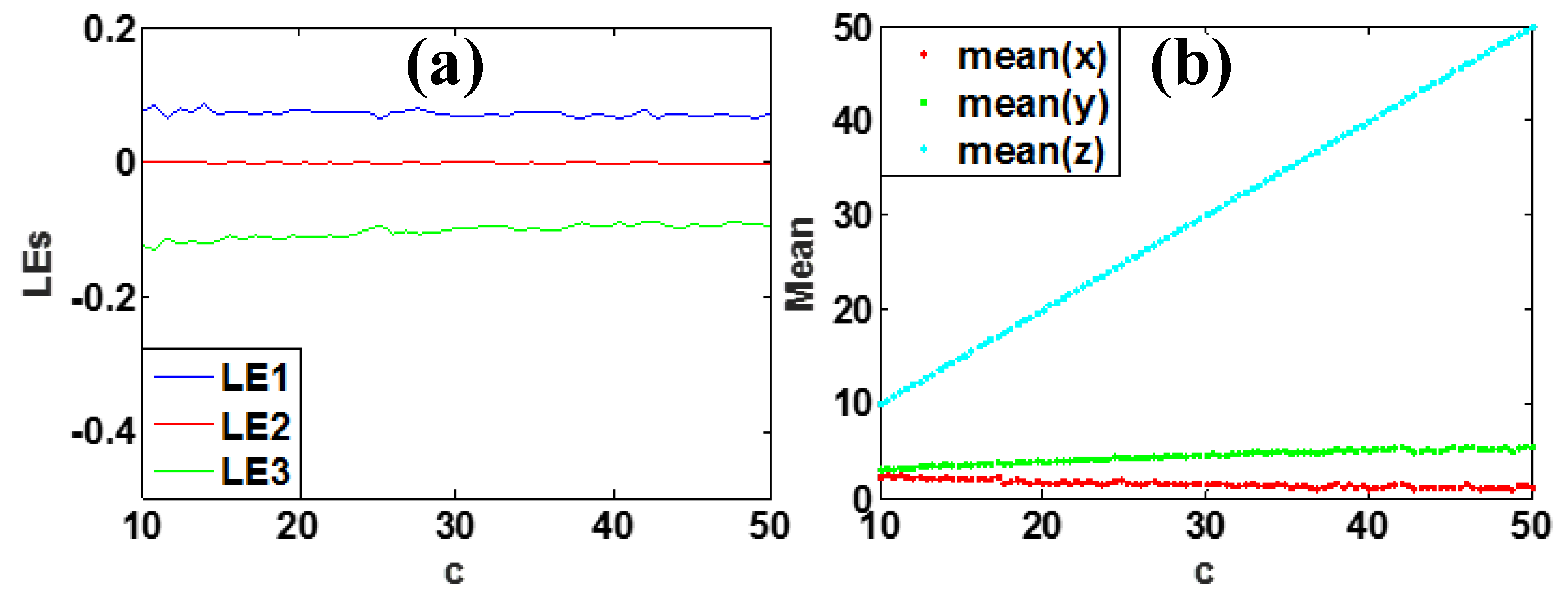
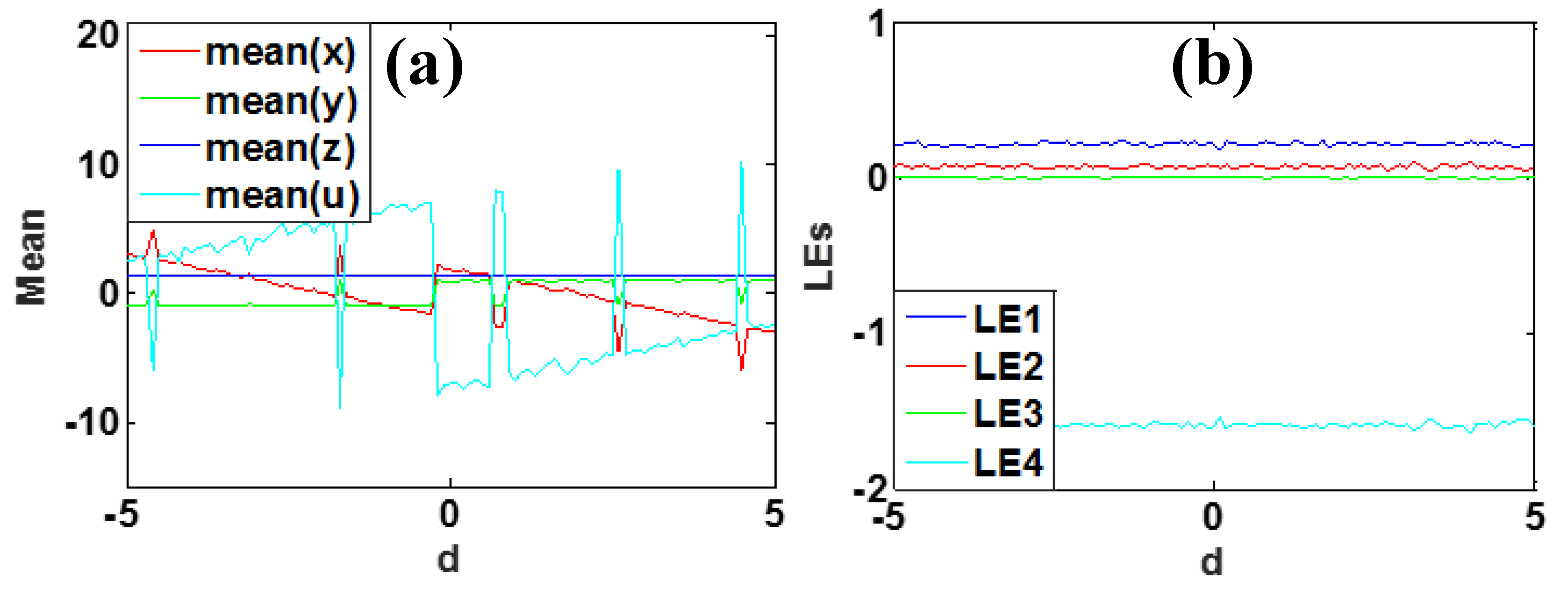
3.5. Mixed Geometric Control
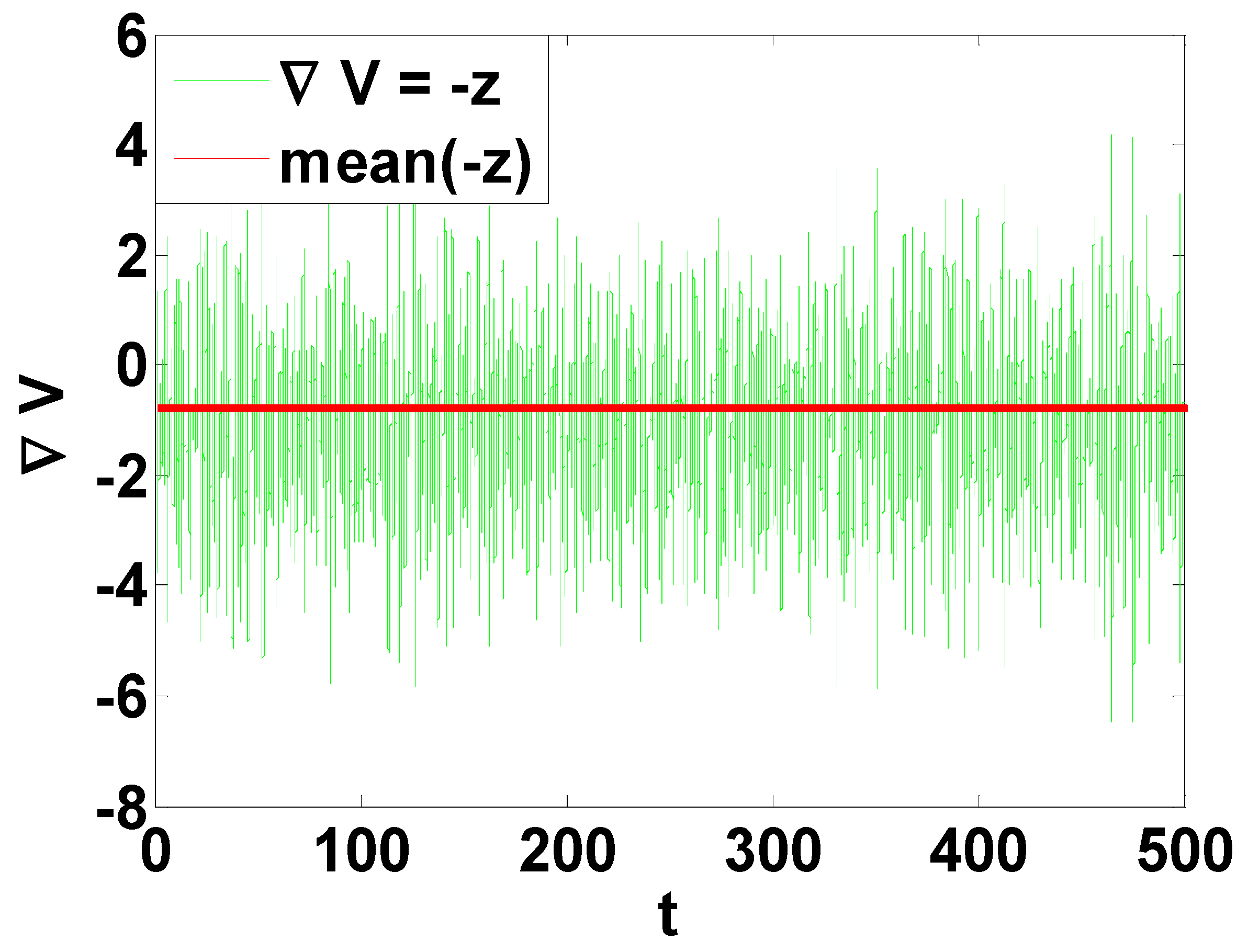
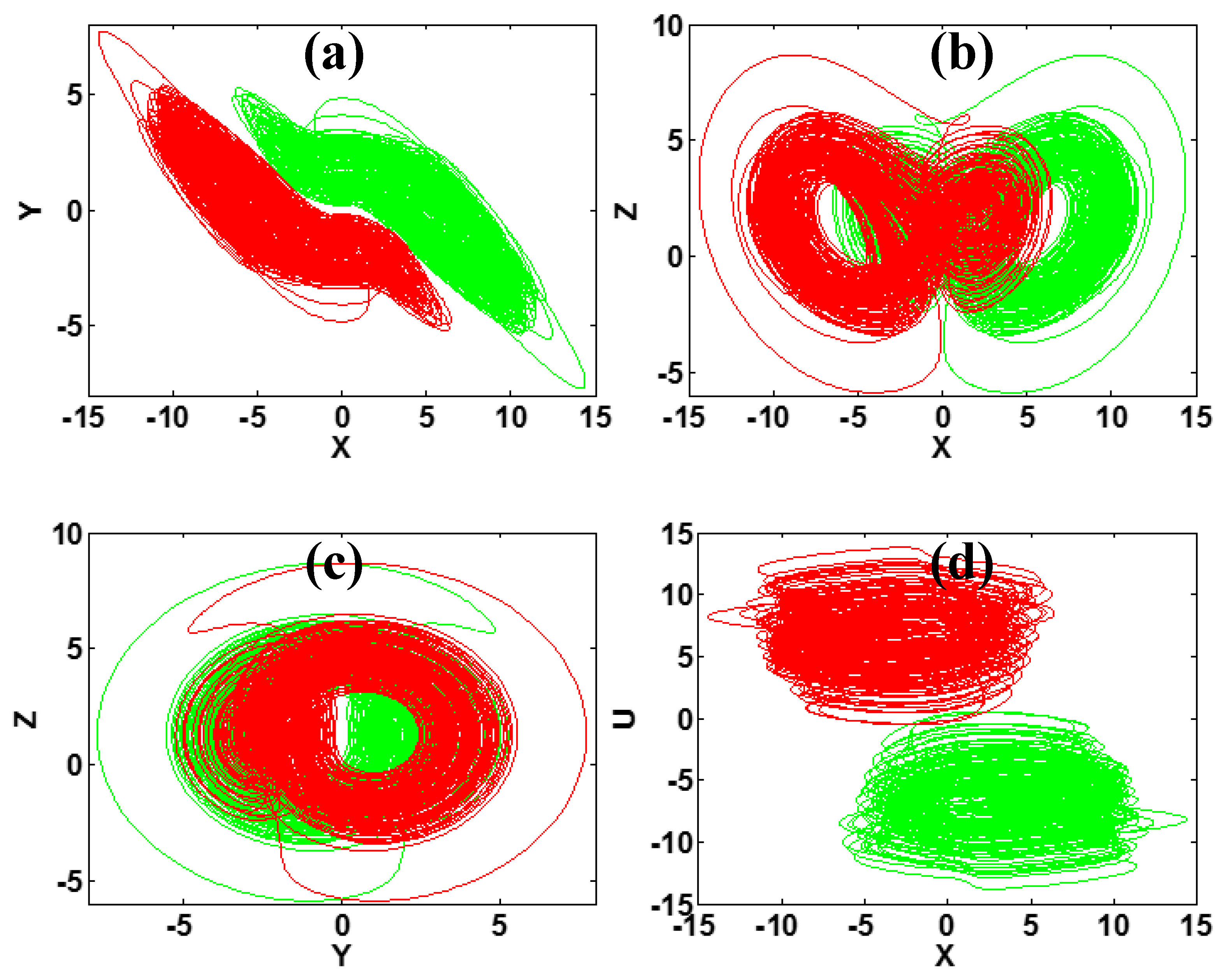
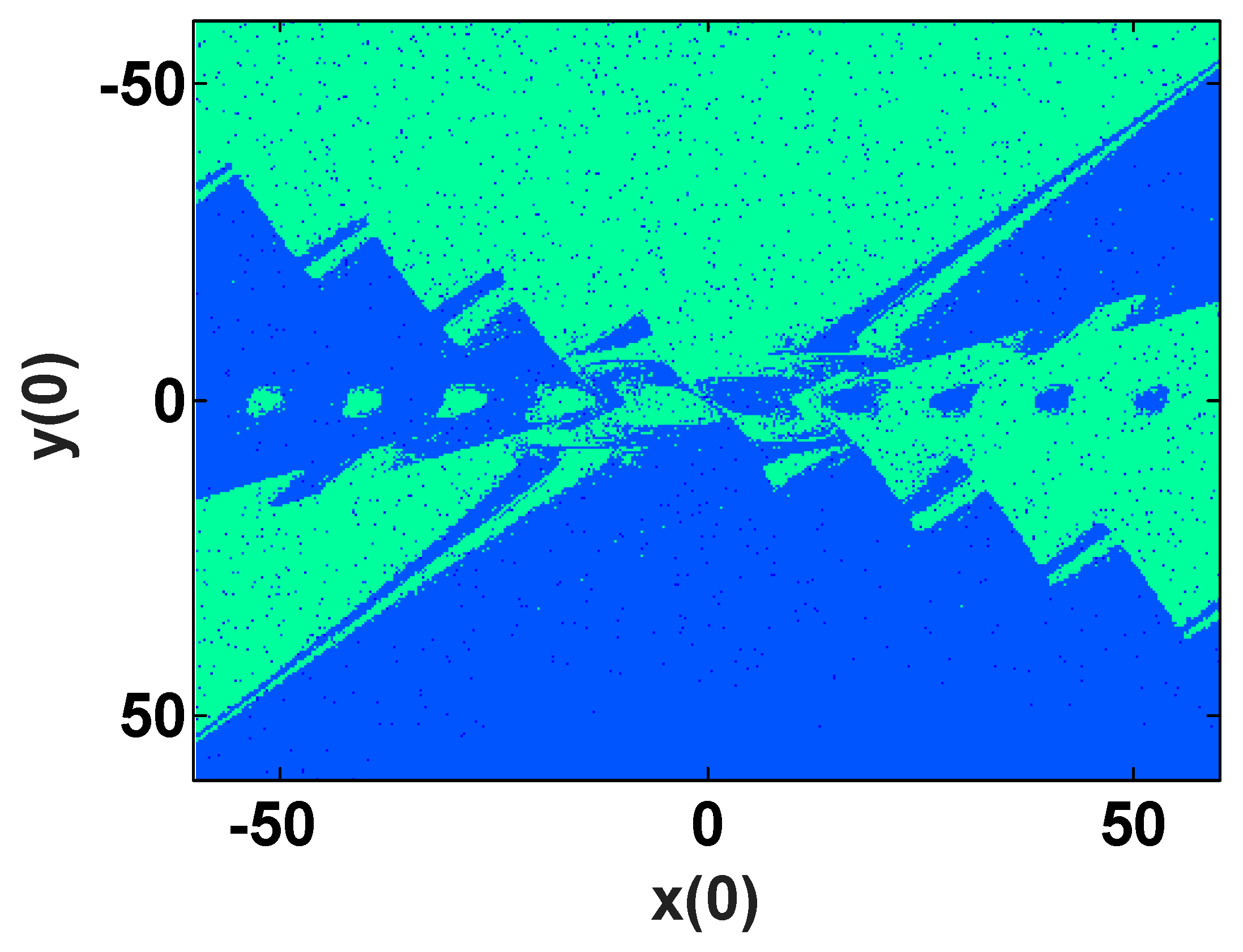
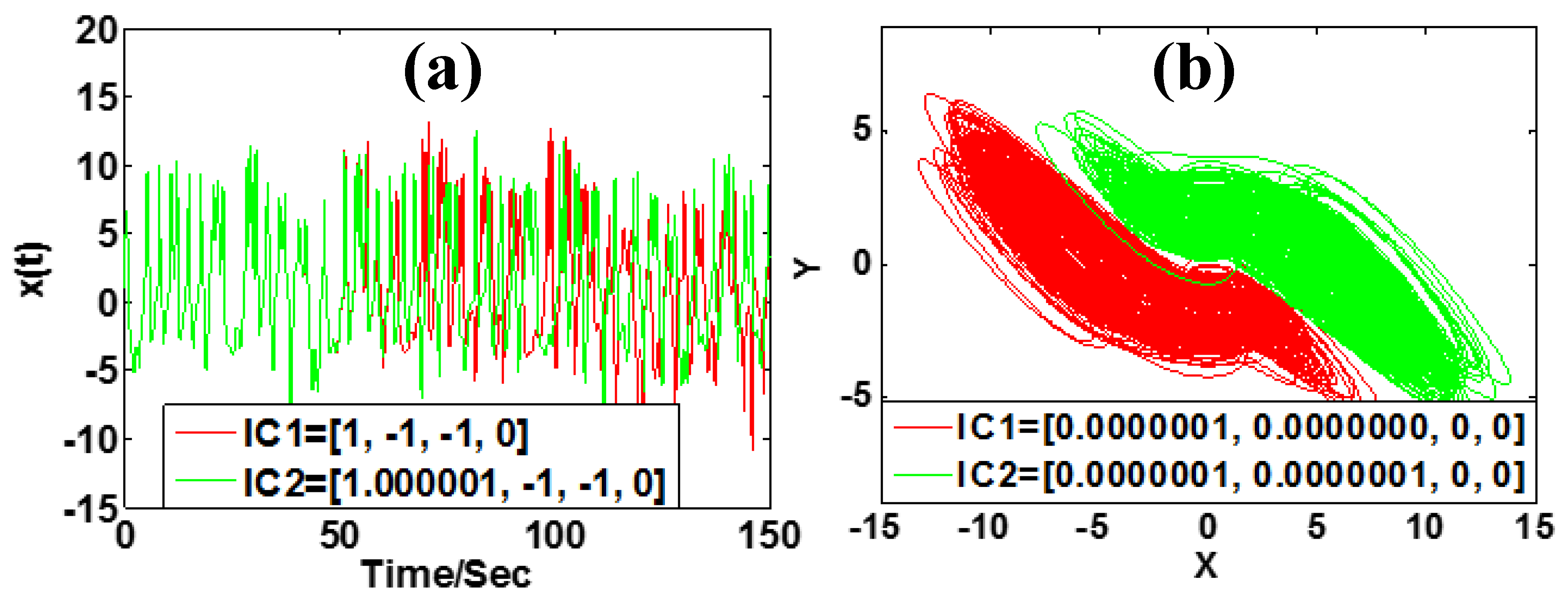
4. Bistability Analysis
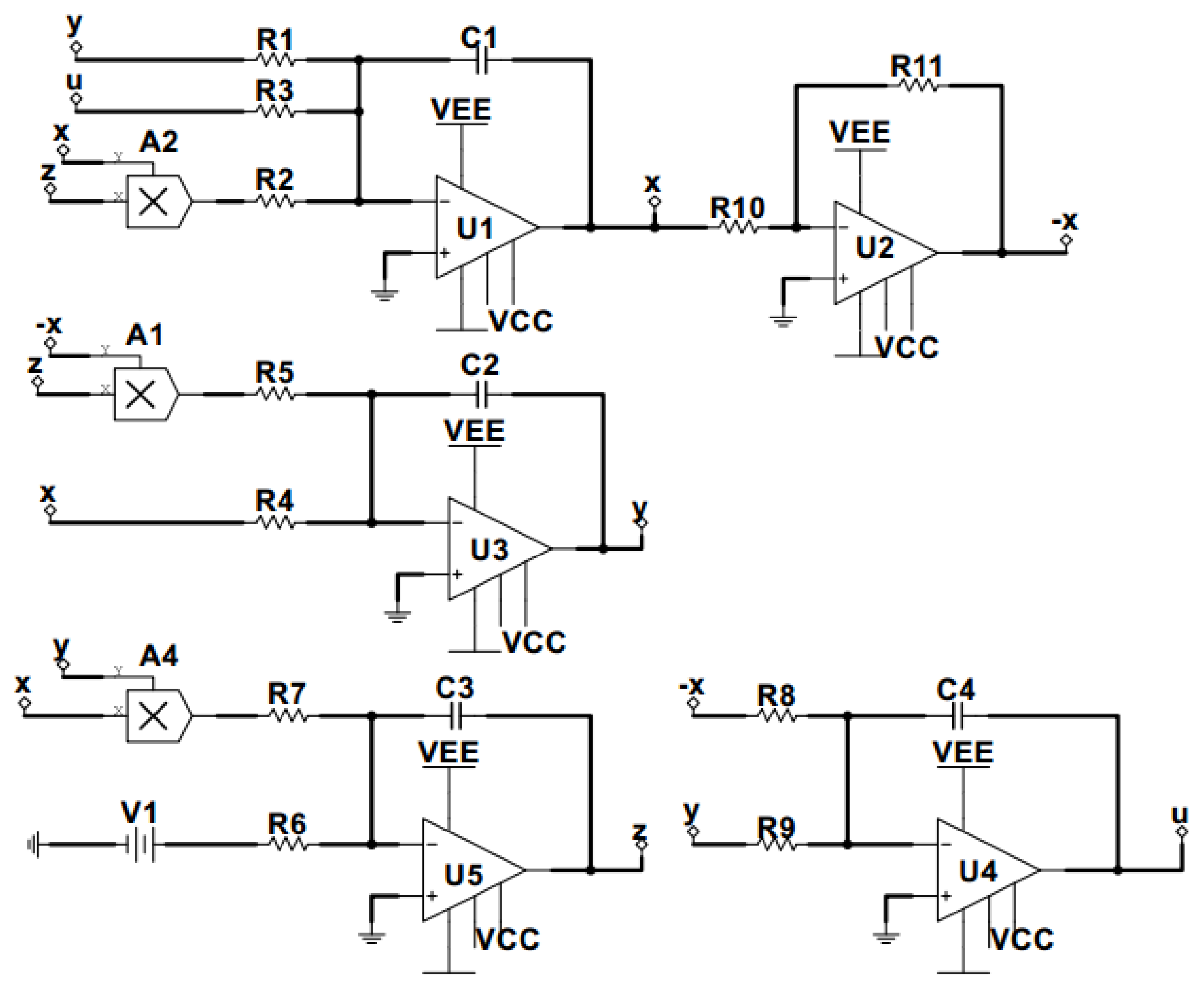
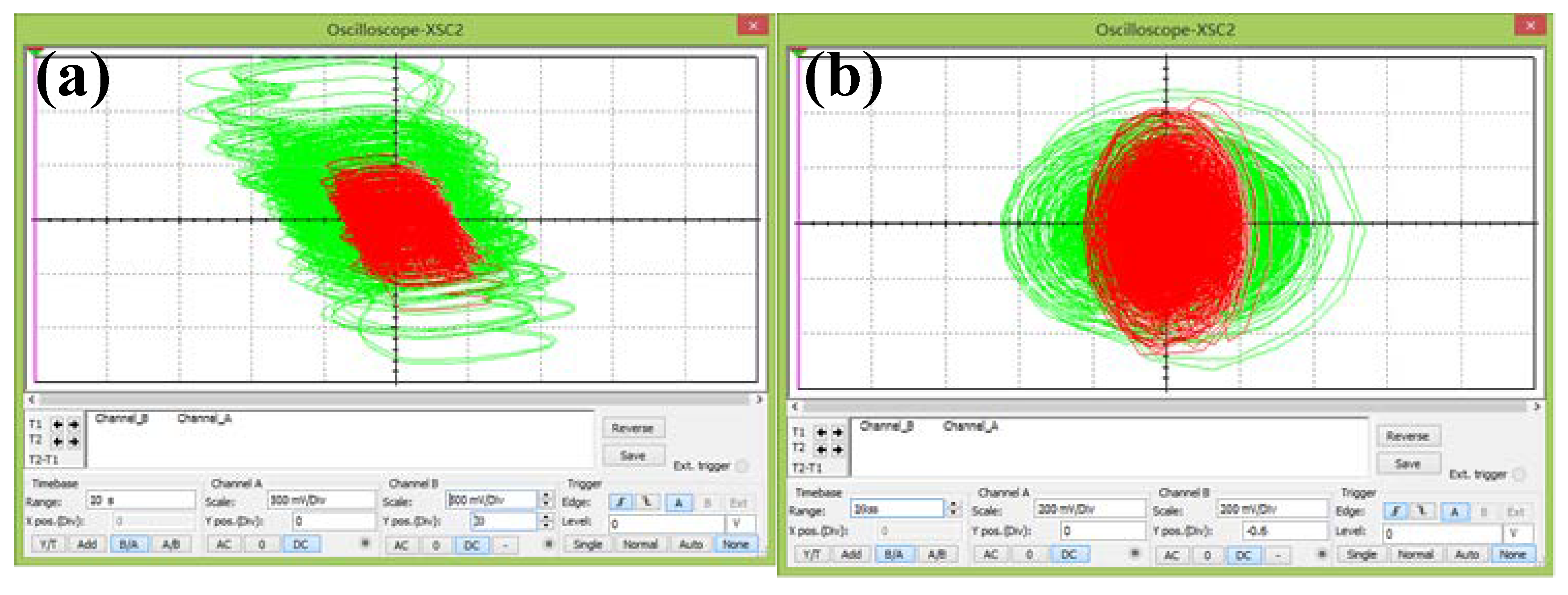
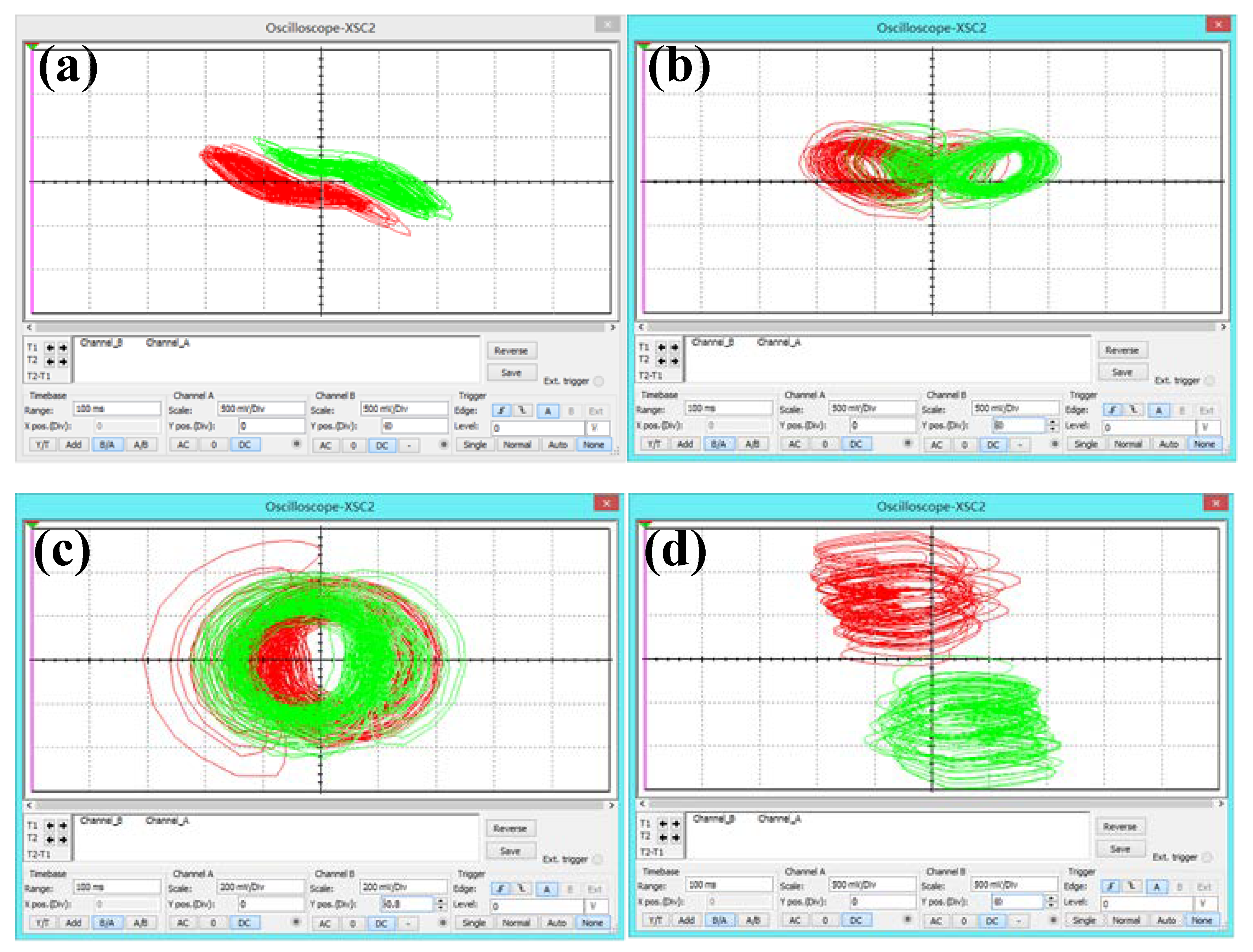
5. Circuit Implementation
6. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Li, C.; Sprott, J.C. Amplitude control approach for chaotic signals. Nonlinear Dyn. 2013, 73, 1335–1341. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Finding coexisting attractors using amplitude control. Nonlinear Dyn. 2014, 78, 2059–2064. [Google Scholar] [CrossRef]
- Chen, H.; Bayani, A.; Akgul, A.; Jafari, M.-A.; Pham, V.-T.; Wang, X.; Jafari, S. A flexible chaotic system with adjustable amplitude, largest Lyapunov exponent, and local Kaplan–Yorke dimension and its usage in engineering applications. Nonlinear Dyn. 2018, 92, 1791–1800. [Google Scholar] [CrossRef]
- Wang, C.; Liu, X.; Xia, H. Multi-piecewise quadratic nonlinearity memristor and its 2N-scroll and 2N + 1-scroll chaotic attractors system. Chaos Interdiscip. J. Nonlinear Sci. 2017, 27, 033114. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Akgul, A.; Li, C.; Zheng, T.; Li, P. A switchable chaotic oscillator with two amplitude-frequency controllers. J. Circuits Syst. Comput. 2017, 26, 1750158. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Akgul, A.; Herbert, H.C.; Iu, H.H.C.; Zhao, Y. A new chaotic oscillator with free control. Chaos 2017, 27, 083101. [Google Scholar] [CrossRef] [PubMed]
- Li, C.; Sprott, J.C.; Yuan, Z.; Li, H. Constructing chaotic systems with total amplitude control. Int. J. Bifurc. Chaos 2015, 25, 1530025. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C.; Xing, H. Constructing chaotic systems with conditional symmetry. Nonlinear Dyn. 2017, 87, 1351–1358. [Google Scholar] [CrossRef]
- Li, C.; Sprott, J.C. Variable-boostable chaotic flows. Optik—Int. J. Light Electron Opt. 2016, 127, 10389–10398. [Google Scholar] [CrossRef]
- Leonov, G.A.; Vagaitsev, V.I.; Kuznetsov, N.V. Localization of hidden Chua’s attractors. Phys. Lett. A 2011, 375, 2230. [Google Scholar] [CrossRef]
- Leonov, G.A.; Vagaitsev, V.I.; Kuznetsov, N.V. Hidden attractor in smooth Chua systems. Phys. D 2012, 241, 1482. [Google Scholar] [CrossRef]
- Rocha, R.; Ruthiramoorthy, J.; Kathamuthu, T. Memristive oscillator based on Chua’s circuit: stability analysis and hidden dynamics. Nonlinear Dyn. 2017, 88, 2577–2587. [Google Scholar] [CrossRef]
- Bao, B.; Xu, Q.; Bao, H.; Chen, M. Extreme multistability in a memristive circuit. Electron. Lett. 2016, 52, 1008–1010. [Google Scholar] [CrossRef]
- Lai, Q.; Nestor, T.; Kengne, J.; Zhao, X. Coexisting attractors and circuit implementation of a new 4D chaotic system with two equilibria. Chaos Solitons Fractals 2018, 107, 92–102. [Google Scholar] [CrossRef]
- Wang, G.Y.; Zheng, Y.; Liu, J.B. A hyperchaotic Lorenz attractor and its circuit implementation. Acta Phys. Sin. 2007, 56, 3113–3120. [Google Scholar]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Bao, H.; Wang, N.; Bao, B.C.; Chen, M.; Jin, P.P.; Wang, G.Y. Initial condition dependent dynamics and transient period in memristor-based hypogenetic jerk system with four line equilibria. Commun. Nonlinear Sci. 2018, 57, 264–275. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Molaie, M. A simple chaotic flow with a plane of equilibria. Int. J. Bifurc. Chaos 2016, 26, 1650098. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Elementary quadratic chaotic flows with no equilibria. Phys. Lett. Sect. A Gen. Atomic Solid State Phys. 2013, 377, 699–702. [Google Scholar] [CrossRef]
- Bao, B.C.; Bao, H.; Wang, N.; Chen, M.; Xu, Q. Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 2017, 94, 102–111. [Google Scholar] [CrossRef]
- Munmuangsaen, B.; Srisuchinwong, B. A hidden chaotic attractor in the classical lorenz system. Chaos Solitons Fractals 2018, 107, 61–66. [Google Scholar] [CrossRef]
- Lai, Q.; Chen, S.M. Research on a new 3d autonomous chaotic system with coexisting attractors. Optik—Int. J. Light Electron Opt. 2016, 127, 3000–3004. [Google Scholar] [CrossRef]
- Wang, C.; Wei, Z.; Yu, P.; Zhang, W.; Yao, M. Study of hidden attractors, multiple limit cycles from hopf bifurcation and boundedness of motion in the generalized hyperchaotic rabinovich system. Nonlinear Dyn. 2015, 82, 131–141. [Google Scholar]
- Zhou, L.; Wang, C.; Zhou, L. A novel no-equilibrium hyperchaotic multi-wing system via introducing memristor. Int. J. Circ. Theor. App. 2018, 46, 84–98. [Google Scholar] [CrossRef]
- Wang, Z.; Cang, S.; Ochola, E.O.; Sun, Y. A hyperchaotic system without equilibrium. Nonlinear Dyn. 2012, 69, 531–537. [Google Scholar] [CrossRef]
- Chlouverakis, K.E.; Sprott, J.C. Chaotic hyperjerk systems. Chaos Solitons Fractals 2006, 28, 739–746. [Google Scholar] [CrossRef]
- Yuan, F.; Wang, G.; Wang, X. Extreme multistability in a memristor- based multi-scroll hyperchaotic system. Chaos 2016, 26, 073107. [Google Scholar] [CrossRef]
- Ruan, J.Y.; Sun, K.H.; Mou, J. Memristor-based Lorenz hyper-chaotic system and its circuit implementation. Acta Phys. Sin. 2016, 65, 190502. [Google Scholar]
- Lai, Q.; Guan, Z.; Wu, Y.; Liu, F.; Zhang, D. Generation of multi-wing chaotic attractors from a lorenz-like system. Int. J. Bifurc. Chaos 2013, 23, 1650177. [Google Scholar] [CrossRef]
- Si, G.; Cao, H.; Zhang, Y. A new four dimensional hyperchaotic Lorenz system and its adaptive control. Chin. Phys. B 2011, 20, 010509. [Google Scholar] [CrossRef]
- Wang, H.; Cai, G.; Miao, S.; Tian, L. Nonlinear feedback control of a novel hyperchaotic system and its circuit implementation. Chin. Phys. B 2010, 19, 030509. [Google Scholar]
- Zhou, L.; Wang, C.; Zhou, L.L. Generating Four-Wing Hyperchaotic Attractor and Two-Wing, Three-Wing, and Four-Wing Chaotic Attractors in 4D Memristive System. Int. J. Bifurc. Chaos 2017, 27, 1750027. [Google Scholar] [CrossRef]
- Pham, V.-T.; Volos, C.; Gambuzza, L.V. A memristive hyperchaotic system without equilibrium. Sci. World J. 2014, 2014, 368986. [Google Scholar] [CrossRef] [PubMed]
- Xiao, J.; Ma, Z.Z.; Yang, Y.H. Dual synchronization of fractional-order chaotic systems via a linear controller. Sci. World J. 2013, 2013, 159194. [Google Scholar] [CrossRef] [PubMed]
- Zhou, P.; Bai, R. One adaptive synchronization approach for fractional-order chaotic system with fractional-order. Sci. World J. 2014, 2, 490364. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Wang, C.H. Multiscroll hyperchaotic system with hidden attractors and its circuit implementation. Int. J. Bifurc. Chaos 2019, 29, 1950117. [Google Scholar] [CrossRef]
- Zhang, S.; Zeng, Y.C.; Li, Z.J.; Wang, M.J.; Xiong, L. Generating one to four-wing hidden attractors in a novel 4D no-equilibrium chaotic system with extreme multistability. Chaos 2018, 28, 013113. [Google Scholar] [CrossRef]
- Wang, Z.L.; Ma, J.; Cang, S.J.; Wang, Z.H.; Chen, Z.Q. Simplified hyper-chaotic systems generating multi-wing non-equilibrium attractor. Optik 2016, 127, 2424–2431. [Google Scholar] [CrossRef]
- Cang, S.; Wang, Z.; Chen, Z.; Jia, H. Analytical and numerical investigation of a new lorenz-like chaotic attractor with compound structures. Nonlinear Dyn. 2014, 75, 745–760. [Google Scholar] [CrossRef]
- Li, C.; Wang, X.; Chen, G. Diagnosing multistability by offset boosting. Nonlinear Dyn. 2017, 90, 1334–1341. [Google Scholar] [CrossRef]




| Reference | Number of Terms | Number of Equilibrium | Amplitude/Frequency Control | Amplitude/Offset Control |
|---|---|---|---|---|
| [15] | 9 | one | no | not mentioned |
| [28] | 10 | line equilibrium | no | not mentioned |
| [30] | 10 | one | no | not mentioned |
| [31] | 9 | one | no | not mentioned |
| [38] | 9 | no | no | not mentioned |
| this work | 9 | no | yes | yes |
| Parameters | Execution Interval | Amplitude Control | Frequency Control | Offset Control |
|---|---|---|---|---|
| a | [6.9, 23.3] | positive control with x | positive | no |
| b | [3, 13] | positive control with x, y, z, u | positive | no |
| c | [10, 50] | positive control with y negative control with x | no | z |
| m | [0.1, 5] | Positive control with x, y, u | no | no |
| n | [−30, 30] | no | no | u |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Li, C.; Lei, T.; Liu, Z.; Tao, C. A Symmetric Controllable Hyperchaotic Hidden Attractor. Symmetry 2020, 12, 550. https://doi.org/10.3390/sym12040550
Zhang X, Li C, Lei T, Liu Z, Tao C. A Symmetric Controllable Hyperchaotic Hidden Attractor. Symmetry. 2020; 12(4):550. https://doi.org/10.3390/sym12040550
Chicago/Turabian StyleZhang, Xin, Chunbiao Li, Tengfei Lei, Zuohua Liu, and Changyuan Tao. 2020. "A Symmetric Controllable Hyperchaotic Hidden Attractor" Symmetry 12, no. 4: 550. https://doi.org/10.3390/sym12040550
APA StyleZhang, X., Li, C., Lei, T., Liu, Z., & Tao, C. (2020). A Symmetric Controllable Hyperchaotic Hidden Attractor. Symmetry, 12(4), 550. https://doi.org/10.3390/sym12040550





