Improved ‘Infotaxis’ Algorithm-Based Cooperative Multi-USV Pollution Source Search Approach in Lake Water Environment

Abstract

This paper studies the cooperation method of multi-cooperative Unmanned Surface Vehicles (USVs) for chemical pollution source monitoring in a dynamic water environment. Multiple USVs formed a mobile sensor network in a symmetrical or asymmetrical formation. Based on ‘Infotaxis’ algorithms for multi-USV, an improved shared probability is proposed for solving the problems of low success rate and low efficiency resulting from the cognitive differences of multi-USV in cooperative exploration. By introducing the confidence factor, the cognitive differences between USVs are coordinated. The success rate and the efficiency of exploration are improved. To further optimize the exploration strategy, the particle swarm optimization (PSO) algorithm is introduced into the ‘Infotaxis’ algorithm to plan the USVs’ exploration path. This method is called the ‘PSO-Infotaxis’ algorithm. The effectiveness of the proposed method is verified by simulation and laboratory experiments. A comparison of the test results shows that the ‘PSO-Infotaxis’ algorithm is superior with respect to exploring efficiency. It can reduce the uncertainty of the estimation for source location faster and has lower exploration time, which is most important for the exploration of a large range of water areas.

1. Introduction

In recent years, frequent sudden pollution accidents have seriously threatened the ecological environment of water. When pollutants are discharged into water, a dynamic spatial and temporal pollution field is formed. When monitoring the water quality, identifying the source of the pollution in a timely and effective fashion is a key problem. Traditional monitoring methods have difficulty tracking and monitoring such dynamic pollution fields. The great advantages of multiple intelligent monitoring USVs in autonomous detection are providing new solutions for water quality monitoring. However, there are still many issues to be studied, especially in water environments such as lakes. Because lake currents are not as directional as rivers, and do not have clear tidal characteristics like oceans, it is difficult to estimate the location of pollution sources quickly and accurately in cases of emergency monitoring with limited individual knowledge. The slow flow velocity and large turbulence, wind field and environmental noise also cause the pollution fields to present discrete local extrema within a local range, meaning that the USV can easily produce incorrect assessments, affecting the detection efficiency.

With the aim of improving the efficiency of pollution source tracing, this study takes multi-USV cooperative monitoring methods as the means, making use of its good spatial expansion characteristics and information fault tolerance, and the monitoring of sudden lake water pollution as the application scenario in which the research is carried out. An innovative N-PSO information trend method is proposed. Probability distribution is used to represent the distribution of pollution sources in space. Information uncertainty under limited prior knowledge is reduced by sharing information among multiple USVs. By introducing the confidence factor, the cognitive differences between USVs are coordinated. The PSO algorithm is combined with an ‘Infotaxis’ algorithm in order to plan the exploration path. This method effectively avoids premature convergence and improves the exploration efficiency of USVs.

2. Related Work

Recently, intelligent mobile devices such as mobile robots have been used more and more in daily life, in engineering, and in the military. Compared with traditional approaches, mobile robots can reach places in harsh environments [1,2,3]. Mobile robots which simulate biological behavior are used to locate chemical sources. These are referred to as olfactory robots [4]. Robots equipped with chemical sensors can track the chemical plume and then locate the chemical source. Olfactory robots have broad prospects in many applications, such as searching for life signs after earthquakes, locating chemical sources of toxic gas leakage, locating ocean hydrothermal vents, locating fire ignition points, and military detection. Cooperative multi-robot systems, such as unmanned ground vehicles, unmanned air vehicles (UAVs), unmanned underwater vehicles (UUVs) or unmanned surface vehicles (USVs), have shown their superiority over sensor networks in the environmental monitoring domain. In this way, perceptive agents are able not only to adapt their measurement capabilities to the changing environmental conditions, but also to cooperate in gathering information and making intelligent decisions. In this study, we focused on a study of cooperative search approach for water pollution source localization.

Chemical concentration trend is a commonly used search method for mobile robots. It relies on local concentration gradient to guide the robot to move toward the chemical source based on simulating the crawling behavior of animals in tracking odorants. In [5], a chemical source search method was proposed based on solid formal principles from the field of fluid mechanics. A mobile sensor network composed of multiple robots is used to sense the ambient fluid velocity and chemical concentration, and calculate derivatives. Fluid dynamics and flux tropism are used to guide the robot to move to the chemical source. In [6], two three-dimensional moth-inspired odor tracking algorithms, Counter-turner and Modified counter-turner, were tested on a robotic platform. Flight tracks show promise in mimicking the flight tracks observed in biological experiments with moths. In [7], the results from a 3-D computer simulation of an autonomous unmanned aerial vehicle (UAV) were presented for tracking a chemical plume to its source. The simulation study includes a simulated dynamic chemical plume, six degrees of freedom, a nonlinear aircraft model, and a bio-inspired navigation algorithm.

For the chemical trend search method, the detected chemical concentration should be sufficiently high to ensure that the average concentration difference measured by the robot at two adjacent locations is greater than the fluctuation error. The ratio of signal to noise depends on the time course and increases with waiting time. Nevertheless, the average concentration may decay rapidly (sometimes exponentially) with increasing distance from the chemical source. A signal-to-noise ratio that is weaker in this way will make the waiting time for concentration detection too long. In addition, during the waiting time, the concentration information may change. Meanwhile, different types of pollution sources emit different pheromones. Some of them are diffused with the flow, and show a clear concentration gradient feature, such as liquid chemical pollutants. Some of them are rapidly diffused at the beginning but form a uniform oil film which will drift along with the water after reaching a certain degree of diffusion, such as the oil pollutants. Some of them emit sporadic pheromones, such as when solid waste is dumped. The environmental factors also have a great impact on morphology. Slowly flowing water and wind fields cause the pheromones to present better continuity. However, turbulence may break up pheromones and make them discrete and irregular. These factors cause the chemical concentration tend search method to be unreliable in complex environments. Robots may lose their tracking targets due to disordered local information, or may obtain inaccurate concentration information due to a high signal-to-noise ratio. Sometimes, they may fall into extreme values of local concentration and make incorrect decisions.

In the last decade, an ‘Infotaxis’ algorithm was proposed, which has been well developed in the past few years. In [8], a strategy of information trend for olfactory tracing was presented. Information entropy plays a similar role as the concentration gradient in the method of chemical concentration trend. The strategy of the ‘Infotaxis’ algorithm is to maximize the expected information gain. By comparing the predicted information gains, the searcher always moves towards the location with maximum information gain. The uncertainties of the probability are reduced continuously with the exploration of robots, until the source location is located. This ‘Infotaxis’ algorithm makes the exploration independent of the concentration gradient, and it can be applied in turbulent environments with unstable concentration cues or in weak sensing environments which is far from the chemical pollution sources.

In lake water environments, because of the wide range of the working space, there are some shortcomings in using a single USV for target detection.

(1) Although the ‘Infotaxis’ algorithm does not depend on the continuous concentration gradient distribution, when a single USV explores within a discrete clue distribution field, it may still terminate the exploration because of losing clues.

(2) Due to the lack of global information, the exploration process is vulnerable to being influenced by sensor information that sets off false alarms, changing environmental information, and other factors, thus resulting in incorrect decision-making. This would lead the efficiency of the exploration to become very low, extending the exploration time.

(3) Due to the limited environmental information obtained, a single USV may fall into local extreme values, resulting in misjudgment.

(4) Once the single USV fails, the task cannot be completed.

With the development of intelligent robots, more and more attention has been paid to multi-agent theory and technology [9,10,11]. Compared with the single robot exploration method, multiple robots can achieve decreased information entropy more quickly and locate the chemical source more effectively. In [12,13,14,15,16], the ‘Infotaxis’ algorithm for multiple cooperative robots was proposed and applied. However, the cooperation strategy of multi-USV still needs to be improved, especially when used in wide spaces such as lakes or oceans. The main issues include:

(1)

Simply overlaying the exploration information of multiple USVs cannot maximize the advantages of the multi-USV system.

(2)

Multi-USV systems that lack cooperation make it easy for USVs to search the same area repeatedly. This will lead to the aggregation of multiple USVs in the same area, thus reducing the efficiency of exploration.

(3)

How can a reasonable cooperation strategy be designed to minimize the impact of environmental uncertainty?

Based on the existing ‘Infotaxis’ algorithm, this study proposes an improved shared probability updating method. To further optimize the exploration strategy, the PSO algorithm is introduced into the ‘Infotaxis’ algorithm to plan the USVs’ exploration path.

3. Study Foundation

3.1. Topological Logic for Cooperative Multiple USVs-Remote Centre

The multi-USV system for water quality monitoring designed in this study is shown in Figure 1. It shows the communication link and collaborative decision-making topology diagram of the Multiple USVs Remote Center.

A single USV has the abilities of autonomous navigation, autonomous driving, autonomous monitoring, and intelligent interaction. Multiple USVs are controlled centrally by the remote center. In addition, due to the limited computing ability of USVs, too much complex computing consumes their energy and extends the detection time. Therefore, the remote center undertakes the computing and decision-making tasks for the cooperative behavior of the USVs. As shown in Figure 1, the remote center includes a cloud server and a remote monitoring center. The cloud server receives data communicated by the USVs, and processes and stores the data. Meanwhile, the cloud server provides the decision-making for USVs’ cooperative behavior, and sends the decisions as commands to the USV. The current 4G technology guarantees the communication rate between the USV and the remote center. Even if a large amount of data is transmitted, there will be no delay. The remote monitoring center is able to issue monitoring tasks, check monitoring data, and monitor the implementation of tasks.

3.2. ‘Infotaxis’ Algorithm

3.2.1. Probabilistic Map Building Method Based on the Measurement of Binary Sensors

Suppose the chemical pollution source is located in an unknown position in the space. The matter released by the chemical source is diffused with the flow or wind field, forming the distribution of the pollutant in the water. A USV is equipped with olfactory (chemical concentration) sensors. It is able to measure the concentration of pollutants. In addition to the concentration information, the detected location, detection times, and other information could become clues for the prediction of chemical pollution sources, known as “pheromones”. The pheromone set detected along the trace ${ㄒ}_t$ at a time $t_i$ implies some information about the source location. The clues found by the USV in the trace ${ㄒ}_t$ can be regarded as information sent to the detector by the chemical pollution source. This information is applied in a Bayesian equation to calculate the posterior probability $P_t\left(r_0\right)$ of the unknown source location $r_0$. ${ㄒ}_t$ and $P_t\left(r_0\right)$ are time-varying variables that are constantly updated. The posteriori probability depends on the detect rate $R\left(r|r_0\right)$ in different locations. Here, $R\left(r|r_0\right)$ denotes the contact rate of a chemical substance that is released from a chemical source at position $r_0$ and which came into contact with the contacter at positon $r$.

Reference [9] gives a common expression for the detection rate in a two-dimensional space.

$$R\left(r|r_0\right)=\frac{R}{ln\left(\frac{\lambda }{a}\right)}exp\left(-\frac{V\left(y-y_0\right)}{2D}\right)K_0\left(\frac{\left|r-r_0\right|}{\lambda }\right)$$

(1)

where $R$ is the release rate of the particles released from the chemical source; $a$ is the size of the explorer; τ is the average lifetime of the particles in the process of propagation; D is the isotropic chemical diffusion rate; V is the velocity in the advection flow field; $K$₀ is the zero-order Bessel function of second kind. $\lambda$ is the characteristic length, and its expression is:

$$\lambda =\sqrt{\frac{D\tau }{1+\frac{V^2\tau }{4D}}}$$

(2)

At time t, the posterior probability of the source location $r_0$ relative to the information collected on the path ${ㄒ}_t$ is:

$$P_t\left(r_0\right)=\frac{L_{r_0}\left({ㄒ}_t\right)}{{\displaystyle \int }{L}_{r_x}\left({ㄒ}_t\right)d{r}_x}=\frac{e^{-{{\displaystyle \int }}_0^{t}R\left((r\left(t^{\prime }\right)|r_0\right)d{t}^{\prime }}{{\displaystyle \prod }}_{i=1}^{H}R\left(r\left(t_i\right)|r_0\right)}{{\displaystyle \int } e^{-{{\displaystyle \int }}_0^{t}R\left((r\left(t^{\prime }\right)|r_0\right)d{t}^{\prime }}{{\displaystyle \prod }}_{i=1}^{H}R\left(r\left(t_i\right)|r_x\right)d{r}_x}$$

(3)

Here, H is the number of hits along the trajectory, $t_i$ are the corresponding times and $L_{r_0}$ denotes the possibility of robot passing the path ${ㄒ}_t$ for a source located at $r_0$ [8]. With the development of the exploration, the path ${ㄒ}_t$ extends continuously, the information collected increases gradually, and the probability map is continually updated.

The $e^{-{{\displaystyle \int }}_0^{t}R\left((r\left(t^{\prime }\right)|r_0\right)d{t}^{\prime }}$ in Equation (3) expresses the item not captured clues, and ${{\displaystyle \prod }}_{i=1}^{H}R\left(r\left(t_i\right){|r}_0\right)$ expresses the item captured clues.

At the time of $t+\Delta t$, the posterior probability of source location $r_0$ is:

$$P_{t+\Delta t}\left(r_0\right)=\frac{P_t\left(r_0\right)e^{-R\left(r\left(t+\Delta t\right)|r_0\right)\Delta t}{R}^{\eta }\left(r\left(t+\Delta t\right)|r_0\right)}{Z_{t+\Delta t}}$$

(4)

Here, $\eta$ is the number of clues touched by the detector within the time interval $\Delta t$, and $Z_{t+\Delta t}$ is the normalized constant. $P_{t+\Delta t}\left(r_0\right)$ means the calculated posterior probability for a source location $r_0$. In Equation (4), the item $e^{-R\left(r\left(t+\Delta t\right){|r}_0\right)\Delta t}{R}^{\eta }\left(r\left(t+\Delta t\right){|r}_0\right)$ represents the likelihood of the detector receiving $\eta$ hits in the interval $\Delta t$. Therefore, $P_t\left(r_0\right)$ can be seen to depend only on the hits received in the $\Delta t$ interval and $P_t\left(r_0\right)$. Thus, keeping track of the whole trajectory and the history of detections is not necessary [8]. According to Equation (4), the detector only needs to record the $P_t\left(r_0\right)$ in time $t$ and the hits received in the $\Delta t$.

3.2.2. ‘Infotaxis’ Algorithm-Based Exploration Using a Single Robot

According to the clues obtained, the explorer needs to choose the best exploratory path to reduce the uncertainty of the judgment of the source location. The purpose of information trend is to rapidly reduce uncertainty based on the information obtained, i.e., to rapidly reduce entropy [8].

At time t, the information entropy of the probability distribution of the source location based on the historical clues obtained by the explorer can be calculated as follows:

$$S_t=-\int P_t\left(r_x\right)log{P}_t\left(r_x\right)d{r}_x$$

(5)

The next detection target of the explorer can be set to the position at which the estimated information entropy is most decreased. If at the next moment, the explorer has eight adjacent points as possible moving target points, as shown in Figure 2, then the explorer needs to determine which location will result in the greatest reduction in entropy at the next detection step.

The estimated change in entropy after detection at the next position can be calculated using the following equation:

$$\overline{\Delta S\left(r_i\to r_j\right)}=P_t\left(r_j\right)\left[-S_t\right]+\left(1-P_t\left(r_j\right)\right)\left[{\displaystyle \sum }_{k=0}^{\infty }{\rho }_k\left(r_j\right)\Delta S_k\right]$$

(6)

where ${\rho }_k\left(r_j\right)$ is the probability of k times touching the cues in the time of $t$. In a conservative case, even if the detector does not move, it will still obtain ${\rho }_k\left(r_j\right)$. Each independent detection satisfies the Poisson equation, ${\rho }_k=h^k\exp \left(-h\right)/k!$, where h is the average number of hits. At position $r_j$,

$$h\left(r_j\right)=\Delta t\int P_t\left(r_0\right)R\left(r_j|r_0\right)d{r}_0$$

(7)

where $R\left(r_j|r_0\right)$ is the cue detection rate; t is the time step.

Through the evaluation of information entropy, the explorer can make the decision as to the next action by choosing the maximum amount of information expected to be obtained. Specifically, at each time step, the explorer chooses the neighboring node with the smallest $\overline{\Delta S}$ value (usually negative) as the moving target.

In this method, the step length of the explorer is definite, that is, the distance from the current position to the adjacent point. In general, the range of each sampling point is the size of a robot. This method is effective, but there are still some shortcomings:

For one thing, within a small range of an indoor space, the size of the node is appropriate. However, in broader outdoor spaces, there are too many points needing to be explored. Therefore, the process is slow.

For another thing, in water environments, the information obtained at adjacent nodes may exhibit minimal difference, for example, the number of hits of the clues at the detection points may similar, thus causing the entropy to drop slower. Therefore, the speed of convergence of the algorithm is slow.

3.2.3. ‘Infotaxis’ Algorithm-Based Exploration Using Multiple Robots

Shared Probability Map Computation Based on Bayesian Framework

The basic method for cooperatively locating chemical pollution sources using multiple robots is information sharing. The explorers work together to build a probabilistic map. Assuming that the detection events of multiple robots are independent, the probability that the $r_0$ position is a chemical pollution source is $P_t\left(r_0|{ㄒ}_{n1}{}_t\right)$, which is calculated by robot $n_1$ according to the cues obtained on its path at moment $t$. Similarly, the probability calculated by the robot $n_2$ is $P_t\left(r_0|{ㄒ}_{n2}{}_t\right)$. According to the Bayesian joint probability [13], under the condition that n numbers of robots have detected clues on their respective paths, the probability that the $r_0$ position is the chemical pollution source can be calculated by:

$$P_t^{sh}\left(r_0\right)=\frac{{{\displaystyle \prod }}_{i=1}^n{P}_i}{{{\displaystyle \prod }}_{i=1}^n{P}_i+{{\displaystyle \prod }}_{i=1}^n\left(1-P_i\right)}$$

(8)

$P^{sh}$ can be understood to be the sharing probability of the source location calculated by multiple explorers. At the same time, the shared probability $P^{sh}\left(r_i\right)$ of each location constitutes a shared probability map.

According to Equation (4), at time $t+\Delta t$, the sharing probability is updated according to the clues added on each robot’s trajectory ${ㄒ}_t^1$ at time interval $\Delta t$:

$$P_{t+\Delta t}^{sh}\left(r_0\right)=\frac{P_t^{sh}\left(r_0\right){{\displaystyle \prod }}_{i=1}^n\left[e^{-R(r_i\left(t+\Delta t\right)|r_0)\Delta t}{R}^{\eta i}(r_i\left(t+\Delta t\right)|r_0)\right]}{Z_{t+\Delta t}}$$

(9)

where $\eta i$ is the number of touches of the clues by the i-th robot during interval $\Delta t$.

From Equation (9), it can be seen that $P_{t+\Delta t}^{\mathrm{sh}}\left(r_0\right)$ depends on $\eta i$ and the sharing probability $P_t^{sh}\left(r_0\right)$ at time t. When $P_t^{sh}\left(r_0\right)$ is known, it is only necessary to record the $\eta i$ of each robot in the time interval $\Delta t$.

Information Entropy Prediction of Multi Robot Exploration

The entropy change of multi robot exploration can be calculated through the following equation:

$$\overline{\Delta S\left(\left\{r_i\right\}\to \left\{r_i^{\prime }\right\}\right)}=-S{P}_t^{\ast }(\{r_i^{\prime }\})+(1-P_t^{\ast }(\{r_i^{\prime }\})){{\displaystyle \sum }}_{k_1=0}^{\infty }\cdots {{\displaystyle \sum }}_{k_n=0}^{\infty }\Delta S_{\left\{k_i\right\}}{{\displaystyle \prod }}_{j=1}^n{\rho }_{kj}\left(r_j^{\prime }\right)$$

(10)

where $P_t^{\ast }={\displaystyle \sum }_j{P}_t\left(r_j^{\prime }\right){\displaystyle \prod }_{k\ne j}\left(1-P_t\left(r_k^{\prime }\right)\right)$ is the probability of the source being found by an explorer, symbol {} represents the set of n possible variables, and n is the number of explorers. $\left\{r_i\right\}=\left\{r_1,r_2,\cdots ,r_n\right\}$, $\left\{r_i^{\prime }\right\}=\left\{r_1^{\prime },r_2^{\prime },\cdots ,r_n^{\prime }\right\}$. Compared with exploration using a single robot, the entropy drop resulting from using multiple robots is faster, and enables the explorer to find the source position more quickly. In the same exploration area, with the increase in the number of robots, the speed of exploration increases. However, the increase in the number of robots also increases the cost of computation. If one robot has l choices at time $t+\Delta t$, for n robots, the possible choice of behavior is $n^l$, and the amount of computation increases exponentially. To simplify computation, some researchers limit the value of $k_j$ [13]. For example, the value of $k_j$ is limited to 0–1, which means that the detection results are simplified into either touching a clue or not touching a clue at position $r_i^{\prime }$.

4. Improved Shared Probability Updating Method Based on Information Confidence Level Judgment

4.1. Method Introduction

In the process of cooperative detection of multiple USVs, due to differences in some factors, such as the distance between the USVs and the chemical source, or the sampling accuracy of the USVs, the pheromones obtained by different USVs may be quite different, which makes the cognitive level of USVs different.

Generally, the USVs that are closer to the chemical source are able to obtain more pheromones, while the USVs that are further away from the chemical source are able to obtain less pheromones. USVs located in different positions may have different cognitive abilities. As shown in Figure 3, the information sampled by the USVs in different positions causes them to have some deviation in estimating the location of the source. The greater the distance between the two USVs is, the greater the difference in the sampled information is, and the greater the deviation of the probability maps obtained. Therefore, when calculating the shared probability map, we need to consider the difference of the cognitive level of each USV. In [16], a correlation parameter was introduced to weigh the cognitive differences among individuals. The smaller the individual cognitive differences are, the greater the individual’s recognition of population information is. On the contrary, the greater the cognitive difference between individuals is, the lower the individual’s recognition of group information is. In this approach, the choice between individual information and population information is considered, but the confidence level of individual information is not considered. In our study, confidence factors are introduced to coordinate the cognitive differences between USVs.

The evaluation of the confidence level between individual mainly considers the following two factors:

(1)

The closer the USV’s sampling location nears to the chemical pollution source, the higher its confidence is. The closer the USV is to the chemical pollution source, the greater the probability that it will sample information indicating excessive chemical substances, thus giving it more confidence.

(2)

The more pheromones that the USV obtains at the sampling position, the higher the confidence assigned to it. The more times a USV touches cues in its position, or the higher the chemical concentration of the sample, the greater its likelihood of approaching a chemical source, thus giving it more confidence.

Based on this, when calculating the source probability of each position in the map, assuming that the position of the assumed target is $r_j$ and the position of the USV i is $r_i$, a distance confidence factor of USV i could be defined as:

$$D_{d_{i,j}}=\frac{2}{n}-\frac{d_{i,j}}{{{\displaystyle \sum }}_{i=1}^n{d}_{i,j}}$$

(11)

where $D_{d_{i,j}}$ is the distance confidence factor, and n represents the total number of USVs, ${\displaystyle \sum }_{k=1}^n{D}_{d_{i,j}}=1$, $d_{i,j}$ is the distance between the target and the USV.

Suppose ${\eta }_i$ is the number of cues that USV $i$ touches in its sampling position at the time interval t.

$$h_i=\frac{{\eta }_i}{{{\displaystyle \sum }}_{i=1}^n{\eta }_i}$$

(12)

Here, $h_{i_k}$ is the clue confidence factor.

The confidence factor obtained by USV $i$ at step $k$ is:

$${\sigma }_i=D_{d_{i,j}}\ast h_i$$

(13)

$${\displaystyle \sum }_{i=1}^n{\sigma }_i=1$$

Equation (9) can be rewritten as:

$$P_{t+\Delta t}^{sh}\left(r_0\right)=\frac{P_t^{sh}\left(r_0\right){{\displaystyle \prod }}_{i=1}^n\left[e^{-R(r_i\left(t+\Delta t\right)|r_0)\Delta t}\ast {\sigma }_i\ast R^{\eta i}(r_i\left(t+\Delta t\right)|r_0\right]}{Z_{t+\Delta t}}$$

(14)

Equation (14) is the updating equation of shared probability with confidence factor. It takes into account the cognitive differences between the individual USVs, and evaluates the cognitive level. The USV with higher confidence is given more weight.

4.2. Case Study

To validate the effectiveness of the proposed algorithm, a simulation of single USV exploration and double USV exploration was carried out, assuming there was a chemical pollution source in an exploration space. The exploration space was mapped with a grid. The environmental and pollutant parameters were as follows: the search space was 10 m × 10 m; the length and width of the unit grid were same as the length of a USV; the chemical release rate of the pollutant source was R = 1; the average life of the released particles was $\tau =2500$; the direction of the flow velocity was along the y axis; the flow velocity was V = 0.2 m/s; and the pollutant diffusion velocity is D = 0.1 m/s (isotropy). The chemical pollution source was located in grid (10, 3).

The case was calculated in MATLAB. The probability maps were separately explored by a single USV, by two USVs cooperating without considering cognitive differences, and by two USVs cooperating in consideration of cognitive differences, respectively. The three moments in the exploration process were recorded as t₁, t₂ and t₃. Figure 4, Figure 5, Figure 6 and Figure 7 are probability maps obtained from several cases at three-time moments.

Figure 4 and Figure 5 are two probabilistic maps which independently explored by two USVs. The initial position of USV 1 is (1, 3), and the initial position of USV 2 is (1, 5). As can be seen from Figure 4, the convergence rate of the source probability is faster because the USV 1 is closer to the source (on a straight line with the current). USV 2 obtains less pheromones and slower probability convergence because of its relatively great distance from the chemical source, as shown in Figure 5. It can be seen that the convergence speed of the source probability is obvious influenced by the following factors: (1) the distance between the target position of the USV obtained information and the position of the chemical pollution source; (2) the angle with the centerline of the water flow through the source position. The farther away from the source the clues are, or the greater the angle with the flow direction, the slower the convergence rate of the source probability is. Due to the different recognition degree between the two USVs, the final judgment of the source location is different, making exploration using a single USV in some complex environments prone to error.

Figure 6 is the source probability map obtained from two USVs without considering the difference of cognition. Figure 7 is the source probability map obtained from two cooperative USVs considering the difference of cognition. In the process of cooperative exploration by multiple USVs, if the cognitive differences of the USVs are not considered, then in the initial stage, the cognitive differences of the USVs made the sharing probability extremely low, thus affecting the convergence speed of the sharing probability, as shown in Figure 6. Despite the USVs’ cognitions exhibit gradual convergence, the overall efficiency of the exploration is still low. The greater the cognitive differences between USVs is, the more obvious the impact is.

Considering the cognitive differences, the convergence rate of the shared probability is greatly improved by using the information confidence judgment-based method, as shown in Figure 7.

5. ‘PSO-Infotaxis’ Algorithm-Based Exploration of Cooperative USVs

According to the above study, it can be seen that there are still some shortcomings in the application of the multi-USV information trend search method.

(1) Multi-USV exploration can only share information about probabilistic maps, but there are no cooperative measures. When exploring, only the information obtained by the individual USV is considered, which lowers the exploring efficiency, and the USV can easily fall into local extreme values and make incorrect judgments.

(2) The exploration method in consideration of cognitive differences can avoid falling into local optimal solutions. Multi-USV cooperation can achieve better fault tolerance, making the detection results more robust. Nevertheless, the method is still based on a simple cooperation method without considering coordination between individual cognition and the population’s experience, which lowers the search efficiency.

(3) The next step of the standard information trend method is to locate the target location adjacent to the explorer. In small spaces, this method is more effective. However, in large areas of space, the exploration step is too small. The speed of convergence is significantly affected by the size of the space.

If the multi-cooperative USV exploration system is regarded as a social population, the behavior of each individual in it will be affected not only by its past experiences and cognition, but also by overall social behaviors. The manner in which this cooperative role can be better achieved, and in which the search strategy can be adjusted in accordance with own-historical experience and group behavior in order to improve the efficiency of method, is the next problem to be solved. A meta-heuristic algorithm, which inspired our study, is a combination of a stochastic and a local search. In [17], a novel adaptation of the multi-group quasi-affine transformation evolutionary algorithm for global optimization was proposed. In [18], a compact pigeon-inspired optimization algorithm was proposed to solve complex scientific and industrial problems with many data packets, including the use of classical optimization problems and the ability to find optimal solutions in many solution spaces with limited hardware resources. Those studies provide a feasible solution to the problem under acceptable computational time and space, and the solution cannot be predicted in advance [19].

In this study, the PSO algorithm is introduced into the information trend search algorithm to plan and adjust the USVs’ exploration path. This method is called the ‘PSO-Infotaxis’ algorithm.

5.1. Basic Idea of Standard PSO

PSO was initially proposed by Eberhart and Kennedy [20,21]. Its basic concept originates from the study of the foraging behavior of birds. The basic PSO algorithm is expressed in the following. Assume that the search space of n dimensions comprises populations with n particles, where the position of each particle can be expressed as a vector of $X_i=\left(X_1,X_2,\cdots ,X_n\right)$^T. According to the objective function, the fitness value corresponding to each particle’s position $X$ can be calculated. The velocity of the i-th particle is expressed as V_i = (V₁, V₂ ⋯ V_n)^T, and its individual extreme values denote the optimum historical position of the particle, which is expressed as $P_i={\left(P_1,P_2,\cdots ,P_n\right)}^T$. The extreme value of the population is the optimum historical position of particle populations, which are expressed as $P_g$. In the t-th iteration, the updating formula of particle velocity and position is as follows:

$$V_i^{t+1}=w{V}_i^t+c_1{r}_1\left(P_i^t-X_i^t\right)+c_2{r}_2\left(P_g^t-X_i^t\right)$$

(15)

$$X_i^{q+1}=X_i^q+V_i^{q+1}$$

(16)

where $w$ is the inertial weight, which represents the degree of inertial motion of a particle in accordance with its own velocity. It is linearly reduced with the number of iterations.

$$w=w_{max}-iter·\frac{w_{max}-w_{min}}{ite{r}_{max}}$$

$$w_{max}=0.9$$

$$w_{min}=0.4$$

$c_1$ and $c_2$ are learning factors which represent the experience learned from the particle and the particle group, respectively. The values of $c_1$ and $c_2$ are usually 2. $r_1$ and $r_2$ are random numbers between 0 and 1 [19].

5.2. ‘Infotaxis’ Algorithm of Multi-USV Exploration Based on Improved PSO

The algorithm proposed in this study is inspired by PSO. The multiple USVs are regarded as particles, and form the particle population $X_i={\left(X_1,X_2,\cdots ,X_n\right)}^T$. When dynamic particles sample in exploratory space, their own knowledge about their previous experience and the shared knowledge with other particles are used as guidance to make local exploratory behavior more efficient. The PSO identifies the knowledge shared by the group as much as possible. Meanwhile, it retains the consideration of the experiences of the particle itself. This makes the cooperation among the multiple USVs more effective.

The speed and position of particles are decided according to PSO. The optimal values of the probability of the source location detected by the USVs are taken as the fitness function. For the particle i, in the t-th iteration, the extreme value is the historically optimal position that possesses the best fitness value on its trajectory. This is the $P_i^t$ in Equation (15). $P_g^t$ is the best location of the fitness function value of the whole particle population. The fitness function of the whole particle population is the shared probability calculated according to Equation (14).

$P_i^t$ and $P_g^t$ can be expressed as follows:

$$P_i^t=\arg \max \left(P_t\left(r_j\right)\right)$$

(17)

$$P_g^t=\arg \max \left(P_t^{sh}\left(r_j\right)\right)$$

(18)

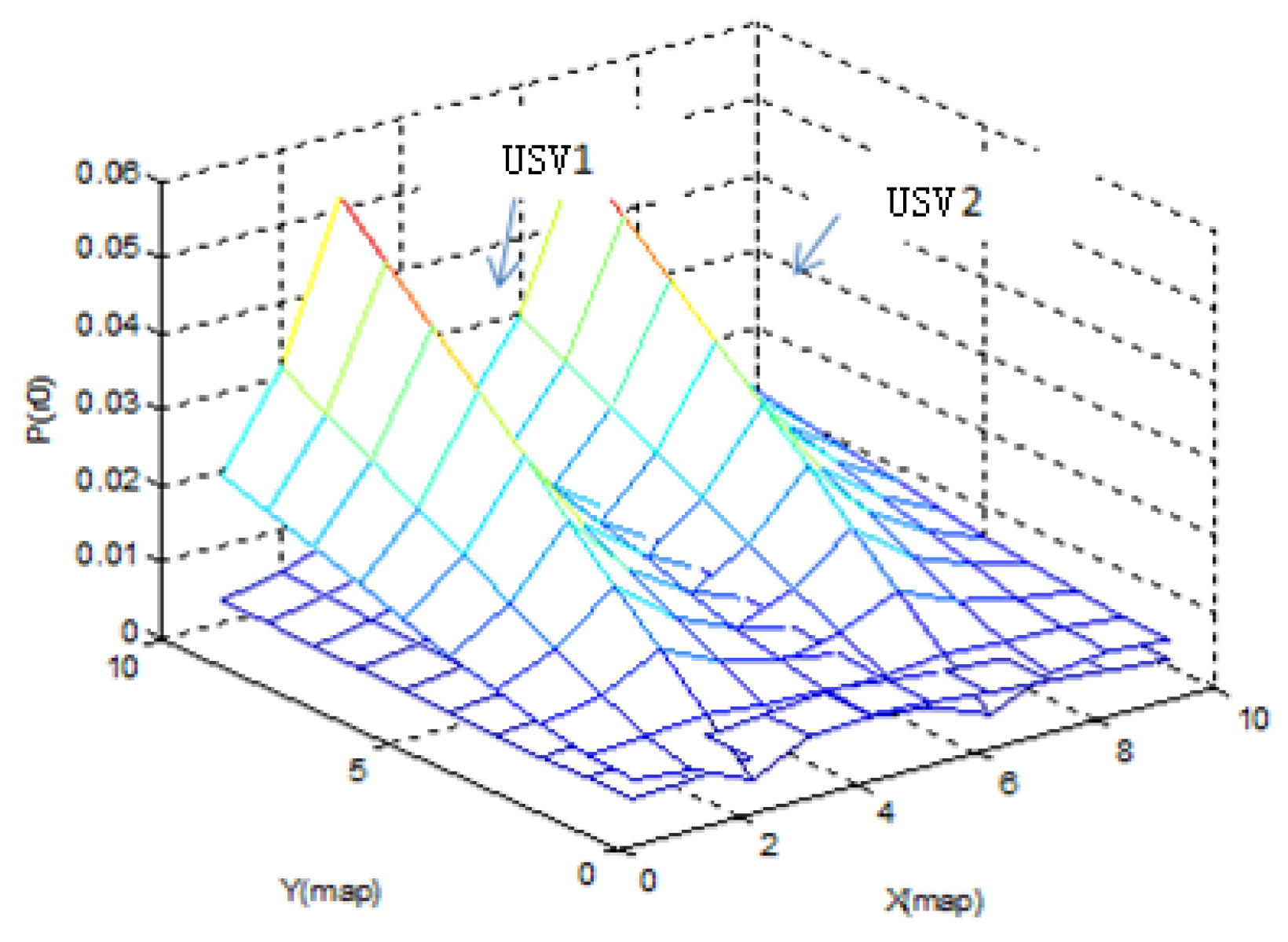
Here, $P_t\left(r_j\right)$ is the probability of source position estimated in USV i’s t-th iteration, and $P_t^{sh}\left(r_j\right)$ is the sharing probability of source position estimated in the multiple USVs’ t-th iteration.

The next exploration position of USV i is calculated from Equations (15) and (16). $V_i^{t+1}$ can be understood as the step length of the USV’s next movement.

To overcome the shortcomings of less numbers of particles, and avoid premature convergence, it is necessary to enrich the diversity of particle selection. This study further improves the standard PSO. The $r_1$ and $r_2$ in Equation (15) respectively take different random values to generate population $V_i^{t+1}={\left(V_1^{t+1},V_2^{t+1},\cdots ,V_n^{t+1}\right)}^T$, where $i$ is the size of the population that is generated. To avoid excessive computation, the value of $i$ is limited to less than 8.

For n particles $V_i^{t+1}=\left(V_1^{t+1},V_2^{t+1},\cdots ,V_n^{t+1}\right)$, take it into Equation (16) and obtain the corresponding position population of each particle: $X_i^{t+1}={\left(X_1^{t+1},X_2^{t+1},\cdots ,X_n^{t+1}\right)}^T$. According to Equation (10), we can calculate the best combination of positions with maximum entropy reduction as the exploration target of USVs at moment $t+1$. The method is iterated until the source of chemical pollution is found or the limit of iterations is reached.

5.3. The Overall Process of the Method

Step 1: The local map is rasterized, where the direction of the X or Y axis on the map corresponds to the direction of the water flow. Initialize the speed and position of particles in the population. The initial probability distribution in each grid cell of the map is $P_{t=0}\left(r_0\right)=\frac{1}{N}$, where N is the number of cells.

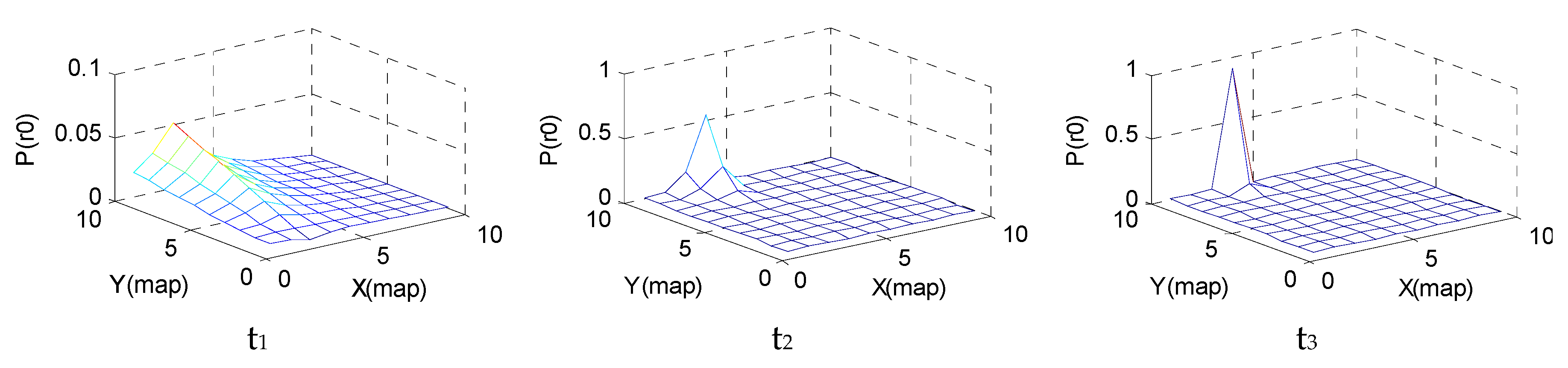
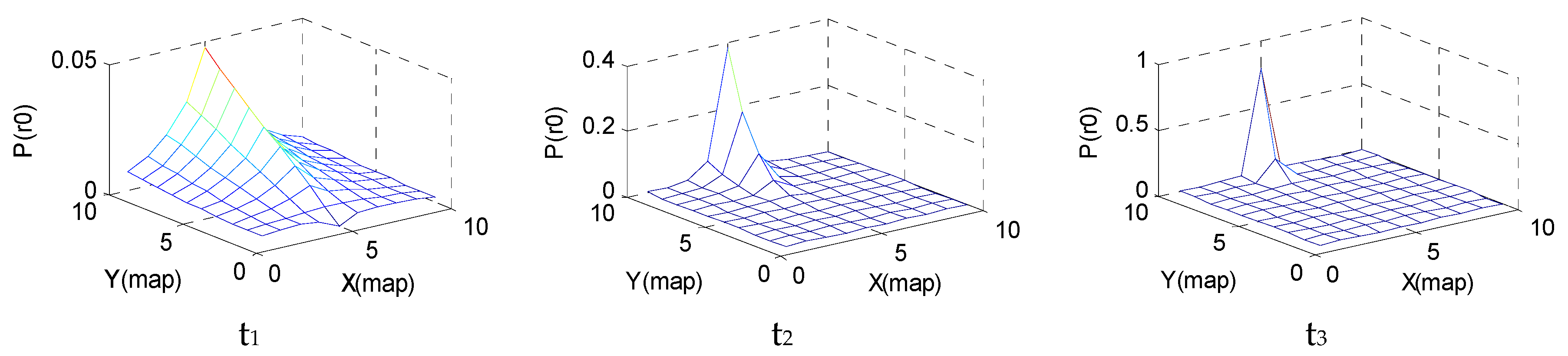
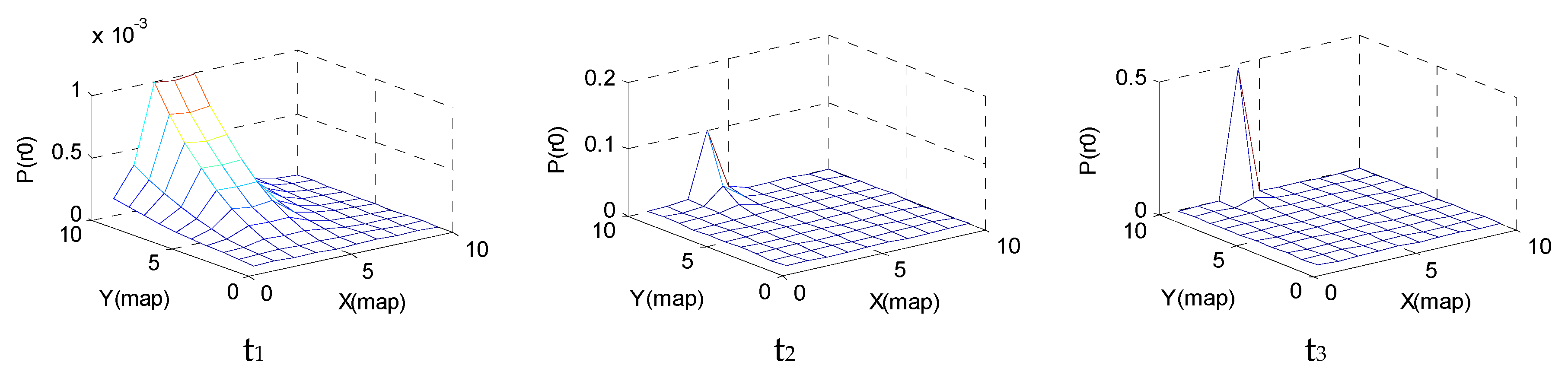
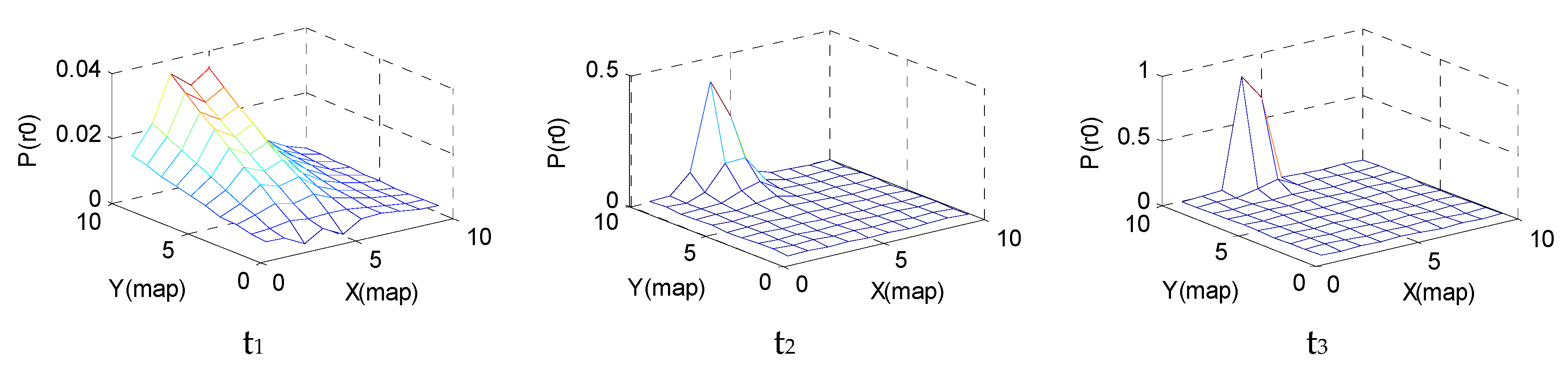
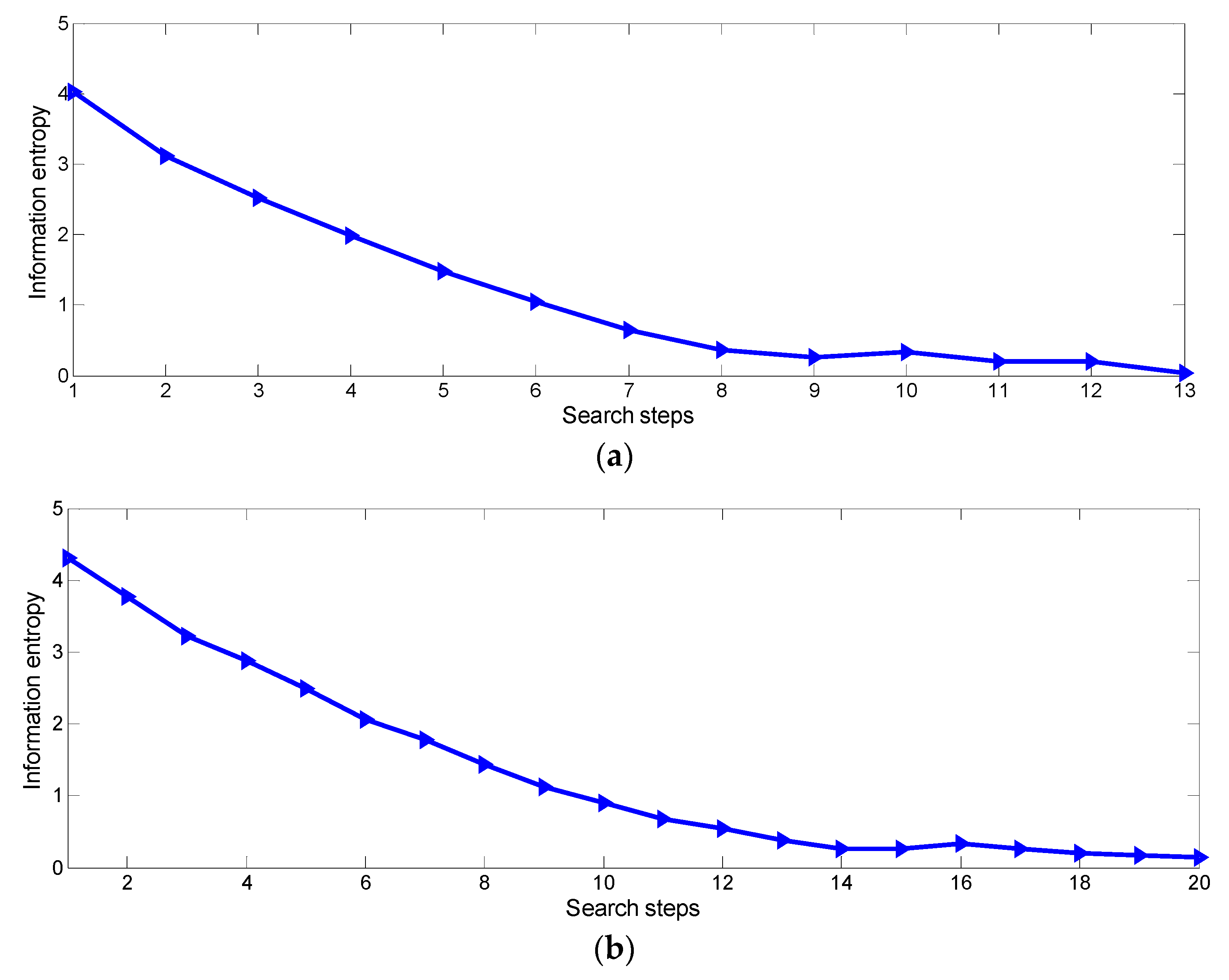
Step 2: According to the clues detected by the particles in their respective positions, the posterior probability distribution on the map is calculated according to Equation (4). The information entropy value based on the historical clues obtained by the particles at time t is calculated through Equation (5). For multiple USVs, the sharing probability is calculated according to Equation (14).

Step 3: The position of the optimal posterior probability of the particle, that is, $P_i^t$ in Equation (15), is updated. The position $P_g^t$, which is the optimal fitness value of the whole particle population, is updated.

Step 4: The speed and location set of each particle are calculated according to Equations (15) and (16).

Step 5: According to Equation (10), the best moving position combination of particles with the greatest entropy drop in each particle population is calculated.

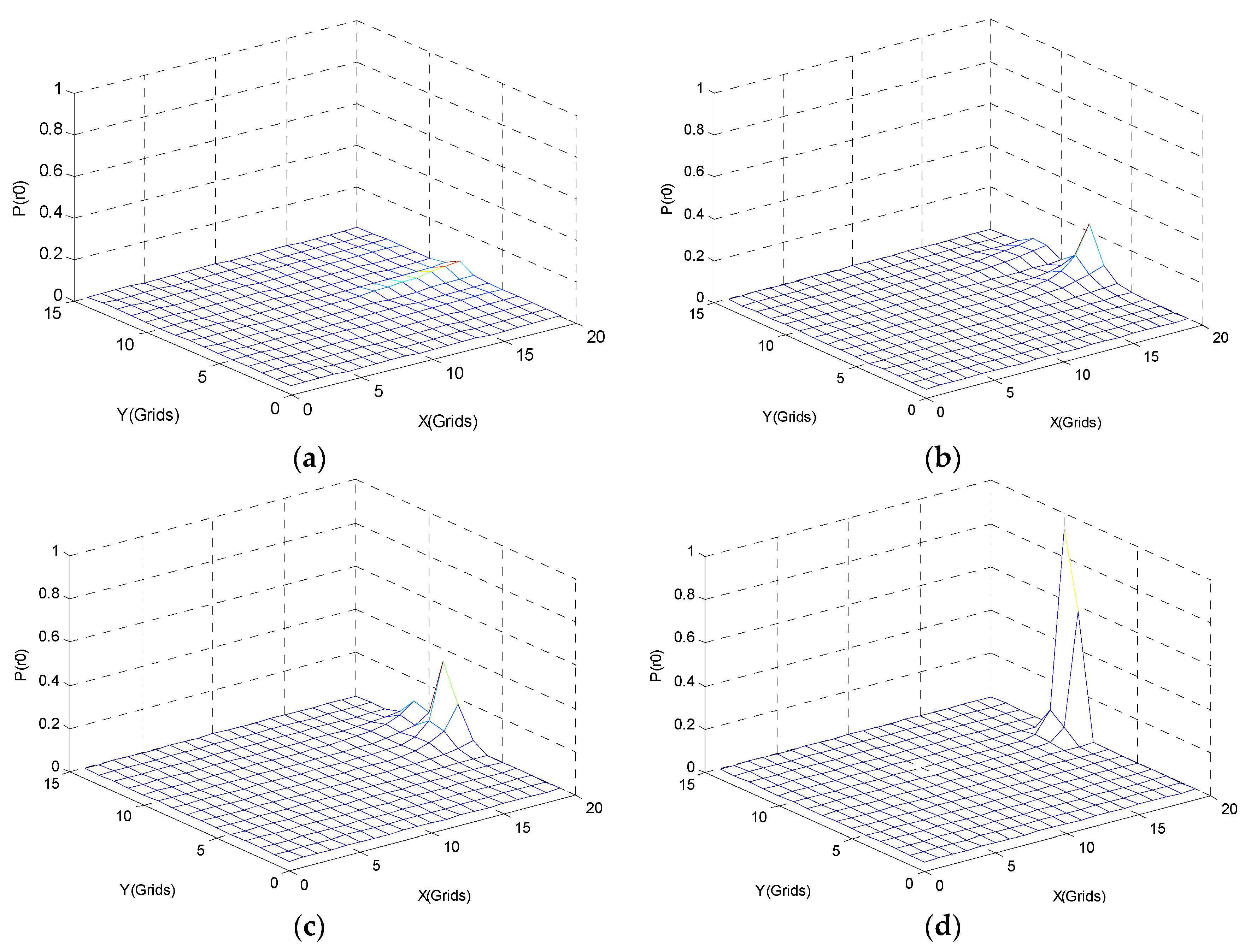
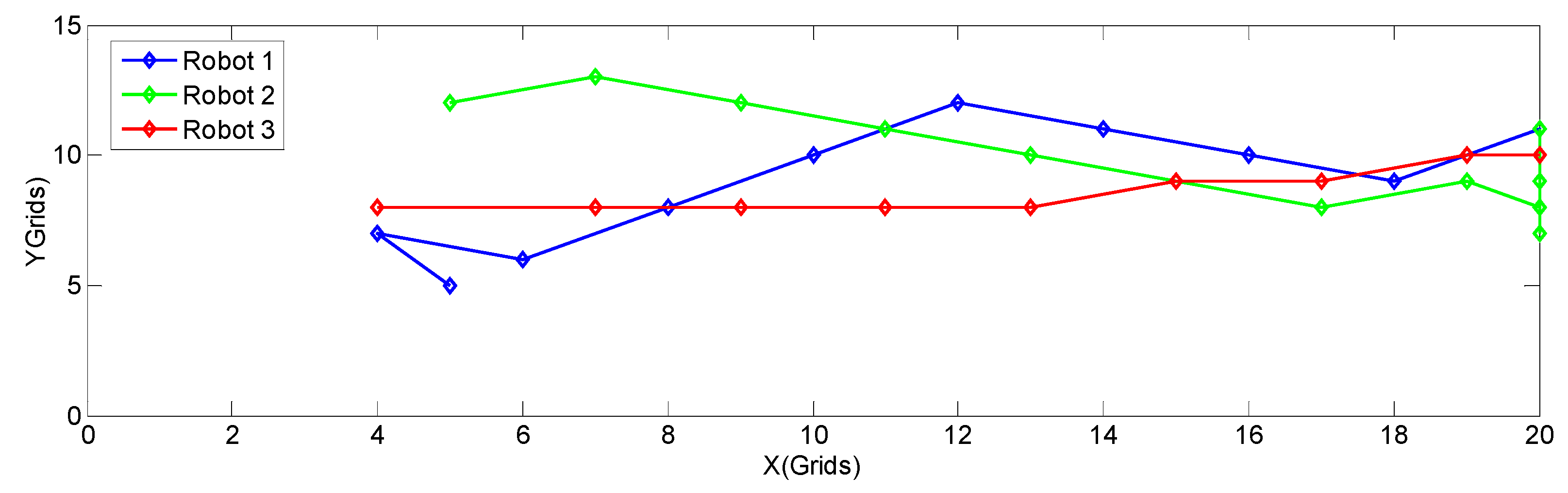
Step 6: The USVs move to their next target points and record the clues obtained.

Step 7: Repeat Step 3 for iteration.

Step 8: If the global fitness value $P_g^t$ reaches a certain limit (in this study set to 0.9), and its position does not change during the set time interval $T_0$, the chemical pollution source confirmation procedure is started. If the chemical pollution source is confirmed, the task is ended. Otherwise, the local map is expanded and Step 1 is repeated to continue execution.

6. Experimental Study

6.1. Construction of Test Platform

To verify the effectiveness of the approach, a chemistry source exploration experiment was designed using three robots. Because of the limitations of the test conditions, the experiment cannot be carried out in an actual lake environment. Therefore, the experiment was carried out indoors in a simulated lake environment. To simulate the propagation process of chemical pollutants in water, a dynamic contaminant diffusion map is projected on the ground by a projector. The projector is short-focal and wide-angle. The size of the mobile robot is 20 cm × 15 cm. The actual size of the mobile USV on water is 120 cm × 30 cm. This means that the actual monitored water environment is scaled down. The exploration area is divided into a 20 cm × 15 cm grid. There are 300 grid cells in the region. The size of each grid cell is 20 cm × 20 cm, which is similar to the actual size of the robot.

According to the convection–diffusion equation [22], the process of drift and diffusion of the pollutant in two-dimensional space is simulated, and the process is expressed by dynamic image. The dynamic image is projected onto the ground. Different concentrations of pollutant are expressed by different gray values. The scene of the polluted water environment simulated by a projected dynamic image is shown in Figure 8. The robot uses a CCD camera to identify the dynamic color changes in the image, which are considered to represent the concentration of pollutants monitored by the USV. If the gray value of the image recognized by robot exceeds the limit value, it can be considered to have detected an above-standard concentration of pollutant. To simulate the number of times the USV touches pollutants in the process of water quality monitoring, the gray level of the color corresponding to water quality is set at several levels. According to the gray value range (0–255), the related grades are divided into several levels. Each level represents the number of contaminant contacts. That is to say, three levels of gray value range respectively represent 1 time, 2 times and 3 times of contact with clues. To avoid the influence of shadow on recognition, the robot carries two cameras, one on each side. This ensures that there is always a camera avoiding the shadowed area at any time, as shown in Figure 8.

6.2. Source Location Tracking Experiment

The location of the pollution source is set at (20,10). The coordinates of the location are the number of grids. The initial location of the three mobile robots is (1,1), (1,2), (1,3). The simulated flow direction is along the negative direction of the X axis. The flow velocity is set to be $v_x=0.02$ m/s. The pollution diffusion velocity is $D_x=D_y=0.01$ m/s. The maximum speed of the robot is 0.3 m/s. There are no obstacles in the exploration area. This experiment simulates the pollutant diffusion process of continuous emission at a fixed point. The robot recognizes the gray value of the projected image which simulates the contaminant in the water. When the robot detects the pollutant exceeding the limit value at a certain position, it then begins the task of tracking the pollutant source.

Figure 9a is the calculated probability map of the pollution source when three robots first detect the above-standard pollutant concentration. Robot 3 first detects excess contamination at position (4,8). Subsequently, robot 3 sends messages to robot 1 and robot 2. They begin cooperative detection. Robot 1 and robot 2 initially detect above-standard pollutant concentration at positions (5,5) and (5,12). The time at which all three robots can simultaneously detect excessive pollutants is regarded as the starting time. According to the location of the above-standard pollutant detected by the three robots and the number of detected times, the probability map of pollutant source can be calculated at the initial moment. It can be seen from the figures that when the above-standard pollutant is detected initially, the calculated probability value is low, because there is no previously accumulated detection data.

Figure 9b shows the source probability distribution at time t = 50 s, and Figure 9c shows the source probability distribution at time t = 80 s. The source probability calculated at these two intermediate moments has obvious extrema in the local region. In addition, the exrema are continually improving. However, several different local extrema appear in the map because of the difference in the recognition degree of the multiple robots. Although cognitive differences are considered in calculation, they are still unavoidable in the calculation results. However, the difference is significantly reduced compared with the algorithm without considering the cognitive difference. Based on the figures, it can be seen from t = 50 s to t = 80 s that the range of the source probability extrema is becoming smaller. This is due to the continuous convergence of cognition of the multiple robots as the exploration process proceeds.

Figure 9d is the source probability map at time t = 182 s. At this time, the extremum of probability has exceeded 0.9, and the extremum region converges to the fixed grid. This means that the source location is very clear. At this time, according to the settings, if the probability extrema of three consecutive computations are all in the same grid, the source location confirmation task will be activated.

Figure 10 shows the trajectory of the three robots. After exploring, the three robots converge near the location of the pollution source. The experimental results show that the three robots cooperate successfully to locate the pollution source, which proves the effectiveness of the proposed method.

In the same scenario, the cooperative exploration strategy of the three robots is changed to the basic ‘Infotaxis’ algorithm without the PSO method. The experimental results are compared with the experimental results using the ‘PSO-Infotaxis’ algorithm.

Figure 11 shows the optimal sharing probabilities of three robots. The optimal shared probability value is the extreme value of probability in the shared probability map. Figure 11a is the optimal sharing probability curve of cooperative exploration by three robots using the ‘PSO-Infotaxis’ algorithm. Figure 11b is the optimal sharing probability curve using the basic ‘Infotaxis’ algorithm. It can be seen that the optimal sharing probability using the ‘PSO-Infotaxis’ algorithm increases rapidly, and the number of exploration steps is less. The robots that use the basic ‘Infotaxis’ algorithm require more exploration steps, with an increase of 75% under the same experimental conditions.

The lower the entropy is, the lower the uncertainty of the source position is. Similarly, the information entropy value of using the ‘PSO-Infotaxis’ algorithm decreases faster than that using the basic ‘Infotaxis’ algorithm, as shown in Figure 12. This shows that the ‘PSO-Infotaxis’ algorithm can reduce the uncertainty of the estimation faster and has a lower exploration time.

6.3. Discussion

In the source location tracking experiment, three robots cooperate to locate the pollution source successfully (as shown in Figure 9 and Figure 10), proving the effectiveness of the proposed method. The comparison experiment compares the optimal sharing probability curve and information entropy curve of ‘PSO-Infotaxis’ algorithm and basic ‘Infotaxis’ algorithm applied by three robots in the same scenario. The more rapidly the optimal sharing probability increases, the faster the source tracking speed is. Information entropy indicates the uncertainty of the estimate of the source position. The lower the information entropy is, the lower the uncertainty of the estimated source position is. From comparison of Figure 11a,b, it can be seen that the optimal sharing probability of using the ‘PSO-Infotaxis’ algorithm increases rapidly, and the number of exploration steps is less. The robots using the basic ‘Infotaxis’ algorithm require more exploration steps, with an increase of 75% under the same experimental conditions. From comparison of Figure 11a,b, it can be seen that the information entropy value of using ‘PSO-Infotaxis’ algorithm decreases faster than that using the basic ‘Infotaxis’ algorithm. This shows that the ‘PSO-Infotaxis’ algorithm can reduce the uncertainty of source location estimation faster while also having a shorter exploration time. The experimental results show that the ‘Infotaxis’ algorithm combined with the PSO algorithm gives a feasible solution to the problem with acceptable efficiency and accuracy.

7. Conclusions

In this study, a chemical pollution source localization approach using multiple cooperative USVs is studied. An improved shared probability updating method based on information confidence judgment is proposed to solve the cognitive difference problem of multiple USVs. The performance method is improved through the introduction of the distance confidence factor and cue confidence factor. The simulation results show that the multi-USV information trend method based on the improved shared probability formula can make up the cognitive differences among the multi-USVs and improve the exploration accuracy of cooperative exploration. To improve the exploratory efficiency of the single-step ‘Infotaxis’ algorithm in exploration decision-making, this study proposes a ‘PSO-Infotaxis’ algorithm to plan the multi-USV walking strategy. An improved PSO algorithm is introduced for the multi-USV information trend exploration method. The experiment platform is built in the laboratory environment. The experiment compares the information trend method using the ‘PSO-Infotaxis’ algorithm and a non-cooperative strategy. The analysis results show that the ‘PSO-Infotaxis’ algorithm is superior to non-cooperative ‘Infotaxis’ algorithm in terms of exploration efficiency.

Due to the limited experimental conditions, this study only verifies the proposed algorithm in the simulated experimental environment. However, in an actual lake water environment, the influencing factors are more complex and unpredictable. Therefore, it is necessary to verify the method of pollution monitoring in the actual environment in future work. Further simplification of the calculation process and the reduction of the calculation workload will be studied.