Abstract
The method of geometric deformation (MGD) is here employed to study compact stellar configurations, which are solutions of the effective Einstein–Dirac coupled field equations on fluid branes. Non-linear, self-interacting, fermionic fields are then employed to derive MGD Dirac stars, whose properties are analyzed and discussed. The MGD Dirac star maximal mass is shown to increase as a specific function of the spinor self-interaction coupling constant, in a realistic model involving the most strict phenomenological current bounds for the brane tension.
1. Introduction
The method of geometrical deformation (MGD) is a protocol emerging in the context of the AdS/CFT membrane paradigm, having general relativity (GR) as a limit that corresponds to rigid branes [1,2,3,4]. The MGD well describes compact stellar configurations in braneworld scenarios [5,6,7]. The MGD has the brane tension, , as a running parameter that encrypts Kaluza–Klein modes and gravity in the bulk as well. A rigid brane corresponds to the GR, , limit. As the brane emulates the universe we live in, cosmological expansion can be implemented from the brane deformation, due to a finite brane tension, into the warped additional dimension of the bulk. In fact, realistic brane-world models take into account a variable brane tension, which is proportional to the brane temperature, according to the Eötvös law [8,9,10].
The MGD is a procedure that derives solutions of the Einstein field equations on the brane, encompassing compact stellar configurations [2,3,4,11]. As a natural step in the membrane paradigm of AdS/CFT [12,13], the holographic entanglement entropy of MGD black holes was computed in [14]. The MGD has observational bounds, derived in [15,16,17,18] in several physical contexts. In the MGD and its extensions (EMGD) [19,20,21,22,23], the finite brane tension governs the deformation of the Schwarzschild solution, in such a way that brane/bulk effects can be implemented. The information entropy was employed to predict critical densities of several types of stars, in the MGD and EMGD contexts [17,18]. Besides, MGD dark glueball stars implementing hidden SU(N) gauge theories [24], whose signature may be detected in eLISA, were scrutinized in [25]. EMGD compact glueball stellar configurations were also studied in [26]. Hydrodynamical analogues of MGD black holes were discussed in [27]. The MGD was also used in [28,29,30,31,32,33,34,35,36,37], that include anisotropic solutions of quasi-Einstein equations [1,38,39,40,41]. Besides, the MGD was employed in the context of the generalized uncertainty principle to study the MGD black hole thermal spectrum [42].
The so called Dirac stars encompass compact stellar configurations generated by fermionic fields [43,44]. Exact solutions for self-gravitating Dirac fields were studied in [45,46,47,48,49,50]. The works [51,52,53] also scrutinize fermionic fields in gravity. Besides, [54] discussed Dirac stars generated by non-Abelian gauge fields. The main aim of this work is to study MGD compact stellar configurations, that are solutions of the effective Einstein–Dirac coupled field equations. The MGD-decoupling method is employed to correct the effective energy-momentum tensor on the brane by fermionic background effects. Non-linear, self-interacting, massive spinor fields are used to derive physical properties of MGD Dirac stellar configurations, with respect to both the finite brane tension and the spinor self-interaction coupling constant. The MGD Dirac star stability is also discussed.
This paper is organized as follows. Section 2 is devoted to introduce a brief review, regarding the MGD applied to stellar configurations on a fluid brane, ruled by a variable tension that encodes the cosmological evolution. In Section 3 the Einstein–Dirac coupled system of ODEs is solved for self-interacting fermionic fields, having the MGD as a natural input. Then, the solutions of the coupled system of ODEs represent MGD Dirac stars, whose observational features are scrutinized and illustrated in several regimes. In Section 4 the conclusions and perspectives are presented.
2. The MGD Setup and Fluid Branes
The MGD procedure is constructed to derive high energy corrections to GR [2,4,23]. Fluid branes have a variable tension that emulates cosmological evolution [8,10]. The extended MGD has been recently employed to derive, in the context of the quantum portrait of black holes, the strictest brane tension bound [18].
The brane Einstein field equations can be derived, by the Gauss–Codazzi projection method, from the Einstein equations in the bulk. Hereon , for is the brane coupling constant, where denotes the Planck mass. The brane metric is governed by the brane effective Einstein field equations
where is the Einstein tensor and stands for the cosmological running parameter on the brane. The energy-momentum tensor in (1) can be split into the following components,
The term denotes the energy-momentum encoding all kind of matter on the brane and is the electric component of the bulk Weyl curvature tensor, taking account the average over the two edges of the symmetric brane, whereas is a tensor whose intricate expression involves quadratic terms of energy-momentum of the brane. Besides, the term comes from an eventual asymmetric embedding of the brane into the bulk, whereas regards the pull back of fields in the bulk that are beyond the standard model, encompassing moduli fields, dilatons and quantum radiation, for instance [10].
Stellar configurations that can be modelled by solutions of Equation (1) are static and spherically symmetric, described by a metric of type
The MGD metric was initially derived in [3,4,11]. One can usually write and , for a more concise notation in what follows. When interior stellar configurations are regarded, nonlinear terms in matter fields, arising from high-energy corrections, set in, what makes analytical solution a hard task to derive. Nevertheless, the MGD and generalizations has been a powerful method to generate analytical solutions [1,2,3,4]. In particular, the MGD generates interior solutions for stellar configurations, that are physically viable.
The MGD method is essentially based on deforming the radial metric component of the interior spacetime associated to a self-gravitating stellar configuration of radius R, where
is the effective stellar configuration radius, for being the compact stellar configuration energy density [2]. This radial metric component deformation, generated by bulk effects, reads [19,20]
where
It contains the usual GR mass function for , and for , whereas the function encrypts anisotropic effects due to bulk gravity on p, and . The function in Equation (5) also depends on the mass, , of the self-gravitating configuration and must be zero in the GR limit, and I is shown below in Equation (9). For interior solutions, the condition must be imposed, precluding singular solutions at . However, in the region , where there is a Weyl fluid surrounding the stellar configuration, . Hence there is a geometric deformation of the Schwarzschild solution. The geometric deformation in vacuum (), hereafter called , will be minimal, reading
The MGD introduces a family of Schwarzschild-like solutions can be generated when it is imposed the Schwarzschild constraint
Hence the Schwarzschild constraint in Equation (10) and the deformed vacuum solution in Equation (8) yield
Yielding an equation for . Next we show the general matching conditions between the generic interior MGD metric characterizing the interior stellar , where is given by Equation (5) with , and the most general exterior solution associated to the Weyl fluid , for , which, according to the expression in Equation (8), can be written as
where the mass . The continuity of the first fundamental form at the stellar surface , when the metric in Equation (12) is considered, yields
whereas the second fundamental form at implies that
where is a unit radial vector and . Using Equation (15) implies , yielding
The Weyl fluid bathing the stellar configuration, described by the functions and , for , implies the matching condition
where , with and . The limit in the second fundamental form in Equation (17) leads to the well-known GR matching condition . Equations (13) and (14) and Equation (17) are the necessary and sufficient conditions for the matching of the interior MGD metric to a spherically symmetric background filled by a Weyl fluid.
Let us now find the explicit MGD function produced by the Schwarzschild solution
Using Equation (18) in Equation (7), we obtain
and the deformed exterior metric reads
which matches the vacuum solution found in [55] in the particular case when , for . The Weyl fluid for the solution (20), (21) is then described by the functions
The function must be specified by considering the deformed Schwarzschild solution (20), (21) in the matching conditions (13), (14) and (17). The first fundamental form leads to the expressions given by Equations (13) and (14), where Equation (13) becomes
whereas the second fundamental form in Equation (17) gives
The matching condition (24) shows that the exterior geometric deformation at the stellar surface is negative. Therefore, the deformed horizon will always be smaller than the Schwarzschild horizon . Hence, bulk effects weaken the strength of the gravitational field of stellar configuration.
Finally, when the explicit geometric deformation (19) is considered in the matching condition (24), the function reads
Showing thus that is always positive and (interior) model-dependent. For instance, we can find by considering the exact interior BW solution found in Ref. [2], where the geometric deformation is given by
where C a constant given by , and . The form of yields [2,3]
implying that
where y is a numerical value, as . It is worth to notice that , so is the expression above plus terms in .
The MGD metric can be rewritten as [2,3]
where
In the general-relativistic limit , the Schwarzschild metric is recovered from the MGD metric.
3. Dirac Stars on Fluid Branes
Compact gravitating configurations on fluid branes, modelled by the MGD with a background spinor field, , of mass m, can be described by the Einstein field Equation (1), coupled to a Dirac equation. To the action that generates the Einstein field equations, it must be added the spinor Lagrangian
where self-interacting spinor fields are implemented by
Here is the set of gamma matrices, that satisfies the Clifford algebra , and is the spinor conjugate. Equation (32) displays non-linear, self-interacting, spinor fields. In fact, compact stellar configurations, which are solutions of the Einstein–Dirac coupled system of equations for linear spinor fields, have mass much smaller than the Chandrasekhar mass. The work [44] considered self-interacting spinor fields, demonstrating that the mass of compact stellar configurations increase several orders of magnitude, encompassing astrophysical stars. A similar approach will be used hereon, in the MGD setup.
Equation (1) can be obtained by varying the bulk Einstein–Hilbert action, when one uses the Gauss–Codazzi equations. In the presence of a spinor field background, one derives the Einstein field equations and the Dirac equation, using the MGD-decoupling method [1]
where is a small parameter driving the MGD decoupling, and the fermionic energy-momentum tensor reads
for . Equation (33) represents the brane Einstein field Equation (1), now corrected by the MGD-decoupling for the spinor energy-momentum tensor in Equation (36).
In order to describe the background spinor field, the following two stationary ansätze for are compatible with the metric (3) [43,44], given by
where are real functions. When one replaces (37) into the field Equations (33) and (34), it yields the coupled systems of ODEs involving also the MGD metric (3):
where, denoting , the following quantities are defined [44]:
The mass of compact stellar configurations, , is usually studied when the spinor field mass, m, is much smaller than the Chandrasekhar mass, .
As the MGD metric (3) is a solution of the Einstein field equations, we want now to verify which are the spinor fields components in (37) that satisfy the coupled system (38)–(40). Hence, numerical integration can be implemented, using boundary conditions near the stellar configuration center, as in [44]:
where quantities indexed by “c” stand for central () values of the respective variables. Some of expansion coefficients in (43) can be derived once Equations (38)–(40) are taken into account. On the other hand, the parameters and are constrained just in order that the Minkowski spacetime be a solution of Equations (38)–(40), in the limit , and .
The lower limit of integration of Equations (38)–(40) is the center of the compact stellar configuration, where is determined. On the other hand, the upper limit of integration is the effective stellar radius where the functions , , and vanish [44]. After numerical integration, the MGD compact stellar configuration mass parameter, , as a function of , has the profile illustrated in Figure 1. Two different values of the coupling constant , driving the spinor field self-interaction in Equation (32), are considered, as well as three different values of the finite brane tension. In fact, as the most strict current bound on the variable brane tension is [18], then in what follows we take the lower brane tension limit , together with and , to study the physical differences among these cases. It is worth to emphasize that the general-relativistic limit corresponds to a rigid brane, making and .
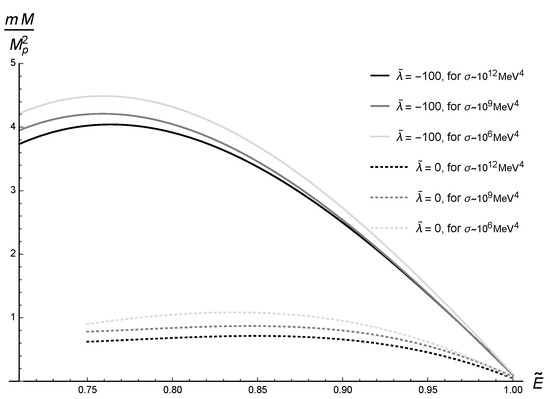
Figure 1.
MGD Dirac star mass, as a function of , shown for two values of the coupling constant, , and for , and . The MGD-decoupling parameter is adopted.
In Figure 1, for fixed values of the spinor coupling constant , there is a peak of the mass, at some value of . The bigger the brane tension, the smaller the maximal mass is, for both analyzed values of . Boson stars were studied in a similar context, where a maximal mass was identified to a transition point, splitting stable and unstable compact stellar configurations [56]. This aspect was emulated and explored for MGD and EMGD compact stellar configurations, from the point of view of the information entropy, by Refs. [17,18].
It is worth to study compact stellar configurations in the regime . Ref. [43] derived the maximal mass of standard Dirac stars. The spinor field mass, m, of the order yields the maximal MGD stellar mass , corresponding to small mass stellar configurations. In fact, the Sun mass reads Kg. Therefore it prevents positive values of , as it implies a decrement of the maximal stellar mass. Studying astrophysical compact stellar configurations requires . Figure 1 shows that the more increases, the bigger the maximal MGD stellar masses are. In addition, for fixed values of , the mass peaks are bigger, the lower the brane tension is.
Figure 2 illustrates how the maximal MGD stellar mass increases as a function of , for different values of the brane tension.
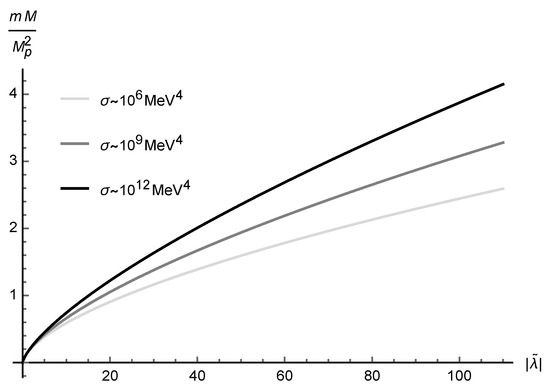
Figure 2.
MGD Dirac star maximal mass, , as a function of , for , and . The MGD-decoupling parameter is adopted.
Figure 2 shows that the bigger the brane tension, the steeper the slope of each plot is. It indicates that more realistic models, involving observational values of the brane tension, yield a MGD Dirac star maximal mass that increases with , however in a lower rate. The general-relativistic limit , is acquired, being very close to the black line plot in Figure 2, as indicated in Ref. [44]. It is worth to emphasize that, when , Figure 2 can be described, for , by the interpolation expression
This emulates the results in Ref. [44] in the MGD-decoupling context.
When coupling spinor fields to the MGD solutions, the resulting compact stellar configurations present distinct profiles, in the and the regimes. Figure 3 illustrates the spinor fields profiles with respect to the (adimensional radius) of the MGD Dirac star, for and .
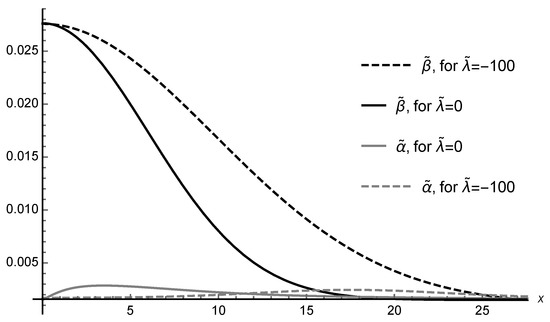
Figure 3.
Spinor fields profiles with respect to the Dirac star radius, x, for and , for a finite brane tension . The MGD-decoupling parameter is adopted.
Similar to bosonic stellar configurations [44], Equations (38)–(40) can be made adimensional, at the regime, by the mappings
Ref. [44] showed that at a large regime, the fermionic field percolates a large range . This implies that terms involving and can be disregarded. Hence, Equation (38) can be led to an analogue of Equation (46). Taking only leading terms in Equations (38) and (39) yields, when ,
Replacing it into Equation (40) yields
Since , then the self-interacting spinor field constant coupling, , is explicitly evinced in Equation (47). Therefore, Equation (47) can be employed to derive the rescaled MGD Dirac star mass, . Numerical analysis yields the solutions of Equations (46) and (47), given in Figure 4,
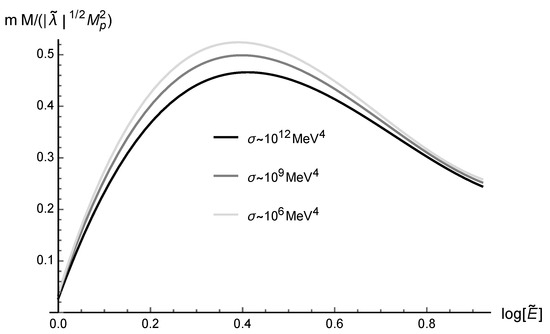
In the general-relativistic, limit, the maximal mass was derived in Ref. [54], being matching Equation (44).
4. Concluding Remarks, Discussion and Outlook
MGD compact stellar configurations, coupled to self-interacting fermionic fields of spin-1/2, were scrutinized. The time-dependent spinor field solutions are asymptotically flat. MGD Dirac stars qualitatively resemble standard Dirac stars, as the MGD parameter is bounded, , by current experimental and observational data [16], together with the most strict bound for the brane tension [18]. Therefore, due to the small physical values of these two parameters that rule the deformation process in the MGD, the numerical solutions plotted in Figure 1, Figure 2, Figure 3 and Figure 4, for MGD Dirac stars, present qualitative profiles that are similar to the standard Dirac stars [44], as expected. The MGD-decoupling parameter was adopted in all the numerical calculations. As discussed in [44], standard Dirac stars generated by linear spinors fields have tiny masses. Including non-linear spinor fields, in particular the self-interaction (32), circumvents this feature. It thus makes possible to approach astrophysical MGD Dirac stars. The MGD Dirac star maximal mass increases as a function of the spinor self-interaction coupling constant, , as illustrated in Figure 2. Moreover, for the strictest phenomenological bound for the brane tension , the MGD Dirac star maximal mass was shown to increase in a lower rate, compared to higher order values of the brane tension.
The spinor self-interaction coupling constant, , in Equation (32), indicates stable compact self-gravitating configurations, whose maximal mass is given by Equation (44). This value of the mass, alternatively written as corresponds to the mass of a MGD Dirac star that has similar order of magnitude as the Chandrasekhar mass, for fermions with mass GeV. In the general-relativistic limit, when and , all the results in Ref. [44] are recovered.
For MGD bosonic stellar configurations formed by Bose–Einstein condensates of gravitons, Ref. [17] showed that a critical local point of the star information entropy, as a function of the stellar configuration mass, indicates a transition between stability and instability against linear perturbations. The extended MGD case was discussed in [18]. In the case here studied, there is a family of MGD Dirac stars, parametrized by central value of the spinor field component. The mass of a MGD Dirac star can be expressed in terms of , existing a local critical mass for each value of , given by the solution of Equation (47). In addition to this analysis, the information entropy of MGD Dirac stars should take place to provide a final answer to their instability/stability conditions. The developments in [57,58] can shed new light on this important problem, that is beyond the scope of this paper.
Funding
This research was funded by The São Paulo Research Foundation (FAPESP) (Grant No. 2017/18897-8) and the National Council for Scientific and Technological Development—CNPq (Grants No. 303390/2019-0, No. 406134/2018-9 and No. 303293/2015-2)
Conflicts of Interest
The authors declare no conflict of interest.The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Ovalle, J. Decoupling gravitational sources in general relativity: from perfect to anisotropic fluids. Phys. Rev. D 2017, 95, 104019. [Google Scholar] [CrossRef]
- Ovalle, J. Non-uniform Braneworld Stars: An Exact Solution. Int. J. Mod. Phys. D 2009, 18, 837. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J. Brane-world stars from minimal geometric deformation, and black holes. Gen. Rel. Grav. 2014, 46, 1669. [Google Scholar] [CrossRef]
- Ovalle, J.; Gergely, L.; Casadio, R. Brane-world stars with a solid crust and vacuum exterior. Class. Quant. Grav. 2015, 32, 045015. [Google Scholar] [CrossRef]
- Antoniadis, I.; Arkani-Hamed, N.; Dimopoulos, S.; Dvali, G.R. New dimensions at a millimeter to a Fermi and superstrings at a TeV. Phys. Lett. B 1998, 436, 257. [Google Scholar] [CrossRef]
- Antoniadis, I. A Possible new dimension at a few TeV. Phys. Lett. B 1990, 246, 377–384. [Google Scholar] [CrossRef]
- Randall, L.; Sundrum, R. A Large mass hierarchy from a small extra dimension. Phys. Rev. Lett. 1999, 83, 3370. [Google Scholar] [CrossRef]
- Abdalla, M.C.B.; Hoff da Silva, J.M.; da Rocha, R. Notes on the Two-brane Model with Variable Tension. Phys. Rev. D 2009, 80, 046003. [Google Scholar] [CrossRef]
- da Rocha, R.; Hoff da Silva, J.M. Black string corrections in variable tension braneworld scenarios. Phys. Rev. D 2012, 85, 046009. [Google Scholar] [CrossRef]
- Gergely, L.A. Eotvos branes. Phys. Rev. D 2009, 79, 086007. [Google Scholar] [CrossRef]
- Ovalle, J. Searching exact solutions for compact stars in braneworld: A Conjecture. Mod. Phys. Lett. A 2008, 23, 3247. [Google Scholar] [CrossRef]
- Boschi-Filho, H.; Braga, N.R.F. Compact AdS space, brane geometry and the AdS / CFT correspondence. Phys. Rev. D 2002, 66, 025005. [Google Scholar] [CrossRef]
- Boschi-Filho, H.; Braga, N.R.F. Isometries of a D3-brane space. Class. Quant. Grav. 2004, 21, 2427–2433. [Google Scholar] [CrossRef][Green Version]
- da Rocha, R.; Tomaz, A.A. Holographic entanglement entropy under the minimal geometric deformation and extensions. Eur. Phys. J. C 2019, 79, 1035. [Google Scholar] [CrossRef]
- Cavalcanti, R.T.; Goncalves da Silva, A.; da Rocha, R. Strong deflection limit lensing effects in the minimal geometric deformation and Casadio-Fabbri-Mazzacurati solutions. Class. Quant. Grav. 2016, 33, 215007. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J.; da Rocha, R. Classical Tests of General Relativity: Brane-World Sun from Minimal Geometric Deformation. EPL 2015, 110, 40003. [Google Scholar] [CrossRef]
- Casadio, R.; da Rocha, R. Stability of the graviton Bose-Einstein condensate in the brane-world. Phys. Lett. B 2016, 763, 434. [Google Scholar] [CrossRef]
- Fernandes-Silva, A.; Ferreira-Martins, A.J.; da Rocha, R. Extended quantum portrait of MGD black holes and information entropy. Phys. Lett. B 2019, 791, 323. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J.; da Rocha, R. Black Strings from Minimal Geometric Deformation in a Variable Tension Brane-World. Class. Quant. Grav. 2014, 31, 045016. [Google Scholar] [CrossRef]
- Casadio, R.; Ovalle, J.; da Rocha, R. The Minimal Geometric Deformation Approach Extended. Class. Quant. Grav. 2015, 32, 215020. [Google Scholar] [CrossRef]
- Ovalle, J.; Linares, F.; Pasqua, A.; Sotomayor, A. The role of exterior Weyl fluids on compact stellar structures in Randall-Sundrum gravity. Class. Quant. Grav. 2013, 30, 175019. [Google Scholar] [CrossRef]
- Ovalle, J. Decoupling gravitational sources in general relativity: The extended case. Phys. Lett. B 2019, 788, 213–218. [Google Scholar] [CrossRef]
- Ovalle, J.; Linares, F. Tolman IV solution in the Randall-Sundrum Braneworld. Phys. Rev. D 2013, 88, 104026. [Google Scholar] [CrossRef]
- Bernardini, A.E.; Braga, N.R.F.; da Rocha, R. Conditional entropy of glueball states. Phys. Lett. B 2017, 765, 81. [Google Scholar] [CrossRef]
- Da Rocha, R. Dark SU(N) glueball stars on fluid branes. Phys. Rev. D 2017, 95, 124017. [Google Scholar] [CrossRef]
- Fernandes-Silva, A.; Ferreira-Martins, A.J.; da Rocha, R. The extended minimal geometric deformation of SU(N) dark glueball condensates. Eur. Phys. J. C 2018, 78, 631. [Google Scholar] [CrossRef]
- da Rocha, R. Black hole acoustics in the minimal geometric deformation of a de Laval nozzle. Eur. Phys. J. C 2017, 77, 355. [Google Scholar] [CrossRef]
- Contreras, E. Minimal Geometric Deformation: the inverse problem. Eur. Phys. J. C 2018, 78, 678. [Google Scholar] [CrossRef]
- Casadio, R.; Contreras, E.; Ovalle, J.; Sotomayor, A.; Stuchlick, Z. Isotropization and change of complexity by gravitational decoupling. Eur. Phys. J. C 2019, 79, 826. [Google Scholar] [CrossRef]
- Rincón, A.; Gabbanelli, L.; Contreras, E.; Tello-Ortiz, F. Minimal geometric deformation in a Reissner-Nordström background. Eur. Phys. J. C 2019, 79, 873. [Google Scholar] [CrossRef]
- Ovalle, J.; Posada, C.; Stuchlík, Z. Anisotropic ultracompact Schwarzschild star by gravitational decoupling. Class. Quant. Grav. 2019, 36, 205010. [Google Scholar] [CrossRef]
- Gabbanelli, L.; Ovalle, J.; Sotomayor, A.; Stuchlik, Z.; Casadio, R. A causal Schwarzschild-de Sitter interior solution by gravitational decoupling. Eur. Phys. J. C 2019, 79, 486. [Google Scholar] [CrossRef]
- Contreras, E.; Bargueño, P. Extended gravitational decoupling in 2 + 1 dimensional space-times. Class. Quant. Grav. 2019, 36, 215009. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; da Rocha, R.; Sotomayor, A.; Stuchlik, Z. Einstein-Klein-Gordon system by gravitational decoupling. EPL 2018, 124, 20004. [Google Scholar] [CrossRef]
- Morales, E.; Tello-Ortiz, F. Compact Anisotropic Models in General Relativity by Gravitational Decoupling. Eur. Phys. J. C 2018, 78, 841. [Google Scholar] [CrossRef]
- Morales, E.; Tello-Ortiz, F. Charged anisotropic compact objects by gravitational decoupling. Eur. Phys. J. C 2018, 78, 618. [Google Scholar] [CrossRef]
- Panotopoulos, G.; Rincón, A. Minimal Geometric Deformation in a cloud of strings. Eur. Phys. J. C 2018, 78, 851. [Google Scholar] [CrossRef]
- Ovalle, J.; Casadio, R.; da Rocha, R.; Sotomayor, A. Anisotropic solutions by gravitational decoupling. Eur. Phys. J. C 2018, 78, 122. [Google Scholar] [CrossRef]
- Gabbanelli, L.; Rincón, A.; Rubio, C. Gravitational decoupled anisotropies in compact stars. Eur. Phys. J. C 2018, 78, 370. [Google Scholar] [CrossRef]
- Pérez Graterol, R. A new anisotropic solution by MGD gravitational decoupling. Eur. Phys. J. Plus 2018, 133, 244. [Google Scholar] [CrossRef]
- Heras, C.L.; Leon, P. Using MGD gravitational decoupling to extend the isotropic solutions of Einstein equations to the anisotropical domain. Fortsch. Phys. 2018, 66, 1800036. [Google Scholar] [CrossRef]
- Casadio, R.; Nicolini, P.; da Rocha, R. Generalised uncertainty principle Hawking fermions from minimally geometric deformed black holes. Class. Quant. Grav. 2018, 35, 185001. [Google Scholar] [CrossRef]
- Herdeiro, C.A.R.; Pombo, A.M.; Radu, E. Asymptotically flat scalar, Dirac and Proca stars: discrete vs. continuous families of solutions. Phys. Lett. B 2017, 773, 654–662. [Google Scholar] [CrossRef]
- Dzhunushaliev, V.; Folomeev, V. Dirac stars supported by nonlinear spinor fields. Phys. Rev. D 2019, 99, 084030. [Google Scholar] [CrossRef]
- Bronnikov, K.A.; Rybakov, Y.P.; Saha, B. Spinor fields in spherical symmetry. Einstein-Dirac and other space-times. Eur. Phys. J. Plus 2020, 135, 124. [Google Scholar] [CrossRef]
- Saha, B. Spinor fields in spherically symmetric space-time. Eur. Phys. J. Plus 2018, 133, 461. [Google Scholar] [CrossRef]
- Saha, B. Non-minimally coupled nonlinear spinor field in Bianchi type-I cosmology. Eur. Phys. J. Plus 2019, 134, 491. [Google Scholar] [CrossRef]
- Saha, B. Nonlinear spinor field in isotropic space-time and dark energy models. Eur. Phys. J. Plus 2016, 131, 242. [Google Scholar] [CrossRef]
- Saha, B. Spinor field with polynomial nonlinearity in LRS Bianchi type-I space?time. Can. J. Phys. 2016, 94, 116–121. [Google Scholar] [CrossRef]
- Cianci, R.; Fabbri, L.; Vignolo, S. Critical exact solutions for self-gravitating Dirac fields. Eur. Phys. J. C 2016, 76, 595. [Google Scholar] [CrossRef]
- Fabbri, L. Least-order torsion-gravity for dirac fields, and their non-linearity terms. Gen. Rel. Grav. 2015, 47, 1837. [Google Scholar] [CrossRef][Green Version]
- Fabbri, L.; Vignolo, S.; Carloni, S. Renormalizability of the Dirac equation in torsion gravity with nonminimal coupling. Phys. Rev. D 2014, 90, 024012. [Google Scholar] [CrossRef]
- Fabbri, L. Conformal Gravity with the most general ELKO Matter. Phys. Rev. D 2012, 85, 047502. [Google Scholar] [CrossRef]
- Dzhunushaliev, V.; Folomeev, V. Dirac Star with SU(2) Yang-Mills and Proca Fields. Phys. Rev. D 2020, 101, 024023. [Google Scholar] [CrossRef]
- Germani, C.; Maartens, R. Stars in the brane world. Phys. Rev. D 2001, 64, 124010. [Google Scholar] [CrossRef]
- Gleiser, M.; Watkins, R. Gravitational Stability of Scalar Matter. Nucl. Phys. B 1989, 319, 733–746. [Google Scholar] [CrossRef]
- Braga, N.R.F. Information versus stability in an anti-de Sitter black hole. Phys. Lett. B 2019, 797, 134919. [Google Scholar] [CrossRef]
- Braga, N.R.F.; da Rocha, R. Configurational entropy of anti-de Sitter black holes. Phys. Lett. B 2017, 767, 386–391. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).