An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem
Abstract
1. Introduction
2. Multi-Objective Aerospace Shell Production Scheduling Problem
2.1. General Problem Description
2.2. Mathematical Formulation
- (1)
- Each operation must be processed once and only once on each machine.
- (2)
- The same job contains a specific sequence of operations, which must be processed in the order of the operations.
- (3)
- There are no dependencies between operations belonging different jobs.
- (4)
- Operations scheduled to designated machines have a deterministic processing time.
- (5)
- Each machine can only process a single operation at a specific time duration.
- (6)
- Once processing is started, it cannot be interrupted.
- (7)
- The situation of a machine failure is not considered.
- (8)
- There are no differences between machines that can perform the same operation.
- (9)
- A machine can start the processing of another operation immediately after completing one operation.
2.3. Multi-Objective Model
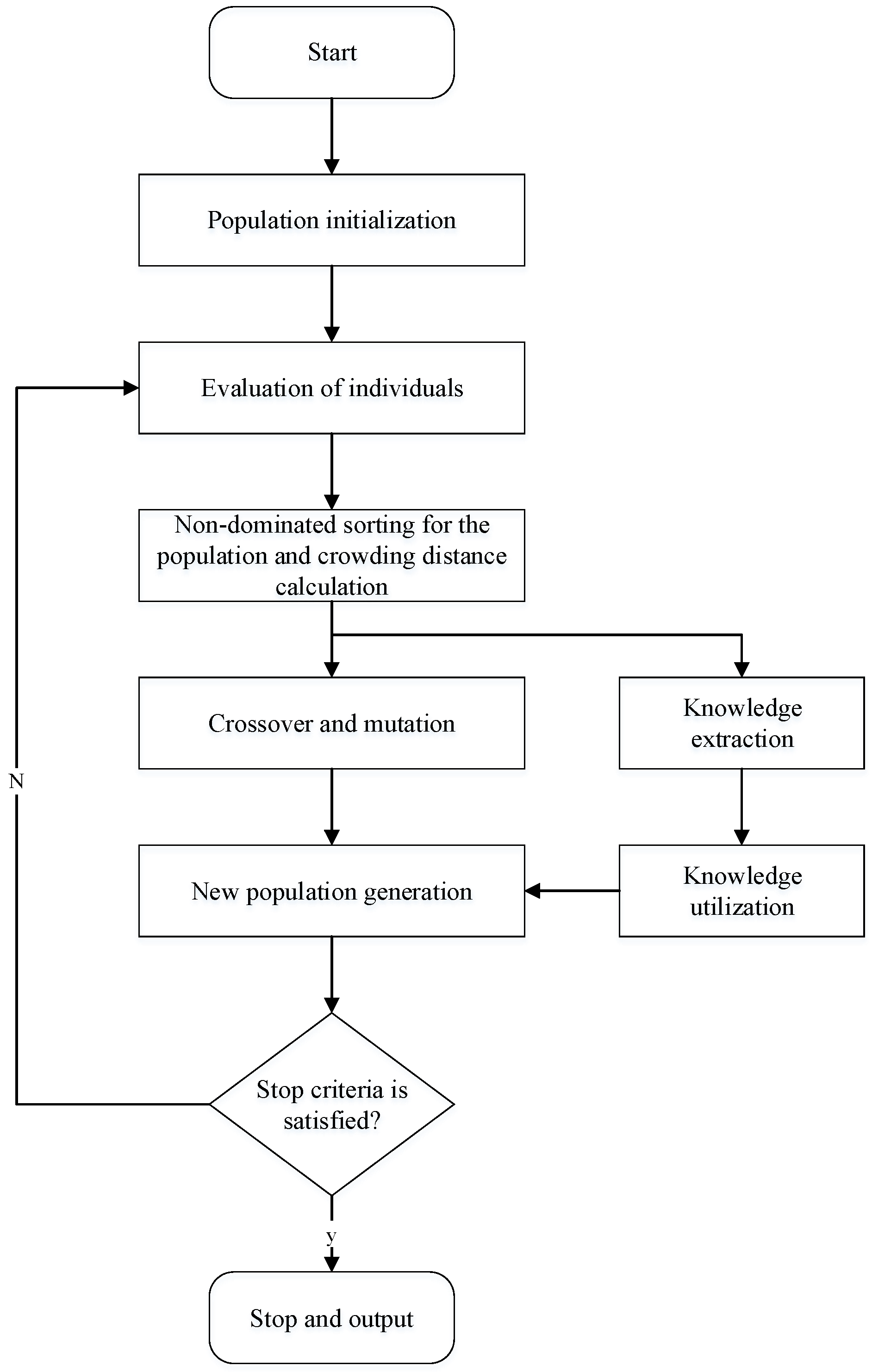
3. An Improved Multi-Objective Evolutionary Algorithm
3.1. Multi-Objective Evolutionary Algorithms
3.2. Mechanism of NSGA-II
3.2.1. Fast Non-Dominated Sorting Mechanism
| Algorithm 1. Fast non-dominated sorting algorithm. |
| For each For each If () then //If p dominates q //Add q to the set of solutions dominated by p Else if () //Increment the domination counter of p If then //p belongs to the first front //Initialize the front counter While //Used to store the members of the next front For each For each If then //q belongs to the next front |
3.2.2. Crowding Distance Calculation
| Algorithm 2. Calculation of crowding distance. |
| Input // is the set of individuals // is the number of individuals in For each i, set =0 //initialize distance For each objective m =sort(,m) //sort using each objective value //so that boundary points are always selected For i=2 to (l-1) |
3.2.3. Partial Order of Individuals
3.3. Chromosome, Crossover and Mutation
3.4. Knowledge-Driven MOEA
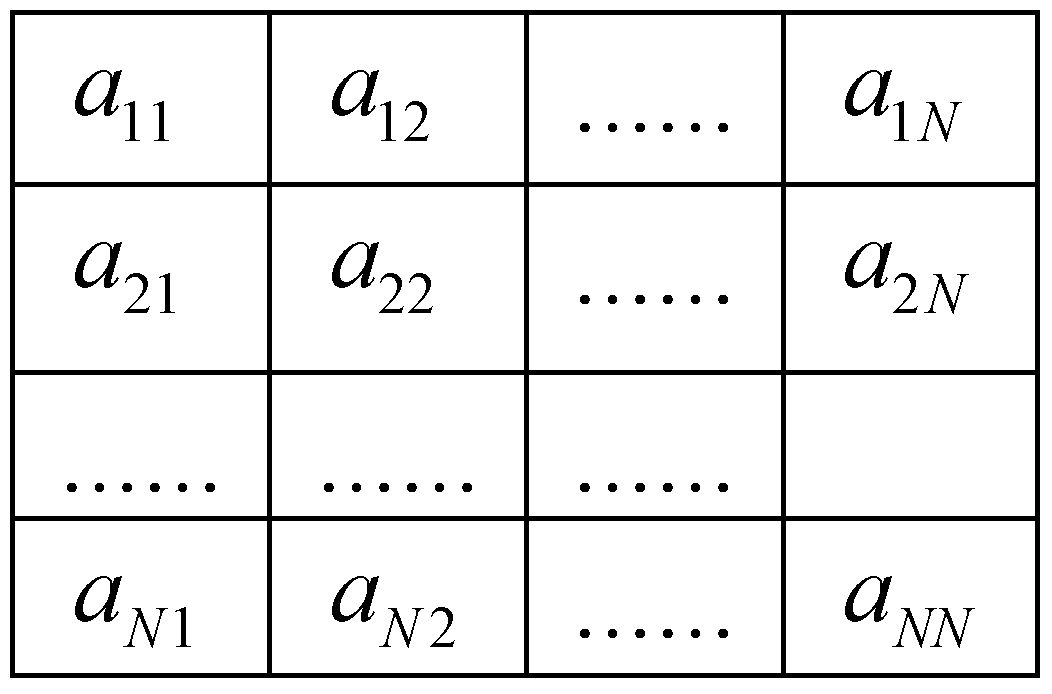
3.4.1. Knowledge Extraction
3.4.2. Knowledge Use
4. Experimental Analysis
4.1. Test Instances
4.2. Parameter Settings
4.3. Experimental Results
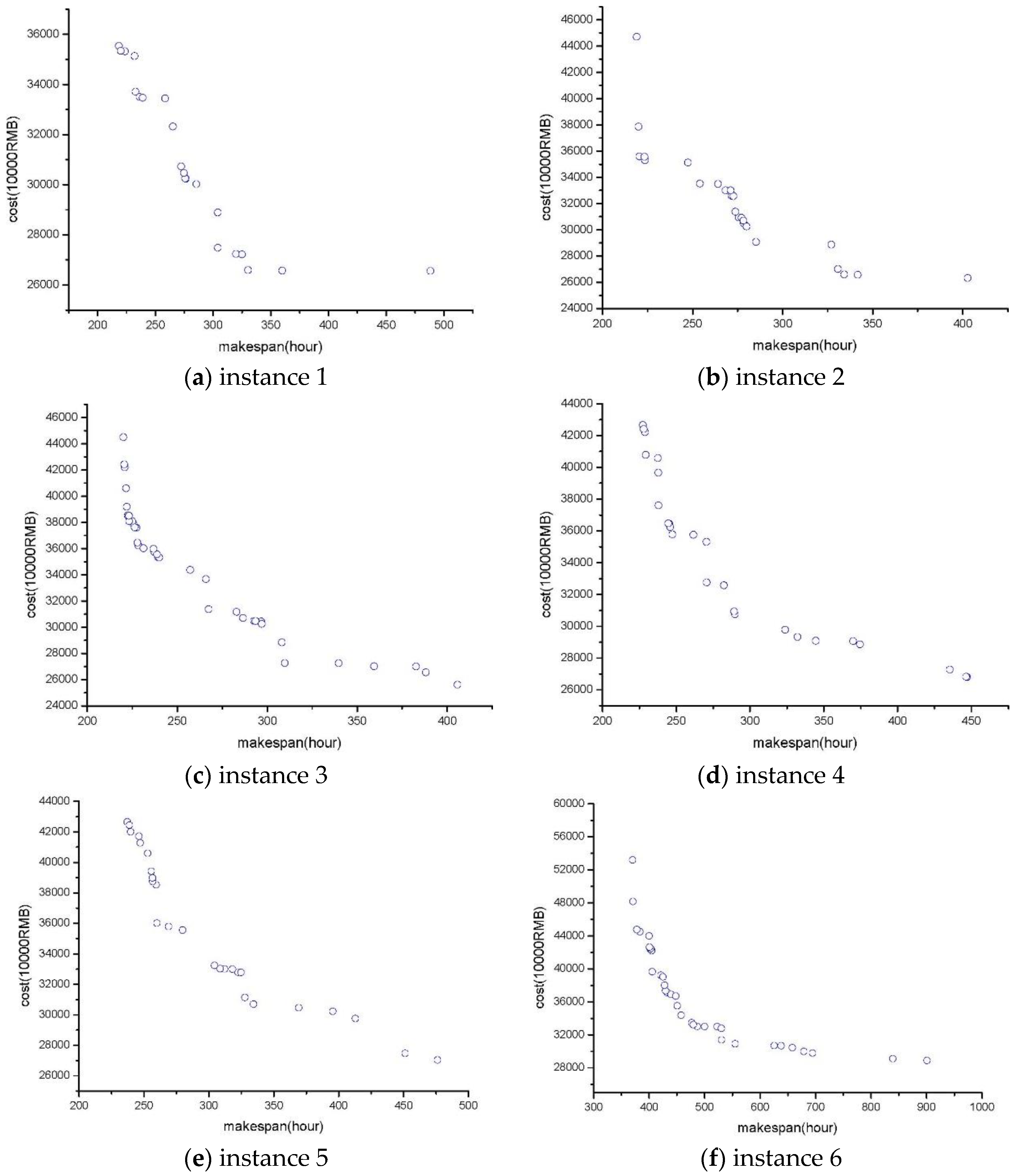
4.3.1. Obtained Non-Dominated Solutions
4.3.2. Performance Comparison
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Corominas, A.; Garcia-Villoria, A.; González, N.-A.; Pastor, R. A multistage graph-based procedure for solving a just-in-time flexible job-shop scheduling problem with machine and time-dependent processing costs. J. Oper. Res. Soc. 2018, 70, 620–633. [Google Scholar] [CrossRef]
- Wu, X.; Liu, X.; Zhao, N. An improved differential evolution algorithm for solving a distributed assembly flexible job shop scheduling problem. Memetic Comput. 2018, 11, 335–355. [Google Scholar] [CrossRef]
- Kavitha, S.; Venkumar, P.; Rajini, N.; Pitchipoo, P. An Efficient Social Spider Optimization for Flexible Job Shop Scheduling Problem. J. Adv. Manuf. Syst. 2018, 17, 181–196. [Google Scholar] [CrossRef]
- Xie, N.; Chen, N. Flexible job shop scheduling problem with interval grey processing time. Appl. Soft Comput. 2018, 70, 513–524. [Google Scholar] [CrossRef]
- Defersha, F.; Bayat-Movahed, S. Linear programming assisted (not embedded) genetic algorithm for flexible jobshop scheduling with lot streaming. Comput. Ind. Eng. 2018, 117, 319–335. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, L.; Wang, S.-Y.; Liu, M. An effective teaching–learning-based optimization algorithm for the flexible job-shop scheduling problem with fuzzy processing time. Neurocomputing 2015, 148, 260–268. [Google Scholar] [CrossRef]
- Gao, K.Z.; Suganthan, P.; Pan, Q.-K.; Chua, T.; Chong, C.S.; Cai, T.-X. An improved artificial bee colony algorithm for flexible job-shop scheduling problem with fuzzy processing time. Expert Syst. Appl. 2016, 65, 52–67. [Google Scholar] [CrossRef]
- Quan, K.P. An effective discrete harmony search algorithm for flexible job shop scheduling problem with fuzzy processing time. Int. J. Prod. Res. 2015, 53, 1–16. [Google Scholar]
- Birgin, E.; Ferreira, J.; Ronconi, D.P. List scheduling and beam search methods for the flexible job shop scheduling problem with sequencing flexibility. Eur. J. Oper. Res. 2015, 247, 421–440. [Google Scholar] [CrossRef]
- Geyik, F.; Dosdoğru, A.T. Process plan and part routing optimization in a dynamic flexible job shop scheduling environment: An optimization via simulation approach. Neural Comput. Appl. 2012, 23, 1631–1641. [Google Scholar] [CrossRef]
- Duarte, J.L.R.; Fan, N.; Jin, T. Multi-process production scheduling with variable renewable integration and demand response. Eur. J. Oper. Res. 2020, 281, 186–200. [Google Scholar] [CrossRef]
- Karner, M.; Glawar, R.; Sihn, W.; Matyas, K. An industry-oriented approach for machine condition-based production scheduling. Procedia CIRP 2019, 81, 938–943. [Google Scholar] [CrossRef]
- Plinere, D.; Aleksejeva, L. Production scheduling in agent-based supply chain for manufacturing efficiency improvement. Procedia Comput. Sci. 2019, 149, 36–43. [Google Scholar] [CrossRef]
- Paithankar, A.; Chatterjee, S. Open pit mine production schedule optimization using a hybrid of maximum-flow and genetic algorithms. Appl. Soft Comput. 2019, 81, 105507. [Google Scholar] [CrossRef]
- Jélvez, E.; Morales, N.; Nancel-Penard, P.; Cornillier, F. A new hybrid heuristic algorithm for the Precedence Constrained Production Scheduling Problem: A mining application. Omega 2019, 102046. [Google Scholar] [CrossRef]
- Samavati, M.; Essam, D.; Nehring, M.; Sarker, R. Production planning and scheduling in mining scenarios under IPCC mining systems. Comput. Oper. Res. 2020, 115, 104714. [Google Scholar] [CrossRef]
- Mai, N.L.; Topal, E.; Erten, O.; Sommerville, B. A new risk-based optimisation method for the iron ore production scheduling using stochastic integer programming. Resour. Policy 2019, 62, 571–579. [Google Scholar] [CrossRef]
- Kaylani, H.; Atieh, A.M. Simulation Approach to Enhance Production Scheduling Procedures at a Pharmaceutical Company with Large Product Mix. Procedia CIRP 2016, 41, 411–416. [Google Scholar] [CrossRef]
- Rawlings, B.C.; Avadiappan, V.; LaFortune, S.; Maravelias, C.T.; Wassick, J.M. Incorporating automation logic in online chemical production scheduling. Comput. Chem. Eng. 2019, 128, 201–215. [Google Scholar] [CrossRef]
- Russell, A.; Taghipour, S. Multi-objective optimization of complex scheduling problems in low-volume low-variety production systems. Int. J. Prod. Econ. 2019, 208, 1–16. [Google Scholar] [CrossRef]
- Lan, T.; Kao, D.; Chiang, M.; Sabharwal, A. An Axiomatic Theory of Fairness in Network Resource Allocation. In Proceedings of the 2010 IEEE INFOCOM, San Diego, CA, USA, 14–19 March 2010; pp. 1–9. [Google Scholar]
- Zabini, F.; Bazzi, A.; Masini, B.M. Throughput versus fairness tradeoff analysis. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5131–5136. [Google Scholar]
- Zhou, A.; Qu, B.-Y.; Li, H.; Zhao, S.-Z.; Suganthan, P.; Zhang, Q. Multiobjective evolutionary algorithms: A survey of the state of the art. Swarm Evol. Comput. 2011, 1, 32–49. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A Fast and Elitist Multiobjective Genetic Algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, H. MOEA/D: A Multiobjective Evolutionary Algorithm Based on Decomposition. IEEE Trans. Evol. Comput. 2007, 11, 712–731. [Google Scholar] [CrossRef]
- Wang, Q.; Luo, H.; Xiong, J.; Song, Y.-J.; Zhang, Z. Evolutionary Algorithm for Aerospace Shell Product Digital Production Line Scheduling Problem. Symmetry 2019, 11, 849. [Google Scholar] [CrossRef]
- Zhang, Z.; Hong, W.-C.; Li, J. Electric Load Forecasting by Hybrid Self-Recurrent Support Vector Regression Model With Variational Mode Decomposition and Improved Cuckoo Search Algorithm. IEEE Access 2020, 8, 14642–14658. [Google Scholar] [CrossRef]
- Hong, W.-C.; Li, M.-W.; Geng, J.; Zhang, Y. Novel chaotic bat algorithm for forecasting complex motion of floating platforms. Appl. Math. Model. 2019, 72, 425–443. [Google Scholar] [CrossRef]


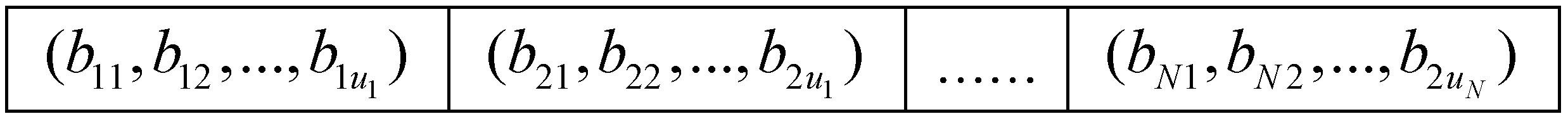

| Symbol | Description |
|---|---|
| n | Number of jobs. |
| e | Number of machine types. |
| i | Index of jobs, i = 1, 2, …, n |
| j | Index of machine types, j = 1, 2, …, e |
| aj | Machine amount of type j |
| j,m | Index of machine for type j, m = 1, 2, …, aj |
| Cj | The unit cost of machine type j. |
| machinej,m | The mth machine for the type j. |
| J | The set of jobs, J = {J1, J2, …, Jn} |
| Fi | The finish time of job i. |
| qi | The number of operations for job i. |
| k | The index of operation for job i. |
| Oi | The set of operation for job i |
| O | The set of all operations, O = {O1, O2, …, On} |
| opri,k | The kth operation of job i. |
| Mach_typei,k | The type of machine that can process operation opri,k. |
| di,k | The duration of operation opri,k. |
| sti,k | The start time of operation opri,k. |
| eti,k | The end time of operation opri,k. |
| xi,k,j,m | Machine assignment index of operation opri,k to machinej,m. |
| M | The set of machines deployed in the production line. |
| s | Index of machine in the set of M, s = 1, 2, …, |M| |
| ytj,m,i,k | At time t, whether a machine machinej,m is processing operation opri,k. |
| Machine Type | Machine Number | Unit Cost (10,000 RMB) |
|---|---|---|
| 1 | 6 | 2300 |
| 2 | 5 | 2850 |
| 3 | 3 | 3100 |
| 4 | 4 | 3250 |
| 5 | 2 | 3750 |
| 6 | 3 | 3650 |
| 7 | 2 | 4000 |
| 8 | 3 | 3350 |
| 9 | 5 | 4200 |
| 10 | 4 | 4050 |
| 11 | 8 | 3900 |
| 12 | 8 | 2550 |
| 13 | 4 | 3450 |
| 14 | 4 | 2865 |
| 15 | 3 | 3674 |
| 16 | 4 | 3890 |
| 17 | 8 | 230 |
| 18 | 7 | 210 |
| 19 | 9 | 240 |
| 20 | 3 | 300 |
| 21 | 4 | 5300 |
| Instance Index | Shell Type 1 | Shell Type 2 | Shell Type 3 | Shell Type 4 |
|---|---|---|---|---|
| instance 1 | 1 | 1 | 1 | 1 |
| instance 2 | 2 | 1 | 1 | 1 |
| instance 3 | 2 | 2 | 1 | 1 |
| instance 4 | 2 | 2 | 2 | 1 |
| instance 5 | 2 | 2 | 2 | 2 |
| instance 6 | 3 | 3 | 3 | 3 |
| Solution | Instance | Makespan | Cost |
|---|---|---|---|
| solution 1 | instance 1 | 218.5 | 35540 |
| solution 2 | instance 1 | 304.2 | 27480 |
| solution 3 | instance 1 | 488.3 | 26560 |
| solution 4 | instance 6 | 370.2 | 53190 |
| solution 5 | instance 6 | 530.1 | 32790 |
| solution 6 | instance 6 | 900.9 | 28900 |
| Instance | KD-MOEA | NSGA-II | MOEA/D |
|---|---|---|---|
| instance 1 | 0.7256 ± 0.0177 (+) | 0.7140 ± 0.0149 (-) | 0.7099 ± 0.0167 (-) |
| instance 1 | 0.7259 ± 0.0167 (+) | 0.7195 ± 0.0178 (~) | 0.7081 ± 0.0211 (-) |
| instance 1 | 0.7168 ± 0.0209 (+) | 0.6950 ± 0.0215 (-) | 0.6873 ± 0.0187 (-) |
| instance 6 | 0.6819 ± 0.0163 (+) | 0.6722 ± 0.0205 (~) | 0.6432 ± 0.0251 (-) |
| instance 6 | 0.6566 ± 0.0333 (+) | 0.6332 ± 0.0183 (-) | 0.6091 ± 0.0224 (-) |
| instance 6 | 0.4998 ± 0.0401 (+) | 0.4487 ± 0.0495 (-) | 0.4221 ± 0.0411 (-) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Q.; Wang, X.; Luo, H.; Xiong, J. An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem. Symmetry 2020, 12, 509. https://doi.org/10.3390/sym12040509
Wang Q, Wang X, Luo H, Xiong J. An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem. Symmetry. 2020; 12(4):509. https://doi.org/10.3390/sym12040509
Chicago/Turabian StyleWang, Qing, Xiaoshuang Wang, Haiwei Luo, and Jian Xiong. 2020. "An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem" Symmetry 12, no. 4: 509. https://doi.org/10.3390/sym12040509
APA StyleWang, Q., Wang, X., Luo, H., & Xiong, J. (2020). An Improved Multi-Objective Evolutionary Approach for Aerospace Shell Production Scheduling Problem. Symmetry, 12(4), 509. https://doi.org/10.3390/sym12040509




