Abstract
Recently, resolving a problem based on multi-criteria decision-making systems has become an attractive method. One of recent techniques is trapezoidal fuzzy VIKOR method which was used for selecting the best option among criteria. This research is aimed to utilize the VIKOR method in prioritization of watershed reforestation in Semarang City, Indonesia. Several criteria have been set for the prioritization of reforestation areas to select watersheds as reforestation targets. In this case, the six criteria and six alternatives were used in order to determine the best priority of reforestation. The result showed that VIKOR method was successfully applied to determine the best option and Kali Garang watershed was the top priority as it has the highest rank and it meets reforestation criteria compared with other watersheds criteria.
1. Introduction
Fuzzy logic is considered as a strong technique of reasoning approaches by associating input with output spaces and mostly used for complicated system which is hardly solved by using a conventional mathematical model [1]. The complexity of models is normally due to less accurate or unclear values of variables or parameters and therefore the mathematical models are hardly defined. VIKOR method is a new technique in fuzzy logic systems which is widely used for decision making problems. This method has been implemented by many researchers. Noordian [2] used the method for selecting the reinforcement of natural fiber composition for car hoods. The results showed that VIKOR method can help identify the type of strengthening of the composition of natural fibers to be applied to laminated metal fibers to car hoods to achieve transit weight reduction. Santawy and Ahmed [3] implemented VIKOR method for scholarship recipient selection. The results showed that the method could help the selection process and determine the scholarship recipients based on the criteria set and weighted by the employer. In addition, Salvius et al. [4] demonstrated the use of VIKOR method to evaluate consulting firms and to evaluate the best company from a number of existing consulting companies. It showed that the VIKOR method can evaluate and rank consulting firms by setting some predetermined criteria to determine the right consulting company. Civic and Vucijak [5] also used the VIKOR method as a method for material selection in wall insulation. They used the appropriate material for wall insulation by using several criteria that have been determined previously. The VIKOR method in this problem could obtain the best material ranking of every material available so the appropriate decision can be opted based on the results of the ranking that has been set. The selected material could reduce production costs, increase energy efficiency, and reduce CO2 emissions. Santawy and Ahmed [6] also used the VIKOR method as a project selection based on capital investment in every company. Several objectives are considered such as economic desires, environmental issues, and technical and social factors. The study showed that the VIKOR method can rank several projects and select one the appropriate one.
Watershed is an area where natural resources, especially vegetation, soil, and water, are found and stored, and a place for humans to use those natural resources to meet their needs [7]. As an area, watershed is also regarded as an ecosystem of the water cycle, and therefore watershed is also defined as an area of land which unites rivers and streams, which has function of conserving naturally rainfall into the sea or the lake [8]. In the study of watersheds, the presence of land boundary must be considered. It is an area of waters that is still influenced by activities in land side [9]. Therefore, watersheds are also defined as natural areas which provide productive benefits and water supply through rivers, groundwater, and/or springs, to fulfill various needs of life for humans, wildlife, and plants. In order to obtain optimal and sustainable benefits, it is crucial to design an objective and rational watershed management planning system. In fact, watershed management planning is dynamic because the processes occurring within watershed, either natural, political, institutional, socio-economic, or technological processes, continue to develop. Reforestation in urban watersheds is, in fact, a crucial issue because it aims to not only preserve urban water supply but also prevent soil erosion [10]. Regarding the importance of watersheds, it is vital to always maintain good conditions of watersheds in order for them to function properly.
An increase in population has caused an increase in the need for lands for humans to live in, making the needs for land very vital at this time. Unfortunately, development carried out by humans often does not pay attention to environmental carrying capacity. This then results in the degradation of land and the physical conditions of the land. In fact, natural resources such as soil and water area are prone to damage or degradation. In addition, other human activities that may damage watersheds are excessive logging or deforestation, human settlement project, conversion of forest land to plantations, and agricultural lands [11].
There are five watersheds in Semarang City—i.e., Garang watershed, Bringin watershed, Karanganyar watershed, Silandak watershed, and Babon Pemali Jratun watershed or the Center for Watershed and Protected Forest Management (BPDAS-HL). In urban areas, watersheds function to maintain water supply and restore watershed functions, so it is necessary to conduct reforestation around watersheds. In fact, reforestation aims to restore, maintain, and improve land conditions, enabling lands to produce and function optimally as something that maintains water systems and protects the environment from anything that occurs in it. Reforestation is an effort to plant trees on degraded lands in the form of vacant land or thicket to restore forest functions. Reforestation is an activity of planting trees in forests or in areas to be afforested. These areas can be either degraded forests or non-forest areas to be afforested. In fact, reforestation is very important to restore water supply and prevent soil erosion. The priority scale of reforestation is determined based on several criteria as a consideration and priority scale for the selection of watersheds to be reforested. The criteria for the selection of reforestation areas are based on watershed conservation, prevention of soil erosion, cost savings, land availability, community support, and government involvement [10]. In fact, the selection of reforestation area requires multiple criteria, which require a multi criteria decision making (MCDM) method [12,13]. The prioritization of reforestation area may contain uncertainty and subjectivity which can be modeled by using theory of fuzzy logic. Fuzzy approach is used to perform quantitative and qualitative analysis and to analyze expert opinions related to the assessment of reforestation area [14,15].
This research analyzed priority scales and decision making alternatives in the selection of reforestation areas using trapezoidal fuzzy VIKOR method (Visekriterijumsko Kompromisno Rangiranje) as a method which could identify the importance of criteria and alternatives, with pairwise comparison values obtained from various expert opinions [16]. Therefore, the objective of this study is also to use fuzzy VIKOR method with multiple criteria decision methods in decision making by ranking system. In this research, besides using the VIKOR method, it also used fuzzy logic to determine the priority scale of reforestation in the watershed (DAS) with a case study in the City of Semarang, Central Java, Indonesia, as critical watersheds. This paper is structured into six sections: (1) Introduction, in which the rationale of the research is briefly introduced; (2) Literature Review, as the background of fuzzy logic theory that is used in the research; (3) Criteria System, where the number of criteria sets has been determined for solving the problems; (4) Methods, where VIKOR method was described and implemented; (5) Case Study, where the watershed in Semarang as a case problem is described; (6) Results and Discussion, which intensively analyzes the results; (7) Conclusion, which provides a summary of the main finding of this research.
2. Literature Reviews
2.1. Preliminaries
Elementary Definitions
Definition 1.
A fuzzy numberis defined as any subset of the real numberand it has membership function ofthat has characteristics as [17]:
is continuos,
for all
is strictly increasing on
for
is strictly decreasing on
for all
Definition 2.
A trapezoidal fuzzy numberis shown by any fuzzy set of the real numberwhich has membership functionand can be expressed as [17,18,19]:
where the interval of this shape is described as:
If then the trapezoidal fuzzy number will coincide with the triangular one.
A trapezoidal fuzzy number can also be defined as where it denotes the smallest possible, most promising, and largest possible values and the membership function as Equation (1) and it is shown in Figure 1.
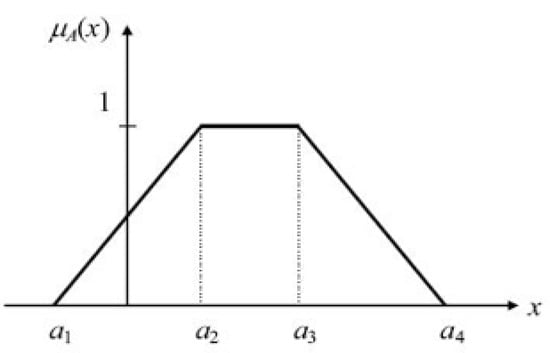
Figure 1.
Trapezoidal fuzzy number of .
While the real number is supported by fuzzy number and is described as [18,20]
2.2. Arithmetic Operations
The arithmetic operations is important to determine two trapezoidal fuzzy numbers, and where the operations are [18,21]:
2.3. Concept of Fuzzy VIKOR
A word is considered to be semantically fuzzy if it cannot be well defined, meaning that it cannot be determined explicitly (correct or false) whether a particular object has the characteristics as meant by such word/term. For example, to determine the quality of data, whether the data can be categorized as ‘good’ or the relative importance of a decision maker, whether it is categorized as ‘very important’. The concept of fuzzy logic is easy to understand because it uses a set theory and it is highly flexible because it is able to adapt to any changes and uncertainties that accompany problems [15,22].
A set is a collection of both concrete and abstract objects which have certain common characteristics. A crisp set is a set that is well defined, meaning that each of the elements in the universal set can always be determined whether it is an element/member of the set [15,23,24]. Normally, a set is characterized by a function, i.e., a function of universal set X to the set {0,1} where 0 (zero) is not an element and 1 (one) is an element. The crisp set is a set of real numbers of which has membership function expressed by a mathematical formula. The triangular fuzzy number and trapezoidal fuzzy number are the most widely used [15] and this study used fuzzy numbers with trapezium membership functions or trapezoidal fuzzy numbers.
3. Criteria System
Multi-criteria decision making (MCDM) is introduced as a method to determine the best alternative from a number of alternatives according to a set of criteria [25]. Criteria are usually chosen in the form of rule of standard and measurements in making decision. Based on the objectives, MCDM can be divided into two models [26]: multi-attribute decision making (MADM) and multi-objective decision making (MODM). Frequently, MCDM and MADM are utilized to describe the same class or category. MADM is normally used in problem solving of discrete spaces while MODM is used to solve problems in continuous space. In general, MADM is used to opt the best alternative from a number alternatives, while MODM is used for designing the best alternative. There are several common features used in MCDM, which are [26]:
- Alternatives. Alternatives are different objects and have the same opportunity to be chosen by the decision maker.
- Attributes. Attributes are often also referred to as characteristics, components, or decision criteria. In most cases, one-level criteria are used, although there is a possibility of using sub-criteria related to the criteria that have been given.
- Conflict between criteria. Some criteria usually have conflicts between one another, for example the profit criteria will conflict with the cost criteria.
- Decision weight. Decision weight indicates the relative importance of each criterion, W = ().
4. Methods
4.1. VIKOR Method
VIKOR is one of MADM methods by determining the alternative approach as an ideal solution in a ranking by using a ranking index based on a certain measure to find the ideal solution [2]. The VIKOR technique was introduced for resolving discrete decision-making on conflicting and non-commensurable criteria. The VIKOR ranking algorithm as follows [26,27].
Step 1. Evaluate the best rating and the worst rating for all the criteria,, if the function represents an advantage then
Step 2. Calculate the values of and as
where is the weight of each criterion.
Step 3. Compute the values of , , , , for formulated:
(veto) is a weight that ranges from 0-1, but usually is considered 0.5.
Step 4. Perform ranking for the alternatives by categorizing each values in decreasing order. The output is set in three ranking lists and denoted as
Step 5. In this step, we conclude that the lower the VIKOR index (), the better the alternative solution.
Alternative with the first ranking is the alternative with the highest ranking if using ascending order based on , becoming the proposed solution if the following two requirements are met:
Requirement 1.
“Acceptable Advantage”: , whereis second-rank alternative based on.
Requirement 2.
“Acceptable Stability”. Alternativehas to become the best ranking based on S and/or R.
If one of these two requirements cannot be met, the proposed solution should follow:
- (i)
- If condition 1 is not met, then is the proposed solution.
- (ii)
- If condition 2 is not met, then and is the proposed solution.
Finally, the best alternative with minimum has been obtained.
4.2. Data Analysis
This study was conducted via both primary as well as secondary data collections, processing and analysis, literature review, as well as relevant government/non-government institutions. In this study, data and information were from primary and secondary data which were then analyzed using trapezoidal fuzzy VIKOR approach to determine priorities [23,25,28] in reforestation. The primary data were obtained using questionnaires regarding the evaluation of the importance of the given criteria and alternatives. The questionnaires were distributed to two (2) BPDAS-HL Pemali Jratun watershed analysis. After that, a numerical simulation was carried out with a case study at BPDAS-HL Pemali Jratun. This was then followed by calculation, starting by testing the consistency of the results of the assessment performed by decision makers. If the assessment was consistent, the next stage was to perform analysis and calculation of the criteria weight which influenced reforestation decision making. The results were used for prioritization in the selection of reforestation areas.
5. Case Study
There are 128 watersheds in Central Java, Indonesia, 35 of which are currently in critical condition. This is due to the increasingly lack of water catchment areas and agricultural practices that do not heed the rules of conservation. Semarang city watershed is one of watersheds that are considered critical. Therefore, it is very appropriate if in this study, the Semarang City watershed has been chosen.
This study was conducted in Semarang City, which is surrounded by five watersheds—namely Garang, Bringin, Karanganyar, Silandak, and Babon Pemali Jratun watershed (Center for Watershed and Protected Forest Management (BPDASHL)). The details can be seen in Figure 2 as follows.
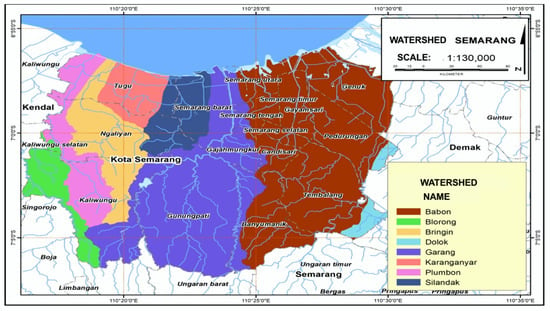
Figure 2.
Study area of watershed boundaries in Semarang City, Central Java, Indonesia. Source: BPDAS-HL Pemali Jratun, 2019.
6. Results and Discussion
The VIKOR method has been implemented for multi-criteria optimization in watershed problems and the result is shown in this section [19,29,30,31,32]. In this research, the trapezoidal fuzzy approach was used by applying linguistic terms to evaluate the ranking of alternatives with respect to criteria as shown in Table 1 and Table 2 [2].

Table 1.
Linguistics terms and appropriate fuzzy values among criteria [2].

Table 2.
Linguistic terms and appropriate fuzzy values among material [2].
Criteria described in Table 1 and Table 2 shows fuzzy number and their corresponding linguistic terms. Moreover, the linguistic variables and corresponding fuzzy set valuae for each criterion is show in Table 3 and Table 4. Let the fuzzy rating for criterion and importance of weight of the decision maker be ordered number fuzzy Xij of an alternative can be evaluated as [33,34]
where

Table 3.
Pairwise comparison among criteria according to decision makers on linguistic scale.

Table 4.
Pairwise comparisons among criteria according to decision makers in trapezoidal fuzzy numbers.
The weight of fuzzy can be defined as
where
According to Chang [35], defuzzification is the process of changing fuzzy number into crisp number. Defuzzification of fuzzy decision matrix and fuzzy weights of each of the criteria into crisp numbers uses the following formula
Si is the value of maximum group utility and Ri is a minimum individual regret of the opponent. These variables can be calculated as
where Si refers to the size of of the best fuzzy value and Ri refers to the size of of the worst fuzzy value, while wj is the weight given to each criterion cj. VIKOR index (Qi) can be obtained using the following formula
(veto) is the weight, ranging from 0-1, but is usually 0.5. The lower the VIKOR index (), the better the alternative solution.
According to Liu [36], hierarchical structure is a step to define the problem in a clearer and more detailed form. The hierarchical structure is arranged based on the views of experts in the concerned field. The top level in the hierarchical structure is the goal of the decision, the middle level is the criteria, while the lowest level is an alternative for decision. The arrangement of the hierarchical structure can be described in Figure 3. The hierarchical structure of the decision-making process applied in the watersheds in Semarang City, Central Java, Indonesia is as follows.
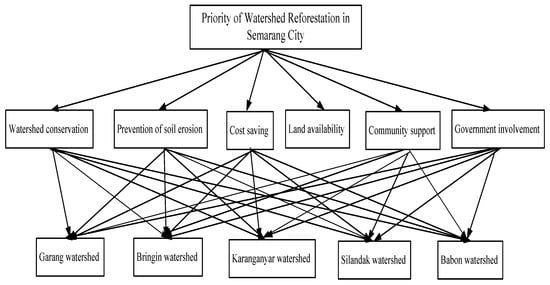
Figure 3.
Structure of hierarchical of the problem.
In this study, the aim is to evaluate DAS alternatives; the used criteria was set according to Hamdan [11]. Other human activities that may damage watersheds are excessive logging or deforestation, human settlement project, conversion of forest land to plantations and agricultural lands, about the criteria in reforestation area selection can be described as follows:.
C1: DAS Preservation
This criterion is set based on the function of sponges and the function of forested DAS pumps. Alternative evaluations in accordance with this criterion, experts do not only consider the DAS capacity but also the current reforestation situation in the area.
C2: Prevention of soil erosion
This criterion is set according to the paying function and the land function of forested DAS. Alternative evaluation according to these criteria, experts consider the risk of erosion of the area.
C3: Cost saving
This criterion reduces the specific costs of the regional planting and maintenance unit. This is considered as a profit criteria.
C4: Land availability
This criterion uses an empty area suitable for reforestation owned by the City of Semarang.
C5: Community Supporting Capacity
This subjective criterion represents social acceptance of the possibility of reforestation projects in the vicinity of certain DAS. Along with the carrying capacity of the environment, this criterion has a socio-economic impact from reforestation projects on communities in the expected area.
C6: Government involvement
This subjective criterion represents the government’s involvement in the possibility of reforestation projects in the DAS area. This criterion involves political consequences and possible risks from reforestation projects.
At the lowest level is an alternative to the DAS decision in Semarang City which is used as an alternative to the network structure of this research hierarchy with the notation A1: Garang DAS, A2: Bringin DAS, A3: Karanganyar DAS, A4: Silandak DAS, and A5: Babon DAS.
This hierarchical structure uses six criteria which described as (C1, …, C6) and six ratings of the alternatives: (A1, …, A6). To obtain the importance level of each criterion in the linguistic scale of the decision makers, it was conducted interviews using questionnaires. The interview results by using the questionnaires with two decision makers (D1 and D2) regarding the importance of each criterion on a linguistic scale are shown in the following Table 3.
Once the results of the questionnaires on a linguistic scale were obtained as shown in Table 3, they were then transformed to trapezoidal fuzzy numbers using Table 1 and the results are presented in the following Table 4.
Trapezoidal fuzzy numbers are generally used both in theory and practice of numbers [36] as trapezoidal fuzzy numbers including uncertainty fuzzy numbers [37]. The assessment of the results of the questionnaires between the alternatives and criteria on a linguistic scale according to decision makers 1 (D1) and 2 (two) (D2) is shown in Table 5.

Table 5.
Pairwise comparisons of alternative with criteria according to decision makers on linguistic scale.
Noordiana [2] used the VIKOR method decision making using linguistic terms to determine the ratings of alternatives compared to criteria with decision makers between alternatives and on linguistic scale criteria according to decisions D1–D5. While this study is used with decision makers D1 and D2. The results on a linguistic scale as shown in Table 5 were then converted into trapezoidal fuzzy numbers by using Table 2 and the results are presented in Table 6 as follows.

Table 6.
Pairwise comparisons of alternative with criteria according to decision makers on fuzzy numbers.
In Table 7, it shows an alternative paired comparison of criteria according to decision makers in fuzzy numbers to find the average value of several decision makers [32]. The multiple attribute group of decision making model is based on aggregating the value of crisp into intuitionistic fuzzy numbers. First, each alternative was evaluated with respect to their attributes, the value of which was provided by the decision maker as a firm number. Second, to normalize the value of a reasonable attribute in a group decision making environment, the maximum value and minimum value were added to the attribute value [38]. To discover the weight of the criteria and the pair, it was made in the form of a matrix. Matrices for criteria weight and pairwise comparison were calculated using Equations (2) and (3), and the outputs are presented in Table 7.

Table 7.
Weight of criteria and pairwise comparisons of alternative with criteria on trapezoidal fuzzy numbers.
The concept of fuzzy logic is easy to understand because it uses the basis of set theory. Moreover, fuzzy logic is very flexible meaning that it is able to adapt to the changes and uncertainties that accompany problems [16]. The set is a collection of objects that are both concrete and abstract that have certain characteristics in common. A crisp set is a set that is explicitly defined, meaning that for each element in the set, the universe can always be determined whether it is a member or not of the set [15]. Once the results as shown in Table 7 were obtained, they were then converted into crisp numbers using Equation (4) (Table 8).

Table 8.
Crisp value of criteria weight and pairwise comparison of alternative with criteria.
The next step was to determine the value of , i.e., the best value of each of the criteria and the value of , i.e., the worst value of each of the criteria (Table 9).

Table 9.
Best value and worst value.
Once the best and worst values of each of the criteria were obtained, the next step was to determine the utility measures—i.e., value of Si and Ri using Equations (5) and (6)—and to determine the VIKOR index (Qi) using Equation (7) (Table 10).

Table 10.
Value of S, R, and Q.
After all , , and on each alternative were subjected to defuzzification, it conducted ranking [39]. The values of , , and were then sorted in ascending order or ranking for alternatives one to five (A1–A5), thus obtaining the results in Table 11.

Table 11.
Final ranking of alternatives.
Next, the optimal solutions were checked in terms of:
Condition 1.
Resulting in 0.67 ≥ 0.25, meaning that Condition 1 was met.
Condition 2.
Based on Table 11, it was known that A1 had the best rankingbased onand, meaning that Condition 2 was met. Conditions 1 and 2 were met, sowas the optimal solution.
Therefore, by using trapezoidal fuzzy VIKOR [19,29,40], it can be seen that Garang watershed was the top priority and met the criteria for reforestation compared to other watersheds. Trapezoidal fuzzy VIKOR method can be applied in other areas, but adjusted to both the conditions of the areas and the criteria pre-determined by experts in their field [18].
7. Conclusions and Future Work
The results of the analysis using trapezoidal fuzzy VIKOR method involving several criteria can be used as a consideration in carrying out prioritization of watershed reforestation in Semarang City. This method is a complex multi-criteria optimization method which focuses on the ranking and selection of a set of alternatives among conflicting and known criteria. It can be seen that the Garang watershed is the top priority and it meets reforestation criteria compared with other watersheds. The trapezoidal fuzzy VIKOR method can be applied in other areas, but adjusted to both the conditions of the areas and the criteria pre-determined by experts in their field.
Future work: For further research, alternatives and criteria on the linguistic scale according to decision makers can be added, so that the data entered is more varied. In addition, the VIKOR method can be applied in other programs as a ranking method to provide an alternative model for integrated watershed management policies in the form of a framework that can be implemented within a certain timeframe, both general for all watersheds and those that are specific on the basis of their critical criterion criteria. Integrated watershed management is very important in order to preserve the environment for the welfare of the community. The VIKOR method can also be applied in other fields of study as a ranking or decision support method.
Author Contributions
All authors have contributed to this research equally. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the Research Fund of OPOC Program Diponegoro University, Indonesia.
Acknowledgments
The authors would like to thank the Center for Watershed and Protected Forest Management (BPDASHL) Pemali Jratun, the Ministry of Environment and Forestry Semarang, Central Java, Indonesia for the recommendation and permits during the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Salman, A.G. Pemodelan Dasar Sistem Fuzzy. Available online: https://socs.binus.ac.id/2012/03/02/pemodelan-dasar-sistem-fuzzy/ (accessed on 25 February 2020).
- Noordiana, M.I.; Sivakumar, D.M.; Ridzuan, M.M. Selection of natural fibre reinforced composites using fuzzy VIKOR for car front hood. Int. J. Mater. Prod. Technol. 2016, 53, 267–285. [Google Scholar]
- Santawy, M.F.; Ahmed, A.N. Evaluating Consulting Firms Using VIKOR. Life Sci. J. 2012, 9, 27–31. [Google Scholar]
- Salvius, P.L.; Adhistya, E.P.; Silmi, F. Implementation of the VIKOR Method for Scholarship Recipient Selection. In Proceedings of the 7th Conference on Information Technology and Electrical Engineering (CITEE 2015), Yogyakarta, Indonesia, 29–30 October 2015. [Google Scholar]
- Civic, A.; Vucijak, B. Multi-criteria optimization of insulation options for warmth of buildings to increase energy efficiency. Procedia Eng. 2014, 69, 911–920. [Google Scholar] [CrossRef]
- Santawy, M.F.; Ahmed, N.N. A VIKOR Approach for Project Selection Problem. Life Sci. J. 2012, 9, 5878–5880. [Google Scholar]
- Paimin Irfan, B.P.; Purwanto Dewi, R.I. Sistem Perencanaan Pengelolaan Daerah Aliran Sungai; Pusat Penelitian dan Pengembangan Konservasi dan Rehabilitasi (P3KR): Bogor, Indonesia, 2012; ISBN 978-602-99218-2-3. [Google Scholar]
- Asdak, C. Hidrologi dan Pengelolaan Daerah Aliran Sungai; Gadjah Mada University Press: Yogyakarta, Indonesia, 2004. [Google Scholar]
- Law of Republic of Indonesia No. 7 of 2004 concerning Water Resources. Available online: http://www.lead-journal.org/content/06118.pdf (accessed on 1 January 2020).
- Kaya, T.; Kahraman, C. Fuzzy multiple criteria forestry decision making based on an integrated VIKOR and AHP approach. Expert Syst. Appl. 2011, 38, 7326–7333. [Google Scholar] [CrossRef]
- Hamdan, M. Analisis Debit Aliran Sungai Sub DAS Ciliwung Hulu Menggunakan MW-SWAT. Bachelor’s Thesis, Bogor Agricultural University, Hilton Kuching, Malaysia, 2010. [Google Scholar]
- Siregar, D.; Nurdiyanto, H.; Sriadhi, S.; Suita, D.; Khair, U.; Rahim, R.; Napitupulu, D.; Fauzi, A.; Hasibuan, A.; Mesran, M.; et al. Multi-Attribute Decision Making with VIKOR Method for Any Purpose Decision. In Proceedings of the 1st International Conference on Green and Sustainable Computing (ICoGeS), Kuching, Malaysia, 25–27 November 2017; IOP Conf. Series: Journal of Physics: Conf. Series. IOP Publishing: Bristol, UK, 2018; Volume 1019, p. 012034. [Google Scholar]
- Wang, Y.J. Ranking tringle and trapezoidal fuzzy numbers based on the relative preference relation. Appl. Math. Model. 2015, 39, 586–599. [Google Scholar] [CrossRef]
- Shouzhen, Z.; Shyi-Ming, C.; KuoLi-Wei, K. Multiattribute decision making based on novel score function of intuitionistic fuzzy values and modified VIKOR method. Inf. Sci. 2019, 488, 76–92. [Google Scholar] [CrossRef]
- Frans, S.J. Himpunan dan Logika Kabur serta Aplikasinya; Graha Ilmu: Yogyakarta, Indonesia, 2006. [Google Scholar]
- Kusumadewi, S.; Purnomo, H. Aplikasi Logika Fuzzy untuk Pendukung Keputusan; Graha Ilmu: Yogyakarta, Indonesia, 2010. [Google Scholar]
- Abbasbandy, S.; Amirfakhrian, M. The nearest trapezoidal form of a generalized left right fuzzy number. Int. J. of Approx. Reason. 2006, 43, 166–178. [Google Scholar] [CrossRef]
- Vincent, F.Y.; Chi, H.T.X.; Dat, L.Q.; Phuc, P.N.K.; Shen, C.H. Ranking generalized fuzzy numbers in fuzzy decision making based on the left and right transfer coefficients and areas. Appl. Math. Model. 2013, 37, 8106–8117. [Google Scholar]
- Wang, T.C.; Liang, L.J.; Ho, C.Y. Multi-criteria decision analysis by using fuzzy VIKOR. In Proceedings of the International Conference on Servise Systems and Service Management, Troyes, France, 25–27 October 2006; Volume 2, pp. 901–906. [Google Scholar]
- Cheng, C.H.; Mon, D.L. Fuzzy System Reliability Analysis by Interval of Confidence. Fuzzy Sets System. 1993, 56, 29–35. [Google Scholar] [CrossRef]
- Cheng, C.H. A new approach for rangking fuzzy number by distance method. Fuzzy Sets Syst. 1998, 95, 307–317. [Google Scholar] [CrossRef]
- Pourebrahim, S.; Mokhtar, M.B.; Taghavi, S. Application of VIKOR and Fuzzy AHP for Conservation Priority Assessment in Coastal Areas: Case of Khuzestan district, Iran. Ocean Coast. Manag. 2014, 98, 20–26. [Google Scholar] [CrossRef]
- Anton, H.; Rorres, C. Elementary Linear Algebra; Erlangga: Jakarta, Indonesia, 2004. [Google Scholar]
- Cruz Carlos, S.; Ricardo, V.J. Extending and relating different approaches for solving fuzzy quadratic problems. Fuzzy Optim. Decis. Mak. 2011, 10, 193–210. [Google Scholar] [CrossRef]
- Wang, B.; Junnian, S.; Jingzheng, R.; Kexin, L.; Haiyan, D.; Xian’en, W. Selecting sustainable energy conversion technologies for agricultural residues: A fuzzy AHP-VIKOR based prioritization from life cycle perspective. Resour. Conserv. Recycl. 2019, 142, 78–87. [Google Scholar] [CrossRef]
- Kusumadewi, S. Fuzzy Multi-Attribute Decision Making (Fuzzy MADM); Graha Ilmu: Yogyakarta, Indonesia, 2006. [Google Scholar]
- Adel-Baset, M.; Chang, V.; Abduallah, G.; Smarandache, F. An integrated neutrosophic ANP and VIKOR method for achieving sustainable supplier selection: A case study in importing field. Comput. Ind. 2019, 106, 94–110. [Google Scholar] [CrossRef]
- Opricovic, S.; Gwo-Hshiung, T. Compromise solution by MCDM methods: A comparative analysis of VIKOR and TOPSIS. Eur. J. Oper. Res. 2004, 156, 445–455. [Google Scholar] [CrossRef]
- Yong, D.C. Theory and Methodology Applications of the extent analysis method on fuzzy AHP. J. Oper. Res. 1996, 95, 649–655. [Google Scholar]
- Yong, D. Plant location selection based on fuzzy TOPSIS. Int. J. Adv. Manuf. Technol. 2006, 28, 839–844. [Google Scholar] [CrossRef]
- Alguliyev, R.M.; Aliguliyev, R.M.; Mahmudova, R.S. Multicriteria Personnel Selection by the Modified Fuzzy VIKOR Method. Sci. World J. 2015. [Google Scholar] [CrossRef]
- Brid, P.; Narwade, R. Fuzzy AHP-Vikor Method for Decision Making for Residential Project. Int. J. Innov. Res. Sci. Eng. Technol. 2017, 6, 17136–17140. [Google Scholar]
- Baležentis, T. Group multi-criteria decision making based upon interval-valued fuzzy numbers: An extension of the MULTIMOORA method. Expert Syst. Appl. 2013, 40, 543–550. [Google Scholar] [CrossRef]
- Hajjari, T. Fuzzy Risk Analysis Based on Ranking of Fuzzy Numbers Via New Magnitude Method. J. Fuzzy Syst. 2017, 12, 17–29. [Google Scholar]
- Chang, D. Applications of the Extent Analysis Method on Fuzzy AHP. Eur. J. Oper. Res. 1996, 95, 649–655. [Google Scholar] [CrossRef]
- Liu, H.C.; Liu, L.; Liu, N.; Mao, L.X. Risk Evaluation in Failure Mode and Effects Analysis with Extended VIKOR Method Under Fuzzy Environment. Expert Syst. Appl. 2012, 39, 12926–12934. [Google Scholar] [CrossRef]
- Shemshadi, A.; Shirazi, H.; Toreihi, M.; Tarokh, M.J. A Fuzzy VIKOR method for supplier selection based on entropy measure for objective weighting. Expert Syst. Appl. 2011, 38, 12160–12167. [Google Scholar] [CrossRef]
- Zhongliang, Y. Aggregating crisp values into intuitionistic fuzzy number for group decision making. Appl. Math. Model. 2014, 38, 2969–2982. [Google Scholar]
- Chen, S.H.; Chen, J.H. Fuzzy risk analysis based on rangking generalized fuzzy numbers with different height and different spreads. Expert Syst. Appl. 2009, 36, 6833–6842. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Hajjari, T. A new approach for ranking of trapezoidal fuzzy numbers. Comput. Math. Appl. 2009, 57, 413–419. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).