Numerical Solution of Direct and Inverse Problems for Time-Dependent Volterra Integro-Differential Equation Using Finite Integration Method with Shifted Chebyshev Polynomials
Abstract
1. Introduction
2. Preliminaries
2.1. Shifted Chebyshev Integration Matrices
2.2. Tikhonov Regularization Method
- Step 1: Set and give an initial regularization parameter .
- Step 2: Compute .
- Step 3: Compute .
- Step 4: Compute .
- Step 5: Compute .
- Step 6: Compute .
- Step 7: If for a tolerance , end. Else, set and return to Step 2.
3. Numerical Algorithms for Direct and Inverse Problems of TVIDE
3.1. Procedure for Solving the Direct TVIDE Problem
3.2. Procedure for Solving Inverse Problem of TVIDE
3.3. Algorithms for Solving the Direct and Inverse TVIDE Problems
| Algorithm 1 Numerical algorithm for solving the direct TVIDE problem via FIM-SCP |
| Input:x, , L, T, N, , , , , , and . Output: An approximate solution .
|
| Algorithm 2 Numerical algorithm for solving the inverse TVIDE problem via FIM-SCP |
| Input:x, p, , , L, T, N, , , , , , , , and . Output: An approximate solution and the source terms at all discretized times.
|
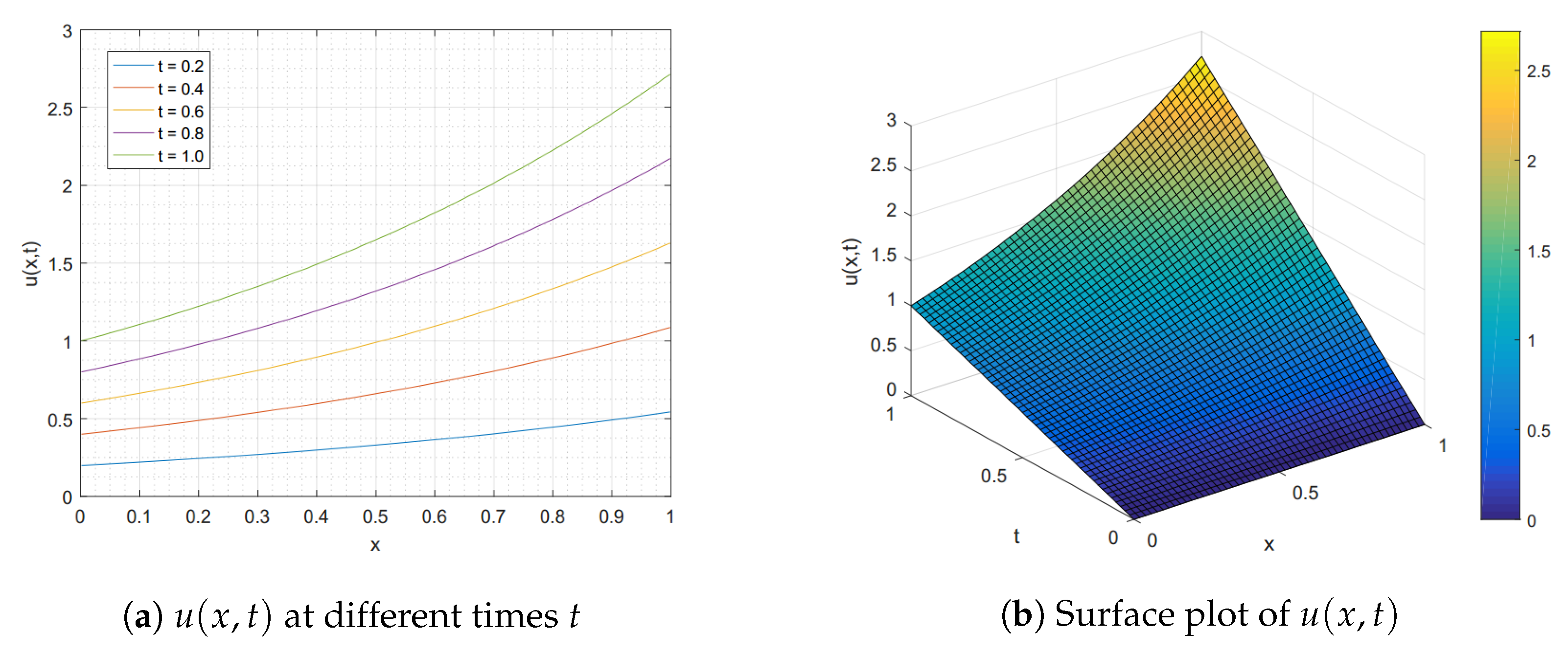
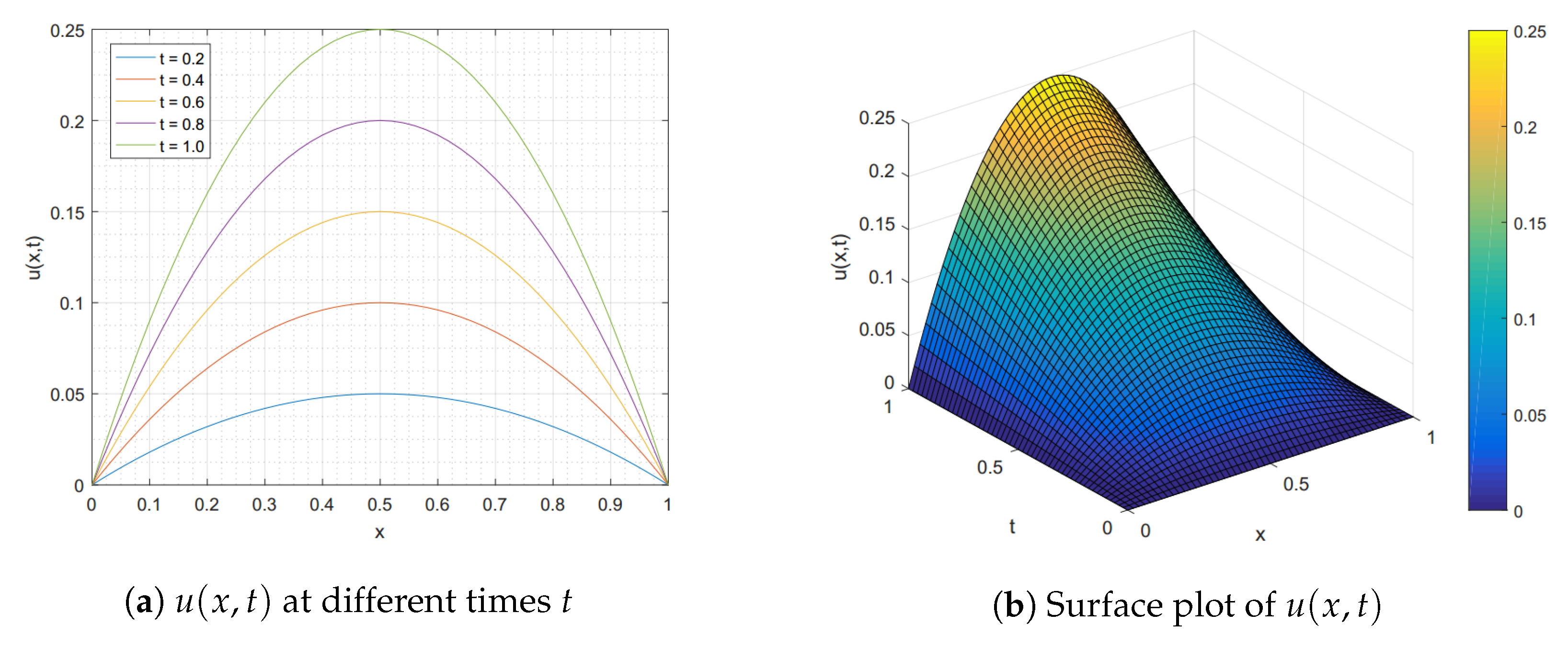
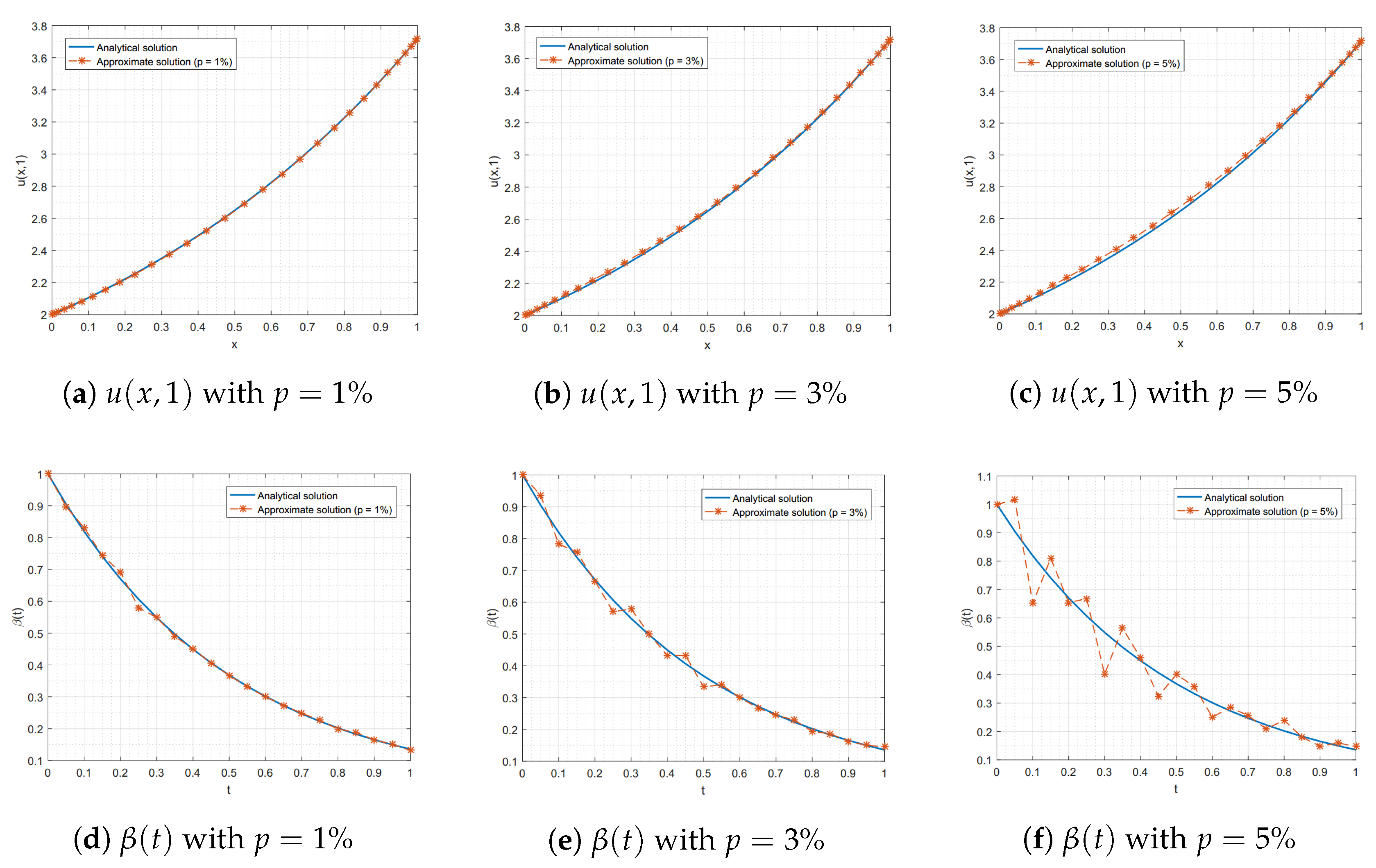
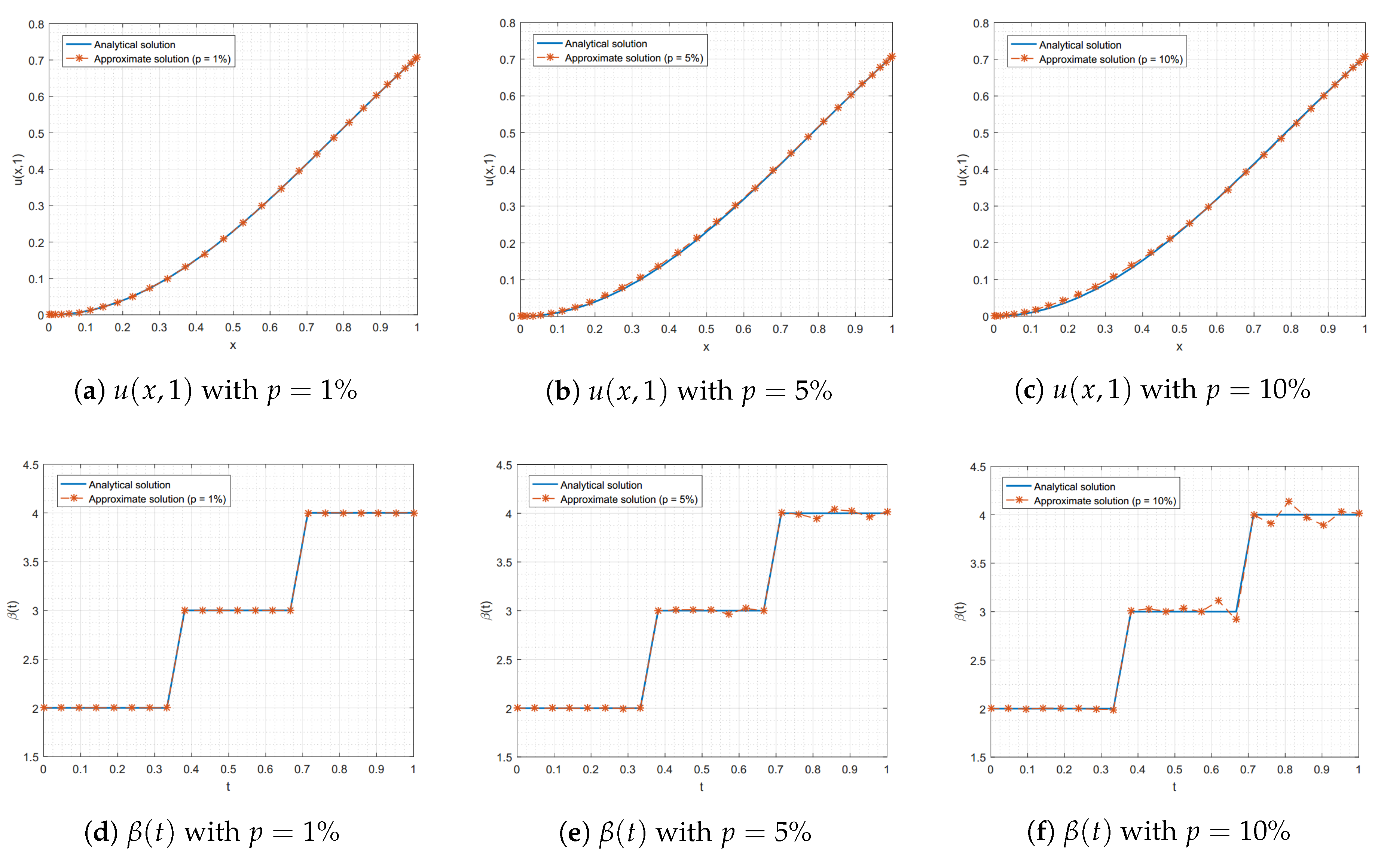
4. Numerical Experiments
5. Conclusions and Discussion
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| FDM | finite difference method |
| FIM | finite integration method |
| FIM-SCP | finite integration method with shifted Chebyshev polynomial |
| IDE | integro-differential equation |
| PDE | partial differential equation |
| TVIDE | time-dependent Volterra integro-differential equation |
References
- Zill, D.G.; Wright, W.S.; Cullen, M.R. Differential Equations with Boundary-Value Problem, 8th ed.; Brooks/Cole, Cengang Learning: Boston, MA, USA, 2013. [Google Scholar]
- Yanik, E.G.; Fairweather, G. Finite element methods for parabolic and hyperbolic partial integro–differential equations. Nonlinear Anal. 1988, 12, 785–809. [Google Scholar] [CrossRef]
- Engle, H. On Some Parabolic Integro–Differential Equations: Existence and Asymptotics of Solution; Lecture Notes in Mathematics, Springer: Berlin, Germany, 1983. [Google Scholar]
- Tang, T. A finite difference scheme for partial integro–differential equations with a weakly singular kernel. Appl. Numer. Math. 1993, 11, 309–319. [Google Scholar] [CrossRef]
- Aguilar, M.; Brunner, H. Collocation methods for second–order Volterra integro–differential equations. Appl. Numer. Math. 1988, 4, 455–470. [Google Scholar] [CrossRef]
- Brunner, H. Implicit Runge–Kutta–Nyström methods for general second–order Volterra integro–differential equations. Comput. Math. Appl. 1987, 14, 549–559. [Google Scholar] [CrossRef][Green Version]
- Jiang, Y.J. On spectral methods for Volterra-type integro–differential equations. J. Comput. Appl. Math. 2009, 230, 333–340. [Google Scholar] [CrossRef]
- Burton, T.A. Volterra Integral and Differential Equations; Academic Press: New York, NY, USA, 1983. [Google Scholar]
- Rahman, M. Integral Equations and Their Applications; WIT Press: Southampton, UK, 2007. [Google Scholar]
- Hu, Q. Stieltjes derivatives and beta–polynomial spline collocation for Volterra integro–differential equations with singularities. SIAM J. Numer. 1996, 33, 208–220. [Google Scholar] [CrossRef]
- Brunner, H. Superconvergence in collocation and implicit Runge–Kutta methods for Volterra–type integral equations of the second kind. Internet Schriftenreihe Numer. Math. 1980, 53, 54–72. [Google Scholar]
- El-Sayed, S.M.; Kaya, D.; Zarea, S. The decomposition method applied to solve high–order linear Volterra–Fredholm integro–differential equations. Internet J. Nonlinear Sci. Numer. Simulat. 2004, 5, 105–112. [Google Scholar] [CrossRef]
- Kabanikhin, S.I. Definitions and examples of inverse and ill–posed problems. J. Inverse Ill-Pose Probl. 2008, 16, 317–357. [Google Scholar] [CrossRef]
- Wen, P.H.; Hon, Y.C.; Li, M.; Korakianitis, T. Finite integration method for partial differential equations. Appl. Math. Model. 2013, 37, 10092–10106. [Google Scholar] [CrossRef]
- Li, M.; Chen, C.S.; Hon, Y.C.; Wen, P.H. Finite integration method for solving multi–dimensional partial differential equations. Appl. Math. Model. 2015, 39, 4979–4994. [Google Scholar] [CrossRef]
- Li, M.; Tian, Z.L.; Hon, Y.C.; Chen, C.S.; Wen, P.H. Improved finite integration method for partial differential equations. Eng. Anal. Bound. Elem. 2016, 64, 230–236. [Google Scholar] [CrossRef]
- Boonklurb, R.; Duangpan, A.; Treeyaprasert, T. Modified finite integration method using Chebyshev polynomial for solving linear differential equations. J. Numer. Ind. Appl. Math. 2018, 12, 1–19. [Google Scholar]
- Rivlin, T.J. Chebyshev Polynomials, From Approximation Theory to Algebra and Number Theory, 2nd ed.; John Wiley and Sons: New York, NY, USA, 1990. [Google Scholar]
- Tikhonov, A.N.; Goncharsky, A.V.; Stepanov, V.V.; Yagola, A.G. Numerical Methods for the Solution of Ill–Posed Problems; Springer: Dordrecht, The Netherlands, 1995. [Google Scholar]
- Sun, Y. Indirect boundary integral equation method for the Cauchy problem of the Laplace equation. J. Sci. Comput. 2017, 71, 469–498. [Google Scholar] [CrossRef]
| x | ||||||
|---|---|---|---|---|---|---|
| 0.1 | ||||||
| 0.3 | ||||||
| 0.5 | ||||||
| 0.7 | ||||||
| 0.9 | ||||||
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rate | Time(s) | Rate | Time(s) | Rate | Time(s) | ||||
| 5 | 1.4584 | 0.0465 | 1.5076 | 0.0456 | 1.5112 | 0.0469 | |||
| 10 | 1.2499 | 0.0487 | 1.2863 | 0.0469 | 1.3040 | 0.0485 | |||
| 15 | 1.1723 | 0.0495 | 1.2008 | 0.0481 | 1.2135 | 0.0501 | |||
| 20 | 1.1327 | 0.0506 | 1.1555 | 0.0516 | 1.1657 | 0.0535 | |||
| 25 | 1.1353 | 0.0521 | 1.1272 | 0.0538 | 1.1365 | 0.0553 | |||
| x | ||||||
|---|---|---|---|---|---|---|
| 0.1 | ||||||
| 0.3 | ||||||
| 0.5 | ||||||
| 0.7 | ||||||
| 0.9 | ||||||
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rate | Time(s) | Rate | Time(s) | Rate | Time(s) | ||||
| 5 | 1.0241 | 0.0524 | 1.0489 | 0.0531 | 1.3720 | 0.0535 | |||
| 10 | 1.0334 | 0.0577 | 1.0278 | 0.0576 | 1.1035 | 0.0576 | |||
| 15 | 1.0208 | 0.0597 | 1.0243 | 0.0585 | 1.0294 | 0.0598 | |||
| 20 | 1.0223 | 0.0609 | 1.0210 | 0.0610 | 1.0203 | 0.0620 | |||
| 25 | 1.0165 | 0.0619 | 1.0182 | 0.0638 | 1.0079 | 0.0641 | |||
| 5 | ||||||
| 10 | ||||||
| 15 | ||||||
| 20 | ||||||
| 5 | ||||||
| 10 | ||||||
| 15 | ||||||
| 20 | ||||||
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rate | Time(s) | Rate | Time(s) | Rate | Time(s) | ||||
| 5 | 1.0046 | 0.0667 | 1.0203 | 0.0655 | 1.6644 | 0.0662 | |||
| 10 | 0.9970 | 0.0679 | 1.0042 | 0.0667 | 1.2409 | 0.0673 | |||
| 15 | 0.9965 | 0.0684 | 1.0001 | 0.0675 | 1.1355 | 0.0693 | |||
| 20 | 1.0003 | 0.0716 | 0.9967 | 0.0722 | 1.0956 | 0.0720 | |||
| 25 | 1.0003 | 0.0776 | 1.0022 | 0.0766 | 1.0699 | 0.0751 | |||
| 6 | ||||||
| 9 | ||||||
| 12 | ||||||
| 15 | ||||||
| 6 | ||||||
| 9 | ||||||
| 12 | ||||||
| 15 | ||||||
| M | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Rate | Time(s) | Rate | Time(s) | Rate | Time(s) | ||||
| 6 | 1.4574 | 0.0704 | 1.4564 | 0.0726 | 1.4563 | 0.0728 | |||
| 9 | 1.3415 | 0.0727 | 1.3406 | 0.0737 | 1.3395 | 0.0746 | |||
| 12 | 1.2758 | 0.0735 | 1.2744 | 0.0753 | 1.2743 | 0.0767 | |||
| 15 | 1.2312 | 0.0749 | 1.2332 | 0.0783 | 1.2337 | 0.0807 | |||
| 18 | 1.2028 | 0.0798 | 1.2031 | 0.0799 | 1.2022 | 0.0828 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boonklurb, R.; Duangpan, A.; Gugaew, P. Numerical Solution of Direct and Inverse Problems for Time-Dependent Volterra Integro-Differential Equation Using Finite Integration Method with Shifted Chebyshev Polynomials. Symmetry 2020, 12, 497. https://doi.org/10.3390/sym12040497
Boonklurb R, Duangpan A, Gugaew P. Numerical Solution of Direct and Inverse Problems for Time-Dependent Volterra Integro-Differential Equation Using Finite Integration Method with Shifted Chebyshev Polynomials. Symmetry. 2020; 12(4):497. https://doi.org/10.3390/sym12040497
Chicago/Turabian StyleBoonklurb, Ratinan, Ampol Duangpan, and Phansphitcha Gugaew. 2020. "Numerical Solution of Direct and Inverse Problems for Time-Dependent Volterra Integro-Differential Equation Using Finite Integration Method with Shifted Chebyshev Polynomials" Symmetry 12, no. 4: 497. https://doi.org/10.3390/sym12040497
APA StyleBoonklurb, R., Duangpan, A., & Gugaew, P. (2020). Numerical Solution of Direct and Inverse Problems for Time-Dependent Volterra Integro-Differential Equation Using Finite Integration Method with Shifted Chebyshev Polynomials. Symmetry, 12(4), 497. https://doi.org/10.3390/sym12040497







