Abstract
In this article, an invariantized finite difference scheme to find the solution of the heat equation, is developed. The scheme is based on a discrete symmetry transformation. A comparison of the results obtained by the proposed scheme and the Crank Nicolson method is carried out with reference to the exact solutions. It is found that the proposed invariantized scheme for the heat equation improves the efficiency and accuracy of the existing Crank Nicolson method.
1. Introduction
Lie’s theory of symmetry groups for differential equations was initiated and utilized for obtaining solutions or reductions of the differential equations [1]. Lie constructed a highly algorithmic technique for the solutions of differential equations. Lie established that several techniques to find the solutions of differential equations can be described and deduced by considering the Lie group analysis of differential equations [2]. Thus, Lie symmetry methodology has a great significance in the theory and applications of differential equations. It is broadly applied by several researchers to solve difficult nonlinear problems. Lie studied the groups of continuous transformations. These transformations (symmetries) can be described by the infinitesimal generators.
The symmetries, which are not continuous are called discrete symmetries. Discrete symmetries have several applications in differential equations, e.g., they are used to simplify the numerical scheme and to find the new exact solutions from the known solutions [3]. The nature of bifurcations in nonlinear dynamical systems are also obtained by using discrete symmetry groups [4]. The procedure to find the discrete symmetries of the differential equations is discussed in [5,6,7,8].
Nowadays, it is a challenging area of research to solve the dynamical equations, as various phenomena in nature are modeled in dynamical systems. Many researchers have considered dynamical systems, e.g., Martinez, Yu Zhang, and Timothy Gordon studied the uses of the control scheme in the classical dynamical systems theory to predict driver behavior and vehicle trajectories [9]. Martinez and Timothy also discussed the uses of machine learning for the systematic understanding of human control behaviors in driving [10]. Lie group theory has became a universal tool for the analysis of dynamical equations. Lie symmetry analysis provides an effective way to solve the partial differential equations.
But recently, interest is rising on the applications of Lie group analysis in the partial differential equations for their numerical solutions. Some work has been dedicated to building those numerical schemes that preserve the symmetries of the given differential equations. Invariantized finite difference schemes by using the idea of moving frame were constructed by Kim [11] and Olver [12]. The technique of discretization that preserves some continuous symmetries of the original differential equation was also studied in [13,14,15,16,17]. In [18], the exact solutions of Fisher’s type equation with the help of Lie symmetries, which are continuous symmetries in nature, are studied. Since most of the partial differential equations have some geometrical properties and some discrete symmetry groups correspond to these geometrical features of partial differential equations [8], the new invaiantized finite difference methods constructed by using these discrete symmetry groups may show better performances than the other finite difference methods.
In this article, first, it is shown that the Crank Nicolson scheme of a diffusion (heat) equation is invariant under a group of the discrete symmetry transformation. Here, a modification is proposed for the invariantization of the Crank Nicolson method given by Kim et al. [19]. This modification is proposed with the help of the composition of discrete and continuous symmetry transformations of the heat equation. It is also shown that the proposed invariantized scheme gives better results, as compared to the other classical finite difference methods.
2. Heat Equation
The homogeneous heat (diffusion) [20] equation
plays a vital role in the study of heat conduction and other diffusion processes, in which a thin metal rod of length L, whose sides are insulated, is considered. The temperature of the bar at the point x and at the time t is represented by . The parameter D is called the thermal conductivity and it depends only upon the material from which the rod is made. For simplicity, we take the parameter then the Equation (1) becomes
2.1. Continuous Symmetry Groups
Equation (2) is a linear and homogenous partial differential equation with one dependent variable w and two independent variables x and t. The point transformation of Equation (2) defines the local diffeomorphism
This transformation maps any surface to the following surface
The heat Equation (2) has infinite dimensional Lie algebra. The infinitesimal generators and the continuous symmetry groups of the Equation (2) [21] are presented in Table 1.

Table 1.
Continuous symmetry transformations of (2).
Due to the arbitrariness of the function appearing in the last generator of Table 1, Lie algebra of Equation (2) is infinite dimensional. Each of the groups given in Table 1 has the property of mapping solutions of heat Equation (2) to the other solutions. For example, consider the explicit form of the projection
where is the group parameter. Computing the induced action on graphs of functions, we conclude that if is any solution to heat Equation (2), so is
2.2. Discrete Symmetry Group
Hydon introduced a technique [7] by which all discrete point symmetries of the partial differential equations can be found on basis of the results [6] that each continuous symmetry generator of a Lie algebra ℓ of a differential equation brings an automorphism that preserve the following commutator relation
Hydon’s method categorizes and factor out all those automorphisms of a Lie algebra ℓ that are equivalent under the action of a Lie symmetry in a Lie group that is generated by the Lie algebra ℓ and provide the most general realization of these automorphisms as point transformations. Finally, by using these point transformations, an entire list of discrete point symmetries of a partial differential equation, is obtained.
The discrete symmetry group of Equation (2) has already been obtained in [8], which is isomorphic to = {group of residues modulo 4} and is generated by
where .
3. Finite Difference Schemes for the Heat Equation
Some finite difference schemes are available in the literature, which help us to find the numerical solutions of the partial differential equations. In this section, the backward difference scheme, forward difference scheme, and the Crank Nicolson method for the heat equation along their stability conditions, are given [22].
3.1. Forward Difference Scheme
The forward difference scheme for heat Equation (2) is given by
where . Here h is the -axis step size and k is the time step size for the grid points , where , for non-negative integers . This scheme is Forward in Time and Centered in Space (FTCS). This method is explicit and converges to the solution for , so is conditionally stable [22].
3.2. Backward Difference Scheme
The backward difference scheme for Equation (2) is given by
This scheme is Backward in Time and Centered in Space (BTCS). This is an implicit and unconditionally stable scheme [22].
3.3. Crank Nicolson Method
The Crank Nicolson method (CNM) for Equation (2) is
The Crank Nicolson method is also implicit and unconditionally stable [22]. It has significant advantages for the time-accurate solutions. The temporal truncation error of CNM is , whereas the truncation error of FTCS and BTCS is .
3.4. Invariantization of the Crank Nicolson Method under the Discrete Symmetry Transformation
It is observed that among the mentioned finite difference schemes for the heat equation, the Crank Nicolson method gives the more accurate results [23], so we are interested in constructing an invariantization of the Crank Nicolson method. In the present subsection, we show that the Crank Nicolson method is invariant under the discrete symmetry transformation (3).
Let be an approximation of at the mesh point . Now, by using the discrete symmetry group of heat equation given in (3), we have the following transformation
By using (5), the Crank Nicolson method transformed to
The finite difference approximation to heat Equation (2) obtained in (7) is similar to the Crank Nicolson method for heat Equation (4). Thus, the Crank Nicolson method remains invariant under the discrete symmetry transformation (3). The consequence of the result obtained in Section 3 can be written in the form of the following theorem.
4. Discrete Symmetry Numerical Scheme For the Heat Equation
Most of the finite difference methods including the Crank Nicolson method are invariant under time, space translations, and scale transformation [24]. It is also proved in the previous literature that the Crank Nicolson method for the heat Equation (2) is invariant under the transformation of the discrete symmetry. Notice that the Galilean boost and projection group are the transformations under which the Crank Nicolson method is not invariant. However, the Crank Nicolson method invariantized by Galilean boost, projection transformations or composition of these transformations, becomes unstable (i.e., does not converge to the exact solution). Nevertheless, by taking the composition of the discrete symmetry group and the projective symmetry group, which is a continuous symmetry group of the heat equation, invariantized Crank Nicolson method converges to the exact solution and gives the more adequate results as compare to other existing finite difference schemes of Equation (2).
In the present section, we construct an invariantization of the Crank Nicolson method for Equation (2) by using the composition of discrete and continuous symmetry groups. The construction of this method is based on the composition of the variable w of these two groups. We deal with the following transformation to construct the new scheme:
where . By transforming the variable w in the Crank Nicolson method (4) with the above transformation for Equation (2), we get:
which can be further simplified as
Since is a continuous parameter and we can choose the optimal value of for which the proposed method gives better performance than the Crank Nicolson method. We choose , where and i is a positive integer, so the above equation takes the form:
The final form of the method is
where
and
Since the Crank Nicolson method for the heat equation is unconditionally stable [22] and the discritized Crank Nicolson method (DCNM) for heat Equation (2) provided in (8) is the invariantization of the Crank Nicolson method, so this method also preserves the unconditional stability condition and therefore converges to the exact solution without having any condition on .
5. Solutions of the Heat Equation
In this section, we find the analytic solution of heat Equation (2) and compare it with the numerical solutions calculated by using the CNM and the proposed method DCNM.
5.1. Analytic Solution
We consider one dimensional homogeneous heat Equation (2) with the following boundary conditions
where , and are two times continuously differentiable functions on , L is the length of the rod and T is the maximum time.
Heat Equation (2) is reduced to an ordinary differential equation by using the following similarity variable
where is obtained from the initial condition with . An exact solution of the system given by the Equations (2) and (9) for particular values of arbitrary functions , , and is given in the following example.
Example 1.
Our aim is to find the solution of (2) with the following initial and boundary conditions
Using the similarity transformation
the above problem is reduced to the following ODE
with the solution .
Hence is the exact solution of the above boundary value problem.
5.2. Numerical Solutions Using CNM and the Proposed Method DCNM
In this subsection, the performance of the proposed method DCNM is investigated by applying it to Example 1. The efficiency of the present method DCNM is shown by calculating the absolute errors, root mean square errors and maximum errors . These errors are computed by the following formulas [18]:
with , where are numerical and are the exact solutions.
To check the computational accuracy of the proposed method (DCNM), we reconsider Example 1 given in the previous subsection, which has the analytic solution [22]. We compare our results of the numerical solutions (DCNM) with the exact solutions and the solutions that are obtained by the Crank Nicolson method for the x-axis step size a time step size and for the time . The comparisons of the numerical solutions obtained by DCNM with the solutions calculated by FTCS, CNM, and the exact solutions are presented in Table 2, where Table 3 is showing the absolute errors of the solutions calculated by FTCS, CNM and the DCNM given in (8) for the different x-axis step sizes. Table 4 shows the values of for fixed and for different values of k, where Table 5 shows the values of for fixed and for different values of h.

Table 2.
The values of for different x.

Table 3.
Absolute errors for different values of x.

Table 4.
for fixed and for different values of k.

Table 5.
for fixed and for different values of h.
Table 6 presents root mean square errors and the maximum errors for DCNM and CNM of Example 1 for the different values of t.

Table 6.
and errors for different values of t.
Figure 1 shows the comparisons between the numerical solutions, obtained by the DCNM given in (8), the Crank Nicolson method, and the exact solutions of Example 1 in 2D for fixed . For and , the graphical representations of the space-time graph of the numerical solutions calculated by the DCNM and exact solutions for the above boundary value problem for are presented in Figure 2 and Figure 3, respectively, and it can be observed that both solutions are very similar.
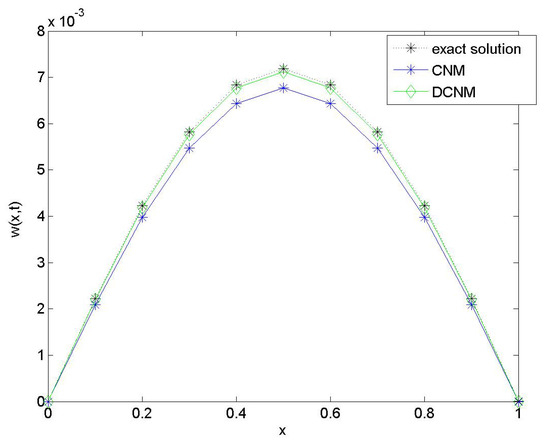
Figure 1.
Comparison of the exact solution with solutions obtained by CNM and DCNM.
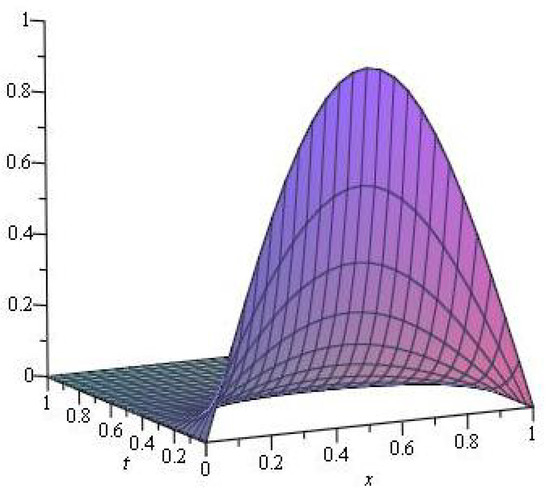
Figure 2.
Space-time graph of DCNM solution for Example 1.
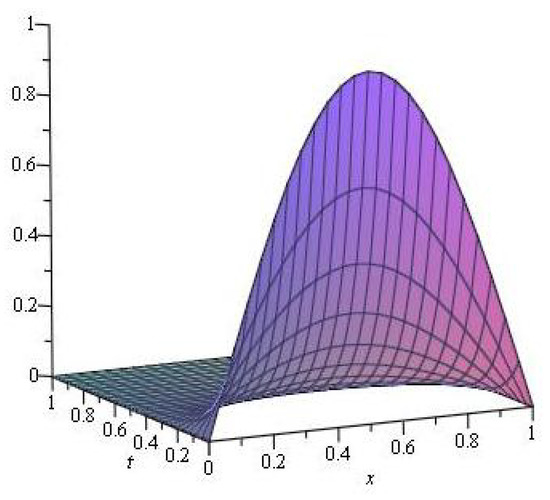
Figure 3.
Space-time graph of exact solution for Example 1.
6. Conclusions
This paper contains the application of the discrete symmetry transformation for the boundary value problem of the diffusion equation. An invariantized finite difference method to find the solution of the heat equation using the composition of discrete symmetry group and projection group of the heat equation is developed. Table 2, Table 3 and Table 4 show that the proposed invariantized method DCNM improves the efficiency and accuracy of the existing Crank Nicolson method.
Similarly, with the help of discrete symmetry groups of partial differential equations, different invariantized finite difference schemes can be constructed to improve the efficiency and performance of the existing finite difference methods.
Author Contributions
All authors have equal contribution to this research and in preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by NUST, Pakistan.
Acknowledgments
The author would like to thanks the editor and anonymous referees for their suggestions and valuable comments that improved the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| FTCS | Forward in Time and Centered in Space |
| CNM | Crank Nicolson Method |
| DCNM | Discritized Crank Nicolson Method |
References
- Lie, S. Theorie der Transjormations Gruppen; Chelsea: New York, NY, USA, 1970. [Google Scholar]
- Yang, H.; Shi, Y.; Yin, B.; Dong, H. Discrete Symmetries Analysis and Exact Solutions of the Inviscid Burgers Equation. Discret. Nat. Soc. 2012, 56, 1–15. [Google Scholar] [CrossRef]
- Ibragimov, N.H. Elementary Lie Group Analysis and Ordinary Differential Equations; John Wiley & Sons: Chichester, UK, 1999. [Google Scholar]
- Golubitsky, M.; Stewart, I.; Schaeffer, D.G. Singularities and Groups in Bifurcation Theory; Springer: New York, NY, USA, 1988. [Google Scholar]
- Hydon, P.E. Discrete point symmetries of ordinary differential equations. R. Soc. Lond. Proc. A 1998, 454, 1961–1972. [Google Scholar] [CrossRef]
- Hydon, P.E. How to construct the discrete symmetries of partial differential equations. Eur. J. Appl. Math. 2000, 11, 515–527. [Google Scholar] [CrossRef][Green Version]
- Hydon, P.E. Symmetry Methods for Differential Equations; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Laine, F.E.; Hydon, P.E. Classification of discrete symmetries of ordinary differential equations. Stud. Appl. Math. 2003, 111, 269–299. [Google Scholar] [CrossRef]
- Garcıa, M.M.; Zhang, Y.; Gordon, T. Modelling Lane Keeping by a Hybrid Open-Closed-Loop Pulse Control Scheme. IEEE Trans. Ind. Inform. 2016, 12, 2256–2265. [Google Scholar] [CrossRef]
- Garcıa, M.M.; Gordon, T. A New Model of Human Steering Using Far-Point Error Perception and Multiplicative Control. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics (SMC2018), Miyazaki, Japan, 7–10 October 2018. [Google Scholar]
- Kim, P. Invariantization of numerical schemes using moving frames. Numer. Math. Springer 2006, 10, 142–149. [Google Scholar] [CrossRef]
- Olver, P.J. Geometric foundations of numerical algorithms and symmetry. Appl. Algebra Eng. Commun. Comput. 2001, 11, 417–436. [Google Scholar] [CrossRef]
- Budd, C.; Dorodnitsyn, V.A. Symmetry-adapted moving mesh schemes for the nonlinear Schrodinger equation. J. Phys. A Math. Gen. 2001, 34, 10387–10400. [Google Scholar] [CrossRef]
- Dorodnitsyn, V.A. Finite difference models entirely inheriting continuous symmetry of original differential equations. Int. J. Mod. Phys. Ser. C 1994, 5, 723–734. [Google Scholar] [CrossRef]
- Dorodnitsyn, V.A.; Kozlov, R.; Winternitz, P. Lie group classification of second order difference equations. J. Math. Phys. 2000, 41, 480–504. [Google Scholar] [CrossRef]
- Valiquette, F.; Winternitz, P. Discretization of partial differential equations preserving their physical symmetries. J. Phys. A Math. Gen. 2005, 38, 9765–9783. [Google Scholar] [CrossRef]
- Budd, C.J.; Iserles, A. Geometric integration: Numerical solution of differential equations on manifolds. Philos. Trans. R. Soc. Lond. A 1999, 357, 945–956. [Google Scholar] [CrossRef]
- Verma, R.; Jiwari, R.; Koksal, M.E. Analytic and numerical solutions of nonlinear diffusion equations via symmetry reductions. Adv. Differ. Equ. 2014, 10, 142–149. [Google Scholar] [CrossRef]
- Kim, P. Invariantization of the Crank-Nicolson method for Burgers’ equation. Phys. D Nonlinear Phenom. 2008, 237, 243–254. [Google Scholar] [CrossRef]
- Stavroulakis, I.P.; Tersian, S.A. Partial Differential Equations: An Introduction with Mathematica and Maple; World Scientific Publishing Company Ltd.: Hackensack, NJ, USA, 2004. [Google Scholar]
- Bluman, G.W.; Kumei, S. Symmetries and Differential Equations; Springer: New York, NY, USA, 1989. [Google Scholar]
- Burden, R.L.; Faires, J.D. Numerical Analysis, 9th ed.; Brooks/Cole Cengage Learning: Boston, MA, USA, 2010. [Google Scholar]
- Kharab, A.; Guenther, R.B. An Introduction to Numerical Methods, A Matlab Approach, 3rd ed.; CRC Press Taylor and Francis Group: New York, NY, USA, 2011. [Google Scholar]
- Marx, C.; Aziz, H. Lie Symmetry preservation by Finite difference Schemes for the Burgers Equation. Symmetry 2010, 2, 868–883. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).