Abstract
We discuss the possibility that inflation is driven by supersymmetry breaking with the scalar component of the goldstino superfield (sgoldstino) playing the role of the inflaton and charged under a gauged R-symmetry. Imposing a linear superpotential allows us to satisfy easily the slow-roll conditions, avoiding the so-called -problem, and leads to an interesting class of small field inflation models, characterised by an inflationary plateau around the maximum of the scalar potential near the origin, where R-symmetry is restored with the inflaton rolling down to a minimum describing the present phase of the Universe. Inflation can be driven by either an F- or a D-term, while the minimum has a positive tuneable vacuum energy. The models agree with cosmological observations and in the simplest case predict a rather small tensor-to-scalar ratio of primordial perturbations. We propose a generalisation of Fayet-Iliopoulos model as a microscopic model leading to this class of inflation models at low energy.
1. Introduction
“A fundamental theory of Nature, such as string theory, should be able to explain at the same time particle physics and cosmology, which are phenomena that involve very different scales from the smallest microscopic four-dimensional (4d) quantum gravity length of cm to the largest macroscopic distances of the size of the observable Universe cm, spanned a region of about 60 orders of magnitude. In particular, besides the 4d Planck mass, there are three very different scales with very different physics corresponding to the electroweak scale, dark energy and inflation” [1]. An interesting possibility is that these scales are related by the dynamics of an underlying fundamental theory, such as string theory. A first step towards this goal is to study possible connections between the electroweak scale of the Standard Model or its possible extension (such as the supersymmetry breaking scale) with that of inflation. An additional constraint would be to impose at the electroweak vacuum the presence of a tiny tuneable cosmological constant in order to accommodate the observed dark energy, without necessarily trying to explain it. Indeed, despite the absence of evidence of low-energy supersymmetry at colliders, it is theoretically likely that supersymmetry plays a role at some more fundamental level. On the other hand, inflation is an attractive paradigm for cosmology but the associated models provide a phenomenological description leaving several unanswered questions, such as the origin of the inflaton field, its fundamental or composite nature and its connection to the rest of particle physics.
“Inflationary models in supergravity (For reviews on supersymmetric models of inflation, see for example [2].) suffer in general from several problems, such as fine-tuning to satisfy the slow-roll conditions, large field initial conditions that break the validity of the effective field theory, and stabilisation of the (pseudo) scalar companion of the inflaton arising from the fact that bosonic components of superfields are always even. The simplest argument to see the fine tuning of the potential is that a canonically normalised kinetic term of a complex scalar field X corresponds to a quadratic Kähler potential that brings one unit contribution to the slow-roll parameter , arising from the proportionality factor in the expression of the scalar potential V. This problem can be avoided in models with no-scale structure where cancellations arise naturally due to non-canonical kinetic terms leading to potentials with flat directions (at the classical level). However, such models require often trans-Planckian initial conditions that invalidate the effective supergravity description during inflation. A concrete example where all these problems appear is the Starobinsky model of inflation [3], despite its phenomenological success” [4].
In [4], we proposed a class of models that avoids all three problems above in which the inflaton is identified with the superpartner of goldstino (See [5,6,7,8] for earlier works relating supersymmetry and inflation), in the presence of a gauged R-symmetry. Indeed, the superpotential in this case is linear and cancels exactly the big contribution to described above. Since inflation takes place at a plateau around the maximum of the scalar potential (hill-top) no large field initial conditions are needed. The pseudo-scalar companion of the inflaton is eaten by the R-gauge field that becomes massive, leaving the inflaton as a single scalar degree of freedom present in the low-energy spectrum. As we will show below, this model provides therefore a minimal realisation of natural small-field inflation in supergravity, compatible with present observations. Moreover, it allows a realistic minimum describing our present Universe with an infinitesimal positive vacuum energy arising due to a cancellation between an F- and D-term contributions to the scalar potential, without affecting the properties of the inflationary plateau, along the lines of Refs. [9,10,11].
In the model we discussed above, the D-term has a constant FI contribution but plays no role during inflation and can be neglected, while the pseudoscalar partner of the inflaton is absorbed by the gauge field that becomes massive away from the origin. Recently, a new FI term was proposed [12] that has three important properties: (1) it is manifestly gauge invariant already at the Lagrangian level; (2) it is associated to a that should not gauge an R-symmetry and (3) supersymmetry is broken by (at least) a D-auxiliary expectation value and the extra bosonic part of the action is reduced in the unitary gauge to a constant FI contribution leading to a positive shift of the scalar potential, in the absence of matter fields. In the presence of matter fields, the FI contribution to the D-term acquires a special field dependence that violates invariance under Kähler transformations.
In a recent work [13], we studied the properties of the new FI term and explored its consequences to the class of inflation models we introduced in [4]. (The new FI term was also studied in [14] to remove an instability from inflation in Polonyi-Starobinsky supergravity.) We first showed that matter fields charged under the gauge symmetry can consistently be added in the presence of the new FI term, as well as a non-trivial gauge kinetic function. We then observed that the new FI term is not invariant under Kähler transformations. On the other hand, a gauged R-symmetry in ordinary Kähler invariant supergravity can always be reduced to an ordinary (non-R) by a Kähler transformation. By then going to such a frame, we find that the two FI contributions to the D-term can coexist, leading to a novel contribution to the scalar potential.
The resulting D-term scalar potential provides an alternative realisation of inflation from supersymmetry breaking, driven by a D- instead of an F-term (See [15,16] for earlier works on D-term inflation). The inflaton is still a superpartner of the goldstino which is now a gaugino within a massive vector multiplet, where again the pseudoscalar partner is absorbed by the gauge field away from the origin. For a particular choice of the inflaton charge, the scalar potential has a maximum at the origin where inflation occurs and a supersymmetric minimum at zero energy, in the limit of negligible F-term contribution (such as in the absence of superpotential). The slow roll conditions are automatically satisfied near the point where the new FI term cancels the charge of the inflaton, leading to higher than quadratic contributions due to its non trivial field dependence.
The Kähler potential can be canonical, modulo the Kähler transformation that takes it to the non R-symmetry frame. In the presence of a small superpotential, the inflation is practically unchanged and driven by the D-term, as before. The maximum is still at the origin but the minimum has a small non-vanishing positive cosmological constant, where supersymmetry is broken by both F- and D-auxiliary expectation values of the same order of magnitude. In general, the model predicts small primordial gravitational waves with a tensor-to-scaler ration r well below the observability limit. However, when higher order terms are included in the Kähler potential, r can be increased to large values [17].
In the following, we will present the main features of these models. A brief review of the proposed single field model for inflation from supersymmetry breaking where the goldstino superpartner plays the role of the inflaton is given in Section 2. Assuming that inflation arises near the maximum of the scalar potential where R-symmetry is restored, supersymmetry breaking is driven predominantly either by an F-term or by a D-term. In Section 3, we introduce an example of the microscopic origin for the effective field theory of the inflation model described above. In Section 4, we discuss the new FI-term and analyse its consequences in the models of inflation driven by supersymmetry breaking.
2. Inflation from Supersymmetry Breaking
The Set Up
Let us consider , supergravity with gauged R-symmetry [18]. The theory contains one chiral multiplet and a corresponding vector multiplet. The chiral multiplet X transforms as:
where q and denote the charge of X and the gauge parameter respectively. The Kähler potential is a function of while we choose the linear superpotential
where f is a constant parameter. Note that X is dimensionless and the reduced Planck mass GeV. Without loss of generality, we choose the gauge kinetic function to be 1. The scalar potential is given by
where the F and D-term potential are
The Kähler covariant derivative is defined by
The moment map is defined by
denotes the Killing vector for X under the R-symmetry, and ; in the present setup, they become . As usual, subscripts stand for partial derivatives: .
We assume the inflaton starts rolling around a local maximum of the potential near the origin , where R-symmetry is preserved. Let us expand the Kähler potential up to quadratic order in :
With this, the F-term potential becomes
and the D-term potential is
By making the change of field variables
the scalar potential becomes
Note that the phase get absorbed by the gauge field in the standard Brout-Englert-Higgs mechanism [19,20,21]. Thus, the scalar potential is only a function of the modulus .
We now indentify the field as the inflaton. However, in order to calculate the slow-roll parameters, we introduce the canonically normalised field satisfying
The slow-roll parameters can be defined in terms of the canonical field as:
Since inflation arises near the maximum , we expand
where we defined . The above equation implies . For simplicity, we focus on the special case where F-term contribution to the scalar potential is dominant. By considering the behaviour near the origin, we can put some constraints on the coefficient A of the quadratic term of the Kähler potential defined on the right-hand side of (7). We can easily show that is required for having a local maximum of the scalar potential at . Furthermore, the slow-roll condition sets an upper bound . Taking these requirements into account, the constraint on A is
We can choose to obtain which is in agreement with CMB observational data. In the following sections we introduce a microscopic model that can generate the coefficient A satisfying the constraint in (15).
3. Microscopic Model
In this section, we introduce an example of the microscopic origin for the effective field theory of the inflation model described in the previous section. It is a “generalisation” version of the Fayet-Iliopoulos (FI) model [22]. The model has a vacuum configuration that spontaneously breaks both gauge symmetry and supersymmetry, leaving (in the decoupling limit) the goldstino as the only light degree of freedom in this sector.
3.1. The Generalised Fayet-Iliopoulos Model
Let us consider a supergravity model with two chiral multiplets and one vector multiplet. As we will show shortly, this theory has a vacuum in which only is lighter than the other degrees of freedom. After integrating out all other heavy degrees of freedom, we will obtain an effective supergravity action for . The UV supergravity action formulated in Poincaré superspace as in [18] is given by
In the following, we will mostly work in supergravity mass units , for notational simplicity. This theory is invariant under a gauged transformation which acts only on matter superfields, which we call transformation. Under , the chiral superfields and the vector superfield transform as, (strictly speaking, this includes a local rotation of the fermionic coordinates and the overall phase rotation because the superpotential also transforms under . Hence, is a gauged R-transformation)
where is chiral. The function is the -invariant Kähler potential,
The gaugino superfield is defined with the super-Poincaré covariant derivatives as
The gauge kinetic function is given by
The logarithmic term cancles the chiral anomaly of through Green-Schwarz mechanism. For more details see [4,23]
The scalar potential in the microscopic model considered in (16) is given by
where is the lowest component of . Note that the first term is the D-term contribution and is the Fayet-Iliopoulos parameter. Below, it is natural to introduce the parameter as
The vacuum which spontaneously breaks and supersymmetry is of the form
Around this vacuum, the fields of are heavier than those of , in the limit of small SUSY breaking scale. The extremisation condition with respect to reads
This provides us a constraint among the parameters , v, x and which we will use in Section 3.4.
Let us consider the approximation where Equation (24) has a unique solution
We can easily see that plays the role of the massless R-Goldstone boson while gets a correction to its mass-squared compared to the global SUSY case by . The mass-squared of also changes to . If this mass is much smaller than the other masses the integrating out condition is satisfied.
For Equation (24) gives two solutions , where
The mass of the vector field is and the mass matrices of are given by
In the following, we assume that the integrating out condition is satisfied, which will be shown explicitly in Section 3.4 with the analysis of the parameter space leading to models of realistic inflation.
3.2. Integrating Out Heavy Fields
The UV action in conformal superspace takes exactly the same form as in the case with the super-Weyl compensators [24]:
After fixing the conformal compensators as , it becomes the action (16). Let us briefly explain the notation. In conformal superspace, there are two important classes of superfields namely chiral and primary superfield. A chiral superfield is defined by
where is the superconformally covariant spinor derivative. A primary superfield of charges (conformal and chiral weights) is defined by
where are the generators for the dilatation, chiral rotation, and special conformal transformations respectively [25] (The local Lorentz index A in stands for the vector and the undotted and dotted spinor indices . Therefore denotes the generators , with , the generators of the S-supersymmetry).
We now explain the notation. For details, see [26]. An action integral with in the third line of (31) is called the D-type action. In order to be invariant under gauge transformation, its integrand must be real primary of charge . On the other hand, action integrals with in the first and second lines of (31) are called the F-type action. Their integrands are required to be chiral primary of charge for gauge invariance. The determinant of the vierbein superfield is real primary of charges , while the chiral density is chiral primary of charges .
The chiral superfields are primaries of charges . They transform under the matter as , where is chiral primary of charges . The vector superfield is primary of charges . It transforms under as .
“The compensators are chiral primaries of charges , and anti-chiral primary of charges , respectively. To guarantee gauge invariance, we assign charges to the compensators as” [26]
is the gauge-invariant Kähler potential defined in (18) and is the chiral primary gaugino superfield of charges , defined here with the superconformally covariant derivatives as (Note that has charges and has charges .)
Let us proceed to integrating out the heavy degrees of freedom. In the unitary gauge , the action reads
where the vector superfield is rescaled to absorb the factor , and is the gauge-fixed Kähler potential,
Recall that .
To integrate out at tree level, we will solve the equation of motion of around its vacuum where higher derivative contributions are neglected. The equation of motion of reads
After making the shift in to remove the tadpole [27], and then neglecting the derivative term, we obtain the following low-energy effective equation of motion
We now integrate out in the following way:
and then eliminate by substituting the exact equation of motion (38). The first and third terms of the action (36) then become
Next, we combine the (low-energy) equation of motion (39) with the second line of (41). This gives us the low-energy effective action,
where is understood as a function of , determined by the (low-energy) equation of motion (39).
3.3. Effective K ähler Potential and Superpotential
We will fix the compensators in such the way that the gauge fixing
makes the effective action (42) into the integral in the Kähler superspace characterised by the effective Kähler potential . This is easy to be realised by
where the second term is the supergravity modification. The gauge fixing (43) simplifies the effective equation of motion (39) into
This gives us an analytic solution for as a function of ,
“Since, the low-energy effective theory obtained in the this section does not have a gauged R symmetry, we need to add another gauged R symmetry to the low-energy theory by hand. Let us denote this additional gauge by . The simplest way to achieve this is by extending the symmetry of the UV theory from to and assuming that the additional does not take part in the integrating out process and survives as the gauged R-symmetry of the low-energy theory. As we summarize in Table 1, transforms under with charge while is singlet under ” [26].

Table 1.
The chiral multiplet and are charged under . Note that becomes the R-symmetry in the low-energy theory and does not play any role during the integrating out process.
In the next section, we will identify the parameter regions in which the scalar potential has a local maximum at the origin by analysing the behaviour of the effective Kähler potential near the origin.
3.4. Inflation from the Effective Low-Energy Theory
For simplicity, we absorb into the vector multiplet. To explore the behaviour near the origin, we first assume the solution of Equation (45) can be written perturbatively in the form
Substituting this into Equation (45) we can show that
After substituting the perturbative solution of in (47) into the effective Kähler potential (44), the effective Kähler potential around the local maximum can be written as
where the first two coefficients are
Then we define the canonically normalized chiral superfield as
We can absorbe the constant term in (49) by a Kähler transformation. Around the origin, the effective Kähler potential becomes
where the first nontrivial coefficients read
In order to having a local maximum at the origin, we need to satisfy the constraint . According to the signs of and of the scalar component c, we can divide the domain in two-dimensional parameter space in which is positive into four regions [26]:
- Region I: with , ,
- Region II: with , ,
- Region III: with , ,
- Region IV: with , .
These four regions are shown in Figure 1a. It turns out that a Minkowski minimum is allowed in Region I and III, while the scalarpotential with parameters in Region II and IV have only de Sitter minimum with a large cosmological constant. We can also show that Region I does not satisfy the integrating out condition. Therefore, we conclude that Region III is the only possible domain that allows for slow-roll inflation with a nearby minimum having a small and tuneable vacuum energy.
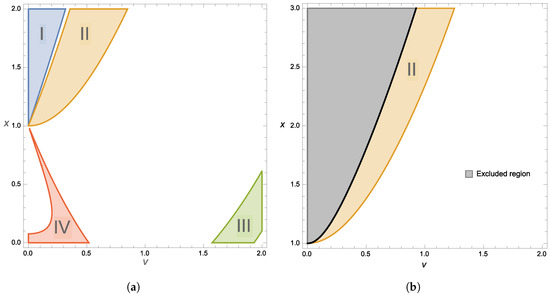
Figure 1.
(a) Allowed parameter space (v, x) with 0 < v < 2.0 and 0 < x < 2.0. The colored regions in which A2 > 0 can be divided into 4 parts, namely I, II, III and IV. (b) Region I and part of Region II are in the excluded area where
where the integrating out condition is not satisfied.
3.5. The Effective Scalar Potential and Slow-Roll Parameters
“We are now exploring the global minimum of the scalar potential and comparing our predictions for inflation with the observational data. To do these, we need the exact expression of the scalar potential which can be achieved by the following way. Using the analytic solution (46) for as a function of , we obtain the scalar potential as a function of instead of ” [26].
Let us combine (44) with (46), the effective Kähler potential can be expressed as a function of the vector multiplet ,
where is a function of . The effective superpotential is
We find the effective D-term potential in terms of given by
where a new parameter . The inflaton field is defined as and it can be written in terms of c with the help of (46) as
For any given value of the parameters v and x, the “physical domain” of c is defined in such a way that . We also define , in terms of c with the help of (58) as
On the other hand, the F-term contribution to effective potential is written as
where the functions and are
To define the slow-roll parameters, we introduce the canonically normalised inflaton field defined through . It can be written in terms of c as
The slow-roll parameters and can be written in terms of c as
The number of e-folds N during inflation period can be obtained by
where and is the value of c at the horizon exit. In the following, we will compare our theoretical predictions to the CMB observational data. The amplitude of density fluctuations , the spectral index and the tensor-to-scalar ratio r can be written in terms of the slow-roll parameters:
evaluated at the horizon exit.
Let us consider for example
The scalar potential for this set of parameters is plotted in Figure 2a,b as a function of c and respectively. Figure 2c shows the relation between c and coordinates where the physical domain is . We also plot the slow-roll parameters in coordinates in Figure 2d.
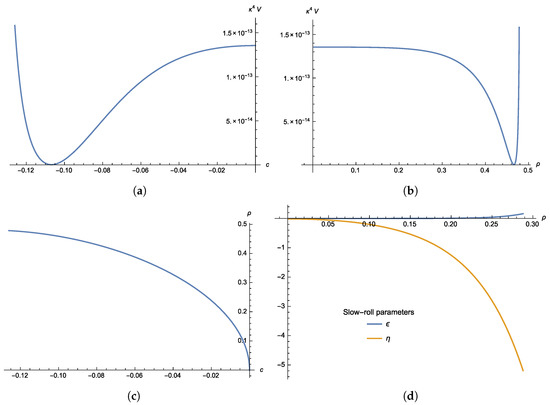
Figure 2.
The scalar potential in Region III of Figure 1 is plotted as a function of the coordinate c in (a) and ρ in (b) with parameters (71) . The inflaton ρ as a function of c is shown in (c). Finally (d) shows the slow-roll parameters ϵ and η.
As it was shown in [26], we can choose the initial condition and (or equivalently, by using (58), and ) to obtain , , and , which are within the -region of Planck’18 data [28].
4. Fayet-Iliopoulos (Fi) D-Terms in Supergravity
In this section, we follow the notation in [25]. The chiral weight in this section is related to the chiral weight of the previous section by .
4.1. Review
In [12] (see also in [29]), a new (constant) FI term was proposed of the form fermions, that can be coupled to supergravity without gauging the R-symmetry. It is non-singular when the D-auxiliary filed has a non vanishing vacuum expectation value (VEV), and the corresponding supergravity Lagrangian is:
where is a constant parameter. In the superconformal formalism, the chiral compensator field , with Weyl and chiral weights , has components . The vector multiplet has weights , and its components are given by . We will use the Wess-Zumino gauge in which the first components . The multiplet is of weights , and given by
The components of can be written as
The corresponding kinetic terms in supergravity Lagrangian for the gauge multiplet are
The operator T () in (73) is defined in [30,31], and can be used to define a chiral (antichiral) multiplet. For example, the chiral multiplet has weights . In global supersymmetry, this corresponds to the usual chiral projection operator . Note that we will drop the notation of h.c. and implicitly assume its presence for every term in the Lagrangian. Finally, the multiplet is a linear multiplet. Its components are given by
The component and the covariant field strength are defined in Equation (17.1) of [25]. In our case, they can be written as
Here is the vierbein, with frame indices and coordinate indices . The gauge fields , , and correspond to Lorentz transformations, dilatations, and symmetry of the conformal algebra respectively, while denotes the gravitino. We define the conformal d’Alembertian by .
Let us consider first the case of pure supergravity coupled to a gauge multiplet with the FI term in (73). The supergravity Lagrangian can be written as
Supersymmetry is broken via a non-vanishing VEV of the D-auxiliary component of the vector multiplet driven by the linear term in D, with the Goldstino being the gaugino. After fixing the compensator , integrating out the auxiliary fields, and choosing the unitary gauge where the Goldstino vanishes, the Lagarangian in component form is [12]:
with a constant superpotential . In the absence of matter, any non-vanishing value of uplifts the vacuum energy by a constant term and supersymetry is broken. It is important to note that the FI term in Equation (73) breaks the Kähler invariance and does not require the gauging of an R-symmetry.
Let us now couple the FI-term given by Equation (73) to additional matter fields charged under the . For simplicity, we focus on a single chiral multiplet X. The Lagrangian is given by
Here , and are a Kähler potential, a superpotential and a gauge kinetic function respectively. The first three terms in Equation (81) are the usual supergravity Lagrangian [25]. Assuming that the multiplet X transforms under the as
where is a gauge multiplet parameter. In the case we consider, the superpotential does not transform under the gauge symmetry therefore the is not an R-symmetry. For a model with a single chiral multiplet, the superpotential must be constant
To ensure gauge invariance of the supergravity action, the Kähler potential must be a function of . However, for notational simplicity, in the following we drop the factors.
Indeed, in this case we can consistently add the FI-term to the theory, similar to [12], and the resulting D-term potential acquires an extra term proportional to
where the Killing vector is . For a constant superpotential (83), the F-term potential reduces to
“From Equation (84) it is easy to see that if the Kähler potential has a term proportional to , the D-term contribution to the scalar potential obtains another constant contribution. For example, if
the D-term potential becomes
The term proportional to is the usual FI term in a non R-symmetric Kähler frame. It can be consistently added to the model with the new FI term proportional to .
In the absence of the extra term, a Kähler transformation
with allows us to recast the model in the form
where . The two models result in the same Lagrangian, at least classically (At the quantum level, a Kähler transformation also introduces a change in the gauge kinetic function f, see for example [24]). However, in the Kähler frame of Equation (89) the superpotential transforms nontrivially under the gauge symmetry. As a consequence, the gauge symmetry becomes an R-symmetry.
Note that the extra term (73) violates the Kähler invariance of the theory, and the two models related by a Kähler transformation are no longer equivalent. The model written in the Kähler frame where the gauge symmetry becomes an R-symmetry in Equation (89) can not be consistently coupled to . A generalized Kähler invariant FI term has been built in [32,33]” [17].
4.2. The Scalar Potential in a Non R-Symmetry Frame
In this section, we work in the Kähler frame where the superpotential does not transform, and take into account the two types of FI terms which were discussed in the last section. For convenience, we repeat here the Kähler potential in Equation (86) and restore the inverse reduced Planck mass :
The superpotential and the gauge kinetic function are set to be constant (In order to cancel the chiral anomalies [4], the gauge kinetic function gets a field-dependent correction . However, the correction turns out to be very small and can be neglected below, since q is chosen to be of order of or smaller):
After performing a change of the field variable where and setting , the full scalar potential is a function of . The F-term contribution to the scalar potential is given by
and the D-term contribution is
Note that we rescaled the second FI parameter by . We are interested in the role of the new FI-term in inflationary models driven by supersymmetry breaking.
For , one finds that for and the potential has a maximum at the origin, and a supersymmetric minimum. Since we set the superpotential to zero, the SUSY breaking is measured by the D-term order parameter, i.e. the Killing potential associated with the gauged , which is given by
“This enters the scalar potential as . So, at the local maximum and during inflation is of order q and supersymmetry is broken. On the other hand, at the global minimum, supersymmetry is preserved and the potential vanishes. Strictly speaking, the supersymetric minimum is not valid because the new FI term becomes singular since the D-auxiliary vanishes. Therefore a small F is required in any case” [17].
For , the potential has still a local maximum at for and . For this choice, the derivatives of the potential have the following properties,
For , the extremum is a local maximum, as desired.
Let us comment on the global minimum after turning on the F-term contribution. As long as , the change in the global minimum is very small, of order , The plot of this change is shown in Figure 3.
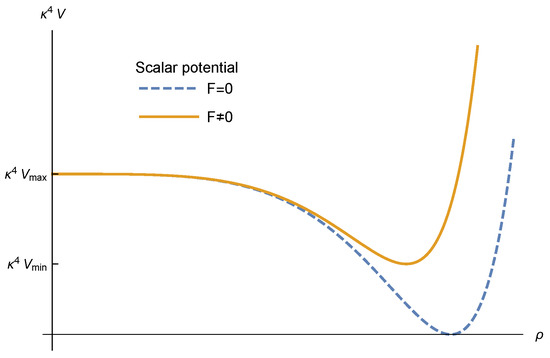
Figure 3.
This plot presents the scalar potentials for and cases. For , we have a local maximum at and the global minimum has zero cosmological constant. For , the origin is still the maximum but the global minimum now has a positive cosmological constant.
Let us comment on super symmetry breaking in the present case , the order parameters are both the Killing potential and the F-term contribution , which read
where the F-term order parameter is defined by
Therefore, near the local maximum, . On the other hand, at the global minimum, both and are of the same order i.e. , assuming that at the minimum is of order , which is true in our models below. This makes tuning of the vacuum energy between the F- and D-contribution in principle possible, along the lines of [4,11].
“Let us consider the case where only the new FI parameter contributes to the potential. In this case, the condition for the local maximum of the scalar potential at can be satisfied for . In the case where F is set to zero, the scalar potential (93) has a minimum at . In order to have , we can choose . However, we find that this choice of parameter does not allow slow-roll inflation near the maximum of the scalar potential. Similar to our previous models [4] it may be possible to achieve both the scalar potential satisfying slow-roll conditions and a small cosmological constant at the minimum by adding correction terms to the Kähler potential and turning on a parameter F. However, here we will focus on case where, as we will see shortly, less parameters are required to satisfy the observational constraints” [17].
4.3. Example for Slow-Roll D-Term Inflation
“In this section we focus on the case and assume that the scalar potential is D-term dominated by choosing . The model has only two free parameters, namely q and . The first parameter controls the overall scale of the potential and it will be fixed by the amplitude of the CMB data. The only free parameter left over is the second parameter . We derive the condition that leads to slow-roll inflation scenarios, where the start of inflation (or, horizon crossing) is near the maximum of the potential at ” [17].
To calculate the slow-roll parameters, we need to introduce the canonically normalised field defined by
The slow-roll parameters can be written in terms of the canonical field as
Since we assume inflation to start near the origin , the expansion of slow-roll parameters for small can be expressed as
Note also that is negative when . We can therefore tune the parameter to avoid the -problem. The observation is that at , the effective charge of X vanishes and thus the -dependence in the D-term contribution (93) becomes of quartic order.
“Note that we obtain the same relation between and as in the model of inflation from supersymmetry breaking driven by an F-term from a linear superpotential and (see Equation (14)) [4]. Thus, there is a possibility to have flat plateau near the maximum that satisfies the slow-roll condition and at the same time a small cosmological constant at the minimum nearby” [17].
The number of e-folds N during inflation is determined by
where we choose . Notice that the slow-roll parameters for small satisfy the simple relation by Equation (100). Therefore, the number of e-folds between and () takes the following simple approximate form as in [4],
as long as the expansions in (100) are valid in the region . Note that we used the approximation , which holds in this case.
“We are now comparing the theoretical predictions of this model to the observational data via the power spectrum of scalar perturbations of the CMB such as the amplitude , tilt and the tensor-to-scalar ratio r. From the relation of the spectral index above, one should have , and thus Equation (102) gives approximately the desired number of e-folds when the logarithm is of order one. Actually, using this formula, we can estimate the upper bound of the tensor-to-scalar ratio r and the Hubble scale following the same argument given in [4]; the upper bounds are given by computing the parameters assuming that the expansions (100) hold until the end of inflation. We then get the bound
where we used , and , which are consistent with our models” [17].
4.4. A Small Field Inflation Model from Supergravity with Observable Tensor-to-Scalar Ratio
“Supergravity models with higher r are of particular interest. In this section we show that our model can get large r at the price of introducing some additional terms in the Kähler potential. Let us consider the previous model with additional quadratic and cubic terms in :” [17].
while the superpotential and the gauge kinetic function remain as in Equation (91). We assume that inflation is driven by the D-term by setting the parameter . The scalar potential in terms of the field variable can be written as:
We now have two additional parameters A and B. These parameters do not affect our previous discussions on the choices of the parameter b because they appear in higher orders in in the scalar potential. Therefore, we can continue with the case. The Formula (102) for the number of e-folds also holds for small even when are not zero because the new parameters appear at order and higher. However these two parameters can increase the value of the tensor-to-scalar ratio r. To obtain , we can choose for example
By choosing the initial condition and , we get the results , , and , which agree with Planck’15 data as shown in Figure 4.
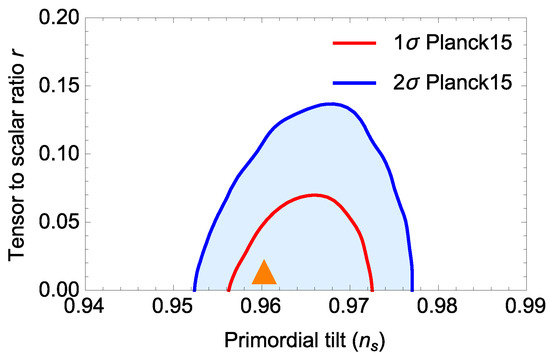
Figure 4.
A plot of the predictions for the scalar potential with , , , , and in the - r plane, versus Planck’15 results.
Note that an application of the new FI term in no-scale supergravity model for inflation can be found for example in [33,34].
5. Conclusions
In summary, in this review we discussed the possibility that inflation is driven by supersymmetry breaking with the scalar component of the goldstino superfield playing the role of the inflaton. Imposing a gauged R-symmetry allows to satisfy easily the slow-roll conditions, leading to an interesting class of small field inflation models, characterised by an inflationary plateau around the maximum of the scalar potential near the origin, where R-symmetry is restored with the inflaton rolling down to a minimum with an infinitesimal tuneable positive vacuum energy. Inflation can be driven by either an F- or a new FI D-term. The corresponding effective field theory can be derived by a microscopic model based on a generalised Fayet-Iliopoulos model of a R-symmetry coupled to supergravity. Going to the Higgs phase in the limit of small supersymmetry breaking scale compared to the mass, the massive vector multiplet can be integrated out leading to an effective field theory for the goldstino chiral multiplet characterised by a linear superpotential and an effective Kähler potential. By implementing the theory with an additional gauged R-symmetry that remains spectator (and unbroken) we were able to provide a microscopic model of inflation by supersymmetry breaking. The above models are in agreement with cosmological observations and in the simplest case predict a rather small tensor-to-scalar ratio of primordial perturbations.
Author Contributions
Investigation, I.A. and A.C.; methodology I.A.; software, A.C.; writing-original draft preparation, A.C.; writing-review and editing, I.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported in part by the Labex “Institut Lagrange de Paris”, in part by a CNRS PICS grant, and in part by the “CUniverse” research promotion project by Chulalongkorn University (grant reference CUAASC).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Borštnik, N.S.M.; Nielsen, H.F.B.; Khlopov, M.Y.; Lukman, D. Proceedings to the 21st International Workshop “What Comes Beyond the Standard Models”, June 23– July 1, 2018, Bled, Slovenia. arXiv, 2019; arXiv:1902.10628. [Google Scholar]
- Lyth, D.H.; Riotto, A. Particle physics models of inflation and the cosmological density perturbation. Phys. Rept. 1999, 314, 1–146. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. 1980, 91B, 99–102. [Google Scholar] [CrossRef]
- Antoniadis, I.; Chatrabhuti, A.; Isono, H.; Knoops, R. Inflation from Supersymmetry Breaking. Eur. Phys. J. C 2017, 77, 724. [Google Scholar] [CrossRef]
- Randall, L.; Thomas, S.D. Solving the cosmological moduli problem with weak scale inflation. Nucl. Phys. B 1995, 449, 229. [Google Scholar] [CrossRef]
- Riotto, A. Inflation and the nature of supersymmetry breaking. Nucl. Phys. B 1998, 515, 413–435. [Google Scholar] [CrossRef]
- Izawa, K.I. Supersymmetry - breaking models of inflation. Prog. Theor. Phys. 1998, 99, 157. [Google Scholar] [CrossRef]
- Buchmuller, W.; Covi, L.; Delepine, D. Inflation and supersymmetry breaking. Phys. Lett. B 2000, 491, 183. [Google Scholar] [CrossRef]
- Antoniadis, I.; Knoops, R. Gauge R-symmetry and de Sitter vacua in supergravity and string theory. Nucl. Phys. B 2014, 886, 43. [Google Scholar] [CrossRef]
- Catino, F.; Villadoro, G.; Zwirner, F. On Fayet-Iliopoulos terms and de Sitter vacua in supergravity: Some easy pieces. JHEP 2012, 1201, 002. [Google Scholar] [CrossRef]
- Antoniadis, I.; Chatrabhuti, A.; Isono, H.; Knoops, R. Inflation from Supergravity with Gauged R-symmetry in de Sitter Vacuum. Eur. Phys. J. C 2016, 76, 680. [Google Scholar] [CrossRef]
- Cribiori, N.; Farakos, F.; Tournoy, M.; van Proeyen, A. Fayet-Iliopoulos terms in supergravity without gauged R-symmetry. JHEP 2018, 1804, 32. [Google Scholar] [CrossRef]
- Antoniadis, I.; Chatrabhuti, A.; Isono, H.; Knoops, R. Fayet-Iliopoulos terms in supergravity and D-term inflation. Eur. Phys. J. C 2018, 78, 366. [Google Scholar] [CrossRef]
- Aldabergenov, Y.; Ketov, S.V. Removing instability of inflation in Polonyi-Starobinsky supergravity by adding FI term. Mod. Phys. Lett. A 2018, 32, 1850032. [Google Scholar] [CrossRef]
- Halyo, E. Hybrid inflation from supergravity D terms. Phys. Lett. B 1996, 387, 43–47. [Google Scholar] [CrossRef]
- Binetruy, P.; Dvali, G.R. D term inflation. Phys. Lett. B 1996, 388, 241–246. [Google Scholar] [CrossRef]
- Antoniadis, I. Inflation From Supersymmetry Breaking. Universe 2019, 5, 30. [Google Scholar] [CrossRef]
- Wess, J.; Bagger, J. Supersymmetry and Supergravity; Princeton University Press: Princeton, NJ, USA, 1992. [Google Scholar]
- Englert, F.; Brout, R. Broken Symmetry and the Mass of Gauge Vector Mesons. Phys. Rev. Lett. 1964, 13, 321–323. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken symmetries, massless particles and gauge fields. Phys. Lett. 1964, 12, 132–133. [Google Scholar] [CrossRef]
- Higgs, P.W. Broken Symmetries and the Masses of Gauge Bosons. Phys. Rev. Lett. 1964, 13, 508. [Google Scholar] [CrossRef]
- Fayet, P.; Iliopoulos, J. Spontaneously Broken Supergauge Symmetries and Goldstone Spinors. Phys. Lett. 1974, 51B, 461–464. [Google Scholar] [CrossRef]
- Antoniadis, I.; Ghilencea, D.M.; Knoops, R. Gauged R-symmetry and its anomalies in 4D N=1 supergravity and phenomenological implications. JHEP 2015, 1502, 166. [Google Scholar] [CrossRef]
- Kaplunovsky, V.; Louis, J. Field dependent gauge couplings in locally supersymmetric effective quantum field theories. Nucl. Phys. B 1994, 422, 57–124. [Google Scholar] [CrossRef]
- Freedman, D.Z.; Proeyen, A.V. Supergravity; Cambridge Univ. Press: Cambridge, UK, 2012. [Google Scholar]
- Antoniadis, I.; Chatrabhuti, A.; Isono, H.; Knoops, R. A microscopic model for inflation from supersymmetry breaking. Eur. Phys. J. C 2019, 79, 624. [Google Scholar] [CrossRef]
- Benakli, K.; Chen, Y.; Goodsell, M.D. Minimal constrained superfields and the Fayet-Iliopoulos model. Eur. Phys. J. C 2018, 78, 711. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. arXiv, 2018; arXiv:1807.06211. [Google Scholar]
- Kuzenko, S.M. Taking a vector supermultiplet apart: Alternative Fayet-Iliopoulos-type terms. Phys. Lett. B 2018, 781, 723. [Google Scholar] [CrossRef]
- Kugo, T.; Uehara, S. N=1 Superconformal Tensor Calculus: Multiplets With External Lorentz Indices and Spinor Derivative Operators. Prog. Theor. Phys. 1985, 73, 235. [Google Scholar] [CrossRef]
- Ferrara, S.; Kallosh, R.; Proeyen, A.V.; Wrase, T. Linear Versus Non-linear Supersymmetry, in General. JHEP 2016, 1604, 65. [Google Scholar] [CrossRef]
- Antoniadis, I.; Chatrabhuti, A.; Isono, H.; Knoops, R. The cosmological constant in Supergravity. Eur. Phys. J. C 2018, 78, 718. [Google Scholar] [CrossRef]
- Antoniadis, I.; Rondeau, F. New Kähler invariant Fayet-Iliopoulos terms in supergravity and cosmological applications. arXiv 2019, arXiv:1912.08117. [Google Scholar]
- Aldabergenov, Y.; Chatrabhuti, A.; Ketov, S.V. Generalized dilaton-axion models of inflation, de Sitter vacua and spontaneous SUSY breaking in supergravity. Eur. Phys. J. C 2019, 79, 713. [Google Scholar] [CrossRef]
Sample Availability: Samples of the compounds...... are available from the authors. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).