Dynamically Generated Inflationary ΛCDM
Abstract
1. Introduction
2. A Simple Model of Unification of Dark Energy and Dark Matter
- The first term in (10) is the standard Einstein–Hilbert action with denoting the scalar curvature with respect to metric in the second order (metric) formalism;
- is particular representative of a non-Riemannian volume-element density (6):
- is general-coordinate invariant Lagrangian of a single scalar field :
3. Inflation and Unified Dark Energy and Dark Matter
- (ii) (37) has a stable minimum for a small finite value : for , where:
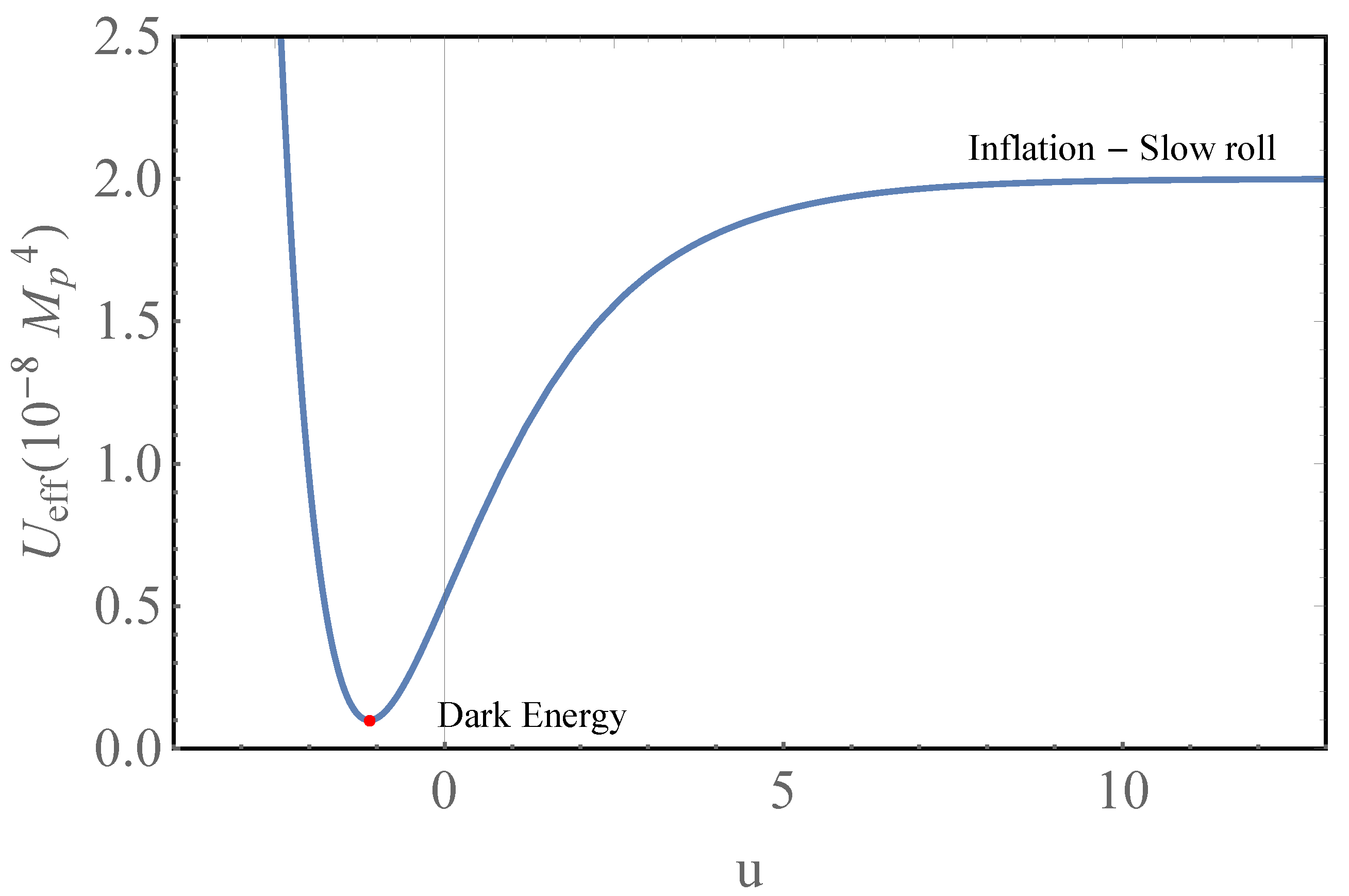
- (iii) As it will be explicitly exhibited in the dynamical system analysis in Section 4, the region of u around the stable minimum at (41) corresponds to the late-time de Sitter expansion of the universe with a slightly varied late-time Hubble parameter (dark energy dominated epoch), wherein the minimum value of the potential:is the asymptotic value at of the dynamical dark energy density [165,166].
4. Cosmological Implications
- (A) Stable critical point:where all three eigenvalues of the stability matrix are negative or with negative real parts (). The stable critical point (57) corresponds to the late-time asymptotics of the universe’s evolution where according to the definitions (52) —the stable minimum of the effective potential (37), so that , the dark matter energy density (48) , and according to (56); i.e., late-time accelerated expansion with .
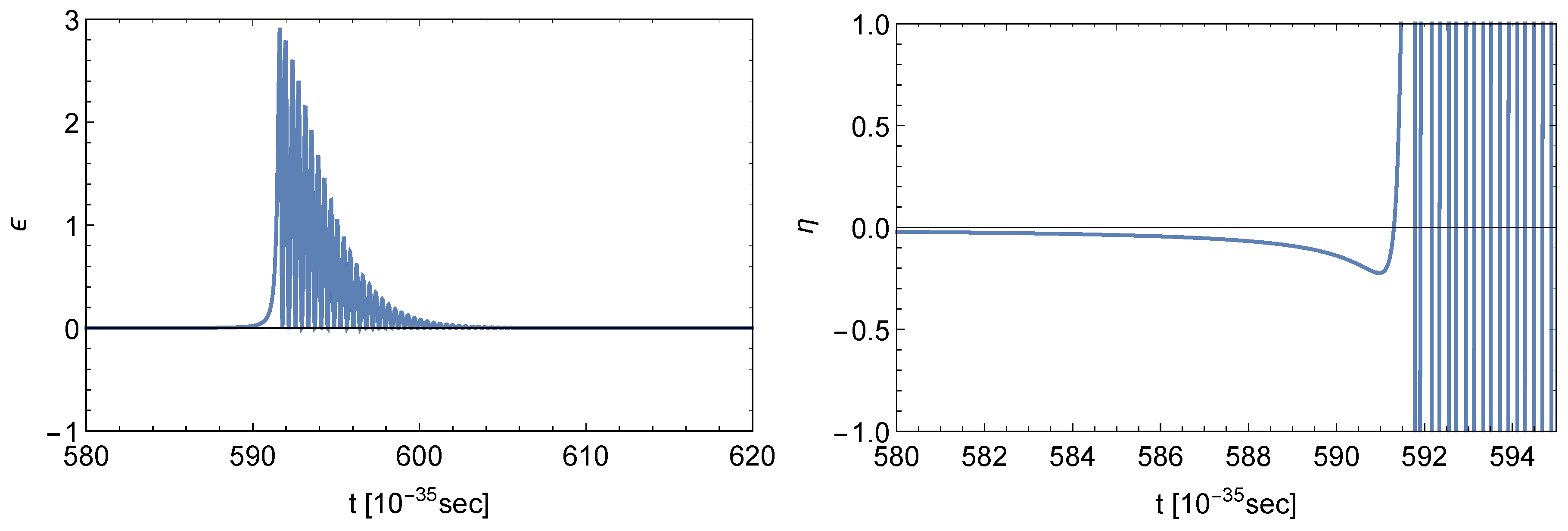
- (B) Unstable critical point:where one of the three eigenvalues of the stability matrix is zero (, , ). According to the definitions (52), in the vicinity of the unstable critical point (58), is very large positive (), so that , is vanishing and we have there a slow-roll inflationary evolution with inflationary scale where the standard slow-roll parameters are very small:
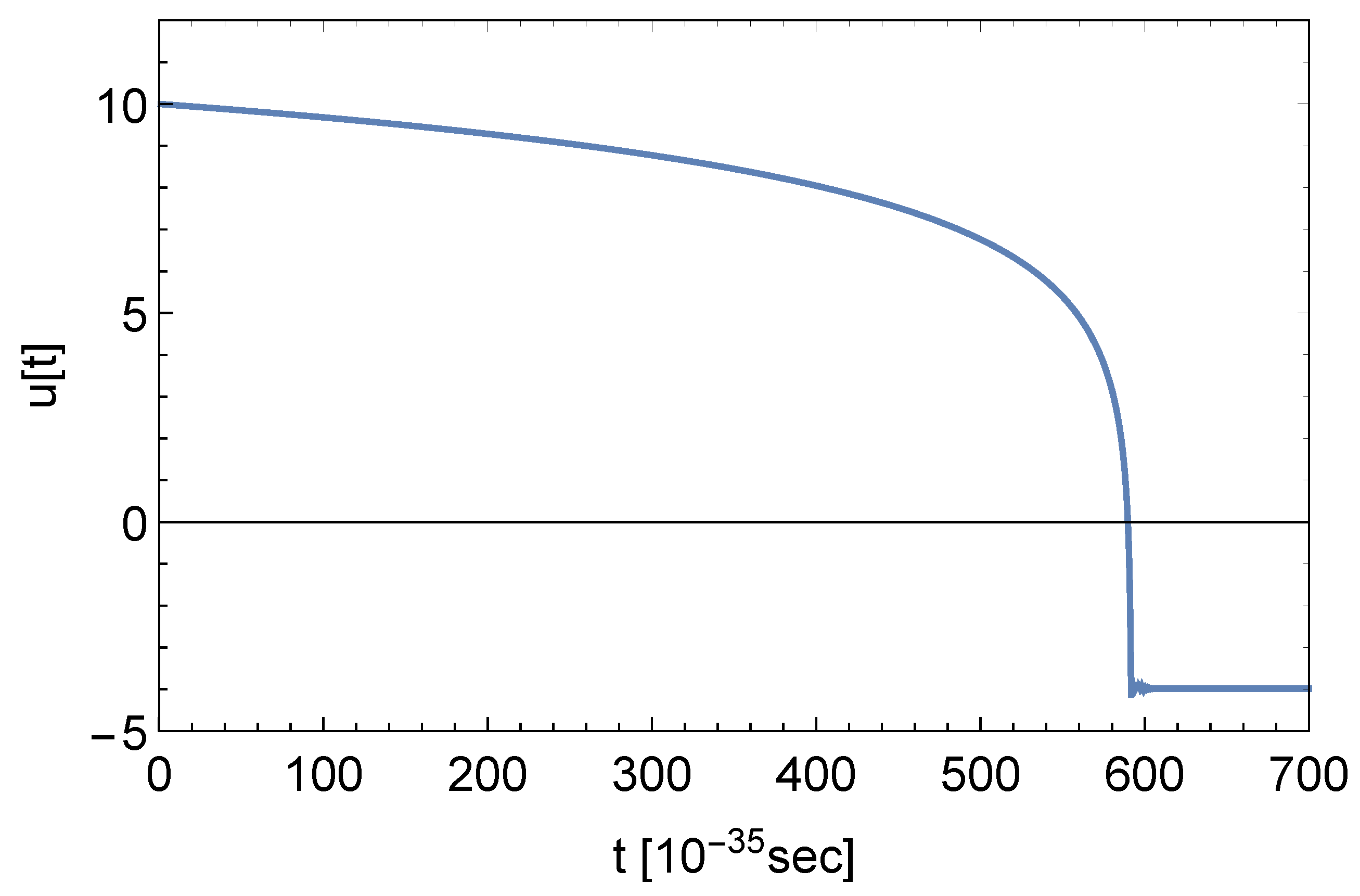
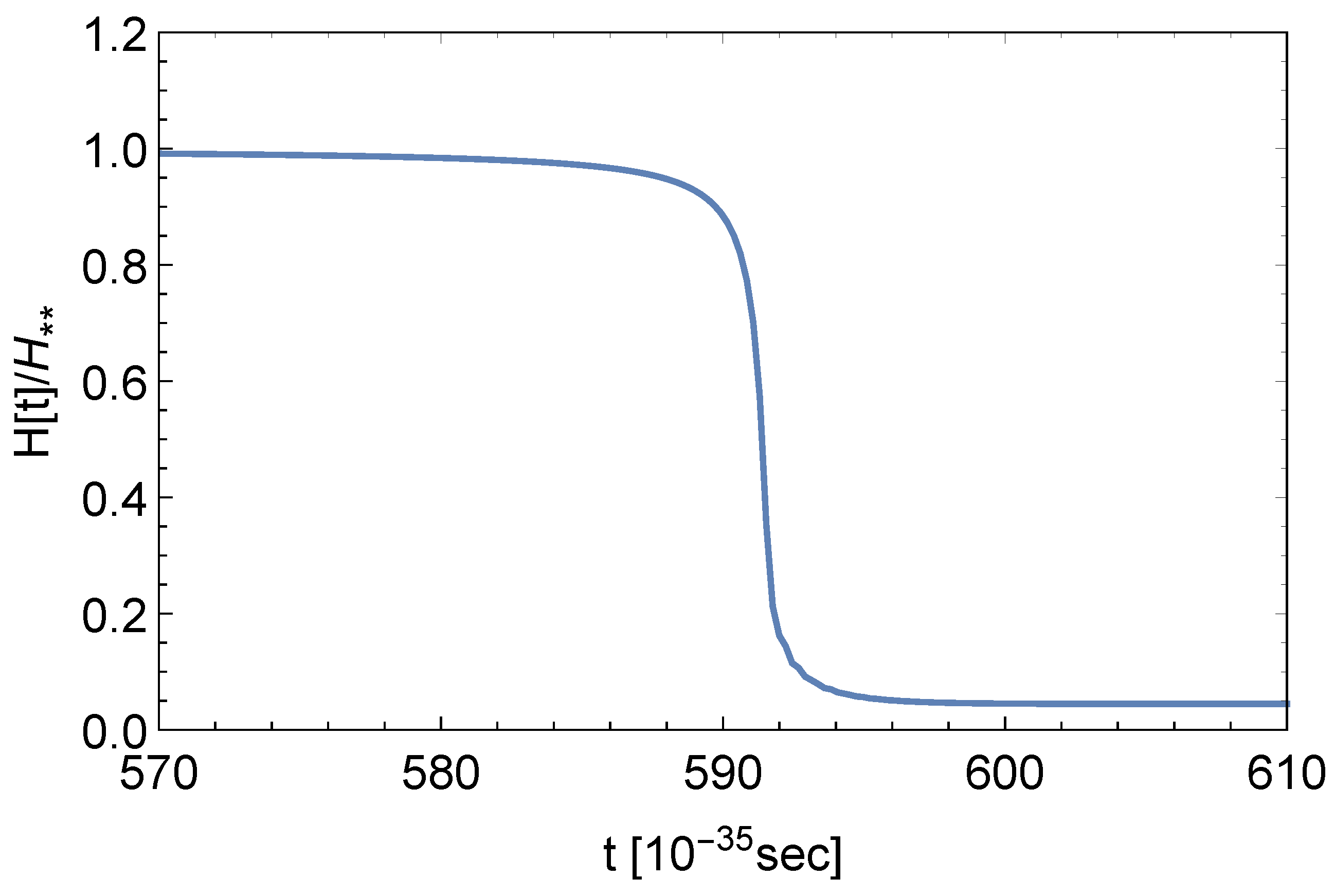
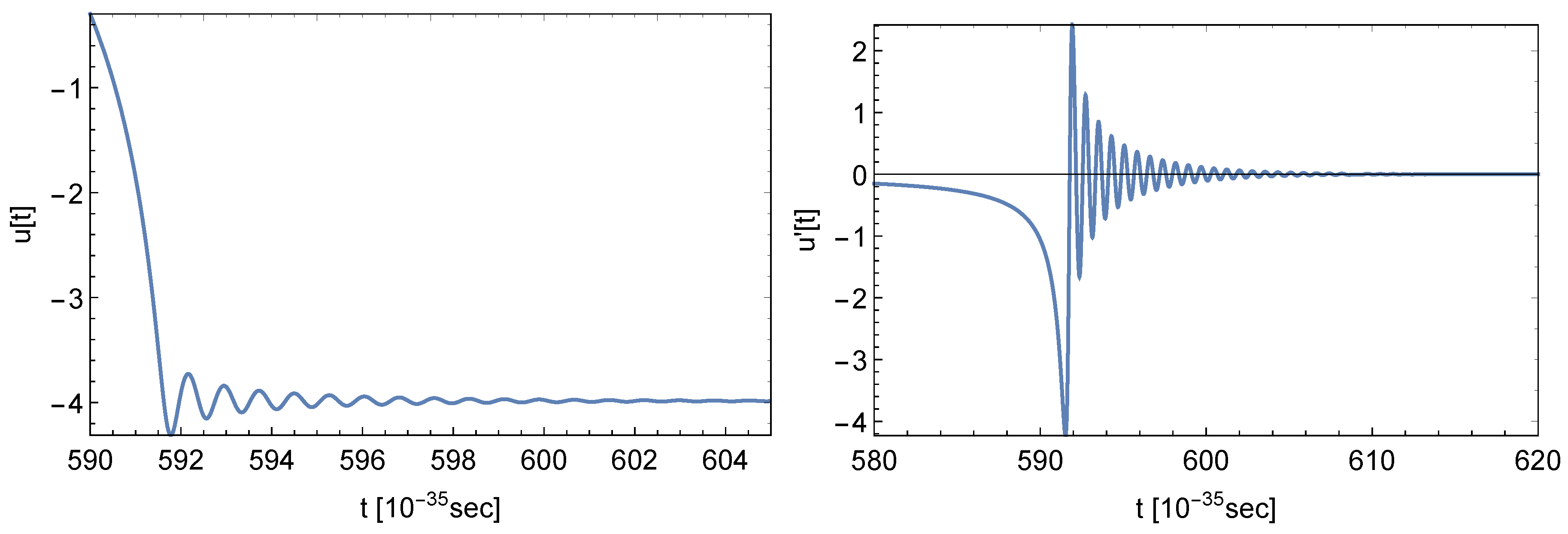
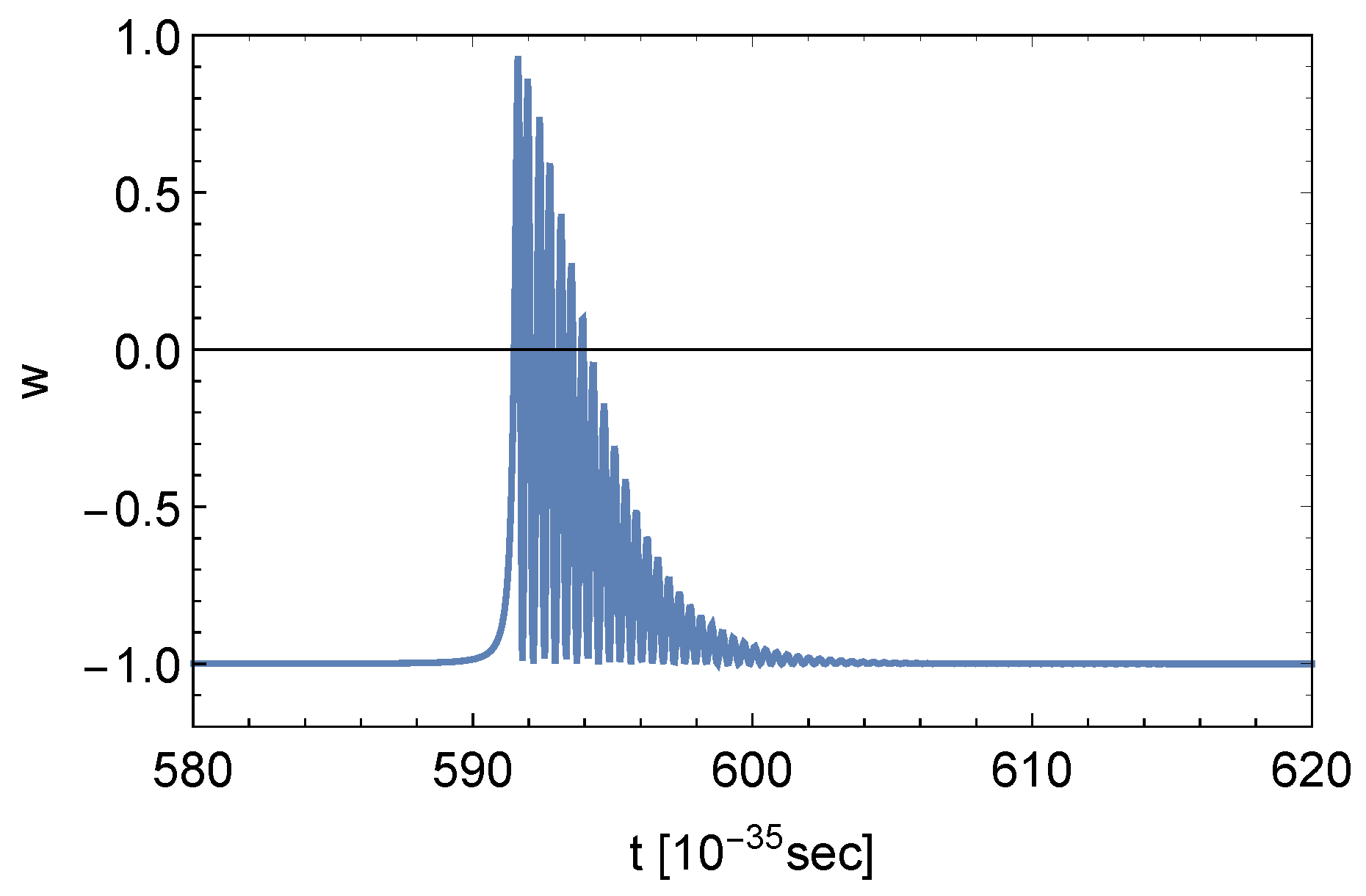
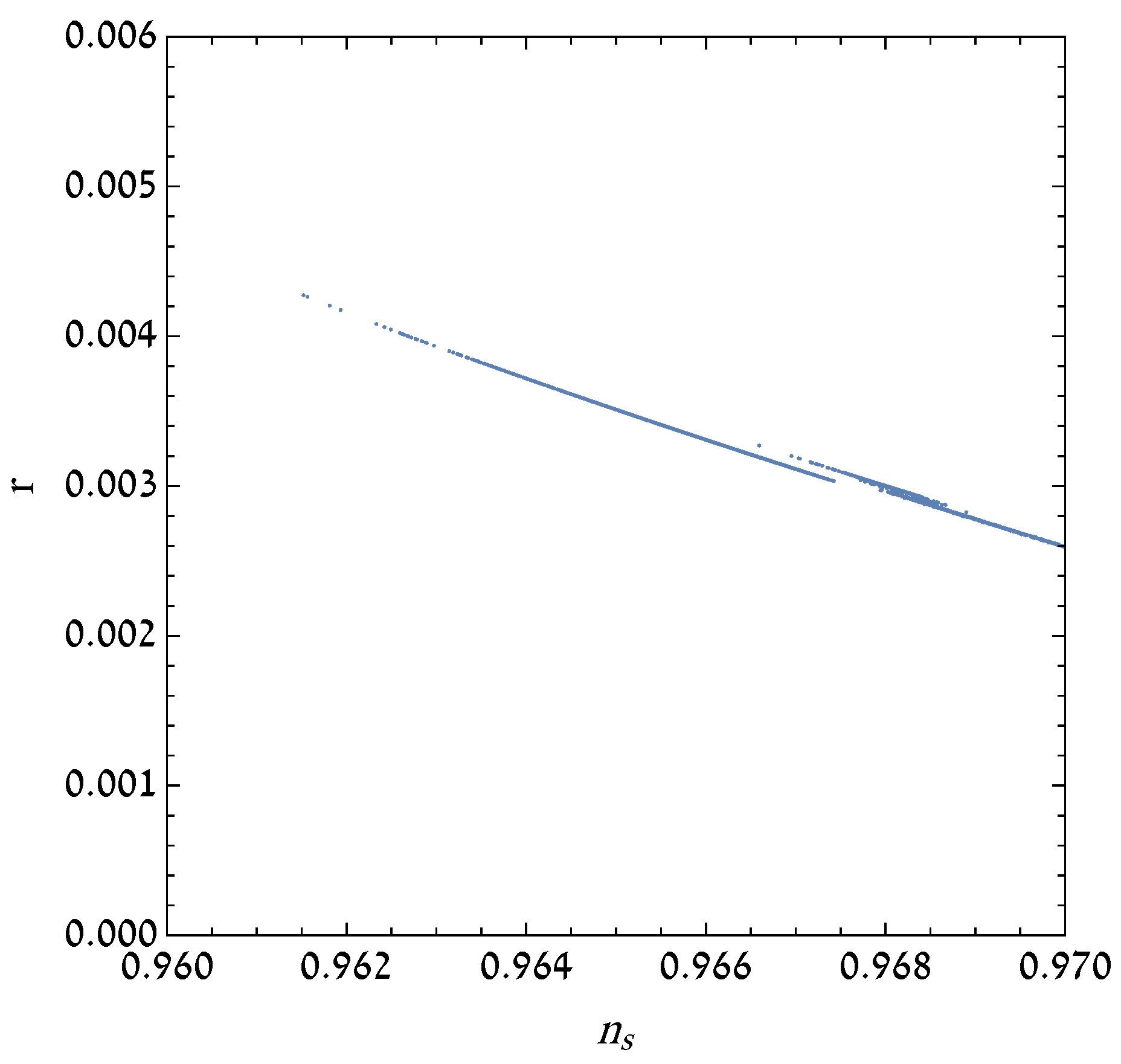
5. Numerical Solutions
6. Conclusions and Outlook
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Perlmutter, S.; Aldering, G.; Goldhaber, G.; Knop, R.A.; Nugent, P.; Castro, P.G.; Deustua, S.; Fabbro, S.; Goobar, A.; Groom, D.E.; et al. Measurements of Omega and Lambda from 42 high redshift supernovae. Astrophys. J. 1999, 517, 565–586. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of dark energy. Int. J. Mod. Phys. 2006, D15, 1753–1936. [Google Scholar] [CrossRef]
- Novikov, E.A. Quantum Modification of General Relativity. Electron. J. Theor. Phys. 2016, 13, 79–90. [Google Scholar]
- Benitez, F.; Gambini, R.; Lehner, L.; Liebling, S.; Pullin, J. Critical collapse of a scalar field in semiclassical loop quantum gravity. Phys. Rev. Lett. 2020, 124, 071301. [Google Scholar] [CrossRef]
- Budge, L.; Campbell, J.M.; De Laurentis, G.; Keith Ellis, R.; Seth, S. The one-loop amplitude for Higgs + 4 gluons with full mass effects. arXiv 2020, arXiv:2002.04018. [Google Scholar]
- Bell, G.; Beneke, M.; Huber, T.; Li, X.Q. Two-loop non-leptonic penguin amplitude in QCD factorization. arXiv 2020, arXiv:2002.03262. [Google Scholar]
- Fröhlich, J.; Knowles, A.; Schlein, B.; Sohinger, V. A path-integral analysis of interacting Bose gases and loop gases. arXiv 2020, arXiv:2001.11714. [Google Scholar]
- D’Ambrosio, F. Semi-Classical Holomorphic Transition Amplitudes in Covariant Loop Quantum Gravity. arXiv 2020, arXiv:2001.04651. [Google Scholar]
- Novikov, E.A. Ultralight gravitons with tiny electric dipole moment are seeping from the vacuum. Mod. Phys. Lett. 2016, A31, 1650092. [Google Scholar] [CrossRef]
- Dekens, W.; Stoffer, P. Low-energy effective field theory below the electroweak scale: Matching at one loop. JHEP 2019, 10, 197. [Google Scholar] [CrossRef]
- Ma, C.T.; Pezzella, F. Stringy Effects at Low-Energy Limit and Double Field Theory. arXiv 2019, arXiv:1909.00411. [Google Scholar]
- Jenkins, E.E.; Manohar, A.V.; Stoffer, P. Low-Energy Effective Field Theory below the Electroweak Scale: Operators and Matching. JHEP 2018, 3, 16. [Google Scholar] [CrossRef]
- Brandyshev, P.E. Cosmological solutions in low-energy effective field theory for type IIA superstrings. Grav. Cosmol. 2017, 23, 15–19. [Google Scholar] [CrossRef]
- Gomez, C.; Jimenez, R. Cosmology from Quantum Information. arXiv 2020, arXiv:2002.04294. [Google Scholar]
- Guth, A.H. The Inflationary Universe: A Possible Solution to the Horizon and Flatness Problems. Phys. Rev. 1981, D23, 347–356. [Google Scholar] [CrossRef]
- Starobinsky, A.A. Spectrum of relict gravitational radiation and the early state of the universe. JETP Lett. 1979, 30, 682–685. [Google Scholar]
- Kazanas, D. Dynamics of the Universe and Spontaneous Symmetry Breaking. Astrophys. J. 1980, 241, L59–L63. [Google Scholar] [CrossRef]
- Starobinsky, A.A. A New Type of Isotropic Cosmological Models Without Singularity. Phys. Lett. 1980, 91B, 99–102. [Google Scholar] [CrossRef]
- Linde, A.D. A New Inflationary Universe Scenario: A Possible Solution of the Horizon, Flatness, Homogeneity, Isotropy and Primordial Monopole Problems. Phys. Lett. 1982, 108B, 389–393. [Google Scholar] [CrossRef]
- Albrecht, A.; Steinhardt, P.J. Cosmology for Grand Unified Theories with Radiatively Induced Symmetry Breaking. Phys. Rev. Lett. 1982, 48, 1220–1223. [Google Scholar] [CrossRef]
- Barrow, J.D.; Ottewill, A.C. The Stability of General Relativistic Cosmological Theory. J. Phys. 1983, A16, 2757. [Google Scholar] [CrossRef]
- Blau, S.K.; Guendelman, E.I.; Guth, A.H. The Dynamics of False Vacuum Bubbles. Phys. Rev. 1987, D35, 1747. [Google Scholar] [CrossRef]
- Cervantes-Cota, J.L.; Dehnen, H. Induced gravity inflation in the standard model of particle physics. Nucl. Phys. 1995, B442, 391–412. [Google Scholar] [CrossRef]
- Berera, A. Warm inflation. Phys. Rev. Lett. 1995, 75, 3218–3221. [Google Scholar] [CrossRef] [PubMed]
- Armendariz-Picon, C.; Damour, T.; Mukhanov, V.F. k - inflation. Phys. Lett. 1999, B458, 209–218. [Google Scholar] [CrossRef]
- Kanti, P.; Olive, K.A. Assisted chaotic inflation in higher dimensional theories. Phys. Lett. 1999, B464, 192–198. [Google Scholar] [CrossRef][Green Version]
- Garriga, J.; Mukhanov, V.F. Perturbations in k-inflation. Phys. Lett. 1999, B458, 219–225. [Google Scholar] [CrossRef]
- Gordon, C.; Wands, D.; Bassett, B.A.; Maartens, R. Adiabatic and entropy perturbations from inflation. Phys. Rev. 2000, D63, 023506. [Google Scholar] [CrossRef]
- Bassett, B.A.; Tsujikawa, S.; Wands, D. Inflation dynamics and reheating. Rev. Mod. Phys. 2006, 78, 537–589. [Google Scholar] [CrossRef]
- Chen, X.; Wang, Y. Quasi-Single Field Inflation and Non-Gaussianities. JCAP 2010, 1004, 27. [Google Scholar] [CrossRef]
- Germani, C.; Kehagias, A. New Model of Inflation with Non-minimal Derivative Coupling of Standard Model Higgs Boson to Gravity. Phys. Rev. Lett. 2010, 105, 011302. [Google Scholar] [CrossRef] [PubMed]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. G-inflation: Inflation driven by the Galileon field. Phys. Rev. Lett. 2010, 105, 231302. [Google Scholar] [CrossRef]
- Feng, C.J.; Li, X.Z.; Saridakis, E.N. Preventing eternality in phantom inflation. Phys. Rev. 2010, D82, 023526. [Google Scholar] [CrossRef]
- Burrage, C.; de Rham, C.; Seery, D.; Tolley, A.J. Galileon inflation. JCAP 2011, 1101, 14. [Google Scholar] [CrossRef]
- Kobayashi, T.; Yamaguchi, M.; Yokoyama, J. Generalized G-inflation: Inflation with the most general second-order field equations. Prog. Theor. Phys. 2011, 126, 511–529. [Google Scholar] [CrossRef]
- Ohashi, J.; Tsujikawa, S. Potential-driven Galileon inflation. JCAP 2012, 1210, 35. [Google Scholar] [CrossRef]
- Paliathanasis, A.; Tsamparlis, M. Two scalar field cosmology: Conservation laws and exact solutions. Phys. Rev. 2014, D90, 043529. [Google Scholar] [CrossRef]
- Dimakis, N.; Paliathanasis, A. Crossing the phantom divide line as an effect of quantum transitions. arXiv 2020, arXiv:2001.09687. [Google Scholar]
- Dimakis, N.; Paliathanasis, A.; Terzis, P.A.; Christodoulakis, T. Cosmological Solutions in Multiscalar Field Theory. Eur. Phys. J. 2019, C79, 618. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. A transition between bouncing hyper-inflation to ΛCDM from diffusive scalar fields. Int. J. Mod. Phys. 2018, A33, 1850119. [Google Scholar] [CrossRef]
- Barrow, J.D.; Paliathanasis, A. Observational Constraints on New Exact Inflationary Scalar-field Solutions. Phys. Rev. 2016, D94, 083518. [Google Scholar] [CrossRef]
- Barrow, J.D.; Paliathanasis, A. Reconstructions of the dark-energy equation of state and the inflationary potential. Gen. Rel. Grav. 2018, 50, 82. [Google Scholar] [CrossRef] [PubMed]
- Olive, K.A. Inflation. Phys. Rept. 1990, 190, 307–403. [Google Scholar] [CrossRef]
- Linde, A.D. Hybrid inflation. Phys. Rev. 1994, D49, 748–754. [Google Scholar] [CrossRef] [PubMed]
- Liddle, A.R.; Parsons, P.; Barrow, J.D. Formalizing the slow roll approximation in inflation. Phys. Rev. 1994, D50, 7222–7232. [Google Scholar] [CrossRef] [PubMed]
- Lidsey, J.E.; Liddle, A.R.; Kolb, E.W.; Copeland, E.J.; Barreiro, T.; Abney, M. Reconstructing the inflation potential: An overview. Rev. Mod. Phys. 1997, 69, 373–410. [Google Scholar] [CrossRef]
- Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Variable gravity: A suitable framework for quintessential inflation. Phys. Rev. 2014, D90, 023512. [Google Scholar] [CrossRef]
- Wali Hossain, M.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Unification of inflation and dark energy à la quintessential inflation. Int. J. Mod. Phys. 2015, D24, 1530014. [Google Scholar] [CrossRef]
- Cai, Y.F.; Gong, J.O.; Pi, S.; Saridakis, E.N.; Wu, S.Y. On the possibility of blue tensor spectrum within single field inflation. Nucl. Phys. 2015, B900, 517–532. [Google Scholar] [CrossRef]
- Geng, C.Q.; Hossain, M.W.; Myrzakulov, R.; Sami, M.; Saridakis, E.N. Quintessential inflation with canonical and noncanonical scalar fields and Planck 2015 results. Phys. Rev. 2015, D92, 023522. [Google Scholar] [CrossRef]
- Kamali, V.; Basilakos, S.; Mehrabi, A. Tachyon warm-intermediate inflation in the light of Planck data. Eur. Phys. J. 2016, C76, 525. [Google Scholar] [CrossRef]
- Geng, C.Q.; Lee, C.C.; Sami, M.; Saridakis, E.N.; Starobinsky, A.A. Observational constraints on successful model of quintessential Inflation. JCAP 2017, 1706, 11. [Google Scholar] [CrossRef]
- Dalianis, I.; Kehagias, A.; Tringas, G. Primordial black holes from α-attractors. JCAP 2019, 1901, 37. [Google Scholar] [CrossRef]
- Dalianis, I.; Tringas, G. Primordial black hole remnants as dark matter produced in thermal, matter, and runaway-quintessence postinflationary scenarios. Phys. Rev. 2019, D100, 083512. [Google Scholar] [CrossRef]
- Benisty, D. Inflation from Fermions. arXiv 2019, arXiv:1912.11124. [Google Scholar]
- Benisty, D.; Guendelman, E.I. Inflation compactification from dynamical spacetime. Phys. Rev. 2018, D98, 043522. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Saridakis, E.N. The Scale Factor Potential Approach to Inflation. arXiv 2019, arXiv:1909.01982. [Google Scholar]
- Gerbino, M.; Freese, K.; Vagnozzi, S.; Lattanzi, M.; Mena, O.; Giusarma, E.; Ho, S. Impact of neutrino properties on the estimation of inflationary parameters from current and future observations. Phys. Rev. 2017, D95, 043512. [Google Scholar] [CrossRef]
- Giovannini, M. Planckian hypersurfaces, inflation and bounces. arXiv 2020, arXiv:2001.11799. [Google Scholar]
- Brahma, S.; Brandenberger, R.; Yeom, D.H. Swampland, Trans-Planckian Censorship and Fine-Tuning Problem for Inflation: Tunnelling Wavefunction to the Rescue. arXiv 2020, arXiv:2002.02941. [Google Scholar]
- Domcke, V.; Guidetti, V.; Welling, Y.; Westphal, A. Resonant backreaction in axion inflation. arXiv 2020, arXiv:2002.02952. [Google Scholar]
- Tenkanen, T.; Tomberg, E. Initial conditions for plateau inflation. arXiv 2020, arXiv:2002.02420. [Google Scholar]
- Martin, J.; Papanikolaou, T.; Pinol, L.; Vennin, V. Metric preheating and radiative decay in single-field inflation. arXiv 2020, arXiv:2002.01820. [Google Scholar]
- Cheon, K.; Lee, J. N = 2 PNGB Quintessence Dark Energy. arXiv 2020, arXiv:2002.01756. [Google Scholar]
- Saleem, R.; Zubair, M. Inflationary solution of Hamilton Jacobi equations during weak dissipative regime. Phys. Scr. 2020, 95, 035214. [Google Scholar] [CrossRef]
- Giacintucci, S.; Markevitch, M.; Johnston-Hollitt, M.; Wik, D.R.; Wang, Q.H.S.; Clarke, T.E. Discovery of a giant radio fossil in the Ophiuchus galaxy cluster. arXiv 2020, arXiv:2002.01291. [Google Scholar] [CrossRef]
- Aalsma, L.; Shiu, G. Chaos and complementarity in de Sitter space. arXiv 2020, arXiv:2002.01326. [Google Scholar]
- Kogut, A.; Fixsen, D.J. Calibration Method and Uncertainty for the Primordial Inflation Explorer (PIXIE). arXiv 2020, arXiv:2002.00976. [Google Scholar]
- Arciniega, G.; Jaime, L.; Piccinelli, G. Inflationary predictions of Geometric Inflation. arXiv 2020, arXiv:2001.11094. [Google Scholar]
- Rasheed, M.A.; Golanbari, T.; Sayar, K.; Akhtari, L.; Sheikhahmadi, H.; Mohammadi, A.; Saaidi, K. Warm Tachyon Inflation and Swampland Criteria. arXiv 2020, arXiv:2001.10042. [Google Scholar]
- Aldabergenov, Y.; Aoki, S.; Ketov, S.V. Minimal Starobinsky supergravity coupled to dilaton-axion superfield. arXiv 2020, arXiv:2001.09574. [Google Scholar]
- Tenkanen, T. Tracing the high energy theory of gravity: an introduction to Palatini inflation. arXiv 2020, arXiv:2001.10135. [Google Scholar]
- Shaposhnikov, M.; Shkerin, A.; Zell, S. Standard Model Meets Gravity: Electroweak Symmetry Breaking and Inflation. arXiv 2020, arXiv:2001.09088. [Google Scholar]
- Garcia, M.A.G.; Amin, M.A.; Green, D. Curvature Perturbations From Stochastic Particle Production During Inflation. arXiv 2020, arXiv:2001.09158. [Google Scholar]
- Hirano, K. Inflation with very small tensor-to-scalar ratio. arXiv 2019, arXiv:1912.12515. [Google Scholar]
- Gialamas, I.D.; Lahanas, A.B. Reheating in R2 Palatini inflationary models. arXiv 2019, arXiv:1911.11513. [Google Scholar]
- Kawasaki, M.; Yamaguchi, M.; Yanagida, T. Natural chaotic inflation in supergravity. Phys. Rev. Lett. 2000, 85, 3572–3575. [Google Scholar] [CrossRef]
- Bojowald, M. Inflation from quantum geometry. Phys. Rev. Lett. 2002, 89, 261301. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Modified gravity with negative and positive powers of the curvature: Unification of the inflation and of the cosmic acceleration. Phys. Rev. 2003, D68, 123512. [Google Scholar] [CrossRef]
- Kachru, S.; Kallosh, R.; Linde, A.D.; Maldacena, J.M.; McAllister, L.P.; Trivedi, S.P. Towards inflation in string theory. JCAP 2003, 310, 13. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unifying phantom inflation with late-time acceleration: Scalar phantom-non-phantom transition model and generalized holographic dark energy. Gen. Rel. Grav. 2006, 38, 1285–1304. [Google Scholar] [CrossRef]
- Ferraro, R.; Fiorini, F. Modified teleparallel gravity: Inflation without inflation. Phys. Rev. 2007, D75, 084031. [Google Scholar] [CrossRef]
- Cognola, G.; Elizalde, E.; Nojiri, S.; Odintsov, S.D.; Sebastiani, L.; Zerbini, S. A Class of viable modified f(R) gravities describing inflation and the onset of accelerated expansion. Phys. Rev. 2008, D77, 046009. [Google Scholar] [CrossRef]
- Cai, Y.F.; Saridakis, E.N. Inflation in Entropic Cosmology: Primordial Perturbations and non-Gaussianities. Phys. Lett. 2011, B697, 280–287. [Google Scholar] [CrossRef]
- Ashtekar, A.; Sloan, D. Probability of Inflation in Loop Quantum Cosmology. Gen. Rel. Grav. 2011, 43, 3619–3655. [Google Scholar] [CrossRef]
- Qiu, T.; Saridakis, E.N. Entropic Force Scenarios and Eternal Inflation. Phys. Rev. 2012, D85, 043504. [Google Scholar] [CrossRef]
- Briscese, F.; Marcianò, A.; Modesto, L.; Saridakis, E.N. Inflation in (Super-)renormalizable Gravity. Phys. Rev. 2013, D87, 083507. [Google Scholar] [CrossRef]
- Ellis, J.; Nanopoulos, D.V.; Olive, K.A. No-Scale Supergravity Realization of the Starobinsky Model of Inflation. Phys. Rev. Lett. 2013, 111, 111301. [Google Scholar] [CrossRef]
- Basilakos, S.; Lima, J.A.S.; Sola, J. From inflation to dark energy through a dynamical Lambda: An attempt at alleviating fundamental cosmic puzzles. Int. J. Mod. Phys. 2013, D22, 1342008. [Google Scholar] [CrossRef]
- Sebastiani, L.; Cognola, G.; Myrzakulov, R.; Odintsov, S.D.; Zerbini, S. Nearly Starobinsky inflation from modified gravity. Phys. Rev. 2014, D89, 023518. [Google Scholar] [CrossRef]
- Baumann, D.; McAllister, L. Inflation and String Theory; Cambridge Monographs on Mathematical Physics; Cambridge University Press: Cambridge, UK, 2015. [Google Scholar] [CrossRef]
- Dalianis, I.; Farakos, F. On the initial conditions for inflation with plateau potentials: the R+R2 (super)gravity case. JCAP 2015, 1507, 44. [Google Scholar] [CrossRef][Green Version]
- Kanti, P.; Gannouji, R.; Dadhich, N. Gauss-Bonnet Inflation. Phys. Rev. 2015, D92, 041302. [Google Scholar] [CrossRef]
- De Laurentis, M.; Paolella, M.; Capozziello, S. Cosmological inflation in F(R,) gravity. Phys. Rev. 2015, D91, 083531. [Google Scholar] [CrossRef]
- Basilakos, S.; Mavromatos, N.E.; Solà, J. Starobinsky-like inflation and running vacuum in the context of Supergravity. Universe 2016, 2, 14. [Google Scholar] [CrossRef]
- Bonanno, A.; Platania, A. Asymptotically safe inflation from quadratic gravity. Phys. Lett. 2015, B750, 638–642. [Google Scholar] [CrossRef]
- Koshelev, A.S.; Modesto, L.; Rachwal, L.; Starobinsky, A.A. Occurrence of exact R2 inflation in non-local UV-complete gravity. JHEP 2016, 11, 67. [Google Scholar] [CrossRef]
- Bamba, K.; Odintsov, S.D.; Saridakis, E.N. Inflationary cosmology in unimodular F(T) gravity. Mod. Phys. Lett. 2017, A32, 1750114. [Google Scholar] [CrossRef]
- Motohashi, H.; Starobinsky, A.A. f(R) constant-roll inflation. Eur. Phys. J. 2017, C77, 538. [Google Scholar] [CrossRef]
- Oikonomou, V.K. Autonomous dynamical system approach for inflationary Gauss–Bonnet modified gravity. Int. J. Mod. Phys. 2018, D27, 1850059. [Google Scholar] [CrossRef]
- Benisty, D.; Vasak, D.; Guendelman, E.; Struckmeier, J. Energy transfer from spacetime into matter and a bouncing inflation from covariant canonical gauge theory of gravity. Mod. Phys. Lett. 2019, A34, 1950164. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I. Two scalar fields inflation from scale-invariant gravity with modified measure. Class. Quant. Grav. 2019, 36, 095001. [Google Scholar] [CrossRef]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Tamvakis, K. Palatini inflation in models with an R2 term. JCAP 2018, 1811, 28. [Google Scholar] [CrossRef]
- Karam, A.; Pappas, T.; Tamvakis, K. Frame-dependence of inflationary observables in scalar-tensor gravity. PoS 2019, CORFU2018, 64. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Saridakis, E.N. Holographic inflation. Phys. Lett. 2019, B797, 134829. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Saridakis, E.N.; Stoecker, H.; Struckmeier, J.; Vasak, D. Inflation from fermions with curvature-dependent mass. arXiv 2019, arXiv:1905.03731. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.; Nissimov, E.; Pacheva, S. Dynamically Generated Inflation from Non-Riemannian Volume Forms. arXiv 2019, arXiv:1906.06691. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Nissimov, E.; Pacheva, S. Dynamically generated inflationary two-field potential via non-Riemannian volume forms. arXiv 2019, arXiv:1907.07625. [Google Scholar] [CrossRef]
- Kinney, W.H.; Vagnozzi, S.; Visinelli, L. The zoo plot meets the swampland: Mutual (in)consistency of single-field inflation, string conjectures, and cosmological data. Class. Quant. Grav. 2019, 36, 117001. [Google Scholar] [CrossRef]
- Brustein, R.; Sherf, Y. Causality Violations in Lovelock Theories. Phys. Rev. 2018, D97, 084019. [Google Scholar] [CrossRef]
- Sherf, Y. Hyperbolicity Constraints in Extended Gravity Theories. Phys. Scr. 2019, 94, 085005. [Google Scholar] [CrossRef]
- Capozziello, S.; De Laurentis, M.; Luongo, O. Connecting early and late universe by f(R) gravity. Int. J. Mod. Phys. 2014, D24, 1541002. [Google Scholar] [CrossRef]
- Gorbunov, D.; Tokareva, A. Scale-invariance as the origin of dark radiation? Phys. Lett. 2014, B739, 50–55. [Google Scholar] [CrossRef]
- Myrzakulov, R.; Odintsov, S.; Sebastiani, L. Inflationary universe from higher-derivative quantum gravity. Phys. Rev. 2015, D91, 083529. [Google Scholar] [CrossRef]
- Bamba, K.; Myrzakulov, R.; Odintsov, S.D.; Sebastiani, L. Trace-anomaly driven inflation in modified gravity and the BICEP2 result. Phys. Rev. 2014, D90, 043505. [Google Scholar] [CrossRef]
- Benisty, D.; Guendelman, E.I.; Vasak, D.; Struckmeier, J.; Stoecker, H. Quadratic curvature theories formulated as Covariant Canonical Gauge theories of Gravity. Phys. Rev. 2018, D98, 106021. [Google Scholar] [CrossRef]
- Aashish, S.; Panda, S. Covariant quantum corrections to a scalar field model inspired by nonminimal natural inflation. arXiv 2020, arXiv:2001.07350. [Google Scholar]
- Rashidi, N.; Nozari, K. Gauss-Bonnet Inflation after Planck2018. arXiv 2020, arXiv:2001.07012. [Google Scholar] [CrossRef]
- Odintsov, S.D.; Oikonomou, V.K. Geometric Inflation and Dark Energy with Axion F(R) Gravity. Phys. Rev. 2020, D101, 044009. [Google Scholar] [CrossRef]
- Antoniadis, I.; Karam, A.; Lykkas, A.; Pappas, T.; Tamvakis, K. Single-field inflation in models with an R2 term. In Proceedings of the 19th Hellenic School and Workshops on Elementary Particle Physics and Gravity (CORFU2019), Corfu, Greece, 31 August–25 September 2019. [Google Scholar]
- Benisty, D.; Guendelman, E.I. Correspondence between the first and second order formalism by a metricity constraint. Phys. Rev. 2018, D98, 044023. [Google Scholar] [CrossRef]
- Chakraborty, S.; Paul, T.; SenGupta, S. Inflation driven by Einstein-Gauss-Bonnet gravity. Phys. Rev. 2018, D98, 083539. [Google Scholar] [CrossRef]
- Mukhanov, V.F.; Chibisov, G.V. Quantum Fluctuations and a Nonsingular Universe. JETP Lett. 1981, 33, 532–535. [Google Scholar]
- Guth, A.H.; Pi, S.Y. Fluctuations in the New Inflationary Universe. Phys. Rev. Lett. 1982, 49, 1110–1113. [Google Scholar] [CrossRef]
- Faraoni, V.; Capozziello, S. Beyond Einstein Gravity; Springer: Dordrecht, The Netherlands, 2011; Volume 170. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D.; Oikonomou, V.K. Modified Gravity Theories on a Nutshell: Inflation, Bounce and Late-time Evolution. Phys. Rept. 2017, 692, 1–104. [Google Scholar] [CrossRef]
- Dimitrijevic, I.; Dragovich, B.; Koshelev, A.S.; Rakic, Z.; Stankovic, J. Cosmological Solutions of a Nonlocal Square Root Gravity. Phys. Lett. 2019, B797, 134848. [Google Scholar] [CrossRef]
- Bilic, N.; Dimitrijevic, D.D.; Djordjevic, G.S.; Milosevic, M.; Stojanovic, M. Tachyon inflation in the holographic braneworld. JCAP 2019, 1908, 034. [Google Scholar] [CrossRef]
- Nojiri, S.; Odintsov, S.D. Unified cosmic history in modified gravity: from F(R) theory to Lorentz non-invariant models. Phys. Rept. 2011, 505, 59–144. [Google Scholar] [CrossRef]
- Berti, E.; Barausse, E.; Cardoso, V.; Gualtieri, L.; Pani, P.; Sperhake, U.; Stein, L.C.; Wex, N.; Yagi, K.; Baker, T.; et al. Testing General Relativity with Present and Future Astrophysical Observations. Class. Quant. Grav. 2015, 32, 243001. [Google Scholar] [CrossRef]
- Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; Basak, S.; et al. Planck 2018 results. X. Constraints on inflation. arXiv 2018, arXiv:1807.06211. [Google Scholar]
- Nojiri, S.; Odintsov, S.D. Modified f(R) gravity consistent with realistic cosmology: From matter dominated epoch to dark energy universe. Phys. Rev. 2006, D74, 086005. [Google Scholar] [CrossRef]
- Lozano, L.; Garcia-Compean, H. Emergent Dark Matter and Dark Energy from a Lattice Model. arXiv 2019, arXiv:hep-th/1912.11224. [Google Scholar]
- Chamings, F.N.; Avgoustidis, A.; Copeland, E.J.; Green, A.M.; Pourtsidou, A. Understanding the suppression of structure formation from dark matter 2013 dark energy momentum coupling. arXiv 2019, arXiv:astro-ph.CO/1912.09858. [Google Scholar]
- Liu, L.H.; Xu, W.L. The running curvaton. arXiv 2019, arXiv:1911.10542. [Google Scholar]
- Cheng, G.; Ma, Y.; Wu, F.; Zhang, J.; Chen, X. Testing interacting dark matter and dark energy model with cosmological data. arXiv 2019, arXiv:1911.04520. [Google Scholar]
- Cahill, K. Zero-point energies, dark matter, and dark energy. arXiv 2019, arXiv:1910.09953. [Google Scholar]
- Bandyopadhyay, A.; Chatterjee, A. Time-dependent diffusive interactions between dark matter and dark energy in the context of k-essence cosmology. arXiv 2019, arXiv:1910.10423. [Google Scholar]
- Kase, R.; Tsujikawa, S. Scalar-Field Dark Energy Nonminimally and Kinetically Coupled to Dark Matter. arXiv 2019, arXiv:1910.02699. [Google Scholar] [CrossRef]
- Ketov, S.V. Inflation, Dark Energy and Dark Matter in Supergravity. In Proceedings of the Meeting of the Division of Particles and Fields of the American Physical Society (DPF2019), Boston, MA, USA, 29 July–2 August 2019. [Google Scholar]
- Mukhopadhyay, U.; Paul, A.; Majumdar, D. Probing Pseudo Nambu Goldstone Boson Dark Energy Models with Dark Matter—Dark Energy Interaction. arXiv 2019, arXiv:1909.03925. [Google Scholar]
- Yang, W.; Pan, S.; Vagnozzi, S.; Di Valentino, E.; Mota, D.F.; Capozziello, S. Dawn of the dark: unified dark sectors and the EDGES Cosmic Dawn 21-cm signal. JCAP 2019, 1911, 44. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Kaganovich, A.B. The Principle of nongravitating vacuum energy and some of its consequences. Phys. Rev. 1996, D53, 7020–7025. [Google Scholar] [CrossRef]
- Gronwald, F.; Muench, U.; Macias, A.; Hehl, F.W. Volume elements of space-time and a quartet of scalar fields. Phys. Rev. 1998, D58, 084021. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Kaganovich, A.B. Dynamical measure and field theory models free of the cosmological constant problem. Phys. Rev. 1999, D60, 065004. [Google Scholar] [CrossRef]
- Guendelman, E.I. Scale invariance, new inflation and decaying lambda terms. Mod. Phys. Lett. 1999, A14, 1043–1052. [Google Scholar] [CrossRef]
- Guendelman, E.I.; Kaganovich, A.B. Absence of the Fifth Force Problem in a Model with Spontaneously Broken Dilatation Symmetry. Ann. Phys. 2008, 323, 866–882. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S.; Vasihoun, M. A New Mechanism of Dynamical Spontaneous Breaking of Supersymmetry. Bulg. J. Phys. 2014, 41, 123–129. [Google Scholar]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Vacuum structure and gravitational bags produced by metric-independent space–time volume-form dynamics. Int. J. Mod. Phys. 2015, A30, 1550133. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Unified Dark Energy and Dust Dark Matter Dual to Quadratic Purely Kinetic K-Essence. Eur. Phys. J. 2016, C76, 90. [Google Scholar] [CrossRef]
- Guendelman, E.; Singleton, D.; Yongram, N. A two measure model of dark energy and dark matter. JCAP 2012, 1211, 44. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Dark Energy and Dark Matter From Hidden Symmetry of Gravity Model with a Non-Riemannian Volume Form. Eur. Phys. J. 2015, C75, 472. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Gravity-Assisted Emergent Higgs Mechanism in the Post-Inflationary Epoch. Int. J. Mod. Phys. 2016, D25, 1644008. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Modified Gravity and Inflaton Assisted Dynamical Generation of Charge Confinement and Electroweak Symmetry Breaking in Cosmology. AIP Conf. Proc. 2019, 2075, 090030. [Google Scholar] [CrossRef]
- Guendelman, E.; Nissimov, E.; Pacheva, S. Unification of Inflation and Dark Energy from Spontaneous Breaking of Scale Invariance. In Proceedings of the 8th Mathematical Physics Meeting, Summer School and Conference on Modern Mathematical Physics, Belgrade, Serbia, 24–31 August 2014; pp. 93–103. [Google Scholar]
- Frieman, J.; Turner, M.; Huterer, D. Dark Energy and the Accelerating Universe. Ann. Rev. Astron. Astrophys. 2008, 46, 385–432. [Google Scholar] [CrossRef]
- Mathews, G.J.; Kusakabe, M.; Kajino, T. Introduction to Big Bang Nucleosynthesis and Modern Cosmology. Int. J. Mod. Phys. 2017, E26, 1741001. [Google Scholar] [CrossRef]
- Liddle, A. Einfuehrung in die Moderne Kosmologie; Wiley-VCH: Berlin, Germany, 2008. [Google Scholar]
- Liddle, A.R. An Introduction to Modern Cosmology; Wiley-VCH: West Sussex, UK, 2003. [Google Scholar]
- Dodelson, S. Modern Cosmology; Academic Press: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Dodelson, S.; Easther, R.; Hanany, S.; McAllister, L.; Meyer, S.; Page, L.; Ade, P.; Amblard, A.; Ashoorioon, A.; Baccigalupi, C.; et al. The Origin of the Universe as Revealed Through the Polarization of the Cosmic Microwave Background. arXiv 2009, arXiv:0902.3796. [Google Scholar]
- Baumann, D.; Cooray, A.; Dodelson, S.; Dunkley, J.; Fraisse, A.A.; Jackson, M.G.; Kogut, A.; Krauss, L.M.; Smith, K.M.; Zaldarriaga, M. CMBPol Mission Concept Study: A Mission to Map our Origins. AIP Conf. Proc. 2009, 1141, 3–9. [Google Scholar] [CrossRef]
- Dodelson, S. Cosmic microwave background: Past, future, and present. Int. J. Mod. Phys. 2000, A15S1, 765–783. [Google Scholar] [CrossRef]
- Dabrowski, M.P.; Garecki, J.; Blaschke, D.B. Conformal transformations and conformal invariance in gravitation. Annalen Phys. 2009, 18, 13–32. [Google Scholar] [CrossRef]
- Angus, C.R.; Smith, M.; Sullivan, M.; Inserra, C.; Wiseman, P.; D’Andrea, C.B.; Thomas, B.P.; Nichol, R.C.; Galbany, L.; Childress, M.; et al. Superluminous Supernovae from the Dark Energy Survey. Mon. Not. R. Astron. Soc. 2019, 487, 2215–2241. [Google Scholar] [CrossRef]
- Zhang, Y.; Yanny, B.; Palmese, A.; Gruen, D.; To, C.; Rykoff, E.S.; Leung, Y.; Collins, C.; Hilton, M.; Abbott, T.M.; et al. Dark Energy Survey Year 1 results: Detection of Intra-cluster Light at Redshift ∼0.25. Astrophys. J. 2019, 874, 165. [Google Scholar] [CrossRef]
- Bahamonde, S.; Böhmer, C.G.; Carloni, S.; Copeland, E.J.; Fang, W.; Tamanini, N. Dynamical systems applied to cosmology: Dark energy and modified gravity. Phys. Rept. 2018, 775–777, 1–122. [Google Scholar] [CrossRef]
- Ade, P.A.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XXII. Constraints on inflation. Astron. Astrophys. 2014, 571, A22. [Google Scholar] [CrossRef]
- Adam, R.; Ade, P.A.; Aghanim, N.; Arnaud, M.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; Bartlett, J.G.; Bartolo, N.; et al. Planck intermediate results-XXX. The angular power spectrum of polarized dust emission at intermediate and high Galactic latitudes. Astron. Astrophys. 2016, 586, A133. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Hall, L.J.; Kolda, C.F.; Murayama, H. A New perspective on cosmic coincidence problems. Phys. Rev. Lett. 2000, 85, 4434–4437. [Google Scholar] [CrossRef]
- Martin, J.; Ringeval, C.; Vennin, V. Encyclopædia Inflationaris. Phys. Dark Univ. 2014, 5–6, 75–235. [Google Scholar] [CrossRef]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benisty, D.; Guendelman, E.I.; Nissimov, E.; Pacheva, S. Dynamically Generated Inflationary ΛCDM. Symmetry 2020, 12, 481. https://doi.org/10.3390/sym12030481
Benisty D, Guendelman EI, Nissimov E, Pacheva S. Dynamically Generated Inflationary ΛCDM. Symmetry. 2020; 12(3):481. https://doi.org/10.3390/sym12030481
Chicago/Turabian StyleBenisty, David, Eduardo I. Guendelman, Emil Nissimov, and Svetlana Pacheva. 2020. "Dynamically Generated Inflationary ΛCDM" Symmetry 12, no. 3: 481. https://doi.org/10.3390/sym12030481
APA StyleBenisty, D., Guendelman, E. I., Nissimov, E., & Pacheva, S. (2020). Dynamically Generated Inflationary ΛCDM. Symmetry, 12(3), 481. https://doi.org/10.3390/sym12030481





