The Analysis of Electronic Circuit Fault Diagnosis Based on Neural Network Data Fusion Algorithm
Abstract
1. Introduction
2. Circuit Pressure Test Problems Based on Electric Flux
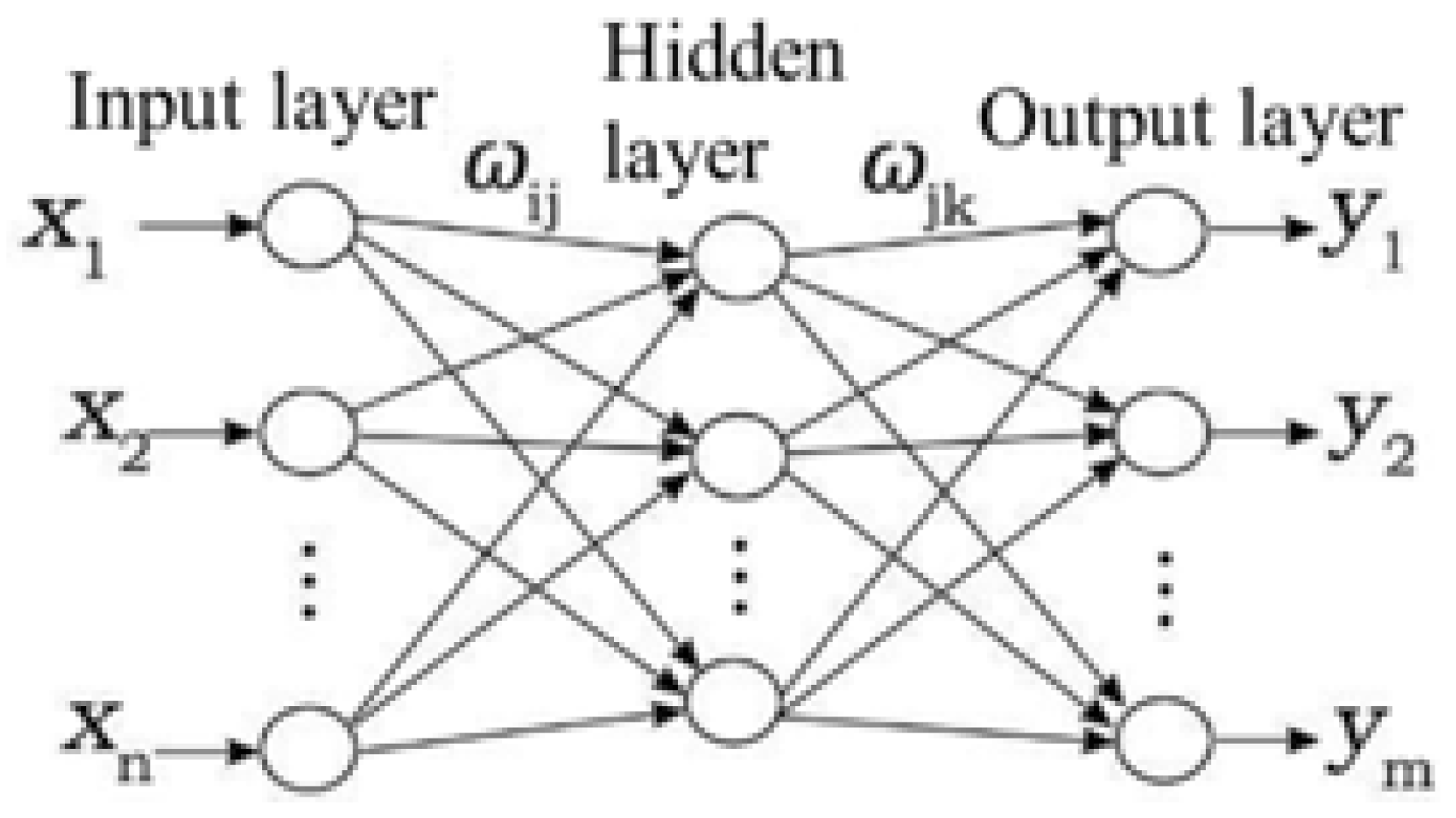
3. Neural Network Model Based on BP Algorithm
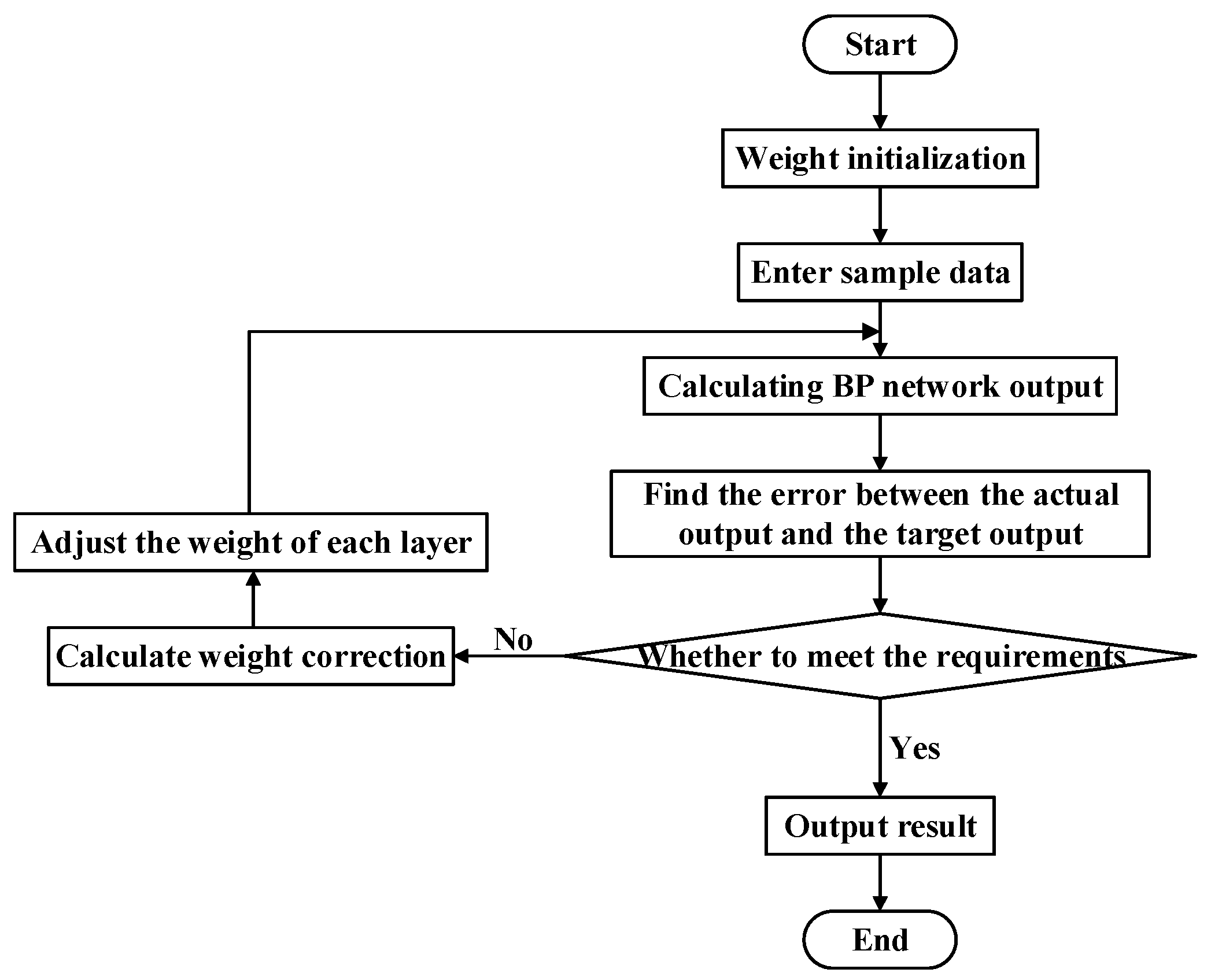
3.1. Algorithm Description
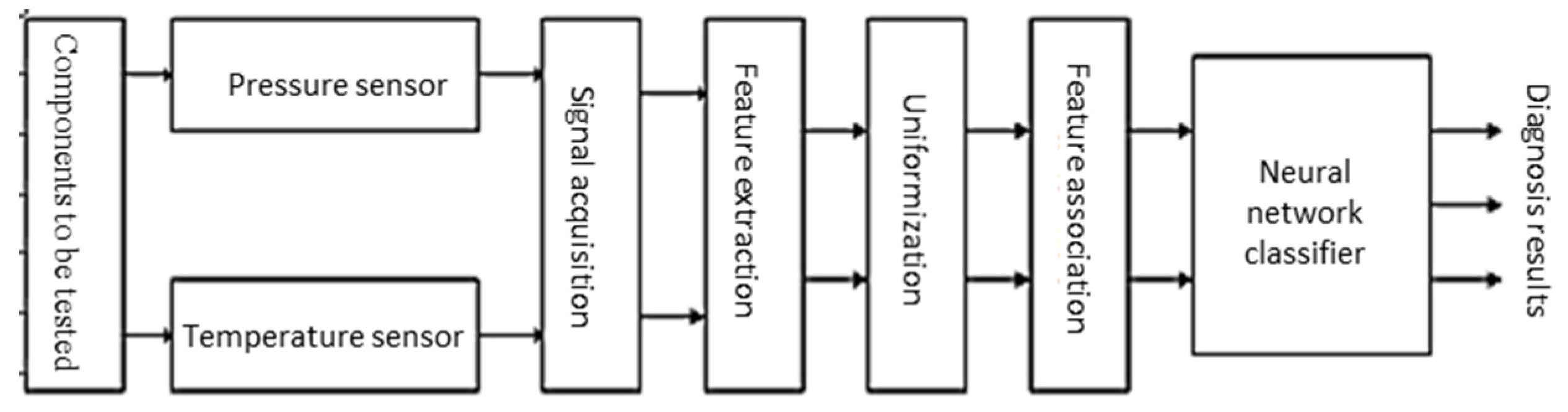
3.2. Diagnosis Steps of Neural Network Information Fusion Fault
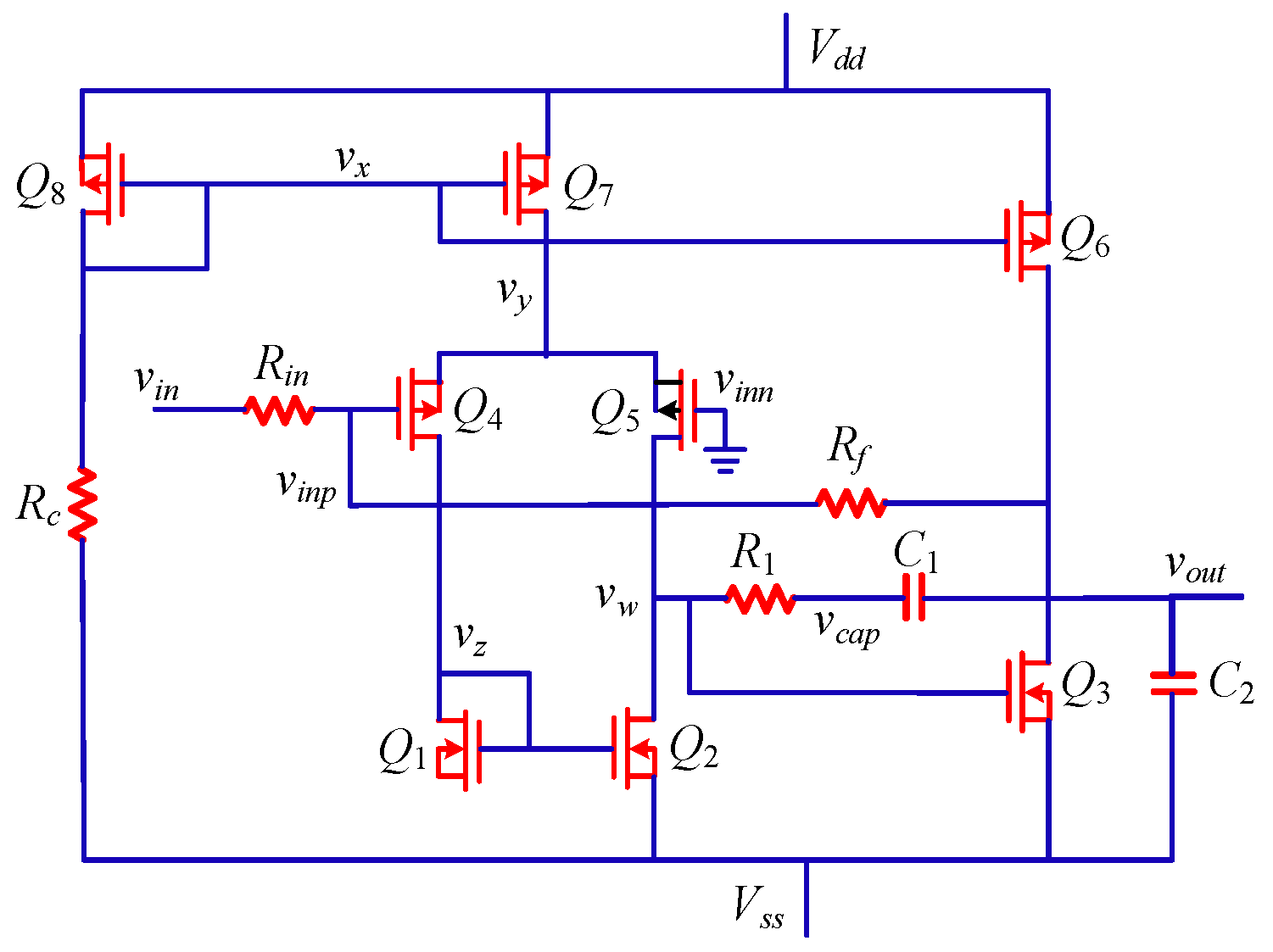
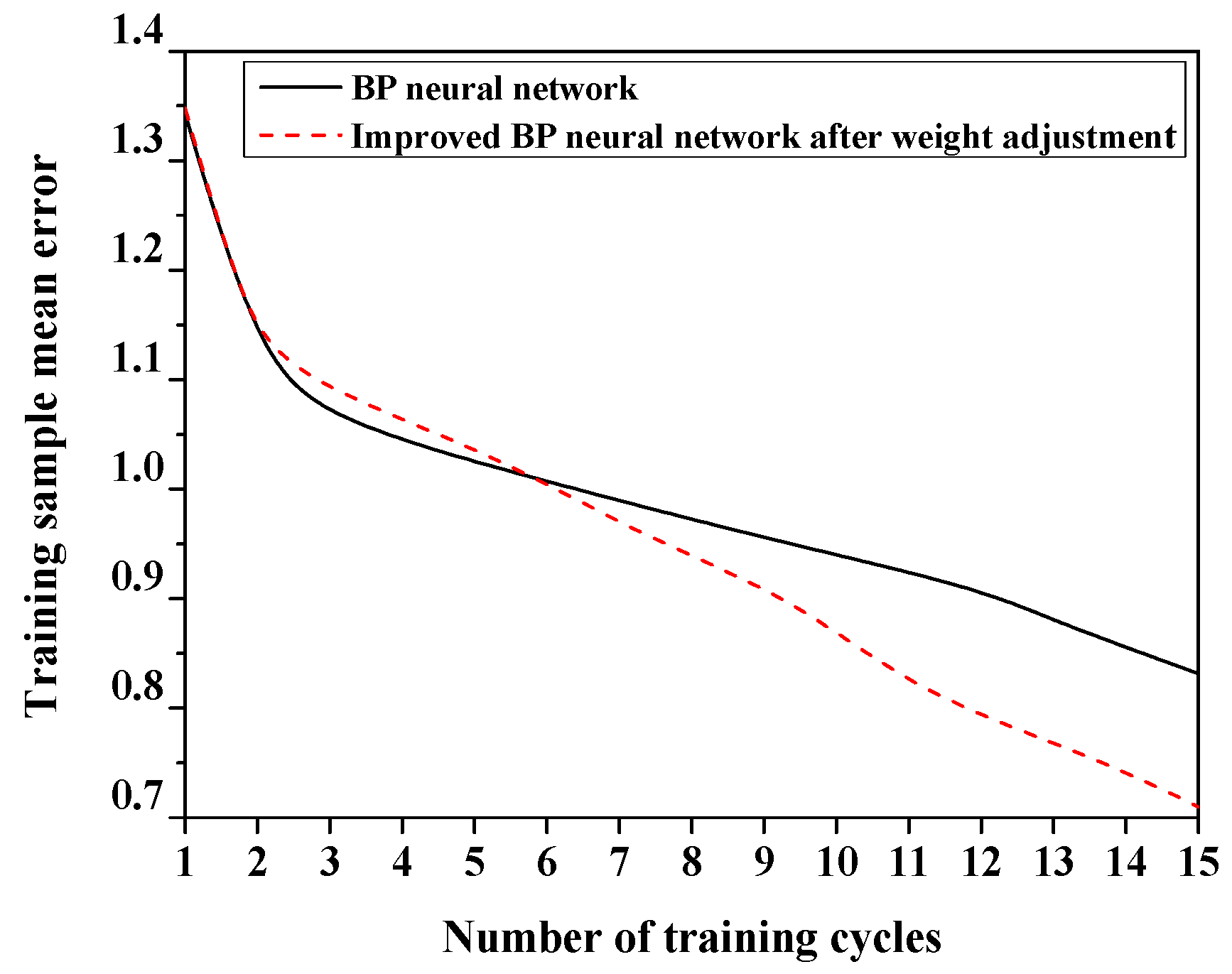
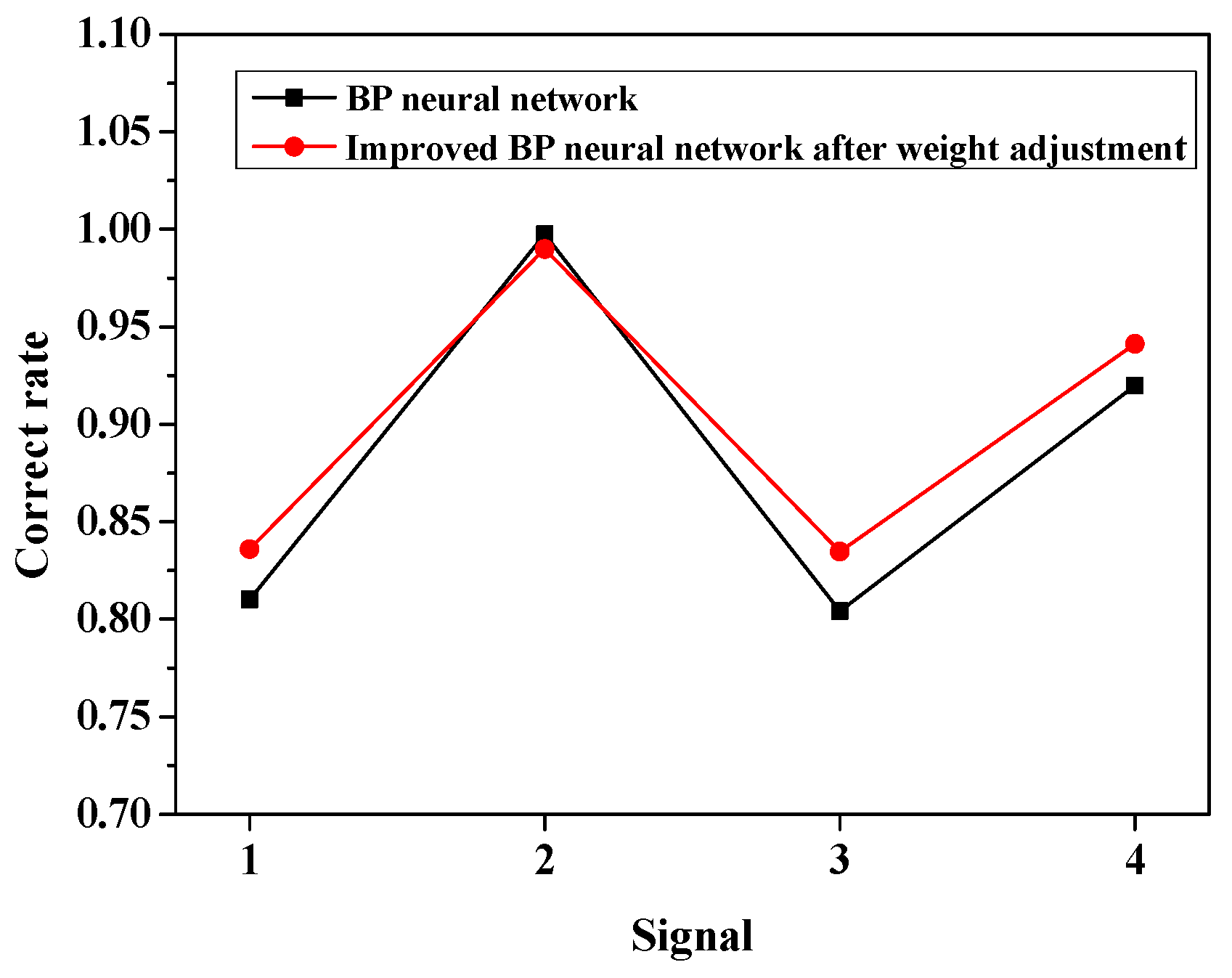
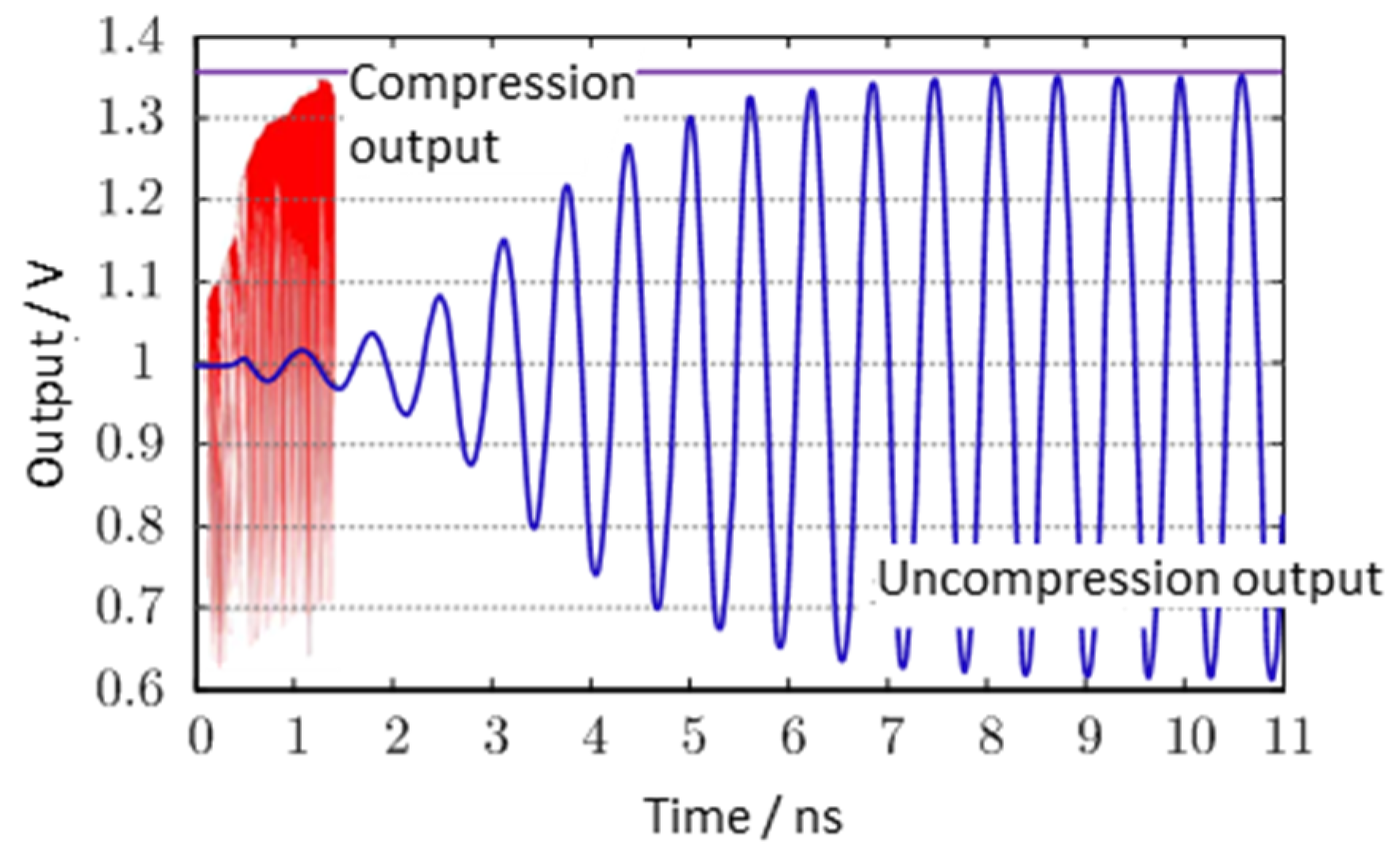
4. Experimental Analysis
5. Conclusions
Funding
Conflicts of Interest
References
- Gan, X.S.; Gao, W.M.; Zhe, D.; Liu, W.D. Research on WNN soft fault diagnosis for analog circuit based on adaptive UKF algorithm. Appl. Soft Comput. 2017, 50, 252–259. [Google Scholar]
- Chen, H.X. Research on multi-sensor data fusion technology based on BP neural network. In Proceedings of the 2015 International Workshop on Wireless Communication and Network (IWWCN2015), Kunming, China, 21−23 August 2015. [Google Scholar]
- Si, L.; Wang, Z.; Liu, X.; Tan, C.; Xu, J.; Zheng, K. Multi-Sensor Data Fusion Identification for Shearer Cutting Conditions Based on Parallel Quasi-Newton Neural Networks and the Dempster-Shafer Theory. Sensors 2015, 15, 28772–28795. [Google Scholar] [CrossRef] [PubMed]
- Tadeusiewicz, M.; Kuczyński, A.; Hałgas, S. Catastrophic Fault Diagnosis of a Certain Class of Nonlinear Analog Circuits. Circuits Syst. Signal Process. 2015, 34, 353–375. [Google Scholar] [CrossRef]
- Zhang, J.; Wu, Y.; Liu, Q.; Gu, F.; Mao, X.; Li, M. Research on High-Precision, Low Cost Piezoresistive MEMS-Array Pressure Transmitters Based on Genetic Wavelet Neural Networks for Meteorological Measurements. Micromachines 2015, 6, 554–573. [Google Scholar] [CrossRef]
- Zhang, B.C.; Xu, R.; Yin, X.J.; Gao, Z. Research on fault diagnosis for rail vehicle compartment of LED lighting system of analog circuit based on WP-EE and BP neural network. In Proceedings of the Control & Decision Conference, Yinchuan, China, 28−30 May 2016. [Google Scholar]
- Liu, M.; Zhang, C.; Liu, X. The study of data fusion for high suspended sediment concentration measuring based on BP neural network. In Proceedings of the 12th IEEE International Conference on Electronic Measurement & Instruments, Qingdao, China, 16−18 July 2015. [Google Scholar]
- Sun, B.; Jiang, C.; Li, M. Fuzzy Neural Network-Based Interacting Multiple Model for Multi-Node Target Tracking Algorithm. Sensors 2016, 16, 1823. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Du, X.; Hong, Y. Mine Internet of Things Data Collection Algorithm Based on Neural Network and Rough Set. J. Comput. Theor. Nanosci. 2015, 12, 6304–6308. [Google Scholar] [CrossRef]
- Shen, C.W.; Ho, J.; Pham, L.; Ting, K. Behavioural Intentions of Using Virtual Reality in Learning: Per-spectives of Acceptance of Information Technology and Learning Style. Virtual Real. 2019, 23, 313–324. [Google Scholar] [CrossRef]
- Zhang, C.; He, Y.; Yuan, L.; Xiang, S. Analog circuit incipient fault diagnosis method using DBN based features extraction. IEEE Access 2018, 6, 23053–23064. [Google Scholar] [CrossRef]
- Ji, L.; Hu, X. Analog circuit soft-fault diagnosis based on sensitivity analysis with minimum fault number rule. Analog Integr. Circuits Signal Process. 2018, 95, 163–171. [Google Scholar] [CrossRef]
- Sobanski, P.; Kaminski, M. Application of artificial neural networks for transistor open-circuit fault diagnosis in three-phase rectifiers. IET Power Electron. 2019, 12, 2189–2200. [Google Scholar] [CrossRef]
- Li, J.W.; Feng, Z.X. Application of the Circuit Theory to the High-Precision Pressure Regulation System in Nuclear Power Plants. J. Comput. Theor. Nanosci. 2016, 13, 1852–1860. [Google Scholar]
- Song, M.; Xu, T.; Xiang, J.; Zhang, X.; Wang, H.; Shou, B.A. Permeability Test Method of the Material for Graphite Pressure Vessel. Materials Science Forum. Trans Tech Publ. Ltd 2017, 898, 1732–1736. [Google Scholar]
- Rida, I.; Almaadeed, N.; Almaadeed, S. Robust gait recognition: A comprehensive survey. IET Biom. 2018, 8, 14–28. [Google Scholar] [CrossRef]
- Jafari, H.P. Stator winding short-circuit fault diagnosis based on multi-sensor fuzzy data fusion. Modares J. Electr. Eng. 2016, 15, 27–34. [Google Scholar]
- Xu, L.; Cao, M.; Song, B.; Zhang, J.; Liu, Y.; Alsaadi, F.E. Open-circuit fault diagnosis of power rectifier using sparse autoencoder based deep neural network. Neurocomputing 2018, 311, 1–10. [Google Scholar] [CrossRef]
- Zhao, G.; Liu, X.; Zhang, B.; Niu, Y.; Liu, G.; Hu, C. A novel approach for analog circuit fault diagnosis based on deep belief network. Measurement 2018, 121, 170–178. [Google Scholar] [CrossRef]
- Shen, C.-W.; Min, C.; Wang, C.-C. Analyzing the trend of O2O commerce by bilingual text mining on social media. Comput. Hum. Behav. 2019, 101, 474–483. [Google Scholar] [CrossRef]
- Wang, X.; Hu, H.; Xiao, L. Multisensor Data Fusion Techniques with ELM for Pulverized-Fuel Flow Concentration Measurement in Cofired Power Plant. IEEE Trans. Instrum. Meas. 2015, 64, 2769–2780. [Google Scholar] [CrossRef]
| Parameter | Value | Description |
|---|---|---|
| Maximum Iterations | 10000 | Maximum iterations in neural network algorithm |
| Neural network scale | 10000 | The size of neural network and the number of HSPICE simulations |
| dt | 1μs | The length of each edge in the neural network and the duration of each SPICE simulation. |
| Total time | 3 h | The total running time of the neural network algorithm tested each time |
| α | 0.5 | Target weight of the state sequencing |
| Fault Components | Sensor and Fusion | Signal Value of the Fault | Fault Diagnosis | ||
|---|---|---|---|---|---|
| 1 | 2 | 3 | |||
| 1 | Temperature | 0.5436 | 0.0782 | 0.0000 | Not sure |
| Pressure | 0.4092 | 0.0743 | 0.2731 | Not sure | |
| Fusion | 0.8906 | 0.1072 | 0.0048 | Component 1 fault | |
| 2 | Temperature | 0.0748 | 0.6161 | 0.0000 | Component 2 fault |
| Pressure | 0.0022 | 0.2935 | 0.1763 | Not sure | |
| Fusion | 0.0527 | 0.9462 | 0.0076 | Component 2 fault | |
| 3 | Temperature | 0.2435 | 0.2424 | 0.3217 | Not sure |
| Pressure | 0.0038 | 0.0036 | 0.1956 | Not sure | |
| Fusion | 0.0098 | 0.0441 | 0.9842 | Component 3 fault | |
| Parallel Times | Index | Literature [14] | Literature [15] | Parallel Compression |
|---|---|---|---|---|
| 1 | Convergence precision | 1.265 × 10 −5 | 4.286 × 10 −5 | 4.149 × 10 −5 |
| Convergence time/μs | 5.368 | 2.418 | 0.156 | |
| 5 | Convergence precision | 3.359 × 10 −5 | 4.173 × 10 −5 | 3.942 × 10 −5 |
| Convergence time/μs | 26.416 | 11.598 | 0.249 | |
| 10 | Convergence precision | 1.287 × 10 −5 | 3.946 × 10 −5 | 2.928 × 10 −5 |
| Convergence time/μs | 55.943 | 28.418 | 0.317 | |
| 15 | Convergence precision | 2.649 × 10 −5 | 2.851 × 10 −5 | 2.516 × 10 −5 |
| Convergence time/μs | 78.634 | 35.76 | 0.729 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N. The Analysis of Electronic Circuit Fault Diagnosis Based on Neural Network Data Fusion Algorithm. Symmetry 2020, 12, 458. https://doi.org/10.3390/sym12030458
Wang N. The Analysis of Electronic Circuit Fault Diagnosis Based on Neural Network Data Fusion Algorithm. Symmetry. 2020; 12(3):458. https://doi.org/10.3390/sym12030458
Chicago/Turabian StyleWang, Nana. 2020. "The Analysis of Electronic Circuit Fault Diagnosis Based on Neural Network Data Fusion Algorithm" Symmetry 12, no. 3: 458. https://doi.org/10.3390/sym12030458
APA StyleWang, N. (2020). The Analysis of Electronic Circuit Fault Diagnosis Based on Neural Network Data Fusion Algorithm. Symmetry, 12(3), 458. https://doi.org/10.3390/sym12030458




