Real Space Theory for Electron and Phonon Transport in Aperiodic Lattices via Renormalization
Abstract
1. Introduction
2. Fibonacci Chains
3. Aperiodic Chains besides Fibonacci
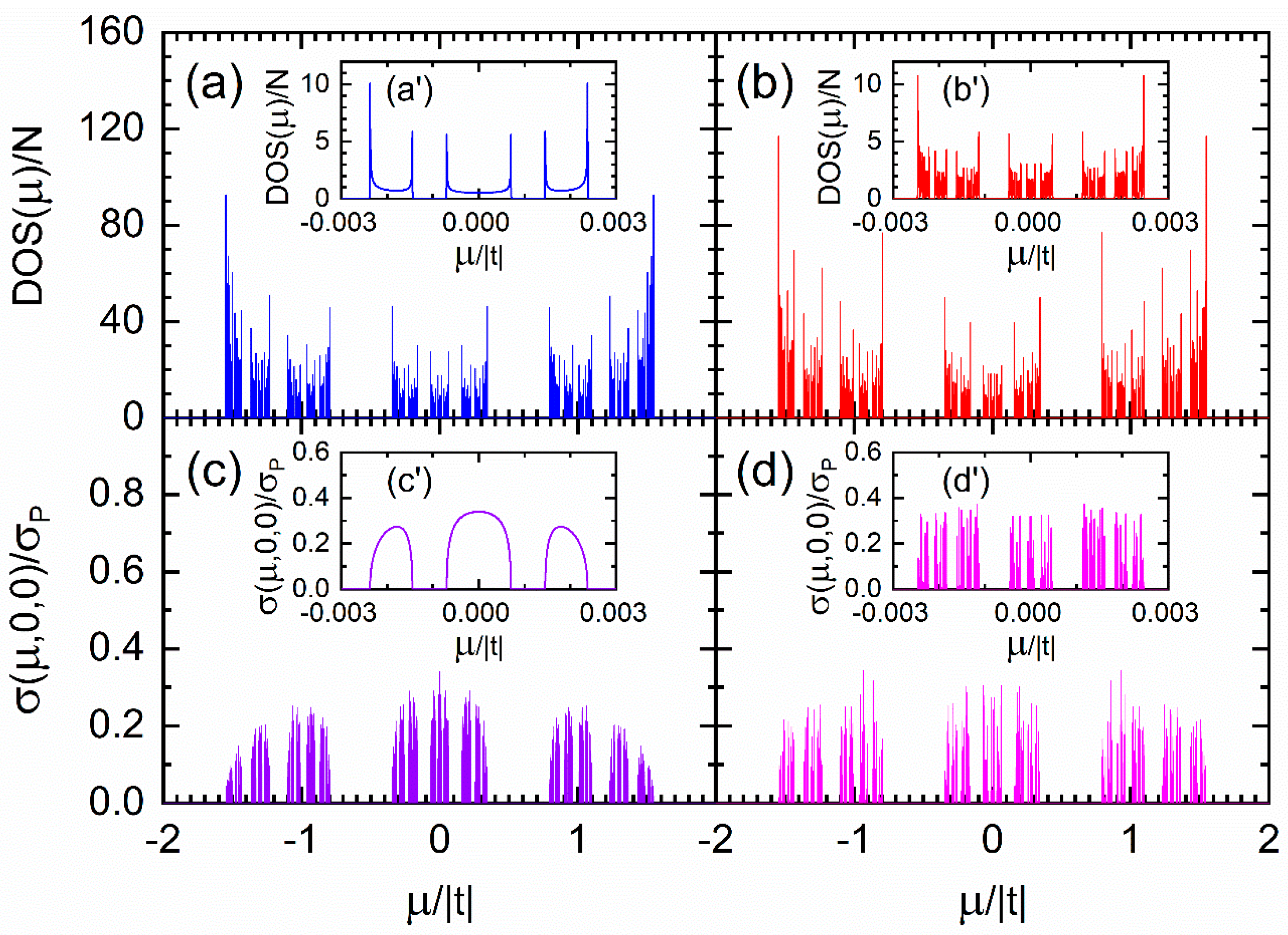
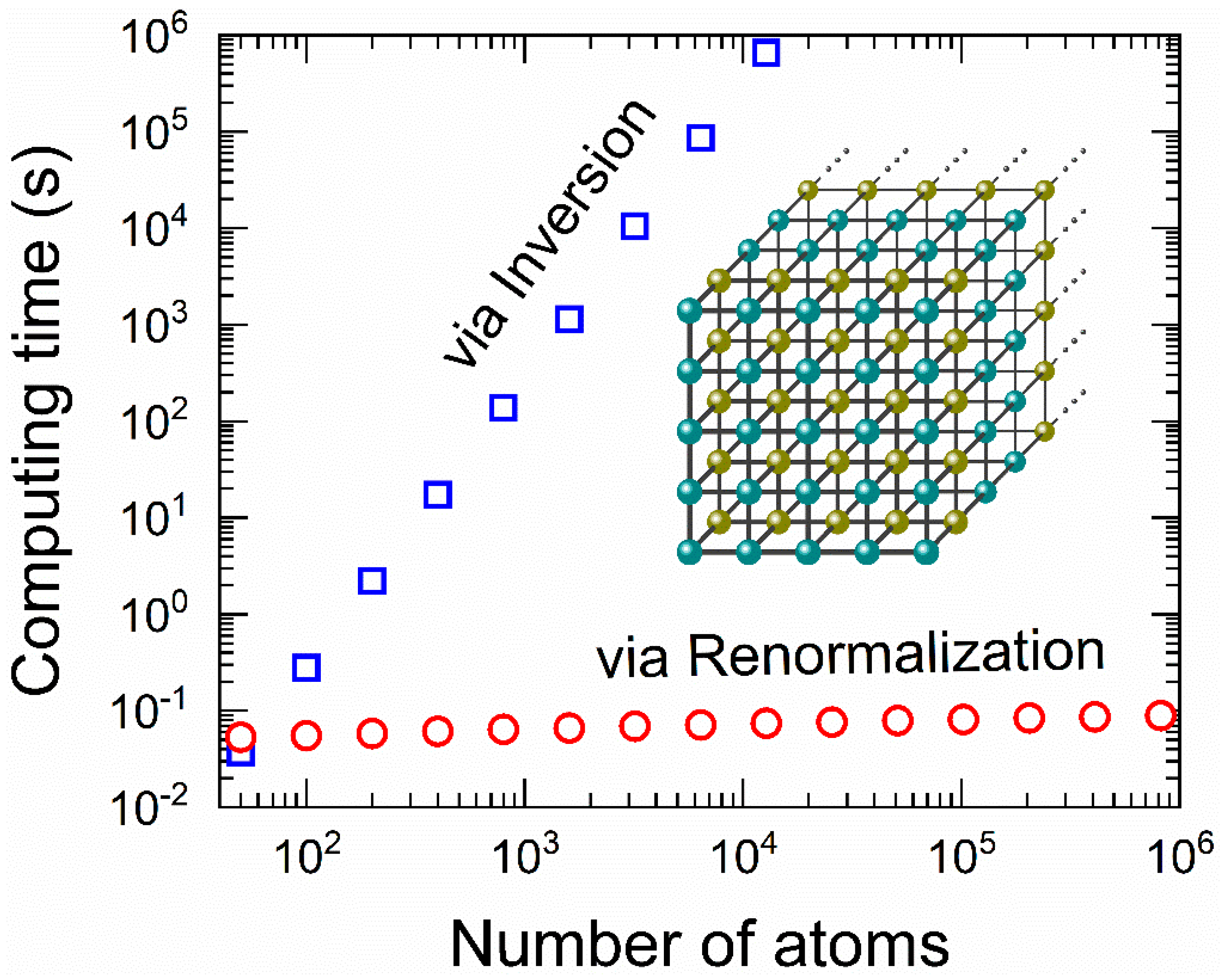
4. Multidimensional Aperiodic Lattices
5. Vibrational Excitations
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| YB | Yottabytes |
| RSRM | Real-space renormalization method |
| CPA | Coherent potential approximation |
| CPU | Central processing unit |
| 1D | One-dimensional |
| 2D | Two-dimensional |
| 3D | Three-dimensional |
| DC | Direct current |
| AC | Alternating current |
| DOS | Density of states |
| IDOS | Integrated density of states |
| GF | Generalized Fibonacci |
| TM | Thue–Morse |
| PD | Period doubling |
| NW | Nanowires |
| IR | Infrared |
| DNA | Deoxyribonucleic acid |
| A | Adenine |
| C | Cytosine |
| G | Guanine |
| T | Thymine |
References
- Chattopadhyay, D.; Queisser, H.J. Electron scattering by ionized impurities in semiconductors. Rev. Mod. Phys. 1981, 53, 745–768. [Google Scholar] [CrossRef]
- Maciá-Barber, E. Thermoelectric Materials: Advances and Applications; CRC Press: Boca Raton, FL, USA, 2015; p. 77. ISBN 978-981-4463-53-9. [Google Scholar]
- Ashcroft, N.W.; Mermin, N.D. Solid State Physics; Saunders College Pub.: Fort Worth, TX, USA, 1976; pp. 615–641. ISBN 0-03-083993-9. [Google Scholar]
- Elliott, R.J.; Krumhansl, J.A.; Leath, P.L. The theory and properties of randomly disordered crystals and related physical systems. Rev. Mod. Phys. 1974, 46, 465–543. [Google Scholar] [CrossRef]
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951–1954. [Google Scholar] [CrossRef]
- Janot, C. Quasicrystals: A Primer, 2nd ed.; Oxford University Press: Oxford, UK, 1994; pp. 223–234. ISBN 978-0-19-965740-7. [Google Scholar]
- Kittel, C. Introduction to Solid State Physics, 8th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2005; pp. 23–42. ISBN 0-471-41526-X. [Google Scholar]
- Kadanoff, L.P. Scaling laws for Ising models near Tc. Physics 1966, 2, 263–272. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization group and critical phenomena. I. Renormalization group and the Kadanoff scaling picture. Phys. Rev. B 1971, 4, 3174–3183. [Google Scholar] [CrossRef]
- Wilson, K.G. Renormalization group and critical phenomena. II. Phase-space cell analysis of critical behavior. Phys. Rev. B 1971, 4, 3184–3205. [Google Scholar] [CrossRef]
- Kramer, B.; MacKinon, A. Localization: Theory and experiment. Rep. Prog. Phys. 1993, 56, 1469–1564. [Google Scholar] [CrossRef]
- Economou, E.N. Green’s Functions in Quantum Physics, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 7–184. ISBN 978-3-540-28838-1. [Google Scholar]
- Oviedo-Roa, R.; Pérez, L.A.; Wang, C. AC conductivity of the transparent states in Fibonacci chains. Phys. Rev. B 2000, 62, 13805–13808. [Google Scholar] [CrossRef]
- Maciá Barber, E. Aperiodic Structures in Condensed Matter: Fundamentals and Applications; CRC Press: Boca Raton, FL, USA, 2009; pp. 132–153. ISBN 978-1-4200-6827-6. [Google Scholar]
- Posamentier, A.S.; Lehmann, I. The Fabulous Fibonacci Numbers; Prometheus Books: New York, NY, USA, 2007; p. 26. ISBN 978-1-59102-475-0. [Google Scholar]
- Dunlap, R.A. The Golden Ratio and Fibonacci Numbers; World Scientific Pub.: Singapore, 1997; pp. 35–49. ISBN 9810232640. [Google Scholar]
- Sánchez, V.; Wang, C. Application of renormalization and convolution methods to the Kubo-Greenwood formula in multidimensional Fibonacci systems. Phys. Rev. B 2004, 70, 144207. [Google Scholar] [CrossRef]
- Kohmoto, M.; Oono, Y. Cantor spectrum for an almost periodic Schrödinger equation and a dynamical map. Phys. Lett. A 1984, 102, 145–148. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B.; Tang, C. Critical wave functions and a Cantor-set spectrum of a one-dimensional quasicrystal model. Phys. Rev. B 1987, 35, 1020–1033. [Google Scholar] [CrossRef] [PubMed]
- Kohmoto, M.; Banavar, J.R. Quasiperiodic lattice: Electronic properties, phonon properties, and diffusion. Phys. Rev. B 1986, 34, 563–566. [Google Scholar] [CrossRef] [PubMed]
- Tang, C.; Kohmoto, M. Global scaling properties of the spectrum for a quasiperiodic Schrodinger equation. Phys. Rev. B 1986, 34, 2041–2044. [Google Scholar] [CrossRef] [PubMed]
- Kohmoto, M. Localization problem and mapping of one-dimensional wave equations in random and quasiperiodic media. Phys. Rev. B 1986, 34, 5043–5047. [Google Scholar] [CrossRef]
- Sutherland, B.; Kohmoto, M. Resistance of a one-dimensional quasicrystal: Power-law growth. Phys. Rev. B 1987, 35, 5877–5886. [Google Scholar] [CrossRef]
- Niu, Q.; Nori, F. Renormalization-group study of one-dimensional quasiperiodic systems. Phys. Rev. Lett. 1986, 57, 2057–2060. [Google Scholar] [CrossRef]
- Zheng, W.M. Global scaling properties of the spectrum for the Fibonacci chains. Phys. Rev. A 1987, 35, 1467–1469. [Google Scholar] [CrossRef]
- Roman, H.E. Hierarchical structure of a one-dimensional quasiperiodic model. Phys. Rev. B 1988, 37, 1399–1401. [Google Scholar] [CrossRef]
- Villaseñor-González, P.; Mejía-Lira, F.; Morán-López, J.L. Renormalization group approach to the electronic spectrum of a Fibonacci chain. Solid State Commun. 1988, 66, 1127–1130. [Google Scholar] [CrossRef]
- Wang, C.; Barrio, R.A. Theory of the Raman response in Fibonacci superlattices. Phys. Rev. Lett. 1988, 61, 191–194. [Google Scholar] [CrossRef]
- Bajema, K.; Merlin, R. Raman scattering by acoustic phonons in Fibonacci GaAs-AlAs superlattices. Phys. Rev. B 1987, 36, 4555–4557. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, A.; Karmakar, S.N.; Moitra, R.K. Exact real-space renormalization-group approach for the local electronic Green’s functions on an infinite Fibonacci chain. Phys. Rev. B 1989, 39, 9730–9733. [Google Scholar] [CrossRef] [PubMed]
- Tsunetsugu, H.; Ueda, K. Ising spin system on the Fibonacci chain. Phys. Rev. B 1987, 36, 5493–5499. [Google Scholar] [CrossRef] [PubMed]
- Ashraff, J.A.; Stinchcombe, R.B. Nonuniversal critical dynamics on the Fibonacci-chain quasicrystal. Phys. Rev. B 1989, 40, 2278–2283. [Google Scholar] [CrossRef]
- Aldea, A.; Dulea, M. Hopping conduction on aperiodic chains. Phys. Rev. Lett. 1988, 60, 1672–1675. [Google Scholar] [CrossRef]
- Miller, A.; Abrahams, E. Impurity conduction at low concentrations. Phys. Rev. 1960, 120, 745–755. [Google Scholar] [CrossRef]
- López, J.C.; Naumis, G.; Aragón, J.L. Renormalization group of random Fibonacci chains. Phys. Rev. B 1993, 48, 12459–12464. [Google Scholar] [CrossRef]
- Barrio, R.A.; Wang, C. Electron Localization in Large Fibonacci Chains. In Quasicrystals and Incommensurate Structures in Condensed Matter; José Yacamán, M., Romeu, D., Castaño, V., Gómez, A., Eds.; World Scientific: Singapore, 1990; pp. 448–464. ISBN 981-02-0001-3. [Google Scholar]
- Capaz, R.B.; Koiller, B.; de Queiroz, S.L.A. Gap states and localization properties of one-dimensional Fibonacci quasicrystals. Phys. Rev. B 1990, 42, 6402–6407. [Google Scholar] [CrossRef]
- Liu, Y.; Sritrakool, W. Branching rules of the energy spectrum of one-dimensional quasicrystals. Phys. Rev. B 1991, 43, 1110–1116. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Karmakar, S.N.; Moitra, R.K. On the nature of eigenstates of quasiperiodic lattices in one dimension. Phys. Lett. A 1992, 168, 301–304. [Google Scholar] [CrossRef]
- Zhong, J.X.; You, J.Q.; Yan, J.R.; Yan, X.H. Local electronic properties of one-dimensional quasiperiodic systems. Phys. Rev. B 1991, 43, 13778–13781. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.X.; Yan, J.R.; You, J.Q.; Yan, X.H. Exact renormalization-group approach for the average Green functions of aperiodic lattices. Phys. Lett. A 1993, 177, 71–75. [Google Scholar] [CrossRef]
- Newman, M.E.J.; Stinchcombe, R.B. Hopping conductivity of the Fibonacci-chain quasicrystal. Phys. Rev. B 1991, 43, 1183–1186. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, A. AC-conductivity of aperiodic chains re-examined. Z. Phys. B 1993, 93, 127–131. [Google Scholar] [CrossRef]
- Piéchon, F.; Benakli, M.; Jagannathan, A. Analytical results for scaling properties of the spectrum of the Fibonacci chain. Phys. Rev. Lett. 1995, 74, 5248–5251. [Google Scholar] [CrossRef]
- Maciá, E.; Domínguez-Adame, F. Physical nature of critical wave functions in Fibonacci systems. Phys. Rev. Lett. 1996, 76, 2957–2960. [Google Scholar] [CrossRef]
- Ghosh, A.; Karmakar, S.N. Electronic properties of quasiperiodic Fibonacci chain including second-neighbor hopping in the tight-binding model. Eur. Phys. J. B 1999, 11, 575–582. [Google Scholar] [CrossRef]
- Sánchez, V.; Pérez, L.A.; Oviedo-Roa, R.; Wang, C. Renormalization approach to the Kubo formula in Fibonacci systems. Phys. Rev. B 2001, 64, 174205. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Exact results of the Kubo conductivity in macroscopic Fibonacci systems: A renormalization approach. J. Alloys Compd. 2002, 342, 410–412. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Electronic transport in quasiperiodic lattices. J. Phys. Soc. Jpn. 2003, 72, 177–178. [Google Scholar] [CrossRef][Green Version]
- Walther, D.; Baltz, R.V. Frequency dependent conductivity of Fibonacci-chains. J. Low Temp. Phys. 2002, 126, 1211–1220. [Google Scholar] [CrossRef]
- Velhinho, M.T.; Pimentel, I.R. Lyapunov exponent for pure and random Fibonacci chains. Phys. Rev. B 2000, 61, 1043–1050. [Google Scholar] [CrossRef]
- Wang, C.; Oviedo-Roa, R.; Pérez, L.A.; Sánchez, V. Electrical conductivity and localization in quasiperiodic lattices. Ferroelectrics 2001, 250, 305–308. [Google Scholar] [CrossRef]
- Naumis, G.G. The stability of the renormalization group as a diagnostic tool for localization and its application to the Fibonacci case. J. Phys. Condens. Matter 2003, 15, 5969–5978. [Google Scholar] [CrossRef][Green Version]
- Vasconcelos, M.S.; Mauriz, P.W.; Albuquerque, E.L.; da Silva, E.F., Jr.; Freire, V.N. Electronic spectra of superlattice with impurities arranged according to a Fibonacci sequence. Appl. Surf. Sci. 2004, 234, 33–37. [Google Scholar] [CrossRef]
- Bakhtiari, M.R.; Vignolo, P.; Tosi, M.P. Coherent transport in linear arrays of quantum dots: The effects of period doubling and of quasi-periodicity. Physica E 2005, 28, 385–392. [Google Scholar] [CrossRef]
- Maciá, E.; Rodríguez-Oliveros, R. Renormalization transformation of periodic and aperiodic lattices. Phys. Rev. B 2006, 74, 144202. [Google Scholar] [CrossRef]
- Sengupta, S.; Chakrabarti, A. Wave propagation in a quasi-periodic waveguide network. Physica E 2005, 28, 28–36. [Google Scholar] [CrossRef]
- Bakhtiari, M.R.; Vignolo, P.; Tosi, M.P. Theory of coherent transport by an ultra-cold atomic Fermi gas through linear arrays of potential wells. Physica E 2006, 33, 223–229. [Google Scholar] [CrossRef][Green Version]
- Maciá, E. Clustering resonance effects in the electronic energy spectrum of tridiagonal Fibonacci quasicrystals. Phys. Status Solidi B 2017, 254, 1700078. [Google Scholar] [CrossRef]
- Hida, K. Quasiperiodic Hubbard Chains. Phys. Rev. Lett. 2001, 86, 1331–1334. [Google Scholar] [CrossRef] [PubMed]
- Arredondo, Y.; Navarro, O. Electron pairing in one-dimensional quasicrystals. Solid State Commun. 2010, 150, 1313–1316. [Google Scholar] [CrossRef]
- Hida, K. New universality class in spin-one-half Fibonacci Heisenberg chains. Phys. Rev. Lett. 2004, 93, 037205. [Google Scholar] [CrossRef] [PubMed]
- Cassels, J.W.S. An Introduction to Diophantine Approximation; Cambridge University Press: Cambridge, UK, 1957; p. 133. ISBN 978-0521045872. [Google Scholar]
- Luck, J.M.; Godreche, C.; Janner, A.; Janssen, T. The nature of the atomic surfaces of quasiperiodic self-similar structures. J. Phys. A Math. Gen. 1993, 26, 1951–1999. [Google Scholar] [CrossRef]
- Maciá, E. Exploiting aperiodic designs in nanophotonic devices. Rep. Prog. Phys. 2012, 75, 036502. [Google Scholar] [CrossRef] [PubMed]
- Gumbs, G.; Ali, M.K. Dynamical maps, Cantor spectra, and localization for Fibonacci and related quasiperiodic lattices. Phys. Rev. Lett. 1988, 60, 1081–1084. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Karmakar, S.N. Renormalization-group method for exact Green’s functions of self-similar lattices: Application to generalized Fibonacci chains. Phys. Rev. B 1991, 44, 896–899. [Google Scholar] [CrossRef]
- Zhong, J.X.; Yan, J.R.; You, J.Q.; Yan, X.H.; Mei, Y.P. Electronic properties of one-dimensional quasiperiodic lattices: Green’s function renormalization group approach. Z. Phys. B Condens. Matter 1993, 91, 127–133. [Google Scholar] [CrossRef]
- Zhong, J.X.; Yan, J.R.; You, J.Q. Renormalization-group approach to the local Green functions of a family of generalized Fibonacci lattices. J. Phys. A Math. Gen. 1991, 24, L949–L954. [Google Scholar] [CrossRef]
- Yan, X.H.; Zhong, J.X.; Yan, J.R.; You, J.Q. Renormalization group of generalized Fibonacci lattices. Phys. Rev. B 1992, 46, 6071–6079. [Google Scholar] [CrossRef]
- Yan, X.H.; You, J.Q.; Yan, J.R.; Zhong, J.X. Renormalization Group on the Aperiodic Hamiltonian. Chin. Phys. Lett. 1992, 9, 623–625. [Google Scholar]
- Oh, G.Y.; Ryu, C.S.; Lee, M.H. Clustering properties of energy spectra for one-dimensional generalized Fibonacci lattices. Phys. Rev. B 1993, 47, 6122–6125. [Google Scholar] [CrossRef] [PubMed]
- Zhong, J.X.; Yan, J.R.; You, J.Q. Exact Green’s functions of generalized Fibonacci lattices. J. Non Cryst. Solids 1993, 153, 439–442. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.; Zhou, P.; Sritrakool, W. Perfect self-similarity of energy spectra and gap-labeling properties in one-dimensional Fibonacci-class quasilattices. Phys. Rev. B 1997, 55, 2882–2889. [Google Scholar] [CrossRef]
- Walther, D.; Baltz, R.V. Path renormalization of quasiperiodic generalized Fibonacci chains. Phys. Rev. B 1997, 55, 8852–8866. [Google Scholar] [CrossRef]
- Chakrabarti, A. The unusual electronic spectrum of an infinite quasiperiodic chain: Extended signature of all eigenstates. J. Phys. Condens. Matter 1994, 6, 2015–2024. [Google Scholar] [CrossRef]
- Barghathi, H.; Nozadze, D.; Vojta, T. Contact process on generalized Fibonacci chains: Infinite-modulation criticality and double-log periodic oscillations. Phys. Rev. E 2014, 89, 012112. [Google Scholar] [CrossRef]
- Wang, C.; Ramírez, C.; Sánchez, F.; Sánchez, V. Ballistic conduction in macroscopic non-periodic lattices. Phys. Status Solidi B 2015, 252, 1370–1381. [Google Scholar] [CrossRef]
- Sánchez, F.; Sánchez, V.; Wang, C. Renormalization approach to the electronic localization and transport in macroscopic generalized Fibonacci lattices. J. Non Cryst. Solids 2016, 450, 194–208. [Google Scholar] [CrossRef]
- Maciá, E. Spectral classification of one-dimensional binary aperiodic crystals: An algebraic approach. Ann. Phys. 2017, 529, 1700079. [Google Scholar] [CrossRef]
- Maciá, E. The role of aperiodic order in science and technology. Rep. Prog. Phys. 2006, 69, 397–441. [Google Scholar] [CrossRef]
- Qin, M.-G.; Ma, H.-R.; Tsai, C.-H. A renormalisation analysis of the one-dimensional Thue-Morse aperiodic chain. J. Phys. Condens. Matter 1990, 2, 1059–1072. [Google Scholar] [CrossRef]
- Zhong, J.X.; You, J.Q.; Yan, J.R. The exact Green function of a one-dimensional Thue-Morse lattice. J. Phys. Condens. Matter 1992, 4, 5959–5965. [Google Scholar] [CrossRef]
- Ghosh, A.; Karmakar, S.N. Trace map of a general aperiodic Thue-Morse chain: Electronic properties. Phys. Rev. B 1998, 58, 2586–2590. [Google Scholar] [CrossRef]
- Cheng, S.-F.; Jin, G.-J. Trace map and eigenstates of a Thue-Morse chain in a general model. Phys. Rev. B 2002, 65, 134206. [Google Scholar] [CrossRef]
- Chakrabarti, A.; Karmakar, S.N.; Moitra, R.K. Role of a new type of correlated disorder in extended electronic states in the Thue-Morse lattice. Phys. Rev. Lett. 1995, 74, 1403–1406. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Chakrabarti, A. Role of an invariant in the existence of delocalized electronic states in generalized models of a Thue-Morse aperiodic chain. Phys. Rev. B 2001, 63, 132201. [Google Scholar] [CrossRef]
- Maciá, E.; Domínguez-Adame, F. Exciton optical absorption in self-similar aperiodic lattices. Phys. Rev. B 1994, 50, 16856–16860. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, D.-C.; Wang, L. Renormalization group approach to the random period doubling lattice. Phys. Lett. A 1995, 207, 293–298. [Google Scholar] [CrossRef]
- Hu, Y.; Tian, D.-C. Spectral properties of the period-doubling lattice: Exact renormalization group study. Z. Phys. B 1996, 100, 629–633. [Google Scholar] [CrossRef]
- Lin, Z.; Kong, X.; Yang, Z.R. Critical behavior of the Gaussian model on a diamond-type hierarchical lattice with periodic and aperiodic interactions. Phys. A 1999, 271, 118–124. [Google Scholar] [CrossRef]
- Liu, Y.; Fu, X.; Han, H.; Cheng, B.; Luan, C. Spectral structure for a class of one-dimensional three-tile quasilattices. Phys. Rev. B 1991, 43, 13240–13245. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Wang, S.; Liu, Y.; Zheng, D.; Zou, N. Electronic properties of a one-dimensional three-tile quasilattice. Phys. Rev. B 1993, 47, 5653–5659. [Google Scholar] [CrossRef] [PubMed]
- Maciá, E. On the nature of electronic wave functions in one-dimensional self-similar and quasiperiodic systems. ISRN Condens. Matter Phys. 2014, 2014, 165943. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef]
- Wang, C.; González, J.E.; Sánchez, V. Enhancement of the thermoelectric figure-of-merit in nanowire superlattices. Mater. Res. Soc. Symp. Proc. 2015, 1735. [Google Scholar] [CrossRef]
- Orellana, P.A.; Domínguez-Adame, F.; Gómez, I.; Ladrón de Guevara, M.L. Transport through a quantum wire with a side quantum-dot array. Phys. Rev. B 2003, 67, 085321. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Kivshar, Y.S. Engineering Fano resonances in discrete arrays. Phys. Rev. E 2005, 72, 056611. [Google Scholar] [CrossRef]
- Chakrabarti, A. Electronic transmission in a model quantum wire with side-coupled quasiperiodic chains: Fano resonance and related issues. Phys. Rev. B 2006, 74, 205315. [Google Scholar] [CrossRef]
- Farchioni, R.; Grosso, G.; Parravicini, G.P. Quenching of the transmittivity of a one-dimensional binary random dimer model through side-attached atoms. Phys. Rev. B 2012, 85, 165115. [Google Scholar] [CrossRef]
- Mardaani, M.; Rabani, H. A solvable model for electronic transport of a nanowire in the presence of effective impurities. Superlattices Microstruct. 2013, 59, 155–162. [Google Scholar] [CrossRef]
- Pal, B. Absolutely continuous energy bands and extended electronic states in an aperiodic comb-shaped nanostructure. Phys. Status Solidi B 2014, 251, 1401–1407. [Google Scholar] [CrossRef][Green Version]
- Nandy, A.; Pal, B.; Chakrabarti, A. Tight-binding chains with off-diagonal disorder: Bands of extended electronic states induced by minimal quasi-one-dimensionality. EPL 2016, 115, 37004. [Google Scholar] [CrossRef]
- Chakrabarti, A. Fano resonance in discrete lattice models: Controlling lineshapes with impurities. Phys. Lett. A 2007, 366, 507–512. [Google Scholar] [CrossRef][Green Version]
- Chattopadhyay, S.; Chakrabarti, A. Electronic transmission in quasiperiodic serial stub structures. J. Phys. Condens. Matter 2004, 16, 313–323. [Google Scholar] [CrossRef]
- Nomata, A.; Horie, S. Self-similarity appearance conditions for electronic transmission probability and Landauer resistance in a Fibonacci array of T stubs. Phys. Rev. B 2007, 76, 235113. [Google Scholar] [CrossRef]
- Ramírez, C.; Sánchez, V. Kubo conductivity of macroscopic systems with Fano defects for periodic and quasiperiodic cases by means of renormalization methods in real space. Phys. Status Solidi A 2013, 210, 2431–2438. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Resonant AC conducting spectra in quasiperiodic systems. Int. J. Comput. Mater. Sci. Eng. 2012, 1, 1250003. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Improving the ballistic AC conductivity through quantum resonance in branched nanowires. Philos. Mag. 2015, 95, 326–333. [Google Scholar] [CrossRef]
- Lambert, C.J. Basic concepts of quantum interference and electron transport in single-molecule electronics. Chem. Soc. Rev. 2015, 44, 875–888. [Google Scholar] [CrossRef]
- Su, T.A.; Neupane, M.; Steigerwald, M.L.; Venkataraman, L.; Nuckolls, C. Chemical principles of single-molecule electronics. Nat. Rev. Mater. 2016, 1, 16002. [Google Scholar] [CrossRef]
- Nomata, A.; Horie, S. Fractal feature of localized electronic states in Fibonacci arrays of Aharonov-Bohm rings. Phys. Rev. B 2007, 75, 115130. [Google Scholar] [CrossRef]
- Sil, S.; Maiti, S.K.; Chakrabarti, A. Metal-insulator transition in an aperiodic ladder network: An exact result. Phys. Rev. Lett. 2008, 101, 076803. [Google Scholar] [CrossRef] [PubMed]
- Chakrabarti, A. Electronic transmission in bent quantum wires. Physica E 2010, 42, 1963–1967. [Google Scholar] [CrossRef][Green Version]
- Farchioni, R.; Grosso, G.; Parravicini, G.P. Electronic transmission through a ladder with a single side-attached impurity. Eur. Phys. J. B 2011, 84, 227–233. [Google Scholar] [CrossRef]
- Pal, B.; Maiti, S.K.; Chakrabarti, A. Complete absence of localization in a family of disordered lattices. EPL 2013, 102, 17004. [Google Scholar] [CrossRef]
- Dutta, P.; Maiti, S.K.; Karmakar, S.N. A renormalization group study of persistent current in a quasiperiodic ring. Phys. Lett. A 2014, 378, 1388–1391. [Google Scholar] [CrossRef][Green Version]
- Pal, B.; Chakrabarti, A. Engineering bands of extended electronic states in a class of topologically disordered and quasiperiodic lattices. Phys. Lett. A 2014, 378, 2782–2789. [Google Scholar] [CrossRef]
- Pal, B.; Chakrabarti, A. Absolutely continuous energy bands in the electronic spectrum of quasiperiodic ladder networks. Physica E 2014, 60, 188–195. [Google Scholar] [CrossRef][Green Version]
- Bravi, M.; Farchioni, R.; Grosso, G.; Parravicini, G.P. Riccati equation for simulation of leads in quantum transport. Phys. Rev. B 2014, 90, 155445. [Google Scholar] [CrossRef]
- Nandy, A.; Chakrabarti, A. Engineering flat electronic bands in quasiperiodic and fractal loop geometries. Phys. Lett. A 2015, 379, 2876–2882. [Google Scholar] [CrossRef]
- Mukherjee, A.; Nandy, A. Spectral engineering and tunable thermoelectric behavior in a quasiperiodic ladder network. Phys. Lett. A 2019, 383, 570–577. [Google Scholar] [CrossRef]
- Mukherjee, A.; Chakrabarti, A.; Römer, R.A. Flux-driven and geometry-controlled spin filtering for arbitrary spins in aperiodic quantum networks. Phys. Rev. B 2018, 98, 075415. [Google Scholar] [CrossRef]
- Mukherjee, A.; Römer, R.A.; Chakrabarti, A. Spin-selective Aharonov-Casher caging in a topological quantum network. Phys. Rev. B 2019, 100, 161108. [Google Scholar] [CrossRef]
- Chakrabarti, A. Electronic states and charge transport in a class of low dimensional structured systems. Physica E 2019, 114, 113616. [Google Scholar] [CrossRef]
- Xu, B.; Zhang, P.; Li, X.; Tao, N. Direct conductance measurement of single DNA molecules in aqueous solution. Nano Lett. 2004, 4, 1105–1108. [Google Scholar] [CrossRef]
- Taniguchi, M.; Kawai, T. DNA electronics. Physica E 2006, 33, 1–12. [Google Scholar] [CrossRef]
- Sponer, J.; Leszczynski, J.; Hobza, P. Structures and energies of hydrogen-bonded DNA base pairs: A nonempirical study with inclusion of electron correlation. J. Phys. Chem. 1996, 100, 1965–1974. [Google Scholar] [CrossRef]
- de Pablo, P.J.; Moreno-Herrero, F.; Colchero, J.; Gómez Herrero, J.; Herrero, P.; Baró, A.M.; Ordejón, P.; Soler, J.M.; Artacho, E. Absence of DC-conductivity in λ-DNA. Phys. Rev. Lett. 2000, 85, 4992–4995. [Google Scholar] [CrossRef]
- Ladik, J.; Biczó, G.; Elek, G. Theoretical estimation of the conductivity of different periodic DNA models. J. Chem. Phys. 1966, 44, 483–485. [Google Scholar] [CrossRef]
- Ladik, J. Energy bands in DNA. Int. J. Quantum Chem. 1970, 5, 307–317. [Google Scholar] [CrossRef]
- Maciá, E.; Roche, S. Backbone-induced effects in the charge transport efficiency of synthetic DNA molecules. Nanotechnology 2006, 17, 3002–3007. [Google Scholar] [CrossRef]
- Maciá, E. Electronic structure and transport properties of double-stranded Fibonacci DNA. Phys. Rev. B 2006, 74, 245105. [Google Scholar] [CrossRef]
- Ketabi, S.A.; Khouzestani, H.F. Electronic transport through dsDNA based junction: A Fibonacci model. Iran. J. Phys. Res. 2014, 14, 67–72. [Google Scholar]
- Joe, Y.S.; Lee, S.H.; Hedin, E.R. Electron transport through asymmetric DNA molecules. Phys. Lett. A 2010, 374, 2367–2373. [Google Scholar] [CrossRef]
- Maciá, E. Electrical conductance in duplex DNA: Helical effects and low-frequency vibrational coupling. Phys. Rev. B 2007, 76, 245123. [Google Scholar] [CrossRef]
- Maciá, E. π-π orbital resonance in twisting duplex DNA: Dynamical phyllotaxis and electronic structure effects. Phys. Rev. B 2009, 80, 125102. [Google Scholar] [CrossRef]
- de Almeida, M.L.; Ourique, G.S.; Fulco, U.L.; Albuquerque, E.L.; de Moura, F.A.B.F.; Lyra, M.L. Charge transport properties of a twisted DNA molecule: A renormalization approach. Chem. Phys. 2016, 478, 48–54. [Google Scholar] [CrossRef]
- Maciá, E. DNA-based thermoelectric devices: A theoretical prospective. Phys. Rev. B 2007, 75, 035130. [Google Scholar] [CrossRef]
- de Moura, F.A.B.F.; Lyra, M.L.; Albuquerque, E.L. Electronic transport in poly(CG) and poly(CT) DNA segments with diluted base pairing. J. Phys. Condens. Matter 2008, 20, 075109. [Google Scholar] [CrossRef]
- Tornow, S.; Bulla, R.; Anders, F.B.; Zwicknagl, G. Multiple-charge transfer and trapping in DNA dimers. Phys. Rev. B 2010, 82, 195106. [Google Scholar] [CrossRef]
- Deng, C.-S.; Xu, H.; Wang, H.-Y.; Liu, X.-L. Renormalization scheme to the charge transfer efficiency of single-strand DNA with long range correlated disorder. Mod. Phys. Lett. B 2009, 23, 951–962. [Google Scholar] [CrossRef]
- Rabani, H.; Mardaani, M. Exact analytical results on electronic transport of conjugated polymer junctions: Renormalization method. Solid State Commun. 2012, 152, 235–239. [Google Scholar] [CrossRef]
- Liu, X.-L.; Xu, H.; Ma, S.-S.; Deng, C.-S.; Li, M.-J. Renormalization-group results of electron transport in DNA molecules with off-diagonal correlation. Physica B 2007, 392, 107–111. [Google Scholar] [CrossRef]
- Wang, L.; Qin, Z.-J. Isolate extended state in the DNA molecular transistor with surface interaction. Physica B 2016, 482, 1–7. [Google Scholar] [CrossRef]
- Mardaani, M.; Rabani, H. An analytical model for magnetoconductance of poly(p-phenylene)-like molecular wires in the tight-binding approach. J. Mag. Mag. Mater. 2013, 331, 28–32. [Google Scholar] [CrossRef]
- Sarmento, R.G.; Fulco, U.L.; Albuquerque, E.L.; Caetano, E.W.S.; Freire, V.N. A renormalization approach to describe charge transport in quasiperiodic dangling backbone ladder (DBL)-DNA molecules. Phys. Lett. A 2011, 375, 3993–3996. [Google Scholar] [CrossRef]
- Ojeda, J.H.; Pacheco, M.; Rosales, L.; Orellana, P.A. Current and Shot noise in DNA chains. Org. Electron. 2012, 13, 1420–1429. [Google Scholar] [CrossRef]
- Pal, T.; Sadhukhan, P.; Bhattacharjee, S.M. Renormalization group limit cycle for three-stranded DNA. Phys. Rev. Lett. 2013, 110, 028105. [Google Scholar] [CrossRef]
- Maji, J.; Bhattacharjee, S.M. Efimov effect of triple-stranded DNA: Real-space renormalization group and zeros of the partition function. Phys. Rev. E 2012, 86, 041147. [Google Scholar] [CrossRef]
- Albuquerque, E.L.; Fulco, U.L.; Freire, V.N.; Caetano, E.W.S.; Lyra, M.L.; de Moura, F.A.B.F. DNA-based nanobiostructured devices: The role of quasiperiodicity and correlation effects. Phys. Rep. 2014, 535, 139–209. [Google Scholar] [CrossRef]
- Lambropoulos, K.; Simserides, C. Tight-binding modeling of nucleic acid sequences: Interplay between various types of order or disorder and charge transport. Symmetry 2019, 11, 968. [Google Scholar] [CrossRef]
- Lifshitz, R. The square Fibonacci tiling. J. Alloys Compd. 2002, 342, 186–190. [Google Scholar] [CrossRef]
- Yang, X.-B.; Liu, Y.-Y. Electronic energy spectrum structure of the two-dimensional Fibonacci quasilattices with three kinds of atoms and one kind of bond length. Acta Phys. Sin. 1995, 4, 510–522. [Google Scholar]
- Ma, H.-R.; Tsai, C.-H. On the energy spectra of one-dimensional quasi-periodic systems. J. Phys. C Solid State Phys. 1988, 21, 4311–4324. [Google Scholar] [CrossRef]
- Merlin, R.; Bajema, K.; Clarke, R.; Juang, F.-Y.; Bhattacharya, P.K. Quasiperiodic GaAs-AIAs heterostructures. Phys. Rev. Lett. 1985, 55, 1768–1770. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.-Y.; Cheng, B.; Zheng, D. Spectral structure of two-dimensional Fibonacci quasilattices. Phys. Rev. B 1991, 43, 10808–10814. [Google Scholar] [CrossRef]
- Yang, X.-B.; Liu, Y.-Y. Splitting rules for spectra of two-dimensional Fibonacci quasilattices. Phys. Rev. B 1997, 56, 8054–8059. [Google Scholar] [CrossRef]
- Yang, X.-B.; Xing, D. Splitting rules for the electronic spectra of two-dimensional Fibonacci-class quasicrystals with one kind of atom and two bond lengths. Phys. Rev. B 2002, 65, 134205. [Google Scholar] [CrossRef]
- Ashraff, J.A.; Luck, J.-M.; Stinchcombe, R.B. Dynamical properties of two-dimensional quasicrystals. Phys. Rev. B 1990, 41, 4314–4329. [Google Scholar] [CrossRef]
- Fu, X.; Liu, Y.-Y. Renormalization-group approach for the local density of states of two-dimensional Fibonacci quasilattices. Phys. Rev. B 1993, 47, 3026–3030. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, V.; Wang, C. Kubo conductivity in two-dimensional Fibonacci lattices. J. Non Cryst. Solids 2003, 329, 151–154. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Convolution and renormalization techniques applied to the Kubo conductivity in quasiperiodic systems. J. Non Cryst. Solids 2004, 345, 518–522. [Google Scholar] [CrossRef]
- Wang, C.; Sánchez, V.; Salazar, F. Fractal quantization of the electrical conductance in quasiperiodic systems. Ferroelectrics 2004, 305, 261–264. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Electronic transport in multidimensional Fibonacci lattices. Philos. Mag. 2006, 86, 765–771. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. Renormalization-convolution approach to the electronic transport in two-dimensional aperiodic lattices. Surf. Sci. 2006, 600, 3898–3900. [Google Scholar] [CrossRef]
- Sánchez, V.; Wang, C. A real-space renormalization approach to the Kubo–Greenwood formula in mirror Fibonacci systems. J. Phys. A Math. Gen. 2006, 39, 8173–8182. [Google Scholar] [CrossRef]
- Sánchez, V.; Sánchez, F.; Ramírez, C.; Wang, C. Non-perturbative analysis of impurity effects on the Kubo conductivity of nano to macroscopic structures. MRS Adv. 2016, 1, 1779–1784. [Google Scholar] [CrossRef]
- Sánchez, V. Renormalization approach to the electrical conductivity of quasiperiodic systems with defects. Comput. Mater. Sci. 2008, 44, 32–35. [Google Scholar] [CrossRef]
- Sánchez, V.; Ramírez, C.; Sánchez, F.; Wang, C. Non-perturbative study of impurity effects on the Kubo conductivity in macroscopic periodic and quasiperiodic lattices. Physica B 2014, 449, 121–128. [Google Scholar] [CrossRef]
- Kohmoto, M.; Sutherland, B. Electronic states on a Penrose lattice. Phys. Rev. Lett. 1986, 56, 2740–2743. [Google Scholar] [CrossRef] [PubMed]
- Kohmoto, M.; Sutherland, B. Electronic and vibrational modes on a Penrose lattice: Localized states and band structure. Phys. Rev. B 1986, 34, 3849–3853. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Barrio, R.A. The electronic band structure of Penrose lattices: A renormalization approach. In Surface Science; Ponce, F.A., Cardona, M., Eds.; Springer Proceedings in Physics: Berlin/Heidelberg, Germany, 1991; Volume 62, pp. 67–70. ISBN 978-3-642-76378-6. [Google Scholar]
- Barrio, R.A.; Wang, C. Some physical inferences from the quasicrystalline topology of Penrose lattices. J. Non Cryst. Solids 1993, 153, 375–379. [Google Scholar] [CrossRef]
- Naumis, G.G.; Barrio, R.A.; Wang, C. Effects of frustration and localization of states in the Penrose lattice. Phys. Rev. B 1994, 50, 9834–9842. [Google Scholar] [CrossRef]
- You, J.Q.; Yan, J.R.; Zhong, J.X.; Yan, X.H. Local electronic properties of two-dimensional Penrose tilings: A renormalization-group approach. Phys. Rev. B 1992, 45, 7690–7696. [Google Scholar] [CrossRef]
- You, J.Q.; Nori, F. The real-space renormalization group and generating function for Penrose lattices. J. Phys. Condens. Matter 1993, 5, 9431–9438. [Google Scholar] [CrossRef]
- Aoyama, H.; Odagaki, T. Bond percolation in two-dimensional quasi-lattices. J. Phys. A Math. Gen. 1987, 20, 4985–4993. [Google Scholar] [CrossRef]
- Tang, L.-H.; Jaric, M.V. Equilibrium quasicrystal phase of a Penrose tiling model. Phys. Rev. B 1990, 41, 4524–4546. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, Z.-H.; Tian, D.-C. Real-space renormalization group approach to the Potts model on the two-dimensional Penrose tiling. Phys. A 1999, 265, 547–556. [Google Scholar] [CrossRef]
- Macé, N.; Jagannathan, A.; Kalugin, P.; Mosseri, R.; Piéchon, F. Critical eigenstates and their properties in one- and two-dimensional quasicrystals. Phys. Rev. B 2017, 96, 045138. [Google Scholar] [CrossRef]
- Takemori, N.; Koga, A. Local electron correlations in a two-dimensional Hubbard model on the Penrose lattice. J. Phys. Soc. Jpn. 2015, 84, 023701. [Google Scholar] [CrossRef]
- Takemori, N.; Koga, A. DMFT study of the local correlation effects in quasi-periodic system. J. Phys. Conf. Ser. 2015, 592, 012038. [Google Scholar] [CrossRef]
- Sánchez, F.; Sánchez, V.; Wang, C. Ballistic transport in aperiodic Labyrinth tiling proven through a new convolution theorem. Eur. Phys. J. B 2018, 91, 132. [Google Scholar] [CrossRef]
- Sire, C.; Mosseri, R.; Sadoc, J.-F. Geometric study of a 2D tiling related to the octagonal quasiperiodic tiling. J. Phys. Fr. 1989, 50, 3463–3476. [Google Scholar] [CrossRef]
- Sire, C. Electronic spectrum of a 2D quasi-crystal related to the octagonal quasi-periodic tiling. Europhys. Lett. 1989, 10, 483–488. [Google Scholar] [CrossRef]
- Takahashi, Y. Quantum and spectral properties of the Labyrinth model. J. Math. Phys. 2016, 57, 063506. [Google Scholar] [CrossRef]
- Takahashi, Y. Products of two Cantor sets. Nonlinearity 2017, 30, 2114–2137. [Google Scholar] [CrossRef]
- Thiem, S.; Schreiber, M. Renormalization group approach for the wave packet dynamics in golden-mean and silver-mean labyrinth tilings. Phys. Rev. B 2012, 85, 224205. [Google Scholar] [CrossRef]
- Thiem, S.; Schreiber, M. Wavefunctions, quantum diffusion, and scaling exponents in golden-mean quasiperiodic tilings. J. Phys. Condens. Matter 2013, 25, 075503. [Google Scholar] [CrossRef][Green Version]
- Torres, M.; Adrados, J.P.; Aragón, J.L.; Cobo, P.; Tehuacanero, S. Quasiperiodic Bloch-like states in a surface-wave experiment. Phys. Rev. Lett. 2003, 90, 114501. [Google Scholar] [CrossRef]
- Callaway, J. Quantum Theory of Solid State; Academic Press: New York, NY, USA, 1974; pp. 19–24. ISBN 0-12-155201-2. [Google Scholar]
- Alfaro, P.; Cisneros, R.; Bizarro, M.; Cruz-Irisson, M.; Wang, C. Raman scattering by confined optical phonons in Si and Ge nanostructures. Nanoscale 2011, 3, 1246–1251. [Google Scholar] [CrossRef] [PubMed]
- Atkins, P.; de Paula, J. Physical Chemistry, 8th ed.; W. H. Freeman and Co.: New York, NY, USA, 2006; pp. 460–468. ISBN 0-7167-8759-8. [Google Scholar]
- Quilichini, M.; Janssen, T. Phonon excitations in quasicrystals. Rev. Mod. Phys. 1997, 69, 277–314. [Google Scholar] [CrossRef]
- Maciá, E. Thermal conductivity and critical modes in one-dimensional Fibonacci quasicrystals. Mater. Sci. Eng. 2000, 294, 719–722. [Google Scholar] [CrossRef]
- Chen, B.; Gong, C.-D. The properties of one-dimensional quasiperiodic lattice’s phonon spectrum. Z. Phys. B Condens. Matter 1987, 69, 103–109. [Google Scholar] [CrossRef]
- You, J.Q.; Yang, Q.B.; Yan, J.R. Phonon properties of a class of one-dimensional quasiperiodic systems. Phys. Rev. B 1994, 41, 7491–7496. [Google Scholar] [CrossRef]
- Zhong, J.X.; Yan, J.R.; Yan, X.H.; You, J.Q. Local phonon properties of the Fibonacci-chain quasicrystal. J. Phys. Condens. Matter 1991, 3, 5685–5691. [Google Scholar] [CrossRef]
- Yan, X.H.; Yan, J.R.; Zhong, J.X.; You, J.Q.; Mei, Y.P. An exact renormalization-group approach for local phonon properties of single-atom and double-atom generalized Fibonacci systems. Z. Phys. B 1993, 91, 467–474. [Google Scholar] [CrossRef]
- Maciá, E. Thermal conductivity of one-dimensional Fibonacci quasicrystals. Phys. Rev. B 2000, 61, 6645–6653. [Google Scholar] [CrossRef]
- Gumbs, G.; Dubey, G.S.; Salman, A.; Mahmoud, B.S.; Huang, D. Statistical and transport properties of quasiperiodic layered structures: Thue-Morse and Fibonacci. Phys. Rev. B 1995, 52, 210–219. [Google Scholar] [CrossRef]
- Ghosh, A.; Karmakar, S.N. Vibrational properties of a general aperiodic Thue-Morse lattice: Role of the pseudoinvariant of the trace map. Phys. Rev. B 2000, 61, 1051–1058. [Google Scholar] [CrossRef]
- Kroon, L.; Riklund, R. Renormalization of aperiodic model lattices: Spectral properties. J. Phys. A Math. Gen. 2003, 36, 4519–4532. [Google Scholar] [CrossRef]
- Ghosh, A. Dynamical properties of three component Fibonacci quasicrystal. Eur. Phys. J. B 2001, 21, 45–51. [Google Scholar] [CrossRef]
- Kono, K.; Nakada, S. Resonant transmission and velocity renormalization of third sound in one-dimensional random lattices. Phys. Rev. Lett. 1992, 69, 1185–1188. [Google Scholar] [CrossRef] [PubMed]
- Springer, K.N.; Van Harlingen, D.J. Resistive transition and magnetic field response of a Penrose-tile array of weakly coupled superconductor islands. Phys. Rev. B 1987, 36, 7273–7276. [Google Scholar] [CrossRef]
- He, S.; Maynard, J.D. Eigenvalue spectrum, density of states, and eigenfunctions in a two-dimensional quasicrystal. Phys. Rev. Lett. 1989, 62, 1888–1891. [Google Scholar] [CrossRef]
- Wang, C.; Fuentes, R.; Navarro, O.; Barrio, R.A.; Barrera, R.G. Wave behavior in anharmonic Penrose lattices. J. Non Cryst. Solids 1993, 153, 586–590. [Google Scholar] [CrossRef]
- González, J.E.; Cruz-Irisson, M.; Sánchez, V.; Wang, C. Thermoelectric transport in poly(G)-poly(C) double chains. J. Phys. Chem. Solids 2020, 136, 109136. [Google Scholar] [CrossRef]
- Wang, C.; Salazar, F.; Sánchez, V. Renormalization plus convolution method for atomic-scale modeling of electrical and thermal transport in nanowires. Nano Lett. 2008, 8, 4205–4209. [Google Scholar] [CrossRef]
- Zhang, Y.-M.; Xu, C.-H.; Xiong, S.-J. Phonon transmission and thermal conductance in Fibonacci wire at low temperature. Chin. Phys. Lett. 2007, 24, 1017–1020. [Google Scholar]
- Andrews, S.C.; Fardy, M.A.; Moore, M.C.; Aloni, S.; Zhang, M.; Radmilovic, V.; Yang, P. Atomic-level control of the thermoelectric properties in polytypoid nanowires. Chem. Sci. 2011, 2, 706–714. [Google Scholar] [CrossRef]
- González, J.E.; Sánchez, V.; Wang, C. Thermoelectricity in periodic and quasiperiodically segmented nanobelts and nanowires. MRS Adv. 2016, 1, 3953–3958. [Google Scholar] [CrossRef]
- González, J.E.; Sánchez, V.; Wang, C. Improving thermoelectric properties of nanowires through inhomogeneity. J. Electron. Mater. 2017, 46, 2724–2736. [Google Scholar] [CrossRef]
- Sánchez, F.; Amador-Bedolla, C.; Sánchez, V.; Wang, C. Quasiperiodic branches in the thermoelectricity of nanowires. J. Electron. Mater. 2019, 48, 5099–5110. [Google Scholar] [CrossRef]
- González, J.E.; Sánchez, V.; Wang, C. Resonant thermoelectric transport in atomic chains with Fano defects. MRS Commun. 2018, 8, 248–256. [Google Scholar] [CrossRef]
- Sutton, A.P. Electronic Structure of Materials; Oxford University Press: New York, NY, USA, 1993; pp. 107–109. ISBN 0-19-851755-6. [Google Scholar]
- Mizutani, U. Hume-Rothery Rules for Structurally Complex Alloy Phases; CRC Press: Boca Raton, FL, USA, 2011; pp. 1–2. ISBN 978-1-4200-9059-8. [Google Scholar]
- Sánchez, F.; Amador-Bedolla, C.; Sánchez, V.; Wang, C. On the role of driving force in molecular photocells. Phys. B Phys. Condens. Matter 2020, 583, 412052. [Google Scholar] [CrossRef]
- Palavicini, A.; Wang, C. Ab-initio determination of porous silicon refractive index confirmed by infrared transmittance measurements of an omnidirectional multilayer reflector. Appl. Phys. B 2018, 124, 65. [Google Scholar] [CrossRef]
- Palavicini, A.; Wang, C. Ab initio design and experimental confirmation of Fabry–Perot cavities based on freestanding porous silicon multilayers. J. Mater. Sci. Mater. Electron. 2020, 31, 60–64. [Google Scholar] [CrossRef]


© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sánchez, V.; Wang, C. Real Space Theory for Electron and Phonon Transport in Aperiodic Lattices via Renormalization. Symmetry 2020, 12, 430. https://doi.org/10.3390/sym12030430
Sánchez V, Wang C. Real Space Theory for Electron and Phonon Transport in Aperiodic Lattices via Renormalization. Symmetry. 2020; 12(3):430. https://doi.org/10.3390/sym12030430
Chicago/Turabian StyleSánchez, Vicenta, and Chumin Wang. 2020. "Real Space Theory for Electron and Phonon Transport in Aperiodic Lattices via Renormalization" Symmetry 12, no. 3: 430. https://doi.org/10.3390/sym12030430
APA StyleSánchez, V., & Wang, C. (2020). Real Space Theory for Electron and Phonon Transport in Aperiodic Lattices via Renormalization. Symmetry, 12(3), 430. https://doi.org/10.3390/sym12030430




