Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model
Abstract
1. Introduction
2. Preliminary
2.1. Conformable Fractional Operator
- 1.
- ;
- 2.
- ;
- 3.
- ;
- 4.
- 5.
- 6.
- 7.
- ; and f is -differentiable at .
2.2. Entropy Generation of Mechanical Systems
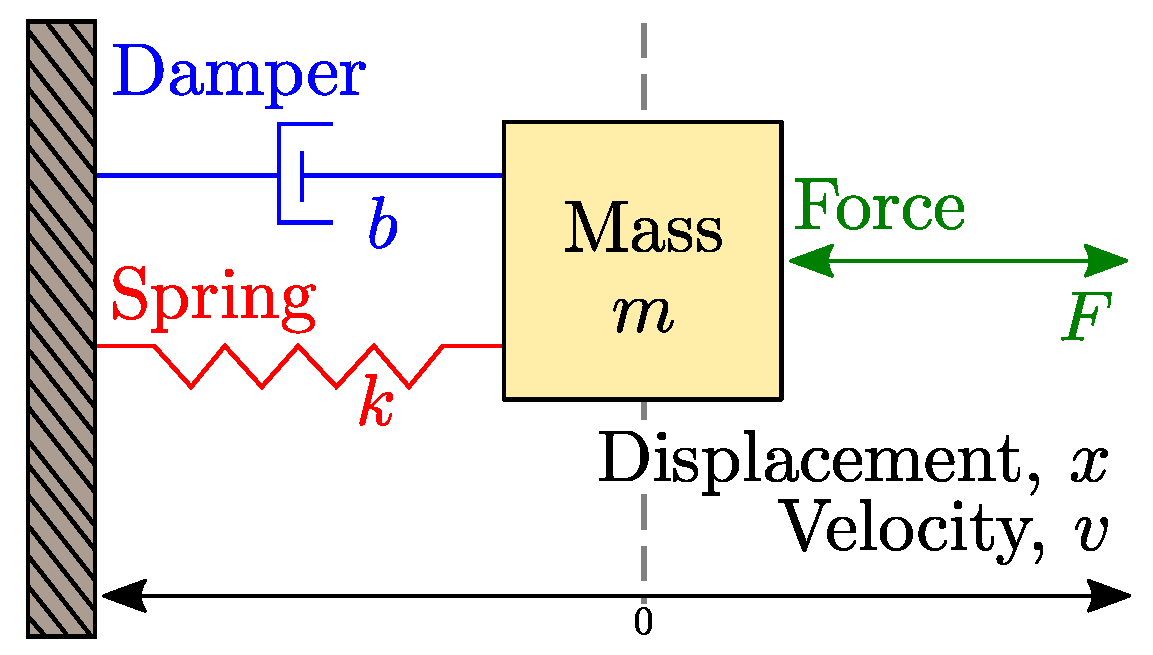
3. Mathematical Models
3.1. Ordinary Model
3.2. Fractional Model
3.3. Conformable Model
3.4. Entropy Production Rate Model
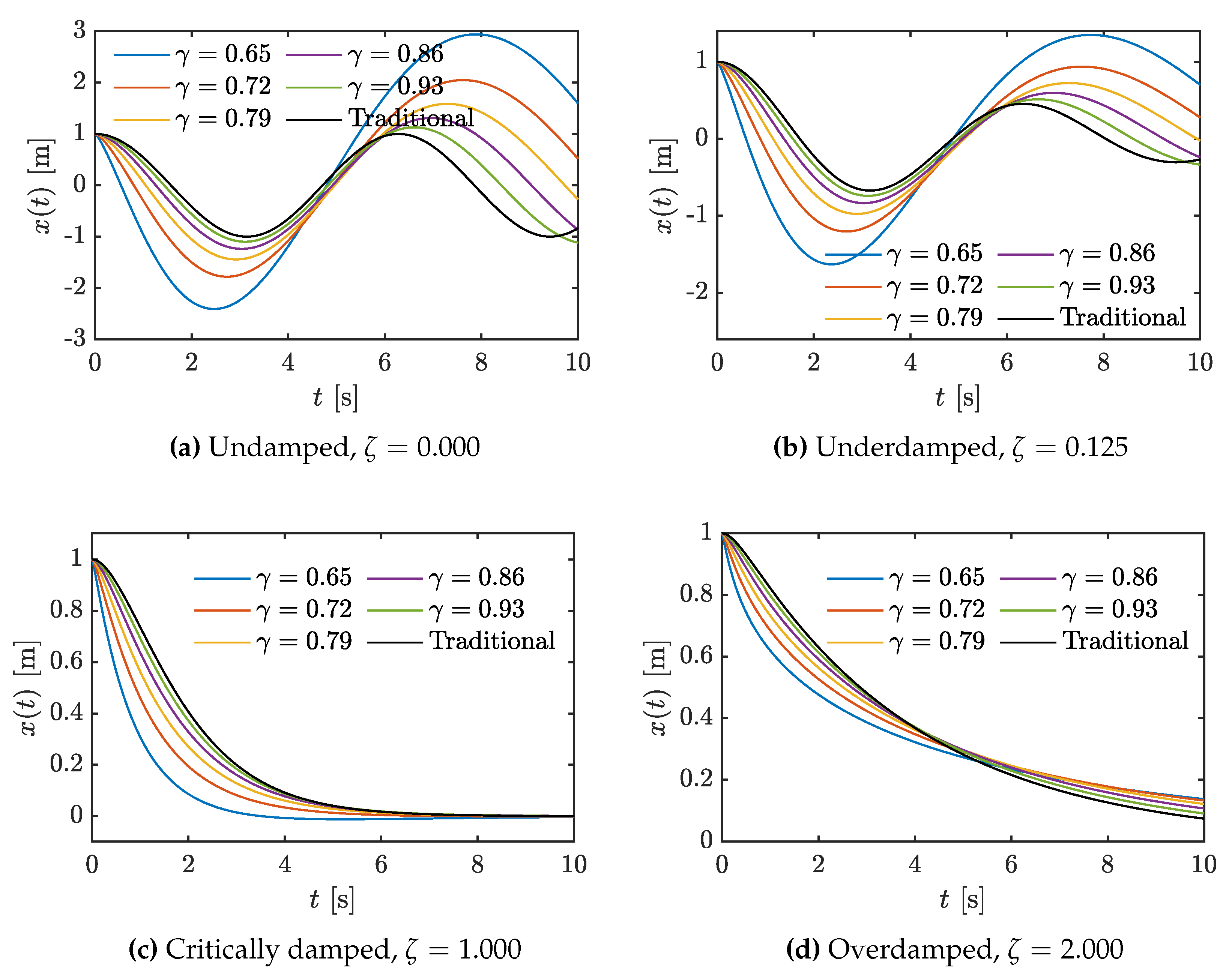
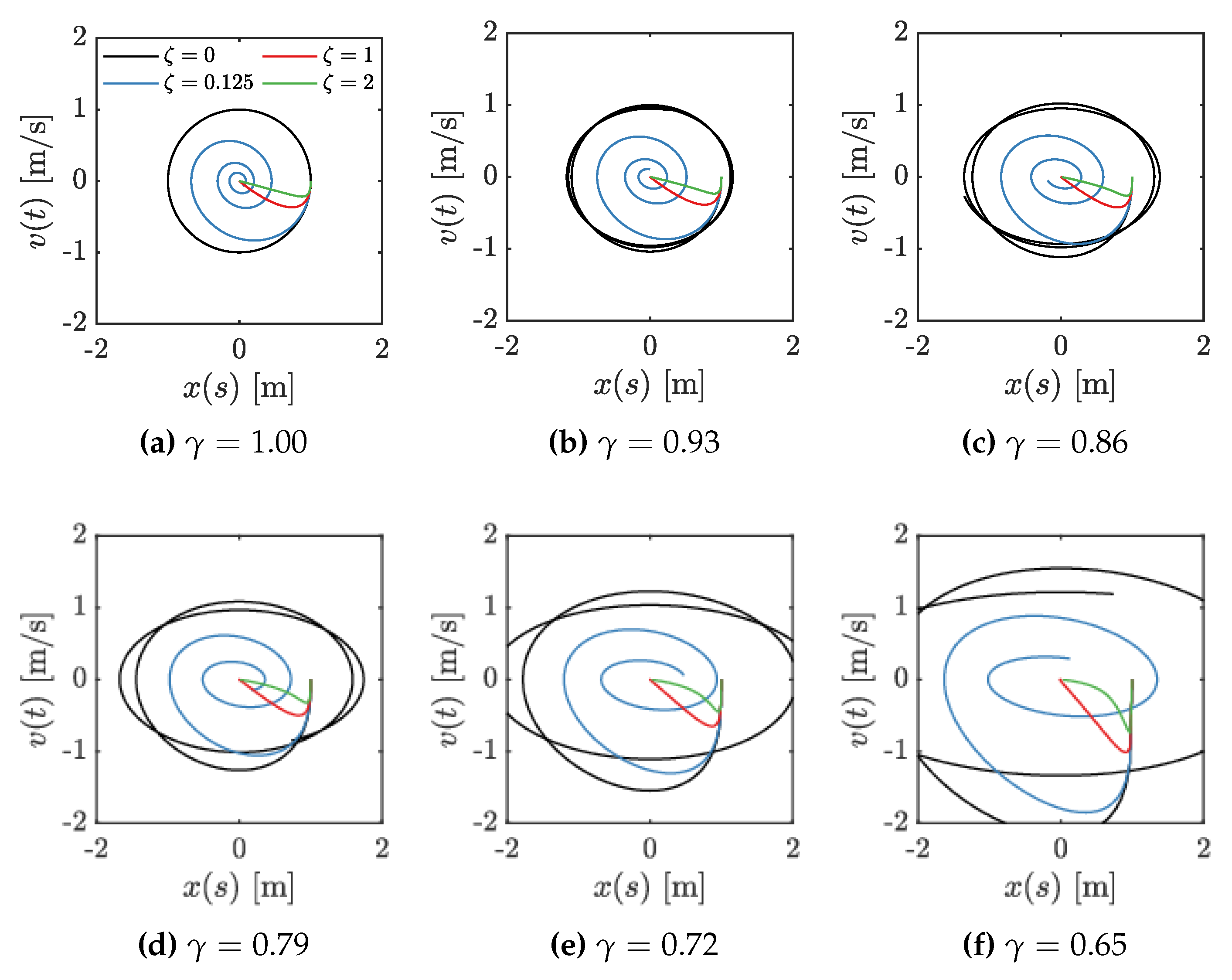
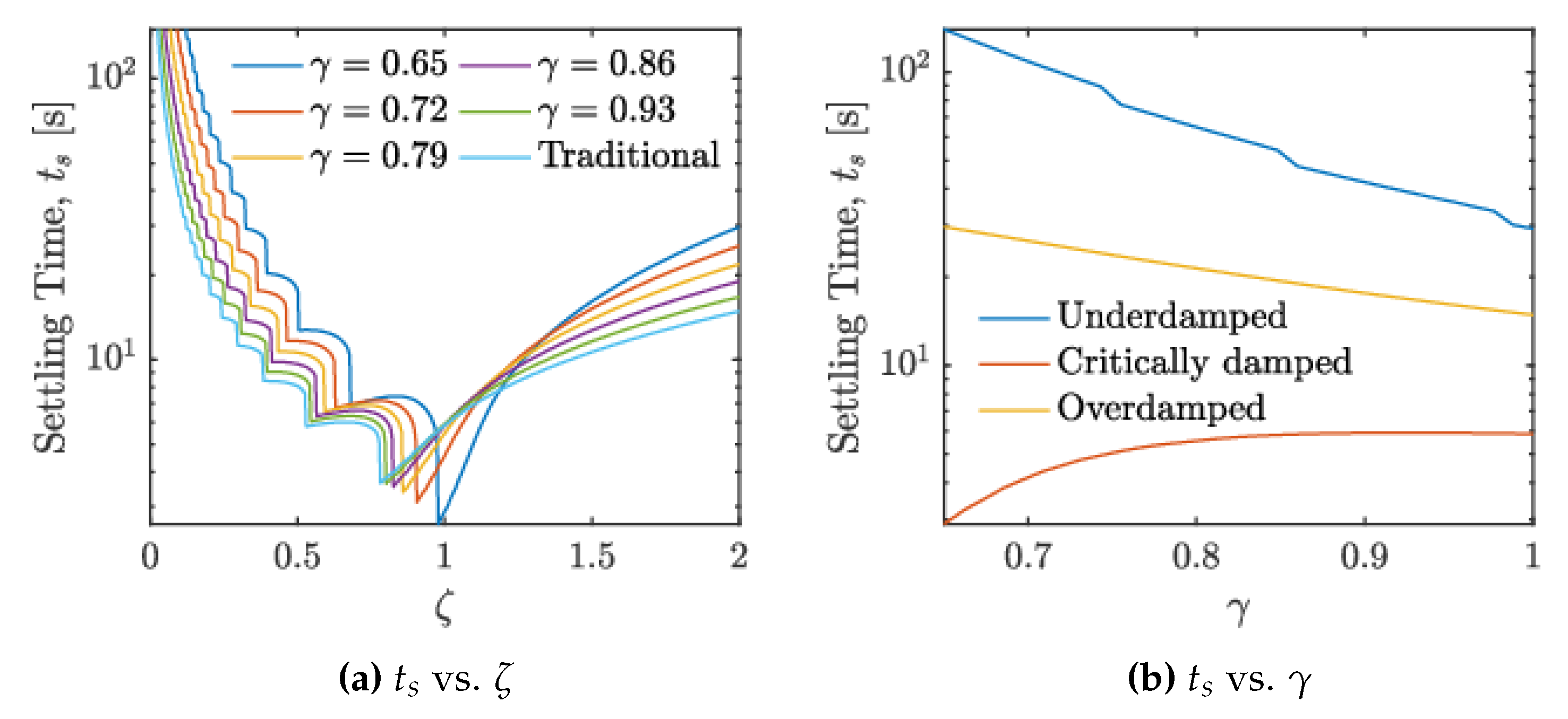
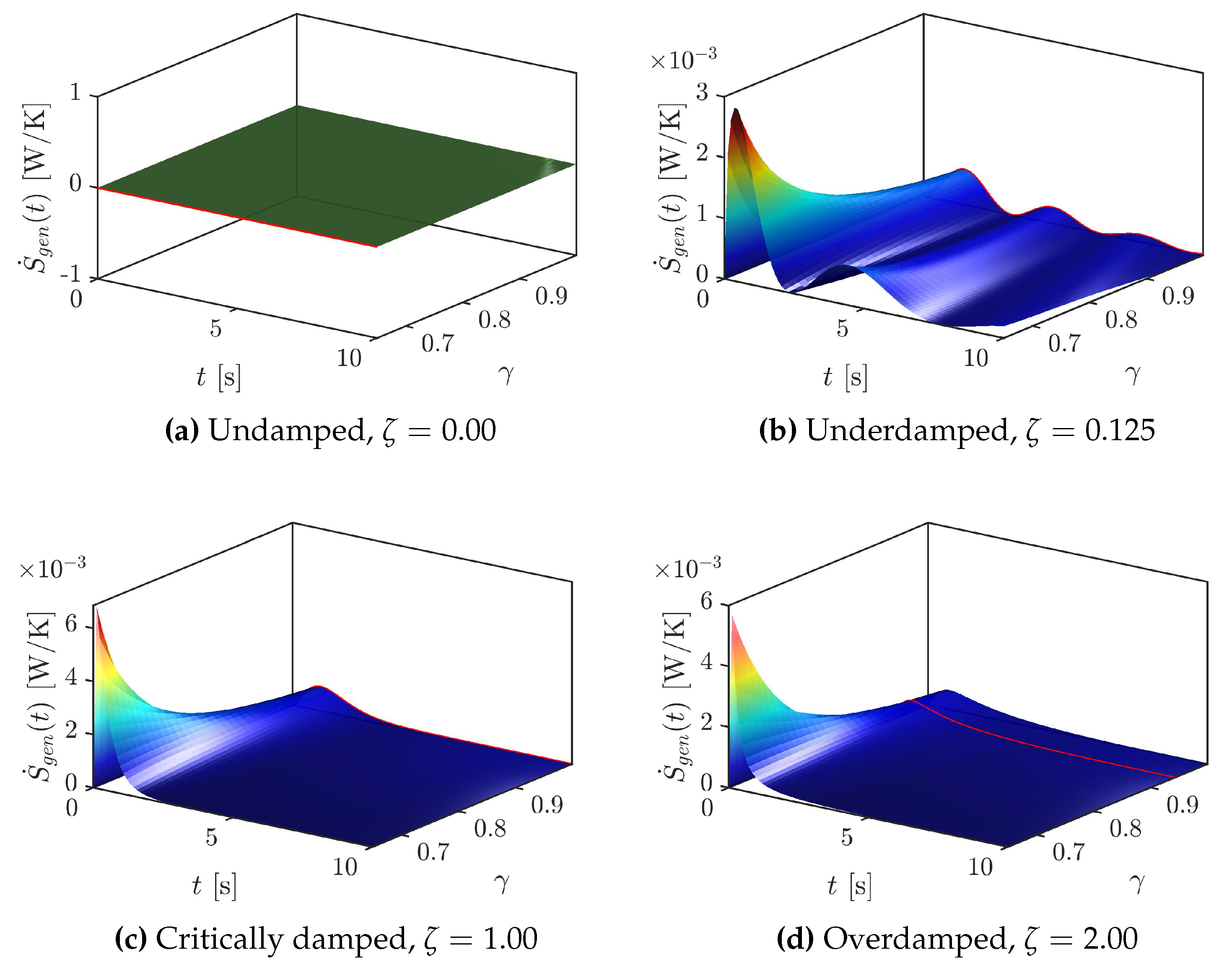
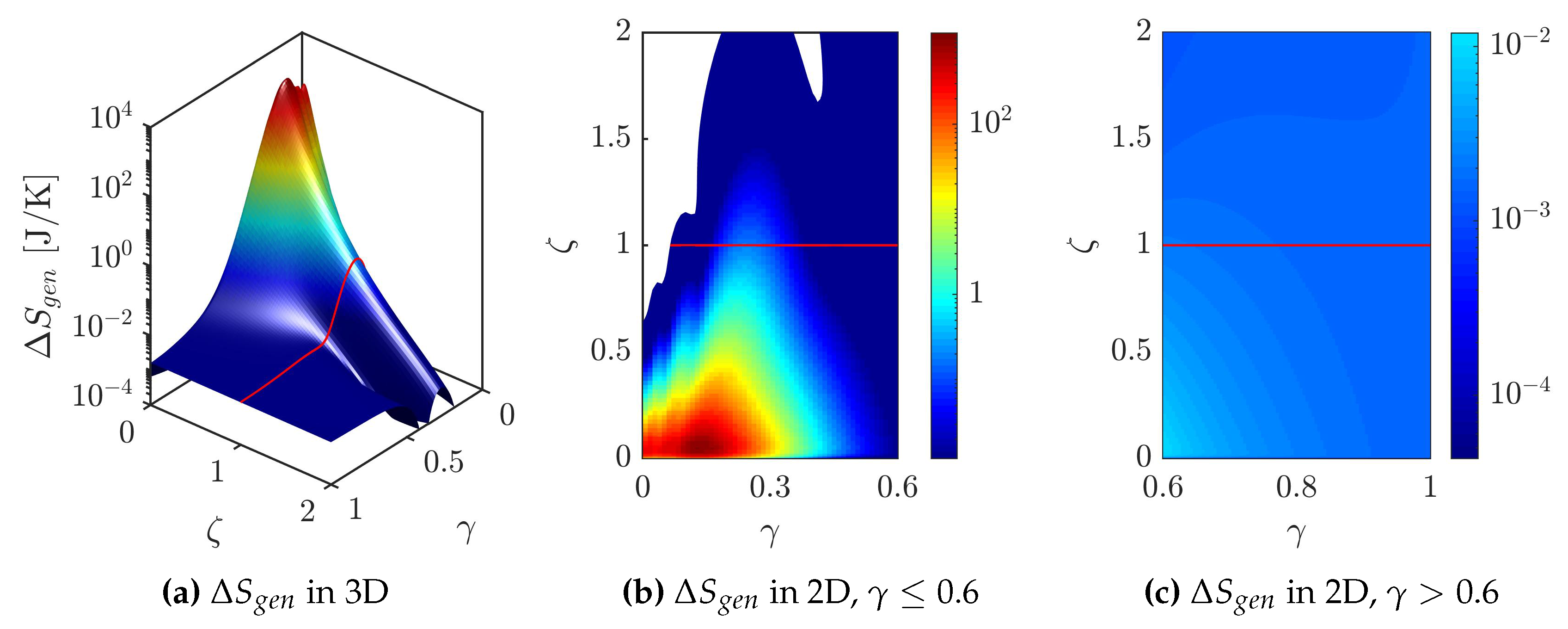
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bai, W.; Dai, J.; Zhou, H.; Yang, Y.; Ning, X. Experimental and analytical studies on multiple tuned mass dampers for seismic protection of porcelain electrical equipment. Earthq. Eng. Eng. Vib. 2017, 16, 803–813. [Google Scholar] [CrossRef]
- Son, L.; Bur, M.; Rusli, M. A new concept for UAV landing gear shock vibration control using pre-straining spring momentum exchange impact damper. J. Vib. Control 2018, 24, 1455–1468. [Google Scholar] [CrossRef]
- Kim, S.M. Lumped element modeling of a flexible manipulator system. IEEE/ASME Trans. Mechatron. 2015, 20, 967–974. [Google Scholar] [CrossRef]
- Wang, D.; Mu, C. Adaptive-critic-based robust trajectory tracking of uncertain dynamics and its application to a spring–mass–damper system. IEEE Trans. Ind. Electron. 2017, 65, 654–663. [Google Scholar] [CrossRef]
- Derakhshandeh, J.F.; Arjomandi, M.; Cazzolato, B.S.; Dally, B. Harnessing hydro-kinetic energy from wake-induced vibration using virtual mass spring damper system. Ocean Eng. 2015, 108, 115–128. [Google Scholar] [CrossRef]
- Takeya, K.; Sasaki, E.; Kobayashi, Y. Design and parametric study on energy harvesting from bridge vibration using tuned dual-mass damper systems. J. Sound Vib. 2016, 361, 50–65. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.T. (Eds.) New Trends in Nanotechnology and Fractional Calculus Applications; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- De Oliveira, E.C.; Tenreiro Machado, J.A. A review of definitions for fractional derivatives and integral. Math. Prob. Eng. 2014, 2014, 238459. [Google Scholar] [CrossRef]
- Machado, J.T.; Mainardi, F.; Kiryakova, V. Fractional calculus: Quo vadimus? (Where are we going?). Fract. Calc. Appl. Anal. 2015, 18, 495–526. [Google Scholar]
- Duarte Ortigueira, M. Fractional Calculus for Scientists and Engineers; Springer: Berlin, Germany, 2011. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013; Volume 2. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and non-singular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Genesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O.C. New exact solutions of Burgers’ type equations with conformable derivative. Waves Random Complex Media 2017, 27, 103–116. [Google Scholar] [CrossRef]
- Morales-Delgado, V.; Gómez-Aguilar, J.; Taneco-Hernández, M. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville-Caputo sense. Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Ertik, H.; Calik, A.E.; Sirin, H.; Sien, M.; Oder, B. Investigation of electrical RC circuit within the framework of fractional calculus. Rev. Mex. Fis. 2015, 61, 58–63. [Google Scholar]
- Abdeljawad, T.; Al-Horani, M.; Khalil, R. Conformable fractional semigroups of operators. J. Semigroup Theory Appl. 2015, 7, 1–9. [Google Scholar]
- Ortega, A.; Rosales, J.J.; Martínez, L.; Cruz-Duarte, J.M. Analysis of projectile motion in view of conformable derivative. Open Phys. 2018, 16, 581–587. [Google Scholar]
- Carreño, C.A.; Rosales, J.J.; Merchán, L.R.; Lozano, J.M.; Godínez, F.A. Comparative analysis to determine the accuracy of fractional derivatives in modeling supercapacitors. Int. J. Circuit Theory Appl. 2019, 47, 1603–1614. [Google Scholar] [CrossRef]
- Rosales, J.J.; Godínez, F.A.; Banda, V.V.; Valencia, G.H. Analysis of the Drude model in view of the conformable derivative. Optik 2019, 178, 1010–1015. [Google Scholar] [CrossRef]
- Ortigueira, M.D.; Tenreiro Machado, J.A. What is a fractional derivative? J. Comput. Phys. 2015, 293, 4–13. [Google Scholar] [CrossRef]
- Zhao, D.; Li, T. On conformable delta fractional calculus on time scales. J. Math. Comput. 2016, 16, 324–335. [Google Scholar] [CrossRef][Green Version]
- Zhao, D.; Luo, M. General conformable fractional derivative and its physical interpretation. Calcolo 2017, 54, 903–917. [Google Scholar] [CrossRef]
- Tarasov, V.E. No nonlocality. No fractional derivative. Commun. Nonlinear Sci. Numerical Simul. 2018, 62, 157–163. [Google Scholar] [CrossRef]
- Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Dynamics of the fractional oscillator. Phys. A Stat. Mech. Its Appl. 2001, 297, 361–367. [Google Scholar] [CrossRef]
- Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Response characteristics of a fractional oscillator. Phys. A Stat. Mech. Its Appl. 2002, 309, 275–288. [Google Scholar] [CrossRef]
- Achar, B.N.; Hanneken, J.W.; Enck, T.; Clarke, T. Damping characteristics of a fractional oscillator. Phys. A Stat. Mech. Its Appl. 2004, 339, 311–319. [Google Scholar] [CrossRef]
- Berman, M.; Cerderbaum, L. Fractional driven-damped oscillator and its general closed form exact solution. Phys. A Stat. Mech. Its Appl. 2018, 505, 744–762. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization: The new thermodynamics of finite-size devices and finite-time processes. J. Appl. Phys. 1996, 79, 1191–1218. [Google Scholar] [CrossRef]
- Bejan, A. Entropy generation minimization, exergy analysis, and the constructal law. Arab. J. Sci. Eng. 2013, 38, 329–340. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Verda, V.; Sciubba, E. Entropy generation analysis as a design tool—A review. Renew. Sustain. Energy Rev. 2015, 43, 1167–1181. [Google Scholar] [CrossRef]
- Sunar, M.; Sahin, A.Z.; Yilbas, B.S. Entropy generation rate in a mechanical system subjected to a damped oscillation. Int. Exergy 2015, 17, 401–411. [Google Scholar] [CrossRef]
- Rosales, J.; Gómez, J.F.; Guía, M.; Tkach, V. Fractional electromagnetic waves. In Proceedings of the 11th International Conference Laser and Fiber-Optical Networks Modeling, Kharkov, Ukraine, 5–8 September 2011. [Google Scholar]
- Atangana, A.; Baleanu, D.; Alsaedi, A. New properties of conformable derivative. Open Math. 2015, 13, 889–898. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Rosales-García, J.J.; Bernal-Alvarado, J.J.; Córdova-Fraga, T.; Guzmán-Cabrera, R. Fractional mechanical oscillators. Rev. Mex. Física 2012, 58, 348–352. [Google Scholar]
- Gómez, F.; Rosales, J.; Guía, M. RLC electrical circuit of non-integer order. Cent. Eur. Phys. 2013, 11, 1361–1365. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.; Morales-Delgado, V.; Taneco- Hernández, M.; Baleanu, D.; Escobar-Jiménez, R.; Al Qurashi, M. Analytical solutions of the electrical RLC circuit via Liouville–Caputo operators with local and non-local kernels. Entropy 2016, 18, 402. [Google Scholar] [CrossRef]
- Ebaid, A.; Masaedeh, B.; El-Zahar, E. A new fractional model for the falling body problem. Chin. Phys. Lett. 2017, 34, 020201:1-3. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz-Duarte, J.M.; Rosales-García, J.J.; Correa-Cely, C.R. Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model. Symmetry 2020, 12, 395. https://doi.org/10.3390/sym12030395
Cruz-Duarte JM, Rosales-García JJ, Correa-Cely CR. Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model. Symmetry. 2020; 12(3):395. https://doi.org/10.3390/sym12030395
Chicago/Turabian StyleCruz-Duarte, Jorge M., J. Juan Rosales-García, and C. Rodrigo Correa-Cely. 2020. "Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model" Symmetry 12, no. 3: 395. https://doi.org/10.3390/sym12030395
APA StyleCruz-Duarte, J. M., Rosales-García, J. J., & Correa-Cely, C. R. (2020). Entropy Generation in a Mass-Spring-Damper System Using a Conformable Model. Symmetry, 12(3), 395. https://doi.org/10.3390/sym12030395





