Residual Control Chart for Binary Response with Multicollinearity Covariates by Neural Network Model

Abstract

Quality control studies have dealt with symmetrical data having the same shape with respect to left and right. In this research, we propose the residual (r) control chart for binary asymmetrical (non-symmetric) data with multicollinearity between input variables via combining principal component analysis (PCA), functional PCA (FPCA) and the generalized linear model with probit and logit link functions, and neural network regression model. The motivation in this research is that the proposed control chart method can deal with both high-dimensional correlated multivariate data and high frequency functional multivariate data by neural network model and FPCA. We show that the neural network r control chart is relatively efficient to monitor the simulated and real binary response data with the narrow length of control limits.

1. Introduction

The current available quality control research has focused on symmetrical data having the same shape with respect to left and right. Data are getting bigger and highly correlated with each other and have asymmetric (non-symmetric) distributions. Therefore, the quality control is facing difficulty to handle highly correlated data so that we have a hard time to get accurate information from the current available control charts. In order to monitor a process mean vector, there have been a number of multivariate control charts including Hotelling $T^2$ distribution [1], mulvariate CUSUM [2] and multivariate EWMA [3]. These current available multivariate control charts have limitations to handle high-dimensional data because of the complexity of the covariance structure. Neural network based methods have been applied to quality control research areas, but there is no research available for residual (r) control charts for binary asymmetrical data with highly correlated multivariate covariates by using neural network regression model. Hence, this is a motivation to propose the r control chart for binary asymmetrical data with multicollinearity between input variables via principal component analysis (PCA), functional PCA (FPCA), and neural network model. To deal with high correlations among independent variables, [4] proposed Poisson, negative binomial, COM-Poisson-based principal component regression-based r-control charts for monitoring dispersed count data. More detailed information for diverse control charts can be found in [5,6]. The novelties with respect to existing strategies in this research have two things. The first one is that the proposed control chart method can deal with high-dimensional correlated multivariate data by neural network model and the second one is that the proposed control chart method can deal high frequency functional multivariate data by FPCA. One of the applications by the proposed statistical process control is monitoring clinical performance which measures binary asymmetrical data such as mortality with patient medical information.

2. Statistical Methods

In this research, we present regression-based r-control charts combining principal component analysis methods (PCA and FPCA) and binary response regression models (generalized linear model and neural network regression model) for binary asymmetrical data with multicollinearity among independent variables.

2.1. Generalized Linear Model and Neural Network Model for Binary Response Data

To introduce the binary response regression models, the generalized linear model (GLM) should be considered first because GLM is both a generalized and flexible model which can consider binary asymmetrical data. The GLM has the following probability density distribution which comes from the exponential family:

$$g\left(y\right|\lambda ,\delta )=exp\left[\frac{y\left(\lambda \right)-a_2\left(\lambda \right)}{a_1\left(\delta \right)}+a_3(y,\delta )\right]$$

(1)

where we denote the response variable to be y, the location parameter to be $\lambda$, the dispersion parameter to be $\delta$, and arbitrary functions to be $a_1(·)$, $a_2(·)$, and $a_3(·)$. We denote $\zeta$ to be the linear predictor for the response, $\mathbf{y}$ so that $\zeta$ is a linear combination of unknown parameters $\mathbf{b}={({\mathbf{b}}_{\mathbf{0}},{\mathbf{b}}_{\mathbf{1}},\dots ,{\mathbf{b}}_{\mathbf{p}})}^{\prime }$ and input variables $\mathbf{x}={(\mathbf{1},{\mathbf{x}}_{\mathbf{1}},\dots ,{\mathbf{x}}_{\mathbf{p}})}^{\prime }$. A link function f such that $E\left(\mathbf{y}\right)={\mathbf{f}}^{-\mathbf{1}}\left(\zeta \right)$ provides the relationship between the linear predictor and the mean of the distribution function. The link function $f(·)$ specified how to convert the expected value $\mu =E\left(\mathbf{y}\right)$ to the linear predictor $\zeta$: i.e.,

$$\zeta =f\left(\mu \right)={\mathbf{x}}^{\prime }\mathbf{b}.$$

(2)

Using a logit model as an example, we have

$$Logit\left[P(\mathbf{y}=\mathbf{1}|\mathbf{x})\right]={\mathbf{x}}^{\prime }\mathbf{b},$$

(3)

where b is the column vector of the fixed-effects regression coefficients. For the (3), it can be written as

$$P(\mathbf{y}=\mathbf{1}|\mathbf{x})=\frac{\mathbf{1}}{\mathbf{1}+{\mathbf{e}}^{-{\mathbf{x}}^{\prime }\mathbf{b}}}=\mathbf{m}\left(\mathbf{x}\right)$$

(4)

With the (4), we can derive the likelihood function for GLMs as follows:

$$L\left(\mathbf{b}\right)=\prod _{\mathbf{i}=\mathbf{1}}^{\mathbf{n}}\mathbf{m}{\left({\mathbf{x}}_{\mathbf{i}}\right)}^{{\mathbf{y}}_{\mathbf{i}}}{\{\mathbf{1}-\mathbf{m}\left({\mathbf{x}}_{\mathbf{i}}\right)\}}^{\mathbf{1}-{\mathbf{y}}_{\mathbf{i}}}.$$

(5)

and so the log-likelihood function is given by

$$l\left(\mathbf{b}\right)=log\mathbf{L}\left(\mathbf{b}\right)=\sum _{\mathbf{1}=\mathbf{1}}^{\mathbf{n}}[{\mathbf{y}}_{\mathbf{i}}log\mathbf{m}\left({\mathbf{x}}_{\mathbf{i}}\right)+(\mathbf{1}-{\mathbf{y}}_{\mathbf{i}})log\{\mathbf{1}-\mathbf{m}\left({\mathbf{x}}_{\mathbf{i}}\right)\}].$$

(6)

Then the maximum-likelihood estimating equation for $\mathbf{b}$ is easily solved via standard softwares (e.g., SAS or R) using the Fisher scoring or Newton-Raphson method.

The GLM with probit link function requires the assumptions that the response is binary and that an underlying latent variable governing the binary process follows a normal distribution. In some cases the GLMs with probit link function can probably gives best goodness-of-fit of the test where response variables are assumed to have normal distributions [7] because the response probability distribution of the GLMs belongs to an exponential family of distributions which employ the methods analogous to the normal linear methods for the normal data [8,9]. Therefore, for asymmetrical (non-normal) distributed data, the GLM with probit link function may not be the best model. Hence, this is another motivation to propose a neural network model based on r control chart for the better predictive accuracy with the non-normal data.

An artificial neural network (ANN) is originally inspired from human brain and ANN resembles biological neural networks which imitate human brain activity through a computer simulations [10,11,12]. Physically, an ANN contains neurons connected by synapses that connected them. The ANN learning process heavily relies on both weights of the connections between the neurons specifying which variables involved in the network and activities of the neurons. The weights are computed by optimizing a learning algorithm. The ANN uses the concept of competition to select the highest probability of inhibiting all neurons [10,11,12]. Specifically, the most basic form of an ANN is a single layer feedforward type of connection among neurons. ANNs have input layers and multiple hidden layers. Lastly, the hidden layers are connected to the output layer, which produces the outputs. In the last decade, the ANN-based statistical process control research has been actively studied. Research papers such as [13] proposed the pattern recognition for bivariate process mean shifts using feature-based ANN and [14] proposed control chart pattern recognition using Radial Basis Function (RBF) neural networks. Recently, [15] proposed statistical process control with Intelligence Based on the Deep Learning Model and reviewed the neural network-based statistical process control. In this paper, we used ’nnet’ R packge [16] for feed-forward neural networks with a single hidden layer, and for multinomial log-linear models. With repeated simulated data (each sample size 1,000 and 10,000 different replications for the case of PCA and each sample size 1000 and 30 different replications for the case of FPCA) and real data, we employed single layer and 30 neurons for the simulation study and real data analysis.

The r-control charts for binary response data uses the GLM models with logit and probit link functions and neural network models employ deviance residuals being independent and asymptotically normally distributed with zero mean and unit variance, i.e., $r_i\sim N(0,1)$ for $i=1,\dots ,n$. In this research, we chose a deviance residual for the GLM models with logit and probit link functions and a neural network model because the R packages for the GLM models with logit and probit link functions and neural network model have a command for producing the deviance residual. It is easy to compare the residuals from both models which are the GLM-based model and neural network model. Ref. [17] proposed Shewhart control limits for the deviance residuals are

$$E\left(r_i\right)\pm k\sqrt{Var\left(r_i\right)}\approx \pm k$$

(7)

where k is defined by the false alarm probability, $\alpha =1/AR{L}_0$, and $AR{L}_0$ is the average run length (ARL) under the process in-control. The ARL is a measure of the performance of control charts for monitoring a process.

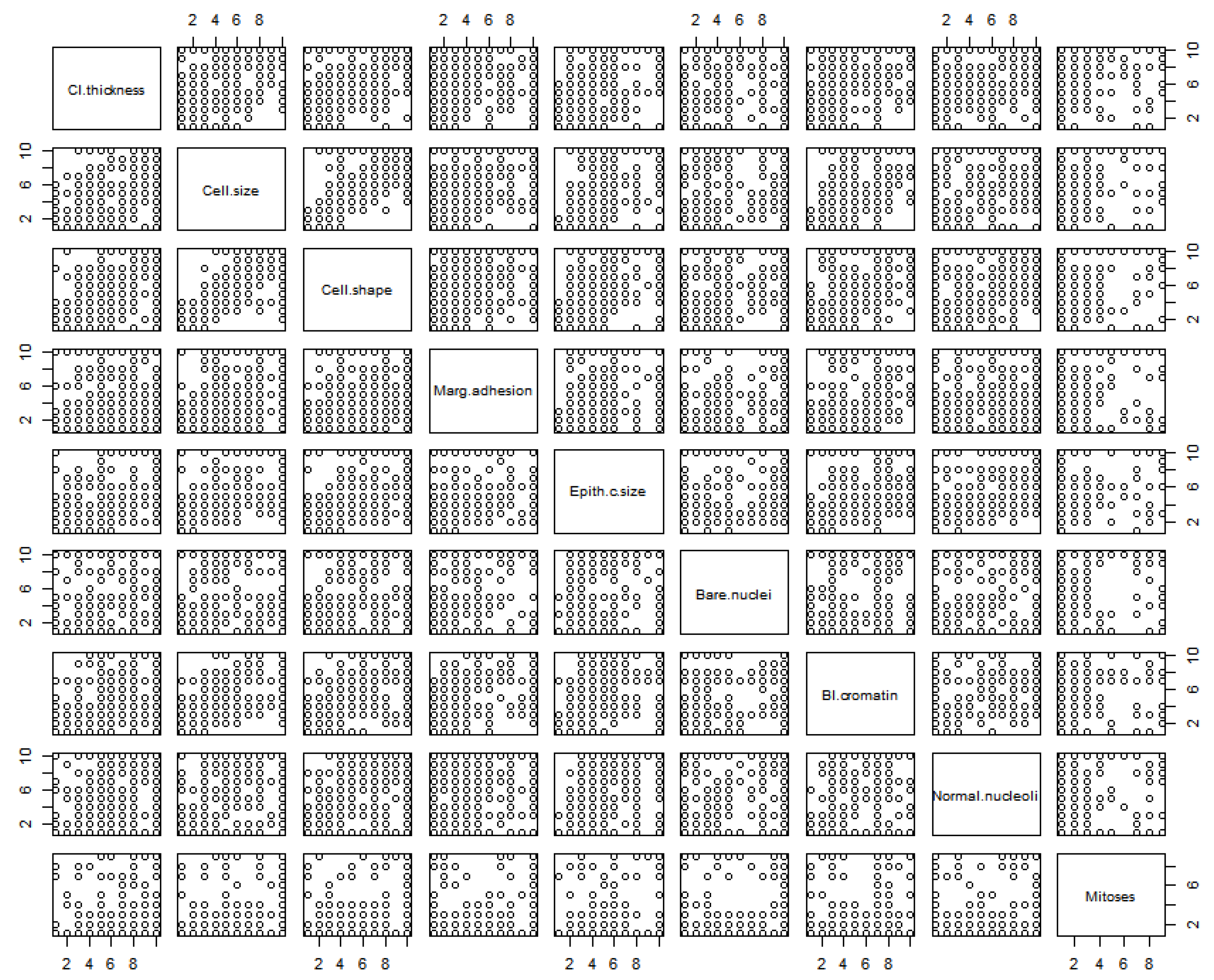
2.2. Dimension Reduction by Principal Component Analysis

The principal component analysis (PCA) is a statistical orthogonal transformation method converting multivariate data set of correlated variables into a set of values of linearly uncorrelated variables called principal components. Hence, the PCA is the most common dimension reduction statistical method which can reduce the dimensionality of multivariate data to the smaller uncorrelated principal components which account for the variation of the original data. The r control chart for binary response regression model with primary principal components by the PCA is a new statistical process control which monitors the binary response variable as a function of uncorrelated PCs. In this paper, we propose a binary response regression model-based r control charts for binary response data overcoming a multicollinearity issue among independent variables.

To verify our proposed method in terms of the model flexibility and performance, we have run simulations for various circumstances: in-control, one inflated, or zero inflated binary data. Through both simulation study and a real data example, we illustrated the good performance of our proposed method.

Ref. [4] denotes $\mathbf{X}$ to be an $n\times q$ matrix of independent variables and $\mathbf{W}$ be the standardized matrix of $\mathbf{X}$ so that each column has mean 0 and standard deviance 1. Let $\mathbf{Q}$ be the matrix of eigenvectors of ${\mathbf{W}}^{\prime }\mathbf{W}$ and $\mathbf{D}$ be the diagonal matrix with eigenvalues of ${\mathbf{W}}^{\prime }\mathbf{W}$ on the diagonal and values of zero everywhere else. Hence, we sort the eigenvalues from largest to smallest such as ${\lambda }_1>{\lambda }_2>\dots >{\lambda }_q$ and sort the eigenvectors in $\mathbf{Q}$ accordingly, and let ${\mathbf{Q}}^{*}$ be this sorted matrix of eigenvectors. Then, the principal components, ${\mathbf{W}}^{*}$, are given by

$${\mathbf{W}}^{*}={\mathbf{WQ}}^{*}.$$

(8)

We can perform a dimensional reduction to the uncorrelated variables ${\mathbf{W}}^{*}$ from the original multivariate high correlated data. Our proposed procedure uses these uncorrelated variables ${\mathbf{W}}^{*}$ to perform GLM with probit, GLM with logit, and neural network regression models.

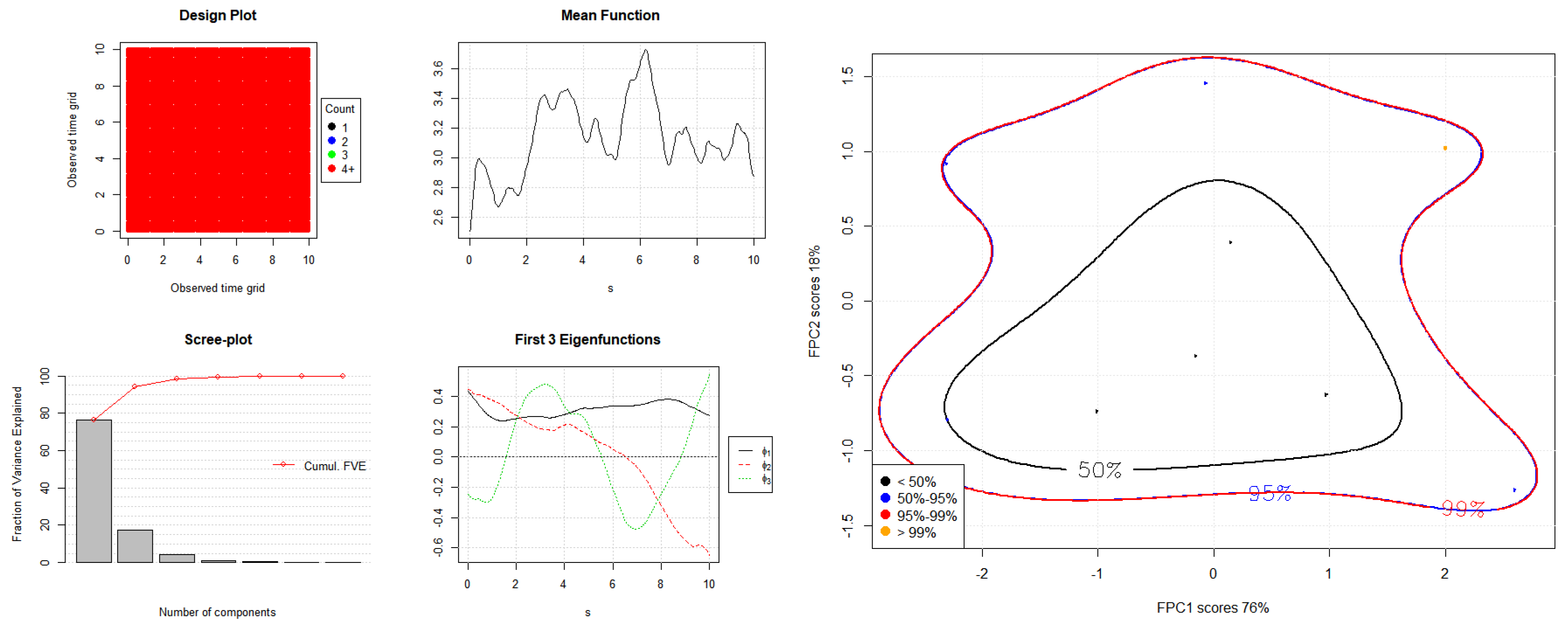
2.3. Dimension Reduction by Functional Principal Component Analysis

Ref. [18] proposed a functional PCA (FPCA) for functional data, which is another dimensional reduction statistical method for explaining the variance of components by using non-liner eigenfunctions and for the multivariate highly correlated data, because FPCA overcomes the high-dimensionality difficulty and efficiently examines the sample covariance structure.

The functional form of $y_i\left(t\right)$ is given by the sum of the weighted basis functions, ${\varphi }_p\left(t\right)$, across the set of times T.

$$\begin{array}{c}\hfill y_i\left(t\right)=\sum _{k=1}^P{c}_{ip}{\varphi }_p\left(t\right),\end{array}$$

(9)

where P is a number of basis functions. In this study, a Fourier basis is used to represent smooth functions as a basis function due to its flexibility and computational advantages. Here, our goal is to obtain a smooth function which fits well into the observed time series, $y_i\left(t_j\right)$. For calculating functional PCA, we employ ’fdapace’ R package [19]. This package is for functional principal component analysis (FPCA) via the principal analysis by the conditional estimation (PACE) algorithm which yields covariance and mean functions, eigenfunctions and principal component (scores). PACE provides fitted continuous trajectories with confidence bands [20,21].

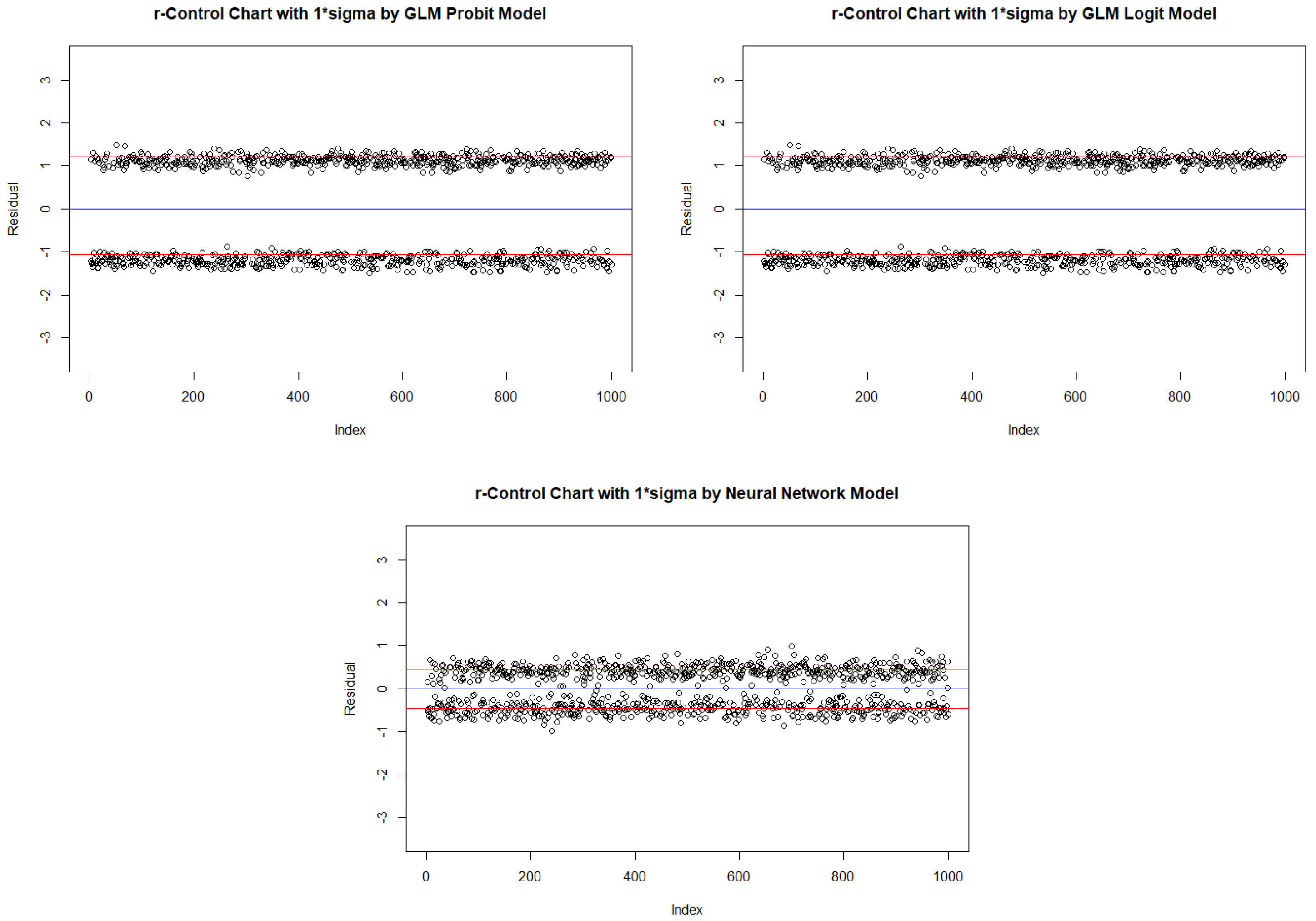
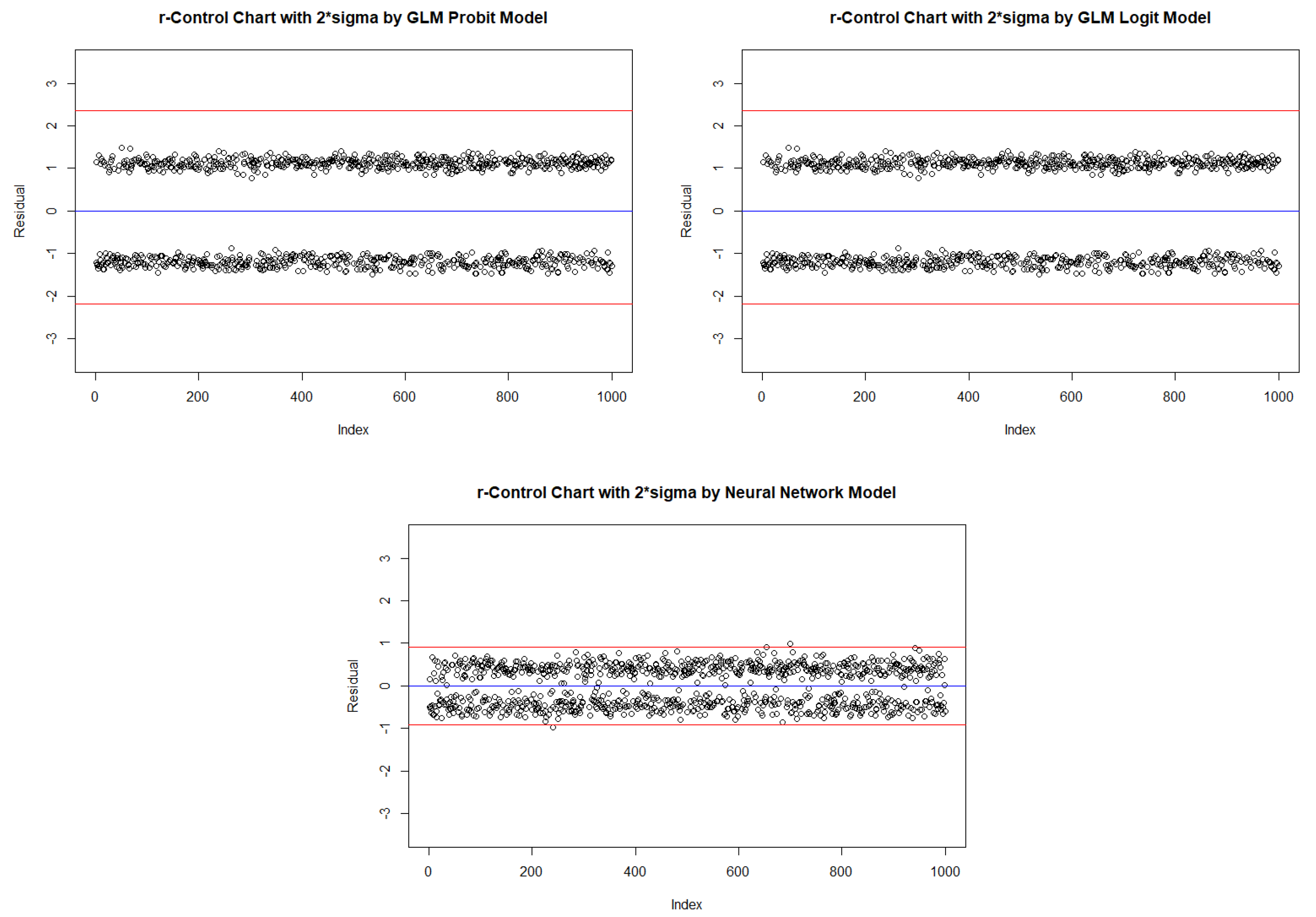
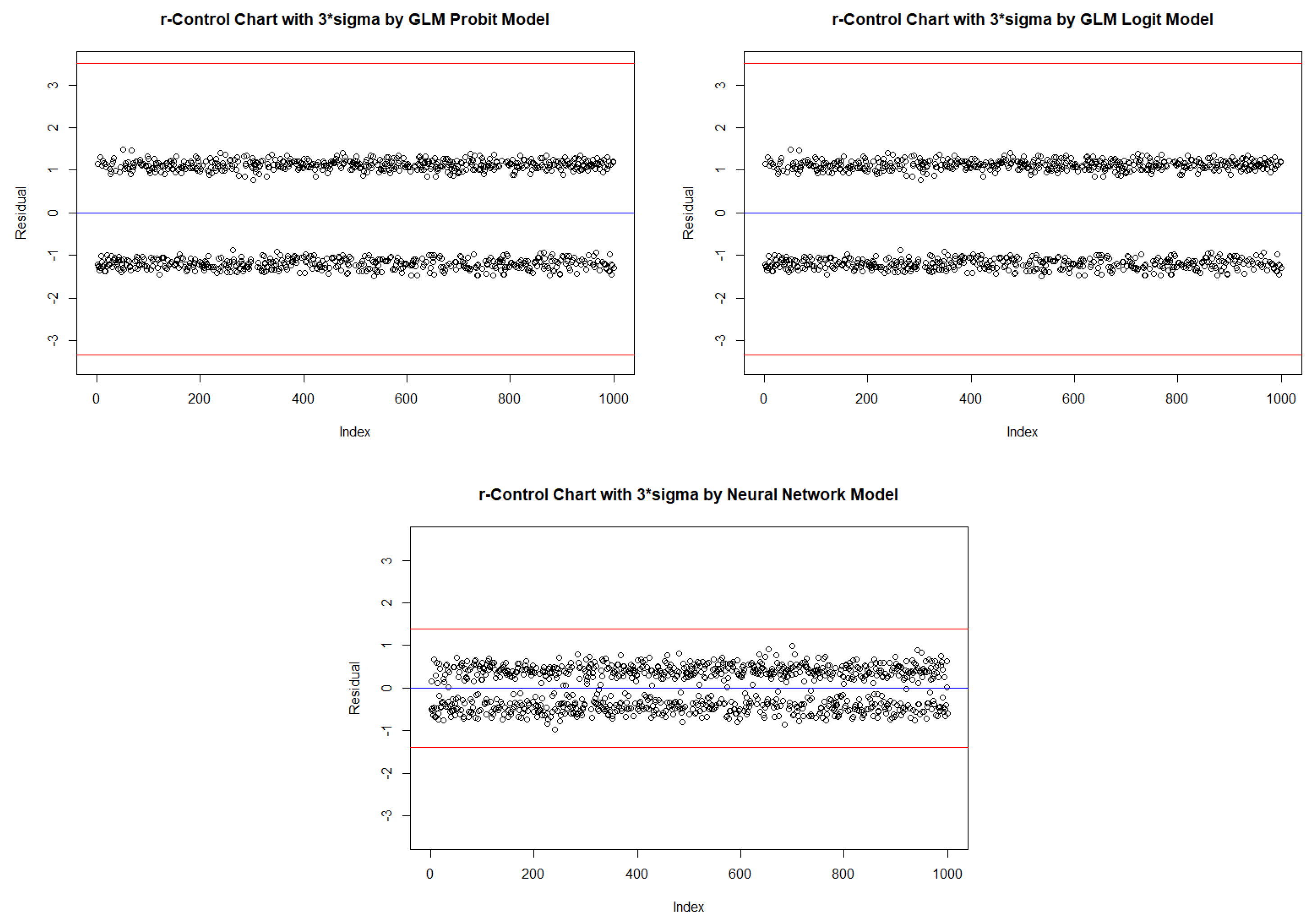
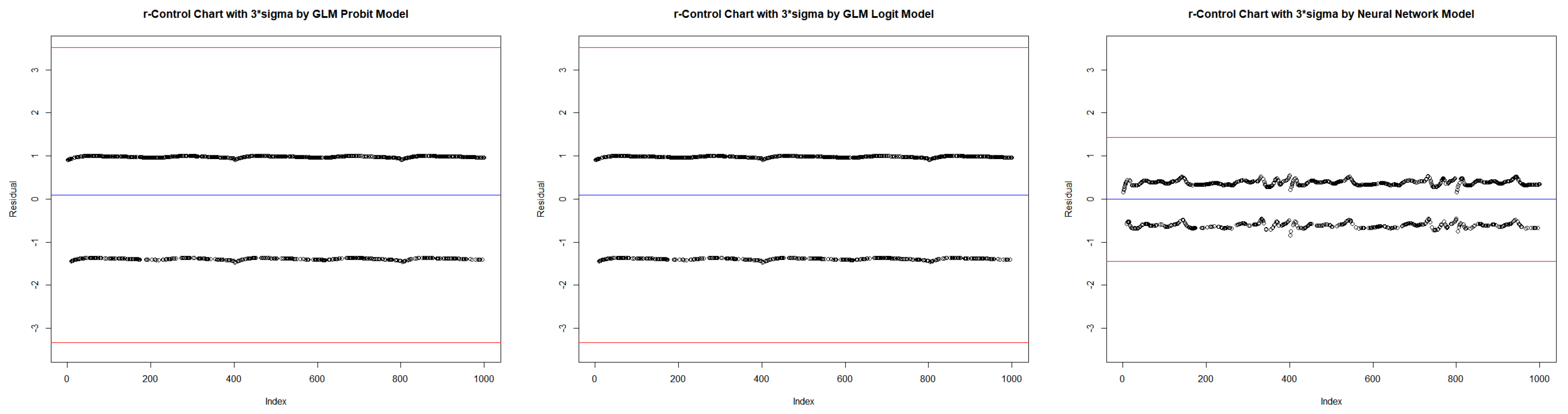
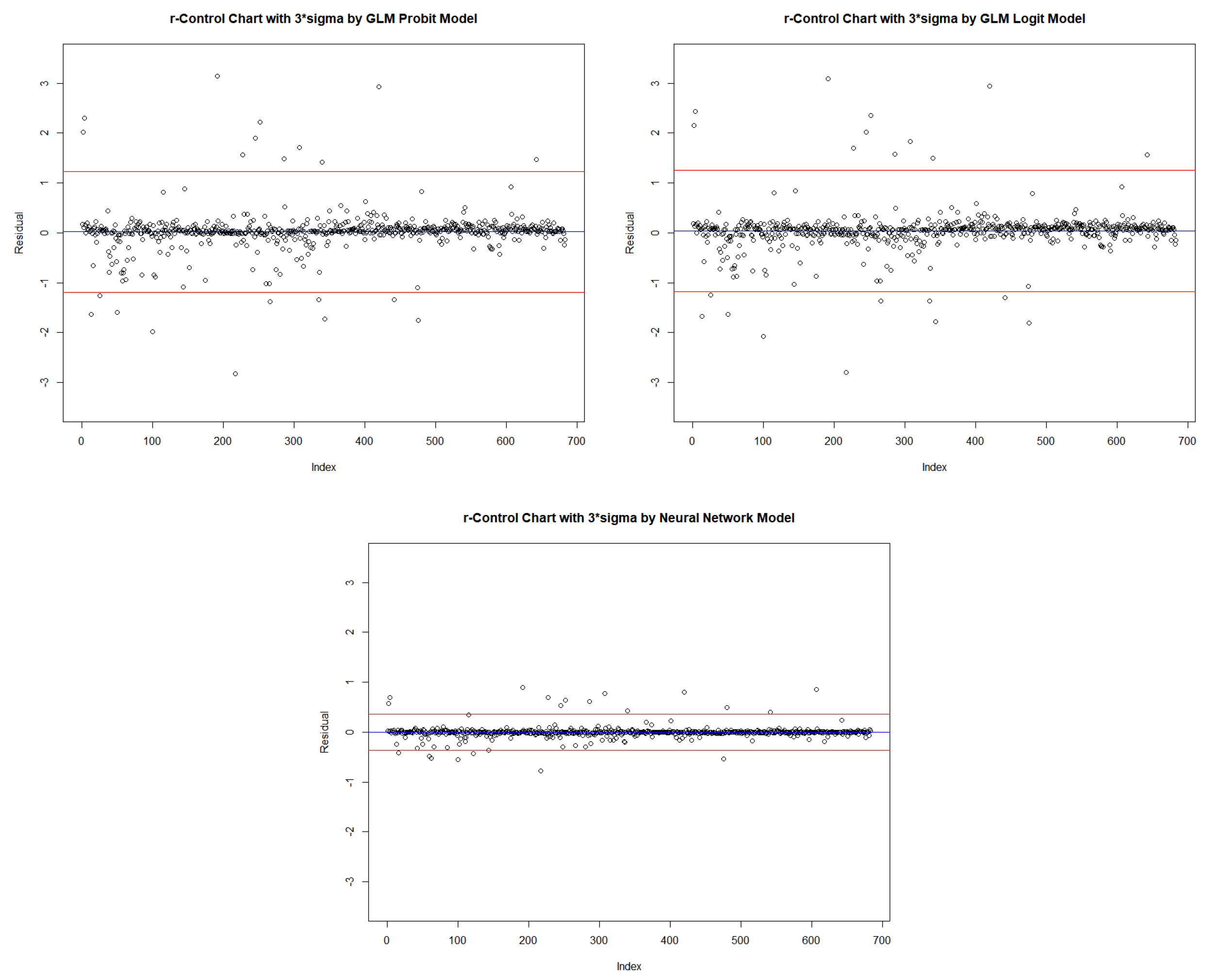
2.4. New Binary response statistical process control Procedure

A new binary response statistical process control procedure for the deviance residuals, r, from binary response regression models that have high correlated multivariate covariates is proposed through the following steps:

• Apply the (functional) principal component analysis in input variables $\mathbf{X}$ and obtain the principal components ${\mathbf{w}}^{*}$ from (8).
• Fit the binary response regression model by using the binary response variable y and the (functional) principal components ${\mathbf{w}}^{*}$ through probit link function, logit link function, and neural network regression models, respectively.
• Obtain the deviance residuals from each model.
• Set k value and obtain the lower and upper control limits of the r-charts using (7).

3. Illustrated Examples

With the proposed method in Section 2, we perform the efficiency comparison among the proposed methods with simulated data and real data.

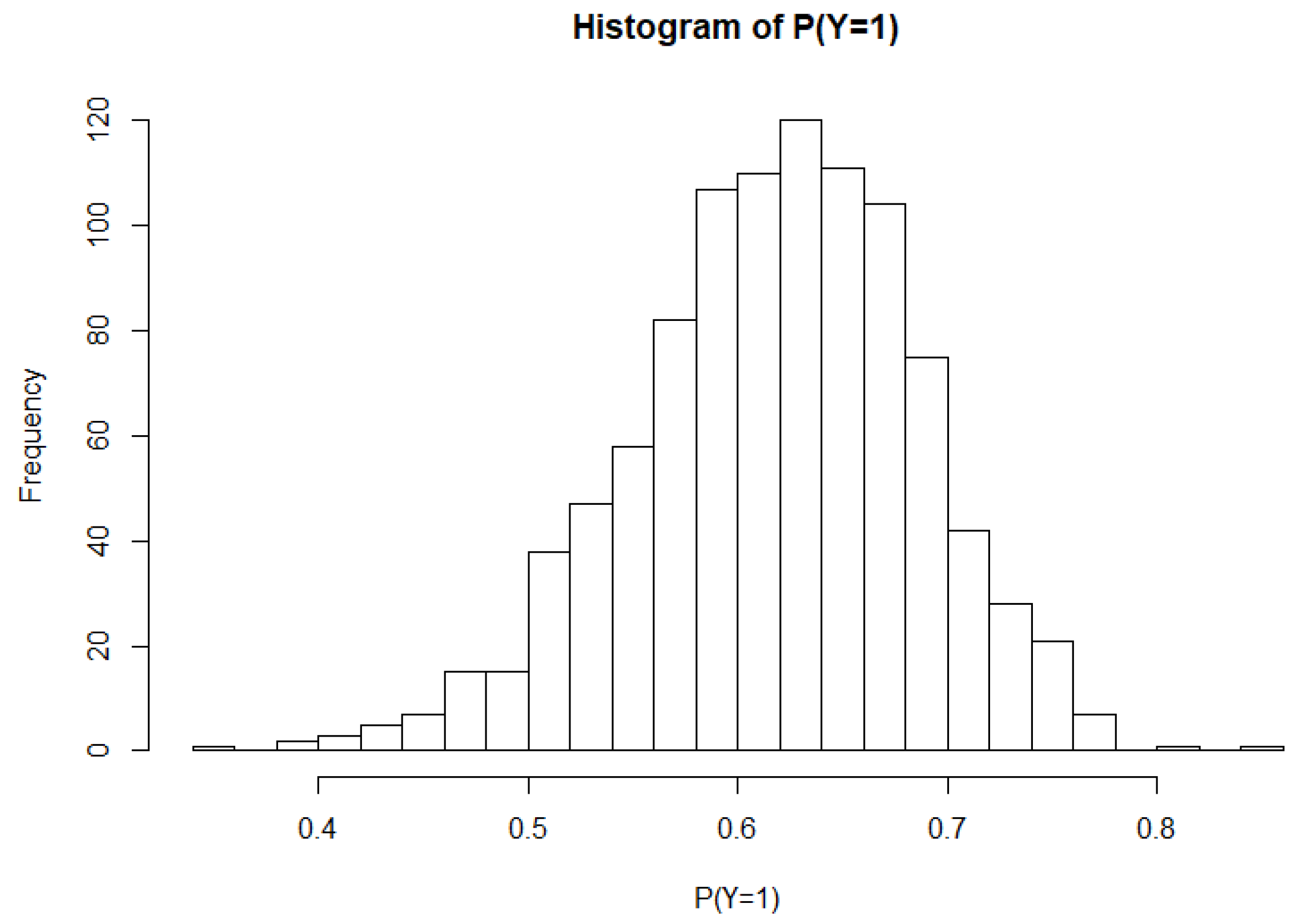
3.1. Simulation Study

In order to compare the r-charts based on binary regression models, we generate simulated data denoting $\mathbf{x}={({\mathbf{x}}_{\mathbf{1}},{\mathbf{x}}_{\mathbf{2}},{\mathbf{x}}_{\mathbf{3}},{\mathbf{x}}_{\mathbf{4}})}^{\prime }$ as input variables which are generated from the multivariate normal distribution with mean $(1,\overrightarrow{2,3},4{)}^{\prime }$ and covariance matrix M as follows:

$$M=\left[\begin{array}{cccc}1& 0.9& 0.2& 0.1\\ 0.9& 1& 0.4& 0.3\\ 0.2& 0.4& 1& 0.7\\ 0.1& 0.3& 0.7& 1\end{array}\right]$$

With each simulated data $\mathbf{x}$, we define the coefficients of parameters ($\beta$’s) to be ${\beta }_0=0.1$, ${\beta }_1=0.25$, ${\beta }_2=-0.5$, ${\beta }_3=0.25$, ${\beta }_4=0.1$ so that $P(y=1)=\frac{1}{1+exp(-0.1-0.25x_1+0.5x_2-0.25x_2-0.1x_4))}$ which passes through an inverse logit function. Then, we generate response variable y randomly by using the Bernoulli distribution with the probability $P(y=1)$ with sample size 1000. For the one (‘1’) inflated case of binary response data, we added 0.1 to the probability $P(y=1)$ such as $P(y=1)+0.1$ and for the zero (‘0’) inflated case of binary response data, we subtracted 0.1 from the probability $P(y=1)$ such as $P(y=1)-0.1$. Also, $P(y=1)$ is used for the in-control dispersion case. In each setup, we perform 10,000 different replications of sample size of 1000.

Table 1. Based on PCA, the coverage probability, expected confidence interval (CI) length, and control limits for the simulated in-control, one inflated-, and zero inflated-dispersion binary data via various r-charts based on GLM with probit, GLM with logit, and neural network models. Neural network model used single layer and 30 neurons. ‘NA’ in the table means that there is no points out of control limits and the number of simulations is 10,000 different replications of sample size of 1000.

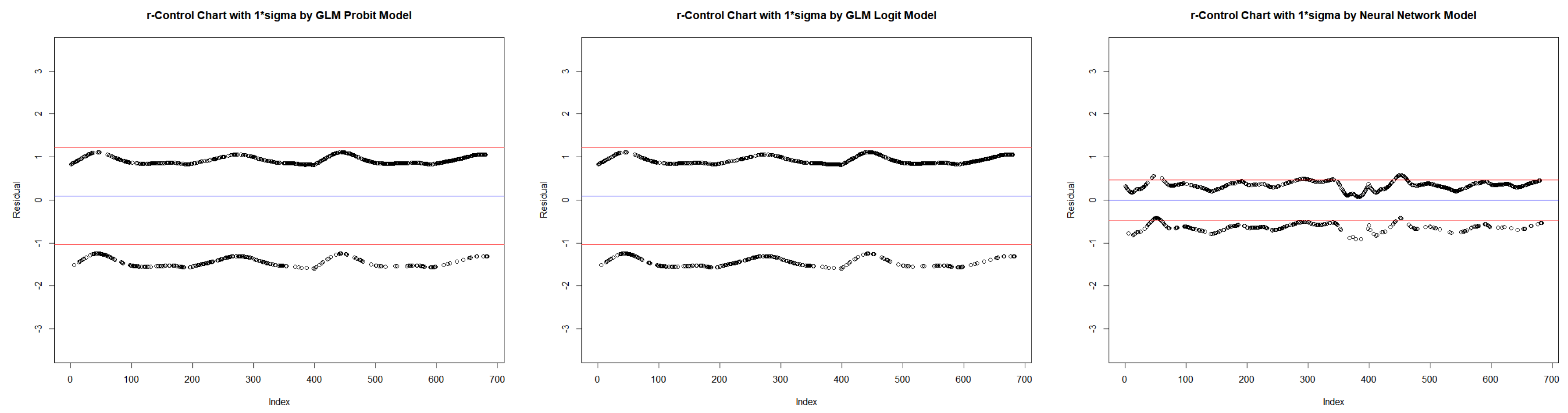
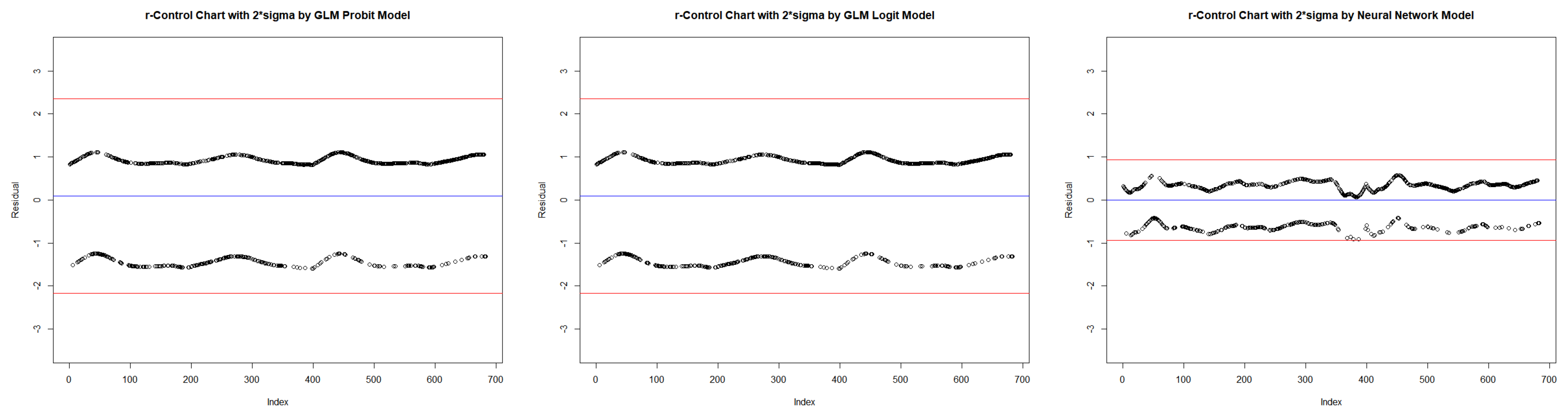
		Probit			Logit			Neural Network
Case	$\mathit{E}\left({\mathit{r}}_{\mathit{i}}\right)\pm \mathit{w}\sqrt{\mathit{V}\mathit{a}\mathit{r}\left({\mathit{r}}_{\mathit{i}}\right)}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$
In-control	ARL	2.590	520.152	NA	2.586	536.938	NA	2.453	322.806	NA
	Center	0.013	0.013	0.013	0.013	0.013	0.013	0.000	0.000	0.000
	LCL	−1.063	−2.202	−3.340	−1.063	−2.201	−3.340	−0.455	−0.911	−1.366
	UCL	1.215	2.354	3.492	1.215	2.354	3.492	0.455	0.911	1.366
	CI Length	2.278	4.555	6.833	2.278	4.555	6.833	0.911	1.821	2.732
	Coverage	0.610	1.000	1.000	0.610	1.000	1.000	0.591	0.998	1.000
One Inflated	ARL	3.532	291.492	NA	3.528	302.546	NA	3.094	62.599	429.500
	Center	0.013	0.013	0.013	0.013	0.013	0.013	0.000	0.000	0.000
	LCL	−0.934	−2.002	−3.069	−0.934	−2.002	−3.069	−0.421	−0.842	−1.263
	UCL	1.200	2.268	3.335	1.200	2.268	3.335	0.421	0.842	1.263
	CI Length	2.135	4.269	6.404	2.135	4.269	6.404	0.842	1.684	2.527
	Coverage	0.717	0.997	1.000	0.717	0.998	1.000	0.677	0.981	1.000
Zero Inflated	ARL	2.177	NA	NA	2.178	NA	NA	2.197	429.347	NA
	Center	0.013	0.013	0.013	0.013	0.013	0.013	0.000	0.000	0.000
	LCL	−1.154	−2.320	−3.486	−1.154	−2.320	−3.486	−0.469	−0.938	−1.406
	UCL	1.179	2.345	3.512	1.179	2.345	3.512	0.469	0.938	1.406
	CI Length	2.333	4.665	6.998	2.333	4.665	6.998	0.938	1.875	2.813
	Coverage	0.536	1.000	1.000	0.536	1.000	1.000	0.555	0.999	1.000

shows the simulation results. By using the deviance residuals for each model and (7) for $k=1,2,3$, we compute the lower control limit (LCL) and upper control limit (UCL) for the process. The expected length of the confidence interval is computed by the average of the length of control limits. The coverage probability is the proportion of the deviance residuals contained in the control limits. The lower control limit and the upper control limit value for r-chart are calculated by means of y minus and plus its one, two and three standard deviations.

The summary statistics of $P(y=1)$ in Figure 1 are that the minimum is 0.3450, the first quartile is 0.5723, the median is 0.6222, the mean is 0.6172, the third quartile is 0.6654 and the maximum is 0.8477. The skewness of $P(y=1)$ is -0.3272 which proves the shape of the simulated data is asymmetry so that it can be more inclined to produce zero value data rather than one value data.

Based on PCA, Table 1 presents the average run length (ARL) results for simulated in-control, one inflated-, and zero inflated-dispersion data via r-charts based on the GLM with probit and logit link function and neural network models. Changes in w that resulted in one, two and three standard deviations from the mean of y are considered. From Table 1, and based on PCA, we can see that the coverage probabilities by the GLMs with probit and logit link functions are slightly greater or equal to the coverage probabilities by the neural network regression model, but the length of the confidence intervals (CIs) for the neural network regression model are much smaller than the the length of the confidence intervals (CIs) for the GLMs with probit and logit link functions and the ARLs of the neural network regression model are much smaller than the the ARLs for the GLMs with probit and logit link function because of the smaller length of CIs.

From Figure 2, Figure 3 and Figure 4 in case of the in-control dispersion based on PCA, we can observe that the residuals of a neural network regression model are much closer to zero than the residuals of the GLM with probit and logit model. Therefore, it is not a surprising result in Table 1 that the r-chart based on the neural network model shows a superiority in all cases in terms of the expected length of the confidence interval. We can say that the r-chart based on the neural network model for monitoring observations has the smallest expected length of the confidence interval with the reasonable coverage probability.

We also see that the r-charts based on the neural network model give the superior performance following the (7), $E\left(r_i\right)\pm k\sqrt{Var\left(r_i\right)}\approx \pm k$ but the r-charts based on the GLM with logit and probit link functions do not give the good performance following the (7). The reason for the difference is probably the tails of the distribution in the GLMs.

For calculating FPCA, we employ ’fdapace’ R package [19] to represent smooth functions with Fourier basis. In order to generate the functional data, we set the number of subjects (N=1000) and the number of measurements per subjects (M=1000). We define the four covariates ($\mathbf{x}$) with four eigencomponents and we define the coefficients of parameters ($\beta$’s) to be ${\beta }_0=0.1$, ${\beta }_1=0.25$, ${\beta }_2=-0.5$, ${\beta }_3=0.25$, ${\beta }_4=0.1$ so that $P(y=1)=\frac{1}{1+exp(-0.1-0.25x_1+0.5x_2-0.25x_2-0.1x_4))}$ which passes through an inverse logit function. To apply the simulated data to the proposed methods, we generate 30 different functional simulated data replications of sample size of 1000 in this study. Based on FPCA,

Table 2. Based on FPCA, the coverage probability, expected confidence interval (CI) length, and control limits for the simulated in-control, one inflated-, and zero inflated-dispersion binary data via various r-charts based on GLM with probit, GLM with logit, and neural network models. Neural network model used single layer and 30 neurons. ‘NA’ in the table means that there is no points out of control limits and and the number of simulations is 30 different replications of sample size of 1000.

		Probit			Logit			Neural Network
Case	$\mathit{E}\left({\mathit{r}}_{\mathit{i}}\right)\pm \mathit{w}\sqrt{\mathit{V}\mathit{a}\mathit{r}\left({\mathit{r}}_{\mathit{i}}\right)}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$
In-control	ARL	2.9	NA	NA	2.9	NA	NA	3.0	NA	NA
	Center	0.076	0.076	0.076	0.076	0.076	0.076	0.000	0.000	0.000
	LCL	−1.074	−2.225	−3.375	−1.074	−2.225	−3.375	−0.482	−0.964	−1.446
	UCL	1.226	2.376	3.527	1.226	2.376	3.527	0.482	0.964	1.446
	CI Length	2.301	4.601	6.902	2.301	4.601	6.902	0.964	1.927	2.891
	Coverage	0.617	1.000	1.000	0.617	1.000	1.000	0.604	1.000	1.000
One Inflated	ARL	4.467	NA	NA	4.467	NA	NA	4.533	423.833	NA
	Center	0.139	0.139	0.139	0.139	0.139	0.139	0.001	0.001	0.001
	LCL	−0.935	−2.009	−3.084	−0.935	−2.009	−3.084	−0.442	−0.884	−1.326
	UCL	1.214	2.288	3.362	1.214	2.288	3.362	0.443	0.885	1.328
	CI Length	2.149	4.298	6.446	2.149	4.298	6.446	0.885	1.769	2.654
	Coverage	0.725	1.000	1.000	0.725	1.000	1.000	0.723	0.999	1.000
Zero Inflated	ARL	2.100	NA	NA	2.100	NA	NA	2.400	NA	NA
	Center	0.016	0.016	0.016	0.016	0.016	0.016	0.000	0.000	0.000
	LCL	−1.160	−2.335	−3.510	−1.160	−2.335	−3.510	−0.495	−0.990	−1.484
	UCL	1.191	2.366	3.542	1.191	2.366	3.542	0.495	0.989	1.484
	CI Length	2.351	4.701	7.052	2.351	4.701	7.052	0.990	1.979	2.969
	Coverage	0.527	1.000	1.000	0.527	1.000	1.000	0.520	1.000	1.000

presents the average run length (ARL) results for simulated in-control, one inflated-, and zero inflated-dispersion data via r-charts based on the GLM with probit and logit link function and neural network models. Changes in w that resulted in one, two and three standard deviations from the mean of y are considered.

From Table 2 which is based on FPCA, we can see the same results as the ones in Table 1 based on PCA. The coverage probabilities by the GLMs with probit and logit link functions are slightly greater or equal to the coverage probabilities by the neural network regression model. The length of the confidence intervals (CIs) for the neural network regression model are much smaller than the the length of the confidence intervals (CIs) for the GLMs with probit and logit link functions but the ARLs of the neural network regression model are not smaller than the the ARLs for the GLMs with probit and logit link function. This result based on FPCA is different from the result based on PCA.

From Figure 5, Figure 6 and Figure 7, in case of the in-control dispersion based on FPCA, we can observe that the residuals of a neural network regression model are much closer to zero than the residuals of the GLM with probit and logit model, which are the same as the figures based on PCA.

From Table 1 and Table 2, we can compare the results for the neural network regression model, the GLMs with probit and logit link functions based on PCA and FPCA. We found the that, for the in-control and the one-inflated cases, the ARLs based on PCA are smaller than the ARLs based on FPCA but, for zero-inflated case, the ARLs based on FPCA are smaller than the ARLs based on PCA. Another interesting result is that, in terms of the ARLs, the GLMs with probit and logit link functions based on FPCA is overall superior than the the neural network regression model. This result is an opposite result compared with the one based on PCA.

3.2. Real Data Analysis

Ref. [22] proposed R package “mlbench" which included Wisconsin breast cancer database named as Breast Cancer. We used Breast Cancer for the illustration of real data analysis in this paper.

The objective of the Wisconsin breast cancer database is to identify each of a number of benign or malignant classes which are binary data (‘0’ and ‘1’). Samples arrive periodically as Dr. Wolberg reports his clinical cases. The database is the chronological grouping of the data. A data frame with 699 observations on 11 variables, one being a character variable, nine being ordered or nominal, and 1 target class. In this paper, We used nine covariates and one target variable such as the Cl.thickness (Clump Thickness), Cell.size (Uniformity of Cell Size), Cell.shape (Uniformity of Cell Shape), Marg.adhesion (Marginal Adhesion), Epith.c.size (Single Epithelial Cell Size), Bare.nuclei (Bare Nuclei), Bl.cromatin (Bland Chromatin), Normal.nucleoli (Normal Nucleoli), Mitoses and Class which is the target binary variable (Y) (‘0’=benigh and ‘1’=malignant).

Table 3. Pearson correlation coefficients of 9 covariates in Breast Cancer.

	Cl.thickness	Cell.size	Cell.shape	Marg.adhesion	Epith.c.size	Bare.nuclei	Bl.cromatin	Normal.nucleoli	Mitoses
Cl.thickness	1.000	0.642	0.653	0.488	0.524	0.593	0.554	0.534	0.355
Cell.size	0.642	1.000	0.907	0.707	0.754	0.692	0.756	0.719	0.465
Cell.shape	0.653	0.907	1.000	0.686	0.722	0.714	0.735	0.718	0.447
Marg.adhesion	0.488	0.707	0.686	1.000	0.595	0.671	0.669	0.603	0.425
Epith.c.size	0.524	0.754	0.722	0.595	1.000	0.586	0.618	0.629	0.481
Bare.nuclei	0.593	0.692	0.714	0.671	0.586	1.000	0.681	0.584	0.349
Bl.cromatin	0.554	0.756	0.735	0.669	0.618	0.681	1.000	0.666	0.354
Normal.nucleoli	0.534	0.719	0.718	0.603	0.629	0.584	0.666	1.000	0.437
Mitoses	0.355	0.465	0.447	0.425	0.481	0.349	0.354	0.437	1.000

presents the Pearson correlation coefficients with the Breast Cancer real data. It shows that nine covariates have strong positive correlation coefficients It means that nine covariates in breast cancer real data positively correlated each other. Figure 8 also showed high correlated pairwise scatter plots of nine covariates in breast cancer real data.

Table 4. PCA summary with nine covariates in Breast Cancer real data.

	Comp.1	Comp.2	Comp.3	Comp.4	Comp.5	Comp.6	Comp.7	Comp.8	Comp.9
Standard deviation	2.430	0.875	0.734	0.680	0.617	0.550	0.543	0.511	0.297
Proportion of Variance	0.656	0.085	0.060	0.051	0.042	0.034	0.033	0.029	0.010
Cumulative Proportion	0.656	0.741	0.801	0.853	0.895	0.928	0.961	0.990	1.000

showed the PCA summary with nine covariates in breast cancer real data. To avoid multicollinearity of the nine covariates, we used principal components for binary response data (Y=Class) via various r-charts based on GLM with probit, GLM with logit, and neural network models.

Based on PCA,

Table 5. Based on PCA, control limits for binary response data (Y=Class) via various r-charts based on GLM with probit, GLM with logit, and neural network models. Neural network model used single layer and 30 neurons.

	Probit			Logit			Neural Network
$E\left(r_i\right)\pm w\sqrt{Var\left(r_i\right)}$	$k=1$	$k=2$	$k=3$	$k=1$	$k=2$	$k=3$	$k=1$	$k=2$	$k=3$
Center	0.022	0.022	0.022	0.038	0.038	0.038	−0.002	−0.002	−0.002
LCL	−0.381	−0.785	−1.188	−0.368	−0.773	−1.178	−0.123	−0.244	−0.365
UCL	0.426	0.829	1.233	0.443	0.849	1.254	0.119	0.240	0.361
CL Length	0.807	1.614	2.421	0.811	1.622	2.433	0.242	0.485	0.727

shows that the r-chart based on neural network model has narrow control limits compared with the r-charts based on the GLM with probit and logit link function models. From Figure 9, Figure 10 and Figure 11, we can observe that the residuals of a neural network regression model are much closer to zero than the residuals of the GLM with probit and logit model. With the narrow control limits of a neural network model, we can monitor the class of the patients with breast cancer by r control chart with important covaraites’ information.

Figure 12 showed the plots of FPCA with nine covariates in Breast Cancer real data so that two main components explain the 94% proportion of variance by FPCA. Hence, we used two main components for the r-chart based regression models.

Based on FPCA,

Table 6. Based on FPCA, control limits for binary response data (Y=death) via various r-charts based on GLM with probit, GLM with logit, and neural network models. Neural network model used a single layer and 30 neurons.

	Probit			Logit			Neural Network
$\mathit{E}\left({\mathit{r}}_{\mathit{i}}\right)\pm \mathit{w}\sqrt{\mathit{V}\mathit{a}\mathit{r}\left({\mathit{r}}_{\mathit{i}}\right)}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$	$\mathit{k}=\mathbf{1}$	$\mathit{k}=\mathbf{2}$	$\mathit{k}=\mathbf{3}$
Center	0.095	0.095	0.095	0.095	0.095	0.095	−0.003	−0.003	−0.003
LCL	−1.034	−2.163	−3.293	−1.034	−2.163	−3.293	−0.470	−0.937	−1.403
UCL	1.225	2.354	3.484	1.225	2.354	3.483	0.464	0.930	1.397
CL Length	2.259	4.518	6.776	2.259	4.518	6.776	0.933	1.867	2.800

shows that the r-chart based on the neural network model has narrow control limits compared with the r-charts based on the GLM with probit and logit link function models. From Figure 13, Figure 14 and Figure 15, we can observe that the residuals of a neural network regression model are much closer to zero than the residuals of the GLM with the probit and logit model which concur to the same result based on PCA. With the narrow control limits of a neural network model, we can monitor the class of the patients with breast cancer by r control chart with important covaraites’ information.

Similar to the simulation data analysis, the r-chart based regression models based on PCA have the the narrower control limits than the r-chart based regression models based on FPCA.

4. Conclusions

In this research, we have presented the binary response regression model-based statistical process control r-charts for dispersed binary asymmetrical data with multicollinearity among input variables. We have demonstrated the proposed method in terms of the model flexibility and performance by running simulations for various circumstances: in-control, one inflated-, or zero inflated-dispersion data. With both simulated data and real data, our proposed method has shown a superiority of the performance. Furthermore, we compared PCA-based binary response regression model-based statistical control r-charts and FPCA-based binary response regression model-based statistical control r-charts with the GLM with probit and logit link function models and neural network model. In case of the dimension reduction by PCA, our proposed approach by a neural network is superior in handling cases of dispersed binary asymmetrical data with multicollinearity among explanatory variables. However, in case of the dimension reduction by FPCA, our proposed approach by neural network is superior in handling cases of dispersed binary asymmetrical data with multicollinearity among explanatory variables but it is not more efficient than the proposed method by the dimension reduction by PCA in this research.

The conclusion in this research is that for the high-dimensional correlated multivariate covariate data, the binary control chart by neural network model is a good statistical process control method and, for high-frequency functional multivariate data, the proposed GLM-based control charts by FPCA are good statistical process control methods. Hence, a cancer clinical study can be investigated by the proposed statistical process control.

Our future research will address the following topics. More general versions of binary asymmetric data will be considered with other machine learning models such as deep learning or multi-layer neural network model. Instead of the deviance residual, quantile residual can also be considered in the binary response regression control charts. Lastly, we need to consider other types of bases for constructing FPCA for further comparison studies with PCA-based models.