An Emergency Decision-Making Method for Probabilistic Linguistic Term Sets Extended by D Number Theory

Abstract

Emergency decision-making has become as one of the hot issues in recent years. The aim of emergency decision-making is to reduce the casualties and property losses. All the processes of emergency decision-making are full of incompleteness and hesitation. The problem of emergency decision-making can be regarded as one of the multi-attribute decision-making (MADM) problems. In this manuscript, a new method to solve the problem of emergency decision-making named D-PLTS is proposed, based on D number theory and the probability linguistic term set (PLTS). The evaluation information given by experts is tidied to be the form of PLTS, which can be directly transferred to the form of the D number, no matter whether the information is complete or not. Furthermore, the integration property of D number theory is carried out to fuse the information. Besides, two examples are given to demonstrate the effectiveness of the proposed method. Compared with some existing methods, the D-PLTS is more straightforward and has less computational complexity. Allocation weights that are more reasonable is the future work for the D-PLTS method.

1. Introduction

In recent years, with the rapid development of society and the economy, a variety of emergency events has become one of the most serious problems [1,2], such as mining accidents [3], fire disasters [4], flood hazards [5], earthquakes [6], gas explosions [7], natural disasters [8], environmental pollution [9], and so on. Since many aspects should be taken into consideration, emergency decision-making can be viewed as one of the multi-attribute decision-making (MADM) problems [10,11,12]. Emergency decision-making aims to minimize the personnel casualties and property losses [13,14]. The speed of response and decisions to be made in a timely manner are the two most important things of emergency decision-making [15]. In the early stage of an unpredicted emergency event, because of the lack of abundant reliable information, the precise evaluation of the information provided by decision-makers is also difficult, while incomplete information is inevitable [16]. There are many tools to represent uncertain or imprecise information, such as fuzzy numbers [17,18,19], intuitionistic fuzzy sets [20], the Z-number [21,22], hesitant fuzzy information [23], inherent fuzzy entropy [24,25], linguistic information [26], Deng entropy [27,28], the R-number [29], rough sets [30], etc. Among them, linguistic information is related to human language, which has been widely employed to represent the evaluation information during the processes of decision-making [31,32,33].

The linguistic information is also named the linguistic term set (LTS) [34,35], which only provides some basic words, such as “bad”, “well”, “excellent”. The number of items in an LTS is just only one at a time, which is deemed as that the statement is assured without any vagueness. Therefore, if the the decision-maker is hesitant to provide his/her opinions, LTS is useless in these situations with uncertainty. The hesitant fuzzy linguistic term set (HFLTS) [36,37] provides a more flexible way to represent linguistic information based on LTS, in which more than one item is allowed [38]. HFLTS can represent more information, but the information is ordered, which still limits its application [39]. Based on this situation, an extend hesitant fuzzy linguistic term set (EHFLTS) was proposed [40], which allows this inconsecutive information. However, the importance degree of information in LTS, HFLTS, and EHFLTS is viewed as the same, which cannot reflect the preference degree of each item. In order to solve this issue, the probabilistic linguistic term set (PLTS) has emerged [41], which involves a parameter to present the preference for items. When the probabilistic factor of PLTS is neglected, it will be degraded to LTS, HFLTS, or EHFLTS, which indicates that PLTS is compatible and generalized. Due to the characteristics of PLTS, it has been widely used for these decision-making areas, such as edge computing [42], sustainable supplier selection [43], risk assessment [44], selecting hotels [45], public health analysis [46], city classifying [47], investment brand selection [48], selecting optimal green enterprises [49], house lease price evaluation [50], and so on.

Dempster–Shafer evidence theory (D-S theory), as a mathematical tool to handle uncertain information, was firstly proposed in 1967 by Dempster [51] and extended by Shafer in 1976 [52]. Compared with classical Bayesian probability, the prior information is not necessary, and the number of elements is also extended from the singleton to the power set in D-S theory. D-S theory, which is often regarded as an extension of the Bayesian theory of probability [53], has been widely applied in many areas, such as data fusion [54,55], target recognition [56,57], risk evaluation [58], decision-making [59,60], reliability assessment [61,62,63,64], and so on. However, there still exist some limitations, when D-S theory is employed, such as the completeness of constraint, independence among bodies of evidence, elements must be mutually exclusive, the “one-vote veto” mechanism, high computational complexity, and so on, as discussed in detail later. In order to solve the above-mentioned deficiencies in D-S theory, D number theory was proposed by Deng in 2012 [65], mirroring the framework of D-S theory. D number theory can be regarded as an extension of D-S theory, since it absorbs the advantages, but overcomes the shortcomings of D-S theory. D number theory has been widely used in many fields, such as human reliability analysis [66], health-care waste treatment assessment [67], risk identification [68,69], supply chain management [70], sustainable evaluation [71], environmental impact assessment [72], motorcycle evaluation [73], decision-making [74], and so forth. Besides, D number theory has been integrated together with other methods, such as the Choquet integral [75] and intuitionistic hesitant fuzzy sets [76], to solve some real-world problems.

Emergency decision-making is always performed in the style of group decision-making, in which experts give their viewpoints with linguistic information habitually while they participate in the process of decision-making. Many methods have been put forward to solve the emergency decision-making problems. For example, Chen and Yu proposed a hybrid emergency decision-making method, integrating the best-worst method and the intuitionistic fuzzy weighted averaging operator (E-IFWA), which was applied in emergency alternative selection [77]. Peng and Garg proposed a composite method based on the interval-valued fuzzy soft set (IVFSS), weighted distance based approximation (WDBA), combinative distance-based assessment (CODAS), and the similarity measure to deal with the problem of mine emergency decision-making [78]. Gao et al. proposed a probabilistic linguistic preference relations (PLPRs) method to solve the problem of petrochemical plant fire accidents [79]. Ju and Huang proposed a hybrid method based on D-S theory and the analytic hierarchy process (AHP) and extended the technique for order preference by similarity to an ideal solution (TOPSIS) to solve the preference ranking of emergency alternatives [80]. The existing methods for emergency decision-making are all based on some commonly used mathematical tools, and they have gained some achievements to some extent. Nevertheless, an inevitable process during the processes of emergency is that crisp numbers are not suitable enough for experts to describe their complicated judgment. Due to the pressure of time and lack of abundant information, experts may be hesitant and even give up providing evaluation information on some alternatives or criteria, which means incomplete information will be presented. That is the incomplete and fuzzy information, which is collectively referred to as uncertain information in this paper, will emerge in the real-life situation. How to deal with the uncertain information in emergency decision-making is still an open issue. There are many tools to deal with this uncertain information, and one of the popular tools is D-S theory. Besides, timeliness is also a key requirement in emergency decision-making, which means the computational effort must be not high. Recently, Li et al. proposed a new method, named DS-PLWA, based on D-S theory and PLTS, to solve the problem of emergency decision-making [3]. In DS-PLWA, there exist at least three potential limitations. The first is the independence among experts in order to ensure the evaluation results given by each expert are all independent. However, this is not always met, especially under emergent situations. The second is the completeness constraint. The fact that information must be complete is one of the strong constraints in D-S theory. The reasonability of the allocation of incomplete information to the whole set is still debatable. In DS-PLWA, the absent information is forced to be assigned to the entire set. The third is the computational complexity. The Dempster combination rule has high computational complexity, as discussed later. However, incomplete information is allowed in D number theory. The computational complexity is also acceptable because of the integration property of the D number, and the independence constraint is also not required in D numbers. Based on the characteristic of PLTS and the merits of D number theory for uncertain information, a new method to deal with emergency decision-making, named D-PLTS, is proposed in this manuscript. The PLTS information can be directly treated as the D number, according to the common feature between D number theory and PLTS. Furthermore, the integration property of D number theory will be carried out to integrate the evaluation information. Compared with the DS-PLWA method, the new proposed method is more straightforward, intuitive, and has less computational complexity, as discussed later.

The remainder of the paper is structured as follows. Section 2 reviews some basic knowledge of the linguistic term set, the hesitant fuzzy linguistic term set, the probabilistic linguistic term set, Dempster–Shafer evidence theory, and D number theory. Section 3 provides the framework and the detailed flow of the new proposed method. Numerical examples are presented in Section 4 to demonstrate the detailed steps of PLTS, and some necessary discussions are also provided. Section 5 concludes the manuscript.

2. Preliminaries

In this Section, some basic concepts of the linguistic term set, the hesitant fuzzy linguistic term set, the probabilistic linguistic term set, Dempster–Shafer evidence theory, and the D number are recalled.

2.1. Linguistic Term Set

The linguistic term set (LTS) can be given as $S=\left\{s_{\sigma }\right|\sigma =-\phi ,\cdots ,-1,0,1,\cdots ,\phi \}$, where $\phi$ is a positive integer and $s_0$ means “no difference” [34]. The items in LTS are the symmetry and sequence. LTS meets the following two rules: (1) if $i>j$, then $s_i>s_j$; and (2) the negation operator can be expressed as $neg\left(s_{\sigma }\right)=s_{-}\sigma$.

Example 1.

Suppose$\sigma =2$, then an LTS S combined with five elements can be presented as$S=\{s_{-2}=worse,s_{-1}=bad,s_0=fair,s_1=good,s_2=better\}$.

In order to extend the application of LTS, Xu extended the integer subscript in LTS to the real number, and LTS can be given as ${{\mathrm{S}}^{\prime }=\{\mathrm{s}}_{\sigma }|\sigma \in [-\pi ,\pi ]\}$ [81]. That is, the operation of LTS can be freely used without consideration of the subscript of LTS. In addition, some operational laws of LTS based on the subscript are given as follows [81].

Definition 1.

Suppose there are two LTSs$S_a,S_b\in S^{\prime }$and$\lambda \in [0,1]$, then:

$$\begin{array}{c}{s}_a\oplus s_b=s_{a+b}\\ s_a\otimes s_b=s_{a\times b}\\ \lambda s_a=s_{\lambda a}\\ {\left(s_a\right)}^{\lambda }=s_{a^{\lambda }}\end{array}$$

(1)

where ⊕ and ⊗ represent the arithmetical operations of addition and multiplication, respectively.

2.2. Hesitant Fuzzy Linguistic Term Set

The traditional LTS can only express one item at a time to a defined degree. When the decision-maker is not sure about his/her viewpoints, LTS is useless in this situation. To address this deficiency, Rodriguez et al. proposed the hesitant fuzzy linguistic term set (HFLTS) [36], which can be defined as follows.

Definition 2.

Let S be an LTS; an HFLTS$H_S$is an ordered finite subset of consecutive LTS in S.

Example 2.

Let$S=\{s_{-2}=worse,s_{-1}=bad,s_0=fair,s_1=good,s_2=better\}$be an LTS, then$b_1=\{s_{-2}=worse,s_{-1}=bad,s_0=fair\}$and$b_2=\{s_0=fair,s_1=good\}$are two HFLTSs. For simplicity, the two HFLTSs can be rewritten as$b_1=\{s_{-2},s_{-1},s_0\}$and$b_2=\{s_0,s_1\}$.

Example 2 indicates that the items in HFLTSs $b_1$ and $b_2$ are limited to a consecutive subset of a given LTS and cannot express this inconsecutive information. Based on this, Wang proposed the extend hesitant fuzzy linguistic term set (EHFLTS) [40] for these inconsecutive subsets in LTS, and it can be defined as follows.

Definition 3.

Let S be an LTS, an EHFLTS$H_S^E$is an ordered finite subset of consecutive LTS in S.

Example 3.

Suppose$S=\{s_{-2}=worse,s_{-1}=bad,s_0=fair,s_1=good,s_2=better\}$is an LTS, and$b_1=\{s_{-2},s_{-1},s_0\}$,$b_2=\{s_0,s_1\}$, and$b_3=\{s_{-2},s_0,s_1\}$are all valid EHFLTSs.

The elements of $s_{-2}$, $s_0$, and $s_1$ in set $b_3$ are not continuous in Example 3, which is the conspicuous difference between HFLTS and EHFLTS.

2.3. Probabilistic Linguistic Term Set

Compared with LTS, both HFLTS and EHFLTS can express more information, especially this uncertain information. However, HFLTS and EHFLTS cannot reflect the degree of importance among these items; in other words, they are regarded as having the same importance. In view of this situation, probabilistic linguistic term sets (PLTS) emerged [41], involving the parameter of probability, and it can be defined as follows.

Definition 4.

Suppose$S=\{s_{\sigma }|\sigma =-\phi ,\cdots ,-1,0,1,\cdots ,\phi \}$is an LTS. A probabilistic linguistic term set (PLTS) can be defined as:

$$\begin{array}{c}\hfill PL\left(p\right)=\left\{({\mathrm{s}}_{\sigma },p_{\sigma })|\sigma =-\phi ,\cdots -1,0,1,\cdots \phi ;p_{\sigma }\ge 0,\sum p_{\sigma }\le 1\right\}\end{array}$$

(2)

where$p_{\sigma }$is the probability of$s_{\sigma }$, indicating the certainty degree of$s_{\sigma }$.

Example 4.

Suppose$S=\left\{s_{\sigma }\right|\sigma =-\phi ,\cdots ,-1,0,1,\cdots ,\phi \}$is an LTS, then:

$$P{L}_1\left(p\right)=\{(s_{-2},0.2),(s_{-1},0.3),(s_0,0.2),(s_1,0.3),(s_2,0)\}$$

and$P{L}_2\left(p\right)=\{(s_{-2},0.4),(s_{-1},0.2),(s_0,0),(s_1,0),(s_2,0)\}$are two PLTSs.

It should be pointed out that the sum of the probabilities of PLTS $P{L}_2\left(p\right)$ in Example 4 is less than one. When some experts are not sure enough to give evaluations or fail to make evaluations due to time pressure, or a lack of sufficient relevant knowledge, or some other subjective and objective restrictions, the PLTS provides a good solution, in which the incomplete information is allowed. Since the probability of zero has no influence on the final results, the PLTS in Example 4 can be rewritten as $P{L}_1\left(p\right)=\{(s_{-2},0.2),(s_{-1},0.3),(s_0,0.2),(s_1,0.3)\}$ and $P{L}_2\left(p\right)=\{(s_{-2},0.4),(s_{-1},0.2))\}$.

2.4. Dempster–Shafer Evidence Theory

Dempster–Shafer evidence theory (D-S theory) is a useful tool to represent and deal with uncertain information [51,52]. Some basic concepts of D-S theory are given as follows.

Let $\Omega =\{{\theta }_1,{\theta }_2\cdots ,{\theta }_n\}$ be a finite set of n mutual exclusive elements. Let $2^{\Omega }$ denote the power set of $\Omega$, and $2^{\Omega }=\{\varnothing ,{\theta }_1,\cdots ,{\theta }_n,{\theta }_1\cup {\theta }_2,{\theta }_1\cup {\theta }_3\cdots ,\Omega \}$.

Definition 5.

For a frame of discernment Ω, a basic probability assignment (BPA) is a mapping$m:2^{\Omega }\to [0,1]$, which is also called the mass function, satisfying:

$$m(\varnothing )=0and\sum _{A\in 2^{\Omega }}m\left(A\right)=1$$

(3)

where ∅ is an empty set and A is any element of$2^{\Omega }$.$m\left(A\right)$represents the support degree of A in a BPA. Equation (3) indicates that the sum of BPAs must be equal to one, which is the complete constraint of D-S theory.

The Dempster combination rule is the core of D-S theory, which provides a way to integrate BPAs [51]. Let $m_1$ and $m_2$ be two BPAs; the Dempster combination rule can be utilized to combine them and generate a new BPA m.

Definition 6.

Dempster’s rule of combination, also named the orthogonal sum, denoted by$m=m_1\oplus m_2$, is defined as follows:

$$m\left(A\right)=\frac{1}{1-k}\sum _{B\cap C=A}{m}_1\left(B\right)m_2\left(C\right)$$

(4)

with:

$$k=\sum _{B\cap C=\varnothing }{m}_1\left(B\right)m_2\left(C\right)$$

(5)

where A, B, and C are the elements of$2^{\Omega }$and k is a normalization constant, called the conflict coefficient between two BPAs. Dempster’s rule of combination satisfies the commutative and associative properties, i.e.,: (1)$m_1\oplus m_2=m_2\oplus m_1$; (2)$(m_1\oplus m_2)\oplus m_3=m_1\oplus (m_2\oplus m_3)$. Thus, if there exist multiple BPAs, the combination of them can be carried out in a pairwise way with any order.

2.5. D Number Theory

The applications of D-S theory are limited, owing to these inherent characteristics. The first is mutually exclusive, that is the elements on the framework of D-S theory must be totally mutually exclusive, which means there must exist a crisp gap among the elements in D-S theory. The second is the completeness constraint, that is the sum of a mass function must be equal to one in D-S theory. However, it is easy to obtain partial information in the real world subjected to kinds of subjective and objective reasons. The third is the independence constraint, that is the BPAs on the same framework of D-S theory must be totally unrelated; however, this is always difficult to meet in real-life situations of decision-making. The fourth is high computational complexity; when the number of element has linear growth, the computational complexity of the Dempster combination rule has exponential growth. If there exist m elements on the framework of D-S theory and n mass functions, the computational complexity of D-S theory is $O\left(m^n\right)$, according to the Dempster combination rule [82,83]. The fifth is the “one-vote-veto”, and there is the famous example of the Zadeh paradox [84], in which once one element is denied, one will be vetoed all the time regardless of how strongly other BPAs support it later.

In order to solve the above-mentioned limitations in D-S theory, a new mathematical tool named D number theory is proposed [65], mirroring the framework of D-S theory, which overcomes the shortcomings, but absorbs the advantages of D-S theory. The above-mentioned deficiencies of D-S theory are all well addressed in D number theory. The mutually exclusive constraint among elements on the framework of the D number is not necessary, which means the framework of D numbers is compatible with D-S theory. The different framework between D-S theory and D numbers is given in Figure 1. The computational complexity of the D number is $O\left(mn\right)$, according to the integration property of the D number. If there are m elements on the framework of the D number and n D numbers, then the computational complexity of the integration operation of the D number is the product of these. The remaining differences between D-S theory and D number are given in

Table 1. The differences between D-S theory and the D number.

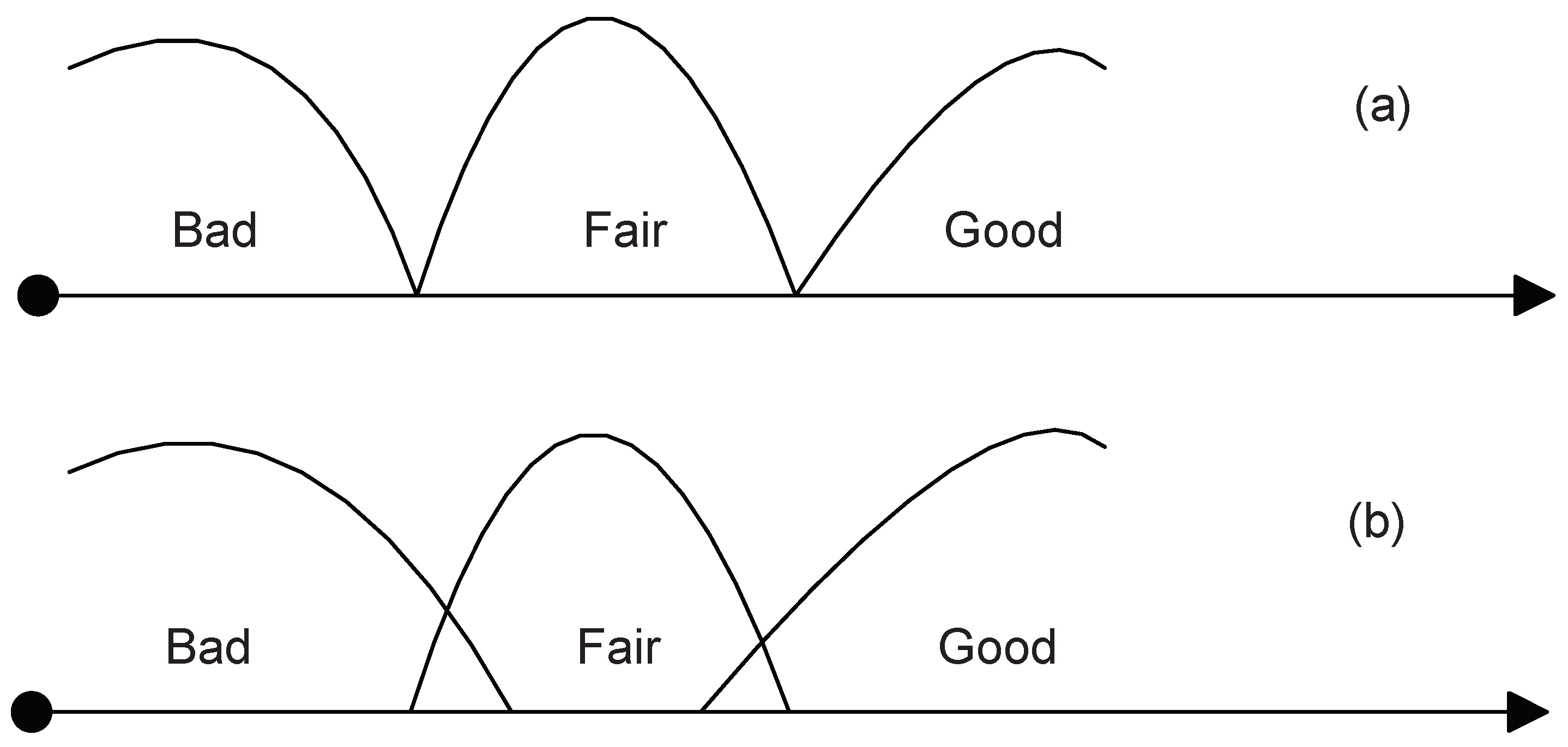
	Mutually Exclusive	Completeness Constraint	Independence Constraint	Computational Complexity	One-vote-veto
D-S theory	Must be	Must be	Must be	O($m^n$)	Exists
D number	Not necessary	Not necessary	Not necessary	O(mn)	Does not exist

.

Some basic concepts of D number theory are shown as follows.

Definition 7.

Let Ω be a finite nonempty set: a D number is a mapping D:$\Omega \to$[0, 1], with:

$$\sum _{A\subseteq \Omega }D\left(A\right)\le 1andD(\varnothing )=0.$$

(6)

where ∅ is an empty set and A is any subset of Ω.

If ${\displaystyle \sum _{A\subseteq \Omega }}D\left(A\right)=1$, the information is said to be complete; otherwise, the information is believed to be incomplete.

For a discrete set $\Omega =\{b_1,b_2,\cdots ,b_i,b_j,\cdots b_n\}$, where $b_i\in R$ and $b_i\ne b_j$ when $i\ne j$, a special form of the D number can be expressed by:

$$\begin{array}{c}\hfill \begin{array}{c}D\left(b_1\right)=v_1\hfill \\ D\left(b_2\right)=v_2\hfill \\ \cdots \hfill \\ D\left(b_i\right)=v_i\hfill \\ D\left(b_j\right)=v_j\hfill \\ \cdots \hfill \\ D\left(b_n\right)=v_n\hfill \end{array}\end{array}$$

(7)

simply denoted as:

$$D=\{(b_1,v_1),(b_2,v_2),\cdots ,(b_i,v_i),(b_j,v_j),\cdots (b_n,v_n)\},$$

where $v_i>0$ and ${\displaystyle \sum _{i=1}^n}{v}_i\le 1$.

Similar to D-S theory, there are also some inherent properties of D number theory as follows.

Property 1.

(Permutation invariability) If the couples of the element and the according value are totally the same in different D numbers, then these D numbers are viewed as the same, but with different orders.

Example 5.

Suppose there are two D numbers,$D_1=\{(b,0.3),(c,0.2),(e,0.4)\}$and$D_2=\{(c,0.2),(e,0.4),(b,0.3)\}$, then$D_1\iff D_2$, where ⇔ means “equal to”.

It should be pointed out that the sum of values of elements of $D_1$ or $D_2$ in Example 5 is less than one, which is allowed in D number theory, but unallowed in D-S theory.

Example 6.

If there are three D numbers:

$$D_1=\{(good,0.3),(bad,0.2),(well,0.5)\},$$

$$D_2=\{(bad,0.2),(well,0.5),(good,0.3)\}$$

and

$$D_3=\{(well,0.5),(bad,0.2),(good,0.3)\}$$

then$D_1\iff D_2\iff D_3$, which means the three D numbers are identical.

Property 2.

(Integration) For a D number,$D=\{(b_1,v_1),\cdots ,(b_i,v_i),\cdots (b_n,v_n)\}$, the integration representation of D number theory is defined as:

$$I\left(D\right)=\sum _{i=1}^n{b}_i{v}_i$$

(8)

where$b_i\in R$,$v_i>0$, and${\displaystyle \sum _{i=1}^n}{v}_i\le 1$.

Example 7.

Suppose a D number:

$$D=\left\{\right(3,0.1),(4,0.3),(5,0.2),(6,0.4\left)\right\},$$

then:

$$I\left(D\right)=3\times 0.1+4\times 0.3+5\times 0.2+6\times 0.4=4.9.$$

3. Proposed Method

In this Section, the D-PLTS model for emergency decision-making will be built based on PLTS and the D number, as shown in Figure 2.

Step 1. Problem description: When an unexpected emergency event happens, some basic information about the incident should be introduced by the organizer to the participants of the decision-making.

Step 2. Preparation for evaluation: The organizer provides an alternatives set T and attribute set A to expert set E. The linguistic term set (LTS) S should also be provided to experts for the evaluation of alternatives.

Step 3. Expert evaluation: According to the information provided by the organizer, experts express their viewpoints for each attribute on each alternative using LTS S. Experts are allowed to give their opinions flexibly, even give up the evaluation according to the real situation. A decision matrix R is built to collect evaluation information provided by experts. The information in R is of the form of LTS, and it should be summarized in a new matrix $R^{\prime }$, in which the information should be the form of PLTS. Because the structure of PLTS is similar to the D number, then the information of PLTS in $R^{\prime }$ can be directly converted to the form of the D number.

Step 4. Weights of the attributes: Different attributes play different roles in the processes of decision-making, and the weights of different attributes should be also involved. There are many methods to allocate weights to each attribute, such as the AHP method, distance measure, etc.

Step 5. Information integration: The integration property of the D number will be used to integrate the evaluation information of alternatives provided by experts, including the weight factor.

Step 6. Rank: According to the integration results of experts on each alternative, the final order will be presented to organizers of the emergency decision-making.

4. Case Study and Discussion

In this section, two examples will be given to illustrate the detailed steps and the effectiveness of the proposed method. A short discussion is given to analyze the advantages of the proposed method.

4.1. Case Study

The case study was the gypsum mine collapse accident in Pingyi, Shandong province, at about 8:00 on 25 December 2015 [3]. The shaking by the collapse was almost equivalent to a magnitude 4.0 earthquake. It was said that there were 29 laborers trapped below. The roadway in the mine was seriously damaged and nearly cut off by the continuous landslides. The geologic structures were also complicated, which was directly related to the rescue. A drilling shaft was necessary in order to rescue the trapped workers as soon as possible. It was reported by the field headquarters that the rescue was complicated, difficult, and high risk. It was a big challenge to drill the shaft, since the gypsum layer of rock was very loose. Any carelessness during the operation would bring about serious consequences to the lives and safety of the trapped workers and the rescue staff.

Step 1. Preparation for evaluation: Ten experts $(E_i,i=1,2\cdots 10)$ being experienced practitioners from the mining industry or emergency rescue were invited by the emergency management department to solve the problem of the rescue of the trapped workers. According to the actual situation and based on the past experience, four possible emergency rescue plans were put forward. In order to select the optimal plan, three attributes (criteria) were presented to the experts by the emergency management. The four possible emergency rescue plans $(T_i,i=1,2,3,4)$ are listed as follows.

$T_1$: A method of excavation of the roadway before the supporting roof;

$T_2$: A method of drilling small holes to send rescue capsules;

$T_3$: A previous method of roadway excavation for the underground mine rescue;

$T_4$: A method of boring big holes to the trapped staff.

The three attributes (criteria) $(A_j,j=1,2,3)$ are given as follows.

$A_1$: speed, the time of rescue for each process;

$A_2$: efficiency, the ratio of rescue benefit to the cost in labor and materials;

$A_3$: possibility, the probability of any process succeeding.

Besides, an LTS S was provided to the experts for evaluation of the four possible alternative plans, as shown in Equation (9).

$$\begin{array}{c}S=\{s_{-3}=none\left(N\right),s_{-2}=verylow\left(VL\right),s_{-1}=low\left(L\right),s_0=fair\left(F\right),s_1=high\left(H\right),\hfill \\ s_2=veryhigh\left(VH\right),s_3=perfect\left(P\right)\}\hfill \end{array}$$

(9)

Step 2. Expert evaluation: According to their specialized knowledge and experience in the mining field and emergency rescue, experts gave their opinions on each attribute of the alternatives using LTS S, as presented in

Table 2. The preliminary evaluation information (LTS) provided by experts.

Experts		${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$	Experts		${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$
$E_1$	$T_1$	F	VH	F	$E_2$	$T_1$	F	VH	L
	$T_2$	VH	-	H		$T_2$	VH	F	H
	$T_3$	H	H	VH		$T_3$	H	H	VH
	$T_4$	VH	VL	H		$T_4$	VH	VL	H
$E_3$	$T_1$	F	VH	L	$E_4$	$T_1$	F	VH	L
	$T_2$	VH	F	VH		$T_2$	P	F	VH
	$T_3$	H	H	VH		$T_3$	H	H	VH
	$T_4$	VH	VL	H		$T_4$	VH	VL	H
$E_5$	$T_1$	H	VH	L	$E_6$	$T_1$	H	VH	L
	$T_2$	P	F	VH		$T_2$	P	F	VH
	$T_3$	H	H	VH		$T_3$	H	VH	VH
	$T_4$	-	L	H		$T_4$	P	F	H
$E_7$	$T_1$	H	VH	L	$E_8$	$T_1$	H	VH	L
	$T_2$	P	F	P		$T_2$	P	-	P
	$T_3$	H	VH	P		$T_3$	H	VH	P
	$T_4$	P	F	H		$T_4$	P	H	H
$E_9$	$T_1$	H	VH	F	$E_{10}$	$T_1$	H	VH	L
	$T_2$	P	F	P		$T_2$	P	F	P
	$T_3$	H	VH	P		$T_3$	H	VH	P
	$T_4$	-	H	H		$T_4$	P	H	-

Note: The symbol “-” indicates no information was provided by the expert, due to the lack of information, pressure of time, or other reasons.

. Taking the intersection value F between the second row and the third column for example, this indicates that the evaluation information for alternative $T_1$ on criterion $A_1$ provided by expert $E1$ is F. The rough information as shown in Table 2 should be tidied for the next step of evaluation. Taking candidate $T_1$ for example, the numbers of evaluation grade F and H on criteria $A_1$ are four and six, respectively, and which can be marked as $\left\{\right(F,4),(H,6\left)\right\}$. Since there were ten experts giving their opinions, then it can be normalized as $\left\{\right(F,0.4),(H,0.6\left)\right\}$, which can be rewritten as $\{(s_0,0.4),(s_1,0.6)\}$ based on Equation (9). Then, summarizing all the evaluation information of LTS from in Table 2, it can be transferred into the form of PLTS information, as shown in

Table 3. Summarized evaluation information in the form of PLTS.

	${\mathit{A}}_1$	${\mathit{A}}_2$	${\mathit{A}}_3$
$T_1$	$\{(s_0,0.4),(s_1,0.6)\}$	$\left\{(s_2,1)\right\}$	$\{(s_{-}1,0.8),(s_0,0.2)\}$
$T_2$	$\{(s_2,0.3),(s_3,0.7)\}$	$\left\{(s_0,0.8)\right\}$	$\{(s_1,0.2),(s_2,0.4),(s_3,0.4)\}$
$T_3$	$\left\{(s_1,1.0)\right\}$	$\{(s_1,0.5),(s_2,0.5)\}$	$\{(s_2,0.6),(s_3,0.4)\}$
$T_4$	$\{(s_2,0.4),(s_3,0.4)\}$	$\{(s_{-}2,0.4),(s_{-}1,0.1),(s_0,0.2),(s_1,0.3)\}$	$\left\{(s_1,0.9)\right\}$

.

As we can see, PLTS information can be viewed as the D number directly, no matter whether the information is complete or not. Then, the evaluation information of PLTS in Table 3 can be presented in the form of the D number as shown in Equation (10).

$$\begin{array}{c}{T}_1:T_{11}=\{(s_0,0.4),(s_1,0.6)\},T_{12}=\{(s_2,1.0),T_{13}=\{(s_{-1},0.8),(s_0,0.2)\}\}\hfill \\ T_2:T_{21}=\{(s_2,0.3),(s_3,0.7)\},T_{22}=\left\{(s_0,0.8)\right\},T_{23}=\{(s_1,0.2),(s_2,0.4),(s_3,0.4)\}\hfill \\ T_3:T_{31}=\left\{(s_1,1.0)\right\},T_{32}=\{(s_1,0.5),(s_2,0.5)\},T_{33}=\{(s_2,0.6),(s_3,0.4)\}\hfill \\ T_4:T_{41}=\{(s_2,0.4),(s_3,0.4)\},T_{42}=\{(s_{-2},0.4),(s_{-1},0.1),(s_0,0.2),(s_1,0.3)\},\hfill \\ T_{43}=\left\{(s_1,0.9)\right\}\hfill \end{array}$$

(10)

where $T_{11}$ represents the evaluation result for alternative $T_1$ on criteria $A_1$, and the remaining are analogous.

Step 3. Weights of the attributes: There are many algorithms to obtain the weight of each attribute. For simplicity, the same weights of the attributes in [3] were adopted as:

$$w_1=0.319,w_2=0.342,w_3=0.339$$

(11)

$w_1$, $w_2$, and $w_3$ correspond to the weights of attributes $A_1,A_2,A_3$, respectively.

Step 4. Information integration: Before utilizing the property integration of the D number, the information of the D number as shown in Equation (10) should be transferred to the form of real numbers, since the D number’s integration operation can only function on the special case of the real number. In this paper, the subscripts of elements in LTS S, as shown in Equation (9), are regarded as the corresponding real numbers for simplicity, then the evaluation information of the D number as shown in Equation (10) can be rewritten as:

$$\begin{array}{c}{T}_1:T_{11}=\{(0,0.4),(1,0.6)\},T_{12}=\{(2,1.0),T_{13}=\{(-1,0.8),(0,0.2)\}\}\hfill \\ T_2:T_{21}=\{(2,0.3),(3,0.7)\},T_{22}=\left\{(0,0.8)\right\},T_{23}=\{(1,0.2),(2,0.4),(3,0.4)\}\hfill \\ T_3:T_{31}=\left\{(1,1.0)\right\},T_{32}=\{(1,0.5),(2,0.5)\},T_{33}=\{(2,0.6),(3,0.4)\}\hfill \\ T_4:T_{41}=\{(2,0.4),(3,0.4)\},T_{42}=\{(-2,0.4),(-1,0.1),(0,0.2),(1,0.3)\},\hfill \\ T_{43}=\left\{(1,0.9)\right\}\hfill \end{array}$$

(12)

Since the weight factor is involved, the integration property of the D number as shown in Equation (8) should be modified as:

$$I\left(T_i\right)=\sum _{j=1}^m\sum _{i=1}^n{w}_j{b}_{ij}{v}_{ij}$$

(13)

Taking $T_1$ for example, based on Equations (11)–(13), the integration of $T_1$ is computed as:

$$\begin{array}{c}I\left(T_1\right)=0.319\times (0\times 0.4+1\times 0.6)+0.342\times (2\times 1.0)\hfill \\ +0.339\times (-1\times 0.8+0\times 0.2)=0.6042\hfill \end{array}$$

(14)

Analogously, the rest of the information of the D number in Equation (12) can be obtained as:

$$I\left(T_2\right)=1.6071,I\left(T_3\right)=1.6456,I\left(T_4\right)=0.7379$$

(15)

Step 5. Rank: Based on Equations (14) and (15), the order of the four D numbers is $I\left(T_3\right)>I\left(T_2\right)>I\left(T_4\right)>I\left(T_1\right)$, which means the rank list of the four alternatives is $T_3\succ T_2\succ T_4\succ T_1$.

As we can see, the result by D-PLTS was the the same as PL-VIKOR method based on the same weights [3,85], which was similar to, but not identical to the DS-PLWA method. The main deference was induced by the weight allocation. In DS-PLWA, the weight was obtained by the distance measure between two mass functions. Since the D number is a novel theory to represent and deal with uncertain information, some rules and characteristics are still under study, including the allocation weight measure of the D number. It was obvious that the final evaluation results were directly influenced by the weight factor, which played a vital role during the process of emergency decision-making. Several methods have been proposed to determine the weight of the attributes in decision-making problems, and they can be divided into three categories as the subjective method, the objective method, and the mixture method. In the real-life practice of emergency decision-making, due to the pressure of time and limited information, the extensive experience of experts is very important. In order to verify the influence of the weight factor to the final evaluation results, another triple value of weights as (0.5, 0.4, 0.1) was adopted, and the final ranking results were $T_2\succ T_3\succ T_1\succ T_4$, which was the same as DS-PLWA [3].

4.2. Discussion

The differences between D-PLTS and DS-PLWA is the differences between D number theory and D-S theory. As discussed in Section 2.5, D number theory originated from D-S theory, and D number theory absorbs the advantages, but well addresses the deficiencies of D-S theory. The most striking place between D-PLTS and DS-PLWA is the manner of dealing with incomplete information. Incomplete information in D-PLTS is allowed, but incomplete information must be supplemented in DS-PLWA through the discount coefficient method in D-S theory.

In order to verify the effectiveness of the proposed method in more occasions, an example from [41] based on TOPSIS and PLTS was adopted. The board of directors of a company, which included five members, was to plan the development of large projects (strategy initiatives) for the next five years. Three possible projects ($x_1$, $x_2$, $x_3$) were marked. The comparison among them was necessary to select the most important of them, as well as order them from the point of view of their importance, taking into account four criteria (categories) suggested by the balanced scorecard methodology: (1) $a_1$: financial perspective; (2) $a_2$: the customer satisfaction; (3) $a_3$: internal business process perspective; and (4) $a_4$: learning and growth perspective. LTS was given as $S=\{s_0=none,s_1=verylow,s_2=low,s_3=medium,s_4=high,s_5=veryhigh,s_6=perfect\}$. For simplicity, $S=\{s_0,s_1,s_2,s_3,s_4,s_5,s_6\}.$ The weight set for attributes $a_1,a_2,a_3$, and $a_4$ is $w=\{0.138,0.304,0.416,0.142\}$, and the collected probabilistic linguistic information decision matrix provided by experts is presented in

Table 4. The collected probabilistic linguistic decision matrix by experts.

	${\mathit{a}}_1$	${\mathit{a}}_2$	${\mathit{a}}_3$	${\mathit{a}}_4$
$x_1$	$\{(s_3,0.4),(s_4,0.6)\}$	$\{(s_2,0.2),(s_4,0.8)\}$	$\{(s_3,0.2),(s_4,0.8)\}$	$\{(s_3,0.4),(s_5,0.6)\}$
$x_2$	$\{(s_5,0.2),(s_3,0.8)\}$	$\{(s_2,0.2),(s_3,0.4),(s_4,0.2)\}$	$\{(s_1,0.2),(s_2,0.4),(s_3,0.2)\}$	$\{(s_3,0.8),(s_4,0.2)\}$
$x_3$	$\{(s_3,0.6),(s_4,0.4)\}$	$\{(s_3,0.6),(s_4,0.2)\}$	$\{(s_3,0.2),(s_4,0.2),(s_5,0.2)\}$	$\{(s_4,0.8),(s_6,0.2)\}$

.

In addition, the D-PLTS model was employed to rank the alternatives $x_1$, $x_2$, and $x_3$, as follows.

The decision matrix in Table 4 can be directly transformed to the D number, and the items of LTS are replaced with their subscripts.

$$\begin{array}{c}{D}_{x1}:D_{11}=\{(3,0.4),(4,0.6)\},D_{12}=\{(2,0.2),(4,0.8)\},\hfill \\ D_{13}=\{(3,0.2),(4,0.8)\},D_{14}=\{(3,0.4),(5,0.6)\}\hfill \\ D_{x2}:D_{21}=\{(5,0.2),(3,0.8)\},D_{22}=\{(2,0.2),(3,0.4),(4,0.2)\},\hfill \\ D_{23}=\{(1,0.2),(2,0.4),(3,0.2)\},D_{24}=\{(3,0.8),(4,0.2)\}\hfill \\ D_{x3}:D_{31}=\{(3,0.6),(4,0.4)\},D_{32}=\{(3,0.6),(4,0.2)\},\hfill \\ D_{33}=\{(3,0.2),(4,0.2),(5,0.2)\},D_{34}=\{(4,0.8),(6,0.2)\}\hfill \end{array}$$

(16)

Taking $x_1$ for example, the integration property of D number theory was used to fuse the attributes as follows.

$$\begin{array}{c}{D}_{x1}:D_{11}=3\times 0.4+4\times 0.6=3.6,D_{12}=2\times 0.2+4\times 0.8=3.6\hfill \\ D_{13}=3\times 0.2+4\times 0.8=3.8,D_{14}=3\times 0.4+5\times 0.6=4.2\hfill \end{array}$$

Considering the weights of each attribute, then the final score of $x_1$ is obtained as:

$$I\left(D_{x1}\right)=3.6\times 0.138+3.6\times 0.304+3.8\times 0.416+4.2\times 0.142=3.7684$$

(17)

Analogously, the finally scores of $x_2$ and $x_3$ are obtained as:

$$I\left(D_{x2}\right)=2.1972,I\left(D_{x3}\right)=2.8828$$

(18)

Based on Equations (17) and (18), the order of the three values was $I\left(D_{x1}\right)\succ I\left(D_{x3}\right)\succ I\left(D_{x2}\right)$. Furthermore, the rank result of the three alternative could be obtained as $x_1>x_3>x_2$ by D-PLTS method, which was the same rank in [41] by the TOPSIS-PLTS method.

5. Conclusions

A critical problem in emergency decision-making is how to select the most desirable alternative. Emergency decision-making is required to be timely and exact, since time is life and money. A suitable rescue and assistance measure aims to reduce the casualties and property losses to the minimum. In this paper, a new method to deal with emergency decision-making was proposed named D-PLTS, based on D number theory and PLTS. The new proposed method could directly deal with the linguistic information of the evaluation provided by experts based on D number theory, which was time saving and possible no matter whether the information was complete or not. In addition, the integration property of D number theory was employed to fuse evaluation information, in which the computational complexity had linear growth, while the amount of information increased. An experiment and a case study comparing other existing methods illustrated that the D-PLTS method was effective.

In conclusion, the advantages of D-PLTS could be summarized as follows: (1) D-PLTS could well address the representation and management of incomplete information, in which incomplete information was allowed; (2) the flowchart of the D-PLTS model was clear and easy to understand; (3) the computational complexity of D-PLTS was smaller than the DS-PLWA method, because of the difference between D-S theory and the D number; (4) the PLTS information could be directly handled with the D number, since they both had the same characteristic. D-PLTS provided a promising way to choose the most suitable alternative in emergency decision-making problems. Due to space limitations, a few examples were used to demonstrate the application of D-PLTS, which could also be applied in other more complicated situations. Furthermore, based on the above-mentioned merits of D-PLTS, it was helpful to determine the most suitable solutions as soon as possible to reduce the property damage and casualties. The D-PLTS model could not only be used for mine emergency decision-making, but would also be suitable for other occasions of decision-making, such as natural disasters, gas explosions, etc. D-PLTS provided a generalized framework to these decision-making problems; therefore, it could be flexibly adjusted according to the real-life situation.

It should be pointed out that the method of allocating weight was not presented in this paper, since there are many methods to obtain weight information according to the actual situation. Furthermore, the allocation of the weight of criteria in decision-making problems by the D-PLTS model is the future work.