1. Introduction
A real stochastic matrix M is a matrix whose row sums or column sums are equal to 1. All the entries of a real stochastic matrix are non-negative. A real symmetric matrix with non-negative entries with row sums and column sums equal to 1 is called doubly stochastic matrix.
A list of
n real numbers, i.e.,
is
realizable if there exists a symmetric doubly stochastic matrix
M with its spectrum denoted by
. Doubly stochastic matrix describes the transitions corresponding to finite state symmetric Markov chains and this transition acts as a special class of this family. Doubly stochastic matrices are the convex hull for transition matrices with element set [
1].
The inverse eigenvalue problems for non-negative doubly stochastic matrices have its origin in work of [
2,
3,
4,
5]. For more details on inverse eigenvalue problems, we refer the reader to [
6,
7,
8,
9,
10] and references therein.
The non-negative matrix
M has a real eigenvalue
such that
for all
i. The eigenvalues
for all
i are the eigenvalues of
M other than
. From the Perron–Frobenius theorem an eigenvector corresponding to
is such that each of its entries are non-negative and sums to 1. For more details, we refer to [
11,
12,
13].
[
14] showed that the eigenvector has the form
corresponding to eigenvalue
for
, where
denotes the real line. The spectrum of a doubly stochastic matrix is bounded by 1, that is
for all
i. Three important eigenvalue problems for doubly stochastic matrices are considered in [
14] whenever there is a possibility that eigenvalues can be placed in complex plane, denoted by
. The first problem deals with necessary and sufficient conditions for
tuples to be the spectrum of a given doubly stochastic matrix. The second problem is about the fact that which real numbers acts as the spectrum of the doubly stochastic matrix. The last problem deals with the study in which set of
n real numbers act as the spectrum of the symmetric doubly stochastic inverse eigenvalue problems.
The matrix
M over a field
such that each row sum and column sum is
, is called the generalization of doubly stochastic matrices by means of Lie theory and algebra
of set of generalized doubly stochastic matrices studied in [
15].
In the literature [
6,
7,
10,
14,
15], much attention has been payed to study the eigenvalues or eigen-spectrum of doubly stochastic matrices. According to the best of our knowledge, however, the study of spectral properties, such as structured singular values for doubly stochastic matrices, is utterly missing from the literature. The current paper deals with the study of the spectral properties, such as singular values and structured singular values for a class of doubly stochastic matrices. The main contribution is to fill this gap which reflects the novelty of our results presented in paper.
The paper is arranged as follows: In
Section 2 we provide definitions of symmetric stochastic matrices, singular values and structured singular values. In
Section 3 we give a detailed explanation of the computation of singular values for symmetric doubly stochastic matrices.
Section 4 of this article contains the geometrical interpretation of eigenvalues and singular values of doubly stochastic matrices. The computation of structured singular values for doubly stochastic matrices is addressed in
Section 5. Whereas the numerical experimentation is discussed in
Section 6.
Section 7 summarizes the conclusions.
3. Computing Singular Values of Doubly Stochastic Matrices
Theorem 1. Let be dimensional symmetric stochastic matrices with row and column sum equals to 1. Let and are singular values with and as left and right singular vectors respectively with for and , are the left and right singular vectors respectively with for . The leading singular vectors and are orthogonal to and for all , respectively. Let be the singular vector corresponding to and then any vector which is orthogonal to is not a singular vector to and
Proof. The result is proved by expanding and taking sum of all components of the singular value problem of the form:
In Equation (
1),
is a singular vector corresponding to a singular value
. The singular vector
is not a singular vector corresponding to singular values
and
Taking sum
of all components of
, we have
because
D is a symmetric stochastic matrix with row and column sums equal to 1. Equation (
2) implies that,
Now, by taking the sum
of righthand side of Equation (
1) gives,
From Equation (
3) and (
4), we have
In turn, this implies that
and
which proves that any vector
orthogonal to vector
which is not a singular vector corresponding to singular values
and
. ☐
Theorem 2. Let be dimensional symmetric stochastic matrices with row and column sum equals to 1. Let and be singular values corresponding to singular vectors as defined in Theorem 1. The matrix is the matrix with and along the main diagonal. The singular values of do not contain original singular values and appearing along the main diagonal of a matrix with The off diagonal of contains the rank-1 matrices and consisting of leading left and right singular vectors corresponding to and , respectively.
Proof. We prove the result by computing the singular vectors of the singular value problem of the form:
In Equation (
6), the set of vectors
for all
is the singular vectors corresponding to singular values
The vector
for all
acts as a singular vector corresponding to
The vector
acts as a singular vector corresponding to singular value
From above discussion it is clear that the vectors of the form
for all
act as a singular vectors for matrix
while the vectors
acts as singular vectors corresponding to singular values
and
of
☐
Theorem 3. Let be two symmetric doubly stochastic matrices. Let and be leading singular values corresponding to singular vectors and , respectively.
Letwith I is an identity matrix with the same dimension as of and and ρ is any constant. The singular values of does not contains the leading singular values of and . The leading singular values are contained in with Proof. We prove the result by computing singular values of singular value problem,
The singular values of
are
,
where
which are the singular values of
Because represent the singular vectors corresponding to singular values can be treated as Similarly for the singular vector holds true. This show that the singular vector corresponding to can be expressed as and finally the vectors act as singular vectors to and ☐
Theorem 4. A two dimensional symmetric doubly stochastic matrix has singular values 1 and if and only if
Proof. To complete the prove its sufficient to see the fact that for
the matrix
is symmetric and doubly stochastic matrix. ☐
Theorem 5. A three dimensional symmetric doubly matrix has singular values if and only if , , and
Proof. The proof is similar to the one in [
15] and hence is omitted. ☐
4. Geometrical Interpretation of Spectrum
In this section, we present the geometrical interpretation of the spectrum of symmetric doubly stochastic matrices. In particular, we discuss the geometry of the eigenspace and singular values and left, right singular vectors of such a class of matrices.
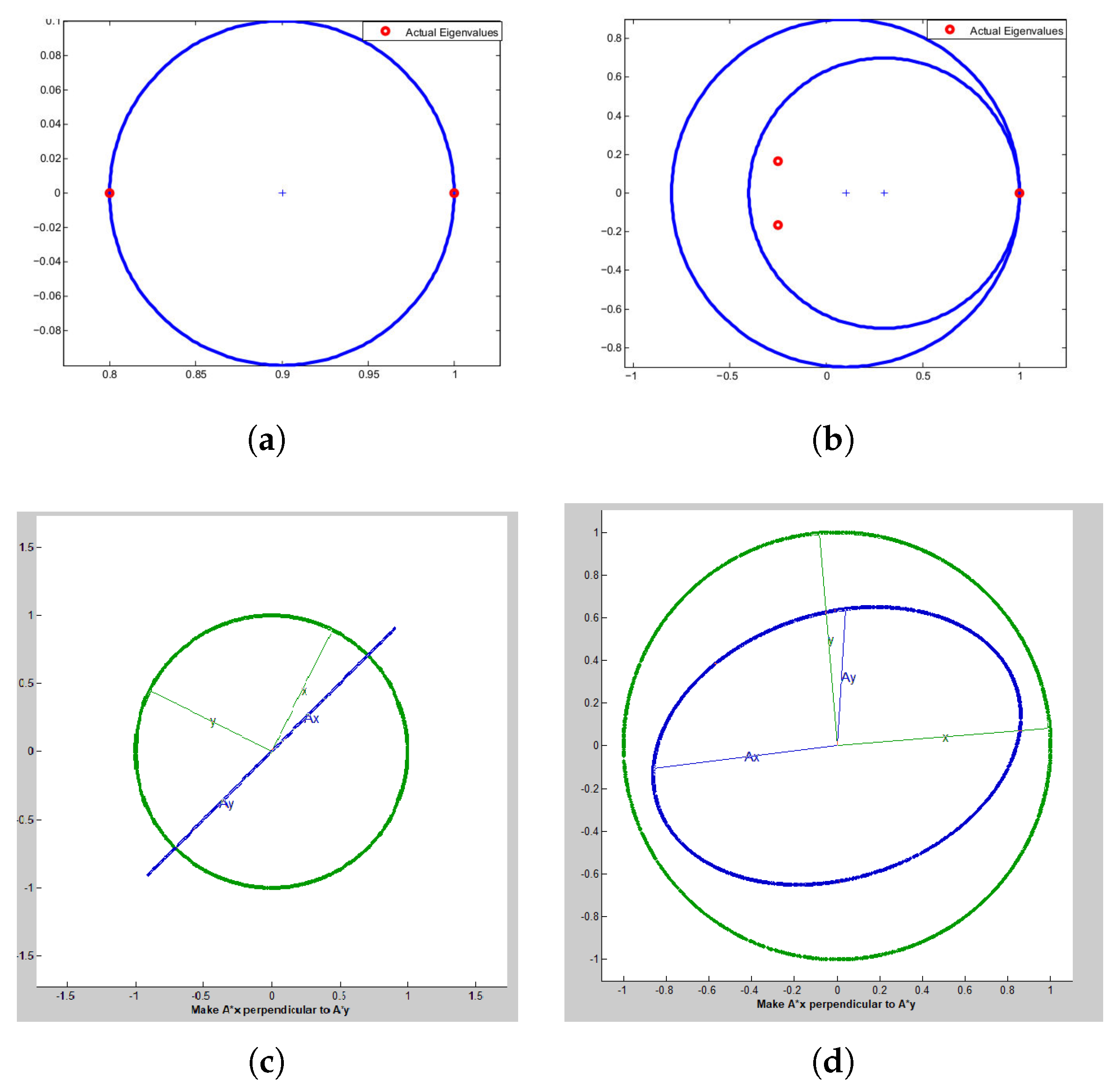
Example 1. We take doubly stochastic matrices and taken from [16] as The spectrum of
is shown in
Figure 1a,b of Example 1, respectively. The maximum eigenvalue for both
is 1 and lies exactly on the spectral circle. The
Figure 1c,d show the geometrical interpretation of the singular values and singular vectors obtained for
of Example 1, respectively.
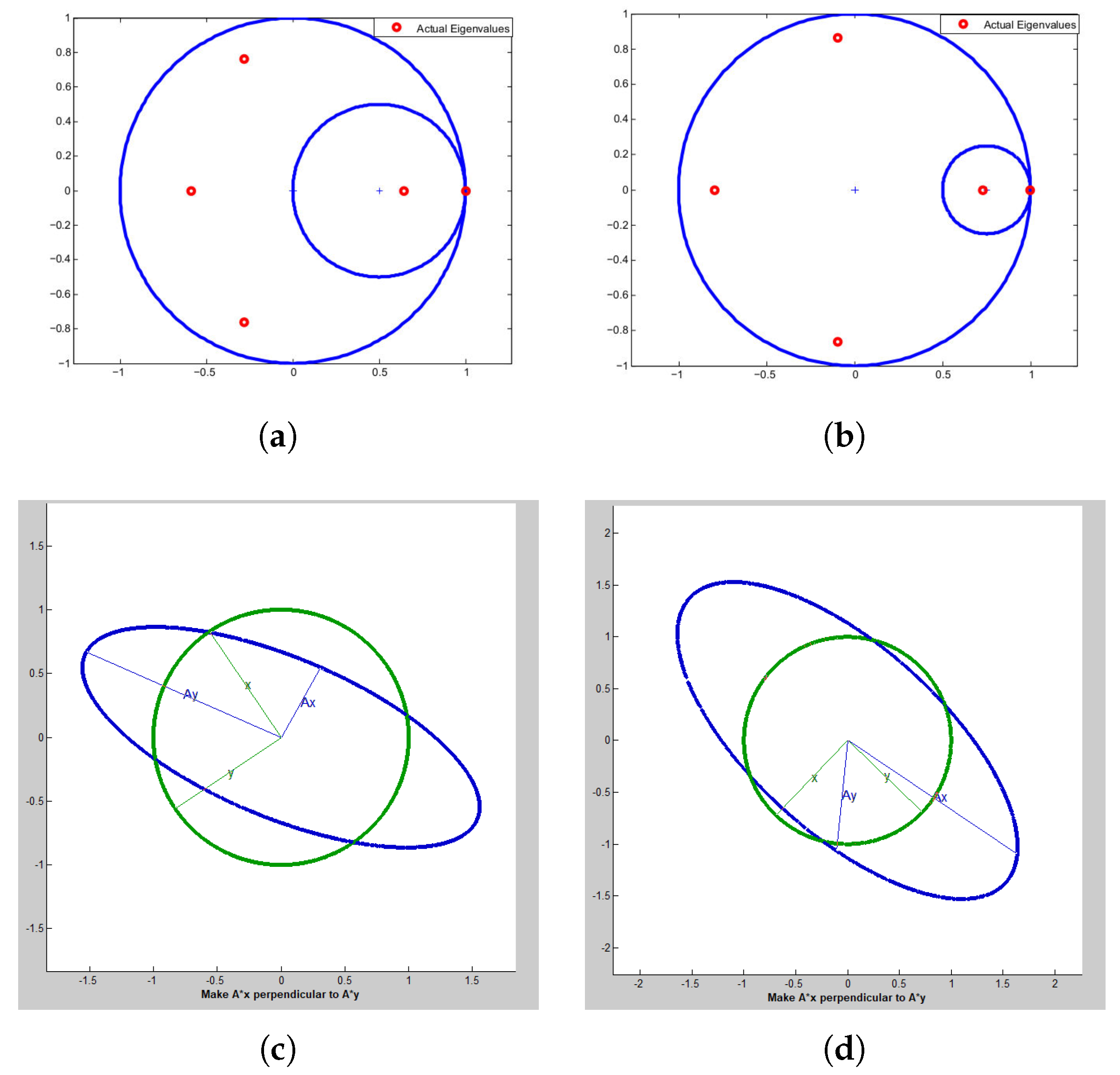
Example 2. We take five dimensional doubly stochastic matrices from [17] as The spectrum of
is shown in
Figure 2a,b of Example 2, respectively. The maximum eigenvalue for both
is 1 and lies exactly on the spectral circle.
Figure 2c,d show the geometrical interpretation of the singular values and singular vectors obtained for
of Example 2, respectively.
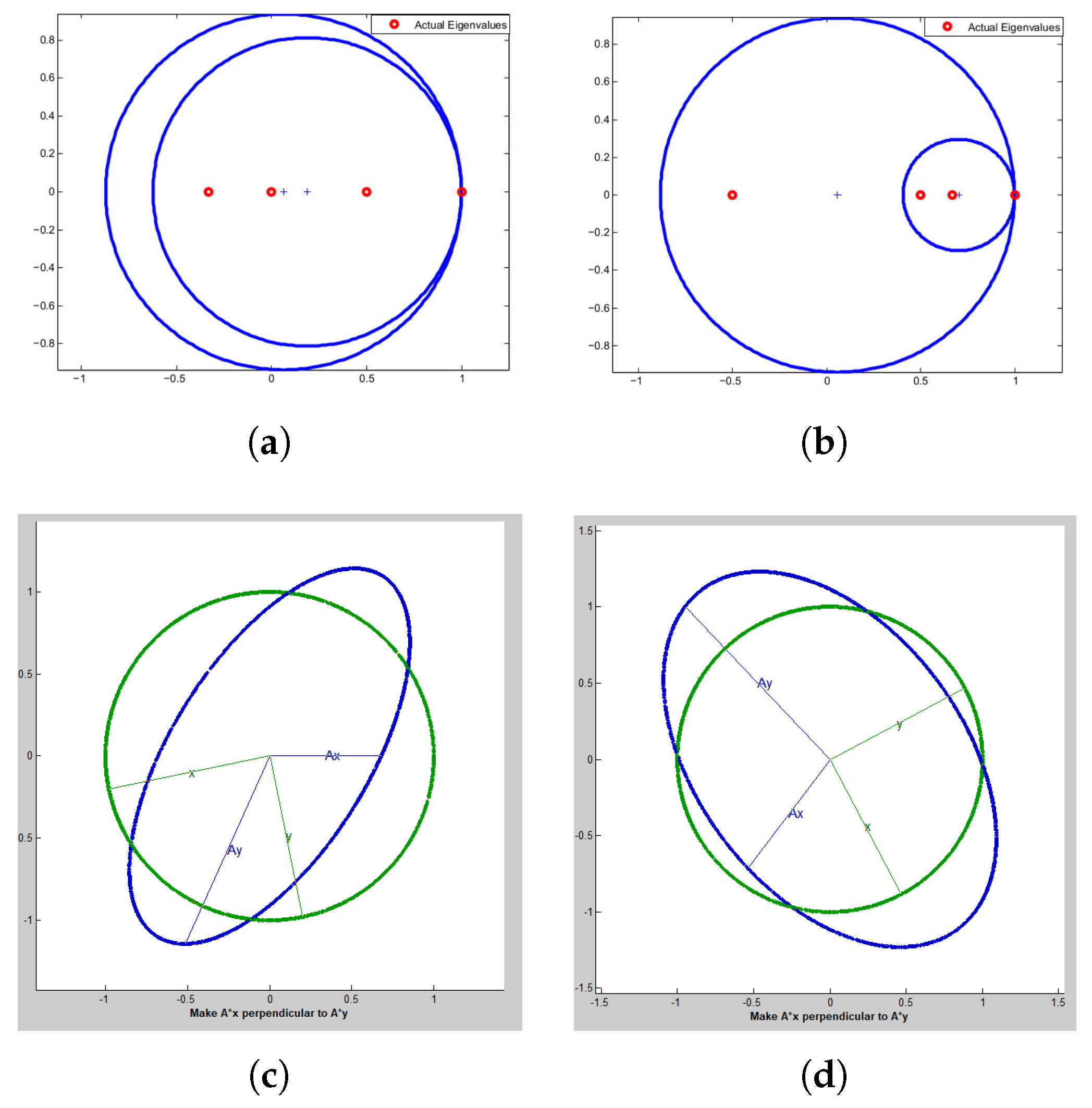
Example 3. We take eight and nine dimensional doubly stochastic matrices from [18]. The largest eigenvalue corresponding to each matrix attains the maximum value 1. The spectrum is shown in Figure 3a,b of Example 3, respectively. The Figure 3c,d show the geometrical interpretation of the singular values and singular vectors of Example 3, respectively. 5. Computing Structured Singular Values
In this section, our aim is to discuss the spectral properties of doubly stochastic matrices based on the computation of Structured Singular Values (SSV). For this purpose, we compute SSV for a class of matrices as considered in
Section 4. SSV is the straight forward generalization of the singular values for the constant matrices. The computation of the exact value of SSV is NP-hard. For this reason, one needs to approximate its bounds, i.e., lower and upper bounds.
From an application point of view, the computation of lower bounds of SSV gives sufficient information about the instability of some feedback system while the upper bounds discuss the stability of feedback system under consideration. The computation of the bounds of SSV presented in this section is based on two powerful mathematical techniques: First technique is based on power method for approximating spectrum [
19]. The upper bound of SSV is computed by means of the balanced/AMI technique [
20] for computing the upper bound from [
21]. The second technique [
22] is based on the low rank ODEs-based techniques in order to approximate the lower bounds of SSV. This technique works on a two level algorithm, i.e., inner-outer algorithm. We give a brief description of inner-outer algorithms in the subsequent subsections.
5.1. Inner-Algorithm
The inner-algorithm is used to solve the minimization problem addressed in Equation (
5). For this purpose, one needs to construct and then solve a gradient system of ordinary differential equations associated with the optimization problem. The construction of system of ODEs involves the approximation of the local extremizers of structured spectral values sets [
22]. Following Theorem 6 helps us to approximate the local extremizer of structured spectral vale sets
Theorem 6. [22]. For a perturbation with the block diagonal structurewith acts as a local extremizer of structured spectral value set. For a simple smallest eigenvalue of matrix valued function with the right and left eigenvetors x and y scaled as and let . The non-degeneracy conditionshold. Then the magnitude of each complex scalar appears to be exactly equal to 1 while each full block possesses a unit 2-norm. Proof. For proof we refer to [
22].
The system of ordinary differential equations corresponding to a perturbation
is to approximate an extremizer of smallest eigenvalue in magnitude, i.e.,
which is obtained as,
where
for
and
is a characteristic function. For further discussion on the construction of system of ordinary differential equations in above equations, we refer to [
22]. ☐
5.2. Outer-Algorithm
The main aim of the outer-algorithm is to vary a small positive parameter
known as the perturbation level. To vary perturbation level a fast Newton’s iteration was used in [
22]. The quantity
provides the approximation of lower bound to SSV.
The fast Newton’s iteration to solve a problem is
To solve Equation (
10), we compute the derivative
To compute , one need following Theorem 7
Theorem 7. [22]. Let be the matrix valued function and let x and y as a function of are right and left eigenvectors of the perturbed matrix . Consider the scaling of vectors x and y accordingly to Theorem 6. Let and consider that the non-degenracy conditions as discussed in Theorem 6 holds true, then it yields that For the proof of the above statement, we refer to [
22].