A Survey on Symmetry Group of Polyhedral Graphs

Abstract

Every three-connected simple planar graph is a polyhedral graph and a cubic polyhedral graph with pentagonal and hexagonal faces is called as a classical fullerene. The aim of this paper is to survey some results about the symmetry group of cubic polyhedral graphs. We show that the order of symmetry group of such graphs divides 240.

1. Introduction

In the present work, all graphs are connected without loops and parallel edges, which we call simple graphs. An automorphism of a graph is a permutation on the set of vertices which preserves the edge set. We denote the image of automorphism $\beta$ of graph $\Gamma$ on the vertex u by $\beta (u)$. The set $Aut(\Gamma )=\{\alpha (u):\alpha$ is an automorphism } with the operation of composition is a permutation group on $V(\Gamma )$ and we call it as automorphism group of $\Gamma$. The first mathematician who considered the graph automorphism was Frucht. In addition, the numerical measures based on automorphisms of a graph have been investigated in reference [1]. A fullerene is a cubic three-connected graph whose faces are pentagons and hexagons. All three connected cubic planar graphs with hexagons and pentagons are called as fullerenes and we donote them by PH-fullerenes, see [2,3]. On the other hand, a three-connected cubic planar graph whose faces are triangles and hexagons is denoted by a TH-fullerene and a SH-fullerene is a three connected cubic planar graph with quadrangles and hexagons. See the references [4,5,6] as well as [7,8,9,10,11], for studying problems concerning with fullerene graphs. In mathematical aspects, fullerenes are member of a big family of larger graphs, namely the polyhedral graphs. In general, a polyhedral graph is three connected planar but in this paper, we just consider cubic polyhedral graphs, see [12,13,14,15]. We denote a cubic polyhedral graph with t triangles, s quadrangles, p pentagonal and h hexagonal faces and no other faces by a $(t,s,p,h)-$polyhedral or briefly a $(t,s,p)$-polyhedral graph. This yields that in a SPH-polyhedral graph all faces are tetragons, pentagons and hexagons. Here, we enumerate the number of edges of a SPH-polyhedral graph F. It is clear that each vertex lies in three faces, because F is 3-regular. In addition, we enumerate each edge two times. Hence, $\left|V\right|=(4s+5p+6h)/3$, $\left|E\right|=(4s+5p+6h)/2=3n/2$ and the number of faces is $f=s+p+h$. The Euler’s formula yields that $n-m+f=2$ and so $(4s+5p+6h)/3-(4s+5p+6h)/2+s+h+p=2$. This means that $p=12-2s$ and $h=n/2+s-10$. Since $p\ge 0$ we get $s\le 6$ and the following cases hold:

Case 1. If $s=0$, then F is a fullerene and $|Aut(F)|$ divides 120.

Cases 2–6. If s is either the number 1 or 2 or 3 or 4 or 5, then p is 10 or 8 or 6 or 4 or 2, respectively.

Case 7. If $s=6$, then one can deduce that $p=0$ and thus F is a SPH-fullerene and $|Aut(F)|$ divides 24.

By above notation, we denote a polyhedral graph with triangles, pentagons and hexagons by a TPH-polyhedral graph. Suppose t is the number of triangles in F, then above discussion yields that $p=12-3s$, $h=n/2+s-10$ and $s\le 4$. If $s=0$, then F is a fullerene. If s is one the integers 1 or 2 or 3, then p is 9 or 6 or 3, respectively. If $s=4$, then $p=0$ and thus F is a TH-fullerene.

One can easily see that in a TSH-polyhedral graph with t triangles, s squares and h hexagons, we yield that $n=(3t+4s+6h)/3$, $m=(3t+4s+6h)/2$ and $f=t+s+h$. Consequently, we obtain either $s=0$ or $s=3$ or $s=6$. If $s=0$, then F is TH-fullerene. If $s=6$, then $t=0$ and F is SH-fullerene. If $s=3$, then $t=2$ and F is a polyhedral graph with exactly two triangles, three squares and h hexagons. The cube graph $Q_3$ is the smallest SPH-polyhedral graph which has no hexagonal face, see Figure 1a. The symmetry group of this graph is isomorphic to ${\mathbb{Z}}_2\times {\mathbb{S}}_4$, see [16]. The pyramid is the smallest TPH-polyhedral graph, see Figure 1b. The smallest TSH-polyhedral graph has no hexagon, see Figure 1c.

Figure 1. The smallest SPH, TPH and TSH polyhedral graphs.

Much research about fullerene was started after producing fullerenes in bulk quantities in 1990, see [17]. Fullerene chemistry is nowadays a well-established field of both theoretical and experimental investigations. The initial enchanting appeal of fullerenes goes back to the high symmetry of these carbon nanostructures, see [18,19] but nowadays the fullerene era is a field of both theoretical and experimental research. The most important problem, with many applications in a large number of area, is finding the symmetry of molecules. There are several ways to determine the symmetry of a molecule. For example, Randić [20,21] and then Balasubramanian [22,23,24,25,26,27,28,29] studied the Euclidean matrix of a chemical graph to find the symmetry group. However, there is a classic theorem in algebraic graph theory which yields the automorphism group of each graph. Suppose $\sigma \in S_n$ is an arbitrary permutation. Then, the permutation matrix P${}_{\sigma }$ is defined as P${}_{\sigma }$ = $\left[x_{ij}\right]$, where x${}_{ij}$ = 1 if i = $\sigma$(j) and 0, otherwise. It is easy to see that the set of all n×n permutation matrices is a group isomorphic to the symmetric group S${}_n$ on n symbols. Moreover, a permutation $\sigma \in S_n$ is a graph automorphism, if it satisfies P${}_{\sigma }$A = AP${}_{\sigma }$, where A is the adjacency matrix of G. In general, the symmetry group and the point-group symmetry of a graph are not isomorphic but about the regular polehedral graphs they are the same. By usung this fact, the authors of [30] computed the symmetry of all fullerenes with up to 70 vertices. In the present paper, we deal with the symmetry properties of fullerene graphs and we compute the symmetry group of several infinite classes of fullerene graphs. One of the aim of computing the symmetry of fullerenes is to enumerate the number of isomers whose number increases very quickly with n. A number of papers deal with the symmetry of fullerene isomers and related species [31,32,33]. The first author computed the automorphism group of some infinite families of fullerene graphs by using GAP programs [34]. Here, we improve the mentioned algorithm to compute the automorphism group of these fullerene graphs. Further, this paper bears some novel results significant for algorithmization of the fullerene graph machine analysis.

2. Main Results

A polyhedral graph with either isolated squares or isolated pentagons is called respectively as ISR or IPR polyhedral graph. Here, we consider only the ISR and IPR polyhedral graphs. In [7] Fowler et al. showed that there are only 28 point groups that a fullerene can be realized. In [35] the author investigated that for a PH-fullerene graph F, $|Aut(F)|$ divides 120. Similar results obtained by Ghorbani et al. in [36,37] who showed that if F is a $TH$-polyhedral graph or a $SH$-polyhedral graph, then $|Aut(F)|$ divides 24 or 48, respectively. They also determined the order of automorphism groups of all TSH, TPH and SPH-polyhedral graphs, see [38]. In other words, they proved the following results.

Proposition 1.

[38] If F is both ISR and IPR, and it is either an SPH or TSH or TPH-polyhedral graph, then for the vertex $u\in V(F)$, we yield that the stabilizer $Aut{(F)}_u$ is trivial or it is isomorphic to one of three groups: the cyclic group $Z_2$, the cyclic group $Z_3$ and the symmetric group $S_3$.

Theorem 1.

[38] Let F be both ISR and IPR, SPH-polyhedral graph, G be a TSH-polyhedral graph and L be a TPH-polyhedral graph. Then $Aut(F)$ is a $\{2,3,5\}$-group and both $Aut(G)$ and $Aut(L)$ are $\{2,3\}$-group. Moreover, $|Aut(F)|$ divides $2^4\times 3\times 5$, $|Aut(G)|$ divides $2^4\times 3$ and $|Aut(L)|$ divides $2^3\times 3$.

In [13] Deza et al. investigated the list of allowed symmetry groups of smallest polyhedral graphs, see [7,14,15].

Theorem 2.

Fora cubic $(t,s,p)$-polyhedral graphs, the possible point groups and the number of vertices of the smallest one are

i. 

$(t,s,p)=(4,0,0)$:

${\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,D_8,A_4,S_4.$

ii. 

$(t,s,p)=(0,6,0):$

$$\begin{gathered} C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,S_3,D_8,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2, \\ {\mathbb{Z}}_2\times S_3,D_{12},D_6,{\mathbb{Z}}_2\times D_{12},{\mathbb{Z}}_2\times D_6,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times D_6. \end{gathered}$$

iii. 

$(t,s,p)=(0,0,12):$

$$\begin{gathered} C_1,{\mathbb{Z}}_2,A_3,,{\mathbb{Z}}_4,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,S_3,S_6,S_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,D_8,{\mathbb{Z}}_2\times {\mathbb{Z}}_5,D_{12},{\mathbb{Z}}_2\times S_3, \\ {A}_4,D_{20},{\mathbb{Z}}_2{D}_{12},D_{24},S_4,A_4\times Z_2,A_5,{\mathbb{Z}}_2\times A_5. \end{gathered}$$

Theorem 3.

Suppose F is a cubic polyhedral graph with at least two face sizes chosen from $\{3,4,5\}$ and no faces of size greater than 6. Then the possible point groups and vertex counts of minimal examples are

i. 

$(t,s,p)=(3,1,1)$:

$C_1,{\mathbb{Z}}_2.$

ii. 

$(t,s,p)=(3,0,3):$

$C_1,{\mathbb{Z}}_2,A_3,S_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_3.$

iii. 

$(t,s,p)=(2,3,0):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,S_3,D_{12}.$

iv. 

$(t,s,p)=(2,2,2):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2.$

v. 

$(t,s,p)=(2,1,4):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2.$

vi. 

$(t,s,p)=(2,0,6):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,S_3,{\mathbb{Z}}_2\times S_3,D_{12}.$

vii. 

$(t,s,p)=(1,4,1):$

$C_1,{\mathbb{Z}}_2.$

viii. 

$(t,s,p)=(1,3,3):$

$C_1,{\mathbb{Z}}_2,A_3,S_3.$

ix. 

$(t,s,p)=(1,2,5):$

$C_1,{\mathbb{Z}}_2.$

x. 

$(t,s,p)=(1,1,7):$

$C_1,{\mathbb{Z}}_2.$

xi. 

$(t,s,p)=(1,0,9):$

$C_1,{\mathbb{Z}}_2,A_3,S_3.$

xii. 

$(t,s,p)=(0,5,2):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_5,D_{20}.$

xiii. 

$(t,s,p)=(0,4,4):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,D_8,{\mathbb{Z}}_4.$

xiv. 

$(t,s,p)=(0,3,6):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,A_3,{\mathbb{Z}}_2\times {\mathbb{Z}}_3,S_3,D_{12}.$

xv. 

$(t,s,p)=(0,2,8):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2,D_8,{\mathbb{Z}}_2\times D_8,D_{16},{\mathbb{Z}}_2\times {\mathbb{Z}}_2\times {\mathbb{Z}}_2,{\mathbb{Z}}_4.$

xvi. 

$(t,s,p)=(0,1,10):$

$C_1,{\mathbb{Z}}_2,{\mathbb{Z}}_2\times {\mathbb{Z}}_2.$

3. Symmetry Group and Group Action

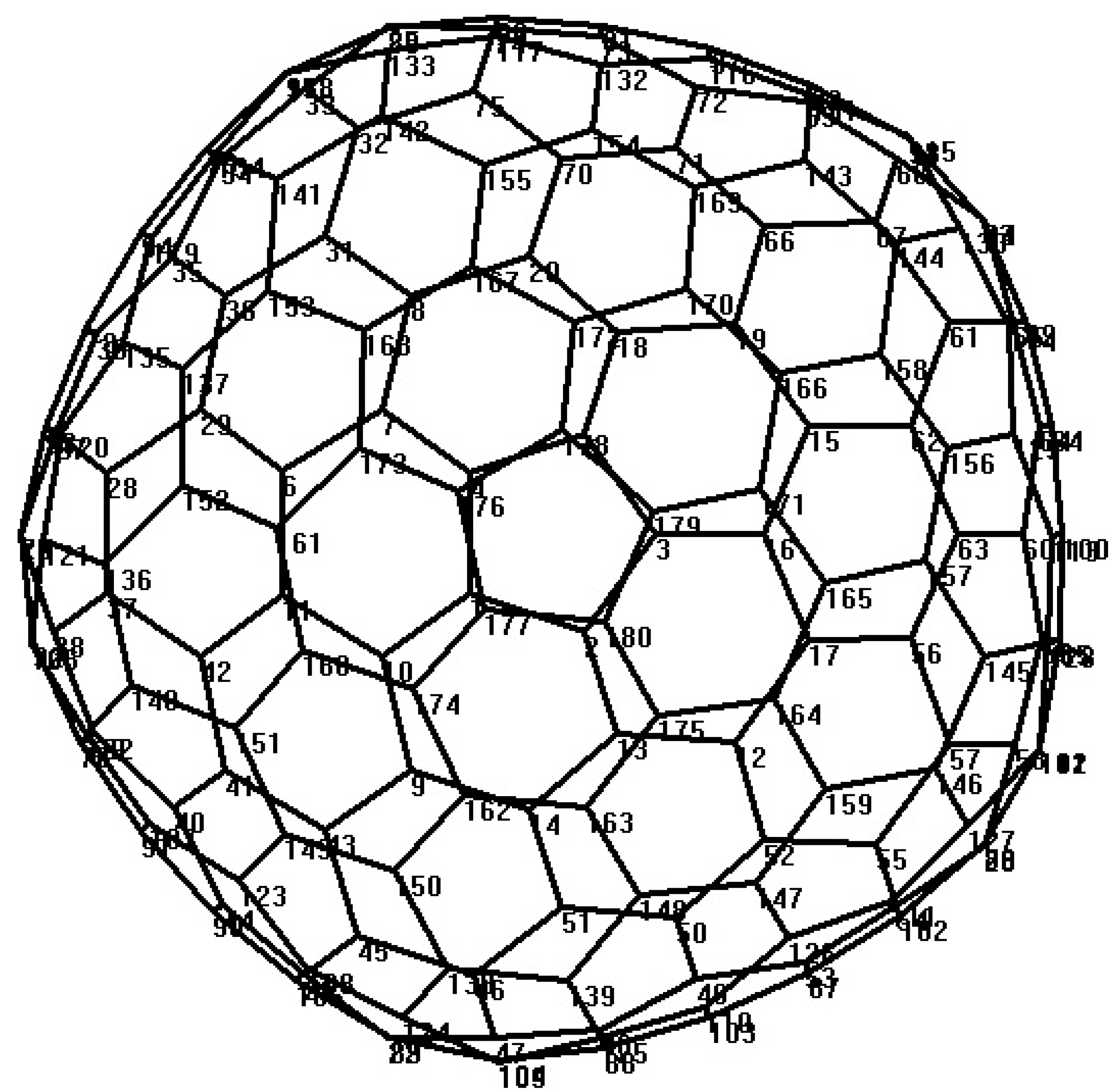
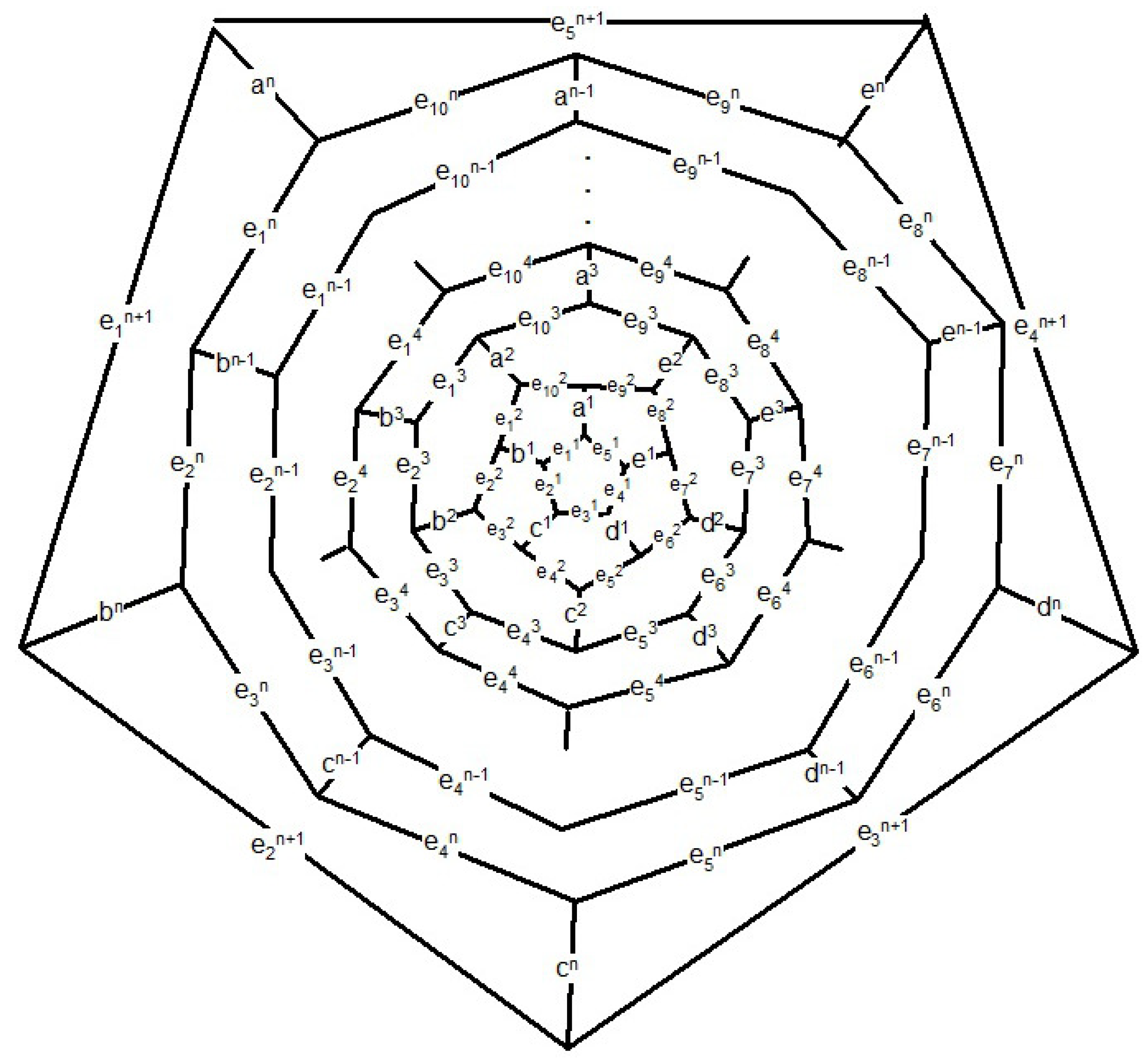
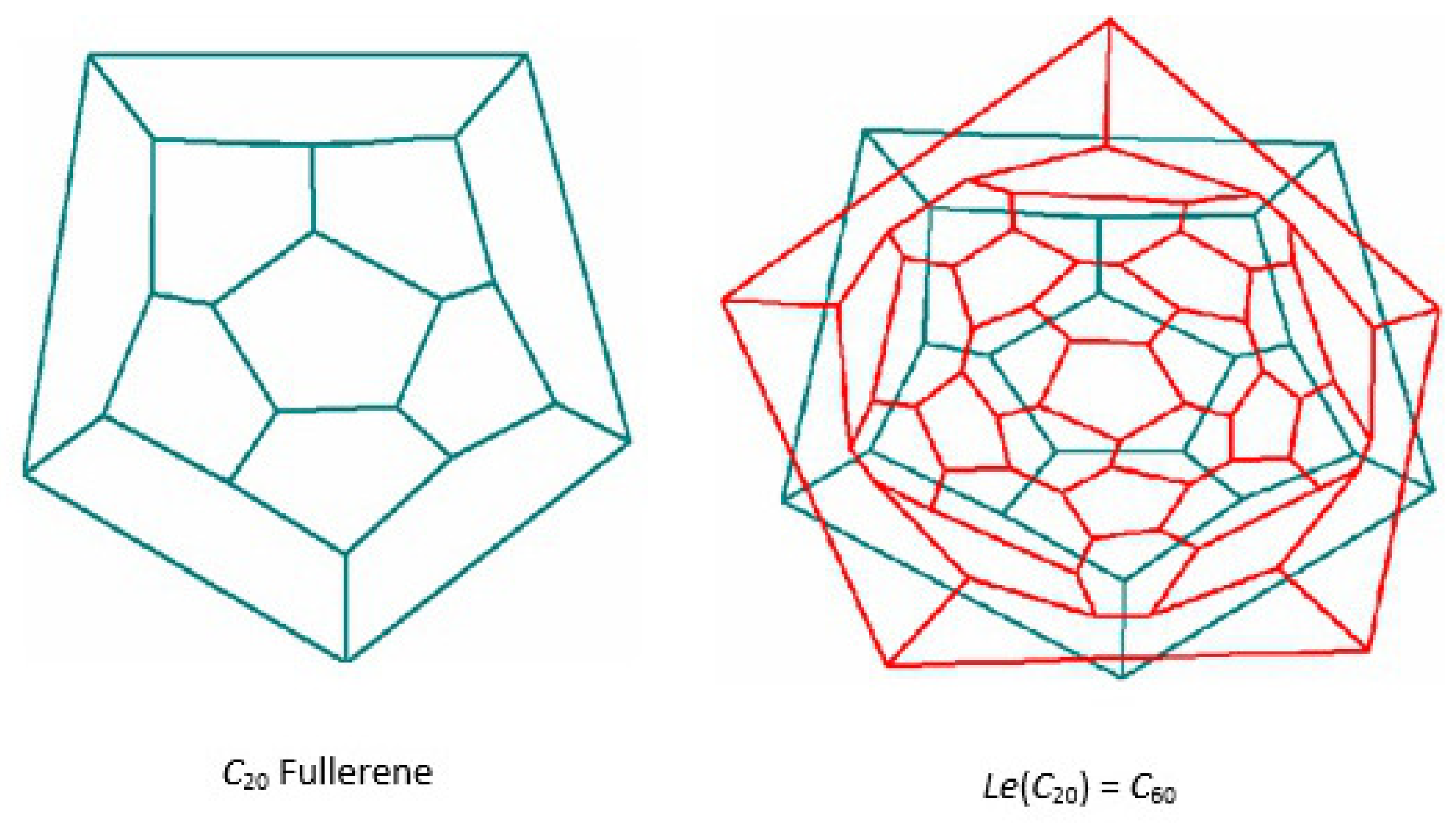
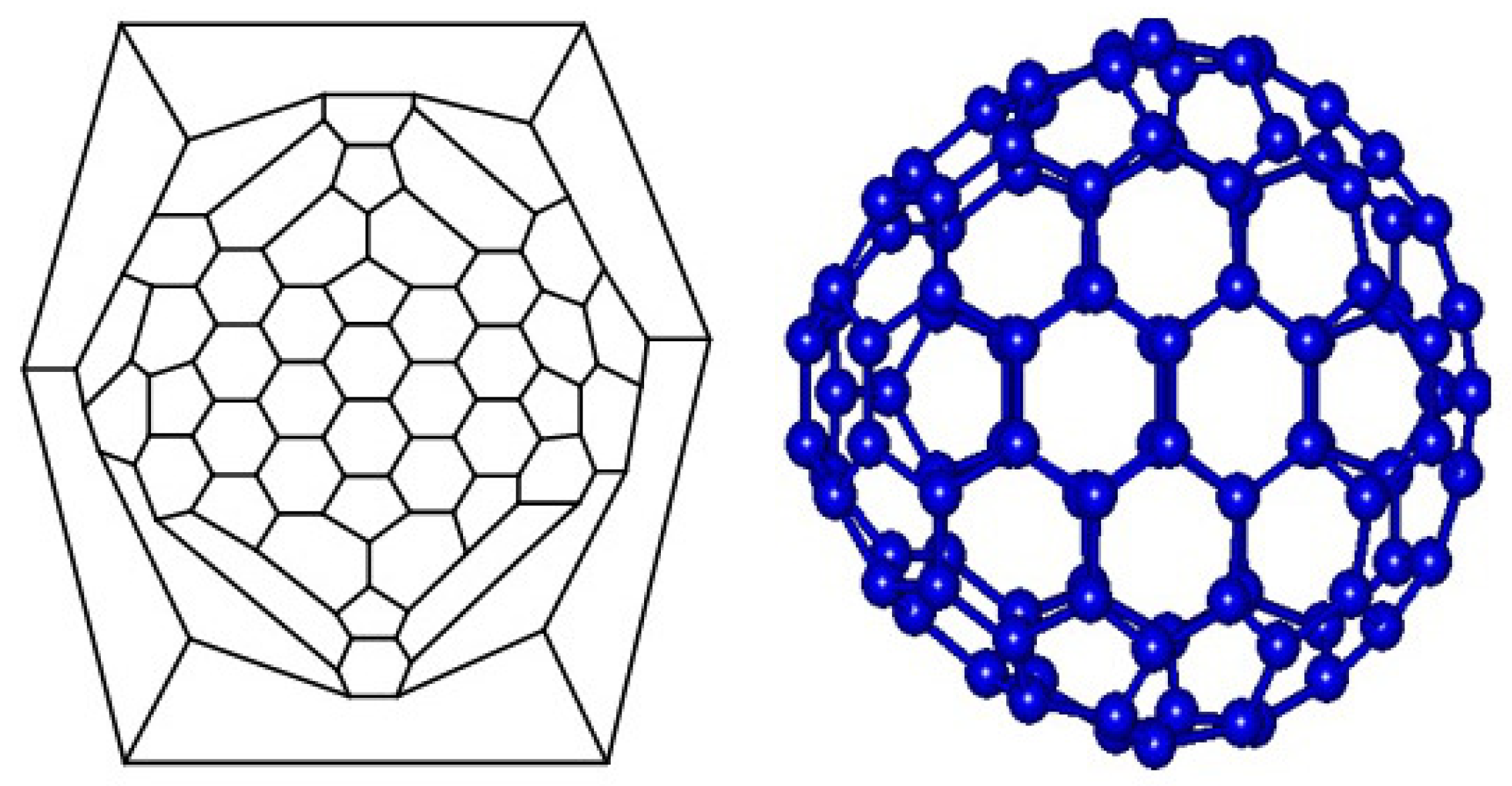
Symmetry has a significant role in the analysis of the structure, bonding and spectroscopy of molecules. A classification of molecules can be done by their symmetry. As we mentioned in the last section, about the fullerene graphs, the symmetry group and the point group are the same. The name point group is also given, because the symmetry elements such as points, lines and planes intersect at a single point. Symmetry elements include mirror planes, axes of rotation, centers of inversion and improper axes of rotation, and all of them are properties related to the structure of the molecule. All molecules have an operation which leaves the molecule where it is and we call it as identity operation. Certain physical properties of molecules are clearly linked to molecular symmetry. For example, molecules with a center of inversion or a mirror plane cannot be chiral. Let F be a fullerene with symmetry group $G=Aut(F)$. The orbit of a vertex $u\in V(F)$ is $u^G=\{u^g,g\in G\}$. The stabilizer of the vertex $u\in V(G)$ is defined as $G_u=\{g\in G:u^g=u\}.$ Let $H=G_u$, then for $u,v\in V(F)$, $H_v$ is denoted by $G_{u,v}$. The orbit-stabilizer theorem implies that $|u^G|.|G_u|=|G|$. For every $g\in G$, let $fix(g)=\{u\in V(F),u^g=u\}$, then we yield the following result.

Lemma 1.

(Cauchy–Frobenius Lemma)Let G acts on set $V(F)$, then the number of orbits of G is

$$O=\frac{1}{\left|G\right|}\sum _{g\in G}\left|fix(g)\right|.$$

(1)

For every edge e = uv and every automorphism $\alpha \in Aut(G)$, define $\overline{\alpha }(e)=\{\alpha (u),\alpha (v)\}.$ Thus, Aut(G) acts on the set of edges by above definition and the Cauchy–Frobenius Lemma for the set of edges can be rewritten as follows:

$$\overline{O}=\frac{1}{|\overline{G}|}\sum _{\overline{g}\in \overline{G}}\left|fix(\overline{g})\right|.$$

(2)

The novelty of this work is that we apply Cauchy–Frobenius Lemma to compute the whole symmetry group of given infinite family of graphs. In the references [37,39], the symmetry group of several infinite families of fullerene graphs have been determined by aid of GAP [34] program, but in this paper we use from the method given in [36,38]. Here is the first attempt to compute the symmetry group by thus way. To explain our method, at first, we investigate the symmetry group of molecular graph $C_{24}$ shown in Figure 2. In [39] the symmetry group of $C_{24}$ is computed and it is isomorphic with the group $Z_2\times S_4$.

Figure 2. 3-D graph of fullerene C${}_{24}$.

Example 1.

Consider now the molecular graph of fullerene $C_{80}$, Figure 3. Here, we show that the symmetry group of fullerene graph $C_{80}$ is isomorphic with a dihedral group of order 20, namely D${}_{20}$. To do this, by using concept of symmetry, one can see that the generators of fullerene graph C${}_{80}$ are as follows:

$$\begin{array}{ccc}\hfill X& =& (2,16)(4,14)(5,18)(6,17)(7,20)(8,19)(9,36)(10,35)(11,34)(12,33)(13,49)\hfill \\ & & (15,51)(21,24)(22,23)(25,37)(26,52)(27,39)(28,50)(29,54)(30,53)(31,56)\hfill \\ & & (32,55)(38,40)(41,42)(43,44)(45,60)(46,59)(47,58)(48,57)(62,67)(63,66)\hfill \\ & & (65,77)(68,80)(69,73)(70,79)(71,78)(72,76)(74,75),\hfill \\ \hfill Y& =& (1,65)(2,66)(3,68)(4,67)(5,48)(6,45)(7,46)(8,47)(9,42)(10,43)(11,44)\hfill \\ & & (12,41)(13,69)(14,70)(15,72)(16,71)(17,36)(18,33)(19,34)(20,35)(21,30)\hfill \\ & & (22,31)(23,32)(24,29)(25,73)(26,74)(27,76)(28,75)(37,77)(38,78)(39,80)\hfill \\ & & (40,79)(49,61)(50,62)(51,64)(52,63)(53,60)(54,57)(55,58)(56,59).\hfill \end{array}$$

By a GAP program, one can see that X${}^2$ = Y${}^2$ = (XY)${}^{10}$ = 1 and X${}^{-1}$(XY)X =(XY)${}^{-1}$.

Figure 3. 3-D graph of fullerene C${}_{80}$.

In continuing, consider the molecular graph of fullerene C${}_{84}$, Figure 4. We prove that the symmetry group of the C${}_{84}$ fullerene is isomorphic to the group S${}_4$. To do this, suppose G is the symmetry group of this fullerene. Then G = ⟨X, Y⟩, where X and Y are the following permutations:

$$\begin{array}{ccc}\hfill X& =& (1,2)(3,4)(5,8)(6,80)(7,81)(9,18)(10,19)(11,20)(12,78)(14,83)(15,82)\hfill \\ & & (17,84)(21,54)(22,77)(23,55)(24,79)(25,76)(26,27)(28,59)(29,60)(30,57)\hfill \\ & & (31,58)(32,66)(33,70)(34,72)(35,67)(36,64)(37,65)(38,74)(39,73)(40,75)\hfill \\ & & (41,56)(42,51)(43,53)(44,52)(45,48)(46,49)(47,50)(61,71)(62,63)(68,69),\hfill \\ \hfill Y& =& (1,76,31,69)(2,59,30,40)(3,79,28,68)(4,58,29,39)(5,51,35,17)\hfill \\ & & (6,84,49,66)(7,83,48,65)(8,80,41,71)(9,77,42,61)(10,78,43,62)\hfill \\ & & (11,81,44,63)(12,82,45,64)(13,55,27,33)(14,20,53,36)(15,19,52,37)\hfill \\ & & (16,54,26,34)(18,56,32,38)(21,72,23,70)(22,74,46,67)(24,73,50,57)\hfill \\ & & (25,75,47,60).\hfill \end{array}$$

Figure 4. 3-D graph of fullerene C${}_{84}$.

Now consider the molecular graph of fullerene $C_{150}$ as given in Figure 5. In [39] it is proved that the symmetry group of C${}_{150}$ is isomorphic with dihedral group D${}_{20}$.

Figure 5. 3-D graph of fullerene C${}_{150}$.

Example 2.

Consider the fullerene graph ${\mathit{C}}_{10n}$ (n is even) as depicted in Figure 6. The vertices of central pentagon is labeled by $\{1^1,2^1,3^1,4^1,5^1\}$. These vertices compose the first layer of $C_{10n}$. The vertices of the second layer are the boundary vertices of five pentagons adjacent with the central pentagon and so on. In [40], it is shown that the following elements are in the automorphism group of fullerene graph ${\mathit{C}}_{10n}$. The automorphism α is a symmetry element in which $fix(\alpha )=\{1^1,{10}^2,{10}^3,\cdots ,{10}^n,5^2,5^3,\cdots ,5^n,3^{n+1}\}$ and σ$=(1^1,1^{n+1},2^1,2^{n+1},3^1,3^{n+1},4^1,4^{n+1},5^1,5^{n+1})(1^2,2^n,3^2,4^n,5^2,6^n,7^2,8^n,9^2,{10}^n)(2^2,3^n,4^2,5^n,6^2,7^n,8^2,9^n,{10}^2,1^n)(1^3,2^{n-1},3^3,4^{n-1},5^3,6^{n-1},7^3,8^{n-1},9^3,{10}^{n-1})(2^3,3^{n-1},4^3,5^{n-1},6^3,7^{n-1},8^3,9^{n-1},{10}^3,1^{n-1})\cdots (1^{n/2},2^{(n+4)/2},3^{n/2},4^{(n+4)/2},5^{n/2},6^{(n+4)/2},7^{n/2},8^{(n+4)/2},9^{n/2},{10}^{(n+4)/2})(2^{n/2},3^{(n+4)/2},4^{n/2},5^{(n+4)/2},6^{n/2},7^{(n+4)/2},8^{n/2},9^{(n+4)/2},{10}^{n/2},1^{(n+4)/2})(1^{(n+2)/2},2^{(n+2)/2},3^{(n+2)/2},4^{(n+2)/2},5^{(n+2)/2},6^{(n+2)/2},7^{(n+2)/2},8^{(n+2)/2},9^{(n+2)/2},{10}^{(n+2)/2}).$ It is clear that ${\alpha }^2={\sigma }^{10}=1,\alpha \sigma \alpha ={\sigma }^{-1}$ and $G=⟨\alpha ,\sigma ⟩\le A=Aut({\mathrm{C}}_{10n})$. On the other hand, every symmetry element which fixes $1^1$, must also fix $\{{10}^2,{10}^3,\cdots ,{10}^n,5^2,5^3,\cdots ,5^n,3^{n+1}\}$. The identity element and the symmetry element α do this. Hence, the orbit-stabilizer property ensures that |A| = | $1^1$${}^A$|.|A${}_{1^1}$| and thus $\left|A\right|=10\times 2=20$ which implies that $A\cong D_{20}.$ The orbits of the automorphism group are given in Table 1.

Figure 6. C${}_{10}$${}_n$,n is even.

Table 1. The structure of orbit elements of $C_{10n}$, n is even.

Vertex	The Structure of Orbit Elements
1${}^1$	$1^1,2^1,3^1,4^1,5^1,1^{n+1},2^{n+1},3^{n+1},4^{n+1},5^{n+1}$
1${}^2$	$1^2,3^2,5^2,7^2,9^2,2^n,4^n,6^n,8^n,{10}^n$
2${}^2$	$2^2,4^2,6^2,8^2,{10}^2,1^n,3^n,5^n,7^n,9^n$
⋮	⋮
1${}^{n/2}$	$1^{n/2},3^{n/2},5^{n/2},7^{n/2},9^{n/2},$
	$2^{(n+4)/2},4^{(n+4)/2},6^{(n+4)/2},8^{(n+4)/2},{10}^{(n+4)/2}$
2${}^{n/2}$	$2^{n/2},4^{n/2},6^{n/2},8^{n/2},{10}^{n/2},$
	$1^{(n+4)/2},3^{(n+4)/2},5^{(n+4)/2},7^{(n+4)/2},9^{(n+4)/2}$
1${}^{(n+2)/2}$	$1^{(n+2)/2},2^{(n+2)/2},3^{(n+2)/2},4^{(n+2)/2},5^{(n+2)/2},$
	$6^{(n+2)/2},7^{(n+2)/2},8^{(n+2)/2},9^{(n+2)/2},{10}^{(n+2)/2}$

Example 3.

Consider the fullerene graph $C_{10n}$ (n is odd) as depicted in Figure 7. Assume that α is a symmetry element with fixpoints $\{1^1,{10}^2,{10}^3,\cdots ,{10}^n,1^{n+1},5^2,5^3,\cdots ,5^n\}$ and σ is a symmetry element by the following permutation presentation: σ$=(1^1,4^{n+1},2^1,5^{n+1},3^1,1^{n+1},4^1,2^{n+1},5^1,3^{n+1})(1^2,7^n,3^2,9^n,5^2,1^n,7^2,3^n,9^2,5^n)(2^2,8^n,4^2,{10}^n,6^2,2^n,8^2,4^n,{10}^2,6^n)(1^3,7^{n-1},3^3,9^{n-1},5^3,1^{n-1},7^3,3^{n-1},9^3,5^{n-1})(2^3,8^{n-1},4^3,{10}^{n-1},6^3,2^{n-1},8^3,4^{n-1},{10}^3,6^{n-1})\cdots (1^{(n+1)/2},7^{(n+3)/2},3^{(n+1)/2},9^{(n+3)/2},5^{(n+1)/2},1^{(n+3)/2},7^{(n+1)/2},3^{(n+3)/2},9^{(n+1)/2},5^{(n+3)/2})(2^{(n+1)/2},8^{(n+3)/2},4^{(n+1)/2},{10}^{(n+3)/2},6^{(n+1)/2},2^{(n+3)/2},8^{(n+1)/2},4^{(n+3)/2},{10}^{(n+1)/2},6^{(n+3)/2}).$ Similar to the last case, one can see $G=⟨\alpha ,\sigma ⟩=Aut({\mathrm{C}}_{10n})$ is isomorphic with dihedral group D${}_{20}$. The orbits of the automorphism group are given in Table 2.

Figure 7. C${}_{10}$${}_n$,n is odd.

Table 2. The structure of orbit elements of $C_{10n}$, n is odd.

Vertex	The Structure of Orbit Elements
1${}^1$	$1^1,2^1,3^1,4^1,5^1,1^{n+1},2^{n+1},3^{n+1},4^{n+1},5^{n+1}$
1${}^2$	$1^2,3^2,5^2,7^2,9^2,1^n,3^n,5^n,7^n,9^n$
2${}^2$	$2^2,4^2,6^2,8^2,{10}^2,2^n,4^n,6^n,8^n,{10}^n$
⋮	⋮
1${}^{(n+1)/2}$	$1^{(n+1)/2},3^{(n+1)/2},5^{(n+1)/2},7^{(n+1)/2},9^{(n+1)/2},$
	$1^{(n+3)/2},3^{(n+3)/2},5^{(n+3)/2},7^{(n+3)/2},9^{(n+3)/2}$
2${}^{(n+1)/2}$	$2^{(n+1)/2},4^{(n+1)/2},6^{(n+1)/2},8^{(n+1)/2},{10}^{(n+1)/2},$
	$2^{(n+3)/2},4^{(n+3)/2},6^{(n+3)/2},8^{(n+3)/2},{10}^{(n+3)/2}$

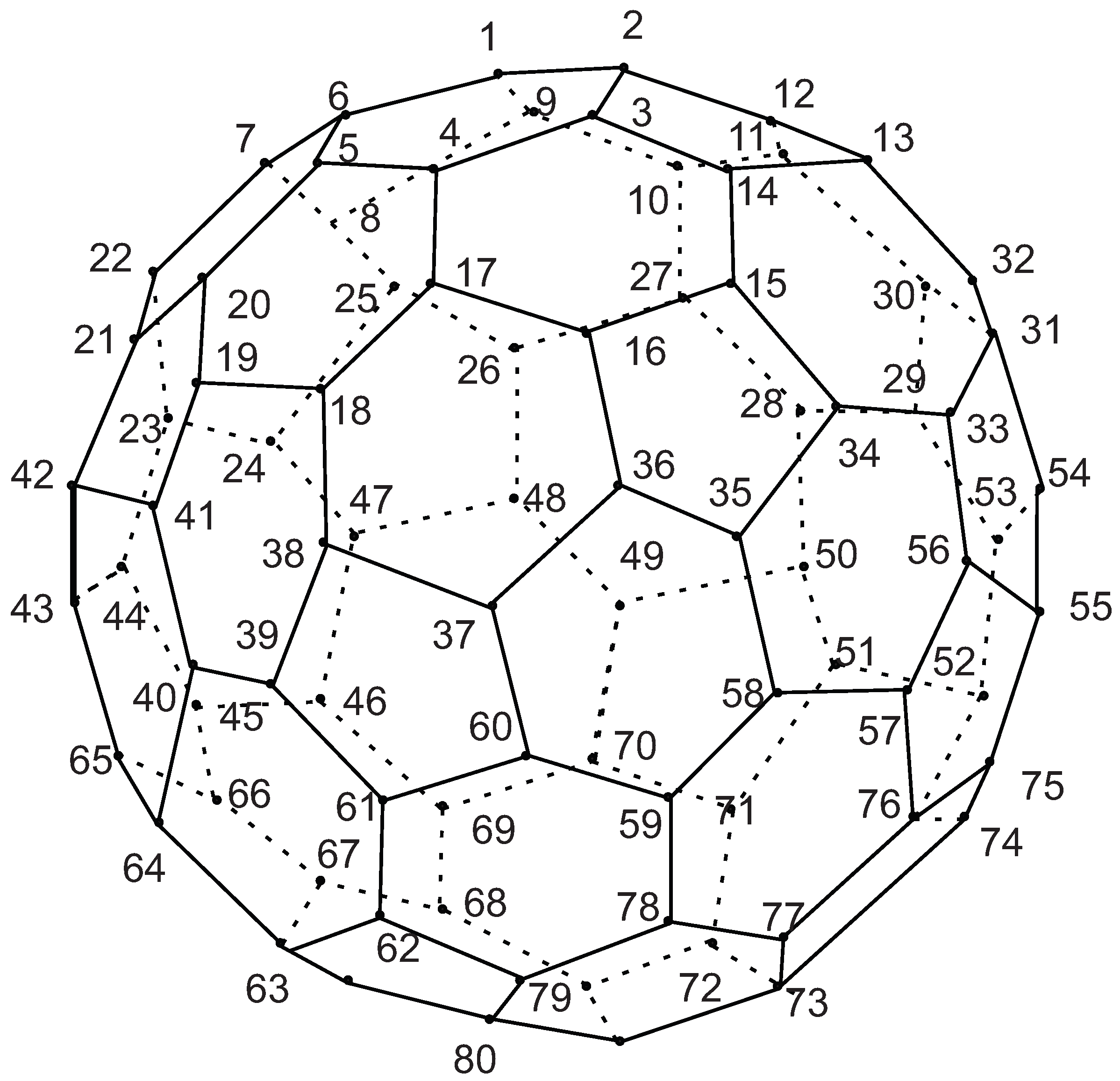
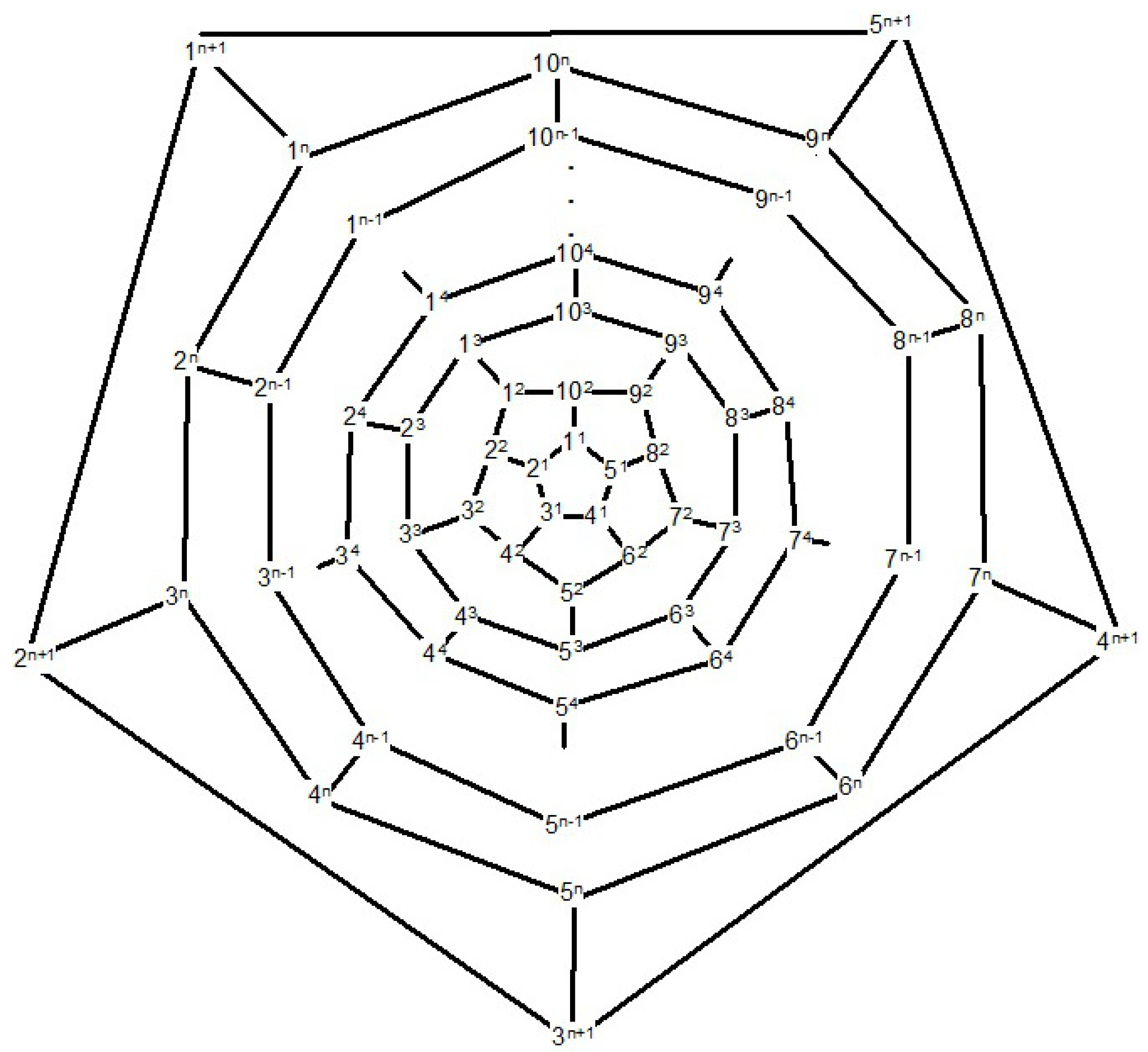
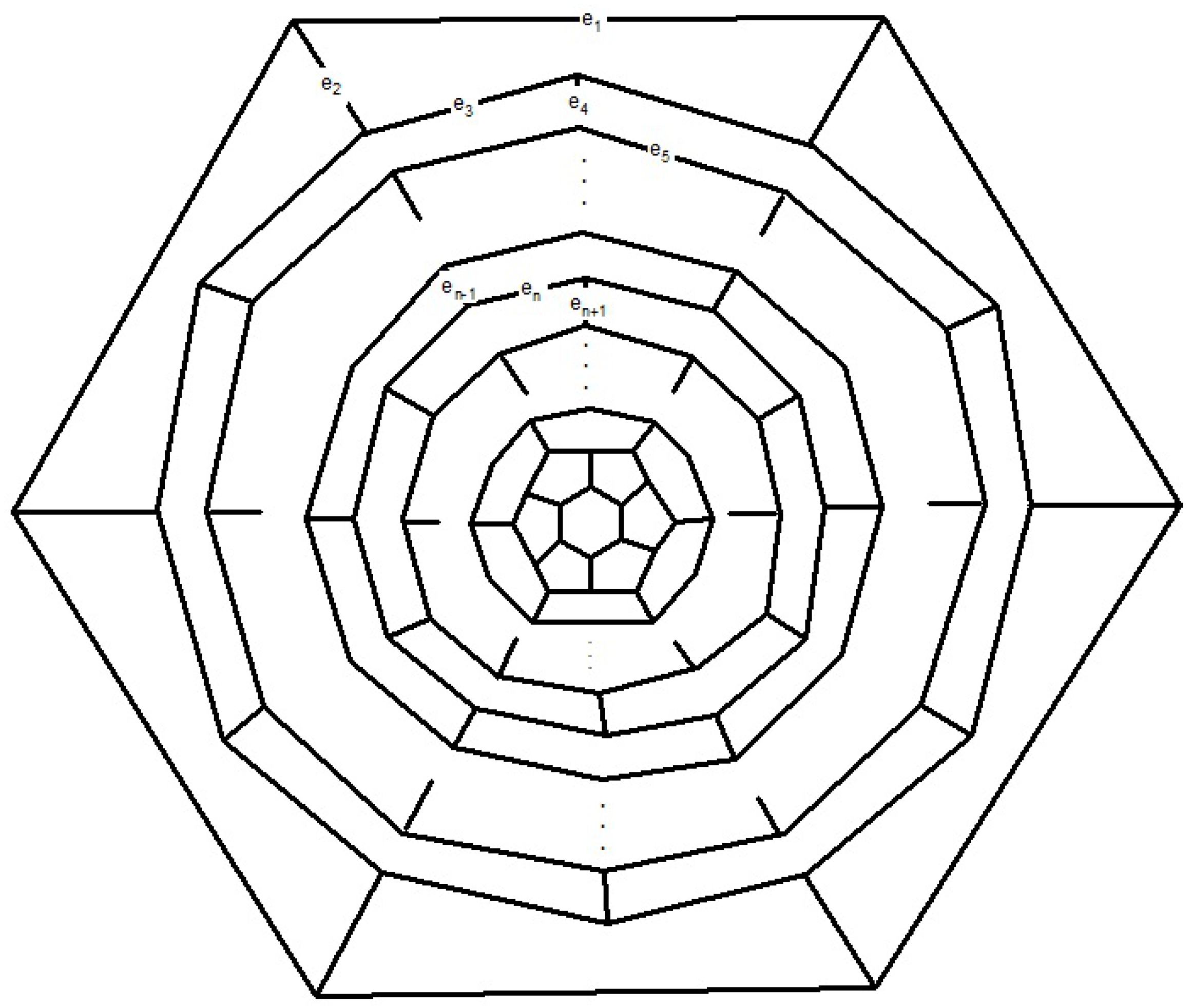
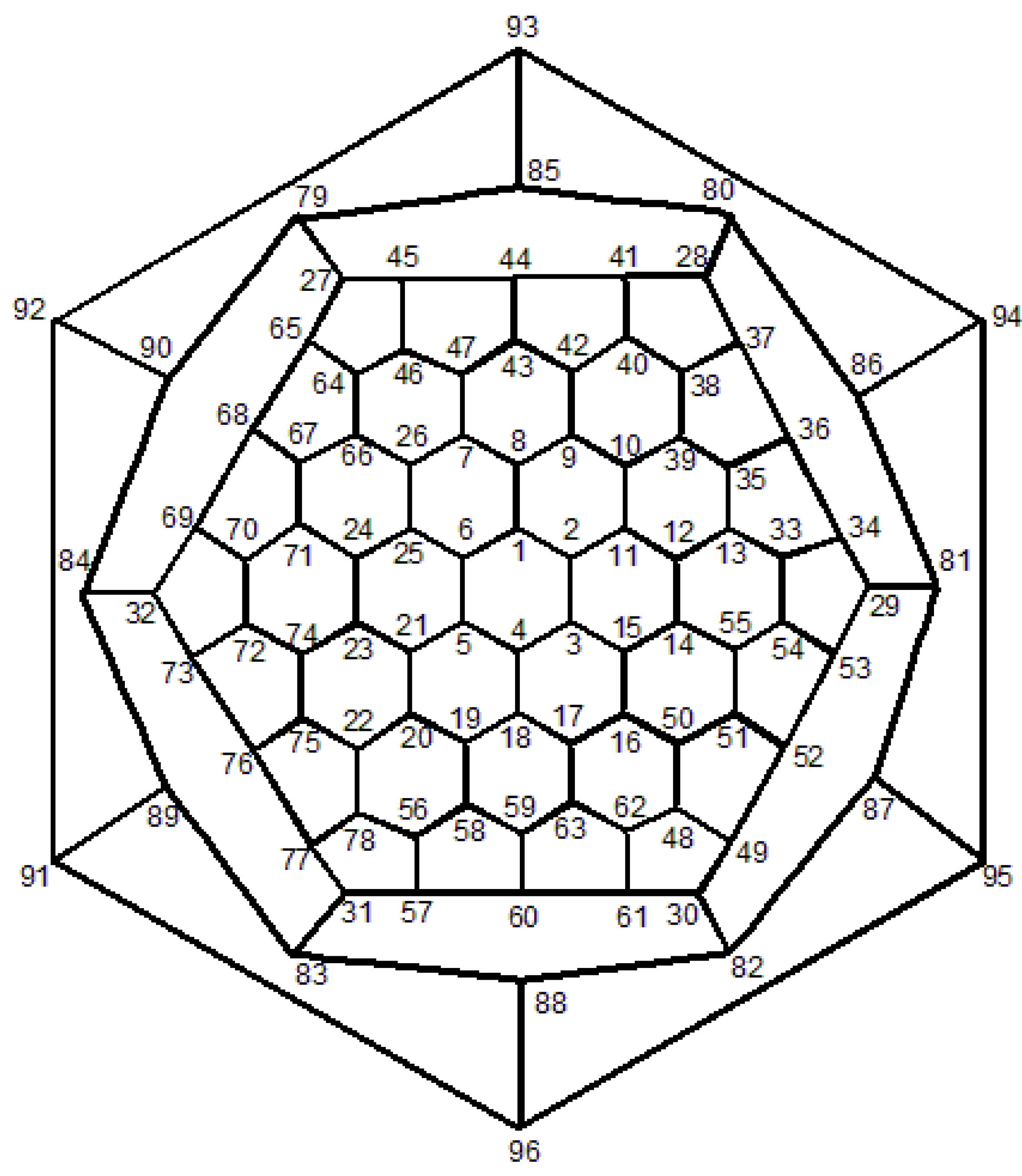
In continuing, we count all orbits of $\Omega =\{$1,…,10n} under the action of automorphism group. Again consider the fullerene graph $C_{10n}$, where n is even, as depicted in Figure 8. We find the presentation of elements $Aut(C_{10n})$. It is not difficult to see that there are five symmetry elements of order 2 in $Aut(C_{10n})$ denoted by ${\alpha }_i,1\le i\le 5$. Clearly, we have $o({\alpha }_i)=2$. In other words, one can easily check that $fix({\alpha }_1)=\{1^1,{10}^2,{10}^3,\cdots ,{10}^n,5^2,5^3,\cdots ,5^n,3^{n+1}\},$ $fix({\alpha }_2)=\{2^1,2^2,2^3,\cdots ,2^n,7^2,7^3,\cdots ,7^n,4^{n+1}\},$ $fix({\alpha }_3)=\{3^1,4^2,4^3,\cdots ,4^n,9^2,9^3,\cdots ,9^n,5^{n+1}\},$ $fix({\alpha }_4)=\{4^1,6^2,6^3,\cdots ,6^n,1^2,1^3,\cdots ,1^n,1^{n+1}\},$ $fix({\alpha }_5)=\{5^1,8^2,8^3,\cdots ,8^n,3^2,3^3,\cdots ,3^n,2^{n+1}\}.$ This means that $fix({\alpha }_i)=2n,(1\le i\le 5)$. Suppose ${\beta }_1$ is an involution that maps $1^1$ to $2^{n+1}$, $2^1$ to $1^{n+1}$, $2^1$ to $2^{n+1}$, $3^1$ to $5^{n+1}$, $4^1$ to $4^{n+1}$, $5^1$ to $3^{n+1}$, $1^2$ to $2^n$, $2^2$ to $1^n$, $3^2$ to ${10}^n$, $4^2$ to $9^n$, $5^2$ to $8^n$, $6^2$ to $7^n$, $7^2$ to $6^n$, $8^2$ to $5^n$, $9^2$ to $5^n$, ${10}^2$ to $3^n$ and so on. It is clear that fix ${\beta }_1=\varphi$. By continuing this method, all permutation presentations of ${\beta }_i$’sare as follows:

$$\begin{array}{ll}\beta {}_1=\hfill & (1^1,2^{n+1})(2^1,1^{n+1})(3^1,5^{n+1})(4^1,4^{n+1})(5^1,3^{n+1})(1^2,2^n)(2^2,1^n)(3^2,{10}^n)(4^2,\hfill \\ \hfill & 9^n)(5^2,8^n)(6^2,7^n)(7^2,6^n)(8^2,5^n)(9^2,4^n)({10}^2,3^n)(1^3,2^{n-1})(2^3,1^{n-1})(3^3,{10}^{n-1})\hfill \\ \hfill & (4^3,9^{n-1})(5^3,8^{n-1})(6^3,7^{n-1})(7^3,6^{n-1})(8^3,5^{n-1})(9^3,4^{n-1})({10}^3,3^{n-1})\cdots (1^{n/2},\hfill \\ \hfill & 2^{(n+4)/2})(2^{n/2},1^{(n+4)/2})(3^{n/2},{10}^{(n+4)/2})(4^{n/2},9^{(n+4)/2})(5^{n/2},8^{(n+4)/2})(6^{n/2},\hfill \\ & 7^{(n+4)/2})(7^{n/2},6^{(n+4)/2})(8^{n/2},5^{(n+4)/2})(9^{n/2},4^{(n+4)/2})({10}^{n/2},3^{(n+4)/2})(1^{(n+2)/2},\hfill \\ \hfill & 2^{(n+2)/2})(3^{(n+2)/2},{10}^{(n+2)/2})(4^{(n+2)/2},9^{(n+2)/2})(5^{(n+2)/2},8^{(n+2)/2})(6^{(n+2)/2},7^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_2=\hfill & (1^1,3^{n+1})(2^1,2^{n+1})(3^1,1^{n+1})(4^1,5^{n+1})(5^1,4^{n+1})(1^2,4^n)(2^2,3^n)(3^2,2^n)(4^2\hfill \\ & ,1^n)(5^2,{10}^n)(6^2,9^n)(7^2,8^n)(8^2,7^n)(9^2,6^n)({10}^2,5^n)(1^3,4^{n-1})(2^3,3^{n-1})(3^3,2^{n-1})\hfill \\ & (4^3,1^{n-1})(5^3,{10}^{n-1})(6^3,9^{n-1})(7^3,8^{n-1})(8^3,7^{n-1})(9^3,6^{n-1})({10}^3,5^{n-1})\cdots (1^{n/2},\hfill \\ & 4^{(n+4)/2})(2^{n/2},3^{(n+4)/2})(3^{n/2},2^{(n+4)/2})(4^{n/2},1^{(n+4)/2})(5^{n/2},{10}^{(n+4)/2})(6^{n/2},\hfill \\ & 9^{(n+4)/2})(7^{n/2},8^{(n+4)/2})(8^{n/2},7^{(n+4)/2})(9^{n/2},6^{(n+4)/2})({10}^{n/2},5^{(n+4)/2})(1^{(n+2)/2},\hfill \\ & t{4}^{(n+2)/2})(2^{(n+2)/2},3^{(n+2)/2})(5^{(n+2)/2},{10}^{(n+2)/2})(6^{(n+2)/2},9^{(n+2)/2})(7^{(n+2)/2},8^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_3=\hfill & (1^1,4^{n+1})(2^1,3^{n+1})(3^1,2^{n+1})(4^1,1^{n+1})(5^1,5^{n+1})(1^2,6^n)(2^2,5^n)(3^2,4^n)(4^2,\hfill \\ & 3^n)(5^2,2^n)(6^2,1^n)(7^2,{10}^n)(8^2,9^n)(9^2,8^n)({10}^2,7^n)(1^3,6^{n-1})(2^3,5^{n-1})(3^3,4^{n-1})\hfill \\ & (4^3,3^{n-1})(5^3,2^{n-1})(6^3,1^{n-1})(7^3,{10}^{n-1})(8^3,9^{n-1})(9^3,8^{n-1})({10}^3,7^{n-1})\cdots (1^{n/2},\hfill \\ & 6^{(n+4)/2})(2^{n/2},5^{(n+4)/2})(3^{n/2},4^{(n+4)/2})(4^{n/2},3^{(n+4)/2})(5^{n/2},2^{(n+4)/2})(6^{n/2},\hfill \\ & 1^{(n+4)/2})(7^{n/2},{10}^{(n+4)/2})(8^{n/2},9^{(n+4)/2})(9^{n/2},8^{(n+4)/2})({10}^{n/2},7^{(n+4)/2})(1^{(n+2)/2},\hfill \\ & 6^{(n+2)/2})(2^{(n+2)/2},5^{(n+2)/2})(3^{(n+2)/2},4^{(n+2)/2})(7^{(n+2)/2},{10}^{(n+2)/2})(8^{(n+2)/2},9^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_4=\hfill & (1^1,5^{n+1})(2^1,4^{n+1})(3^1,3^{n+1})(4^1,2^{n+1})(5^1,1^{n+1})(1^2,8^n)(2^2,7^n)(3^2,6^n)(4^2,\hfill \\ & 5^n)(5^2,4^n)(6^2,3^n)(7^2,2^n)(8^2,1^n)(9^2,{10}^n)({10}^2,9^n)(1^3,8^{n-1})(2^3,7^{n-1})(3^3,6^{n-1})\hfill \\ & (4^3,5^{n-1})(5^3,4^{n-1})(6^3,3^{n-1})(7^3,2^{n-1})(8^3,1^{n-1})(9^3,{10}^{n-1})({10}^3,9^{n-1})\cdots (1^{n/2},\hfill \\ & 8^{(n+4)/2})(2^{n/2},7^{(n+4)/2})(3^{n/2},6^{(n+4)/2})(4^{n/2},5^{(n+4)/2})(5^{n/2},4^{(n+4)/2})(6^{n/2},\hfill \\ & 3^{(n+4)/2})(7^{n/2},2^{(n+4)/2})(8^{n/2},1^{(n+4)/2})(9^{n/2},{10}^{(n+4)/2})({10}^{n/2},9^{(n+4)/2})(1^{(n+2)/2},\hfill \\ & 8^{(n+2)/2})(2^{(n+2)/2},7^{(n+2)/2})(3^{(n+2)/2},6^{(n+2)/2})(4^{(n+2)/2},5^{(n+2)/2})(9^{(n+2)/2},{10}^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_5=\hfill & (1^1,1^{n+1})(2^1,5^{n+1})(3^1,4^{n+1})(4^1,3^{n+1})(5^1,2^{n+1})(1^2,{10}^n)(2^2,9^n)(3^2,8^n)(4^2,\hfill \\ & 7^n)(5^2,6^n)(6^2,5^n)(7^2,4^n)(8^2,3^n)(9^2,2^n)({10}^2,1^n)(1^3,{10}^{n-1})(2^3,9^{n-1})(3^3,8^{n-1})\hfill \\ & (4^3,7^{n-1})(5^3,6^{n-1})(6^3,5^{n-1})(7^3,4^{n-1})(8^3,3^{n-1})(9^3,2^{n-1})({10}^3,1^{n-1}\cdots (1^{n/2},\hfill \\ & {10}^{(n+4)/2}(2^{n/2},9^{(n+4)/2})(3^{n/2},8^{(n+4)/2})(4^{n/2},7^{(n+4)/2})(5^{n/2},6^{(n+4)/2})(6^{n/2},\hfill \\ & 5^{(n+4)/2})(7^{n/2},4^{(n+4)/2})(8^{n/2},3^{(n+4)/2})(9^{n/2},2^{(n+4)/2})({10}^{n/2},1^{(n+4)/2})(1^{(n+2)/2},\hfill \\ & {10}^{(n+2)/2})(2^{(n+2)/2},9^{(n+2)/2})(3^{(n+2)/2},8^{(n+2)/2})(4^{(n+2)/2},7^{(n+2)/2})(5^{(n+2)/2},6^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_6=\hfill & (1^1,3^{n+1})(2^1,4^{n+1})(3^1,5^{n+1})(4^1,1^{n+1})(5^1,2^{n+1})(1^2,6^n)(2^2,7^n)(3^2,8^n)(4^2,\hfill \\ & 9^n)(5^2,{10}^n)(6^2,1^n)(7^2,2^n)(8^2,3^n)(9^2,4^n)({10}^2,5^n)(1^3,6^{n-1})(2^3,7^{n-1})(3^3,8^{n-1})\hfill \\ & (4^3,9^{n-1})(5^3,{10}^{n-1})(6^3,1^{n-1})(7^3,2^{n-1})(8^3,3^{n-1})(9^3,4^{n-1})({10}^3,5^{n-1}\cdots (1^{n/2},\hfill \\ & 6^{(n+4)/2})(2^{n/2},7^{(n+4)/2})(3^{n/2},8^{(n+4)/2})(4^{n/2},9^{(n+4)/2})(5^{n/2},{10}^{(n+4)/2})(6^{n/2},\hfill \\ & 1^{(n+4)/2})(7^{n/2},2^{(n+4)/2})(8^{n/2},3^{(n+4)/2})(9^{n/2},4^{(n+4)/2})({10}^{n/2},5^{(n+4)/2})(1^{(n+2)/2},\hfill \\ & 6^{(n+2)/2})(2^{(n+2)/2},7^{(n+2)/2})(3^{(n+2)/2},8^{(n+2)/2})(4^{(n+2)/2},9^{(n+2)/2})(5^{(n+2)/2},{10}^{(n+2)/2}).\hfill \end{array}$$

$Aut(C_{10n})$ includes four rotational elements ${\gamma }_i$ ($1\le i\le 4$) and four permutations ${\sigma }_i$ ($1\le i\le 4$) of order 10 with the following permutation presentations:

$$\begin{array}{ll}{\gamma }_1=\hfill & (1^1,2^1,3^1,4^1,5^1)(1^2,3^2,5^2,7^2,9^2)(2^2,4^2,6^2,8^2,{10}^2)(1^3,3^3,5^3,7^3,9^3)(2^3,4^3,\hfill \\ & 6^3,8^3,{10}^3)\cdots (1^{n-1},3^{n-1},5^{n-1},7^{n-1},9^{n-1})(2^{n-1},4^{n-1},6^{n-1},8^{n-1},{10}^{n-1})(1^n,3^n,\hfill \\ & 5^n,7^n,9^n)(2^n,4^n,6^n,8^n,{10}^n)(1^{n+1},2^{n+1},3^{n+1},4^{n+1},5^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_2=\hfill & (1^1,3^1,5^1,2^1,4^1)(1^2,5^2,9^2,3^2,7^2)(2^2,6^2,{10}^2,4^2,8^2)(1^3,5^3,9^3,3^3,7^3)(2^3,6^3,\hfill \\ & {10}^3,4^3,8^3)\cdots (1^{n-1},5^{n-1},9^{n-1},3^{n-1},7^{n-1})(2^{n-1},6^{n-1},{10}^{n-1},4^{n-1},8^{n-1})(1^n,5^n,\hfill \\ & 9^n,3^n,7^n)(2^n,6^n,{10}^n,4^n,8^n)(1^{n+1},3^{n+1},5^{n+1},2^{n+1},4^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_3=\hfill & (1^1,5^1,4^1,3^1,2^1)(1^2,9^2,7^2,5^2,3^2)(2^2,{10}^2,8^2,6^2,4^2)(1^3,9^3,7^3,5^3,3^3)(2^3,{10}^3,\hfill \\ & 8^3,6^3,4^3)\cdots (1^{n-1},9^{n-1},7^{n-1},5^{n-1},3^{n-1})(2^{n-1},{10}^{n-1},8^{n-1},6^{n-1},4^{n-1})(1^n,9^n,\hfill \\ & 7^n,5^n,3^n)(2^n,{10}^n,8^n,6^n,4^n)(1^{n+1},5^{n+1},4^{n+1},3^{n+1},2^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_4=\hfill & (1^1,4^1,2^1,5^1,3^1)(1^2,7^2,3^2,9^2,5^2)(2^2,8^2,4^2,{10}^2,6^2)(1^3,7^3,3^3,9^3,5^3)(2^3,8^3,\hfill \\ & 4^3,{10}^3,6^3)\cdots (1^{n-1},7^{n-1},3^{n-1},9^{n-1},5^{n-1})(2^{n-1},8^{n-1},4^{n-1},{10}^{n-1},6^{n-1})(1^n,7^n,\hfill \\ & 3^n,9^n,5^n)(2^n,8^n,4^n,{10}^n,6^n)(1^{n+1},4^{n+1},2^{n+1},5^{n+1},3^{n+1}).\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_1=\hfill & (1^1,5^{n+1},5^1,4^{n+1},4^1,3^{n+1},3^1,2^{n+1},2^1,1^{n+1})(1^2,{10}^n,9^2,8^n,7^2,6^n,5^2,4^n,3^2,\hfill \\ & 2^n)(2^2,1^n,{10}^2,9^n,8^2,7^n,6^2,5^n,4^2,3^n)(1^3,{10}^{n-1},9^3,8^{n-1},7^3,6^{n-1},5^3,4^{n-1},3^3,\hfill \\ & 2^{n-1})(2^3,1^{n-1},{10}^3,9^{n-1},8^3,7^{n-1},6^3,5^{n-1},4^3,3^{n-1})\cdots (1^{n/2},{10}^{(n+4)/2},9^{n/2},\hfill \\ & 8^{(n+4)/2},7^{n/2},6^{(n+4)/2},5^{n/2},4^{(n+4)/2},3^{n/2},2^{(n+4)/2})(2^{n/2},1^{(n+4)/2},{10}^{n/2},9^{(n+4)/2},\hfill \\ & 8^{n/2},7^{(n+4)/2},6^{n/2},5^{(n+4)/2},4^{n/2},3^{(n+4)/2})(1^{(n+2)/2},{10}^{(n+2)/2},9^{(n+2)/2},8^{(n+2)/2},\hfill \\ & 7^{(n+2)/2},6^{(n+2)/2},5^{(n+2)/2},4^{(n+2)/2},3^{(n+2)/2},2^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_2=\hfill & (1^1,1^{n+1},2^1,2^{n+1},3^1,3^{n+1},4^1,4^{n+1},5^1,5^{n+1})(1^2,2^n,3^2,4^n,5^2,6^n,7^2,8^n,9^2,\hfill \\ & {10}^n)(2^2,3^n,4^2,5^n,6^2,7^n,8^2,9^n,{10}^2,1^n)(1^3,2^{n-1},3^3,4^{n-1},5^3,6^{n-1},7^3,8^{n-1},9^3,\hfill \\ & {10}^{n-1})(2^3,3^{n-1},4^3,5^{n-1},6^3,7^{n-1},8^3,9^{n-1},{10}^3,1^{n-1}\cdots (1^{n/2},2^{(n+4)/2},3^{n/2},\hfill \\ & 4^{(n+4)/2},5^{n/2},6^{(n+4)/2},7^{n/2},8^{(n+4)/2},9^{n/2},{10}^{(n+4)/2})(2^{n/2},3^{(n+4)/2},4^{n/2},5^{(n+4)/2},\hfill \\ & 6^{n/2},7^{(n+4)/2},8^{n/2},9^{(n+4)/2},{10}^{n/2},1^{(n+4)/2})(1^{(n+2)/2},2^{(n+2)/2},3^{(n+2)/2},4^{(n+2)/2},\hfill \\ \hfill & 5^{(n+2)/2},6^{(n+2)/2},7^{(n+2)/2},8^{(n+2)/2},9^{(n+2)/2},{10}^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_3=\hfill & (1^1,2^{n+1},4^1,5^{n+1},2^1,3^{n+1},5^1,1^{n+1},3^1,4^{n+1})(1^2,4^n,7^2,{10}^n,3^2,6^n,9^2,2^n,\hfill \\ & 5^2,8^n)(2^2,5^n,8^2,1^n,4^2,7^n,{10}^2,3^n,6^2,9^n)(1^3,4^{n-1},7^3,{10}^{n-1},3^3,6^{n-1},9^3,2^{n-1},\hfill \\ & 5^3,8^{n-1})(2^3,5^{n-1},8^3,1^{n-1},4^3,7^{n-1},{10}^3,3^{n-1},6^3,9^{n-1})\cdots (1^{n/2},4^{(n+4)/2},7^{n/2},\hfill \\ \hfill & {10}^{(n+4)/2},3^{n/2},6^{(n+4)/2},9^{n/2},2^{(n+4)/2},5^{n/2},8^{(n+4)/2})(2^{n/2},5^{(n+4)/2},8^{n/2},\hfill \\ \hfill & 1^{(n+4)/2},4^{n/2},7^{(n+4)/2},{10}^{n/2},3^{(n+4)/2},6^{n/2},9^{(n+4)/2})(1^{(n+2)/2},4^{(n+2)/2},7^{(n+2)/2},\hfill \\ \hfill & {10}^{(n+2)/2},3^{(n+2)/2},6^{(n+2)/2},9^{(n+2)/2},2^{(n+2)/2},5^{(n+2)/2},8^{(n+2)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_4=\hfill & (1^1,4^{n+1},3^1,1^{n+1},5^1,3^{n+1},2^1,5^{n+1},4^1,2^{n+1})(1^2,8^n,5^2,2^n,9^2,6^n,3^2,{10}^n,7^2,\hfill \\ \hfill & 4^n)(2^2,9^n,6^2,3^n,{10}^2,7^n,4^2,1^n,8^2,5^n)(1^3,8^{n-1},5^3,2^{n-1},9^3,6^{n-1},3^3,{10}^{n-1},7^3,\hfill \\ \hfill & 4^{n-1})(2^3,9^{n-1},6^3,3^{n-1},{10}^3,7^{n-1},4^3,1^{n-1},8^3,5^{n-1})\cdots (1^{n/2},8^{(n+4)/2},5^{n/2},\hfill \\ \hfill & 2^{(n+4)/2},9^{n/2},6^{(n+4)/2},3^{n/2},{10}^{(n+4)/2},7^{n/2},4^{(n+4)/2})(2^{n/2},9^{(n+4)/2},6^{n/2},3^{(n+4)/2},\hfill \\ \hfill & {10}^{n/2},7^{(n+4)/2},4^{n/2},1^{(n+4)/2},8^{n/2},5^{(n+4)/2})(1^{(n+2)/2},8^{(n+2)/2},5^{(n+2)/2},2^{(n+2)/2},\hfill \\ \hfill & 9^{(n+2)/2},6^{(n+2)/2},3^{(n+2)/2},{10}^{(n+2)/2},7^{(n+2)/2},4^{(n+2)/2}).\hfill \end{array}$$

Hence, C${}_{10}$${}_n$ (n is even) has $\frac{n-2}{2}\times 2+2=n$ orbits and each of them has 10 vertices, see Table 1.

Figure 8. C${}_{10}$${}_n$,n is even.

It is not difficult to see that $|fix(\overline{{\alpha }_i})|=n+2$$(1\le i\le 5)$, $|fix(\overline{{\beta }_j})|=2$$(1\le j\le 5)$ and $|fix(\overline{{\beta }_6})|=|fix(\overline{{\gamma }_k})|=|fix(\overline{{\sigma }_l})|=0$$(1\le k\le 4),(1\le l\le 4)$. By considering the action of $Aut(C_{10n})$ on the set of edges and using Equation (3.1), one can prove that the number of orbits is $n+1$ for which n is even. These are $O(e_1^1),O(e^1),O(e_1^2),O(e^2),\cdots ,O(e_1^{(n-2)/2}),O(e^{(n-2)/2}),O(e_1^{n/2},O(e^{n/2}),O(e_1^{(n+2)/2}).$ Hence, we proved the following theorem.

Theorem 4.

Consider the fullerene graph $C_{10n}$, then there are n+1 orbits for which n is even under the action of automorphism group on the set of edges.

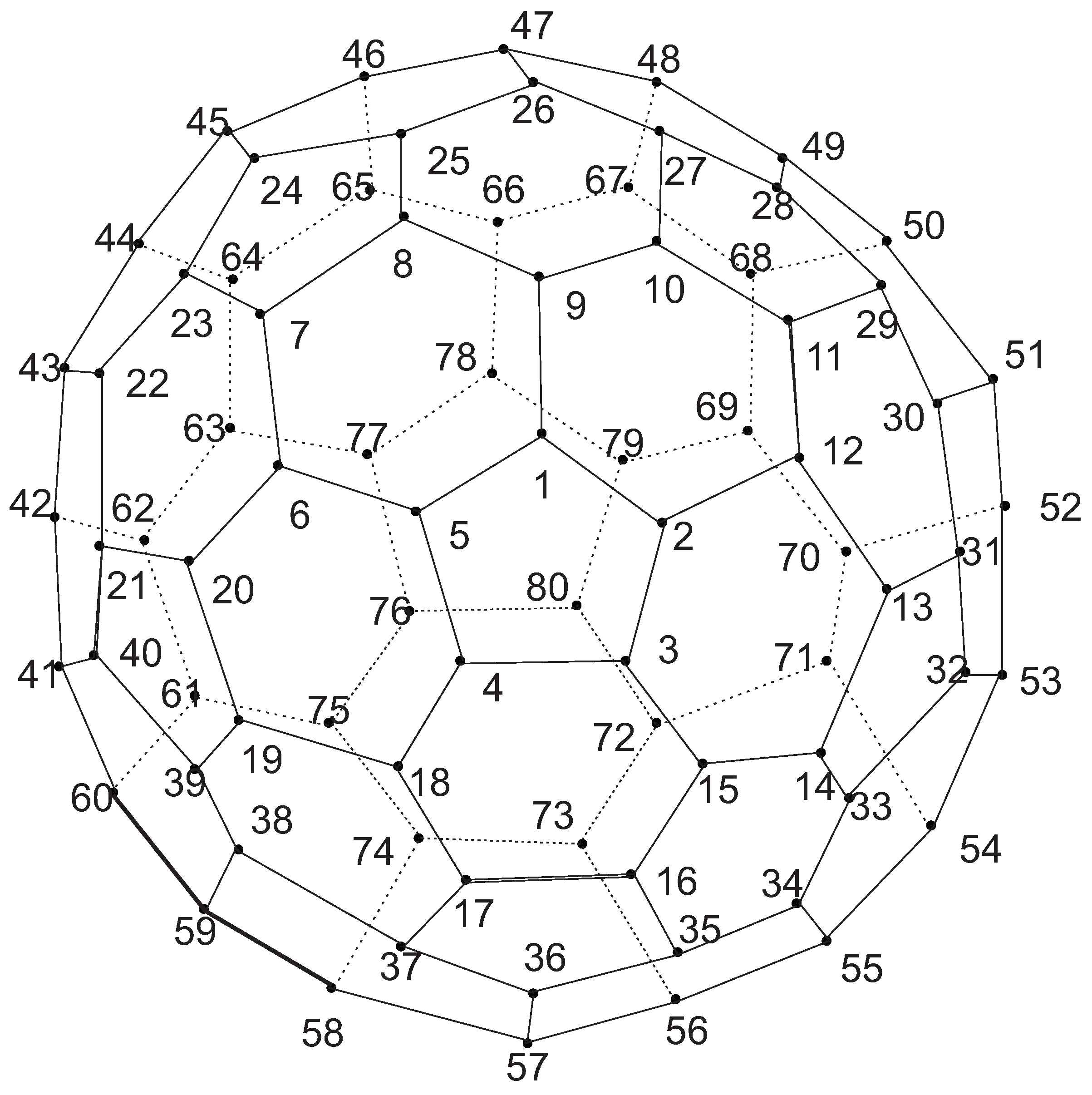
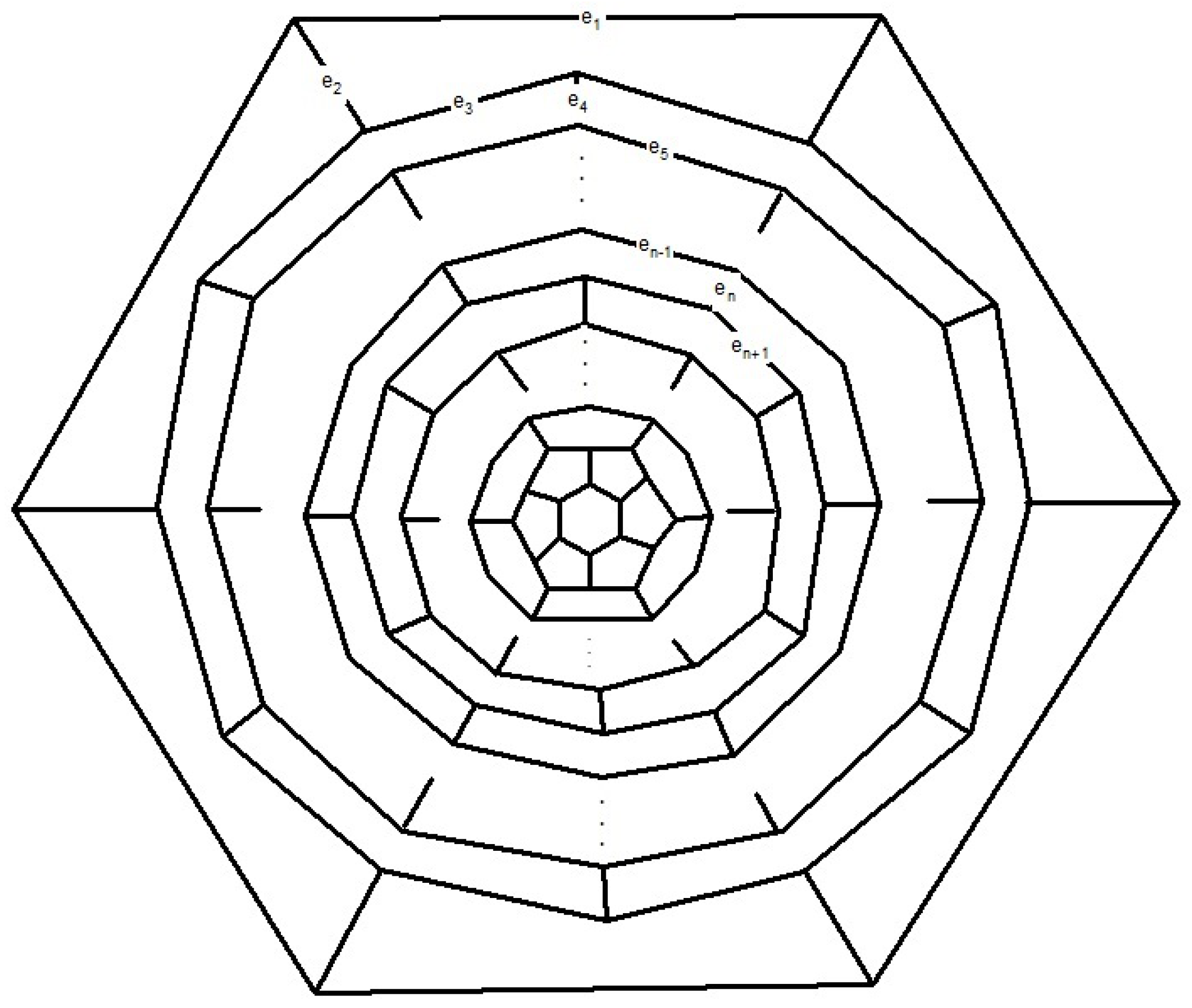
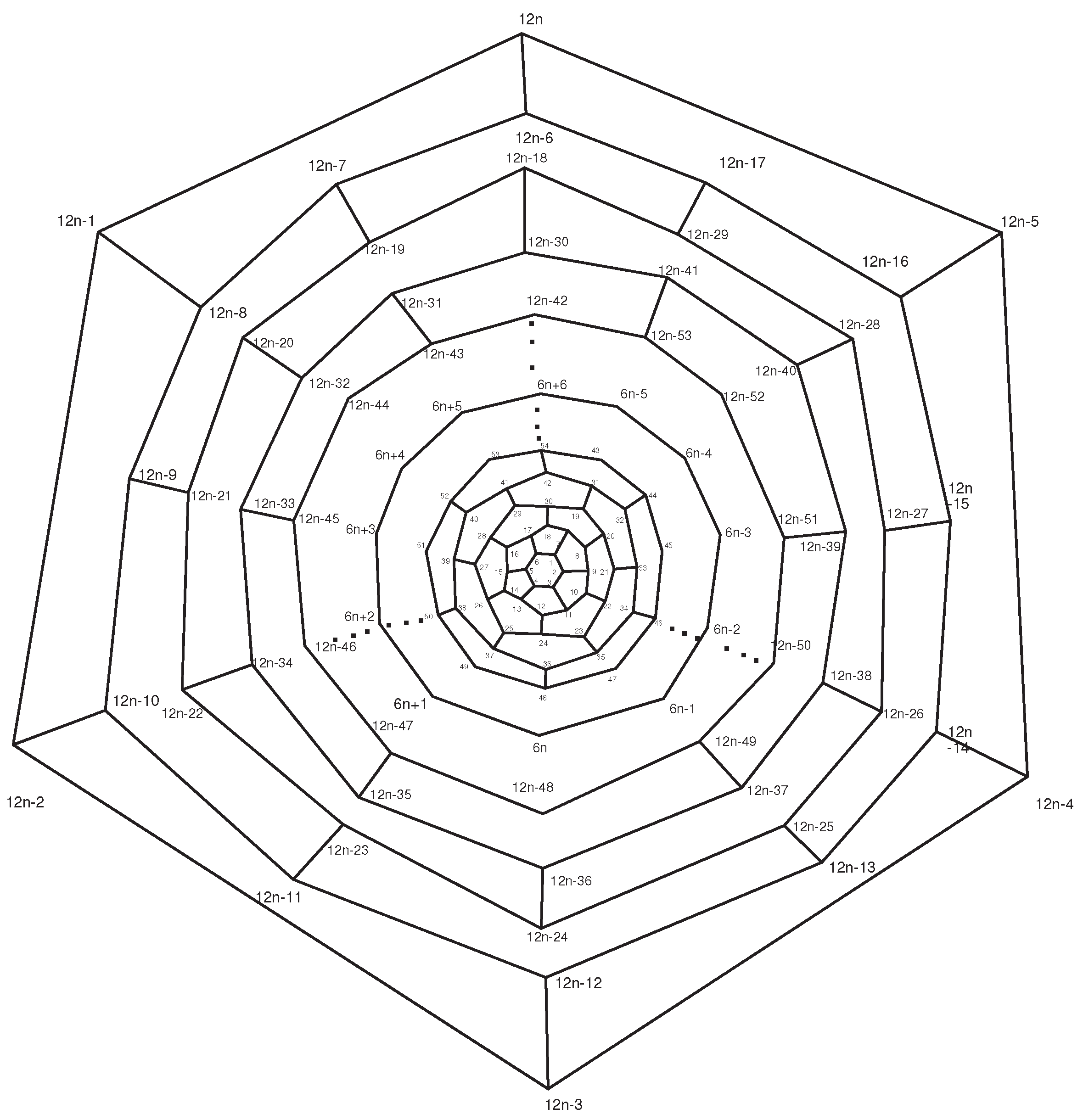
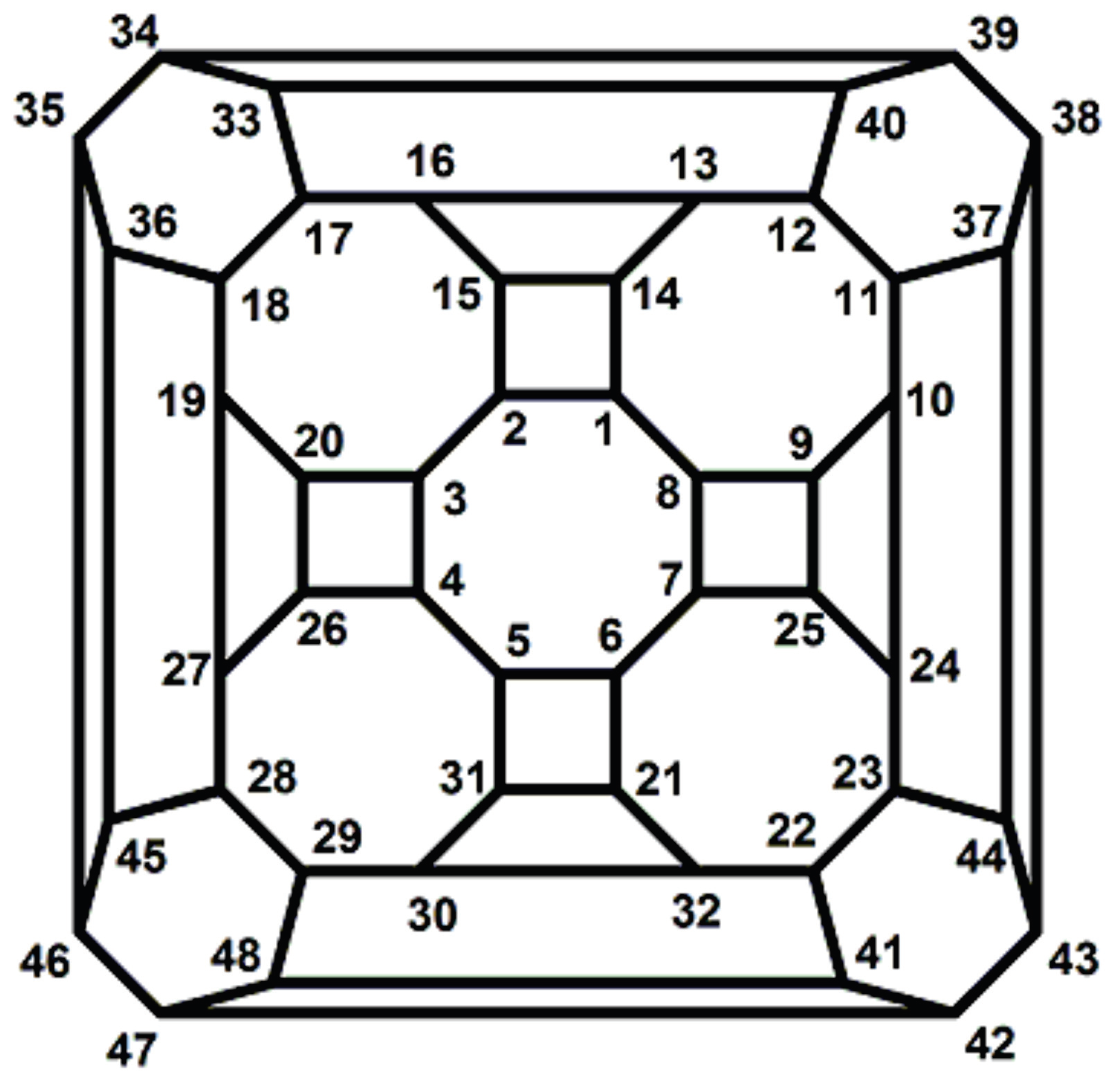
Now consider the fullerene graph $C_{10n}$, where n is odd, as depicted in Figure 9. There are five symmetry elements of order 2 in $Aut(C_{10n})$ denoted by ${\alpha }_i,1\le i\le 5$. Clearly, we have $o({\alpha }_i)=2$. In other words, one can easily check that $fix({\alpha }_1)=\{1^1,{10}^2,{10}^3,\cdots ,{10}^n,1^{n+1},5^2,5^3,\cdots ,5^n\},$ $fix({\alpha }_2)=\{2^1,2^2,2^3,\cdots ,2^n,2^{n+1},7^2,7^3,\cdots ,7^n\},$ $fix({\alpha }_3)=\{3^1,4^2,4^3,\cdots ,4^n,3^{n+1},9^2,9^3,\cdots ,9^n\},$ $fix({\alpha }_4)=\{4^1,6^2,6^3,\cdots ,6^n,4^{n+1},1^2,1^3,\cdots ,1^n\},$ $fix({\alpha }_5)=\{5^1,8^2,8^3,\cdots ,8^n,5^{n+1},3^2,3^3,\cdots ,3^n,2^{n+1}\}.$ This means that $fix({\alpha }_i)=2n,(1\le i\le 5)$. Similar to the last one, the presentation of other elements of $Aut(C_{10n})$ are as follows:

$$\begin{array}{ll}{\beta }_1=\hfill & (1^1,1^{n+1})(2^1,2^{n+1})(3^1,3^{n+1})(4^1,4^{n+1})(5^1,5^{n+1})(1^2,1^n)(2^2,2^n)(3^2,3^n)(4^2,4^n)\hfill \\ & (5^2,5^n)(6^2,6^n)(7^2,7^n)(8^2,8^n)(9^2,9^n)({10}^2,{10}^n)(1^3,1^{n-1})(2^3,2^{n-1})(3^3,3^{n-1})(4^3,\hfill \\ & 4^{n-1})(5^3,5^{n-1})(6^3,6^{n-1})(7^3,7^{n-1})(8^3,8^{n-1})(9^3,9^{n-1})({10}^3,{10}^{n-1})\cdots (1^{(n+1)/2},\hfill \\ & 1^{(n+3)/2})(2^{(n+1)/2},2^{(n+3)/2})(3^{(n+1)/2},3^{(n+3)/2})(4^{(n+1)/2},4^{(n+3)/2})(5^{(n+1)/2},5^{(n+3)/2})\hfill \\ & (6^{(n+1)/2},6^{(n+3)/2})(7^{(n+1)/2},7^{(n+3)/2})(8^{(n+1)/2},8^{(n+3)/2})(9^{(n+1)/2},9^{(n+3)/2})\hfill \\ & ({10}^{(n+1)/2},{10}^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_2=\hfill & (1^1,3^{n+1})(2^1,2^{n+1})(3^1,1^{n+1})(4^1,5^{n+1})(5^1,4^{n+1})(1^2,3^n)(2^2,2^n)(3^2,1^n)(4^2,\hfill \\ & {10}^n)(5^2,9^n)(6^2,8^n)(7^2,7^n)(8^2,6^n)(9^2,5^n)({10}^2,4^n)(1^3,3^{n-1})(2^3,2^{n-1})(3^3,1^{n-1})\hfill \\ & (4^3,{10}^{n-1})(5^3,9^{n-1})(6^3,8^{n-1})(7^3,7^{n-1})(8^3,6^{n-1})(9^3,5^{n-1})({10}^3,4^{n-1}\cdots \hfill \\ & (1^{(n+1)/2},3^{(n+3)/2})(2^{(n+1)/2},2^{(n+3)/2})(3^{(n+1)/2},1^{(n+3)/2})(4^{(n+1)/2},{10}^{(n+3)/2})\hfill \\ & (5^{(n+1)/2},9^{(n+3)/2})(6^{(n+1)/2},8^{(n+3)/2})(7^{(n+1)/2},7^{(n+3)/2})(8^{(n+1)/2},6^{(n+3)/2})\hfill \\ & (9^{(n+1)/2},5^{(n+3)/2})({10}^{(n+1)/2},4^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_3=\hfill & (1^1,4^{n+1})(2^1,3^{n+1})(3^1,2^{n+1})(4^1,1^{n+1})(5^1,5^{n+1}(1^2,5^n)(2^2,4^n)(3^2,3^n)(4^2,\hfill \\ & 2^n)(5^2,1^n)(6^2,{10}^n)(7^2,9^n)(8^2,8^n)(9^2,7^n)({10}^2,6^n)(1^3,5^{n-1})(2^3,4^{n-1})(3^3,3^{n-1})\hfill \\ & (4^3,2^{n-1})(5^3,1^{n-1})(6^3,{10}^{n-1})(7^3,9^{n-1})(8^3,8^{n-1})(9^3,7^{n-1})({10}^3,6^{n-1})\cdots \hfill \\ & (1^{(n+1)/2},5^{(n+3)/2})(2^{(n+1)/2},4^{(n+3)/2})(3^{(n+1)/2},3^{(n+3)/2})(4^{(n+1)/2},2^{(n+3)/2})\hfill \\ & (5^{(n+1)/2},1^{(n+3)/2})(6^{(n+1)/2},{10}^{(n+3)/2})(7^{(n+1)/2},9^{(n+3)/2})(8^{(n+1)/2},8^{(n+3)/2})\hfill \\ & (9^{(n+1)/2},7^{(n+3)/2})({10}^{(n+1)/2},6^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_4=\hfill & (1^1,5^{n+1})(2^1,4^{n+1})(3^1,3^{n+1})(4^1,2^{n+1})(5^1,1^{n+1})(1^2,7^n)(2^2,6^n)(3^2,5^n)(4^2,\hfill \\ & 4^n)(5^2,3^n)(6^2,2^n)(7^2,1^n)(8^2,{10}^n)(9^2,9^n)({10}^2,8^n)(1^3,7^{n-1})(2^3,6^{n-1})(3^3,5^{n-1})\hfill \\ & (4^3,4^{n-1})(5^3,3^{n-1})(6^3,2^{n-1})(7^3,1^{n-1})(8^3,{10}^{n-1})(9^3,9^{n-1})({10}^3,8^{n-1})\cdots \hfill \\ & (1^{(n+1)/2},7^{(n+3)/2})(2^{(n+1)/2},6^{(n+3)/2})(3^{(n+1)/2},5^{(n+3)/2})(4^{(n+1)/2},4^{(n+3)/2})\hfill \\ & (5^{(n+1)/2},3^{(n+3)/2})(6^{(n+1)/2},2^{(n+3)/2})(7^{(n+1)/2},1^{(n+3)/2})(8^{(n+1)/2},{10}^{(n+3)/2})\hfill \\ & (9^{(n+1)/2},9^{(n+3)/2})({10}^{(n+1)/2},8^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_5=\hfill & (1^1,1^{n+1})(2^1,5^{n+1})(3^1,4^{n+1})(4^1,3^{n+1})(5^1,2^{n+1})(1^2,9^n)(2^2,8^n)(3^2,7^n)(4^2,\hfill \\ & 6^n)(5^2,5^n)(6^2,4^n)(7^2,3^n(8^2,2^n)(9^2,1^n)({10}^2,{10}^n)(1^3,9^{n-1})(2^3,8^{n-1})(3^3,7^{n-1})\hfill \\ & (4^3,6^{n-1})(5^3,5^{n-1})(6^3,4^{n-1})(7^3,3^{n-1})(8^3,2^{n-1})(9^3,1^{n-1})({10}^3,{10}^{n-1})\cdots \hfill \\ & (1^{(n+1)/2},9^{(n+3)/2})(2^{(n+1)/2},8^{(n+3)/2})(3^{(n+1)/2},7^{(n+3)/2})(4^{(n+1)/2},6^{(n+3)/2})\hfill \\ & (5^{(n+1)/2},5^{(n+3)/2})(6^{(n+1)/2},4^{(n+3)/2})(7^{(n+1)/2},3^{(n+3)/2})(8^{(n+1)/2},2^{(n+3)/2})\hfill \\ & (9^{(n+1)/2},1^{(n+3)/2})({10}^{(n+1)/2},{10}^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\beta }_6=\hfill & (1^1,2^{n+1})(2^1,1^{n+1})(3^1,5^{n+1})(4^1,4^{n+1})(5^1,3^{n+1})(1^2,1^n)(2^2,{10}^n)(3^2,9^n)(4^2,\hfill \\ & 8^n)(5^2,7^n)(6^2,6^n)(7^2,5^n)(8^2,4^n)(9^2,3^n)({10}^2,2^n)(1^3,1^{n-1})(2^3,{10}^{n-1})(3^3,9^{n-1})\hfill \\ & (4^3,8^{n-1})(5^3,7^{n-1})(6^3,6^{n-1})(7^3,5^{n-1})(8^3,4^{n-1})(9^3,3^{n-1})({10}^3,2^{n-1})\cdots \hfill \\ & (1^{(n+1)/2},1^{(n+3)/2})(2^{(n+1)/2},{10}^{(n+3)/2})(3^{(n+1)/2},9^{(n+3)/2})(4^{(n+1)/2},8^{(n+3)/2})\hfill \\ & (5^{(n+1)/2},7^{(n+3)/2})(6^{(n+1)/2},6^{(n+3)/2})(7^{(n+1)/2},5^{(n+3)/2})(8^{(n+1)/2},4^{(n+3)/2})\hfill \\ & (9^{(n+1)/2},3^{(n+3)/2})({10}^{(n+1)/2},2^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_1=\hfill & (1^1,2^1,3^1,4^1,5^1)(1^2,3^2,5^2,7^2,9^2)(2^2,4^2,6^2,8^2,{10}^2)(1^3,3^3,5^3,7^3,9^3)(2^3,4^3,\hfill \\ & 6^3,8^3,{10}^3)\cdots (1^{n-1},3^{n-1},5^{n-1},7^{n-1},9^{n-1})(2^{n-1},4^{n-1},6^{n-1},8^{n-1},{10}^{n-1})(1^n,3^n,\hfill \\ & 5^n,7^n,9^n)(2^n,4^n,6^n,8^n,{10}^n)(1^{n+1},2^{n+1},3^{n+1},4^{n+1},5^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_2=\hfill & (1^1,3^1,5^1,2^1,4^1)(1^2,5^2,9^2,3^2,7^2)(2^2,6^2,{10}^2,4^2,8^2)(1^3,5^3,9^3,3^3,7^3)(2^3,6^3,\hfill \\ & {10}^3,4^3,8^3)\cdots (1^{n-1},5^{n-1},9^{n-1},3^{n-1},7^{n-1})(2^{n-1},6^{n-1},{10}^{n-1},\hfill \\ & 4^{n-1},8^{n-1})(1^n,5^n,9^n,3^n,7^n)(2^n,6^n,{10}^n,4^n,8^n)(1^{n+1},3^{n+1},5^{n+1},2^{n+1},4^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_3=\hfill & (1^1,5^1,4^1,3^1,2^1)(1^2,9^2,7^2,5^2,3^2)(2^2,{10}^2,8^2,6^2,4^2)(1^3,9^3,7^3,5^3,3^3)(2^3,{10}^3,\hfill \\ & 8^3,6^3,4^3)\cdots (1^{n-1},9^{n-1},7^{n-1},5^{n-1},3^{n-1})(2^{n-1},{10}^{n-1},8^{n-1},6^{n-1},4^{n-1})(1^n,9^n,\hfill \\ & 7^n,5^n,3^n)(2^n,{10}^n,8^n,6^n,4^n)(1^{n+1},5^{n+1},4^{n+1},3^{n+1},2^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\gamma }_4=\hfill & (1^1,4^1,2^1,5^1,3^1)(1^2,7^2,3^2,9^2,5^2)(2^2,8^2,4^2,{10}^2,6^2)(1^3,7^3,3^3,9^3,5^3)(2^3,8^3,\hfill \\ & 4^3,{10}^3,6^3)\cdots (1^{n-1},7^{n-1},3^{n-1},9^{n-1},5^{n-1})(2^{n-1},8^{n-1},4^{n-1},{10}^{n-1},6^{n-1})(1^n,7^n,\hfill \\ & 3^n,9^n,5^n)(2^n,8^n,4^n,{10}^n,6^n)(1^{n+1},4^{n+1},2^{n+1},5^{n+1},3^{n+1}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_1=\hfill & (1^1,2^{n+1},3^1,4^{n+1},5^1,1^{n+1},2^1,3^{n+1},4^1,5^{n+1})(1^2,3^n,5^2,7^n,9^2,1^n,3^2,5^n,7^2,\hfill \\ & 9^n)(2^2,4^n,6^2,8^n,{10}^2,2^n,4^2,6^n,8^2,{10}^n)(1^3,3^{n-1},5^3,7^{n-1},9^3,1^{n-1},3^3,5^{n-1},7^3,\hfill \\ & 9^{n-1})(2^3,4^{n-1},6^3,8^{n-1},{10}^3,2^{n-1},4^3,6^{n-1},8^3,{10}^{n-1})\cdots (1^{(n+1)/2},3^{(n+3)/2},\hfill \\ & 5^{(n+1)/2},7^{(n+3)/2},9^{(n+1)/2},1^{(n+3)/2},3^{(n+1)/2},5^{(n+3)/2},7^{(n+1)/2},9^{(n+3)/2})(2^{(n+1)/2},\hfill \\ & 4^{(n+3)/2},6^{(n+1)/2},8^{(n+3)/2},{10}^{(n+1)/2},2^{(n+3)/2},4^{(n+1)/2},6^{(n+3)/2},8^{(n+1)/2},{10}^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_2=\hfill & (1^1,3^{n+1},5^1,2^{n+1},4^1,1^{n+1},3^1,5^{n+1},2^1,4^{n+1})(1^2,5^n,9^2,3^n,7^2,1^n,5^2,9^n,3^2,\hfill \\ & 7^n)(2^2,6^n,{10}^2,4^n,8^2,2^n,6^2,{10}^n,4^2,8^n)(1^3,5^{n-1},9^3,3^{n-1},7^3,1^{n-1},5^3,9^{n-1},3^3,\hfill \\ & 7^{n-1})(2^3,6^{n-1},{10}^3,4^{n-1},8^3,2^{n-1},6^3,{10}^{n-1},4^3,8^{n-1})\cdots (1^{(n+1)/2},5^{(n+3)/2},\hfill \\ & 9^{(n+1)/2},3^{(n+3)/2},7^{(n+1)/2},1^{(n+3)/2},5^{(n+1)/2},9^{(n+3)/2},3^{(n+1)/2},7^{(n+3)/2})(2^{(n+1)/2},\hfill \\ & 6^{(n+3)/2},{10}^{(n+1)/2},4^{(n+3)/2},8^{(n+1)/2},2^{(n+3)/2},6^{(n+1)/2},{10}^{(n+3)/2},4^{(n+1)/2},8^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_3=\hfill & (1^1,4^{n+1},2^1,5^{n+1},3^1,1^{n+1},4^1,2^{n+1},5^1,3^{n+1})(1^2,7^n,3^2,9^n,5^2,1^n,7^2,3^n,9^2,\hfill \\ & 5^n)(2^2,8^n,4^2,{10}^n,6^2,2^n,8^2,4^n,{10}^2,6^n)(1^3,7^{n-1},3^3,9^{n-1},5^3,1^{n-1},7^3,3^{n-1},9^3,\hfill \\ & 5^{n-1})(2^3,8^{n-1},4^3,{10}^{n-1},6^3,2^{n-1},8^3,4^{n-1},{10}^3,6^{n-1})\cdots (1^{(n+1)/2},7^{(n+3)/2},\hfill \\ & 3^{(n+1)/2},9^{(n+3)/2},5^{(n+1)/2},1^{(n+3)/2},7^{(n+1)/2},3^{(n+3)/2},9^{(n+1)/2},5^{(n+3)/2})(2^{(n+1)/2},\hfill \\ & 8^{(n+3)/2},4^{(n+1)/2},{10}^{(n+3)/2},6^{(n+1)/2},2^{(n+3)/2},8^{(n+1)/2},4^{(n+3)/2},{10}^{(n+1)/2},6^{(n+3)/2}),\hfill \end{array}$$

$$\begin{array}{ll}{\sigma }_4=\hfill & (1^1,5^{n+1},4^1,3^{n+1},2^1,1^{n+1},5^1,4^{n+1},3^1,2^{n+1})(1^2,9^n,7^2,5^n,3^2,1^n,9^2,7^n,5^2,\hfill \\ & 3^n)(2^2,{10}^n,8^2,6^n,4^2,2^n,{10}^2,8^n,6^2,4^n)(1^3,9^{n-1},7^3,5^{n-1},3^3,1^{n-1},9^3,7^{n-1},5^3,\hfill \\ & 3^{n-1})(2^3,{10}^{n-1},8^3,6^{n-1},4^3,2^{n-1},{10}^3,8^{n-1},6^3,4^{n-1})\cdots (1^{(n+1)/2},9^{(n+3)/2},\hfill \\ & 7^{(n+1)/2},5^{(n+3)/2},3^{(n+1)/2},1^{(n+3)/2},9^{(n+1)/2},7^{(n+3)/2},5^{(n+1)/2},3^{(n+3)/2})(2^{(n+1)/2},\hfill \\ & {10}^{(n+3)/2},8^{(n+1)/2},6^{(n+3)/2},4^{(n+1)/2},2^{(n+3)/2},{10}^{(n+1)/2},8^{(n+3)/2},6^{(n+1)/2},4^{(n+3)/2}).\hfill \end{array}$$

So, C${}_{10}$${}_n$ (n is odd) has $\frac{n-1}{2}\times 2+1=n$ orbits which each have 10 vertices, see Table 2.

Figure 9. C${}_{10}$${}_n$,n is odd.

By similar argument, we have the following theorem.

Theorem 5.

Consider the fullerene graph $C_{10n}$ (n is odd), then there are n+1 orbits under the action of automorphism group on the set of edges. These are $O(e_1^1),O(e^1),O(e_1^2),O(e^2),\cdots ,O(e^{(n-1)/2}),O(e_1^{(n+1)/2}),O(e^{(n+1)/2}).$

Now consider the fullerene graph $C_{12n}$ ($nisodd$) as depicted in Figure 10.

Figure 10. The fullerene graph C${}_{12}$${}_n$ (n is odd).

Theorem 6.

Consider the fullerene graph C${}_{12}$${}_n$ (n is odd), then there are n + 1 orbits under the action of automorphism group on the set of edges.

Proof. 

Suppose n is an odd number. The graph $C_{12n}$ has n + 1 levels such that the first and the last levels have six edges and the other levels have 12 edges. There are six edges between i-th and i + 1-th levels. We call them as i-th set of vertical edges. By rotation $\rho ={60}^{\circ }$ around the central hexagon, one can see that the edges of the first level and the last level are in the same orbit. In addition, suppose $\alpha$ is a reflection which maps the central hexagon to the last one. One can prove that i-th and $n+1$-th $(1\le i\le n-1/2)$ set of edges of vertical edges are in the same orbit under the action of <ρ, α>. Note that in the case that i = (n + 1)/2, we have an orbit of size 6 and the other orbits are of size 12. In addition, by a similar argument, one can see that the edges of the j-th and n + 2-th $(1\le j\le n+1/2)$ levels are in the same orbit. In other words, $C_{12n}$ has $1+(n-1)/2$ orbits of size 12, $n-1/2$ orbits of size 24 and one orbit of size 6. This means that the number of orbits of $C_{12n}$ on the set of edges is n + 1. ☐

Similarly, if n is even, see Figure 11, the following theorem can be obtained.

Figure 11. The fullerene graph C${}_{12}$${}_n$ (n is even).

Theorem 7.

Consider the fullerene graph C${}_{12}$${}_n$ (n is even), then there are n + 1 orbits under the action of automorphism group on the set of edges.

Now consider the fullerene graph $C_{24n}$ as given in Figure 12.

Figure 12. C${}_{24}$${}_n$,n is even.

Theorem 8.

For the fullerene graph C${}_{24}$${}_n$$(n\ge 2)$, we have

$$Aut(C_{24n})\cong D_{24}.$$

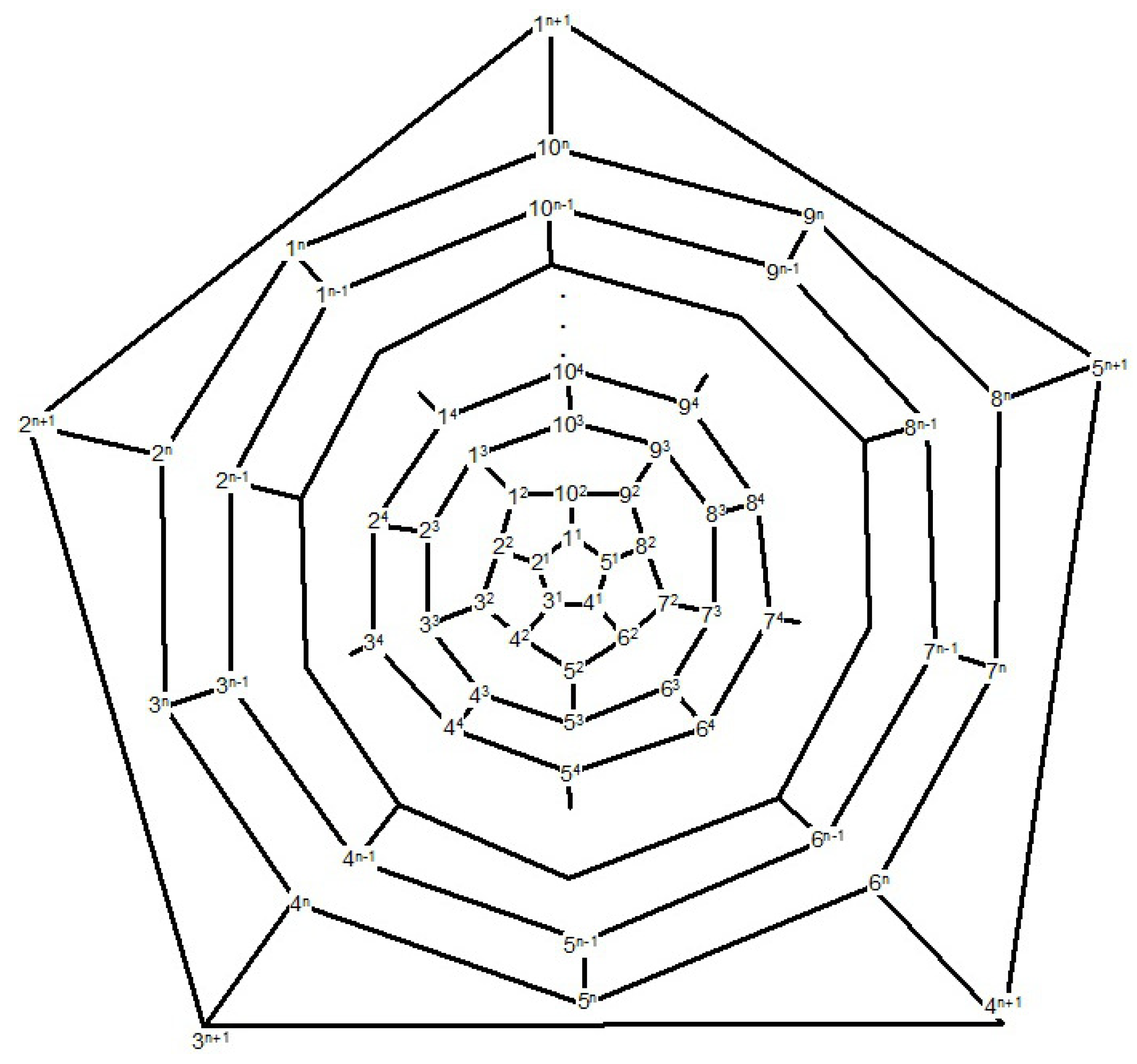
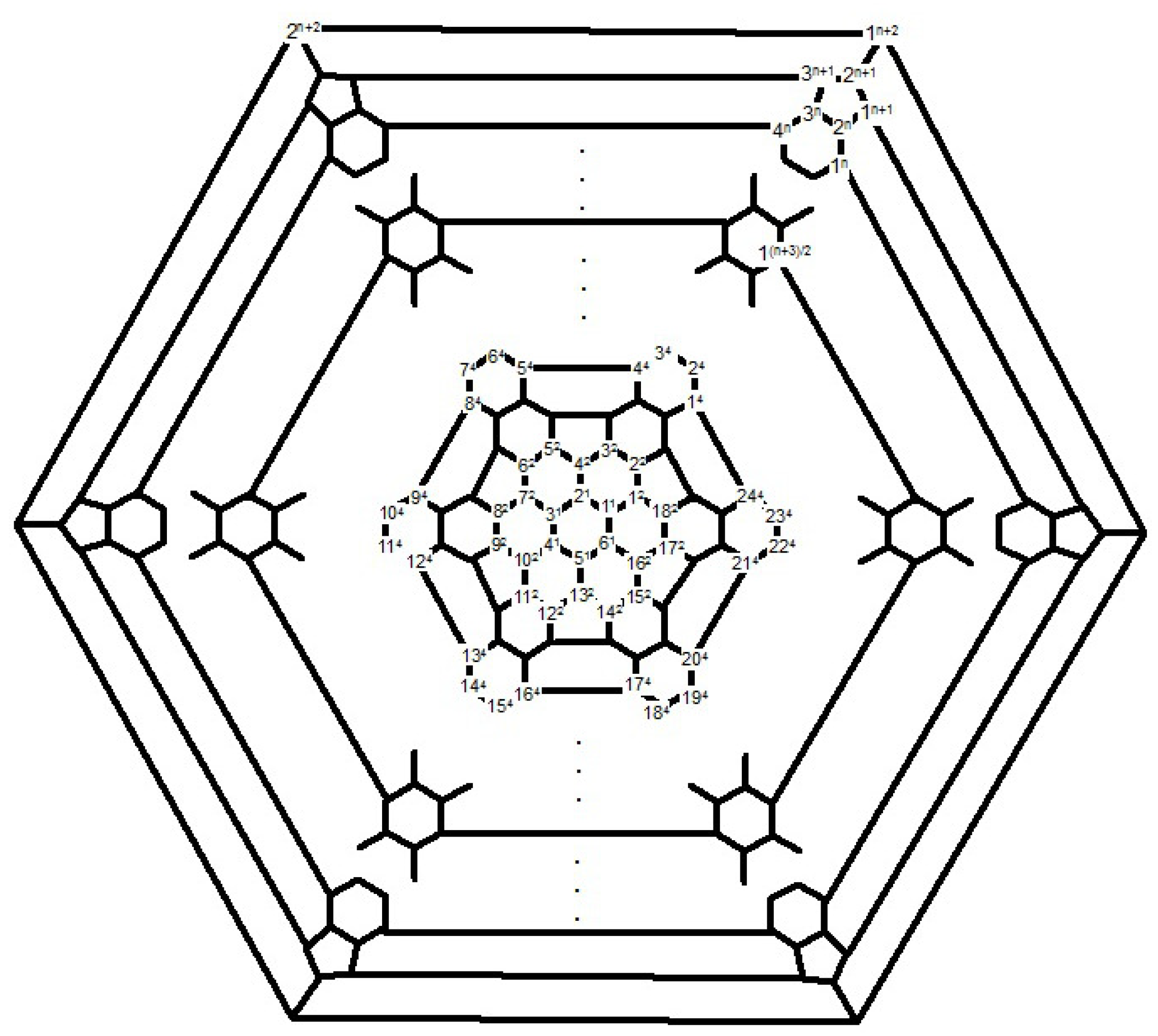
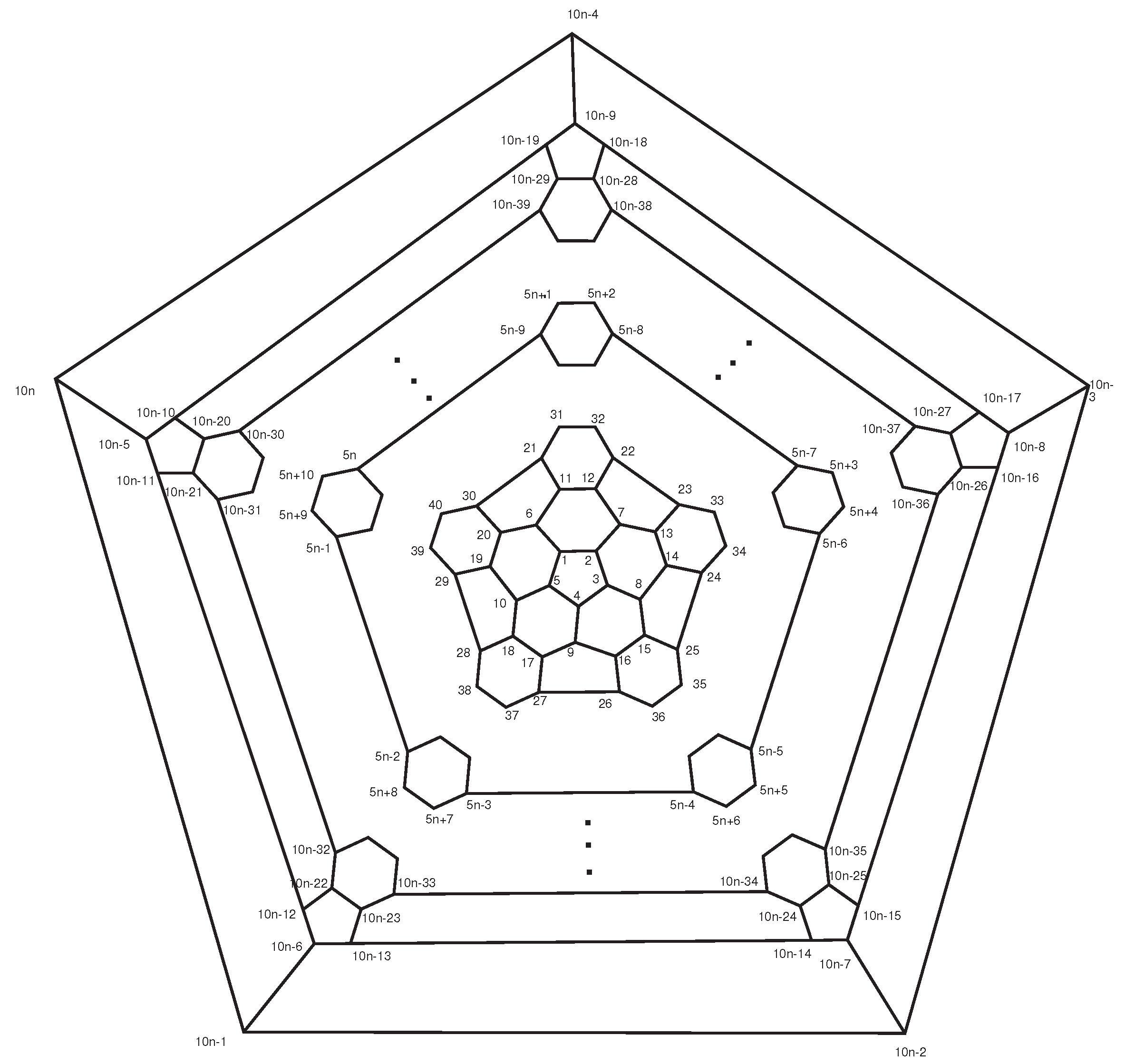
Proof. 

First, we compute the full automorphism group G = $Aut(C_{24n})$ of fullerene C${}_{24}$${}_n$, where n is even as depicted in Figure 12. Suppose a is a symmetry element in which $fix(a)=\{1^1,1^2,4^1,{10}^2\}$ and b denotes the element of order 12 such that permutation presentation of b is as follows:

b = (1${}^1$, 1${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$) (1${}^2$, 2${}^{n+1}$, 4${}^2$, 5${}^{n+1}$, 7${}^2$, 8${}^{n+1}$, 10${}^2$, 11${}^{n+1}$, …, 16${}^2$, 17${}^{n+1)}$ (2${}^2$, 3${}^{n+1}$, 5${}^2$, 6${}^{n+1}$, 8${}^2$, 9${}^{n+1}$, 11${}^2$, 12${}^{n+1}$, …, 17${}^2$, 18${}^{n+1}$) (3${}^2$, 4${}^{n+1}$, 6${}^2$, 7${}^{n+1}$, 9${}^2$, 10${}^{n+1}$, 12${}^2$, 13${}^{n+1}$, …, 18${}^2$, 1${}^{n+1}$) (1${}^i$, 3${}^{n-i+3}$, 5${}^i$, 7${}^{n-i+3}$, 9${}^i$, 11${}^{n-i+3}$, 13${}^i$, 15${}^{n-i+3}$, …, 21${}^i$, 23${}^{n-i+3}$) (2${}^i$, 4${}^{n-i+3}$, 6${}^i$, 8${}^{n-i+3}$, 10${}^i$, 12${}^{n-i+3}$, 14${}^i$,1 6${}^{n-i+3}$, …, 22${}^i$, 24${}^{n-i+3}$) (3${}^i$, 5${}^{n-i+3}$, 7${}^i$, 9${}^{n-i+3}$, 11${}^i$, 13${}^{n-i+3}$, 15${}^i$, 17${}^{n-i+3}$, …, 23${}^i$, 1${}^{n-i+3}$) (4${}^i$, 6${}^{n-i+3}$, 8${}^i$, 10${}^{n-i+3}$, 12${}^i$, 14${}^{n-i+3}$, 16${}^i$, 18${}^{n-i+3}$, …, 24${}^i$, 2${}^{n-i+3}$), where (3≤i≤(n+2)/2).

Clearly, $G\ge ⟨\mathrm{a},\mathrm{b}⟩$ and the orbit-stabilizer property shows that $\left|G\right|=|{(1^1)}^G|\times |G_{1^1}|$. By considering the action of subgroup G${}_1$ on the set of vertices, it can be found that any symmetry of fullerene C${}_{24}$${}_n$ which fixes two vertices $1^1$ and $1^2$ must also fixes the opposite vertices $4^1$ and ${10}^2$. Applying again the orbit-stabilizer property yields $|G_{1^1}|=|{(1^2)}^{G_{1^1}}|\times |G_{1^1}{}_{{}_{1^2}}|.$ It is easy to prove that $|G_{1^1}{}_{{}_{1^2}}|$ = 2, $|{(1^2)}^{G_{1^1}}|=1$ and $|{(1^1)}^G|=12$. Hence |G| = 24. On the other hand, $|⟨\mathrm{a},\mathrm{b}⟩|=24$ and this leads us to conclude that $G=⟨\mathrm{a},\mathrm{b}⟩\cong D_{24}$. 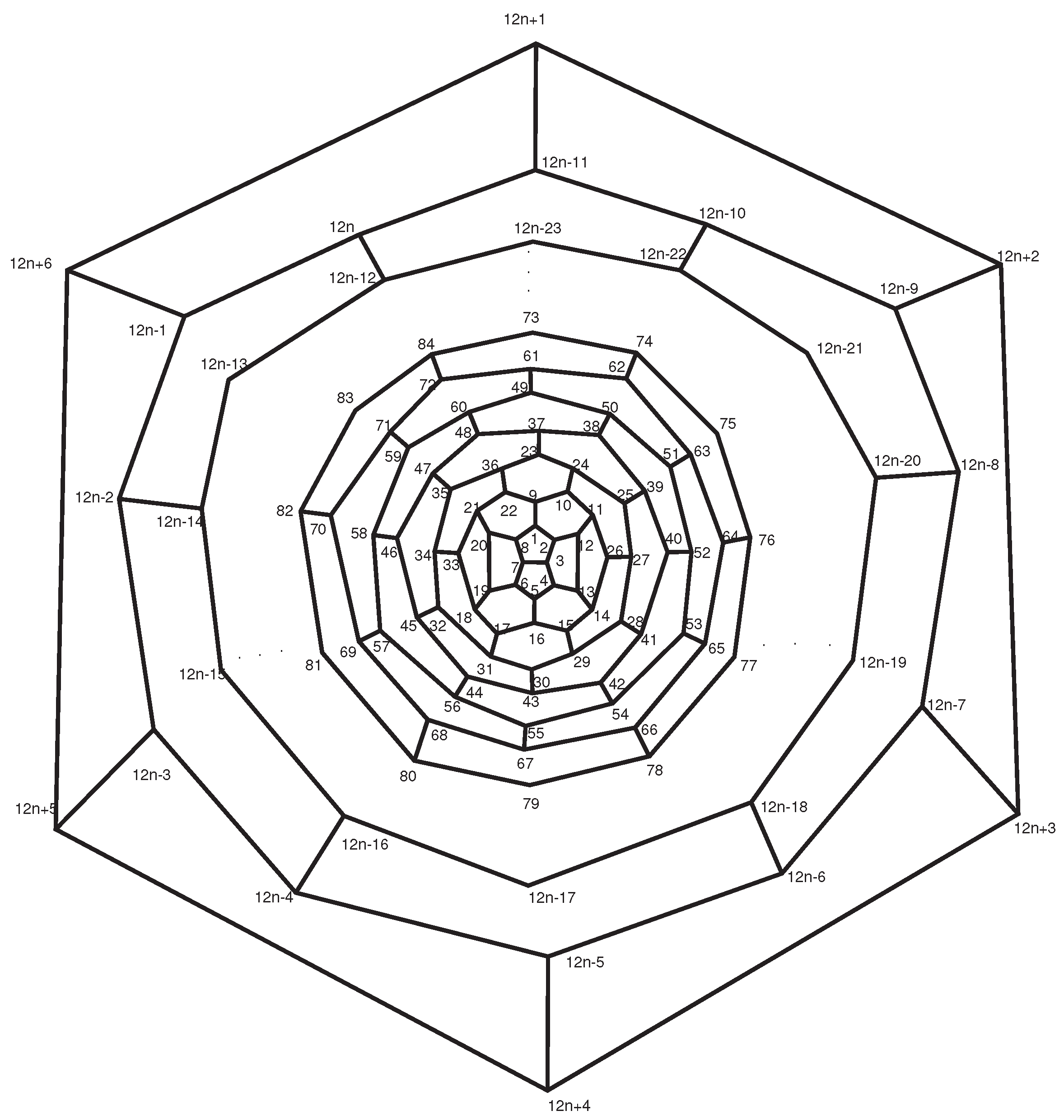Now suppose n is odd (see Figure 13), $fix(a)=\{1^1,1^2,4^1,{10}^2\}$ and b = (1${}^1$, 1${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$, 2${}^1$, 2${}^{n+2}$) (1${}^2$, 2${}^{n+1}$, 4${}^2$, 5${}^{n+1}$, 7${}^2$, 8${}^{n+1}$, 10${}^2$, 11${}^{n+1}$, …, 16${}^2$, 17${}^{n+1}$) (2${}^2$, 3${}^{n+1}$, 5${}^2$, 6${}^{n+1}$, 8${}^2$, 9${}^{n+1}$, 11${}^2$, 12${}^{n+1}$, …, 17${}^2$, 18${}^{n+1}$) (3${}^2$, 4${}^{n+1}$, 6${}^2$, 7${}^{n+1}$, 9${}^2$, 10${}^{n+1}$, 12${}^2$, 13${}^{n+1}$, …, 18${}^2$, 1${}^{n+1}$) (1${}^i$, 3${}^{n-i+3}$, 5${}^i$, 7${}^{n-i+3}$, 9${}^i$, 11${}^{n-i+3}$, 13${}^i$, 15${}^{n-i+3}$, …., 21${}^i$, 23${}^{n-i+3}$) (2${}^i$, 4${}^{n-i+3}$, 6${}^i$, 8${}^{n-i+3}$, 10${}^i$, 12${}^{n-i+3}$, 14${}^i$, 16${}^{n-i+3}$, …, 22${}^i$, 24${}^{n-i+3}$) (3${}^i$, 5${}^{n-i+3}$, 7${}^i$, 9${}^{n-i+3}$, 11${}^i$, 13${}^{n-i+3}$, 15${}^i$, 17${}^{n-i+3}$, …, 23${}^i$, 1${}^{n-i+3}$) (4${}^i$, 6${}^{n-i+3}$, 8${}^i$, 10${}^{n-i+3}$, 12${}^i$, 14${}^{n-i+3}$, 16${}^i$, 18${}^{n-i+3}$, …, 24${}^i$, 2${}^{n-i+3}$) (1${}^{(n+3)/2}$, 3${}^{(n+3)/2}$, 5${}^{(n+3)/2}$, 7${}^{(n+3)/2}$, …, 21${}^{(n+3)/2}$, 22${}^{(n+3)/2}$) (2${}^{(n+3)/2}$, 4${}^{(n+3)/2}$, 6${}^{(n+3)/2}$, 8${}^{(n+3)/2}$,…, 22${}^{(n+3)/2}$, 24${}^{(n+3)/2}$), where (3≤i≤(n-3)/2). By similar argument $G=⟨\mathrm{a},\mathrm{b}⟩\cong D_{24}$. In general, we can conclude that the symmetry elements C${}_{24}$${}_n$ have the cycle types as given in Table 3. ☐

Figure 13. C${}_{24}$${}_n$,n is odd.

Table 3. The cycle type of automorphism group of fullerene C${}_{24}$${}_n$.

Permutations	Cycle Type
1	$1^{24n}$
6	$1^4{2}^{12n-2}$
7	$2^{12n}$
2	$3^{8n}$
2	$4^{6n}$
2	$6^{4n}$
4	${12}^{2n}$

By applying Equation (1) the fullerene graph C${}_{24}$${}_n$ has $(24n+6\times 4)/24=n+1$ orbits under the action of automorphism group on the set of vertices.

Theorem 9.

[41] The automorphism group of fullerene graph $A_{12n+4}(n\ge 4)$ is isomorphic with symmetric group $S_3$.

Proof. 

Consider the labeling of the fullerene graph $A_{12n+4}$ as shown by Figure 14. Suppose $\alpha =(2,5,8)(3,6,9)\dots (12n+2,12n+4,12n),$ and $\beta =(2,8)(3,7)\dots (12n+2,12n)$. Clearly, $S_3\cong ⟨\alpha ,\beta ⟩\le A=Aut(A_{12n+4})$. On the other hand, $\left|A\right|=|1^A\left|\right|A_1|$. Clearly, each automorphism which fixes points 1 and 2 must fixes $\{7,11,17,\cdots 12n-1,12n+2\}$, $|A_1|=|A_{1,2}\left|\right|2^{A_1}|=2\times 3$. Hence $1^A=\{1\}$ and, thus, $\left|A\right|=6$ which implies that $A\cong S_3.$ ☐

Figure 14. Labeling the vertices of fullerene graph $A_{12n+4}$.

Theorem 10.

[41] The automorphism group of fullerene graph $B_{12n+6}(n\ge 6)$ is isomorphic with group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$.

Proof. 

Consider the graph $B_{12n+6}$ shown in Figure 15. Clearly, $\alpha ,\beta$ are automorphisms of fullerene graph $B_{12n+6}$:

$$\begin{array}{l}\alpha =(1,5)(2,4)(6,8)\dots (12n+1,12n+4)(12n+2,12n+3)(12n+5,12n+6),\hfill \\ \beta =(2,8)(3,7)(4,6)\dots (12n+3,12n+5)(12n+2,12n+6).\hfill \end{array}$$

Then $G=⟨\alpha ,\beta ⟩\le A=Aut(B_{12n+6})$. Since every automorphism that fixes point 3 also fixes the points $\{7,26,27,33,\dots ,12n-8,12n-2\}$, the orbit-stabilizer property implies that $\left|A\right|=|3^A\left|\right|A_3|=2\times 2$. Therefore, $A\cong {\mathbb{Z}}_2\times {\mathbb{Z}}_2.$ ☐

Figure 15. Labeling the vertices of the fullerene graph $B_{12n+6}$.

Further, this group is isomorphic to the Abelian group ${\mathbb{Z}}_2\times {\mathbb{Z}}_2$ of order 4 and the cycle types of elements of S are as given in Table 4.

Table 4. Cycle type of automorphism group of fullerene C${}_{12}$${}_{n+6}$.

Permutations	Cycle Type
1	$1^{12n+6}$
1	$1^4{2}^{6n+1}$
1	$1^6{2}^{6n}$
1	$2^{6n+3}$

Theorem 11.

[42] The automorphism group of the fullerene graph $A_{12n}(n\ge 4)$ is isomorphic with dihedral group $D_{24}$.

Proof. 

Let n be an even number and consider the fullerene $A_{12n}$ in Figure 16. Consider two permutations $\alpha ,\beta$ with the following permutation representations:

$$\begin{array}{ccc}\hfill \alpha & =& (2,6)(3,5)\cdots (12n-5,12n)(12n-4,12n-1)(12n-3,12n-2),\hfill \\ \hfill \beta & =& (1,12n-2,2,12n-1,3,12n,4,12n-5,5,12n-4,6,12n-3)\dots \hfill \\ & & (6n-5,6n+2,6n-3,6n+4,6n-1,6n+6,6n+1,6n-4,6n+3,\hfill \\ & & 6n-2,6n+5,6n).\hfill \end{array}$$

One can prove that ${\alpha }^2={\beta }^{12}=1,\alpha \beta \alpha ={\beta }^{-1}$ and thus $A=Aut(A_{12n})\ge ⟨\alpha ,\beta ⟩\cong D_{24}$. On the other hand, the identity element and the symmetry element $\alpha$ fixes 1. Hence, the orbit-stabilizer property implies that $\left|A\right|=|1^A|.|A_1|$ and thus $\left|A\right|=12\times 2$ and thus $A\cong D_{24}$. By a similar method, if n is odd (as depicted in Figure 17), the automorphism group is isomorphic with dihedral group $D_{24}$. ☐

Figure 16. Labeling the vertices of fullerene graph $A_{12n}$, n is even.

Figure 17. Labeling the vertices of fullerene graph $A_{12n}$, n is odd.

Theorem 12.

[42] The automorphism group of the fullerene graph ${\mathrm{A}}_{10n}(n\ge 7)$ is isomorphic with dihedral group $D_{20}$.

Proof. 

Consider the fullerene graph ${\mathrm{A}}_{10n}$, n is even, as depicted in Figure 18. Two permutations $\alpha$ and $\beta$ by the following presentation are in the automorphism group:

$$\begin{array}{ccc}\hfill \alpha & =& (1,2)(3,5)\dots (10n-3,10n)(10n-2,10n-1),\hfill \\ \hfill \beta & =& (1,10n)(2,10n-1)\cdots (3,10n-2)(4,10n-3)(5,10n-4),\hfill \\ \hfill \gamma & =& (1,2,3,4,5)(6,7,8,9,10)\dots (10n-4,10n-3,10n-2,10n-1,10n).\hfill \end{array}$$

Suppose $\beta \gamma =\rho$, it is clear that ${\alpha }^2={\rho }^{10}=1,\alpha \rho \alpha ={\rho }^{-1}$ and thus $\Gamma =⟨\alpha ,\rho ⟩\le A=Aut({\mathrm{A}}_{10n})$ is isomorphic with dihedral group D${}_{20}$. A symmetry element which fixes 4 (such as identity and $\alpha$) must also fixes {9, 10n-9, 10n-4}. Apply the orbit-stabilizer property to obtain |A| = |4${}^A$|.|A${}_4$| and thus $\left|A\right|=10\times 2=20$. This yields $A\cong D_{20}.$ Now, consider the fullerene graph ${\mathrm{A}}_{10n}$, where n is odd, as depicted in Figure 19. A similar argument shows that ${Aut(\mathrm{A}}_{10n})\cong D_{20}$. ☐

Figure 18. Labeling the vertices of fullerene graph ${\mathrm{A}}_{10n}$, n is even.

Figure 19. Labeling the vertices of fullerene graph ${\mathrm{A}}_{10n}$, n is odd.

4. Leapfrog Operation

Suppose C${}_n$ is a fullerene on n vertices. By means an operation which is called the Leapfrog principle, we can construct bigger fullerenes with the same symmetry group. To do this, put an extra vertex into the centre of each face of C${}_n$. Then connect these new vertices with all the vertices surrounding the corresponding face. Then the dual polyhedron is again a fullerene with $3n$ vertices, 12 pentagonal and (3n/2)-10 hexagonal faces, see [43,44]. For example, in Figure 20 it is shown that Le(C${}_{20}$) = C${}_{60}$.

Figure 20. The Fullerene C${}_{20}$ and Le(C${}_{20}$).

Here, we compute the symmetry group of fullerenes constructed by Leapfrog. Consider the molecular graph of the fullerene $C_{3^n\times 20}$ as given in Figure 21. From the Leapfrog principle, one can see that the symmetry group G of these fullerenes is isomorphic to the group $I_h=Z_2\times A_5$ of order 120 and the cycle types of elements of G are as given in Table 5.

Figure 21. 3-D graphs of fullerene $C_{3^n\times 20}$, n = 2.

Table 5. Cycle type of automorphism elements of fullerene C${}_{3^n\times 20}$.

Permutations	Cycle Type
1	$1^{3^n\times 20}$
16	$2^{3^n\times 10}$
15	$1^{3^{n-1}\times 4}{2}^{3^{n-1}\times 28}$
20	$3^{3^{n-1}\times 20}$
24	$5^{3^n\times 4}$
20	$6^{3^{n-1}\times 10}$

Now consider the molecular graph of the fullerene $F_{3^n\times 34}$, Figure 22. In [40] it is proved that the symmetry group G of these fullerenes is isomorphic to the group S${}_3$ of order 6 and the cycle types of elements of G are as given in Table 6.

Figure 22. 3-D graph of fullerene $C_{3^n\times 34}$, n = 1.

Table 6. Cycle type of automorphism group of fullerene $F_{3^n\times 34}$.

Permutations	Cycle Type
1	$1^{3^n\times 34}$
3	$1^{6n}{2}^{17\times 3^n-3n}$
2	$3^{3^{n-1}\times 34}$

Finally, consider the molecular graph of the fullerene $C_{3^n\times 34}$, Figure 23 and Figure 24. In [40] it is shown that the symmetry group of this fullerene is isomorphic with a cyclic group of order 2, namely $Z_2$ and the cycle types of elements are given in Table 7 and Table 8.

Figure 23. 2-D and 3-D graphs of fullerene C${}_{34}$.

Figure 24. 2-D and 3-D graphs of fullerene $C_{3^n\times 34}$, n = 2.

Table 7. Cycle type of automorphism group of fullerene $C_{3^n\times 34}$ (n is even).

Permutations	Cycle Type
1	$1^{3^n\times 34}$
1	$1^{6\times 3^{n/2}}{2}^{34\times 3^n-6\times 3^{n/2}}$

Table 8. Cycle type of automorphism group of fullerene $C_{3^n\times 34}$ (n is odd).

Permutations	Cycle Type
1	$1^{3^n\times 34}$
1	$1^{4\times 3^{(n-1)/2}}{2}^{34\times 3^n-4\times 3^{(n-1)/2}}$

5. The Symmetry Group of Non-Classical Fullerenes

Here, we introduce an infinite class of cubic polyhedral graph composed of quadrilateral, hexagonal and octagonal faces, see Figure 25. This class of cubic polyhedral graphs has exactly $16n$ vertices where $n\ge 3$. We denote this new family of cubic polyhedral graph by $F_{16n}$. Let $s,h,o,n$ and m be the number of squares, hexagons and octagons, carbon atoms and bonds between them, in a given $(4,6,8)$ cubic polyhedral graph F. Since each atom lies in exactly 3 faces and each edge lies in 2 faces, the number of atoms is $n=(4s+6h+8o)/3$, the number of edges is $m=(4s+6h+8o)/2=3/2n$ and the number of faces is $f=s+h+o$. By Euler’s formula $n-m+f=2$ and then $s+h+o=2+n/2$. This leads us to conclude that $s=12,h=8n-16$ and $o=6$, for $n\ge 3$.

Figure 25. The polyhedral graph $F_{16n}$, where $n=3$.

Example 4.

Here, we compute the order of automorphism group of polyhedral graph $F_{48}$ depicted in Figure 25. We compute the order of $G=Aut(F_{16n})$ of symmetries of the polyhedral graph $F_{16n}$, for $n=3$ depicted in Figure 26. Clearly, the automorphism group of $F_{16n}$ for $n\ge 3$ can be computed similarly. If α denotes the rotation of the $F_{16n}$ through an angle of ${90}^{\circ }$ around an axis through the midpoints of the front and back faces, then the corresponding permutation is $\alpha =(1,3,5,7)(2,4,6,8)(9,15,26,21)(10,16,27,32)(11,17,28,22)(12,18,29,23)(13,19,30,24)(14,20,31,25)(33,45,41,37)(34,46,42,38)(35,47,43,39)(36,48,44,40).$ Thus the orbit of the subgroup $⟨\alpha ⟩$ is $1^{⟨\alpha ⟩}=\{1,3,5,7\}$. Now, consider the axis symmetry element which fixes no vertices, it is as follows: $\beta =(1,2)(3,8)(4,7)(5,6)(9,20)(10,19)(11,18)(12,17)$ $(13,16)(14,15)(21,31)(22,29)(23,28)(24,27)(25,26)(30,32)(33,40)(34,39)(35,38)(36,37)(41,48)(42,47)(43,46)(44,45).$ Clearly, $G\ge ⟨\alpha ,\beta ⟩.$ According to the orbit-stabilizer property $\left|G\right|=|2^G|\times |G_2|$ while no element fixes 2. This means that $|G_2|=1$ and so $\left|G\right|=|2^G|$. It is clear that $2^{⟨\alpha ,\beta ⟩}=\{1,2,3,4,5,6,7,8\}$ and thus, $|2^{⟨\alpha ,\beta ⟩}|=8$. On the other hand, every automorphism preserves the adjacency and thus there is no vertex u other than $\{1,2,3,4,5,6,7,8\}$ and a permutation $\sigma \in Aut(F_{16n})$ with $\sigma (u)=2$. This implies that $2^G=\{1,2,3,4,5,6,7,8\}$ and hence $\left|G\right|=8$. It is not difficult to see that $|⟨\alpha ,\beta ⟩|=8$ where ${\alpha }^4={\beta }^2=1$ and $\beta \alpha \beta ={\alpha }^{-1}.$ One can verify then $G=⟨\alpha ,\beta ⟩\cong D_8$ and the proof is complete.

Figure 26. Labeling of fullerene $F_{96}$.

In general, we have the following theorem.

Theorem 13.

The automorphism group $Aut(F_{16n})$ is isomorphic with dihedral group $D_8$.

Now, consider an infinite class of polyhedral graphs with exactly $12n+72$ vertices, where n is an integer greater than or equal with 2. That’s why we name this new family of polyhedral graphs by $F_{12n+72}$.

Example 5.

Consider the fullerene graph $F_{96}$ depicted in Figure 26. If α denotes the rotation of $F_{96}$ through an angle of ${60}^{\circ }$ around an axis through the midpoints of the front and back faces, then the corresponding permutation is

$$\begin{array}{cc}\hfill \alpha & =(1,2,3,4,5,6)(7,10,14,17,20,24)(8,11,15,18,21,25)(9,12,16,19,23,26)\\ & (13,50,58,74,66,42)(22,71,47,39,55,63)(27,28,29,30,31,32)\\ & (33,48,56,72,64,40)(34,49,57,73,65,41)(35,51,59,75,67,43)\\ & (36,52,60,76,68,44)(37,53,61,77,69,45)(38,54,62,78,70,46)\\ & (79,80,81,82,83,84)(85,86,87,88,89,90)(91,96,95,94,93,92).\end{array}$$

Thus, an orbit of $⟨\alpha ⟩$ containing the vertex 1 is $1^{⟨\alpha ⟩}=\{1,2,3,4,5,6\}$. Now, consider the axis symmetry element which fixes vertices $\{1,4,8,18,43,44,59,60,85,88,92,95\}$, the corresponding permutation is

$$\begin{array}{cc}\hfill \beta & =(2,6)(3,5)(7,9)(10,26)(11,25)(12,24)(13,71)(14,23)(15,21)(16,20)\\ & (17,19)(22,50)(27,28)(29,32)(30,31)(33,70)(34,69)(35,67)(36,68)\\ & (37,65)(38,64)(39,66)(40,46)(41,45)(42,47)(48,78)(49,77)(51,75)\\ & (52,76)(53,73)(54,72)(55,74)(56,62)(57,61)(58,63)(79,80)(81,84)\\ & (82,83)(86,90)(87,89)(91,93)(94,96).\end{array}$$

Let $G=Aut(F_{96})$, clearly $G\ge ⟨\alpha ,\beta ⟩$ and the orbit-stabilizer property implies that $\left|G\right|=|1^G|\times |G_1|$. Any symmetry of the polyhedral graph $F_{96}$ which fixes vertex 1 must also fixes the opposite vertex 4. By again applying the orbit-stabilizer property, we found that $|G_1|=|4^{G_1}|\times |G_{1,4}|$. It is easy to prove that $|G_{1,4}|=2$ and hence $\left|G\right|=12$. On the other hand, $|⟨\alpha ,\beta ⟩|=12,$ where ${\alpha }^4={\beta }^2=1,\beta \alpha \beta ={\alpha }^{-1}$. This leads us to conclude that $G=⟨\alpha ,\beta ⟩\cong D_{12}$.

In general, we have the following theorem.

Theorem 14.

The automorphism group $Aut(F_{12n+72})$ is isomorphic with dihedral group $D_{12}$.