Abstract
We propose a new chaotic map combined with delay and cascade, called tent delay-sine cascade with logistic map (TDSCL). Compared with the original one-dimensional simple map, the proposed map has increased initial value sensitivity and internal randomness and a larger chaotic parameter interval. The chaotic sequence generated by TDSCL has pseudo-randomness and is suitable for image encryption. Based on this chaotic map, we propose an image encryption algorithm with a symmetric structure, which can achieve confusion and diffusion at the same time. Simulation results show that after encryption using the proposed algorithm, the entropy of the cipher is extremely close to the ideal value of eight, and the correlation coefficients between the pixels are lower than 0.01, thus the algorithm can resist statistical attacks. Moreover, the number of pixel change rate (NPCR) and the unified average changing intensity (UACI) of the proposed algorithm are very close to the ideal value, which indicates that it can efficiently resist chosen-plain text attack.
1. Introduction
With the development of information technologies, data security has aroused wide public concern. As an important data format, images occupy a large proportion of network data. Their secure transmission plays a vital role in personal and military privacy. In recent years, many chaotic image encryption algorithms have been proposed [1,2,3,4,5,6,7,8,9,10] due to the excellent properties of chaotic maps, such as initial value sensitivity and intrinsic randomness.
Researchers have improved the single chaotic map or combined multiple chaotic maps to improve chaotic properties, producing larger secret key spaces and more random chaotic sequences. Pak et al. [3] proposed a structure to modify two same chaotic maps to produce better performance than a single map [11,12,13,14]. Li et al. [15] improved the logistic map using linear delay. Zhou et al. [6] proved that cascading chaotic maps can increase the Lyapunov exponent, and many chaotic maps can be generated with the cascade model. Hua et al. [4] combined the logistic map and sine map to generate a two-dimensional (2D) map. This paper proposes a new framework that combines the cascade model and delay. This framework rationally integrates three chaotic maps to overcome the performance flaws of one-dimensional (1D) chaotic maps [16]. The experimental results showed that the chaotic maps produced by this model have initial value sensitivity and a large parameter interval.
Based on the proposed chaotic map, we constructed a new image encryption algorithm. Generally, image encryption algorithms can be divided into two steps: confusion and diffusion. Confusion involves randomly changing the position of pixels. The two commonly used confusion algorithms are: performing row and column confusion on a image, and reshaping a two-dimensional image into a vector, and then performing position confusion on it [17,18,19]. The basic diffusion methods are based on an XOR operation or mod operation after addition [20,21].
In this paper, a new simultaneous confusion and diffusion algorithm is proposed, which is applied in the vertical and horizontal directions based on an XOR operation. After analysis, the algorithm can resist chosen-plain text attacks and statistical attacks.
2. Chaotic Map
This section proposes a new chaotic map with delay and cascade using tent, sine, and logistic maps, which we have named tent delay-sine cascade with logistic map (TDSCL). Through the combination of these three kinds of maps, we verified that this new chaotic map has excellent chaotic complexity using the following analysis and comparison.
2.1. The Structure of Chaotic Maps
First, this section reviews three chaotic maps including tent map, sine map, and logistic map. Based on these three chaotic maps, the TDSCL map is generated. The tent map is defined mathematically as [22]:
where is the control parameter with the range of [0, 1].
The structure of the sine map is defined as [23]:
where is the control parameter with a range of [0, 1], and the map is chaotic with . For all , is bounded within [0, 1]. The diagrams of bifurcation are shown in Figure 1b.
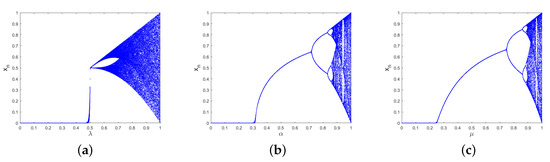
Figure 1.
The bifurcation diagram for the (a) tent map, (b) sine map, and (c) logistic map.
The logistic map is a simple 1D chaotic map. As a discrete chaotic map, Figure 1c shows its bifurcation, with outputs in the range of [0, 1] and an initial input value in [0, 1]. The structure of the logistic map is defined by [24]:
where is the control parameter in the range of [0, 1].
The above three chaotic maps all have flaws, producing no chaotic behavior in some ranges of parameters. Specifically, these three maps only show chaotic characteristics at the rightmost part of the parameter variation range, and the chaotic interval may be discontinuous. To overcome these flaws, we designed a novel chaotic map structure, which is shown in Figure 2. As shown in Figure 2, represents the tent map with a delay item input, and the sine map is indicated by . Then, the outputs of and are added as the input of . The function is taken as in this paper, and cascaded with , thereby obtaining the output result of the chaotic map.
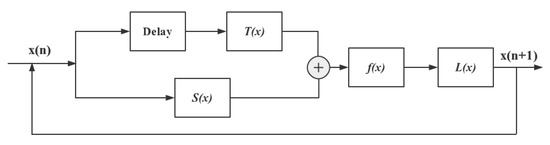
Figure 2.
The structure of the tent delay-sine cascade with logistic map (TDSCL).
Here, the control parameters for the tent map and the sine map are set to 1, and the parameter for the logistic map is used as the control parameter for this new map. Equations (4) and (5) show the mathematical formulae. The circle symbol in Equation (4) represents the composition of two functions. Compared to the 1D delay and linearly coupled logistic chaotic map (DLCL) [15] and a two-dimensional logistic-modulated sine-coupling logistic chaotic map (LSMCL) [1], the structure of TDSCL produces better chaotic performance. In the following section, we use the trajectory, Lyapunov exponent, and permutation entropy (PE) to analyze the characteristics of chaotic maps.
2.2. Chaotic Performance of TDSCL
2.2.1. Chaotic Trajectory
For a chaotic system, the trajectory on the phase plane can show the randomness of outputs [25]. The larger the space occupied by the trajectory, the better the random outputs of the chaotic systems. Figure 3 shows the trajectories of TDSCL, DLCL, and LSMCL. The trajectory of TDSCL can fill the entire phase space compared to DLCL and LSMCL. This indicates that the sequence generated by the TDSCL chaotic map has better randomness and ergodicity.
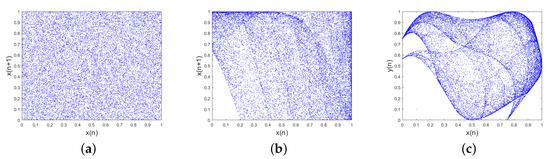
Figure 3.
Trajectories for (a) TDSCL with = 1, (b) delay and linearly coupled logistic chaotic map (DLCL) with = 1, and (c) logistic-modulated sine-coupling logistic chaotic map (LSMCL) with .
2.2.2. Lyapunov Exponent
One of the most important features of a chaotic system is a strong sensitivity to initial values. The Lyapunov exponent (LE) [26] provides a quantitative description of the initial state sensitivity of a chaotic system. A maximum Lyapunov exponent of the chaotic map greater than 0 indicates that the system is in a chaotic state. For a two-dimensional chaotic system, if the system’s two Lyapunov exponents are greater than 0, then the system is in a hyperchaotic state.
In Figure 4a–c, the Lyapunov exponents of TDSCL, DLCL, and LSMCL are calculated. From these diagrams, TDSCL displays hyperchaotic behavior when approximately . When , the maximum Lyapunov exponent of TDSCL is close to 9.2. Therefore, compared with the other two maps, TDSCL not only has a larger chaotic state interval, but also a larger Lyapunov exponent in a large continuous interval. Compared with DLCL and LSMCL, TDSCL is more sensitive to small changes in the initial value of the system and has better unpredictability.
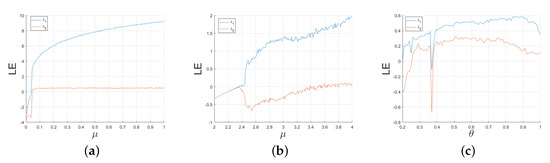
Figure 4.
Lyapunov exponent: (a) TDSCL, (b) DLCL, and (c) LSCML.
2.2.3. Permutation Entropy
The permutation entropy can be used to measure the complexity of chaotic sequences [27]. For a given chaotic system, an entropy of the generated chaotic sequence close to 1 indicates that the chaotic system has unpredictability. As shown in Figure 5, the PE of DLCL is close to 1, only when in the interval of [0.7, 1], and the permutation entropy of LSMCL is always less than 0.8. The permutation entropy value of TDSCL is very close to 1 when . This indicates that the chaotic sequences generated by TDSCL have more complex dynamic behaviour.
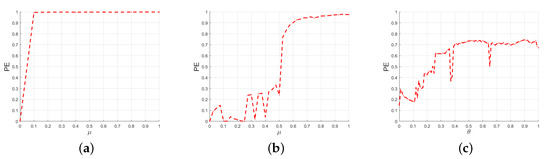
Figure 5.
Permutation entropy for (a) TDSCL, (b) DLCL, and (c) LSCML.
3. Image Encryption Algorithm
In the proposed algorithm, the secret key consists of 16 parameters {, , , , , , , , , , , , , , , and }, where are the first two values of the chaotic sequence, is the control parameter of the chaotic map, and is related to the length of the generated chaotic sequence. As shown in Figure 6, the first step in the encryption algorithm obtaining chaotic sequences is based on the key. Then, confusion and diffusion are performed simultaneously. The details of the algorithm are introduced below.
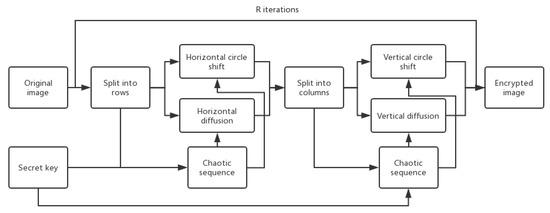
Figure 6.
The image encryption architecture.
3.1. Simultaneous Horizontal Confusion and Diffusion
- Step 1. Generate diffusion matrix .
Iterate Equation (4) times with initial value and control parameter . are the height and width of the image I that is being processed, respectively. Then, the diffusion matrix is obtained by the generated chaotic sequence using Equation (6).
where and . is the matrix of M by N, each value of which is derived from the chaotic sequence . With the given parameter , the generated chaotic sequence has considerable randomness.
- Step 2. Set .
- Step 3. Obtain begin index and circle shift the first row of the image right by pixels
Obtain from the secret key and and calculate the initial value as well as iteration time of chaotic map by adjusting them with the pixel value of image I according to Equation (7).
where:
Then, using initial value and parameter , iterate Equation (4) times. Obtain and according to Equation (9).
- Step 4. Horizontal diffusion.
The horizontal diffusion operation is performed based on the XOR operation. The operation process is as follows:
where
- Step 5. Circle shift horizontally by pixels.
- Step 6. Let and repeat steps 3 to 5 until all rows have been processed.
3.2. Simultaneous Vertical Confusion and Diffusion
The simultaneous operation of vertical confusion and diffusion is similar to the process introduced in the subsection above.
- Step 1. Generate diffusion matrix .
Iterate the formula in Equation (4) times with initial value and control parameter . Then, the diffusion matrix is obtained according to:
where and .
- Step 2. Set .
- Step 3. Generate index and circle shift the first column of the image by pixels.
Obtain from the secret key and adjust them with the pixel value of image I according to Equation (12).
where:
Then, using the initial value and parameter , iterate Equation (4) times. Obtain and according to Equation (14).
- Step 4. Vertical diffusion.
The vertical diffusion process is as follows:
where:
- Step 5. Circle shift vertically by pixels.
- Step 6. Let , and repeat steps 3 to 5 until all columns have been processed.
4. Experiment Results and Analysis
4.1. Simulation Results
To verify the feasibility of the encryption algorithm proposed in this paper, some pictures were used for testing. Figure 7 shows the original images in the first column, the encrypted images in the second column, and the decrypted images in the last column.


Figure 7.
Simulation results of the proposed image encryption algorithm: (a,d) original images, (b,e) encrypted images, and (c,f) decrypted images.
4.2. Secret Key Space
In the proposed algorithm, the secret key contains 16 parameters. The parameters of the chaotic map are double precise, and the parameters related to the number of iterations are in the range of 0 to 1000. Thus, the secret key space can reach , which is large enough to resist statistical attacks.
4.3. Statistical Analysis
4.3.1. Correlation Coefficient Analysis
In plain images, the correlation between adjacent pixels is fairly strong, and the correlation between adjacent pixels can be used by the attacker to obtain some useful information. Therefore, after image encryption, the correlation between adjacent pixels of the encrypted image is closer to 0, indicating that the pixel distribution is random. We selected 4000 pairs of adjacent pixels in plain images and encrypted images, and then calculated the correlation coefficient of two horizontal, vertical and diagonal adjacent pixels using Equation (16):
where and represent the expectation and variance of variable x, respectively. Table 1 shows the experimental results of the tested images by performing the encryption in two rounds. The correlation coefficient of three directions is close to 0 after the encryption.

Table 1.
The correlation coefficient in three directions for tested images.
Figure 8 shows the correlation of the Lena image and its cipher image. The adjacent pixel pairs of the plain image in all directions are densely on the line of , and the adjacent pixel pairs of the cipher image in all directions are evenly distributed in the rectangular area.
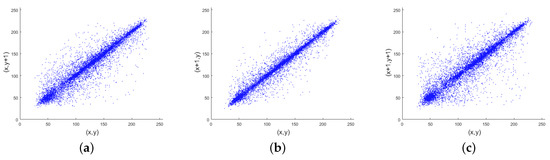
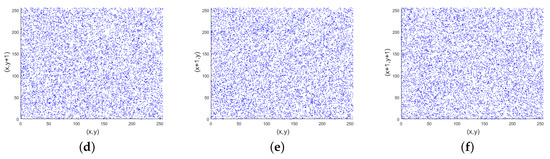
Figure 8.
Adjacent pixels correlation analysis: the correlation between two horizontal, vertical, and diagonal pixels in (a–c) a plain image and (d–f) an encrypted image.
4.3.2. Histogram Analysis
An image histogram can reflect the frequency distribution of pixel values in an image [15]. In this experiment, Figure 9 shows the histograms of the plain and cipher images. The histogram of the cipher image has a balanced pixels distribution. This indicates that it is difficult for the attackers to obtain valid statistical information from the encrypted image. As the pixel values of the encrypted image have no obvious regularity, the attacker cannot obtain the original image through brute force analysis of the cipher. Therefore, the encryption system proposed in this paper has the ability to resist statistical attacks.
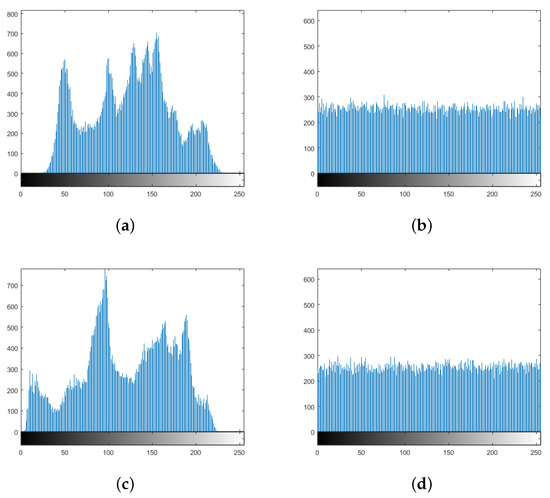
Figure 9.
Histograms of (a,b) Lena and the encrypted image and (c,d) Pepper and the encrypted image.
4.4. Key Sensitivity Test
Key sensitivity can be tested by the number of pixel change rate (NPCR) and the unified average changing intensity (UACI) [28]. In this test, we calculated the NPCR and UACI of two encrypted images based on changing a small value, set to for keys. The mathematical formulas for calculating NPCR and UACI are defined as [29]:
where and are the cipher image generated by the original key and the changed key in the key sensitivity test, respectively. The ideal values of NPCR and UACI are 99.6094% and 33.4635% for an 8-bit grey scale image, respectively [1]. Table 2 lists the simulation results. The NPCR and UACI of our proposed algorithm are very close to the expected value. The analysis results showed that the algorithm can resist chosen-plain text attacks.

Table 2.
The number of pixel change rate (NPCR) and the unified average changing intensity (UACI) of different images for key sensitivity.
4.5. Resistance Against Chosen-plain Text Attack
To resist chosen-plain text attacks, an encryption system must have strong plaintext sensitivity. Similarly, plaintext sensitivity can use the same key to encrypt two distinct plaintext images, and calculate the NPCR and UACI values of the two images. We calculated the average NPCR and UACI for obtaining two cipher images 200 times, by performing two rounds of encryption in Table 3.

Table 3.
The NPCR and UACI of chosen-plain text analysis.
4.6. Information Entropy
Information entropy reflects the uncertainty of an image [30]. The larger the entropy, the greater the uncertainty. The entropy of an image was calculated according to Equation (19)
where L is the number of pixel grey levels, and is the probability that the grey value i appears. From Table 4, the information entropy of the encrypted images approaches the ideal value of eight, which indicates that the encrypted images have considerable uncertainty.

Table 4.
The information entropy of different images.
4.7. Comparison with Other Methods
Table 5 compares the correlation coefficient, the ability against chosen-plain text attacks, and information entropy between the proposed algorithm and others’ using 4.2.05.tiff. Our algorithm performs one and two rounds of encryption, and the results are listed in Table 5. The correlation coefficient of our algorithm is closer to 0, which indicates that the encrypted image has less visible information using our algorithm. For NPCR and UACI, our proposed algorithm is closer to the ideal values compared with the other three algorithms. This algorithm has a good ability to resist chosen-plain text attacks.

Table 5.
Comparison of the proposed method and other methods.
Moreover, the entropy of the encrypted image using the proposed algorithm with two iterations is larger than others. We show that the entropy of the encrypted image with two iterations is larger than that of one iteration.
4.8. Encryption Efficiency Analysis
In this paper, the simulation is performed on Inter(R) Core(TM) i7-6700K CPU @ 4.00 GHz with 16.0 GB in MATLAB R2019b. The average encryption time of a 256 × 256 image is 0.425 s, and the decrypted time is 0.452 s. To analyze the proposed encryption algorithm, the encryption throughput (ET) and number of cycles [33] are calculated by:
The ET of the proposed algorithm is 0.1471 MBps (million byte per second) and the algorithm needs 25,932.68 cpu cycles to finish one-byte operation.
5. Conclusions
In this paper, we constructed a new chaotic map, named TDSCL, which combines the delay tent map with the sine map, which is then cascaded with the logistic map. Compared with the DLCL and LSMCL methods, the simulation results indicated with the chaotic map that our proposed method has a larger Lyapunov exponent and permutation entropy, which demonstrates that it has a better initial value sensitivity and randomness. In addition, we proposed an image encryption algorithm with simultaneous confusion and diffusion in the vertical and horizontal directions. We analyzed the algorithm in terms of the key space, key sensitivity, ability against chosen-plain text attacks, and information entropy. The simulation results showed that this algorithm can resist statistical attacks and chosen-plain text attacks.
Author Contributions
Conceptualization, G.Z.; methodology, G.Z.; software, W.D.; validation, G.Z.; formal analysis, G.Z.; investigation, G.Z.; resources, G.Z.; writing—original draft preparation, G.Z.; writing—review and editing, W.D., L.L.; visualization, G.Z.; supervision, G.Z.; project administration, G.Z.; funding acquisition, G.Z. All authors have read and agreed to the published version of the manuscript.
Funding
The authors would like to thank the National Key R&D Program of China (Grant Nos. 2018YFB1003205 and 2017YFE0111900) and the 2019 Gansu Key Talent project for their support.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhu, H.; Zhao, Y.; Song, Y. 2D Logistic-Modulated-Sine-Coupling-Logistic Chaotic Map for Image Encryption. IEEE Access 2019, 7, 14081–14098. [Google Scholar] [CrossRef]
- Wu, J.; Liao, X.; Yang, B. Image encryption using 2D Hénon-Sine map and DNA approach. Signal Process. 2018, 153, 11–23. [Google Scholar] [CrossRef]
- Pak, C.; Huang, L. A new color image encryption using combination of the 1D chaotic map. Signal Process. 2017, 138, 129–137. [Google Scholar] [CrossRef]
- Hua, Z.; Jin, F.; Xu, B.; Huang, H. 2D Logistic-Sine-coupling map for image encryption. Signal Process. 2018, 149, 148–161. [Google Scholar] [CrossRef]
- Li, B.; Liao, X.; Jiang, Y. A novel image encryption scheme based on logistic map and dynatomic modular curve. Multimed. Tools Appl. 2018, 77, 8911–8938. [Google Scholar] [CrossRef]
- Zhou, Y.; Hua, Z.; Pun, C.M.; Chen, C.P. Cascade chaotic system with applications. IEEE Trans. Cybern. 2014, 45, 2001–2012. [Google Scholar] [CrossRef] [PubMed]
- Xie, J.; Yang, C.; Xie, Q.; Tian, L. An encryption algorithm based on transformed logistic map. In Proceedings of the 2009 International Conference on Networks Security, Wireless Communications and Trusted Computing, Wuhan, China, 25–26 April 2009; Volume 2, pp. 111–114. [Google Scholar]
- Wu, X.; Zhu, B.; Hu, Y.; Ran, Y. A novel colour image encryption scheme using rectangular transform-enhanced chaotic tent maps. IEEE Access 2017, 5, 6429–6436. [Google Scholar] [CrossRef]
- Cai, S.; Huang, L.; Chen, X.; Xiong, X. A Symmetric Plaintext-Related Color Image Encryption System Based on Bit Permutation. Entropy 2018, 20, 282. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, G.; Sun, K. Improved cryptanalysis and enhancements of an image encryption scheme using combined 1D chaotic maps. Entropy 2018, 20, 843. [Google Scholar] [CrossRef]
- Pak, C.; An, K.; Jang, P.; Kim, J.; Kim, S. A novel bit-level color image encryption using improved 1D chaotic map. Multimed. Tools Appl. 2019, 78, 12027–12042. [Google Scholar] [CrossRef]
- Wang, X.; Qin, X.; Liu, C. Color image encryption algorithm based on customized globally coupled map lattices. Multimed. Tools Appl. 2019, 78, 6191–6209. [Google Scholar] [CrossRef]
- Wang, H.; Xiao, D.; Chen, X.; Huang, H. Cryptanalysis and enhancements of image encryption using combination of the 1D chaotic map. Signal Process. 2018, 144, 444–452. [Google Scholar] [CrossRef]
- Wang, X.; Zhu, X.; Zhang, Y. An image encryption algorithm based on Josephus traversing and mixed chaotic map. IEEE Access 2018, 6, 23733–23746. [Google Scholar] [CrossRef]
- Li, S.; Ding, W.; Yin, B.; Zhang, T.; Ma, Y. A novel delay linear coupling logistics map model for color image encryption. Entropy 2018, 20, 463. [Google Scholar] [CrossRef]
- Nkandeu, Y.P.K.; Tiedeu, A. An image encryption algorithm based on substitution technique and chaos mixing. Multimed. Tools Appl. 2019, 78, 10013–10034. [Google Scholar] [CrossRef]
- Hua, Z.; Xu, B.; Jin, F.; Huang, H. Image encryption using josephus problem and filtering diffusion. IEEE Access 2019, 7, 8660–8674. [Google Scholar] [CrossRef]
- Huang, L.; Cai, S.; Xiong, X.; Xiao, M. On symmetric color image encryption system with permutation- diffusion simultaneous operation. Opt. Lasers Eng. 2019, 115, 7–20. [Google Scholar] [CrossRef]
- Ur Rehman, A.; Liao, X. A novel robust dual diffusion/confusion encryption technique for color image based on Chaos, DNA and SHA-2. Multimed. Tools Appl. 2019, 78, 2105–2133. [Google Scholar] [CrossRef]
- Li, S.; Yin, B.; Ding, W.; Zhang, T.; Ma, Y. A Nonlinearly Modulated Logistic Map with Delay for Image Encryption. Electronics 2018, 7, 326. [Google Scholar] [CrossRef]
- Li, M.; Lu, D.; Xiang, Y.; Zhang, Y.; Ren, H. Cryptanalysis and improvement in a chaotic image cipher using two-round permutation and diffusion. Nonlinear Dyn. 2019, 96, 31–47. [Google Scholar] [CrossRef]
- Shan, L.; Qiang, H.; Li, J.; Wang, Z.Q. Chaotic optimization algorithm based on Tent map. Control Decis. 2005, 20, 179–182. [Google Scholar]
- Li, C.; Lin, D.; Lü, J.; Hao, F. Cryptanalyzing an image encryption algorithm based on autoblocking and electrocardiography. IEEE MultiMedia 2018, 25, 46–56. [Google Scholar] [CrossRef]
- Pareek, N.K.; Patidar, V.; Sud, K.K. Image encryption using chaotic logistic map. Image Vis. Comput. 2006, 24, 926–934. [Google Scholar] [CrossRef]
- Paar, V.; Buljan, H. Bursts in the chaotic trajectory lifetimes preceding controlled periodic motion. Phys. Rev. E Stat. Phys. Plasmas Fluids Related Interdisciplinary Top. 2000, 62, 4869–4872. [Google Scholar] [CrossRef]
- Amigo, J.M.; Kocarev, L.; Szczepanski, J. Discrete Lyapunov Exponent and Resistance to Differential Cryptanalysis. IEEE Trans. Circuits Syst. II Express Briefs 2007, 54, 882–886. [Google Scholar] [CrossRef]
- Bandt, C.; Pompe, B. Permutation entropy: A natural complexity measure for time series. Phys. Rev. Lett. 2002, 88, 174102. [Google Scholar] [CrossRef]
- Ahmad, J.; Khan, M.A.; Hwang, S.O.; Khan, J.S. A compression sensing and noise-tolerant image encryption scheme based on chaotic maps and orthogonal matrices. Neural Comput. Appl. 2017, 28, 953–967. [Google Scholar] [CrossRef]
- Wu, Y.; Noonan, J.P.; Agaian, S. NPCR and UACI randomness tests for image encryption. Cyber J. Multidisciplinary J. Sci. Technol. J. Sel. Areas Telecommun. JSAT 2011, 1, 31–38. [Google Scholar]
- Wu, Y.; Zhou, Y.; Saveriades, G.; Agaian, S.; Noonan, J.P.; Natarajan, P. Local Shannon entropy measure with statistical tests for image randomness. Inf. Sci. 2013, 222, 323–342. [Google Scholar] [CrossRef]
- Enayatifar, R.; Abdullah, A.H.; Isnin, I.F.; Altameem, A.; Lee, M. Image encryption using a synchronous permutation-diffusion technique. Opt. Lasers Eng. 2017, 90, 146–154. [Google Scholar] [CrossRef]
- Niyat, A.Y.; Moattar, M.H.; Torshiz, M.N. Color image encryption based on hybrid hyper-chaotic system and cellular automata. Opt. Lasers Eng. 2017, 90, 225–237. [Google Scholar] [CrossRef]
- Farajallah, M. Chaos-Based Crypto and Joint Crypto-Compression Systems for Images and Videos. Ph.D. Thesis, Universite de Nantes, Nantes, France, 2015. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).