Symmetric Key Encryption Based on Rotation-Translation Equation

Abstract

In this paper, an improved encryption algorithm based on numerical methods and rotation–translation equation is proposed. We develop the new encryption-decryption algorithm by using the concept of symmetric key instead of public key. Symmetric key algorithms use the same key for both encryption and decryption. Most symmetric key encryption algorithms use either block ciphers or stream ciphers. Our goal in this work is to improve an existing encryption algorithm by using a faster convergent iterative method, providing secure convergence of the corresponding numerical scheme, and improved security by a using rotation–translation formula.

1. Introduction

Cryptography is a practice and study of techniques of hidden data transfer so that only the intended receivers can extract and read the data [1]. It is the study of mathematical methods related to different aspects of informational security such as data origin, entity authentication, data integrity and confidentiality. The source data, which is to be protected by cryptography, is called plaintext. The procedure of transforming plaintext into an unreadable form termed ciphertext is called encryption. Decryption is the reverse process, recovering the plaintext back from a ciphertext. A cryptographic system is a set of algorithms, seeded by key that encrypt given messages into ciphertext and recover them back into input data. The scheme for a secret key encryption is first proposed by Shannon [2].

There are two categories of key-based cryptographic algorithms: symmetric key (secret key) cryptography and public key (asymmetric key) cryptography. In the first category, a sender and recipient share a private key known only to both of them. The same key is used for encryption and decryption. The most commonly used symmetric algorithms are AES (Advanced Encryption Standard) [3], Cha Cha [4], Blowfish [5], and IDEA (International Data Encryption Algorithm) [6]. By contrast, for asymmetric key cryptography, two keys are used: the first one is made publicly available to senders for encrypting plaintext while the second key is kept secret and is used by the receivers for decrypting the ciphertext. The most ordinarily exploited asymmetric schemes are the Rivest–Shamir–Adleman (RSA) cryptosystem [7] and ECC (Elliptic-curve cryptography) [8]. Symmetric encryption schemes are usually faster than public key counterparts and thus are preferred for encrypting big data.

In symmetric key cryptography, either stream ciphers or block ciphers can be used. An example of stream cipher is the Vigenere Cipher. These types of ciphers encrypt the letters or digits (typically bytes) of a message one at a time, while block ciphers take a number of bits and encrypt them as a single unit. Until now, many symmetric data encryption algorithms have been proposed. Some of them use classical schemes for text encryption. In [9], an extension of a public key cryptographic scheme to support a private key cryptographic scheme which is a mix of AES and ECC is presented. Plain text encryption based on AES, Blowfish, and SALSA20 is designed and experimentally evaluated in [10].

Some of them use chaotic equations for text encryption. In Reference [11], a novel scheme for digital image encryption based on a mix of chaos theory and DNA calculation is presented. In [12], a chaos-based pseudorandom generation scheme based on a six-dimensional chaotic system is proposed. A text encryption architecture is given. Novel symmetric data encryption algorithms based on logistic chaotic formula are presented in [13,14,15]. A chaotic logistic map filtered with binary function is proposed to text encryption scheme in Reference [16]. In [17], a chaos-based encryption technique based on logistic, pinchers, and sine-circle maps is proposed. An algorithm of chaotic data encryption system by using private characteristic of electrocardiogram (ECG) signal and logistic map is designed in [18]. In [19,20], the chaotic behaviour of a Chua system is used in novel text encryption scheme designs. A novel pseudorandom bit generation scheme based on rotation equations is proposed in [21]. The technique has good statistical properties measured by test packages. A novel encryption method based on modified pulsed-coupled spiking neurons circuit is presented in Reference [22]. In [23], a modified quadratic map for numeric sensor data encryption is proposed.

2. Symmetric Key Encryption Algorithms Based on Numerical Methods

One of the first published works that consider symmetric key encryption algorithm based on numerical methods is by Ghosh in [24] (see also [25,26]), where it is shown that any nonlinear function with one variable $f\left(z\right)$ can be defined as a key. The encryption process then is defined as finding the solution of the equation

$$f\left(z\right)-c_i=0,$$

(1)

where $c_i$ represents the numerical code of the ith symbol in the plaintext (e.g., the ASCII code). The function $f\left(z\right)$ must be chosen in such a way that the corresponding formula (1) has at least one real root for any i. Then, the set of roots $\left\{z_i^{*}\right\}$ represents the ciphertext. On the receiver side, each entry $z_i^{*}$ is decoded by substituting it into $f\left(z\right)$ giving rise to the plaintext character $c_i=f\left(z_i^{*}\right)$ (the value $f\left(z_i^{*}\right)$ must be appropriately rounded to recover $c_i$). In [24], as a key function $f\left(z\right)$, the authors use a cubic polynomial and, for the numerical solution of equations $f\left(z\right)-c_i=0$, they use the Newton’s iterative method. We have to mention that, in solving nonlinear Equation (1), we can use different iterative methods. Analogous to this algorithm, an example of a public key cryptosystem based on numerical methods is considered in [27].

It is important to say that the main weaknesses of such algorithms can be summarized in the following:

• Lack of rules on how to choose the function f and suitable iterative method so that the convergence of the process is always guaranteed.
• Vulnerability to attack because in these types of algorithms the same letter is encoded with the same real number of each occurrence in the plaintext.

Our aim in the present work is to develop a new algorithm that solves the disadvantages mentioned above. In order to achieve this, the new scheme will be based on employing numerical iterative methods and rotation–translation formula.

3. On Numerical Methods and Rotation–Translation Equation

3.1. On Numerical Methods for Solving Nonlinear Equations

Although the Newton’s iterative method

$$z_{k+1}=z_k-\frac{f\left(z_k\right)}{f^{\prime }\left(z_k\right)},k=0,1,2,\dots$$

(2)

is one of the most popular and commonly used methods, numerical analysis offers many iterative methods that can be used in the stage of solution of Equation (1). In general to calculate the roots of nonlinear equations (of the type (1)), we have to use approximate (iterative) methods. When studying an iterative method, two of the most important aspects to consider are:

• the convergence speed of the iteration,
• an interval of convergence and the rules for choosing the initial approximations.

Most of the known iterative algorithms for solving nonlinear equations are only locally convergent, i.e., before using such a method, we need to locate the unknown root at a sufficiently small interval. Even if the root sought is located at the appropriate interval, if we do not choose the initial approximation in a proper way, the process may not be convergent. Usually, iterative methods of this type require the following convergence conditions:

• need to have an interval $[a,b]$ containing a single root of f, and
• the derivatives $f^{\prime }$ and $f^{″}$ must not have zeros in the interval $[a,b]$.

Then, the corresponding iterative process converges to the sought root for an initial approximation $z_0$ which is the end of the interval $[a,b]$, where $f\left(z_0\right)f^{″}\left(z_0\right)>0$ (or $f\left(z_0\right)f^{″}\left(z_0\right)<0$).

For some examples of more computationally efficient and higher order iterative methods, we refer the reader to [28].

In the encryption algorithm that we will introduce later, we will use the following iterative function

$$z_{k+1}=z_k-\frac{h\left(z_k\right)}{2}\left(\frac{3f^{\prime }\left(u_k\right)+f^{\prime }\left(z_k\right)}{3f^{\prime }\left(u_k\right)-f^{\prime }\left(z_k\right)}\right),k=0,1,2,\dots$$

(3)

where $h\left(z_k\right)=\frac{f\left(z_k\right)}{f^{\prime }\left(z_k\right)}$ and $u_k=z_k-\frac{3}{2}h\left(z_k\right)$. This iterative algorithm is explored by Jarrat in [29], and it is known as Jarrat’s method (see also [30]).

The reason we prefer iteration method (3) over method (2) is its faster convergence. The order of convergence of Jarrat’s method is four, while the one of Newton’s method is only two (see [30]). In addition, method (3) has higher computational efficiency, although at each step of the iteration one value of f and two values of $f^{\prime }$ are calculated (while in the Newton’s method, one value of f and one value of $f^{\prime }$ are calculated). Thus, if the function f is a polynomial, then calculating the value of the function f is always more complex than calculating its derivative $f^{\prime }$.

3.2. Base of Rotation–Translation Equation

In order to avoid the vulnerability to statistical attack, we include additional randomness by using the following space contraction formula based on rotation–translation equation of the form [31]

$$\begin{array}{cc}\hfill x_{k+1}& =a+b(x_{k}cos{\theta }_k-y_{k}sin{\theta }_k),\hfill \\ \hfill y_{k+1}& =b(x_{k}sin{\theta }_k+y_{k}cos{\theta }_k),\hfill \end{array}$$

(4)

where the angle of rotation is

$$\begin{array}{cc}\hfill {\theta }_k& =c+\frac{d}{x_k^2+y_k^2}.\hfill \end{array}$$

(5)

The translation value is $a=6$, the space contraction value is $b=0.8<1$, and rotation values are $c=a/2$ and $d=a$. The rotation–translation Equation (4) with initial conditions $x_0=0.233$, $y_0=-0.67$ is presented in Figure 1.

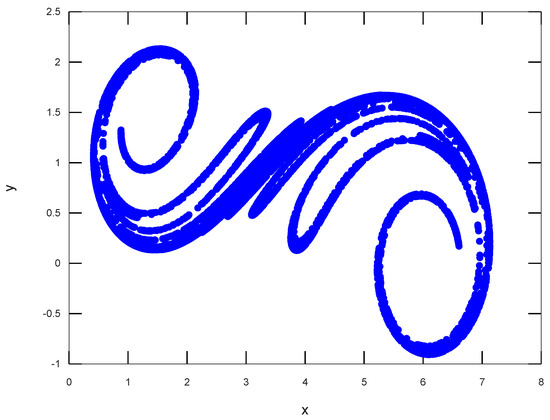
Figure 1. Space contraction.

4. Proposed Encryption Algorithm Based on Numerical Method and Rotation–Translation Equation

Here, we describe an encryption algorithm based on space contraction and numerical method. Any nonlinear function or polynomial f with one variable can be defined as part of a key.

We consider plaintext P with byte length of L. The initial values $x_0$ and $y_0$ from Equation (4), and an initial iteration number $M_0$, are determined. The rotation–translation formula, Equation (4), is iterated for $M_0$ times.

The proposed algorithm based on numerical method and space contraction is given below:

• Read the symbols from the plaintext data and get the ASCII values of the different symbols;
• Construct a system of L nonlinear equations by subtracting the ASCII values from the function f and equate with zero;
• Solve individually the nonlinear equations and put the results ${\alpha }_i$ into an array B;
• The loop of Equation (4) continues, and as an output, two real numbers $x_i$ and $y_i$ are generated. We take the sum of $x_i$ and $y_i$ to produce the real number $d_i=x_i+y_i$, which is put into an array R.
• Return to Step 4 until a stream of real numbers R with length L is reached.
• We get the sum of the two arrays B and R to produce E, the output array of real numbers.

Remark 1.

In Step 2 of Encryption algorithm, it is desirable that the function or polynomial f is such that each equation of the type $f\left(z\right)-c_i=0$ has at least one real root, and it is easy to determine the initial approximation, which guarantees the convergence of the iterative process.

4.1. Approaches for Choosing a Nonlinear Function

In the following, we consider two example functions that are suitable for selecting in the above algorithm.

4.1.1. Nonlinear Function

Let $f\left(z\right)$ has the following form

$$f\left(z\right)=e^z-z^2-p,$$

(6)

where p is a real parameter such that $p\ge 1$. For its first derivative,

$$f^{\prime }\left(z\right)=e^z-2z,$$

we conclude that $f^{\prime }\left(z\right)>0$ for all $z\in \mathbb{R}$, i.e., the function $f\left(z\right)$ is monotonically increasing for all $z\in \mathbb{R}$. This and the limits

$$\underset{z\to -\infty }{lim}f\left(z\right)=-\infty \mathrm{and}\underset{z\to \infty }{lim}f\left(z\right)=\infty$$

show that the function $f\left(z\right)$ has only one real root. From the second derivative of f

$$f^{″}\left(z\right)=e^z-2,$$

and because $f^{″}\left(z\right)>0$ for $\forall z>ln2$, it follows that the function $f\left(z\right)$ is convex for $z\in (ln2,\infty )$.

Therefore, all these properties are also valid for the functions

$$g_i\left(z\right)=f\left(z\right)-c_i,$$

where $c_i$ is an integer value (the corresponding ASCII code). Then, for any i, the function $g_i\left(z\right)$ is monotonous, convex, and has a real root in the interval $(ln2,\infty )$. Indeed, it can be shown that each one function $g_i\left(z\right)$ has a real root in the finite interval $(ln2,6)$.

4.1.2. Polynomial Function

We consider a fifth degree monic polynomial having the following form:

$$f\left(z\right)=z^5-z^4+z^3-p{z}^2+qz-(p+2q),$$

(7)

where p and q are real parameters such that $p,q\in [1,10]$. From the fundamental theorem of algebra, it follows that $f\left(z\right)$ has at least one real root. Using the Descartes’ rules of sign, we can prove that $f\left(z\right)$ has no negative real root, hence it has at least one real positive root (see Appendix A). Examining the first two derivatives of f, it can be shown that the function $f\left(z\right)$ is monotonically increasing, convex and has a real root in the interval $\left(\frac{9}{8},\infty \right)$, for any $p,q\in [1,10]$. By using the bounding theorems (see Appendix A), it can be shown that $f\left(z\right)$ has a real root in the finite interval $\left(\frac{9}{8},2{|p+2q|}^{1/5}\right)$.

4.2. An Example of Encryption

In order to demonstrate the proposed algorithm, we will use the following example:

The text to be encrypted: “Shumen university”.

As a key function, we use the polynomial

$$f\left(z\right)=z^5-z^4+z^3-z^2+z-3,$$

which is obtained by Equation (7) in the case of $p=q=1$. During the encryption process (Step 3 of the Algorithm), we have to solve in series nonlinear equations of the type

$$f\left(z\right)-c_i=0,$$

(8)

where $c_i$ represents the ASCII code of the i-th character in the text, i.e., $c_i\in [1,255]$. From the analysis of the polynomial (7) and using the bounding theorems for the roots of polynomials, we deduce that Equation (8) has a real root in the interval $\left(\frac{9}{8},6\right)$ for any $c_i\in [1,255]$. Moreover, this interval is such that the iterative process (3) is convergent to the solution for any initial approximation $z_0\in \left(\frac{9}{8},6\right)$. For this reason, we use the same initial approximation for each Equation (8) obtained during the encryption process, namely the middle point of the interval: $z_0=\frac{6+9/8}{2}\approx 3.56$.

We solve all the equations by iterative function (3) and by using the following stopping criteria

• $\left|f\right(z_k\left)\right|\le ϵ$, and
• $|z_k-z_{k+1}|\le ϵ$,

where $ϵ={10}^{-15}$.

As a result, for all the equations, the stopping criteria are reached after three iterations. For comparison, if we use the Newton iterative method (2) instead of the Jarrats’ method for solving the corresponding equations, with the same initial approximation, we get six iterations for each equation, see Table 1.

Table 1. Number of iterations for Jarrats’method (JM) and Newton method (NM), and generated arrays.

Letter	ASCII	NM	JM	Array B	Array R	Array E
(Char)	Code	Iterations	Iterations	Reached Root (${\mathit{\alpha }}_{\mathit{i}}$)	${\mathit{d}}_{\mathit{i}}$	${\mathit{e}}_{\mathit{i}}={\mathit{\alpha }}_{\mathit{i}}+{\mathit{d}}_{\mathit{i}}$
S	83	6	3	2.596938615169214	1.13761418319195	3.73455279836116
h	104	6	3	2.707594514758099	3.83246813052273	6.54006264528082
u	117	6	3	2.767550880788345	2.58986907946370	5.35741996025204
m	109	6	3	2.731316748315844	4.91511042783787	7.64642717615371
e	101	6	3	2.692927857503279	2.09200715087053	4.78493500837380
n	110	6	3	2.735958159508397	7.52948634851868	10.2654445080271
	94	6	3	2.657327240630354	0.10782288092075	2.76515012155110
U	85	6	3	2.608365856583876	5.70292778455835	8.31129364114222
n	110	6	3	2.735958159508397	1.30796668243219	4.04392484194058
i	105	6	3	2.712409561369016	7.38162948307289	10.0940390444419
v	118	6	3	2.771941812496392	0.13478345799064	2.90672527048704
e	101	6	3	2.692927857503279	5.23813805178474	7.93106590928801
r	114	6	3	2.754198397484480	1.66157719938621	4.41577559687069
s	115	6	3	2.758679632039476	7.40857522965636	10.1672548616958
i	105	6	3	2.712409561369016	0.16954303210037	2.88195259346938
t	116	6	3	2.763130305077092	6.32301454738480	9.08614485246189
y	121	6	3	2.784941120909602	0.81874887373720	3.60368999464681

The output array of real numbers E is in the last column of Table 1, and this is the encrypted text that the recipient receives.

4.3. Brute-Force Attack Analysis

The set of all initial values constitutes the key size. The key size of the novel encryption algorithm has the following initial key values $x_0$, $y_0$, $M_0$ and at least three real coefficients $a_i$ of the polynomial f (for monic polynomial f of degree $n\ge 3$). The two seeds $x_0$ and $y_0$ are constructed by randomly choosing two floating-point values that belonging to the intervals $[0.5,7]$ and $[-0.8,2]$, respectively. The novel encryption algorithm does not propose weak keys. As stated in the IEEE Standard for floating-point arithmetic [32], the computational precision of the 64-bit floating point variable is about ${10}^{-15}\approx 2^{49}$. The key size of the novel encryption is ${\left(2^{49}\right)}^5+2^{32}>2^{248}$, which is sufficient enough to defeat brute-force attack [33]. The key space is comparable to state-of-the-art chaos-based encryption algorithms; for example, [10,13,16].

4.4. Statistical Test Analysis of the Proposed Encryption

In an attempt to evaluate randomness of the improved encryption algorithm, we used NIST [34], ENT [35], and PractRand [36] statistical test applications. The output numbers $e_i$ from array E are converted to bytes as follows: $s_i=mod\left(abs\left(integer(e_i\times {10}^{15})\right)\right),256)$, where $integer\left(e\right)$ calculates the integer part of e, truncating the value at the decimal point, $abs\left(e\right)$ calculates the absolute value of e, and $mod(e,w)$ calculates the reminder after division. The bytes $s_i$ are produced. Using the improved encryption, ${10}^3$ sequences of 125,000 bytes are produced.

The NIST suite software (version sts-2.1.2) includes 15 statistical tests: monobit, block frequency, cumulative sums forward and reverse, runs, longest run of ones, rank, Fourier, non-overlapping templates, overlapping templates, universal, approximate entropy, serial one and two, linear complexity, random excursion, and random excursion variant.

The output results of the first 13 tests are in Table 2. The minimum hit rate for each statistical test with the excluding of the random excursion variant test is approximately 980 for a sample size of 1000 byte stings. The minimum hit rate for the random excursion variant test is approximately 600 for a sample size of 614 byte strings. The random excursion test outputs 8 p-values which are tabulated in Table 3. The random excursion variant test calculates 18 randomness probability numbers: p-values, and they are in Table 4.

Table 2. NIST test suite results.

NIST Test	p-Value	Success Rate
Monobit	0.556460	992/1000
Block frequency	0.010093	981/1000
Cumulative sums forward	0.399442	993/1000
Cumulative sums reverse	0.299736	993/1000
Runs	0.605916	986/1000
Longest run of ones	0.605916	988/1000
Rank	0.830808	988/1000
Fourier	0.200115	980/1000
Non overlapping templates	0.498222	990/1000
Overlapping templates	0.859637	992/1000
Universal	0.653773	988/1000
Approximate entropy	0.693142	988/1000
Serial one	0.894918	990/1000
Serial two	0.282626	986/1000
Linear complexity	0.051942	995/1000

Table 3. NIST Random excursion test results.

State	p-Value	Success Rate
−4	0.696617	610/614
−3	0.746463	606/614
−2	0.211467	610/614
−1	0.501472	606/614
+1	0.933509	607/614
+2	0.584363	605/614
+3	0.873629	610/614
+4	0.672912	608/614

Table 4. NIST Random excursion variant test results.

State	p-Value	Success Rate
−9	0.283657	608/614
−8	0.444875	607/614
−7	0.699986	609/614
−6	0.775401	607/614
−5	0.876173	610/614
−4	0.921867	607/614
−3	0.135745	607/614
−2	0.036332	610/614
−1	0.574229	612/614
+1	0.345203	609/614
+2	0.366645	607/614
+3	0.517714	610/614
+4	0.024235	612/614
+5	0.990938	612/614
+6	0.447934	610/614
+7	0.232430	609/614
+8	0.193732	611/614
+9	0.659297	611/614

The improved encryption algorithm passed successfully all the NIST tests.

The ENT application includes six tests to bit or byte sequences. We tested a stream of 125,000,000 bytes (1,000,000,000 bits) of the improved encryption and tabulated the output results in Table 5. The novel encryption passed successfully all the ENT tests.

Table 5. ENT test results.

ENT Test	Input of Bits	Input of Bytes
Entropy	1.000000	7.999999
Optimum compression	Reduce size by 0%	Reduce size by 0%
${\chi }^2$ square	0.16, exceed 68.56 %	242.28, exceed 70.66%
Arithmetic mean value	0.5000	127.5055
Monte Carlo for $\pi$	3.141226994 (error 0.01%)	3.141226994 (error 0.01%)
Serial correlation	−0.000002	0.000180

The third suite is PractRand. We tested our improved encryption algorithm for strings up to 1 GB (bytes) in length, passing all statistical tests successfully as shown in Table 6.

Table 6. PractRand test results.

Test Name	Raw	Processed	Evaluation
BCFN(2,13):!	R = +0.0	“pass”	normal
BCFN(2+0,13−0)	R = −0.7	p = 0.608	normal
BCFN(2 + 1,13 − 0)	R = +2.3	p = 0.172	normal
BCFN(2 + 2,13 − 1)	R = −0.1	p = 0.504	normal
BCFN(2 + 3,13 − 1)	R = −2.2	p = 0.812	normal
BCFN(2 + 4,13 − 2)	R = −4.4	p = 0.968	normal
BCFN(2 + 5,13 − 3)	R = −1.1	p = 0.669	normal
BCFN(2 + 6,13 − 3)	R = −4.1	p = 0.960	normal
BCFN(2 + 7,13 − 4)	R = +4.8	p = 0.032	normal
BCFN(2 + 8,13 − 5)	R = +3.3	p = 0.093	normal
BCFN(2 + 9,13 − 5)	R = −0.3	p = 0.524	normal
BCFN(2 + 10,13 − 6)	R = −4.3	p = 0.981	normal
BCFN(2 + 11,13 − 6)	R = −0.9	p = 0.614	normal
BCFN(2 + 12,13 − 7)	R = +1.6	p = 0.219	normal
BCFN(2 + 13,13 − 8)	R = −2.7	p = 0.914	normal
DC6-9x1Bytes-1	R = −1.0	p = 0.795	normal
Gap-16:!	R = +0.0	“pass”	normal
Gap-16:A	R = +0.0	p = 0.614	normal
Gap-16:B	R = −3.2	p = 0.987	normal
(Low1/8)BCFN(2,13):!	R = +0.0	“pass”	normal
(Low1/8)BCFN(2+0,13 − 1)	R = −1.7	p = 0.754	normal
(Low1/8)BCFN(2+1,13 − 2)	R = +1.0	p = 0.336	normal
(Low1/8)BCFN(2+2,13 − 3)	R = +1.7	p = 0.243	normal
(Low1/8)BCFN(2+3,13 − 3)	R = −0.7	p = 0.605	normal
(Low1/8)BCFN(2+4,13 − 4)	R = +2.7	p = 0.138	normal
(Low1/8)BCFN(2+5,13 − 5)	R = −0.3	p = 0.528	normal
(Low1/8)BCFN(2+6,13 − 5)	R = −0.9	p = 0.626	normal
(Low1/8)BCFN(2+7,13 − 6)	R = −2.3	p = 0.838	normal
(Low1/8)BCFN(2+8,13 − 6)	R = −2.4	p = 0.853	normal
(Low1/8)BCFN(2+9,13 − 7)	R = +1.6	p = 0.223	normal
(Low1/8)BCFN(2+10,13 − 8)	R = +3.1	p = 0.096	normal
(Low1/8)DC6-9x1Bytes-1	R = −0.5	p = 0.730	normal
(Low1/8)Gap-16:!	R = +0.0	“pass”	normal
(Low1/8)Gap-16:A	R = −0.1	p = 0.675	normal
(Low1/8)Gap-16:B	R = −1.7	p = 0.888	normal

The different statistical tests clearly show the high quality of the proposed algorithm. Table 7 summarizes some of the computed values of our proposed scheme with other algorithms. The performance test of the novel scheme is based on the average response time with data size of 1 MB. The execution is done on mobile Dell Inspiron computer i7-3630QM (2.4 GHz, 8GB RAM).

Table 7. Comparison of our improved symmetric key encryption with other algorithms.

Algorithm	Key Size	Correlation	Entropy	Arithmetic Mean	Performance Evaluation
Proposed	$2^{248}$	−0.000002	7.999999	127.5055	0.105
[14] Murillo-Escobar	$2^{128}$	−0.002100	7.994500	-	-
[21] Stoyanov 2015	$2^{100}$	0.000001	7.999998	127.4982	0.19
[37,38] AES-128	$2^{128}$	−0.002100	7.954880	127.5281	0.12

Based on the good test outputs, we can infer that the novel text encryption based on numerical method and rotation–translation formula has satisfying statistical characteristics and provides a reasonable level of security.

5. Conclusions

We have presented an improved encryption algorithm based on numerical method and rotation–translation formula. The new method uses a faster convergent iterative algorithm and adds additional randomness by using the space contraction equation. Two exemplary ways of constructing nonlinear functions or polynomials with corresponding properties are described. In the examples considered, we demonstrate how to determine the interval containing the desired root and in which the iterative method is guaranteed to be convergent. Our security analysis shows that the improved encryption scheme can be successfully used for information security.

Appendix A.1. Real Roots Counting of Polynomials

Consider a monic polynomial of degree n

$$f\left(x\right)=x^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0.$$

From the fundamental theorem of algebra, it follows that f has n real or complex roots, counting multiplicities. If the coefficients $a_0,a_1,\dots ,a_{n-1}$ are all real, then the complex roots occur in conjugate pairs.

Using the following Descartes’ rules of sign, we can count the number of real positive zeros of f.

Descartes’ rules

Let p be the number of variations in the sign of the coefficients $a_n,a_{n-1},\dots ,a_0$ (where $a_n=1$ and the zero coefficients are ignored). Let m be the number of real positive zeros of f. Then,

• $m\le p$;
• $p-m$ is an even integer.

A negative zero of $f\left(x\right)$, if exists, is a positive zero of $f(-x)$.

Appendix A.2. Bounds of Real Roots of Polynomials

The first result in the theory of the location of polynomial zeros is due to Gauss, which is improved by Cauchy in [39], where he proves the following theorem.

Theorem A1 (Cauchy).

Let

$$f\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$$

be a polynomial with complex coefficients, where $n\ge 1$ and $a_n\ne 0$. Then, all the zeros of $f\left(x\right)$ lie inside the circle of radius

$$r=1+\underset{0\le k\le n-1}{max}\left|\frac{a_k}{a_n}\right|$$

about the origin.

Another bound given by Lagrange is:

Let

$$f\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$$

be a polynomial with complex coefficients, where $n\ge 1$ and $a_n\ne 0$. Then, all the zeros of $f\left(x\right)$ lie inside the circle of radius

$$r=2max\left(\left|\frac{a_{n-1}}{a_n}\right|,{\left|\frac{a_{n-2}}{a_n}\right|}^{1/2},\dots ,{\left|\frac{a_0}{a_n}\right|}^{1/n}\right)$$

about the origin.

The next theorem is about bounding positive real roots of polynomials with real coefficients due to Cauchy.

Theorem A2 (Cauchy).

Let

$$f\left(x\right)=a_n{x}^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$$

be a polynomial with real coefficients, where $n\ge 1$ and $a_n>0$ and which has $s>0$ strictly negative coefficients. Then, every positive real root of $f\left(x\right)$ is no larger than r:

$$r=max\left({\left|s\frac{a_{n-1}}{a_n}\right|}^{1/i}:1\le i\le nand{a}_{n-i}<0\right).$$

More recent and sharper results are obtained by Joyal, Labelle, and Rahman [40] by proving.

Theorem A3.

If $M={max}_{0\le i<n-1}\left|a_i\right|$, then all the zeros of the monic polynomial

$$f\left(x\right)=x^n+a_{n-1}{x}^{n-1}+\dots +a_{1}x+a_0$$

are contained in the disc

$$\left|x\right|\le \frac{1}{2}\left(1+|a_{n-1}|+\sqrt{(1-|a_{n-1}{\left|\right)}^2+4M}\right).$$