Abstract
In this paper, the fractional-order variant of Puu’s system is introduced, and, comparatively with its integer-order counterpart, some of its characteristics are presented. Next, an impulsive chaos control algorithm is applied to suppress the chaos. Because fractional-order continuous-time or discrete-time systems have not had non-constant periodic solutions, chaos suppression is considered under some numerical assumptions.
1. Introduction
The impulsive control concept has a long history that is based on the mathematical foundation of impulsive differential equations. Most examples of impulsive phenomena can be found in mechanical systems with impacts where a sudden change in their states appears, but also in population dynamics, biotechnology processes, chemistry, engineering, medicine, spacecraft optimal control, and so on. Impulsive systems can be studied via the mathematical tool based on impulsive differential or discrete equations. In the last few decades, differential equations with impulses can be found in e.g., nanoelectronic devices, chaotic spread-spectrum communication systems, or electrical engineering applications, and so on (see, e.g., [1,2]). On the other side, there are classes of systems like biological systems, economical systems where discrete time models seem to be more realistic than the continuous ones.
There exist several kinds of impulses [3]—for example, systems where the impulses are applied at fixed time-moments (see, e.g., one of the first references [4]) and also systems where the impulses are applied at variable times [5].
Due to the memory and hereditary properties of the fractional derivatives (see [6,7]), the discrete-time or continuous-time systems of fractional order (FO) are more suitable than integer-order systems.
While the definition of fractional derivative for continuous-time real functions has been formulated in the late 19th Century by Liouville, Grunwald, Letnikov, and Riemann, the first definition of a fractional difference operator was made by Diaz and Olser in 1974 [8]. Nowadays, differential or difference equations of FO represent useful models in viscoelasticity, mechatronics, seismology, aerodynamics, electrical circuits, biophysics, biology, blood flow phenomena, chemistry, control theory, etc (see, e.g., [9]).
In this paper, the fractional order (FO) variant of the Puu’s system is numerically analyzed and compared with its integer order (IO) counterpart. Using the results on non-existence of exact periodic solutions of FO discrete systems, one consider the periodicity as computationally approached. Moreover, using an impulsive algorithm, the chaotic motion can be suppressed.
2. Puu’s Fractional Order System
In 1939, Paul Samuelson [10] introduced the standard principle of acceleration to consumption used in one of the first formal mathematical models for business cycles, while Sir John Hicks (1950) later improved the Samuelson model [11], introducing the “floor” and “roof” to depreciation levels.
Starting from the standard Samuelson-Hicks model, in 1989, Puu and Sushko [12] developed the discrete dynamical income system of integer order (IO) with cubic nonlinearity of integer order, modeled by the following cubic initial value problem (IVP)
with a real parameter.
It is usual to have multiple attractors for a dynamical system. Each of them can be considered as the attractor for a given initial condition within its own attraction basin. In the bifurcation diagram vs. , presented in Figure 1a, the Puu system of IO (1) reveals two symmetric regions representing regular and chaotic attractors generated by two symmetric (negative and positive) initial conditions within two attraction basins (Due to its symmetry, the coexistence of symmetric attractors is a feature of the Puu system. Like for the cubic logistic map , the oddness of the map (1) induces an equivariance that is a -symmetry [13,14].). Therefore, attractors corresponding to in the upper (bottom) region present non-symmetric new generated points. The successive bifurcations of these points lead to chaos via the standard period-doubling cascade. In addition, note the sudden crisis—at , the previous two non-symmetric chaotic attractors (red and blue, respectively) collide and give birth to a symmetric chaotic attractor that covers both positive and negative values of x. Details on similar dynamics but related to the cubic logistic map can be found in [15].
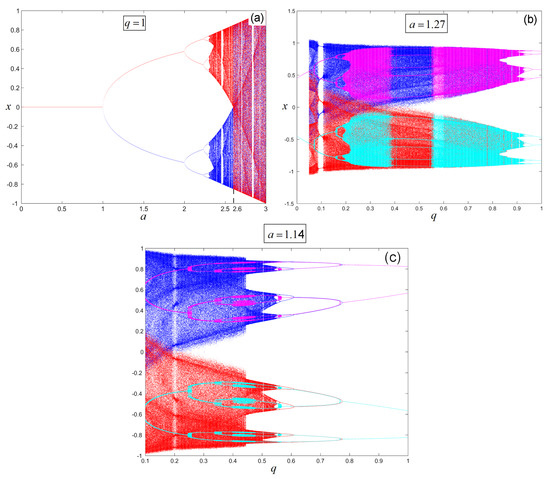
Figure 1.
Bifurcation diagrams of the Puu system of IO and FO. (a) bifurcation of the Puu system of IO vs. parameter a; (b) bifurcation of the Puu system of FO vs. q for ; (c) bifurcation of the Puu system of FO for .
Let us consider the FO Puu discrete system. Following the approach in [16] (see also [17], where the synchronization of the FO Puu is considered), the Caputo-like Puu system of FO can be modeled by the following general IVP of FO:
where is the Caputo-like delta difference of order , and represents the isolated time scale. With the cubic right-hand side , the IVP (2) reads
Theorem.
[16,18] The IVP (3) admits the following discrete integral
In (4), represents the Gamma function.
The local Lyapunov exponent , can be approximated numerically at the first n iterations with the following relation [19]:
where the tangent map , obtained by the linearization of (5) along the orbit , is
Like the solution x, the tangent map at the moment n also presents the so-called discrete memory effect (or time history) i.e., the numerical determined value at the moment n depends on all previous values. Because in relations (5) and (6), the term presents divergency problems, to deal numerically with R for large values of n, one can use the relation . In this way, the numerical experiments can be extended for n up to a couple thousand.
The bifurcation diagrams of the Puu system of FO vs. q, generated within and , for and (Figure 1b,c, respectively), reveal symmetrical transitions to chaos and, also, contrary to its IO part, attractors’ coexistence.
Hereafter, only the two merged “positive” regions (blue and cyan) located most entirely in the positive axis are considered. The other two “negative” symmetric regions (red and light blue) can be generated with and , respectively. As can be seen, both “positive” and “negative” attractors corresponding to maintain the odd symmetry existing in the integer order system and the bifurcations in the positive (negative) axis are non-symmetric.
Remark 1.
As for the case of fractional differential equations, contrary to integer order difference equations, fractional difference equations do not admit exact periodic but only asymptotically periodic solutions (see, e.g., [20,21,22], respectively). Therefore, notions like “stable cycle”, “chaos control”, and even “chaos” (as consisting in infinitely many unstable periodic motions), in continuous-time or discrete-time systems of FO seem to not be adequate. Up to a considered enough tiny computational error, the apparent periodic orbits are called here “computationally periodic orbits” (CPOs). Therefore, in this paper, the chaos suppression means to obtain stable CPOs.
To study some orbit , the relations (5) and (6) together with time series, histograms, and the ‘0–1’ test [23] will be used. Because we are interested in chaos suppression, the value of the parameter a is chosen so that the system evolves chaotic for all initial conditions. Thus, for , the system behaves chaotically for all initial conditions.
One of the tools generated by the ‘0–1’ test [23], which can be easily numerically implemented starting from a time series related to the considered dynamical continuous or discrete system, is the asymptotic growth rate, K, which gives important information to distinguish chaotic behavior from regular behavior. Note that the ‘0-1’ test does not need the system equations, but only a time series of the system. If , then the underlying dynamics are chaotic, while, if , the system behaves along some stable CPO. It is commonly assumed that about 2000 elements in the considered time series, after transients are discarded, are enough. In this paper, after the first 1000 iterations neglected, 1500 elements give enough accurate results.
While the integer order system develops, as usual, stronger chaos once the bifurcation parameter a increases (Figure 1a), the FO system presents chaos extinction with the increase of a (Figure 1b,c).
Hereafter, the case will be considered.
Another interesting property of the FO Puu system, contrary to its integer order counterpart, is the coexistence of stable CPOs with chaotic attractors. For example, in Figure 2, two zoomed areas are presented (Figure 2b,c) from the bifurcation diagram for in Figure 2a. Both zoomed areas reveal, for some parameter values of a, the coexistence of a chaotic attractor with a stable CPO (dotted lines at and ).
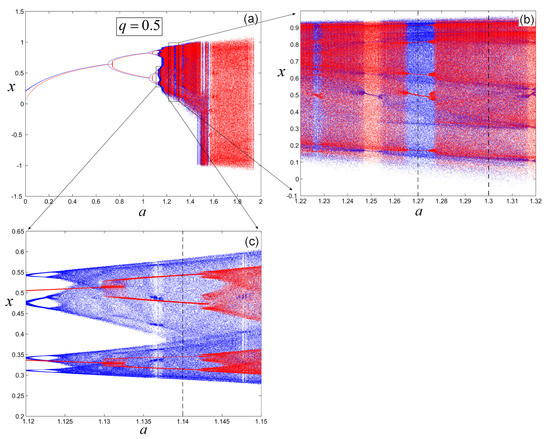
Figure 2.
Bifurcations of the Puu system of FO. (a) bifurcation vs. a for ; (b) zoomed region for ; (c) zoomed region for .
Consider within a stable CP window of period-5 for (red plot) coexisting with its chaotic counterpart (blue plot) in Figure 2b. The coexistence of the underlying stable CPO and the chaotic attractor is studied in Figure 3. Figure 3a,b present superimposed, the time series entirely and the last 100 iterations, respectively; in Figure 3c,d, superimposed, the Lyapunov exponent and the asymptotic growth rate, K, are represented, while in Figure 3e,f plot the histograms of the coexisting attractors. The chaotic attractor generated from (blue plot in Figure 3a,b is characterized by the evolution of the time series, the K value, which is close to 1, and the positiveness of the superimposed Lyapunov exponent (Figure 3d) and the histogram in Figure 3f. The stable CPO revealed after about 900 neglected iterations from the considered 2500 iterations, generated from (red plot in Figure 3a,b), is characterized by the evolution of the time series, the K value, and the superimposed , in which both are close to 0 (Figure 3c), and the discrete five peaks bars in the histogram (Figure 3e) indicating the branches of the cycle, numbered 1–5 in the zoomed time series in Figure 3b. Note that the zero value of seems to indicate a kind of Neimark–Sacker bifurcation, generating the stable CPO of period-5 which coexists with the chaotic attractor. In addition, as can be seen in Figure 3c,d, this kind of bifurcation seems to be not singular, but this subject does not represent the purpose of this paper.
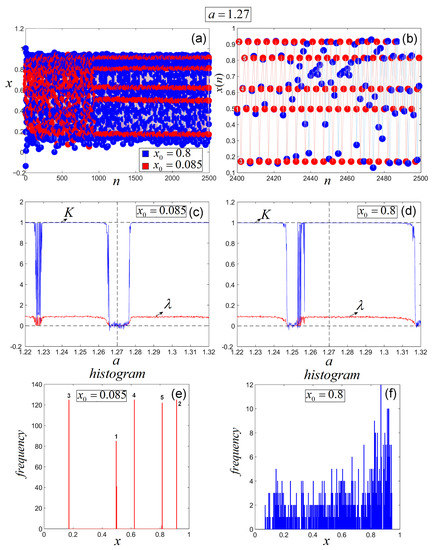
Figure 3.
Attractors coexistence for and and . (a) superimposed time series, (b) Last 100 iterations of the time series; Numbered points indicate the CPO periodicity, (c) Asymptotic growth rate K and exponent for the attractor generated with , (d) asymptotic growth rate K and exponent for the attractor generated with , (e) histogram of the attractor generated with ; bars indicate the CPO elements revealed in (b), (f) histogram of the attractor generated with .
3. Chaos Suppression in the FO Puu System
Being a model proposed in economy, where chaos is usually present, chaos suppression could represent an important task. A simple and efficient way used in this paper is to apply constant periodic impulses every steps. The numerical form of the impulsive algorithm is
where (here the cubic map (1)), and the impulse some relative small real number.
Numerically, the control algorithm (7) reads as follows: after the new value of x is calculated at the moment , , if n is multiple of steps, is perturbed with .
The algorithm is suitable to systems where the state variable is accessible to perturbations and has been successfully utilized for discontinuous systems of FO [24], continuous fractional-order systems of IO [25], discrete systems of FO [26], and discrete systems of IO [27]. The stability of impulsive fractional difference equations is studied in [28]. Some analytical study, such as boundness and periodicity, that applied to a discrete economical supply and demand system can be found in [29].
Consider the case and when the both coexisting chaotic attractors of the Puu’s system of FO are chaotic (see Figure 2b). This means that for whatever initial conditions the system evolves along one of the two chaotic attractors (red or blue).
To not modify the system structure, values are chosen to be relatively small, here of order. The effectiveness of the algorithm (7) can be deduced form the bifurcation diagram of the controlled system vs. for and fixed . The stable windows reveal the values generating stable CPOs. While the chaotic orbits are identified by the positiveness of the Lyapunov exponent, , the chaotic evolution of the underlying time series, dense set of bars in histograms, and , the COPs have negative (or zero) Lyapunov exponent, computationally periodic behavior in the time series, discrete bars in histograms and .
The case , when the system is impulsed at every step, is presented in Figure 4a,d for chosen in the two mentioned attraction basins, and , respectively. As can be seen in the bifurcation diagrams, the impulsive algorithm applied within the two attraction basins preserves the existence of the two previously existing chaotic attractors, but also generates stable CP windows in the . Obviously, it is desirable to find those values for which both coexisting chaotic attractors are stable. However, for , the periodic windows cannot suppress simultaneously the chaos in both chaotic attractors (see dotted green and black lines). For example, for (dotted black lines in Figure 4a,d), the chaotic attractor corresponding to of the impulsed system is stabilized and evolves along a stable CPO of period-5 (see the five intersections of the green dotted line in Figure 4a, the time series in Figure 4b and the history in Figure 4c), but the coexisting attractor corresponding to of the impulsed system is chaotic for the same value of (see Figure 4d–f). The stability within the periodic windows is revealed by the Lyapunov exponent (blue plot) and the asymptotic growth rate K (red plot) which are approximately 0.
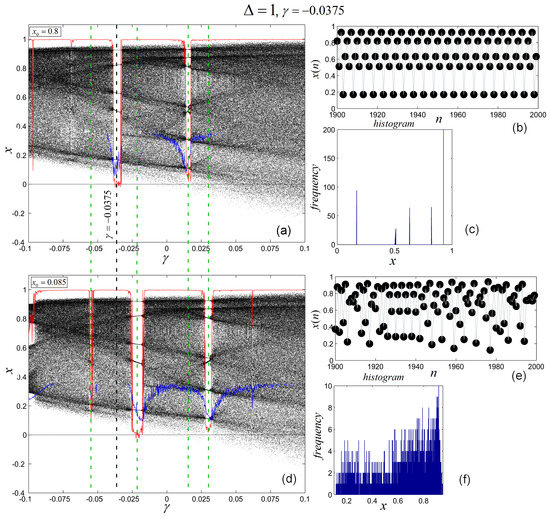
Figure 4.
Impulsive algorithm applied for and (dotted green line). (a,d) bifurcation diagrams of the impulsed system for and (top) and (bottom) respectively, (b,e) last 100 iterations of time series for and , respectively, (c,f) histograms for for and , respectively.
Concluding, for , it is possible that, depending on the initial conditions, the system evolves regularly but also chaotically. This impediment can be avoided if , when the system is impulsed only every two steps. Now, both chaotic attractors can be controlled for a large interval of values (Figure 5). Thus, for , the impulsed system evolves, for whatever initial condition, along a stable CPO: a stable CPO of period-8, for (Figure 5a–c), and also a stable CPO of period-4, for (Figure 5d–f).
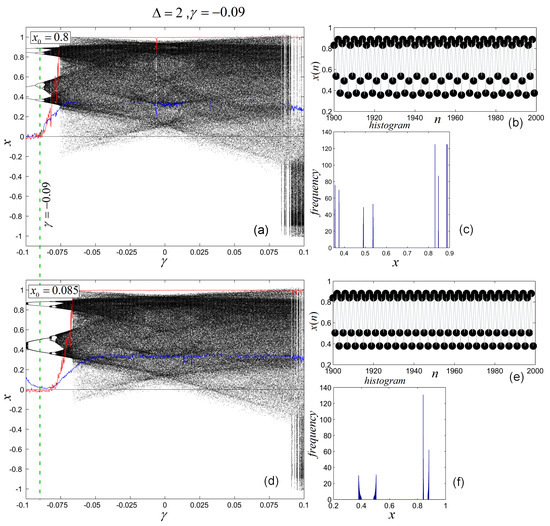
Figure 5.
Chaos suppression with the impulsive algorithm for and (dotted green line). (a,d) bifurcation diagrams of the impulsed system for and (top) and (bottom), respectively, (b,e) last 100 iterations of time series for and , respectively, (c,f) histograms for for and , respectively.
Chaos suppression can also be realized with higher values of . For example, for (Figure 6), if one sends an impulse to the system at every three steps, for (see dotted green line), and one obtains two stable CPOs of multiple periods.
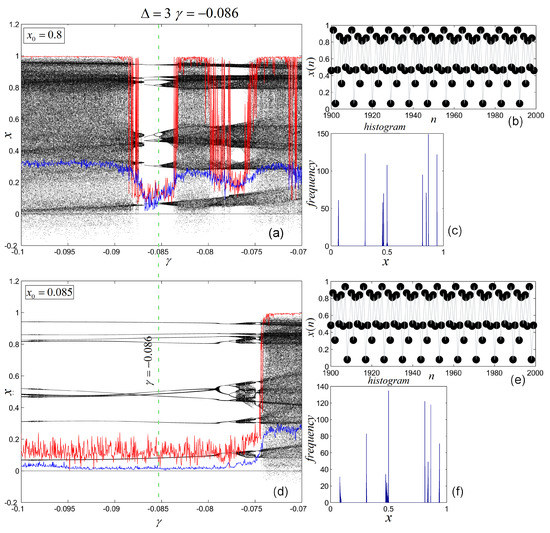
Figure 6.
Chaos suppression for and (dotted green line). (a,d) bifurcation diagrams of the impulsed system for and (top) and (bottom), respectively, (b,e) last 100 iterations of time series for and , respectively, (c,f) histograms for and , respectively.
Next, let the averaged energy of the impulsed system, , which can be determined with the following relation:
for N sufficiently large (see e.g., [30] for the averaged energy applied to a generalized logistic map).
The variation of the averaged energy vs. , for the considered cases , for , is presented in Figure 7. Note that, if the system is impulsed rarer, i.e., , the energy of the impulsed system (red) is smaller than that of the not impulsed system, (horizontal dotted line) for most of values, while, if the system is impulsed more often, i.e., (black) or (blue), the necessary energy for the controlled system (vertical dotted lines) is bigger than . In addition, for positive values of (not considered in this work), , for all considered values for . As expected, when is negative, the system increases the energy.
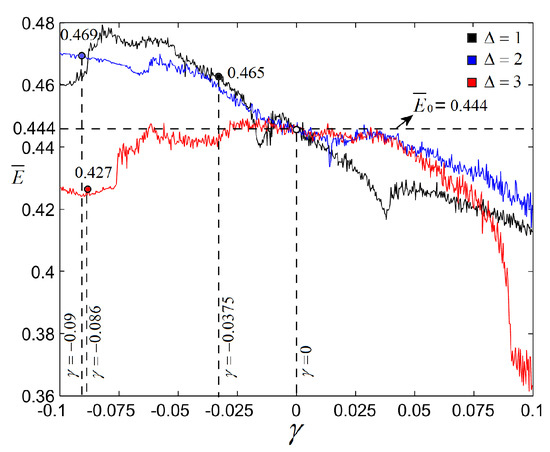
Figure 7.
Superimposed averaged energy , for (black), (blue) and (red). The horizontal dotted line represents the average energy of the not impulsed system.
4. Conclusions
In this paper, the FO variant of the Puu system has been considered and some of its properties are characterized comparatively with its IO counterpart. Contrary to the IO variant, the FO variant presents significant symmetries. In addition, contrary to the FO continuous-time systems, the chaos in the Puu system of FO reduces once the fractional order q increases.
Because, as usual for FO systems, the system does not admit periodic orbits, instead “periodic orbit”, the notion of “computationally periodic orbit” has been introduced. In this way, the door of everything that involves “periodicity”, such as stable/unstable cycles, chaos, chaos control, remains open for study. Note that another approach of this kind of orbits would be done via “almost periodicity” notion (see, e.g., [31]).
Using the impulsive algorithm (7), which perturbs periodically the state variable with the value , chaos can be suppressed. The values of can be determined from the bifurcation diagram of the impulsed system vs. . In this paper, the perturbations are negative, but, depending on the considered system, positive values can also be used (see the mentioned references). Note that, in nature, these kinds of perturbations can be shocks, and can appear in natural disasters, ecology, or can be used in ecosystems management, harvesting, etc.
As for other examples of nonlinear discrete FO systems modeled by Caputo’s derivative, chaos in Puu’s system of FO vanishes when the bifurcation parameter approaches 1. Therefore, the problem of chaos suppression makes sense only for relatively smaller values of the fractional order q, where the considered system behaves chaotically.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Lakshmikantham, V.; Bainov, D.; Simeonov, P. Theory of Impulsive Differential Equations; World Scientific Publishing Co. Pte. Ltd.: Singapore, 1989. [Google Scholar]
- Yang, T. Impulsive Control Theory; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Bonotto, E.M.; Bortolan, M.C.; Caraballo, T.; Collegari, R. A survey on impulsivedynamical systems. Electron. J. Qual. Theory 2016, 7, 1–27. [Google Scholar]
- Rozhko, V.F. A certain class of almost periodic motions in systems with pulses. Differ. Uravn. 1972, 8, 2012–2022. (In Russian) [Google Scholar]
- Kaul, S.K. On impulsive semidynamical systems. J. Math. Anal. Appl. 1990, 150, 120–128. [Google Scholar] [CrossRef][Green Version]
- Oldham, K.B.; Spanier, J. The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. In Mathematics in Science and Engineering; Academic Press: New York, NY, USA, 1974; Volume 11. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. In Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Diaz, J.B.; Olser, T.J. Differences of fractional order. Math. Comput. 1974, 28, 185–202. [Google Scholar] [CrossRef]
- Tenreiro Machado, J.A.; Silva, M.F.; Barbosa, R.S.; Jesus, I.S.; Reis, C.M.; Marcos, M.G.; Galhano, A.F. Some applications of fractional calculus in engineering. Math. Probl. Eng. 2010, 2010, 639801. [Google Scholar] [CrossRef]
- Samuelson, P.A. Interactions between the multiplier analysisand the principle of acceleration. Rev. Econ. Stat. 1939, 21, 75–78. [Google Scholar] [CrossRef]
- Hicks, J.R. A Contribution to the Theory of the Trade Cycle; Oxford University Press: Oxford, UK, 1950. [Google Scholar]
- Puu, T.; Sushko, I. A business cycle model with cubic nonlinearity. Chaos Soliton. Fract. 2004, 19, 597–612. [Google Scholar] [CrossRef]
- Rogers, T.; Whitley, D.C. Chaos in the cubic mapping. Math. Model. 1983, 4, 9–25. [Google Scholar] [CrossRef]
- Chossat, P.; Golubitsky, M. Iterates of maps with symmetry. SIAM J. Math. Anal. 1988, 19, 1259–1270. [Google Scholar] [CrossRef]
- King, G.; Stewart, I. Symmetric Chaos. Math. Sci. Eng. 1992, 185, 257–315. [Google Scholar] [CrossRef]
- Wu, G.-C.; Baleanu, D. Discrete fractional logistic map and its chaos. Nonlinear Dyn. 2014, 75, 283–287. [Google Scholar] [CrossRef]
- Xin, B.; Liu, L.; Hou, G.; Ma, Y. Chaos Synchronization of Nonlinear Fractional Discrete Dynamical Systems via Linear Control. Entropy 2017, 19, 351. [Google Scholar] [CrossRef]
- Goodrich, C.; Peterson, A.C. Discrete Fractional Calculus; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Wu, G.-C.; Baleanu, D. Jacobian matrix algorithm for Lyapunov exponents of the discrete fractional maps. Commun. Nonlinear Sci. Numer. Simulat. 2015, 22, 95–100. [Google Scholar] [CrossRef]
- Tavazoei, M.S.; Haeri, M. A proof for non existence of periodic solutions in time invariant fractional order systems. Automatica 2009, 45, 1886–1890. [Google Scholar] [CrossRef]
- Diblik, J.; Feckan, M.; Pospisil, M. Nonexistence of periodic solutions and S-asymptotically periodic solutions in fractional difference equations. Appl. Math. Comput. 2015, 257, 230–240. [Google Scholar] [CrossRef]
- Cuevas, C.; Souza, J. S-asymptotically ω-periodic solutions of semilinear fractional integro-differential equations. Appl. Math. Lett. 2009, 22, 865–870. [Google Scholar] [CrossRef]
- Gottwald, G.; Melbourne, I. A new test for chaos in deterministic systems. Proc. R. Soc. A 2004, 460, 603–611. [Google Scholar] [CrossRef]
- Danca, M.-F.; Garrappa, R. Suppressing chaos in discontinuous systems of fractional order by active control. Appl. Math. Comput. 2015, 257, 89–102. [Google Scholar] [CrossRef][Green Version]
- Danca, M.-F.; Tang, W.K.S.; Wang, Q.; Chen, G. Suppressing chaos in fractional-order systems by periodic perturbations on system variables. Eur. Phys. J. B 2013, 86, 79. [Google Scholar] [CrossRef]
- Danca, M.-F.; Feckan, M.; Kuznetsov, N. Chaos control in the fractional order logistic map via impulses. Nonlinear Dyn. 2019, 98, 1219–1230. [Google Scholar] [CrossRef]
- Danca, M.-F.; Codreanu, S.; Bako, B. Detailed analysis of a nonlinear prey-predator model. J. Biol. Phys. 1997, 23, 11–20. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.-C.; Baleanu, D. Stability analysis of impulsive fractional difference equations. Fract. Calc. Appl. Anal. 2018, 21, 354–375. [Google Scholar] [CrossRef]
- Danca, M.-F.; Feckan, M. Hidden chaotic attractors and chaos suppression in an impulsivediscrete economical supply and demand dynamical system. Commun. Nonlinear Sci. 2019, 74, 1–13. [Google Scholar] [CrossRef]
- Stavroulaki, M.; Sotiropoulos, D. The Energy of Generalized Logistic Maps at Full Chaos. Chaotic Model. Simul. 2012, 3, 543–550. [Google Scholar]
- Akhmet, M. Almost Periodicity in Chaos. In Almost Periodicity, Chaos, and Asymptotic Equivalence; Springer: Cham, Switzerland, 2020; Volume 27. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).