Rayleigh-Bénard Convection of Paramagnetic Liquid under a Magnetic Field from Permanent Magnets
Abstract
1. Introduction
2. Computational Methods
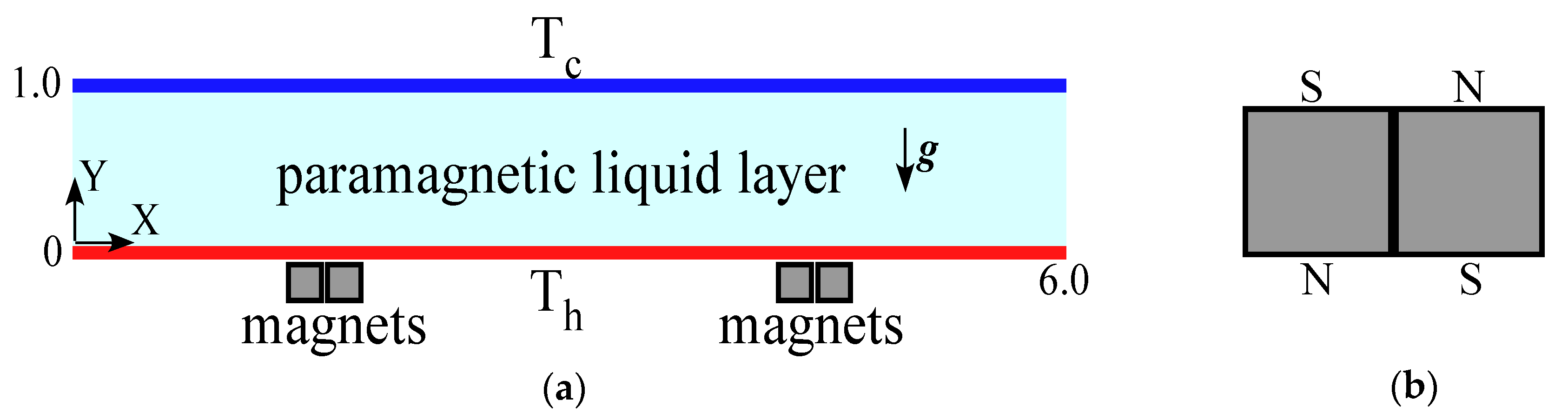
2.1. Schematic Model
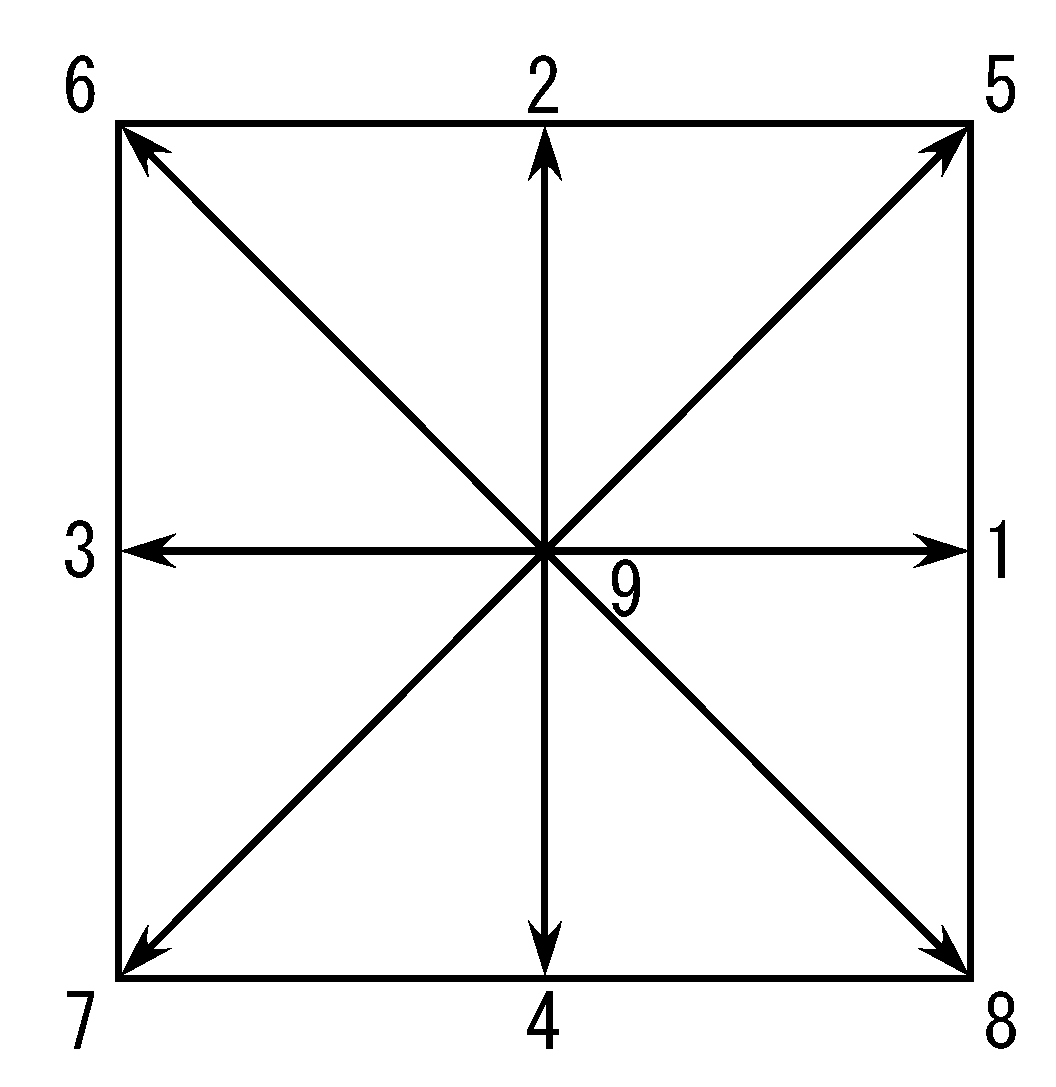
2.2. Lattice Boltzmann Heat and Fluid Flow Simulation
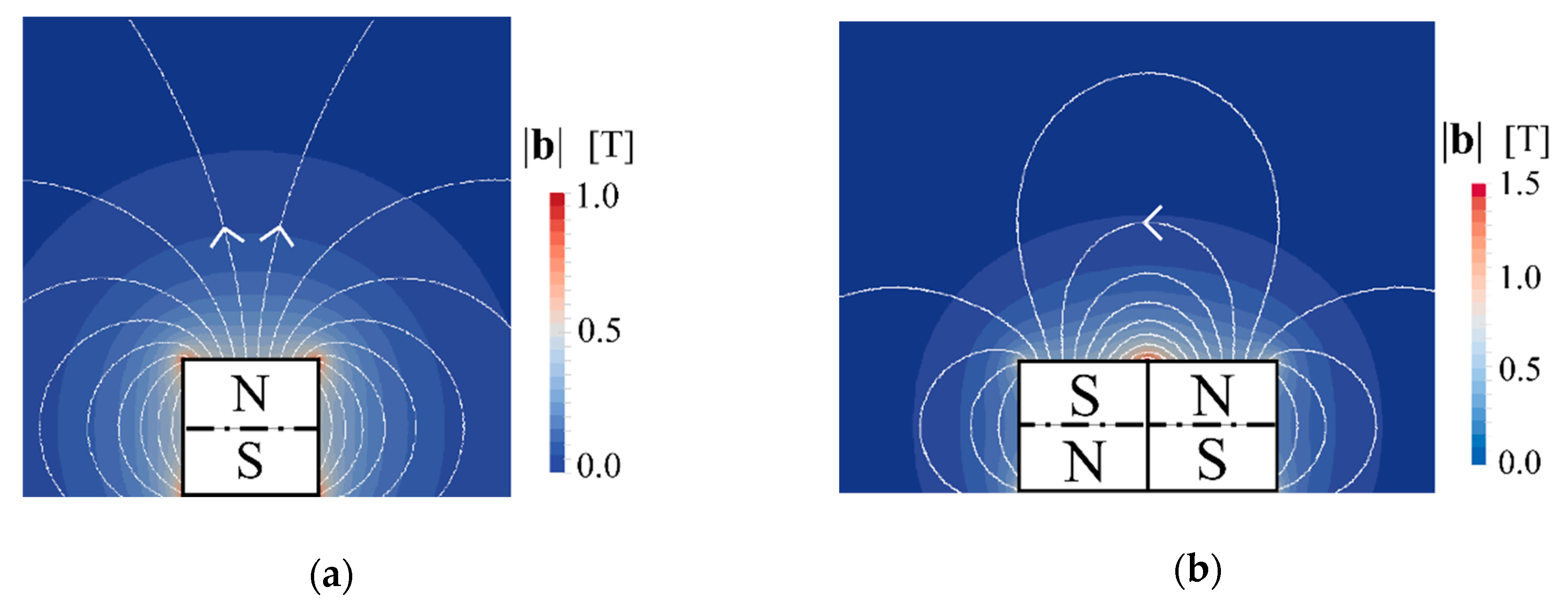
2.3. Magnetic Field Simulation
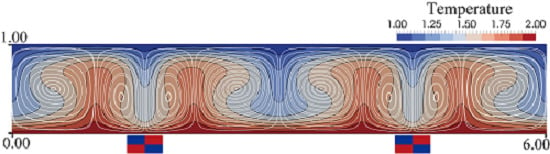
3. Results and Discussion
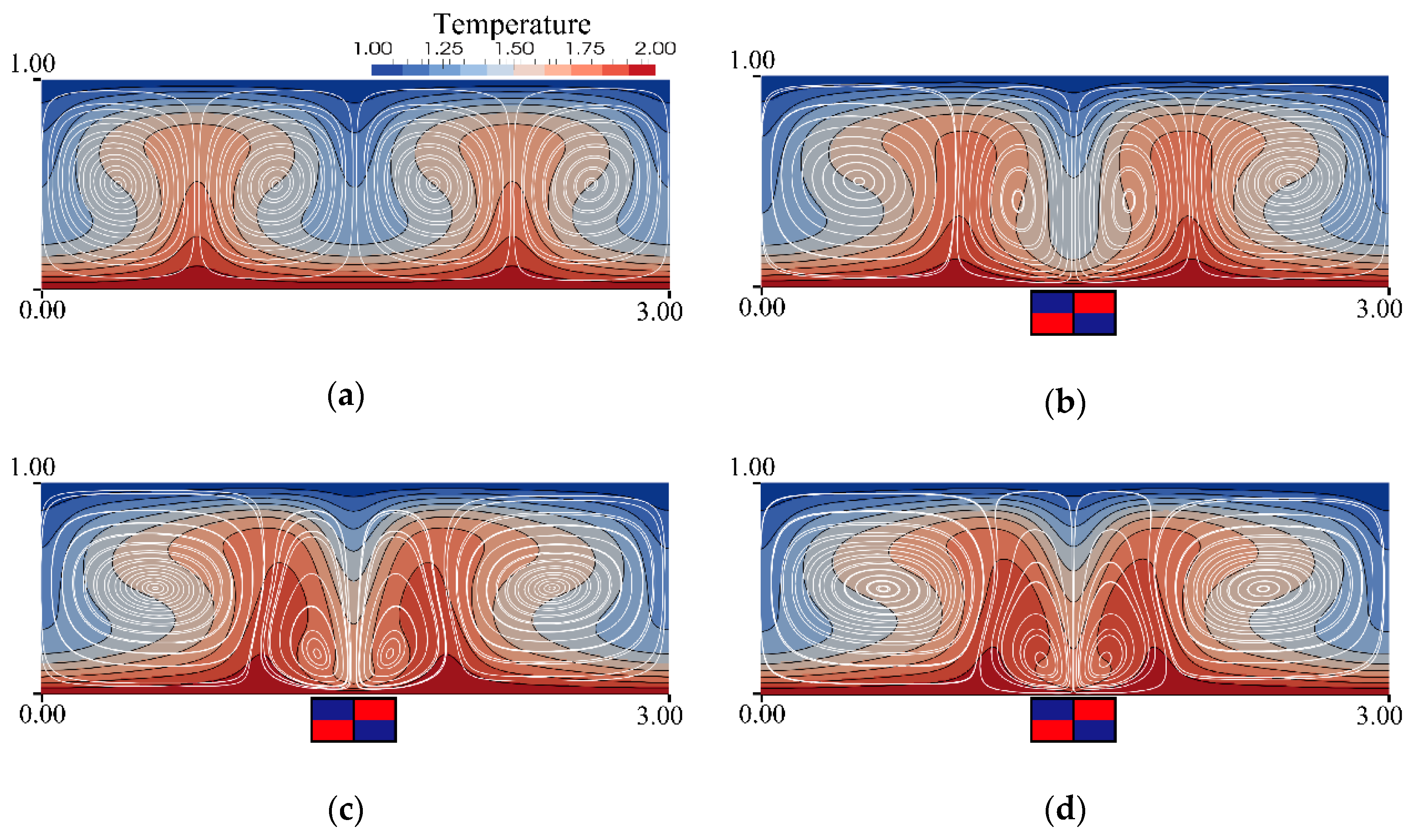
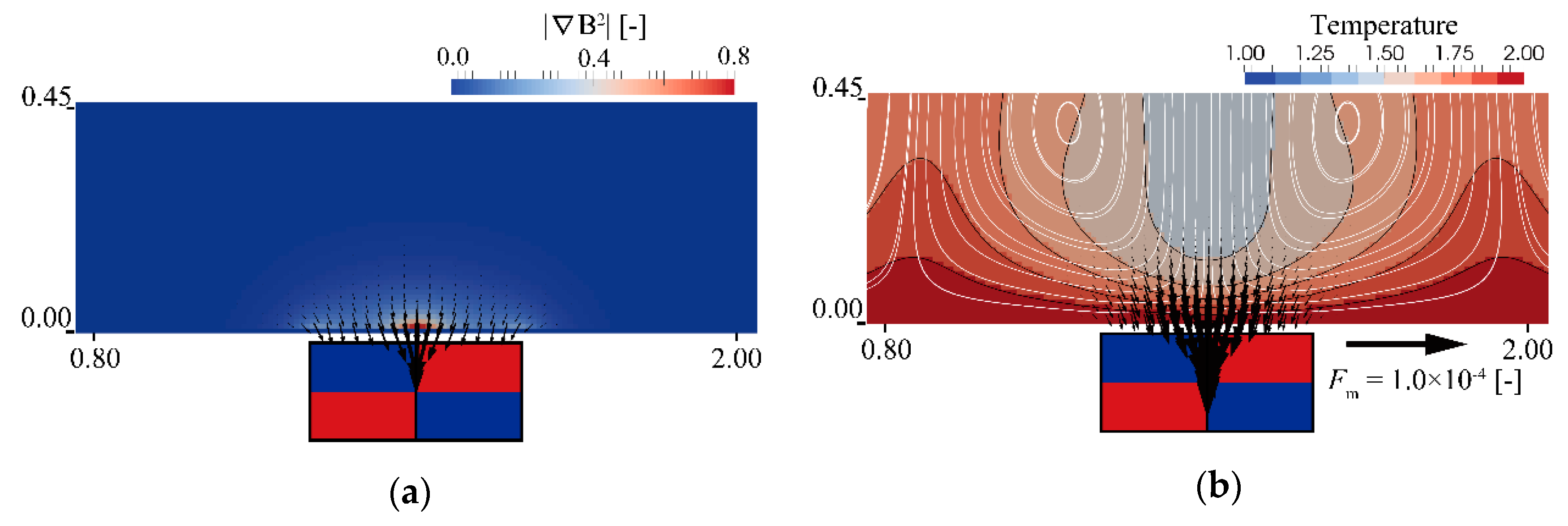
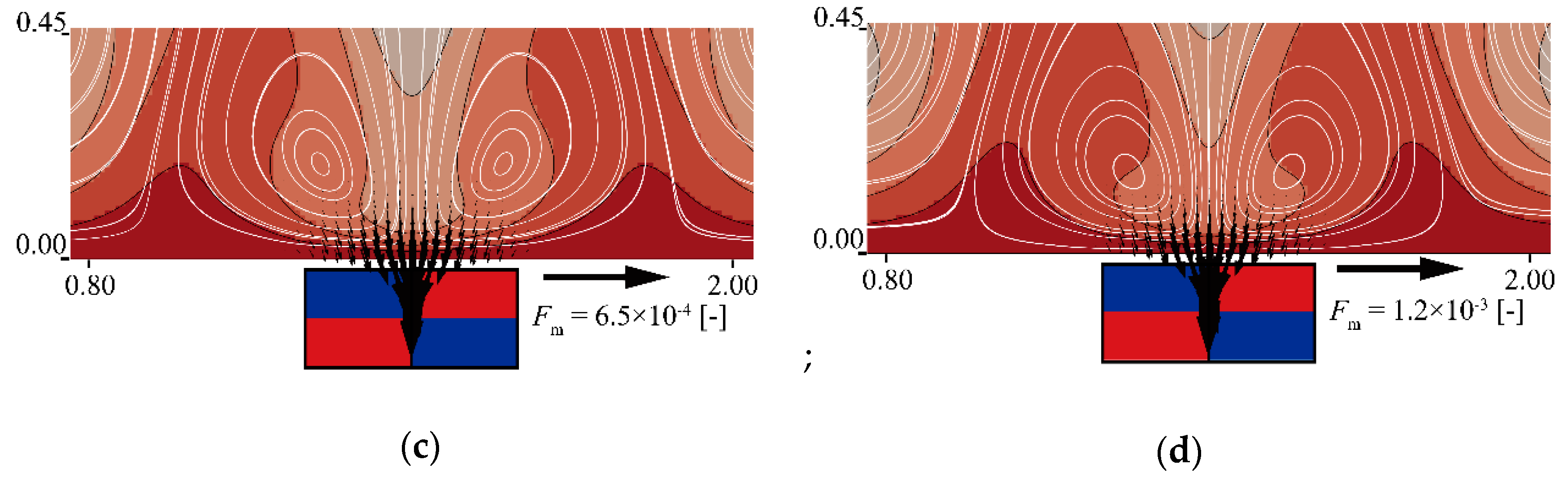
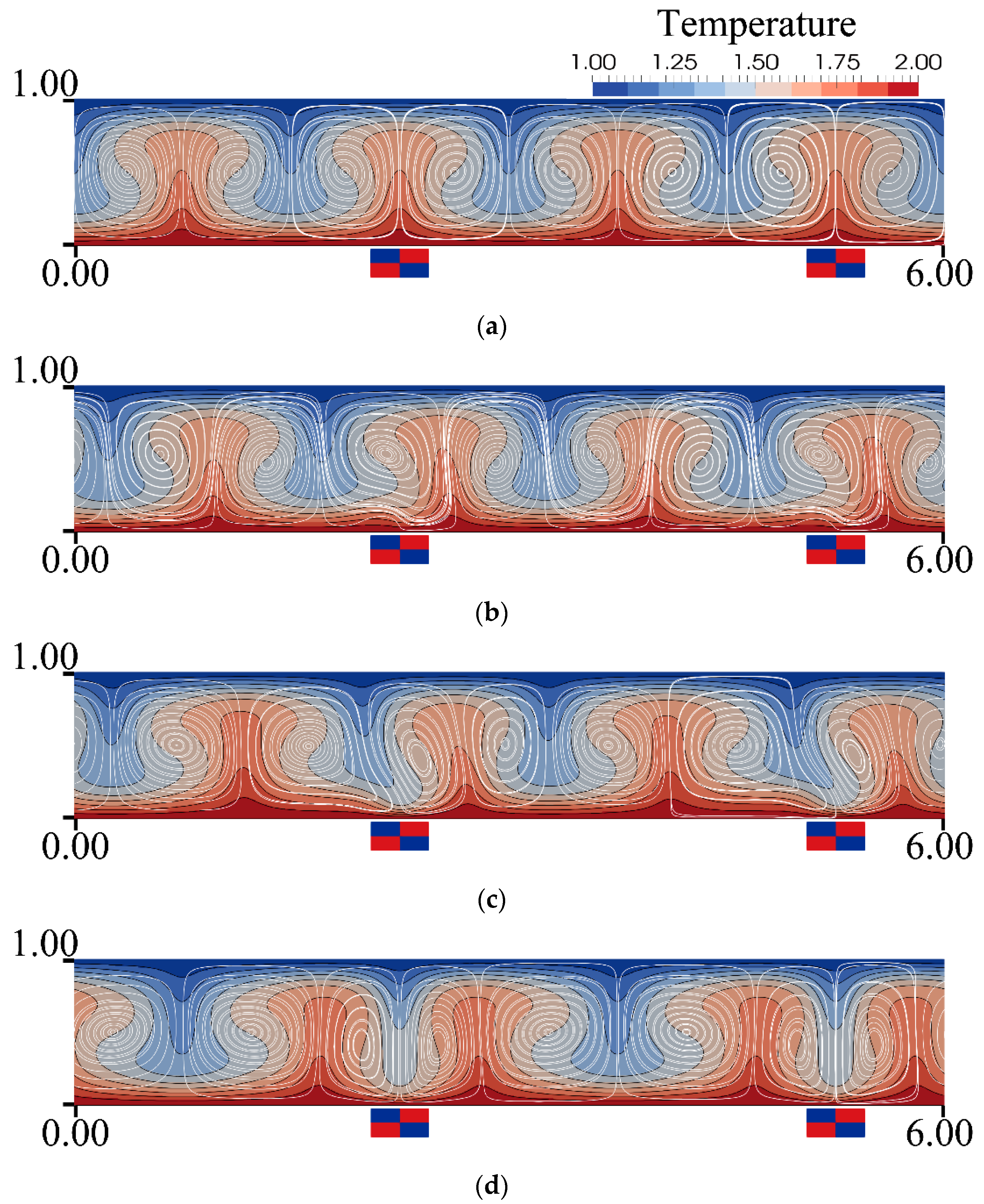
3.1. Heat and Fluid Flow with and without Magnetic Field
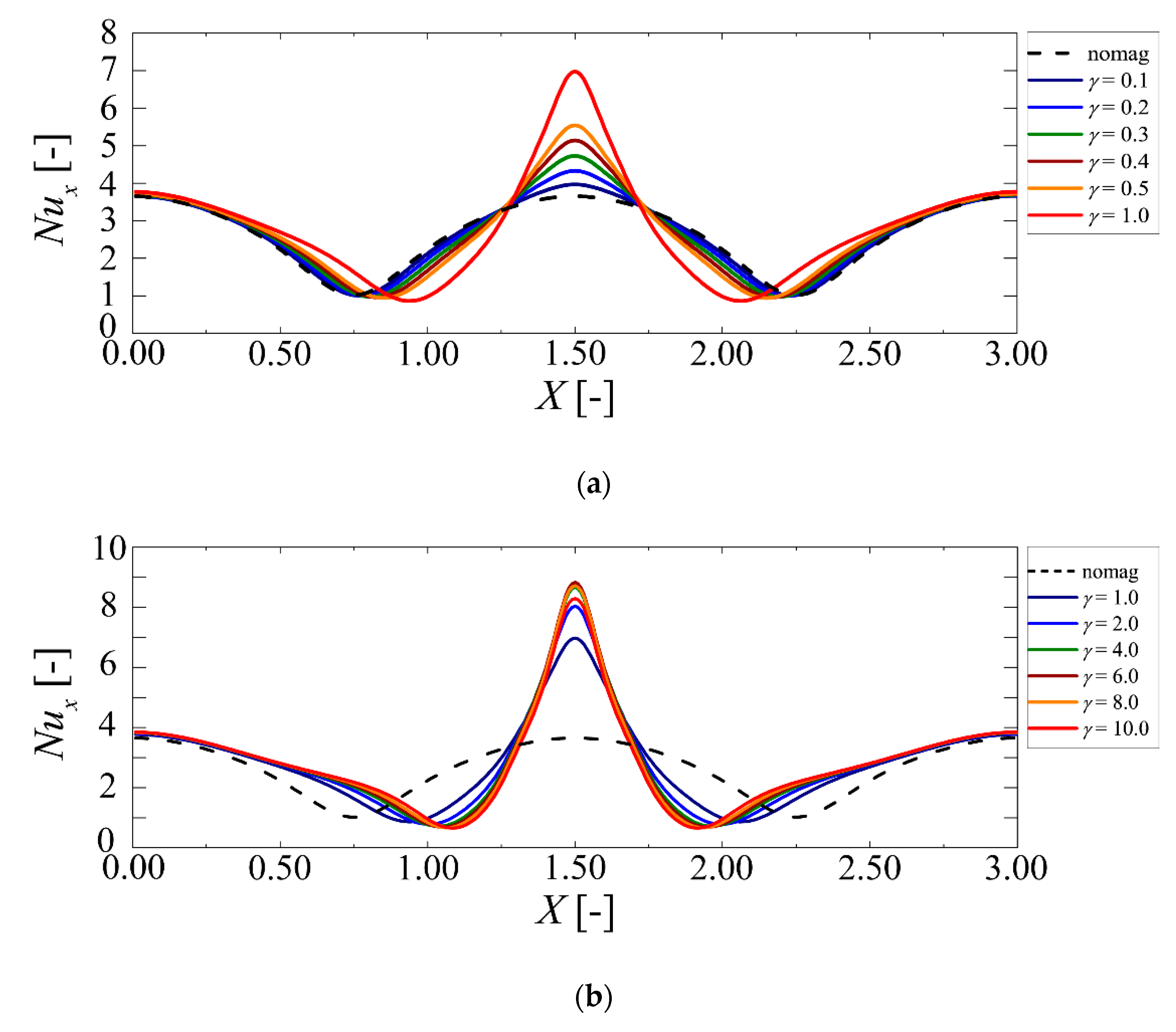
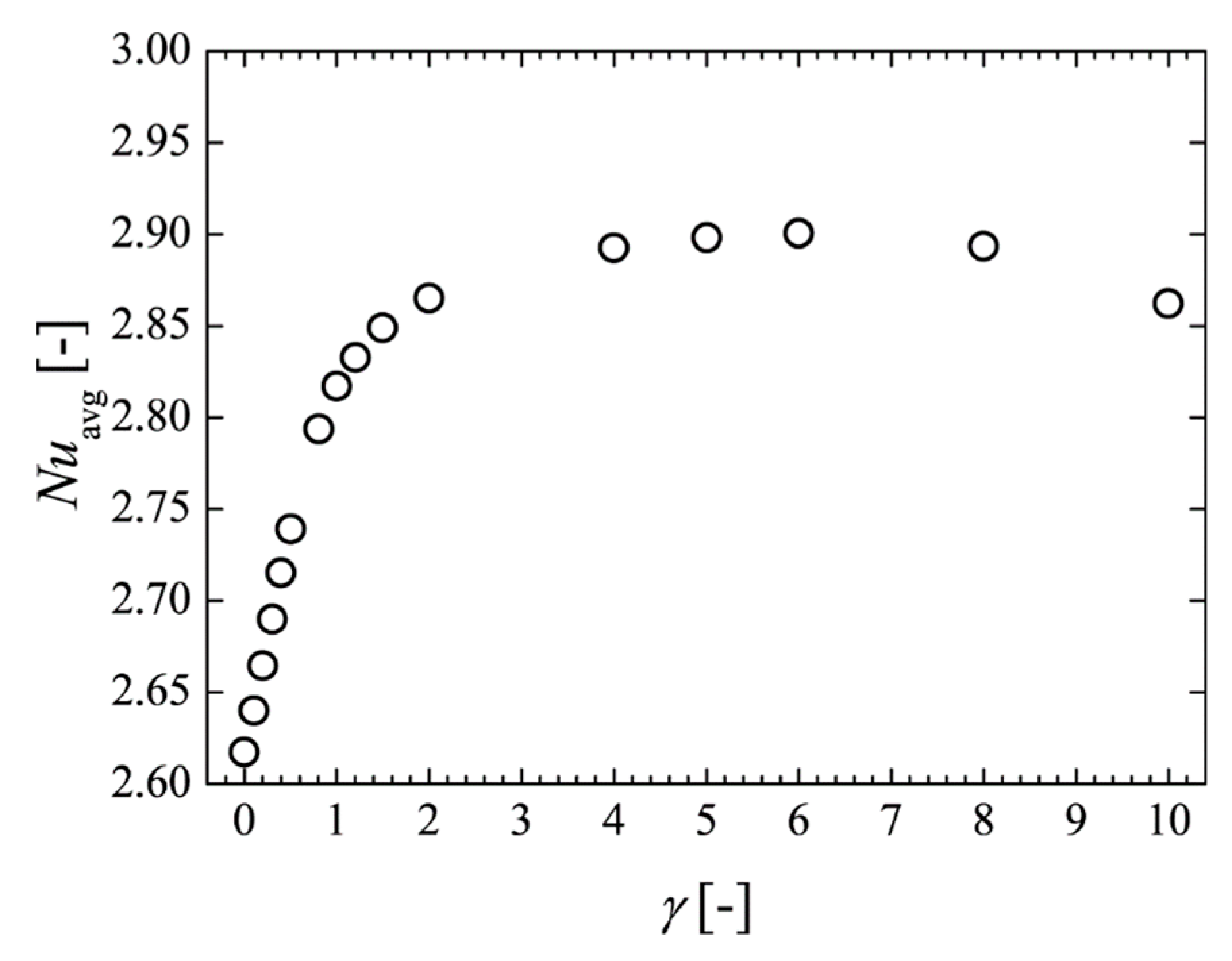
3.2. Effect on Heat Transfer
3.3. Roll Cell Shifting by Magnet Location
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Chong, K.L.; Wagner, S.; Kaczorowski, M.; Shishkina, O.; Xia, K.Q. Effect of Prandtl number on heat transport enhancement in Rayleigh-Bénard convection under geometrical confinement. Phy. Rev. Fluids 2018, 3, 013501. [Google Scholar] [CrossRef]
- Pandey, A.; Scheel, J.D.; Schumacher, J. Turbulent superstructures in Rayleigh-Bénard convection. Nat. Commun. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bouffard, M.; Choblet, G.; Labrosse, S.; Wicht, J. Chemical convection and stratification in the earth’s outer core. Front. Earth Sci. 2019, 7, 1–19. [Google Scholar] [CrossRef]
- Grants, I.; Gerbeth, G. Rayleigh-Bénard instability of Czochralski configuration in a transverse magnetic field. J. Cryst. Growth 2012, 358, 43–50. [Google Scholar] [CrossRef]
- Howle, L.E. Control of Rayleigh-Bénard convection in a small aspect ratio container. Int. J. Heat Mass Transfer. 1997, 40, 817–822. [Google Scholar] [CrossRef]
- Chandrasekhar, S. Hydrodynamic and Hydromagnetic Stability; Dover Publications Inc.: New York, NY, USA, 1981. [Google Scholar]
- Aurnou, J.M.; Olson, P.L. Experiments on Rayleigh-Bénard convection, magnetoconvection and rotating magnetoconvection in liquid gallium. J. Fluid Mech. 2001, 430, 283–307. [Google Scholar] [CrossRef]
- Burr, U.; Müller, U. Rayleigh-Bénard convection in liquid metal layers under the influence of a horizontal magnetic field. J. Fluid Mech. 2002, 453, 345–369. [Google Scholar] [CrossRef]
- Yoshikawa, H.N.; Tadie Fogaing, M.; Crumeyrolle, O.; Mutabazi, I. Dielectric Rayleigh-Bénard convection under microgravity conditions. Phys. Rev. E 2013, 87, 043003. [Google Scholar] [CrossRef]
- Carruthers, J.R.; Wolfe, R. Magnetothermal convection in insulating paramagnetic fluids. J. Appl. Phys. 1968, 39, 5718–5722. [Google Scholar] [CrossRef]
- Jiang, C.; Feng, W.; Zhong, H.; Zhu, Q.; Zeng, J. Magnetic and gravitational convection of air in a porous cubic enclosure with a coil inclined around the Y axis. Trans. Porous Med. 2014, 102, 167–183. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Zhang, J.L.; Song, K.W.; Wang, L.B. Numerical study of the sensing mechanism of the oxygen concentration sensor based on thermal magnet convection. Int. J. Therm. Sci. 2016, 99, 71–84. [Google Scholar] [CrossRef]
- Pleskacz, Ł.; Fornalik-Wajs, E. Identification of the structures for low Reynolds number flow in the strong magnetic field. Fluids 2019, 4, 21. [Google Scholar] [CrossRef]
- Braithwaite, D.; Beaugnon, E.; Tournier, R. Magnetically Controlled Convection in a Paramagnetic Fluid. Nature 1991, 354, 134–136. [Google Scholar] [CrossRef]
- Maki, S.; Tagawa, T.; Ozoe, H. Average heat transfer rates measured and numerically analyzed for combined convection of air in an inclined cylindrical enclosure due to both magnetic and gravitational fields. Exp. Ther. Fluid Sci. 2003, 27, 891–899. [Google Scholar] [CrossRef]
- Maki, S.; Ataka, M.; Tagawa, T.; Ozoe, H.; Mori, W. Natural Convection of a Paramagnetic Liquid Controlled by Magnetization Force. AIChE J. 2005, 51, 1096–1103. [Google Scholar] [CrossRef]
- Tagawa, T.; Ujihara, A.; Ozoe, H. Numerical computation for Rayleigh-Bénard convection of water in a magnetic field. Int. J. Heat Mass Trans. 2003, 46, 4097–4104. [Google Scholar] [CrossRef]
- Weiss, S.; Ahlers, G. Magnetic-field effect on thermal convection of a nematic liquid crystal at large Rayleigh numbers. J. Fluid Mech. 2013, 716, R7-1–R7-11. [Google Scholar] [CrossRef][Green Version]
- Kaneda, M.; Fujiwara, H.; Wada, K.; Suga, K. Natural convection of paramagnetic fluid along a vertical heated wall under a magnetic field from a single permanent magnet. J. Magn. Magn. Mater. 2020, 502, 166574. [Google Scholar] [CrossRef]
- Kaneda, M.; Nazato, K.; Fujiwara, H.; Wada, K.; Suga, K. Effect of magnetic field on natural convection inside a partially-heated vertical duct: Experimental study. Int. J. Heat Mass Transf. 2019, 132, 1231–1238. [Google Scholar] [CrossRef]
- Guo, Z.; Zhen, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef]
- Fakhari, A. Rahimian, Phase-field modeling by the method of lattice Boltzmann equations. Phys. Rev. E 2010, 81, 036707. [Google Scholar] [CrossRef] [PubMed]
- Maki, S.; Tagawa, T.; Ozoe, H. Enhanced convection or quasi-conduction states measured in a super-conducting magnet for air in a vertical cylindrical enclosure heated from below and cooled from above in a gravity field. J. Heat Transf. 2002, 124, 667–673. [Google Scholar] [CrossRef]
- Clever, R.M.; Busse, F.H. Transition to time-dependent convection. J. Fluid Mech. 1974, 65, 625–645. [Google Scholar] [CrossRef]
- Inamuro, T.; Yoshino, M.; Inoue, H.; Mizuno, R.; Ogino, F. A lattice Boltzmann method for a binary miscible fluid mixtures and its application to a heat-transfer problem. J. Comput. Phys. 2002, 179, 201–215. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wada, K.; Kaneda, M.; Suga, K. Rayleigh-Bénard Convection of Paramagnetic Liquid under a Magnetic Field from Permanent Magnets. Symmetry 2020, 12, 341. https://doi.org/10.3390/sym12030341
Wada K, Kaneda M, Suga K. Rayleigh-Bénard Convection of Paramagnetic Liquid under a Magnetic Field from Permanent Magnets. Symmetry. 2020; 12(3):341. https://doi.org/10.3390/sym12030341
Chicago/Turabian StyleWada, Kengo, Masayuki Kaneda, and Kazuhiko Suga. 2020. "Rayleigh-Bénard Convection of Paramagnetic Liquid under a Magnetic Field from Permanent Magnets" Symmetry 12, no. 3: 341. https://doi.org/10.3390/sym12030341
APA StyleWada, K., Kaneda, M., & Suga, K. (2020). Rayleigh-Bénard Convection of Paramagnetic Liquid under a Magnetic Field from Permanent Magnets. Symmetry, 12(3), 341. https://doi.org/10.3390/sym12030341