1. Introduction
The study of the wave processes in elastic shells is widely used in various technical fields. The propagation of deformation waves in elastic, viscoelastic and nonlinear viscoelastic shells was considered in [
1]. However, the case of the interaction of shells with a viscous incompressible fluid is not considered. In [
2,
3,
4,
5,
6], the interaction of the shell with a viscous incompressible fluid was considered, without taking into account the wave phenomena, and the influence of local terms of inertia was not studied, as well.
Various methods are used to solve coupled and uncoupled problems of the interaction of a fluid with an elastic body. At the first stage, when solving the uncoupled problems, the interaction of a fluid with a solid is considered. The friction and pressure acting on the fluid from the side of the solid are determined. Thus, it is assumed that the body deformation does not influence the fluid motion. At the second stage the obtained parameters are substituted into the equations of elastic body dynamics, and longitudinal and normal (deflection) displacements are found. In this way, the stress-strain state of the elastic structure, as the goal of the uncoupled problem, is determined.
In the case of the coupled problem, the fluid and the elastic body dynamics equations are solved simultaneously, taking into account the boundary conditions. The presented approach provides a more precise studying the deformation waves of nonlinear elastic shells containing a viscous fluid of constant density, taking into account the inertia of its motion.
Surrounding elastic media and construction damping in two coaxial shells with viscous incompressible in the gap between them do not allow discovery of the exact solution of the problem of the deformation waves propagation. This leads to the necessity of applying numerical methods [
7].
Mathematical models of the wave process in infinite long coaxial cylinder elastic shells are obtained by means of two-scale expansion by a small parameter, as in [
1,
8]. They differ from the known ones by the presence of viscous incompressible fluid between the shells with rigid non-linearity with application of the coupled hydroelasticity problems. These problems are described by shell dynamics equations and by incompressible viscous fluid ones with corresponding boundary condition in the form of the generalized modified Korteweg–de Vries equations system. The numerical solution is the carry-out difference scheme for the equations similar to the Crank–Nicholson one [
9].
The effects of an incompressible viscous fluid between the shells on the behavior of the deformation wave in the coaxial shells are revealed. The presence of a strain wave in the outer shell leads to the appearance of a strain wave in the inner shell, which was not at the initial moment of time, and there is an “energy transfer” (through the fluid layer) from the outer shell to the inner one, which is accompanied by a nonmonotonic decrease in the wave amplitude in the outer shell and, as a result, a nonmonotonic decrease in the velocity of its distribution. In this case, a nonmonotonic increase of the amplitude occurs in the inner shell. The amplitudes and the velocities fluctuate, and in the course of time they become equal.
Taking into account the movement of the fluid and the surrounding elastic media leads to the wave velocity change, and the structural damping and fluid viscous friction cause wave amplitude decrease.
2. Results
2.1. Defining and Resolving Relations of the Physically Nonlinear Theory of Shells
Two coaxial indefinitely long elastic shells with viscous impressible fluid in the gap between them present the subject of the study.
To derive the equations of motion of cylinder shells element in the displacements for Kirchhoff-Love model we consider the material with nonlinear dependence of tension tensor components on deformation tensor ones.
A. A. Ilyushin’s deformation theory [
10] connects the components of the stress tensor
,
with the components of the strain tensor
,
and the square of the strain intensity
[
11,
12].
where
are the coordinates in the systems in the median surfaces of the two shells;
E is Young’s modulus;
m is the constant of the material, determined from the experiments on tension or compression;
is the Poisson’s ratio of the shell material.
We consider axisymmetric coaxial cylindrical shells. We denote: is the radius of the inner surface of the outer shell; is the radius of the outer surface of the inner shell; are the radii of the median surfaces; is the shell thickness; is the longitudinal elastic displacement; is the deflection directed to the center of curvature ( for the outer shell, for the inner one); is the thickness of the fluid layer in the annular section of the pipe . Wherein , .
We write down the relation between the components of the strains and elastic displacements in the form
Where
x is the longitudinal coordinate along the median surface;
z is the normal coordinate in the shell
. We write down the square of the strain intensity in the form of
Formulas (
1)–(
3) demonstrate cubic dependence of stress tensor components on the elastic displacements. We determine the forces in the middle surface of the shell and the moment using the following formulas
The dynamics equations of the shells are written down in in the form of
where
t is time;
is the density of the shell material;
,
are the stresses from the side of the fluid inside the annular section;
for the outer shell,
for the inner shell;
is structural damping coefficient in the longitudinal direction;
l is wave length;
coefficient subgrade reaction [
13,
14];
r,
x are the cylindrical coordinates in the coordinates’ system with the center on axis if symmetry of the shells. The direction of the axis
x coincides with the direction of the axis
x of the coordinates’ systems on the median surfaces of the shells.
2.2. The Asymptotic Method for Studying the Equations of Shells with a Fluid
The estimates made in dimensionless variables characterize the problems under consideration. For wave problems, the shell is considered infinite. For longitudinal waves, dimensionless variables and dimensionless parameters are introduced in the shell. We take wavelength
l for the characteristic length, and
,
for the characteristic values of elastic displacements
is the propagation velocity of longitudinal elastic waves in the shell. We put
where
is the small parameter of the problem. We introduce independent variables in the form of
where
is the fast time;
c is the wave velocity.
We represent the dependent variables as an asymptotic expansion
By substituting (
1)–(
4), (
6)–(
9) in Equation (
5) for the first term of the asymptotic expansion (
9), we obtain the equations system
Thus,
—is the arbitrary function and the dimensionless wave velocity
and therefore the wave velocity is equal to
—the wave velocity in the rod. Since the shell has the infinite length, then
For the second term of the asymptotic expansion (
9), we obtain the system of equations in the approximation
We substitute relation (
11) into Equation (
12) and obtain the system for the second expansion member
Eliminating the terms
,
from the left-hand sides of the equation from system (
13), we obtain the resolving equations.
The resulting equation is a modified Korteweg–de Vries equation (MKdV) for . In the absence of the fluid, the right-hand side of the equation is zero and the modified Korteweg–de Vries equation (MKdV) is obtained. It is necessary to determine the right side by solving the equations of hydrodynamics.
The incompressibility of the fluid is justified by the fact that its movement velocity, caused by the shell’s elastic displacements, is much less than the sound velocity.
2.3. The Study of the Stresses Acting on the Shell from the Side of the Fluid Inside
We consider two coaxial infinitely long elastic shells in
Figure 1, inside of which there is a viscous incompressible fluid.
The equation of motion of an incompressible viscous fluid and the continuity equation in a cylindrical coordinate system
in the case of an axisymmetric flow [
15] are written in the form of
At the boundary, the shells and fluid in
Figure 1 with
the conditions of fluid sticking are satisfied [
15]
here
,
are projections on the axis of the cylindrical coordinate system of the velocity vector;
p is the pressure in the fluid;
is the density of the fluid;
is the kinematic viscosity coefficient. The stresses from the side of the fluid layer are determined by the formulas
Here is the normal to the middle surface of the i-th shell, , , are the unit vectors of the cylindrical coordinate system, the center of which is located on the geometric axis. If we carry the stress on the unperturbed surface of the shell, we can assume— and , .
We introduce dimensionless variables and parameters
We expand pressure and velocity components in powers by a small parameter
Substituting (
18) and (
19) into the hydrodynamic problem (
15) and (
16) in the zero approximation by
(hydrodynamic theory of lubrication) for the first terms of expansion (
19), we obtain the equations
and boundary conditions
At the first step of the iteration, we set
(hydrodynamic theory of lubrication) [
15]. By taking into account the boundary conditions we obtain from the equations of fluid motion
At the second step of the iteration, by substituting the found values
into the equations of fluid dynamics, we find
The convergence of the iteration method is justified in [
2]. Considering that the variables (
8) are introduced and bearing in mind (
11), under
, we find
We find the expression in the right-hand side of Equation (
14). Considering that
and flat
,
due to the smallness of
,
for the first equation, we have
For the second equation, we have
2.4. The Coaxial Shells Dynamics Equations
The system of equations takes this form, taking into account the found right-hand side of (
26) and (
27)
We can also introduce the notation
,
,
,
, where
We put
and obtain a system of equations generalizing the modified Korteweg–de Vries equations.
In the absence of the damping in longitudinal direction
and the influence of elastic media
the system (
31) takes the form of
with the exact solution
In the absence of fluid and damping in the longitudinal direction
, the system of equations decomposes into two independent MKdV equations
These equations have the solutions
which can be taken as initial conditions at
.
Under the initial condition in the presence of the fluid between the shells and structural damping in the longitudinal direction, a numerical solution of the equations systems is required
2.5. Computing Experiment
For numerical simulation, we consider a difference scheme for the equations similar to the Crank–Nicholson one for the heat equation [
9]
3. Discussion
The subject matter of the research is studying the effects of the incompressible viscous fluid in the behavior of the deformation waves in the coaxial shells. The performed numerical experiments make it possible to evaluate the effects of viscous incompressible fluid presence between the inner and outer shells and the influence of the fluid movement inertia on the behavior of the nonlinear deformation waves. The influence of structural damping in the shells and the influence elastic media surrounding the outer shell are taken into account, as well.
Under the presence of the deformation wave in the outer shell and its absence in the inner shell at first the amplitudes are aligned, and then they fall and disappear.
In
Figure 2, the adequacy of the difference scheme and the system of resolving equations is checked. The solutions of the difference equations coincide with the exact solution of the resolving equations. The velocity of the wave is supersonic.
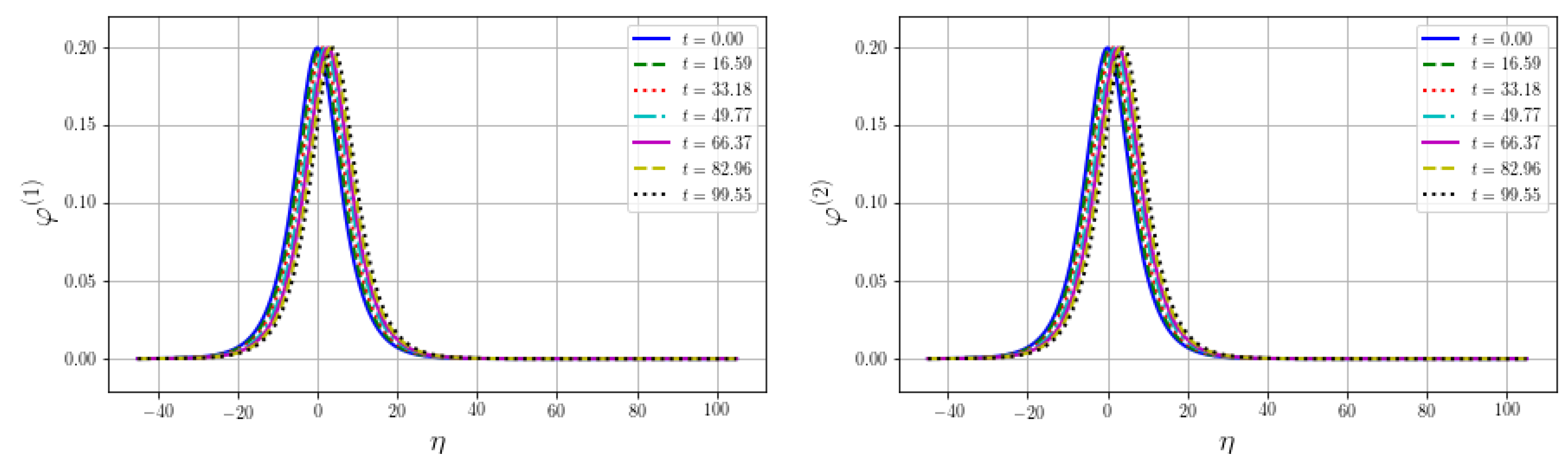
In
Figure 3, at the initial moment of time, the deformation wave is specified in the outer shell; the deformation wave is absent in the inner shell. There is a transfer of energy from the outer shell to the inner one. In the outer shell the wave amplitude decreases, and in the inner shell it grows, until the amplitudes equalize and become equal to the half of the initial amplitude of the outer shell. In this case, the wave velocity in the outer shell is greater than the wave velocity in the inner shell. The velocity of the wave is supersonic and more than
Figure 2. This occurs due to the influence of the elastic environment, which can be seen both from the exact solution (
37) and from the calculations.
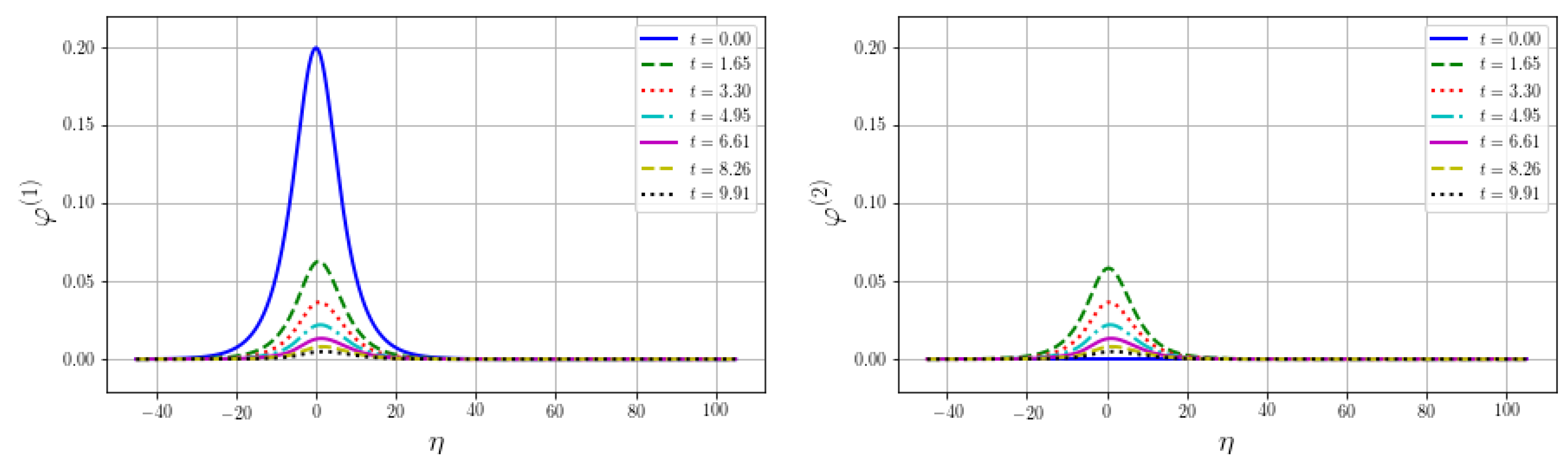
Figure 4 shows the effect of structural damping in the longitudinal direction. In the outer shell the wave amplitude decreases, and in the inner shell it grows, until the amplitudes equalize and then begin to fall in both shells.
4. Conclusions
Deformation waves in an elastic shell can emerge, for example, due to piezoelectric element acting. The propagation of such waves presents the subject matter of numerous and various investigations. The presence of the fluid in the gap between two coaxial shells is of primary importance in studying the deformation waves propagation. The mathematical model of this phenomena presents the coupled problem of hydroelasticity.
The hydroelastic equations for two coaxial shells with viscous incompressible fluid between them are reduced to the system of two generalized modified Korteweg–de Vries equations. Structural damping in the longitudinal direction in the shells and the presence of the media surrounding the outer shell are the important factors influencing deformation waves propagation. The solution of nonlinear equations of shells’ dynamics was carried out by means of two-scale asymptotic expansions method. This made it possible to consider the equations’ non-linearity.
The solution of the equations of fluid mechanics with corresponding boundary conditions was carried out by means of the method of asymptotic series expansions in powers of small parameters of the problem. This expansion lead to the linear equations of hydrodynamics lubrication theory with consideration of the inertia local member. The latter equations were solved by means of the iteration method with justification of its usage.
Under the absence of structural damping and surrounding elastic media, the obtained resolving equation system possesses the exact solution. This made it possible to test the proposed difference scheme for numerical study of the problem. The numerical experiment allowed to take into account the influence of all factors of the problem under consideration.
The novelty of the study is presented in the fact that the energy is transferred in the presence of the fluid between the shells. In this case, the amplitude in the outer shell decreases, and in the inner one it grows until they become equal. Moreover, the effect of structural damping leads to the wave amplitudes decrease.
The obtained results are new and demonstrate the possibility of using nonlinear waves in the shells for transmitting information over long distances. Thus, the obtained results justify the necessity of energy boost into the outer shell by means of piezoelectric elements for compensating the losses caused by structural damping.