Abstract
Motivated by the lubrication processes naturally appearing in numerous industrial applications (such as steam turbines, pumps, compressors, motors, etc.), we study the lubrication process of a slipper bearing consisting of two coaxial cylinders in relative motion with an incompressible micropolar fluid (lubricant) injected in the thin gap between them. The asymptotic approximation of the solution to the governing micropolar fluid equations is given in the form of a power series in terms of the small parameter representing the thickness of the shaft. The regular part of the approximation is obtained in the explicit form, allowing us to acknowledge the effects of fluid’s microstructure clearly through the presence of the microrotation viscosity in the expressions for the first-order velocity and microrotation correctors. We provide the construction of the boundary layer correctors at the upper and lower boundary of the shaft along with the construction of the divergence corrector, allowing us to improve our overall estimate. The derived effective model is rigorously justified by proving the error estimates, evaluating the difference between the original solution of the considered problem and the constructed asymptotic approximation.
MSC:
35C20; 35Q35; 76M45
1. Introduction
The classical Navier–Stokes model has a serious limitation as it does not take into account the microstructure of the fluid. In order to overcome this issue, the model of micropolar fluids was proposed in the 1960s by Eringen in his well-known paper (see [1]). The micropolar fluid model is based on the introduction of a microrotation field (angular velocity field of rotation) describing effects such as rotation and shrinking of the fluid particles. As a consequence, a new vector equation derived from the law of conservation of angular momentum is added to the Navier–Stokes system. In this way, we obtain a coupled system of partial differential equations that are well suited for modeling the behavior of various non-Newtonian fluids including liquid crystals, animal blood, muddy fluids, certain polymeric fluids, and even water at small scales. For this reason, there exist a vast number of recent results concerning the engineering applications of the model, primarily in biomedicine and blood flow modeling (see, e.g., [2,3,4,5]), as well as a number of papers providing rigorous mathematical treatment of various effective models for micropolar fluids (see, e.g., [6,7,8,9,10,11]). A comprehensive survey of the modern mathematical theory underlying the micropolar fluid model can be found in the monograph [12].
The study of lubrication problems can be traced back to the pioneering work of Reynolds in 1886 (see [13]), where the thin film flow was treated heuristically without giving a relation between the derived model and the Navier–Stokes equations. A formal relation between the Navier–Stokes equations in a thin domain and the Reynolds equations using asymptotic analysis was provided by Capriz, Elrod, and Wannier (see [14,15,16]). Rigorous mathematical treatment of the Reynolds equations for a flow between two plain surfaces was addressed by Bayada, Chambat, and Cimatti (see [17,18]). Bourgeat, Mikelić, and Tapiero provided a similar result in [19] with rigorous mathematical treatment for a non-Newtonian fluid. Furthermore, Assemien, Bayada, and Chambat provided a study of the weak inertial effects in the asymptotic behavior of a thin film flow (see [20]), while Bourgeat and Marušić–Paloka justified the nonlinear model for a fast flow through a rough thin domain (see [21,22]). Moreover, the asymptotic behavior of the viscous flow in an infinite thin layer between two fixed, plain surfaces was investigated by Nazarov in [23].
The rigorous mathematical treatments of a thin curved pipe stationary flow including an investigation of the effects of flexion and torsion on the flow were provided by Marušić–Paloka for a Newtonian fluid (see [24]) and by Pažanin for a micropolar fluid (see [25]). On the other hand, the nonstationary flows were the subject of investigation by Castineira, Marušić–Paloka, Pažanin, and Rodriguez for a Newtonian fluid (see [26]) and Pažanin and Radulović for a micropolar fluid (see [27]). Finally, the rigorous mathematical justification of an asymptotic model for the lubrication problem with a Newtonian fluid in a curved domain, namely a rotating shaft appearing in real-life situations, was provided by Duvnjak and Marušić–Paloka (see [28,29]). At this point, it is important to emphasize that the latter result inspired us to consider the more general case of the lubrication process of a rotating shaft filled with a non-Newtonian fluid, namely the micropolar fluid. The main advantage of considering the micropolar fluid is that it takes into account the microstructure of the fluid. Although a lower-dimensional model for the considered problem was recently formally derived in [30] by the authors of this paper, the justification of its usage is still missing in the literature. The justification of the derived model represents the main novelty of this work. By proving the corresponding error estimates, we provide the order of accuracy of the newly proposed model indicating its range of applicability, and this represents our main contribution.
In this paper, we consider the lubrication process of a slipper bearing consisting of two coaxial cylinders in relative motion. One belongs to the shaft, which is rotating with some constant angular velocity , while the other is a lubricated (not perfectly smooth) surface of support. The circular shaft is of radius R and height l. Between the shaft and the support, there is a thin gap (the domain ) of thickness , completely filled with an incompressible micropolar fluid (the lubricant). The problem under consideration is commonly found in various real-life applications primarily including the study of the optimal design of lubrication devices consisting of slipper bearings. These devices naturally appear in industrial machinery with a large horse power having high loads and speeds including steam turbines, pumps, compressors, and motors (see [31]).
In Section 2, we write down the micropolar fluid system of equations posed in the thin domain . In Section 3, due to the curved geometry of the domain under consideration, we first write our micropolar fluid system of equations in the cylindrical coordinates. Then, we seek the solution of our original problem as a power series in terms of the small parameter , representing the thickness of the domain, and derive the explicit expressions for the velocity and microrotation in the regular part of the expansion. However, as the boundary conditions at the upper and lower part of the shaft were neglected in the process, we correct the approximation by constructing the boundary layer correctors. Moreover, as the residual in the divergence equation is not small enough to provide us with satisfactory error estimates, we construct the divergence corrector as well. Finally, in Section 4, we estimate, in suitable norms, the difference between the original solution of our problem and the constructed asymptotic solution in terms of the small parameter . In this way, we justify the usage of the formally derived simplified, effective model. As mentioned above, to the best of our knowledge, a rigorous mathematical treatment of the lubrication problem of a rotating shaft filled with micropolar fluid is still missing in the literature, and this represented the motivation to tackle this problem.
2. Setting of the Problem
Due to the curved geometry of the domain, we describe it using cylindrical coordinates . We denote by the change of variables and assume that the film thickness is , where is a small positive parameter. The domain of the flow is given by:
where the function is of class , -periodic, and bounded in the sense , for (see Figure 1).
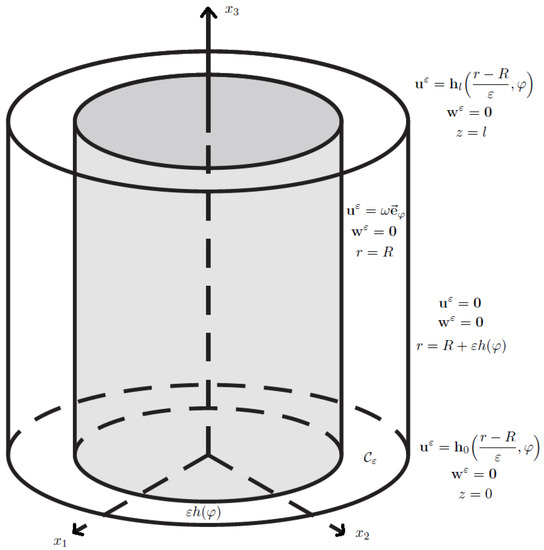
Figure 1.
The considered domain .
In the following, we assume a low Reynolds number regime.
The flow in is governed by the micropolar fluid system of equations:
In view of the application we aim to model, we consider the following boundary conditions:
Here, is the velocity field, is the pressure, whereas represents the microrotation field. The constants appearing in the system of Equation (1) are given by , , , and , where is the Newtonian viscosity, is the microrotation viscosity, while , and are the coefficients of angular viscosities. The external sources of linear and angular momentum are given by the functions and .
We also assume that the functions , , where:
are -periodic with respect to and satisfy the following:
3. Asymptotic Analysis
Taking into account the curved geometry of the domain, it is appropriate to write our original problem (1) and (2) in cylindrical coordinates. The micropolar system of equations in cylindrical coordinates reads (see, e.g., [33]):
and:
where the velocity and microrotation field are given in the form:
and we introduced the differential operator:
for a scalar function .
3.1. Asymptotic Expansion
We construct the formal asymptotic expansion of the solution to the problem (1) and (2) in the following way:
where , while the external force functions are given in the form:
It is important to emphasize that the components and can be neglected due to the small thickness of the domain in the component . Furthermore, applying the same argument, we can assume that the external force functions and are independent of .
In the sequel, we compute the zero-order approximation and first-order correctors of the approximation given by (6). The procedure is the following: plugging the approximation into the governing system of Equations (4) and (5), collecting the terms by the same powers of , and solving the obtained recursive sequence of problems.
It is important to note that we will not take into account the boundary conditions at the lower and upper part of the boundary in the formal derivation of the model, leading to the boundary layer effects. In order to address those effects as well, we need to construct the boundary layer correctors, which is done in Section 3.3.
3.2. Regular Part of the Expansion
We plug the asymptotic expansion (6) into the micropolar system of Equations (4) and (5) and collect terms by the same powers of , leading to a recursive sequence of problems. The computations presented in Section 3.2, which are related to the regular part of the expansion, were presented by Marušić–Paloka, Pažanin, and Radulović in [30], and we recall them for the sake of the readers’ convenience.
3.2.1. Zero-Order Approximation
Collecting the terms by order , we obtain the following system of equations for the zero-order approximation for the velocity and pressure :
with the boundary conditions:
The incompressibility condition yields:
We conclude from (7)–(9) that , , , and the solution of (7) and (8) is given in the form:
Plugging (10) into , we obtain the following equation:
Integrating the equation with respect to over and taking into account the boundary conditions , we obtain the Reynolds equation for :
endowed with the following boundary conditions:
where are chosen in order to satisfy the compatibility conditions for the boundary layer correctors and are given in the form (see Section 3.3):
The problem (12)–(14) is well posed due to the condition and assuming that is -periodic in and that vanishes in the neighborhood of and (see, e.g., [28,29]).
The microrotation zero-order approximation is given as the solution of the following problem:
We solve it by putting:
It is important to emphasize at this point that the expressions for the velocity given by (10) have been derived in [28,29] for a Newtonian fluid and, as expected, do not feel the effects of the microstructure of the fluid. Furthermore, the same effects are not present in the expressions for the microrotation given in explicit form (16). We thus continue our computations in order to capture those effects and try to compute the higher order correctors.
3.2.2. First-Order Corrector
Collecting the terms by , we obtain the system of equations for the first-order velocity and pressure corrector :
From the incompressibility equation , we obtain:
The solution of the problem (17) is given in the following form:
Comparing the above expressions for the velocity given by (19) with the ones derived in [28,29] for a Newtonian fluid, we notice that we have obtained the additional effects we were seeking in the computation of the first-order corrector. Namely, we observe the influence of the microstructure of the fluid on the fluid flow, explicitly acknowledged through the presence of the microrotation viscosity constant a in the derived expressions.
Now, plugging (19) into leads to the Reynolds equation for the first-order pressure corrector :
which can be rewritten as:
and endowed with the boundary conditions:
where are chosen in order to satisfy the compatibility conditions for the boundary layer correctors and are given in the form (see Section 3.3):
where:
for . The problem (20)–(24) is well posed due to the condition and assuming , are -periodic in and that the functions , vanish in the neighborhood of and (see, e.g., [28,29]).
The first-order microrotation corrector is the solution of the following problem:
leading to:
We observe that the first-order velocity and microrotation correctors and given in explicit form by (19) and (26) take into account the effects of the microstructure of the fluid through the presence of the microrotation viscosity coefficient a in the expressions.
We have thus completed the computations for the regular part of the expansion. Since we have not taken into account the conditions at the lower and upper part of the boundary in the derivation of the model, we need to construct the boundary layer correctors in order to acknowledge the boundary layer effects. This will be addressed in the following section.
3.3. Boundary Layer Correctors
We computed our asymptotic approximation in order to satisfy the boundary conditions at and given by , , and . However, the conditions at and given by and were not taken into account in the process, and as a result, the computed asymptotic approximation did not necessarily satisfy these conditions. For this reason, we needed to construct boundary layer correctors in the vicinity of and .
In the boundary layer near , we seek the expansion in the following form:
where and is the new dilated variable used to describe the fast changes of the solution in the boundary layer.
Near , we seek the expansion in the form:
where .
3.3.1. Zero-Order Approximation
The boundary layer approximation is the solution of the following system of equations:
posed in the infinite strip , where .
Integrating over , we obtain the compatibility condition:
leading to:
For every , the system (27) admits unique solutions exponentially decaying as (see, e.g., [32]).
The zero-order microrotation boundary layer approximation is given by:
For every , the system (28) admits unique solutions exponentially decaying as (see, e.g., [32]).
We treat the boundary layer on the opposite side in much the same way. The boundary layer zero-order approximations are defined on the infinite strip , where . The problem for is analogous to the one for , while the problem for is analogous to the one for . The well possedness and exponential decay are analogous as for and . The expression for is given in the form (14).
3.3.2. First-Order Corrector
The first-order velocity and pressure boundary layer corrector satisfies:
The compatibility condition for problem (29) is given in the following form:
leading to:
We now obtain:
and:
where the coefficients are given by (see [28,29]):
For every , the system (29) admits unique solutions
exponentially decaying as (see, e.g., [32]).
The first-order velocity and pressure boundary layer corrector at satisfies:
For every , the system (30) admits unique solutions exponentially decaying as (see, e.g., [32]).
Again, we treat the boundary layer on the opposite side in much the same way. The first-order boundary layer correctors are defined on , where . The problem for is analogous to the one for , while the problem for is analogous to the one for . The well possedness and exponential decay results are analogous as for and . The expression for is given in the form (23).
We have thus completed the derivation of our asymptotic solution, which we write down explicitly in the next section.
3.4. Asymptotic Solution
The asymptotic approximation of the original problem (1)–(3) is now given in the form:
where , , , and are given by (10), (16), (19), and (26), and are the solutions of the Reynolds problems (12)–(14) and (21)–(24), while , , , , , are the solutions of the problems (27), (28), (29), (30), and , , , , , are solutions of the analogous problems posed on the opposite side .
Although we have corrected the boundary layer effects by constructing the appropriate boundary layer correctors in Section 3.3, the residual in the divergence equation is not small enough to obtain satisfactory error estimates. In order to correct this, we construct the divergence corrector in the forthcoming section. In this manner, our overall estimate will be improved, which will be rigorously addressed in Section 4.
3.5. Divergence Corrector
In order to improve the accuracy of our approximation, we add the divergence corrector in the form , where:
Now, plugging the approximation given by:
into the divergence equation , we obtain:
Taking into account the relations (9), (18), , and the analogous divergence equation relations for the boundary layer correctors and at , Equation (32) reduces to:
where . Using a simple change of variables, we finally obtain from (33) the following estimate:
We now completed the derivation of our model. We constructed the formal part of the expansion, the boundary layer correctors at the lower and upper part of the boundary, and the divergence corrector. In the next section, we aim to justify the usage of the model derived in the present section rigorously. This will be achieved by providing the error estimates in suitable norms for the difference between the solution of our original problem and the constructed asymptotic approximation.
4. Justification of the Derived Model
In this section, we provide the rigorous justification of the derived lower dimensional model by estimating the difference between the solution of our original problem (1)–(3) and the computed asymptotic solution given by (31) via error estimates in suitable norms.
We first recall the following technical results proved in [28,29].
Lemma 1.
There exists a constant such that:
for any such that for .
Lemma 2.
There exists such that:
where , , η, for , for , and the identity holds:
and the estimate:
We now define as the solution of the problem:
where . We now obtain from (36) the following estimate:
where and
The main result of this section can be stated as follows:
Theorem 1.
Remark 1.
The estimates in the norm would be worthless because the domain is shrinking, implying for any bounded . For this reason, we express the error estimate in the rescaled norm .
Proof.
The asymptotic approximation satisfies the following system of equations:
where , , , and we denote:
Introducing the difference:
we deduce the following system of equations:
We obtain from Lemma 2 the existence of a function with the same trace as on satisfying the estimate:
We now multiply Equation by and integrate over to obtain:
We estimate the terms on the right-hand side of (43) using Poincaré’s inequality (35) and (39) and (42):
We now obtain from (43) and (44) the estimate:
leading to:
The problem satisfied by is given by the following system of equations:
where , , , , and we denote:
Denoting the differences:
we obtain the following system of equations:
We now multiply by and integrate over to obtain:
We handle the terms on the right-hand side of (47) using Poincaré’s inequality (35) and the estimate (39):
Taking into account (45), for sufficiently small , we obtain from (47) and (48):
Now, using the estimate (39), from (49), we get:
leading to:
From (45) and (49), we directly deduce:
Now, we obtain easily from (50) and (51) the estimates:
and:
yielding and .
Now, let be the solution of:
Assuming that , it follows from Lemma 2 that there exists at least one solution of the problem (52) satisfying the estimate:
Multiplying by , we obtain:
We estimate the right-hand side of (54) using Poincaré’s inequality (35) and the estimates (39), (49), (51), and (53) as follows:
We now obtain from (54) and (55):
Finally, we have from (56):
providing:
thus obtaining the estimate . □
We thus provided the rigorous justification of the model derived in Section 3 via error estimates in suitable norms. In the final section, we provide the main highlights and the contribution of our work, as well as possible further extensions of the research presented in this paper.
5. Conclusions
In this paper, using the methods of rigorous asymptotic analysis, we derived and justified the effective model describing the lubrication process of a rotating shaft with incompressible micropolar fluid. As we considered the lubrication process in a curved geometry naturally appearing in various real-life applications, our results were relevant in the modeling of lubrication devices consisting of a slipper bearing. These devices naturally appear in industrial machinery primarily including steam turbines, pumps, compressors, and motors. The computed asymptotic approximation given in the form of a powers series in terms of the small parameter , representing the thickness of the shaft, acknowledges the effects of the fluid’s internal structure through the presence of the microrotation viscosity a. We can verify this by looking at the derived explicit expressions (19) and (26) for the velocity and microrotation first-order correctors.
The main contribution of this paper is twofold. Firstly, in order to improve the accuracy of the derived asymptotic approximation (not necessarily satisfying the boundary conditions at the lower and upper boundary of the shaft), we constructed the boundary layer correctors for the velocity, pressure, and microrotation. Moreover, as the residual in the divergence equation was not small enough, to provide satisfactory error estimates, we also constructed the divergence corrector. In this way, our overall estimates were improved.
Secondly, the derived model was rigorously justified by proving the error estimates, evaluating the difference between the original solution of the problem and the derived asymptotic approximation in suitable norms. We strongly believe that the derived model could prove useful in industrial applications, in particular ones including the study of the optimal design of lubrication devices in the industrial machinery mentioned above.
Finally, it would be natural to consider the thermal effects on the lubrication process of a rotating shaft with micropolar fluid as a possible further extension of the research presented in this paper. More precisely, one can consider the thermodynamic closure of the problem (1)–(3) by adding the heat equation to the problem, namely:
where denotes the fluid temperature, while k is the thermal conductivity. Employing a similar asymptotic approach as here, it is reasonable to expect that one can derive and rigorously justify a lower dimensional model for the above-mentioned problem, allowing us to observe the thermal effects on the lubrication process clearly.
Another possibility for further research is to consider the lubrication process of a rotating shaft with a time-dependent micropolar fluid flow. The governing non-stationary micropolar fluid system of equations is given by (see, e.g., [6] and [27]):
Our goal in this case would be to derive an asymptotic model taking into account additional effects involving time. More precisely, we would need to obtain an asymptotic approximation where the effect of the time derivative would be explicitly acknowledged in the derived expressions.
This will be the subject of our future work.
Author Contributions
E.M.–P. (Supervision), I.P. (Methodology), M.R. (Formal Analysis). All authors have read and agreed to the published version of the manuscript.
Funding
Croatian Science Foundation (projects: AsAn, MultiFM).
Acknowledgments
The first and the third author of this work were supported by the Croatian Science Foundation (scientific project: Asymptotic analysis of boundary value problems in continuum mechanics (AsAn)). The second author of this work was supported by the Croatian Science Foundation (scientific project: Multiscale problems in fluid mechanics (MultiFM)). The authors would like to thank the referees for their helpful comments and suggestions that helped to improve the paper significantly.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Eringen, A.C. Theory of micropolar fluids. J. Math. Mech. 1966, 16, 1–18. [Google Scholar] [CrossRef]
- Abdullah, I.; Amin, N. A micropolar fluid model of blood flow through a tapered artery with a stenosis. Math. Methods Appl. Sci. 2010, 33, 1910–1923. [Google Scholar] [CrossRef]
- Ahmed, A.; Nadeem, S. Effects of magnetohydrodynamics and hybrid nanoparticles on a micropolar fluid with 6–types of stenosis. Results Phys. 2017, 7, 4130–4139. [Google Scholar] [CrossRef]
- Haghighi, A.R.; Shahbazi, M. Mathematical modeling of micropolar fluid flow through an overlapping arterial stenosis. Int. J. Biomath. 2015, 08, 1550056. [Google Scholar] [CrossRef]
- Maddah, S.; Navidbahksh, M.; Atefi, G. Continuous model for dispersion of discrete blood cells with an ALE formulation of pulsatile fluid flow in a flexible tube. J. Dispers. Sci. Technol. 2013, 34, 1165–1172. [Google Scholar] [CrossRef]
- Beneš, M.; Pažanin, I.; Radulović, M. Rigorous derivation of the asymptotic model describing a nonsteady micropolar fluid flow through a thin pipe. Comput. Math. Appl. 2018, 76, 2035–2060. [Google Scholar] [CrossRef]
- Boukrouche, M.; Paoli, L. Asymptotic analysis of a micropolar fluid flow in a thin domain with a free and rough boundary. SIAM J. Math. Anal. 2012, 44, 1211–1256. [Google Scholar] [CrossRef]
- Dupuy, D.; Panasenko, G.; Stavre, R. Asymptotic solution for a micropolar flow in a curvilinear channel. Z. FÜr Angew. Math. Und Mech. 2008, 88, 793–807. [Google Scholar] [CrossRef]
- Panasenko, G.; Pileckas, K. Asymptotic analysis of the nonsteady viscous flow with a given flow rate in a thin pipe. Appl. Anal. 2012, 91, 559–574. [Google Scholar] [CrossRef]
- Panasenko, G.; Pileckas, K. Asymptotic analysis of the non–steady Navier–Stokes equations in a tube structure I. The case without boundary–layer–in–time. Nonlinear Anal. 2015, 122, 125–168. [Google Scholar] [CrossRef]
- Panasenko, G.; Pileckas, K. Asymptotic analysis of the non–steady Navier–Stokes equations in a tube structure II. General case. Nonlinear Anal. 2015, 125, 582–607. [Google Scholar] [CrossRef]
- Lukaszewicz, G. Micropolar Fluids: Theory and Applications. Modeling and Simulation in Science, Engineering and Technology; Birkhäuser: Boston, MA, USA, 1999. [Google Scholar]
- Reynolds, O. On the theory of lubrication and its application to Beauchamp Tower’s Experiment. Philos. Trans. R. Soc. Lond. 1886, 177, 157–234. [Google Scholar]
- Capriz, G. On the vibrations of shaft rotating on lubricated bearings. Ann. Di Mat. Pura Ed Appl. 1960, 50, 223–248. [Google Scholar] [CrossRef]
- Elrod, H.G. A derivation of the basic equations for hydrodynamics lubrication with a fluid having constant properties. Q. Appl. Math. 1960, 17, 349–359. [Google Scholar] [CrossRef]
- Wannier, G.H. A contribution to the hydrodynamics of lubrication. Q. Appl. Math. 1950, 8, 1–31. [Google Scholar] [CrossRef]
- Bayada, G.; Chambat, M. The transition between the Stokes equations and the Reynolds equation: A mathematical proof. Appl. Math. Optim. 1986, 14, 73–93. [Google Scholar] [CrossRef]
- Cimatti, G. A rigorous justification of the Reynolds Equation. Q. Appl. Math. 1987, 45, 627–644. [Google Scholar] [CrossRef][Green Version]
- Bourgeat, A.; Mikelić, A.; Tapiéro, R. Dérivation des équations moyennées eécrivant un écoulement non Newtonien dans un domain de faible épaisseur. Comptes Rendus De L’AcadÉmie Des Sci. 1993, 316, 965–970. [Google Scholar]
- Assemien, A.; Bayada, G.; Chambat, M. Inertial Effects in the Asymptotic Behavior of a Thin Film Flow. Asymptot. Anal. 1994, 9, 177–208. [Google Scholar] [CrossRef]
- Bourgeat, A.; Marušić–Paloka, E. Loi d’écoulement non linéaire entre deux plaques ondulées. Comptes Rendus De L’AcadÉmie Des Sci. 1995, 321, 1115–1120. [Google Scholar]
- Bourgeat, A.; Marušić–Paloka, E. Nonlinear Effects for Flow in Periodically Constricted Channel Caused by High Injection Rate. Math. Model. Methods Appl. Sci. 1998, 08, 379–405. [Google Scholar] [CrossRef]
- Nazarov, S.A. Asymptotic solution to the Navier–Stokes problem on the flow of a thin layer of fluid. Sib. Math. J. 1990, 31, 296–307. [Google Scholar] [CrossRef]
- Marušić–Paloka, E. The effects of flexion and torsion on a fluid flow through a curved pipe. Appl. Math. Optim. 2001, 44, 245–272. [Google Scholar] [CrossRef]
- Pažanin, I. Effective flow of micropolar fluid through a thin or long pipe. Math. Probl. Eng. 2011, 2011, 127070. [Google Scholar] [CrossRef]
- Castineira, G.; Marušić–Paloka, E.; Pažanin, I.; Rodriguez, J.M. Rigorous justification of the asymptotic model describing a curved–pipe flow in a time–dependent domain. Z. Fur Angew. Math. Und Mech. 2019, 99, 1–39. [Google Scholar] [CrossRef]
- Pažanin, I.; Radulović, M. Asymptotic analysis of the nonsteady micropolar fluid flow through a curved pipe. Appl. Anal. 2018, 1–48. [Google Scholar] [CrossRef]
- Duvnjak, A.; Marušić–Paloka, E. Derivation of the Reynolds equation for lubrication of a rotating shaft. Arch. Math. 2000, 36, 239–253. [Google Scholar]
- Duvnjak, A.; Marušić-Paloka, E. Correctors for Reynolds equation describing the process of lubrication of a rotating shaft. In Trends in Applications of Mathematics to Mechanics; Loss, G., Gues, O., Nouri, A., Eds.; 2000; pp. 272–281. Available online: https://books.google.com.hk/books?hl=en&lr=&id=up1vdhnE90YC&oi=fnd&pg=PA272&dq=Correctors+for+Reynolds+equation+describing+the+process+of+lubrication+of+a+rotating+shaft&ots=mpLTiU0q74&sig=3Ht8V_E1AK_U5SAQGBNjbsh-_xk&redir_esc=y&hl=zh-CN&sourceid=cndr#v=onepage&q=Correctors%20for%20Reynolds%20equation%20describing%20the%20process%20of%20lubrication%20of%20a%20rotating%20shaft&f=false (accessed on 11 February 2020).
- Marušić–Paloka, E.; Pažanin, I.; Radulović, M. On the lubrication of a rotating shaft with incompressible micropolar fluid. Proc. Top. Probl. Fluid Mech. 2020, 2020, 1–8. [Google Scholar]
- Vats, P.; Sharma, B.C.; Sharma, S. Heat transfer through journal bearing: A case study. Int. J. Res. Eng. Techonol. 2016, 03, 1–6. [Google Scholar] [CrossRef]
- Galdi, G.P. An Introduction to the Mathematical Theory of the Navier–Stokes Equations, I, II; Springer: Berlin, Germany, 1994. [Google Scholar]
- Hughes, T.J.R.; Marsden, J.E. A Short Course in Fluid Mechanics; Publish or Perish: Boston, MA, USA, 1976. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).