Blind Audio Watermarking Based on Parametric Slant-Hadamard Transform and Hessenberg Decomposition
Abstract
1. Introduction
2. Related Research
3. Background Information
3.1. Parametric Slant-Hadamard Transform (PSHT)
3.2. Hesssenberg Decomposition (HD)
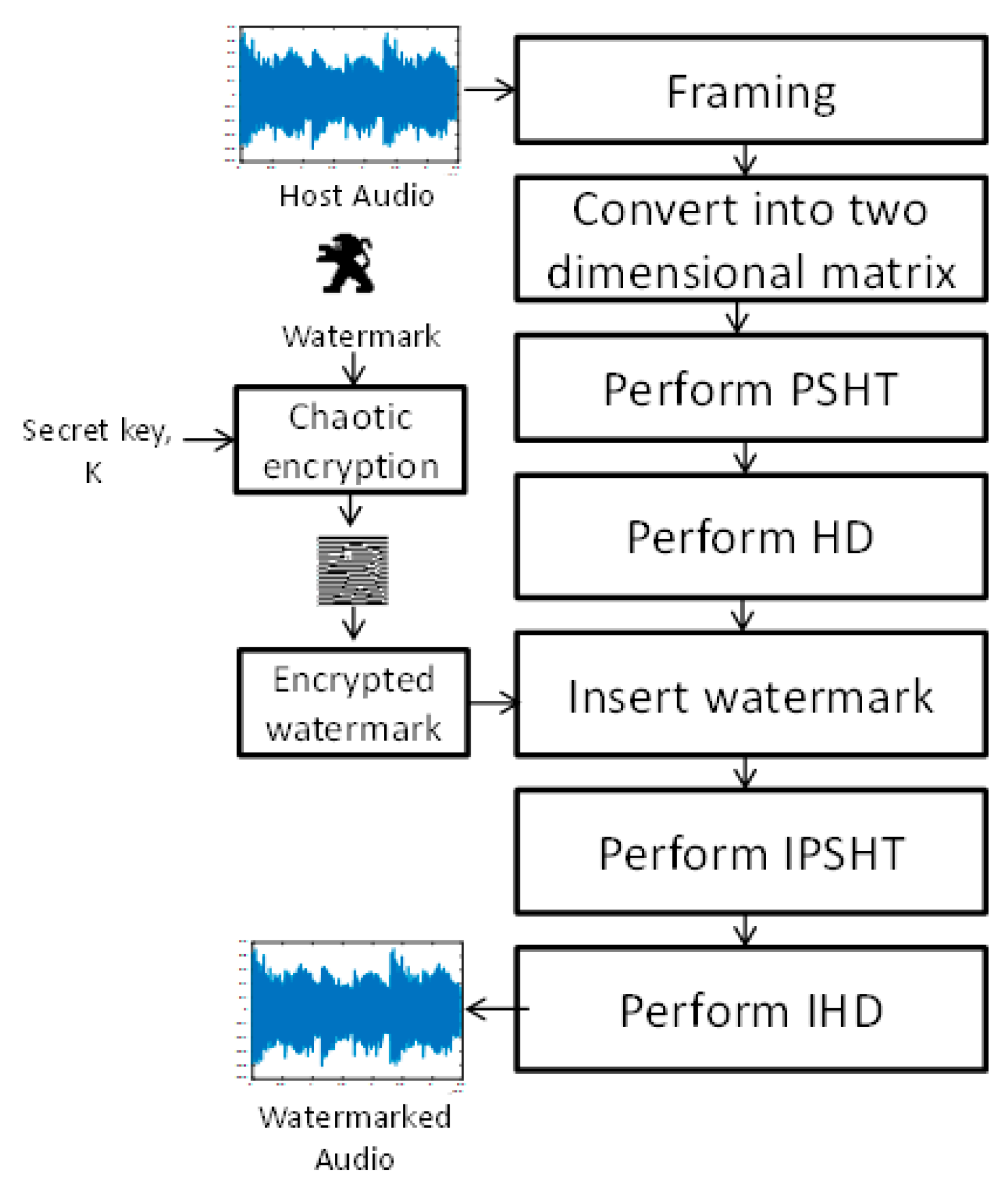
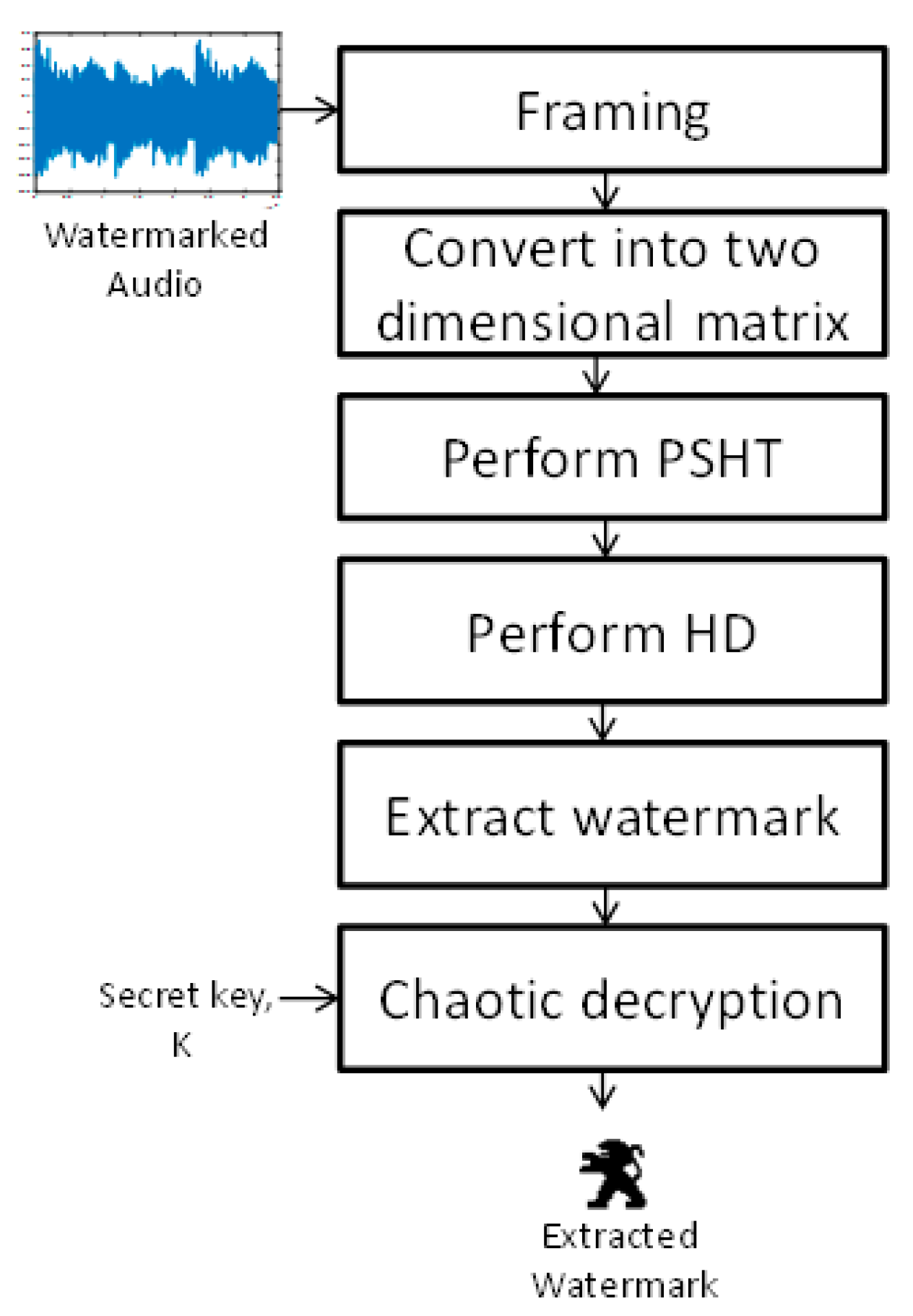
4. Proposed Watermarking Algorithm
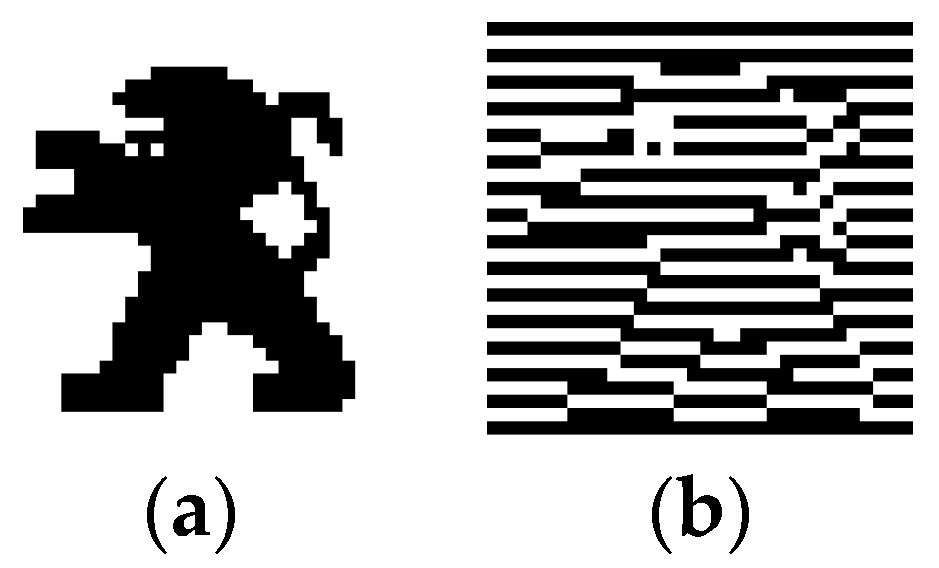
4.1. Watermark Preprocessing
| Algorithm 1: Watermark Preprocessing |
| Variable Declaration: |
| W (i = 1, 2, …., M; j = 1, 2, …., M): the watermark image |
| : logistic mapping parameter |
| a, b: real parameters |
| binary sequence |
| predefined threshold value |
| new one dimensional sequence from Wi |
| encrypted watermark sequence |
| Watermark Preprocessing Procedure: |
| Let (1)∈ (0,1) |
| for i = 1: M do |
| calculate using Equation (7) |
| calculate using Equation (8) |
| calculate using Equation (9) |
| end for |
| return encrypted watermark sequence |
4.2. Watermark Embedding Process
| Algorithm 2: Watermark Embedding |
| Variable Declaration: |
| Y: host audio signal |
| F: segmented non-overlapping frame |
| frame represented in dimensional matrix with size m×m |
| transformed matrix |
| non-overlapping bloc |
| sum of absolute mean of the block |
| : block with maximum sum of absolute mean |
| : Hessenberg matrix |
| : the 2nd order Euclidean normalization |
| : quantization coefficient for embedding |
| Watermark Embedding Procedure: |
| for i = 1: do |
| convert the frame coefficients into two dimensional matrix |
| apply PSHT on to obtain |
| for j = 1: N do |
| subdividing into non-overlapping block |
| calculate the sum of absolute mean of each block using Equation (10) |
| end for |
| select block with maximum sum of absolute mean |
| apply HD on matrix using Equation (11) |
| calculate using Equation (12) |
| calculate and |
| update into using Equations (13) and (14) |
| modify the largest Hessenberg coefficient using Equation (15) |
| apply inverse HD on matrix using Equation (16) |
| apply inverse PSHT on |
| reshape properly |
| reshape properly. |
| end for |
| return watermarked audio |
4.3. Watermark Extraction Process
| Algorithm 3: Watermark Extraction |
| Variable Declaration: |
| : attacked watermarked audio signal |
| F: attacked watermarked frame |
| watermarkedframe represented in two dimensional matrix with size m×m |
| modified transformed matrix |
| modified non-overlapping block |
| sum of absolute mean of modified the block |
| : modified block with maximum sum of absolute mean |
| : modified Hessenberg matrix : modified the 2ndorder |
| Euclidean normalization |
| : quantization coefficientfor extraction |
| Watermark Extraction Procedure: |
| for i = 1: do |
| convert the coefficients of the frame into two dimensional matrix |
| apply PSHT on to obtain |
| for j = 1: N do |
| subdividing into non-overlapping block |
| calculate the sum of absolute mean of each block |
| end for |
| select block with maximum sum of absolute mean |
| apply HD on matrix |
| calculate |
| calculate and |
| calculate using the Equation (17) |
| calculate using the Equation (18) |
| reshape |
| end for |
| return watermark |
5. Experimental Results and Discussion
5.1. Imperceptibility Analysis
5.1.1. Subjective Analysis
5.1.2. Objective Analysis
5.2. Robustness Analysis
- Noise addition: Additive white Gaussian noise (AWGN) was added with a watermarked signal until the signal had an SNR of 20 dB.
- Cropping: A number of 1000 samples of the watermarked audio were removed from different positions, and then, these samples were replaced with the watermarked audio signal attacked by additive white Gaussian noise.
- Re-sampling: The watermarked signal with a sample rate of 44.1 kHz was sampled to 22.05 kHz and again resampled by a rate of 44.1 kHz.
- Re-quantization: The watermarked audio was quantized from 16 bit to 8 bit.
- Compression: The watermarked signal was compressed using MPEG-1 layer 3 compression (128 kbps).
- Noise Reduction: Noise reduction was successfully done from the watermarked audio with the help of “Hiss removal” function.
- Echo addition: Echo signal containing a delay time of 150 ms and decay rate of 35% was applied to the watermarked signal.
- Distortion: The watermarked audio signal was distorted within a range of 0 dB to −10 dB.
- Amplification: The watermarked audio was amplified (enlarged) by 1.25 times of its original amplitude.
- Delay: A delay time of 150 ms was used and the volume of the delayed signal contains 3% of the original signal.
- Invert: The watermarked audio signal was fully inverted to obtain the inverted form of the actual watermark signal.
- Low-Pass Filter: A low-pass filter with a cut-off frequency of 15,000 Hz was applied to the watermarked audio.
5.3. Data Payload
5.4. Security Analysis
5.5. Computation Time Analysis
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Xiang, Y.; Hua, G.; Yan, B. Digital Audio Watermarking: Fundamentals, Techniques and Challenges; Springer: Singapore, 2017. [Google Scholar]
- Cvejic, N. Digital Audio Watermarking Techniques and Technologies: Applications and Benchmarks; IGI Global: Hershey, PA, USA, 2007. [Google Scholar]
- Pandey, M.K.; Parmar, G.; Gupta, R. Audio watermarking by spreading echo in time domainusing pseudo noise gray sequence. In Proceedings of the IEEE International Conference on Industrial Instrumentation and Control (ICIC), Pune, India, 28–30 May 2015; pp. 740–743. [Google Scholar]
- Kaur, A.; Dutta, M.K.; Soni, K.M.; Taneja, N. Localized & self-adaptive audio watermarking algorithm in the wavelet domain. J. Inf. Secur. Appl. 2017, 33, 1–15. [Google Scholar]
- Tsai, S.E.; Yang, S.M. An effective watermarking method based on energy averaging in audio signals. Math. Probl. Eng. 2018, 2018, 6420314. [Google Scholar] [CrossRef]
- Pourhashemi, S.M.; Mosleh, M.; Erfani, Y. Audio watermarking based on synergy between Lucas regular sequence and Fast Fourier Transform. Multimed. Tools Appl. 2019, 78, 22883–22908. [Google Scholar] [CrossRef]
- Dhar, P.K.; Shimamura, T. Blind audio watermarking in transform domain based on singular value decomposition and exponential-log operations. Radioengineering 2017, 26, 552–561. [Google Scholar] [CrossRef]
- Karnjana, J.; Unoki, M.; Aimmanee, P.; Wutiwiwatchai, C. Audio watermarking scheme based on singular spectrum analysis and psychoacoustic model with self-synchronization. J. Electr. Comput. Eng. 2016, 2016, 5067313. [Google Scholar] [CrossRef]
- Liu, H.; Liu, X.; Shi, B.; Chen, T.; Wang, J. Multifunctional audio watermarking algorithm based on Chaotic Scrambling. J. Comput. Methods Sci. Eng. 2017, 17, 443–454. [Google Scholar] [CrossRef]
- Dhar, P.K.; Shimamura, T. Blind SVD-based audio watermarking using entropy and log-polar transformation. J. Inf. Secur. Appl. 2015, 20, 74–83. [Google Scholar] [CrossRef]
- Hwang, M.J.; Lee, J.; Lee, M.; Kang, H.G. SVD-based adaptive QIM watermarking on stereo audio signals. IEEE Trans. Multimed. 2018, 20, 45–54. [Google Scholar] [CrossRef]
- Luo, Y.; Peng, D.; Sang, Y.; Xiang, Y. Dual-domain audio watermarking algorithm based on flexible segmentation and adaptive embedding. IEEE Access 2019, 7, 10533–10545. [Google Scholar] [CrossRef]
- Hu, H.T.; Lee, T.T. High-performance self-synchronous blind audio watermarking in a unified FFT framework. IEEE Access 2019, 7, 19063–19076. [Google Scholar] [CrossRef]
- Choudhary, S.; Nath, K.; Panda, J. Double layered audio zero-watermarking using DWT and DSSS. In Proceedings of the International Conference on Communication and Signal Processing (ICCSP), Chennai, India, 6–8 April 2017; pp. 0419–0423. [Google Scholar]
- Irawati, I.D.; Budiman, G.; Ramdhani, F. QR-based watermarking in audio subband using DCT. In Proceedings of the International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC), Bandung, Indonesia, 5–7 December 2018; pp. 136–141. [Google Scholar]
- Gupta, A.K.; Agarwal, A.; Singh, A.; Vimal, D.; Kumar, D. Blind audio watermarking using adaptive quantization and Lifting wavelet transform. In Proceedings of the IEEE 5th International Conference on Signal Processing and Integrated Networks (SPIN), Noida, India, 22–23 February 2018; pp. 556–559. [Google Scholar]
- Weina, W. Digital audio blind watermarking algorithm based on audio characteristic and scrambling encryption. In Proceedings of the IEEE 2nd Advanced Information Technology, Electronic and Automation Control Conference (IAEAC), Chongqing, China, 25–26 March 2017; pp. 1195–1199. [Google Scholar]
- Tang, X.; Ma, Z.; Niu, X.; Yang, Y. Robust audio watermarking algorithm based on empirical mode decomposition. Chin. J. Electron. 2016, 25, 1005–1010. [Google Scholar] [CrossRef]
- Safitri, I.; Ginanjar, R.R.; Rizal, A. Adaptive multilevel wavelet BCH code method in the audio watermarking system. In Proceedings of the IEEE International Conference on Control, Electronics, Renewable Energy and Communications (ICCREC), Yogyakarta, Indonesia, 26–28 September 2017; pp. 55–59. [Google Scholar]
- Sulistyawan, V.N.; Budiman, G.; Safitri, I. Histogram-based audio watermarking with synchronization in stationary audio subband. In Proceedings of the IEEE International Conference on Control, Electronics, Renewable Energy and Communications (ICCEREC), Bandung, Indonesia, 5–7 December 2018; pp. 195–201. [Google Scholar]
- Sakai, H.; Iwaki, M. Audio watermarking method based on phase-shifting having robustness against band-pass filtering attacks. In Proceedings of the IEEE 7th Global Conference on Consumer Electronics (GCCE), Nara, Japan, 9–12 October 2018; pp. 343–346. [Google Scholar]
- Agaian, S.; Tourshan, K.; Noonan, J.P. Parametric Slant-Hadamard transforms with applications. IEEE Signal Process. Lett. 2002, 9, 375–377. [Google Scholar] [CrossRef]
- Seddik, H.; Sayadi, M.; Fnaiech, F.; Cheriet, M. Image watermarking based on the Hessenberg transform. Int. J. Image Graph. 2009, 9, 411–433. [Google Scholar] [CrossRef]


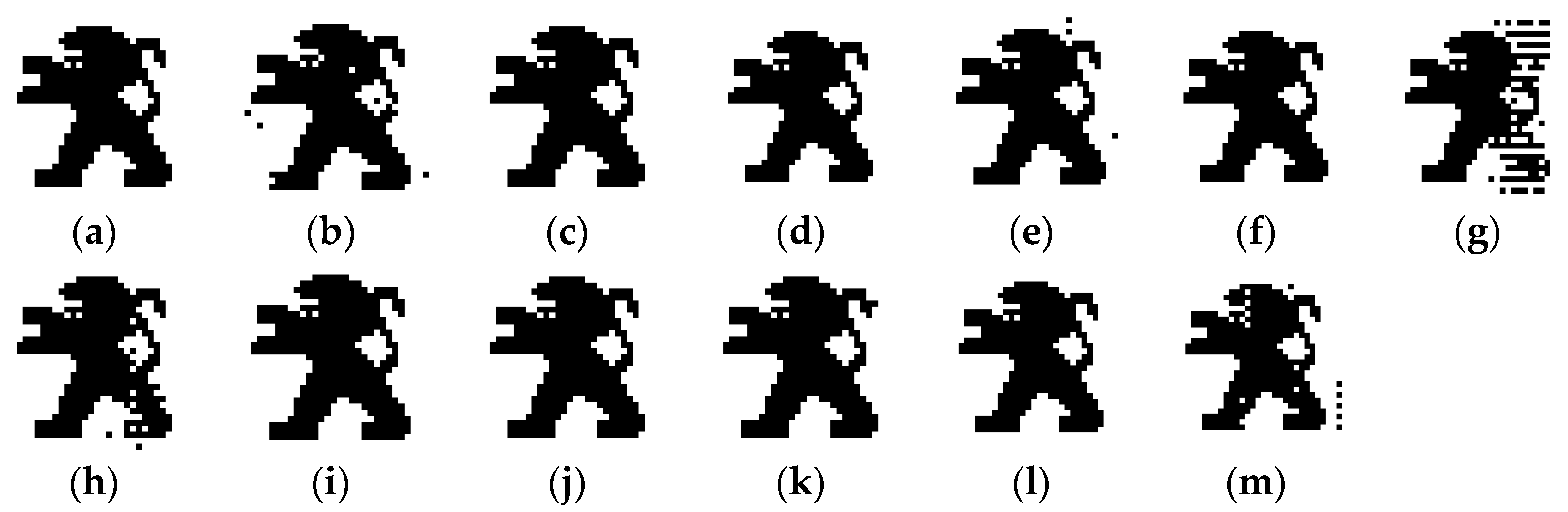


| SDG | ODG | Description | Quality |
|---|---|---|---|
| 5 | 0 | Imperceptible | Excellent |
| 4 | −1 | Perceptible, but not annoying | Good |
| 3 | −2 | Slightly annoying | Fair |
| 2 | −3 | Annoying | Poor |
| 1 | −4 | Very annoying | Bad |
| Audio Signal | MOS | Correct Detection | SNR | ODG |
|---|---|---|---|---|
| Pop | 4.90 | 54% | 43.81 | −0.46 |
| Classical | 5.00 | 48% | 47.75 | −0.35 |
| Jazz | 5.00 | 48% | 47.08 | −0.37 |
| Rock | 4.90 | 54% | 47.60 | −0.38 |
| Average | 4.95 | 51% | 46.56 | −0.39 |
| Reference | Method | SNR | MOS |
|---|---|---|---|
| [4] | Energy averaging | 41.47 | - |
| [5] | Localized and self-adaptive algorithm | 31.40 | 3.7 |
| [6] | LRS-FFT | 44.81 | - |
| [7] | DCT-SVD-ELO | 33.47 | 4.88 |
| [8] | SSA-PM | 25.61 | - |
| [9] | Multifunctional algorithm | 23.33 | - |
| [10] | DCT-SVD-LPT | 37.20 | 4.85 |
| [11] | SVD-QIM | 19.39 | - |
| [12] | FS-AE | 33.6 | - |
| Proposed | PSHT-HD | 46.56 | 4.95 |
| Attack | Pop | Classical | Jazz | Rock |
|---|---|---|---|---|
| No attack | 1 | 1 | 1 | 1 |
| Noise Addition | 0.9986 | 0.9995 | 0.9911 | 1 |
| Noise Reduction | 1 | 1 | 1 | 1 |
| Echo Addition | 1 | 1 | 1 | 1 |
| Cropping | 0.9978 | 0.9977 | 0.9988 | 0.9982 |
| Re-quantization | 0.9968 | 1 | 0.9992 | 1 |
| Compression (MP3) | 0.9566 | 0.9459 | 0.9619 | 0.9643 |
| Re-sampling | 0.9836 | 1 | 0.9943 | 0.9893 |
| Distortion | 0.9766 | 1 | 0.9895 | 0.9992 |
| Amplification | 0.9944 | 1 | 0.9871 | 1 |
| Delay | 0.9944 | 0.9976 | 0.9895 | 1 |
| Invert | 1 | 1 | 1 | 1 |
| Low-Pass Filtering | 0.9649 | 0.9871 | 0.9822 | 0.9919 |
| Attack | Pop | Classical | Jazz | Rock |
|---|---|---|---|---|
| No attack | 0 | 0 | 0 | 0 |
| Noise Addition | 0.37 | 0.88 | 1.07 | 0 |
| Noise Reduction | 0 | 0 | 0 | 0 |
| Echo Addition | 0 | 0 | 0 | 0 |
| Cropping | 0.24 | 0.026 | 0.14 | 0.20 |
| Re-quantization | 0.39 | 0 | 0.09 | 0 |
| Compression (MP3) | 5.18 | 6.54 | 4.59 | 4.30 |
| Re-sampling | 1.67 | 0 | 0.68 | 0.88 |
| Distortion | 2.83 | 0 | 1.27 | 0.09 |
| Amplification | 0.68 | 0 | 1.56 | 0 |
| Delay | 0.49 | 0.29 | 1.27 | 0 |
| Invert | 0 | 0 | 0 | 0 |
| Low-Pass Filtering | 4.54 | 1.56 | 2.15 | 0.98 |
| Reference | Method | Noise Addition | Resampling | Re-Quantization | MP3 Compression |
|---|---|---|---|---|---|
| Proposed | PSHT-HD | 0.58(20 dB) | 0.81(22.05 kHz) | 0.12 (8 Bits/Sample) | 5.15(128 kbps) |
| [4] | Energy averaging | - | 8.0(22.05 kHz) | - | 5.0(128 kbps) |
| [5] | Localized and self-adaptive algorithm | 6.03(30 dB) | 0(22.05 kHz) | 0.14(8 bits/sample) | 6.20(64 kbps) |
| [6] | LRS-FFT | 5.17(-) | 6.56(22.05 kHz) | 4.94(8 bits/sample) | 6.88(128 kbps) |
| [7] | DCT-SVD-ELO | 0.91(-) | 0.88(22.05 kHz) | 0.23(8 bits/sample) | 6.13 (32 kbps) |
| [8] | SSA-PM | 2.50(36 dB) | 6.06(22.05 kHz) | 8.83(16 bits/sample) | 9.44(128 kbps) |
| [9] | Multifunctional algorithm | 4.22(-) | 0(22.05 kHz) | - | 7.48(32 kbps) |
| [10] | DCT-SVD-LPT | 0.83(-) | 1.56(22.05 kHz) | 0(8 bits/sample) | 3.91(128 kbps) |
| [11] | SVD-QIM | 10.25(30 dB) | 4.88(16 kHz) | - | 17.76(128 kbps) |
| [12] | FS-AE | 7.23(20 dB) | - | - | 6.04(48 kbps) |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dhar, P.K.; Chowdhury, A.H.; Koshiba, T. Blind Audio Watermarking Based on Parametric Slant-Hadamard Transform and Hessenberg Decomposition. Symmetry 2020, 12, 333. https://doi.org/10.3390/sym12030333
Dhar PK, Chowdhury AH, Koshiba T. Blind Audio Watermarking Based on Parametric Slant-Hadamard Transform and Hessenberg Decomposition. Symmetry. 2020; 12(3):333. https://doi.org/10.3390/sym12030333
Chicago/Turabian StyleDhar, Pranab Kumar, Azizul Hakim Chowdhury, and Takeshi Koshiba. 2020. "Blind Audio Watermarking Based on Parametric Slant-Hadamard Transform and Hessenberg Decomposition" Symmetry 12, no. 3: 333. https://doi.org/10.3390/sym12030333
APA StyleDhar, P. K., Chowdhury, A. H., & Koshiba, T. (2020). Blind Audio Watermarking Based on Parametric Slant-Hadamard Transform and Hessenberg Decomposition. Symmetry, 12(3), 333. https://doi.org/10.3390/sym12030333






