A Systematic Literature Review on Outlier Detection in Wireless Sensor Networks

Abstract

A wireless sensor network (WSN) is defined as a set of spatially distributed and interconnected sensor nodes. WSNs allow one to monitor and recognize environmental phenomena such as soil moisture, air pollution, and health data. Because of the very limited resources available in sensors, the collected data from WSNs are often characterized as unreliable or uncertain. However, applications using WSNs demand precise readings, and uncertainty in data reading can cause serious damage (e.g., health monitoring data). Therefore, an efficient local/distributed data processing algorithm is needed to ensure: (1) the extraction of precise and reliable values from noisy readings; (2) the detection of anomalies from data reported by sensors; and (3) the identification of outlier sensors in a WSN. Several works have been conducted to achieve these objectives using several techniques such as machine learning algorithms, mathematical modeling, and clustering. The purpose of this paper is to conduct a systematic literature review to report the available works on outlier and anomaly detection in WSNs. The paper highlights works conducted from January 2004 to October 2018. A total of 3520 papers are reviewed in the initial search process. Later, these papers are filtered by title, abstract, and contents, and a total of 117 papers are selected. These papers are examined to answer the defined research questions. The current paper presents an improved taxonomy of outlier detection techniques. This will help researchers and practitioners to find the most relevant and recent studies related to outlier detection in WSNs. Finally, the paper identifies existing gaps that future studies can fill.

1. Introduction

The wireless sensor network (WSN) consists of a set of distributed and interconnected sensors located in a target area. It aims to monitor and recognize environmental phenomena such as soil moisture, air pollution, and health data [1]. Low-cost devices and easy-to-deploy sensor nodes have found a variety of applications in positioning and tracking [2], health care [3], environmental monitoring [4], etc.

Figure 1 shows some WSN applications in different fields.

However, there are still many critical challenges that need to be tackled via reliable technology. Usually, sensors are deployed in harsh environments with an unattended operation, which may lead to the sensor or network failures. Therefore, it is important for sensors to have not only a fault tolerance system but also the ability to do self-calibrating, self-recovering, self-repairing, and self-testing. In some scenarios such as health applications, it is important to have accurate data collection in the network. Data reliability in sensor networks is the area of focus for many applications.

Usually, data retrieved from WSNs have low reliability due to missing values, inconsistent or duplicate data, errors, noise, and malicious attacks. Low-quality sensors may compromise memory, battery functionality, communication efficacy, and computation ability, thus leading to inaccurate WSN sensory data [5]. Sensor nodes are vulnerable to the effects of the environment as well. A WSN with high density employs hundreds or thousands of sensor nodes within a setting, which may eventually result in malfunction nodes, leading to inaccurate and insufficient data. These nodes are susceptible to malevolent attacks such as eavesdropping, black holes, and denial of service (DoS) [6].

In the field of WSNs, measurements that significantly differ from the normal pattern of sensed data are declared as outliers [7]. The potential causes of outliers are noise and errors, events, and malicious attacks. Outlier detection in WSNs is the process of identifying data instances that deviate from the rest of the data patterns based on certain measurements [8].

Outliers can occur for different reasons, and understanding their source helps to decide what actions to take after detecting them [9]. Many studies have investigated abnormal data detection under various terms such as anomaly detection, fraud detection, and outlier detection [10]. In the WSN context, the outlier also is defined as an anomaly or divergence which is unusual behavior in comparison with the majority of sensory data as indicated in Figure 2. The outlier data can be classified into two main classes, including single and batch outlier data. An outlier is single when data are far from a group of sensory data, whereas batch outliers are bulk data points that continuously occurred over a period. According to the related literature, there are no general definitions of outliers or anomalies. Therefore, in

Table 1. Outlier detection definitions from previous studies.

Reference	Definition
[11]	“A process to identify data points that are very different from the rest of the data based on a certain measure.”
[12]	“An observation which deviates so much from the other observations as to arouse suspicions that it was generated by a different mechanism.”
[13]	“An observation that deviates a lot from other observations and can be generated by a different mechanism.”
[14]	“An outlier is an observation or subset of observations that appears to be inconsistent with the rest of the set of data.”
[15]	“An outlier is a data point which is significantly different from other data points, or does not conform to the expected normal behavior, or conforms well to a defined abnormal behavior.”
[16]	“A spatial-temporal point, which non-spatial attribute values are significantly different from those of other spatially and temporally referenced points in its spatial or/and temporal neighborhoods, is considered as a spatial-temporal outlier.”
[17]	“A point is considered to be an outlier if, in some lower-dimensional projection, it is present in a local region of abnormal low density.”
[18]	“If the removal of a point from the time sequence results in a sequence that can be represented more briefly than the original one, then the point is an outlier.”
[19]	“Outliers are points that do not belong to clusters of a dataset or clusters that are significantly smaller than other clusters.”
[15]	“Outliers are points that lie in the lower local density with respect to the density of their local neighborhoods.”

, this study shows a set of common definitions of anomalies and outliers proposed by several researchers.

As shown in Figure 3, several sources for outliers have been categorised as follows: noise or error, events, and malicious attacks [20]. An event-based sensor network sends information to the base station after an event occurs in the network. Query and data-driven methods are different from event detection. In query and data-driven methods, sensor nodes reply to queries issued by sink nodes.

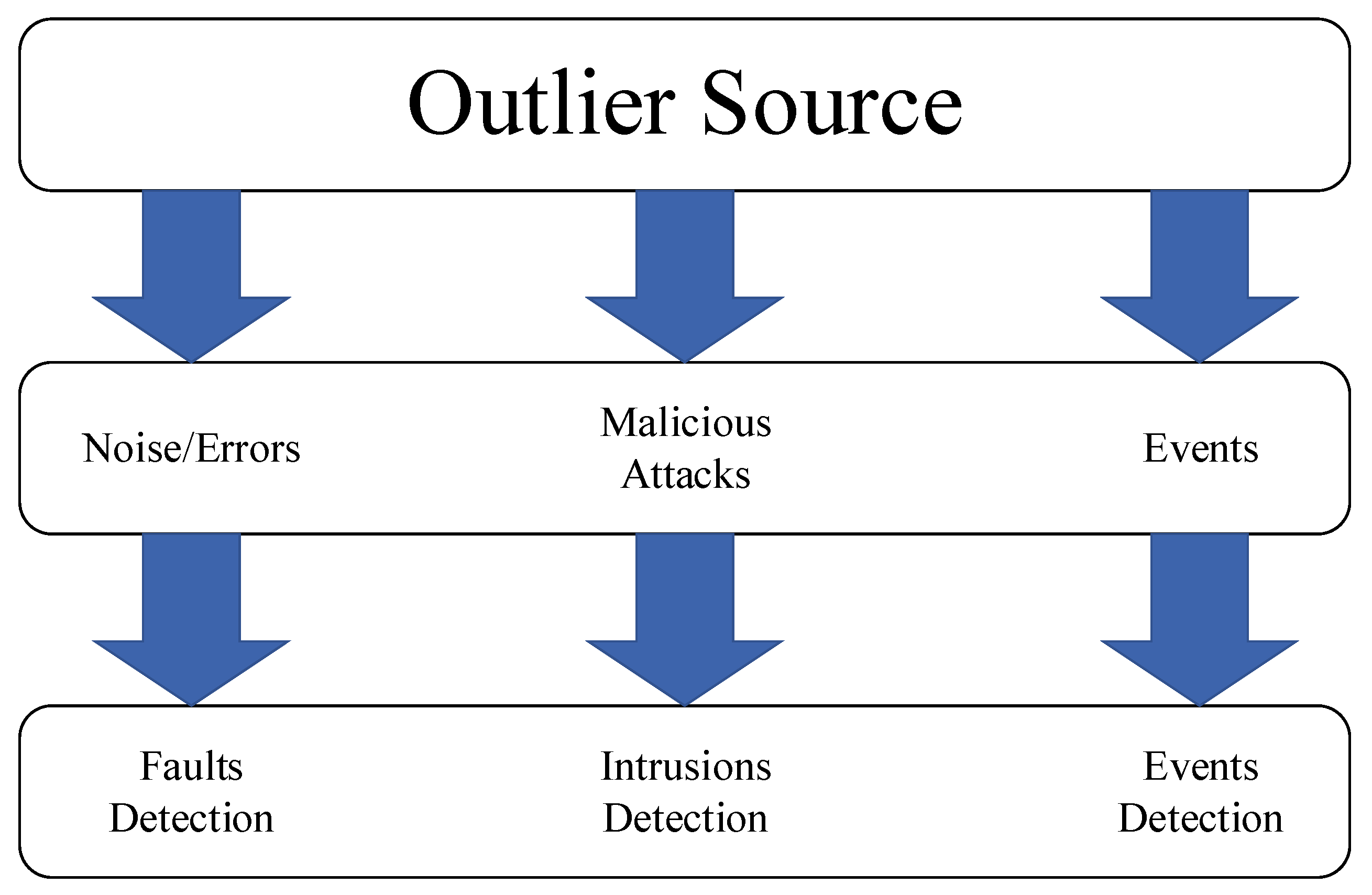
• An event-based network is different from a monitoring sensor network. Some typical event examples are earthquake monitoring, flood, volcanic eruption alarm, rainfall and flood detection, weather changes, chemical hazardous alert, air pollution, air quality monitoring, and fireplace detection. In mutuality with inaccurate data, outliers generated by events tend to have an especially smaller probability of incidence [21]. Deleting the outlier event from the dataset can cause loss of necessary and important data from relevant events [22]. Several techniques are proposed for event detection such as [23,24,25].
• Noise or error that is based on noise in measurement may occur because of several sources, like a sensor fault or sensor misbehavior [20]. Faulty data are ordinarily described as a modification in the dataset that is disparate from the rest of the data. Error or noise can result in several changes associated with the environment, including harshness and the difficulties of the preparation areas. If possible, faulty data, as well as noisy data, must be corrected or deleted [20].
• Malicious attacks are associated with the security of the network. Outliers based on malicious attacks begin with a sensor node that is compromised by the attacker and the injection of unreliable or corrupt data into the network topology. Malicious attacks are classified into passive and active attacks. A passive attack changes sensory data with the aim of interrupting the decision-making system of the network [20], whereas an active attack has an effect on network functionality and performance. This attack can slow or even shut down the network [26].

Usually, identifying outliers amongst a vast data are a difficult task [27]. The two primary challenges in detecting outliers within WSNs are ensuring less resource consumption and achieving high accuracy. These challenges should be overcame to ensure the accuracy and the reliability of data retrieved from sensors for further processes [27].

This paper presents a detailed overview of techniques that are dedicated to detecting outliers in WSNs, compares existing methods, and discusses future research prospects. Although some works have used prior studies’ outcomes to assess the present state of the work in this area, no work has been conducted to systematically synthesize and review outlier detection in WSNs. Therefore, this study systematically collects, analyzes, and synthesizes all papers linked with outlier detection in WSNs in order to highlight emerging methods, themes, taxonomies, and datasets. This paper presents a systematic literature review (SLR) conducted on a large pool of papers proposing anomaly detection techniques across several research parts and domain applications. 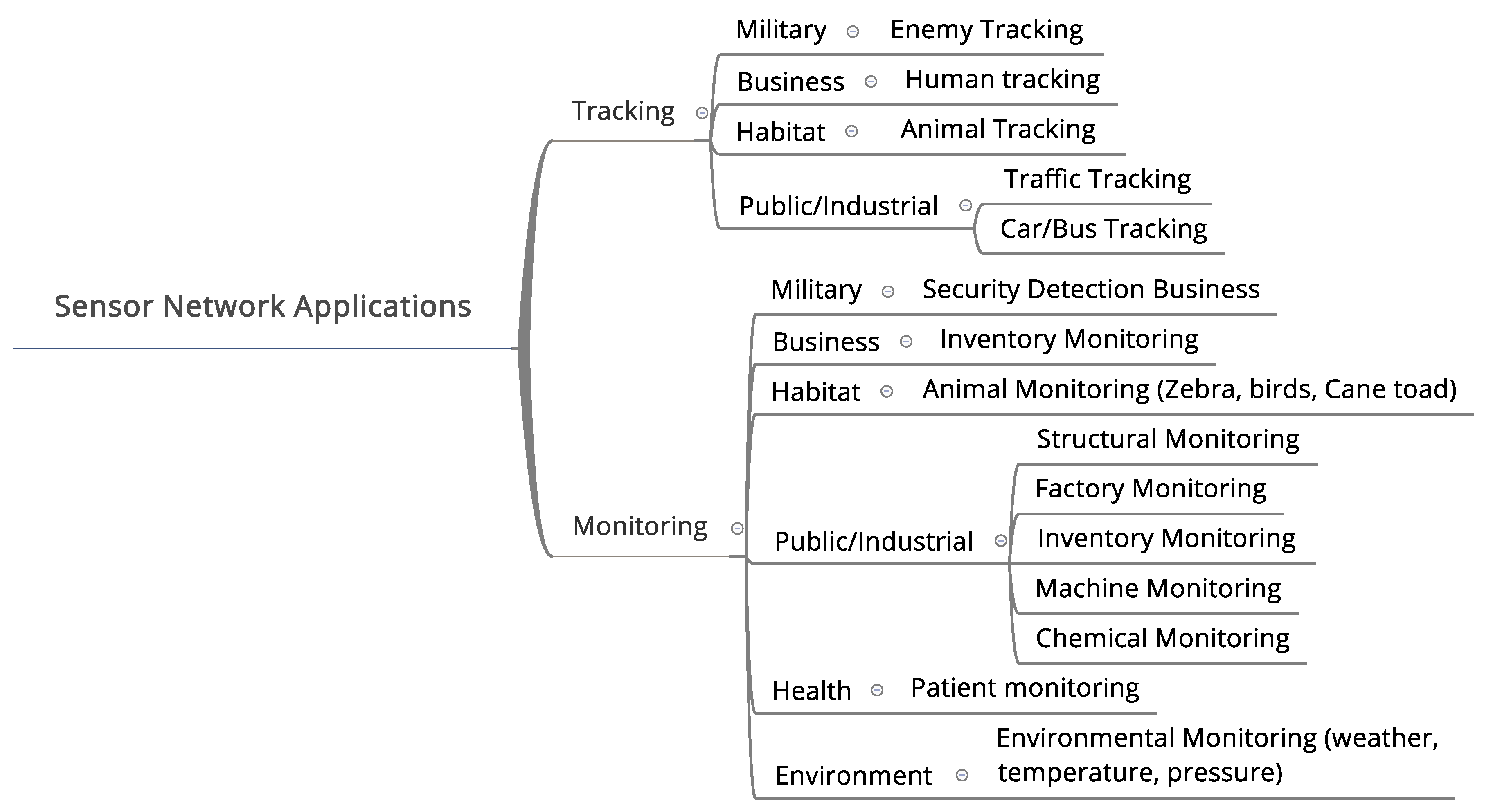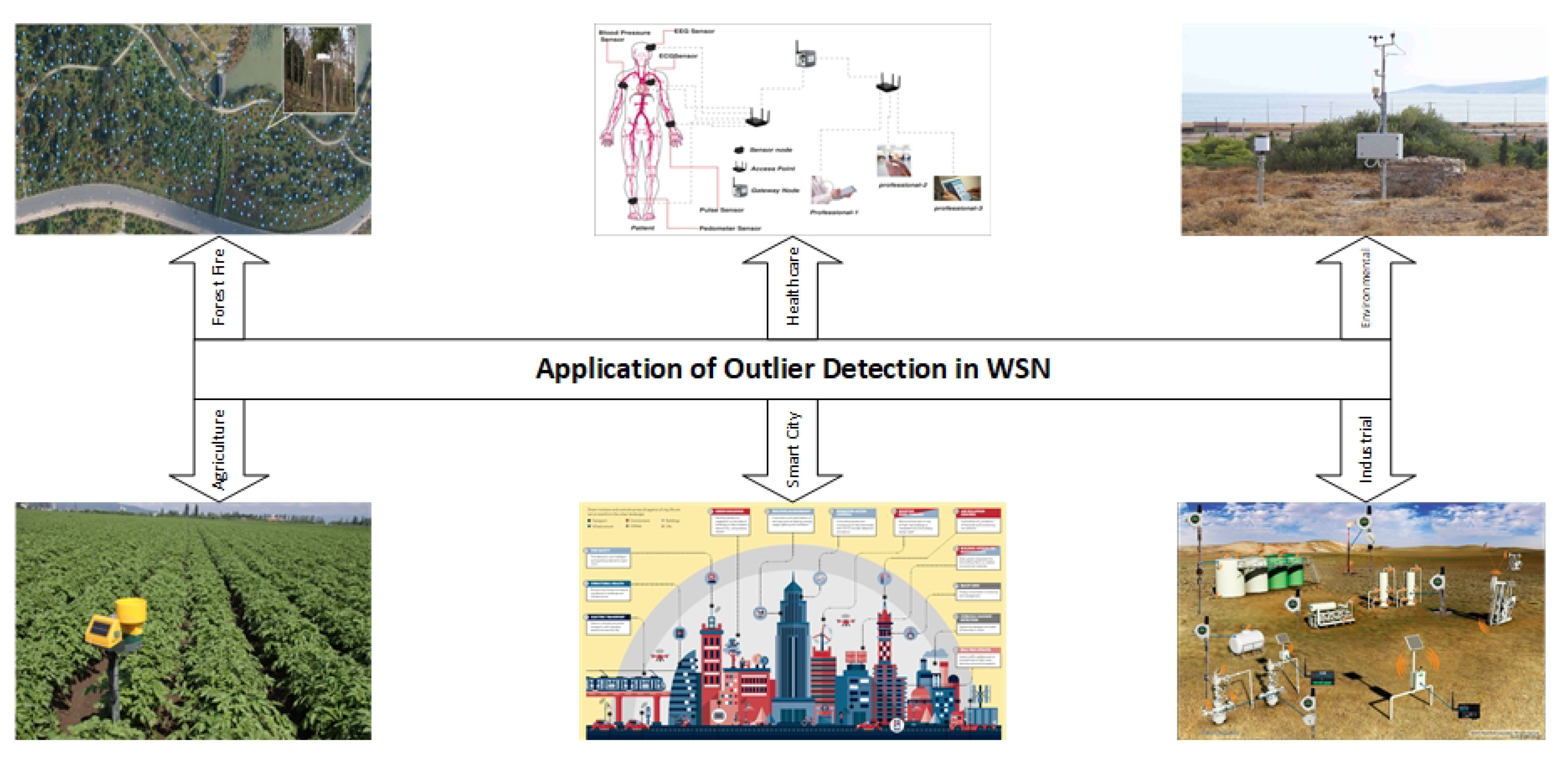The remainder of this study is organized as follows: Section 2 describes applications of outlier detection in WSN. Section 3 illustrates the methodology that is employed in this study, whereas Section 4 discusses the planning review, and Section 5 explains how the review was conducted. Next, Section 6 provides answers to research questions (RQ), and Section 7 compares methods for detecting outliers. Finally, the study is concluded in Section 9.

2. Application of Outlier Detection in WSNs

Anomaly or outlier detection is a main function of the data mining procedure, as illustrated in Figure 4. Outlier detection can help in preventing malicious attacks and identifying sensors with outlier data to provide reliable data for decision-makers. Many lifetime and real-time applications use outlier detection:

• Environmental monitoring: Many sensors such as temperature, humidity, air pollution, and wind speed sensors are deployed in harsh environments to monitor and analyze environmental factors.
• Industrial monitoring: Sensors such as vibration, pressure, or temperature sensors are installed on sensitive equipment to monitor the state of this equipment.
• Healthcare monitoring: Small sensors are used to monitor patients’ vital state. These sensors are implemented in the patient’s body in different positions to monitor blood pressure, heart rate, or enzymes and minerals.
• Smart cities: Different kinds of sensors such as parking sensors, dustbin sensors, and pedestrian sensors are used to make cities more comfortable for citizens.
• Forest fire detection: Forests are monitored to prevent fires using a variety of sensor nodes. Thousands of them are deployed in the target area to predict and prevent forest fires.

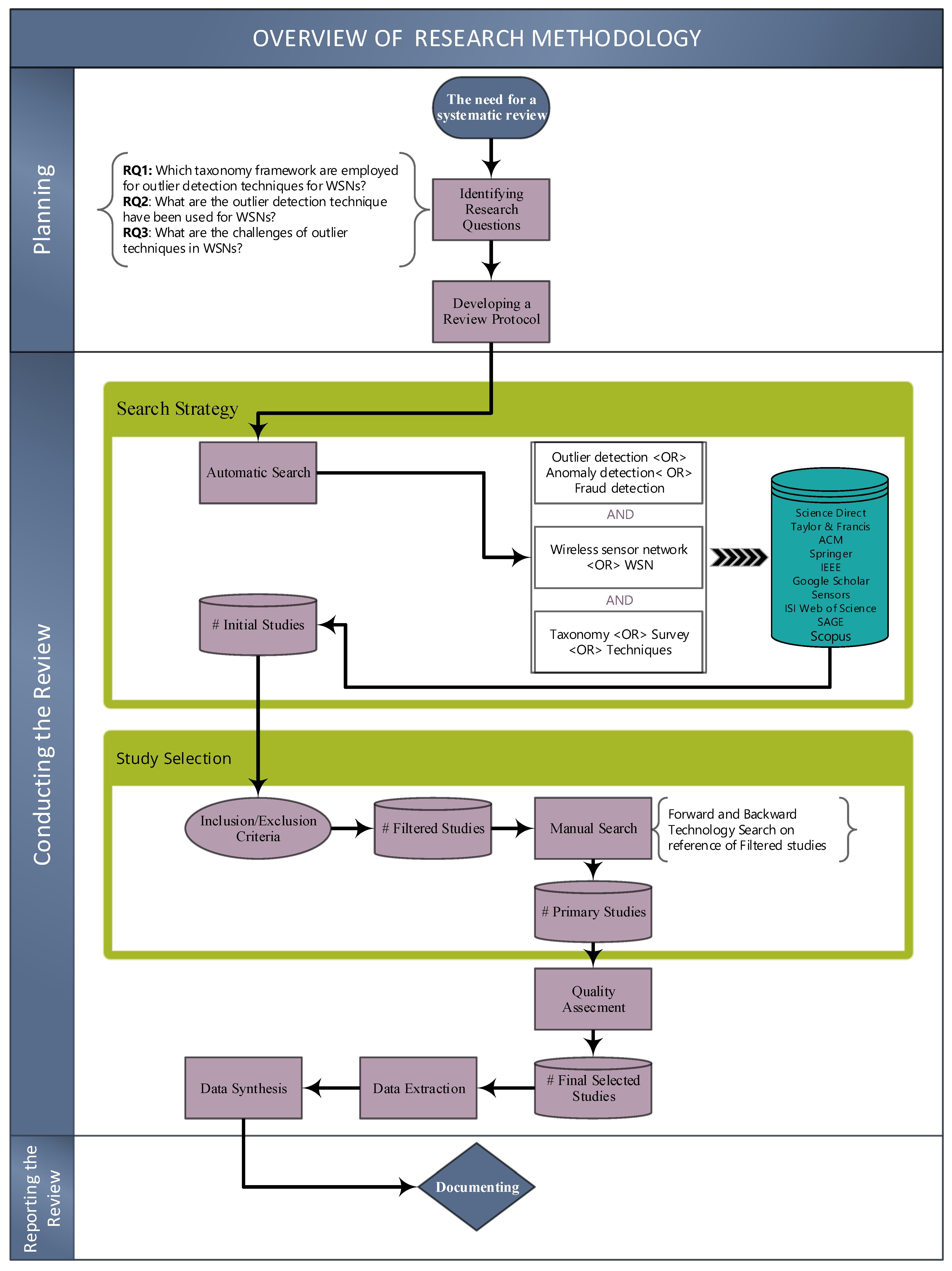
3. Review Method

We used SLR as the methodology to study current research work regarding outlier detection. The ‘systematic literature review provides a means for the evaluation and interpretation of the available research which is pertinent to a specific topic area, RQ, or a phenomenon of interest’ [28,29,30]. This study employed the SLR guidelines and standards proposed by Kitchenham [31], which consist of a set of well-defined stages conducted in line with a predefined protocol. The aim of performing SLR is to systematically collect, evaluate, and interpret all the published studies relevant to the predefined RQs in order to deliver comprehensive information for the research community. The SLR was selected to gather data regarding cutting-edge notions, to list the benefits of certain approaches, and to find a research gap that may be bridged via investigation [32]. According to [31], the SLR approach has three phases: ‘planning, conducting, and reporting the review’. These phases consist of the following processes: (1) identifying RQs; (2) developing a review protocol; (3) determining both exclusion and inclusion criteria; (4) selecting search strategy and study process; (5) quality assessment (QA); and (6) extracting and synthesizing data. As illustrated in Figure 5, for performing SLR, we summarized the methodological steps. In the following section, the details of these steps are explained.

4. Planning the Review

The planning phase begins by determining the need for SLR, identifying RQs, and developing a review protocol. The review protocol is as follows:

4.1. The Need for a Systematic Review

Although many strategies have been suggested for detecting specific subsets of WSN outliers, there is still a need for more comprehensive outlier detection strategies. This study looked into the various methods that have been developed for outlier detection in the literature review, besides those that have tried to provide an overview of the vast literature on techniques, classifications, taxonomies, and comparisons. Numerous techniques for detecting outliers have been developed for a specific application or a single study area. This survey significantly expands the discussion in several directions according to the following research questions.

4.2. Identifying Research Questions

To achieve the main objectives of this study, we propose three key research questions:

• RQ1: What is the designed taxonomy and framework for outlier detection techniques in WSNs?
• RQ2: What are the outlier detection techniques that have been used in WSNs?
• RQ3: What are the challenges in current outlier detection techniques in WSNs?

4.3. Developing a Review Protocol

The review protocol is considered an important step in conducting the SLR. It helps to determine the methods that will be applied in the systematic review. The main aim of the review protocol is to decrease study bias and differentiate SLR from traditional methods of reviewing the literature [31]. This review protocol categorizes the ‘review background, search strategy, development of RQs, extraction of data, criteria for study selection, and data synthesis’. The relevant RQs and review background are explained above. The following section provides details about other elements.

5. Conducting the Review

The review begins with a study selection and extraction and synthesis of data.

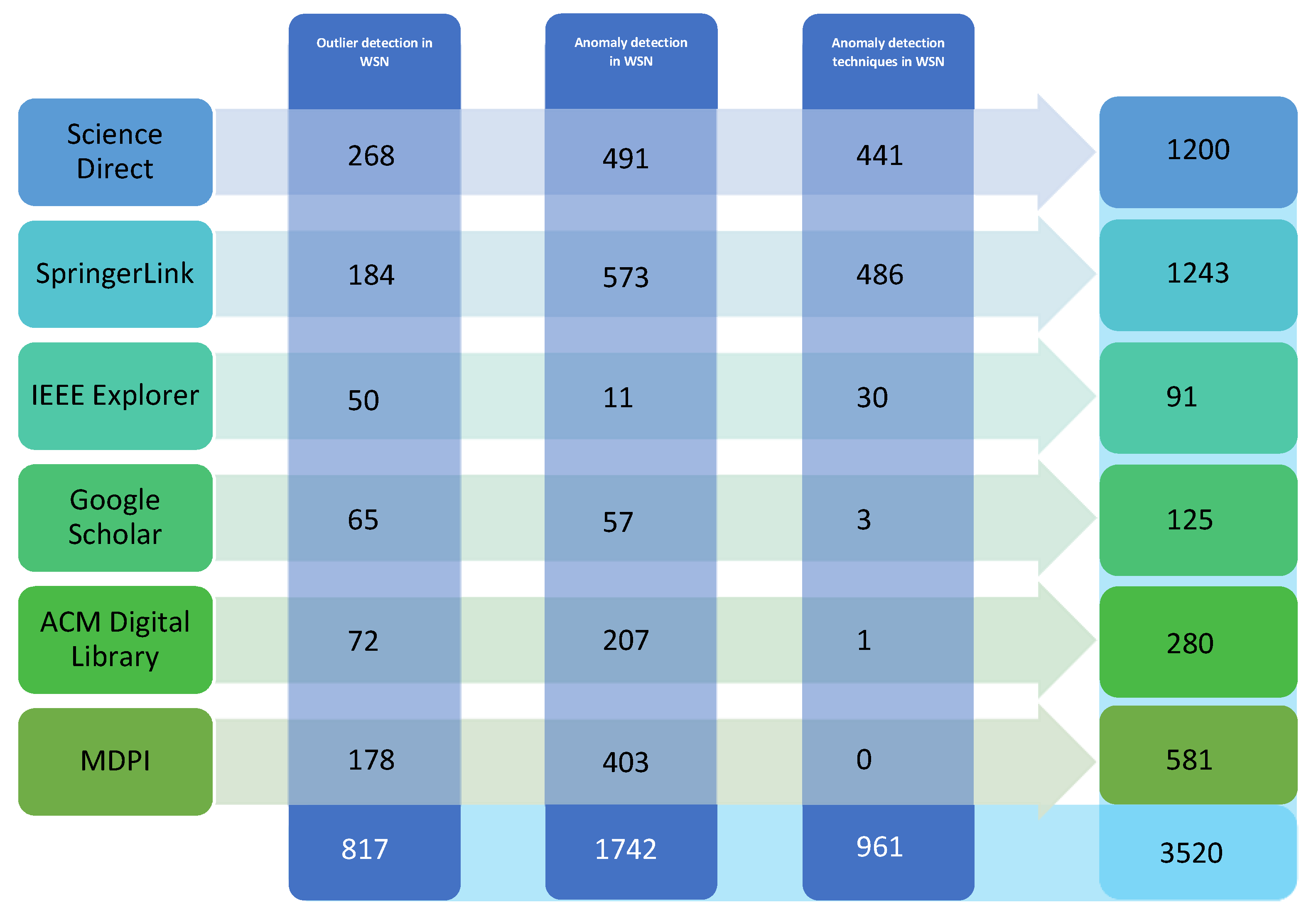
5.1. Search Strategy

The search strategy has a significant impact on data extraction from selected papers. A search strategy can assist scholars in obtaining as many relevant studies as possible [33]. Figure 5 illustrates the two steps of search strategies: manual and automatic. Both manual and automatic search approaches are employed for investigating the content of a review. This allows more studies to be incorporated and a wide range of academic publications to be covered. An automatic search can be employed to find primary studies on anomaly detection in WSNs. Web searches can be conducted based on search keywords in online library databases. Based on [34]’s suggestions, the search strategy was not limited to only a certain type of article; rather, it included a wide range of relevant and high-impact-factor publications in online libraries. The following online databases (with their assigned link) were included in the search strategy:

• Science Direct (http://www.sciencedirect.com/),
• SpringerLink (http://www.springer.com/in/),
• IEEE Explorer (http://www.ieee.org/index.html),
• Taylor and Francis Online (http://www.tandfonline.com/),
• ACM Digital Library (https://dl.acm.org/),
• MDPI (https://www.mdpi.com/).

The proposed study aimed to identify articles that were relevant to the domain. The main research keywords included are: ‘anomaly detection in WSN’, ‘outlier detection in WSN’, and ‘anomaly detection techniques in WSN’. A string of words was used to make sure that no relevant publication was missed. The search was limited to the year range of 2004 to October 2018 (more than 10 years). The search exposed a big volume of literature, including journal publications, conference proceedings, and many other published materials. All included digital repositories were manually searched using the predefined keywords.

The details of the overall search process based on the defined keywords in the given libraries are shown in Figure 6.

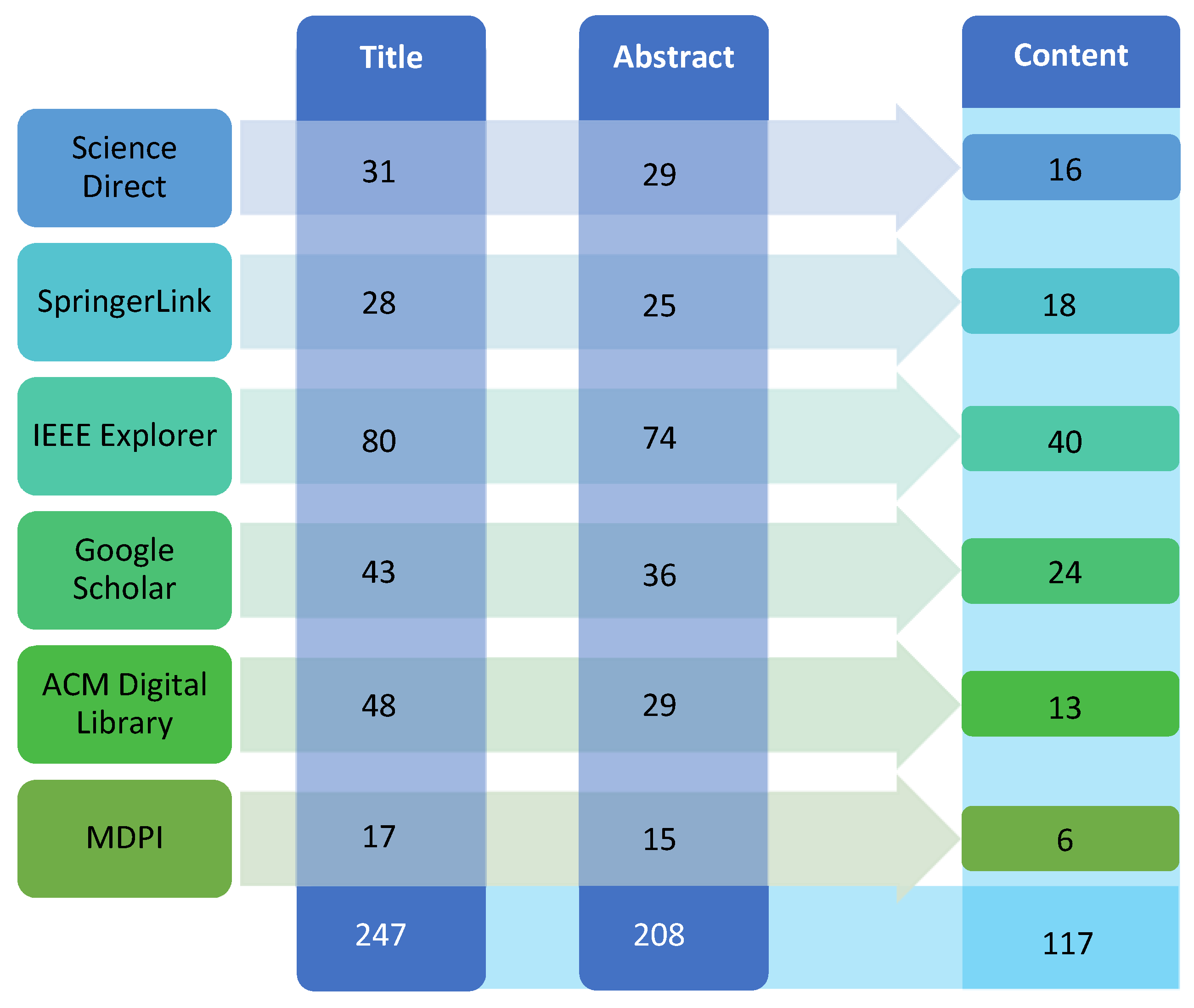
5.2. Criteria for Inclusion and Exclusion Articles

Exclusion and inclusion criteria ensure that only relevant studies are incorporated in data analysis. Because this review focused on understanding outlier detection in WSNs, only papers published in the English language from 2004 to 2018 were included in this study. The reason for selecting this particular time-frame was that the term ‘outlier’ has been gradually utilized in many studies since 2004, and several articles have covered the topic of outlier detection as of 2014. Thus, this study aimed to systematically collect, analyze, and synthesize articles until 2018. Studies unrelated to outlier detection in WSNs were discarded.

Table 2. Criteria for inclusion and exclusion of the articles.

Inclusion Criteria	Exclusion Criteria
Studies are written in English	Studies whose full text is not available
Studies are published between 2004−2018	Duplicated studies
Studies are published in the above selected database	Studies that are not related to outlier detection in wireless network domain
Studies that provide answers to the research questions	Articles that did not match the inclusion criteria

shows the criteria applied.

5.3. Manual Search

Based on [34], a forward and backward search was employed to trace the citations of primary studies. We used the Google Scholar search engine to find studies that were cited in the selected primary studies. The manual search also ensured that the systematic review of the research was relatively complete and comprehensive and that we did not miss anything. Mendeley (https://www.mendeley.com) was employed for sorting and managing all the studies and to remove duplicate studies.

5.4. Process for Selection of Studies

The primary aim of the selection process (primary studies) was to identify relevant studies to SLR. This search was performed by adhering to the steps outlined in the previous section. As a result, 3520 research articles were retrieved via the automatic search. Using Mendeley, the duplicated articles were removed. Initially, each folder of the library was checked manually, and all the articles were properly named by their titles. The duplications in these publications were removed by checking the titles in each folder. The initial selection filtering process was performed manually for all the libraries by title, and a total of 247 articles were obtained. Based on Kitchenham’s [35] recommendations, these articles were then filtered manually by abstract, and a total of 208 articles were included. In the last step, these articles were again filtered manually by content, and finally, a total of 117 articles were selected. The details of the selected papers by title, abstract, and contents are given in Figure 7. The list of year-wise publications is shown in

Table 3. Year-wise breakup of selected publications.

2018	2017	2016	2015	2014	2013	2012	2011	2010	2009	2008	2007	2006	2005	2004
												[2]
												[4]
												[5]
									[8]			[22]
								[6]	[36]			[37]
								[38]	[39]			[40]
	[20]	[41]			[42]			[43]	[44]			[45]
	[46]	[47]			[48]			[49]	[50]	[51]		[52]
[53]	[54]	[55]		[56]	[57]	[26]		[58]	[59]	[60]	[11]	[61]
[62]	[63]	[64]	[13]	[65]	[66]	[67]		[68]	[59]	[69]	[70]	[71]
[72]	[73]	[74]	[75]	[76]	[77]	[78]	[1]	[79]	[80]	[81]	[82]	[83]
[84]	[85]	[86]	[87]	[88]	[89]	[90]	[91]	[92]	[93]	[94]	[95]	[96]	[17]
[97]	[98]	[99]	[100]	[101]	[102]	[103]	[104]	[105]	[106]	[107]	[108]	[109]	[24]
[110]	[111]	[112]	[113]	[114]	[115]	[116]	[117]	[118]	[119]	[120]	[121]	[122]	[123]
[124]	[125]	[126]	[127]	[128]	[129]	[130]	[131]	[132]	[133]	[134]	[135]	[136]	[137]	[138]

. The list of final selected papers along with the titles and citations is given in

Table 4. Primary Studies.

S-ID	Reference	Year	Type	Methodology	Taxonomy	Dataset
S1	[53]	2018	Journal	Support Vector Machines	Classification	Smart city datset
S2	[87]	2015	Journal	Quarter-sphere support vector machine (QSSVM)	Classification	–
S3	[55]	2015	Journal	Bayesian network	Classification	Mica2Dot sensor nodes dataset at Berkeley Lab
S4	[89]	2013	Journal	Survey	–	–
S5	[64]	2016	Conference	Support vector machine technique within a sliding window-based learning algorithm	Classification and Spectral Decomposition	univariate datasets: an artificial dataset, in addition to the Well-Log and Dow Jones dataset
S6	[74]	2016	Journal	Support vector machine and a sliding window learning	Classification and Spectral Decomposition	Benchmark three-tank system
S7	[101]	2014	Journal	Review Paper	–	–
S8	[47]	2016	Conference	Nearest neighbor	Classification	Intel Berkeley base
S9	[13]	2015	Journal	Naïve bayesian	Classification	Intel Berkeley Research Lab
S10	[41]	2016	Conference	Kernel principal component analysis (KPCA)	Statistical	Intel Berkeley (IBRL), Grand-St- Bernard (GStB), and Sensor- scope (LUCE)
S11	[92]	2010	Journal	Rule, LLSE, time series forecasting, and HMMs	–	Sensor Scope, INTEL Lab, GDI, NAMOS
S12	[6]	2010	Journal	Survey	–	–
S13	[26]	2012	Journal	Survey	–	–
S14	[75]	2015	Journal	KPCA based Mahalanobis kernel	Statistical and Classification	Intel Berkeley Research Lab (IBRL), Grand St. Bernard (GStB), Sensorscope Lausanne Urban Canopy Experiment (LUCE)
S15	[86]	2016	Journal	STODM algorithm and the fuzzy logic	–	St.Bernard wireless sensor network
S16	[119]	2009	Conference	Review	–	–
S17	[71]	2006	Journal	K-Means	Clustering	Dataset generated from multivariate Gaussian distribution
S18	[99]	2016	Journal	Cross calibration	–	Simulated dataset
S19	[109]	2006	Journal	Localized fault detection	–	–
S20	[137]	2005	Journal	Bayesian algorithm	Classification based	–
S21	[114]	2014	Journal	Multi criteria	statistical	Dataset acquired from a real world
S22	[24]	2005	Conference	Boundary detection	–	–
S23	[115]	2013	Journal	Fault-tolerant	Clustering	–
S24	[112]	2016	Journal	Data compression	–	Events collected data from different locations
S25	[113]	2015	Journal	Automatic data quality control	–	Real dataset
S26	[138]	2004	Journal	review Survey	–	–
S27	[133]	2009	Journal	Pareto algebra	Statistical	Simulated dataset
S28	[46]	2017	Journal	Dynamically aggregated neighboring information	Nearest Neighbor based	Dataset from Sensor Scope Grand St. Bernard scenario
S29	[131]	2011	Journal	–	–	–
S30	[8]	2009	Journal	Survey	–	–
S31	[82]	2007	Journal	Aggregation tree	Classification	Dataset provided by Berkeley research lab
S32	[37]	2006	Journal	Bayesian and Neyman Pearson	Statistical	Simulated dataset
S33	[139]	2013	Journal	Survey	–	–
S34	[108]	2007	Conference	Bayesian	Classification	Simulated dataset and actual environmental dataset collected in the forest
S35	[90]	2012	Journal	Hierarchical Bayesian spatio temporal (HBST) modeling	Classification	Three simulated datasets
S36	[140]	2014	Journal	Systematic Literature Review	–	–
S37	[22]	2006	Conference	Clustering	Clustering	Simulated dataset from the Great Duck Island project
S38	[128]	2014	Journal	Review of anomaly detection methods	–	–
S39	[116]	2012	Journal	Support vector machine	Classification	synthetic and real
S40	[11]	2007	Journal	Histogram	Statistical	Dataset of temperature records
S41	[58]	2010	Journal	Bayesian network	Classification	Simulated dataset
S42	[107]	2008	Journal	Bayesian network	Classification	Dataset gathered from deployed sensor networks in existing Australian coal mines
S43	[70]	2007	Journal	Two localized algorithms	–	Simulated dataset
S44	[48]	2013	Journal	k-nearest neighbor	Nearest neighbor	Real WSN dataset
S45	[93]	2009	Journal	Clustering	Clustering	Dataset acquired from the UCI Machine Learning Repository
S46	[67]	2012	Journal	Time series analysis and geostatistics	Statistics	Real dataset from the Swiss Alps
S47	[54]	2017	Journal	Bayesian network	Classification	Dataset of Intel Lab
S48	[63]	2017	Journal	Support vector machine	Classification	UCI dataset and IBRL dataset of WSNs
S49	[85]	2017	Journal	Segment-based anomaly detection	–	Dataset of real-word received signal strength (RSS)
S50	[73]	2017	Conference	Five different classifiers: bayesian network, neural network, nearest neighbors, support vector machine, and decision tree	Classification	Dataset from WSN in static and dynamic environments
S51	[141]	2014	Journal	Voronoi diagram based network	–	Dataset of IRBL
S52	[1]	2011	Journal	Survey	–	–
S53	[36]	2009	Journal	Non-parametric and unsupervised methods	Statistical	Simulated data
S54	[120]	2008	Journal	Survey	–	–
S55	[78]	2012	Journal	Support vector machine	Classification	Two synthetic datasets and a real dataset gathered at the Grand St. Bernard, Switzerland
S56	[5]	2006	Conference	Non Parametric	Statistical	Simulated dataset and real dataset from Pacific Northwest region
S57	[25]	2009	Conference	Bayesian network and support vector machine	Classification	Simulated dataset and real dataset from Grand-St-Bernard, Switzerland
S58	[69]	2008	Conference	Quarter sphere Support vector machine (SVM)	Classification	Dataset of Intel Berkeley Research Laboratory
S59	[123]	2005	Conference	Gaussian distribution	Statistical	Simulated data
S60	[105]	2010	Conference	Survey	–	–
S61	[122]	2006	Journal	Lightweight methods	–	Simulated data
S62	[118]	2010	Conference	Discrete Wavelet Transform (DWT) and the self-organizing map (SOM)	Classification	Synthetic dataset and actual dataset collected from a wireless sensor network
S63	[43]	2010	Journal	Neighborhood	Nearest neighbor	Real life datasets (Annealing and Cancer)
S64	[132]	2010	Conference	Optimization	–	Real and synthetic datasets
S65	[121]	2007	Conference	Quarter sphere support vector machines	Classification	Real dataset gathered from a deployment of wireless sensors in the Great Duck Island project
S66	[134]	2008	Conference	Hyperellipsoidal support vector machine	Classification	Real dataset from the Great Duck Island Project
S67	[68]	2010	Journal	Support vector machine (CESVM) and one class quarter sphere support vector machine	Classification	Synthetic and real datasets: GDI, Ionosphere, Banana, and Synth
S68	[83]	2006	Conference	Bayesian Networks	Classification	Dataset of habitat monitoring on Great duck island
S69	[106]	2009	Conference	One class support vector machine	Classification	Synthetic and real datasets of the Sensor Scope System
S70	[61]	2006	Conference	Wavelet based outlier correction and DTW distance	–	Simulated dataset
S71	[40]	2006	Journal	Outlier detection algorithm	Statistical	–
S72	[142]	2007	Journal	kernel density estimation and mico cluster	Statistical and classification	–
S73	[57]	2013	Journal	k-nearest neighbor	Clustering based and nearest neighbor based	Intel Berkeley research lab and synthetic dataset
S74	[136]	2006	Conference	Unsupervised learning	Classification and nearest neighbor	Dataset of the KDD-Cup 1999 network
S75	[143]	2007	Journal	Hierarchical Bayesian model within a decision theoretic framework	Classification	Simulated dataset
S76	[51]	2008	Conference	Density estimation	Statistical	Datasets from the UCI Machine Learning Repository and a number of synthetic datasets
S77	[81]	2008	Conference	One class Support Vector machine	Classification	Simulated datasets
S78	[45]	2006	Conference	linear regression and control chart	statistical	Dataset of the observation of the air pollution taken in Kuala Lumpur
S79	[144]	2007	Journal	One sided and two sided median	Statistical	Dataset of a flight data recorder (FDR)
S80	[145]	2006	Journal	Bayesian network	Classification	Simulated datasets
S81	[8]	2009	Journal	Survey	–	–
S82	[146]	2005	Journal	Local search heuristic	–	Real life datasets (lymphography and cancer) and synthetic datasets
S83	[39]	2009	Journal	Squence-based method	Statistical	Real life datasets (lymphography and cancer)
S84	[130]	2012	Journal	Neural Network and Rough set	Classification	Simulated Data
S85	[92]	2010	Journal	Rules, Time series analysis, learning, and estimation methods	–	Real World datasets
S86	[147]	2006	Conference	Dynamic bayesian networks	Classification	SERF windspeed sensor dataset streams from Corpus Christi Bay
S87	[148]	2011	Journal	Bayesian networks	Classification	–
S88	[149]	2006	Conference	Neighboring network	Nearest neighbor	Dataset of meteorological from various neighboring ground stations in the island of Crete in Greece
S89	[60]	2008	Journal	Distance	Nearest neighbor	Real and synthetic datasets
S90	[38]	2010	Journal	Kernel Density Estimation	Statistical	Real dataset from Intel Berkeley Research lab
S91	[49]	2010	Journal	Fuzzy clustering	Clustering	Three datasets
S92	[150]	2011	Journal	Support vector machine	Classification	Real dataset collected from a closed neighborhood from a WSN deployed in Grand-St-Bernard
S93	[151]	2011	Journal	Clustering	Clustering	Real dataset obtained from Intel Lab’s web site and synthetic dataset
S94	[80]	2009	Conference	Hyper-ellipsoidal	Clustering	Real life dataset called the IBRL and a synthetic dataset
S95	[44]	2009	Journal	Statistical analysis	Statistical	Dataset from a real sensor network obtained from the Intel Berkeley Research Laboratory (IBRL)
S96	[42]	2013	Journal	Linear regression	Statistical	Real medical dataset with many (both real and synthetic) anomalies
S97	[56]	2014	Journal	Hyperspherical clusters	Clustering	Two real sensor network deployment datasets and two synthetic datasets for evaluation purposes, namely the IBRL, GDI, Banana and Gaussmix datasets
S98	[77]	2013	Journal	Fuzzy clustering	Clustering and Statistical	Real dataset from 54 sensors deployed at the Intel Berkeley Research Lab and artificial datasets from Intel Lab
S99	[66]	2013	Journal	Principal component analysis (PCA)	Clustering	Real sensed dataset collected by 54 Mica2Dot sensors deployed in Intel Berkeley Research Lab
S100	[152]	2006	Journal	Support vector machine	Classification	Dataset of the wide area airborne mine detection (WAAMD) and hyperspectral digital imagery collection experiment (HYDICE)
101	[153]	2011	Conference	Tukey and relative entropy statistics	Statistical	Dataset from RUBiS
102	[59]	2009	Journal	Sequence Miner	Clustering	Synthetic dataset and real dataset
103	[129]	2013	Journal	Survey	–	–
104	[76]	2014	Journal	Decision tree	Classification	Intel Berkley lab dataset
105	[27]	2011	Conference	Temporal technique	Statistical technique combined with nearest neighbor technique	Real datasets in different fields
106	[20]	2017	Journal	Survey	–	–
107	[62]	2018	Journal	DUCF protocol of based on fuzzy logic interface system	Clustering	Real dataset
108	[72]	2018	Journal	Case Study	Machine learning&Classification	–
109	[84]	2018	Journal	Support vector machine	Classification	Real dataset
110	[126]	2016	Journal	Kriging	Clustering	Real dataset
111	[127]	2015	Journal	Support vector machine	Classification	Dataset of multiple intelligent monitoring in intensive care (MIMIC)
112	[98]	2017	Conference	support vector machine	Classification	IBRL dataset
113	[97]	2018	Conference	support vector machine	Classification	IBRL real dataset
114	[111]	2017	Conference	support vector machine	Classification	Intel Berkeley Research Laboratory (IBRL)
115	[125]	2017	Conference	Neural network	Classification	Real dataset
116	[110]	2018	Conference	Bayesian network	Classification	–
117	[124]	2018	Journal	K-medoids	Clustering	Synthetic datasets provided by NS2 and R studio

.

5.5. Applying Quality Assessment (QA)

The next stage was involved in assessing the quality of the selected studies by using QA, as it is recommended by Kitchenham [35]. The QA was performed for all the articles and with respect to each research question. For assessing the quality of each article, this study used four RQs as QA criteria:

• QA1: Is the topic addressed in the paper related to anomaly detection in WSN?
• QA2: Is the research methodology defined in the article?
• QA3: Is there a sufficient explanation of the background in which the study was performed?
• QA4: Is there a clear declaration concerning the research objectives?

These four QA criteria were tested among the 117 research papers to determine their reliability. The QA was comprised of three stages of quality schema, high, medium, and low [154], in which the quality of the paper relied on its loading score. For example, papers that satisfied the criteria were awarded a score of 2, papers that partially satisfied the criteria were awarded a score of 1, and papers that did not provide any information regarding the question and did not satisfy the criteria were awarded a score of 0. Consequently, based on the four defined criteria, studies with a score of 5 or above were considered with high quality, studies with a score of 4 were considered with medium quality, and studies with a score below 4 were considered with low quality.

Table 5. Quality assessment criterion.

S_ID	QA1	QA2	QA3	QA4	Score
S1	2	2	2	2	8
S2	2	2	2	2	8
S3	2	1	1	2	6
S4	2	2	1	1	6
S5	2	2	1	2	7
S6	2	1	2	2	7
S7	1	2	1	1	5
S8	2	2	2	2	8
S9	2	2	2	2	8
S10	2	2	2	2	8
S11	1	1	2	2	6
S12	2	1	2	2	7
S13	2	2	2	2	8
S14	2	2	2	2	8
S15	2	1	2	2	7
S16	2	2	2	2	8
S17	2	2	2	2	8
S18	2	1	2	2	7
S19	2	2	2	2	8
S20	2	2	2	2	8
S21	2	1	2	2	7
S22	2	2	2	2	8
S23	2	2	2	2	8
S24	2	1	2	2	7
S25	2	2	2	2	8
S26	2	2	2	2	8
S27	2	1	2	2	7
S28	2	2	2	2	8
S29	2	2	2	2	8
S30	2	1	2	2	7
S31	2	2	2	2	8
S32	2	2	2	2	8
S33	2	1	2	2	7
S34	2	2	2	2	8
S35	2	2	2	2	8
S36	2	1	2	2	7
S37	2	2	2	2	8
S38	2	2	2	2	8
S39	2	1	2	2	7
S40	2	2	2	2	8
S41	2	2	2	2	8
S42	2	1	2	2	7
S43	1	2	1	1	5
S44	2	1	1	1	4
S45	1	2	1	1	5
S46	1	1	2	1	5
S47	1	2	1	2	6
S48	2	2	1	2	7
S49	2	1	1	1	5
S50	2	1	2	1	6
S51	1	1	1	1	4
S52	1	1	1	1	4
S53	1	2	2	1	6
S54	1	2	1	1	5
S55	2	1	2	1	6
S56	2	1	1	1	5
S57	2	1	1	2	6
S58	2	1	1	1	5
S59	2	1	1	2	6
S60	2	1	2	2	7
S61	2	2	2	1	7
S62	2	1	1	1	5
S63	2	1	1	2	6
S64	2	1	2	2	7
S65	2	1	1	2	6
S66	2	2	2	1	7
S67	2	1	1	1	5
S68	1	2	2	2	7
S69	2	2	1	2	7
S70	2	1	1	1	5
S71	2	1	1	1	5
S72	2	2	1	1	6
S73	2	2	2	2	8
S74	2	1	1	2	6
S75	2	1	1	1	5
S76	1	2	2	1	6
S77	1	2	1	1	5
S78	2	1	1	1	5
S79	2	1	2	2	7
S80	1	2	2	1	6
S81	1	2	2	2	7
S82	2	1	2	1	6
S83	1	1	2	1	5
S84	1	1	0	1	3
S85	1	2	0	1	4
S86	1	1	1	1	4
S87	1	1	1	1	4
S88	1	2	0	1	4
S89	2	2	1	1	6
S90	1	1	1	1	4
S91	2	1	1	1	5
S92	2	1	1	1	5
S93	1	1	1	1	4
S94	2	0	1	1	4
S95	2	1	1	1	5
S96	2	2	2	2	8
S97	1	1	2	1	5
S98	2	1	1	1	5
S99	2	1	1	2	6
S100	2	1	1	1	5
S101	2	1	1	1	5
S102	2	2	1	1	6
S103	2	1	1	2	6
S104	2	2	1	1	6
S105	2	2	2	1	7
S106	1	1	2	2	6
S107	2	1	2	1	6
S108	2	2	1	2	7
S109	1	2	2	1	6
S110	1	2	1	1	5
S111	2	1	1	1	5
S112	2	1	2	2	7
S113	1	1	2	1	5
S114	2	1	1	1	5
S115	2	1	1	2	6
S116	1	1	2	2	6
S117	2	1	2	1	6

presents the QA list of every study.

5.6. Data Extraction and Synthesis

A form for data extraction was developed at this phase to accurately key in all data. This was done by cautiously analyzing each study and extracting appropriate information through Mendeley and Microsoft Excel spreadsheets. The columns considered in the review were as follows: Study ID, authors, publication date, type (e.g., journal, conference proceeding), methodology, technique-based taxonomy, and datasets. Retrieval of this information was related to both research objectives and RQs.

Table 6. Data extraction of primary studies.

Extracted Data	Description
Study ID	Unique identity for each article
Authors	authors’ names
Year	Publication Date
Type	Journal or conference
Methodology	e.g., bayesian network, k-nearest neighbor (kNN), support vector machine, etc
Taxonomy	Comparative techniques that are addressed in each paper
datasets	e.g., simulated data, real data, etc.

presents the items embedded in the form, whereas Table 4 shows the data extracted from the selected 117 research papers based on the form. The extracted data were synthesized for discursive analysis to address several issues related to WSN, including advantages and disadvantages, classification, and methods.

5.7. Publication Sources Overview

The list of selected papers published from the year 2004 until the year 2018 is presented in Figure 8. A gradual increase was noted in the number of papers published in the field of detecting outlier detection in WSNs. This shows the increasing interest in this domain, particularly after 2005. The year 2012 saw an increase of 12 studies, compared to only seven studies for 2014 and 2015. However, 2006 had the highest publication rate with 15 studies based on their reliability, an increase in the number of impact factor journals, and an increase in the number of computer science conferences. Figure 8 shows that 83 research papers were retrieved from journals (71%), and 34 papers were from conference proceedings (29%).

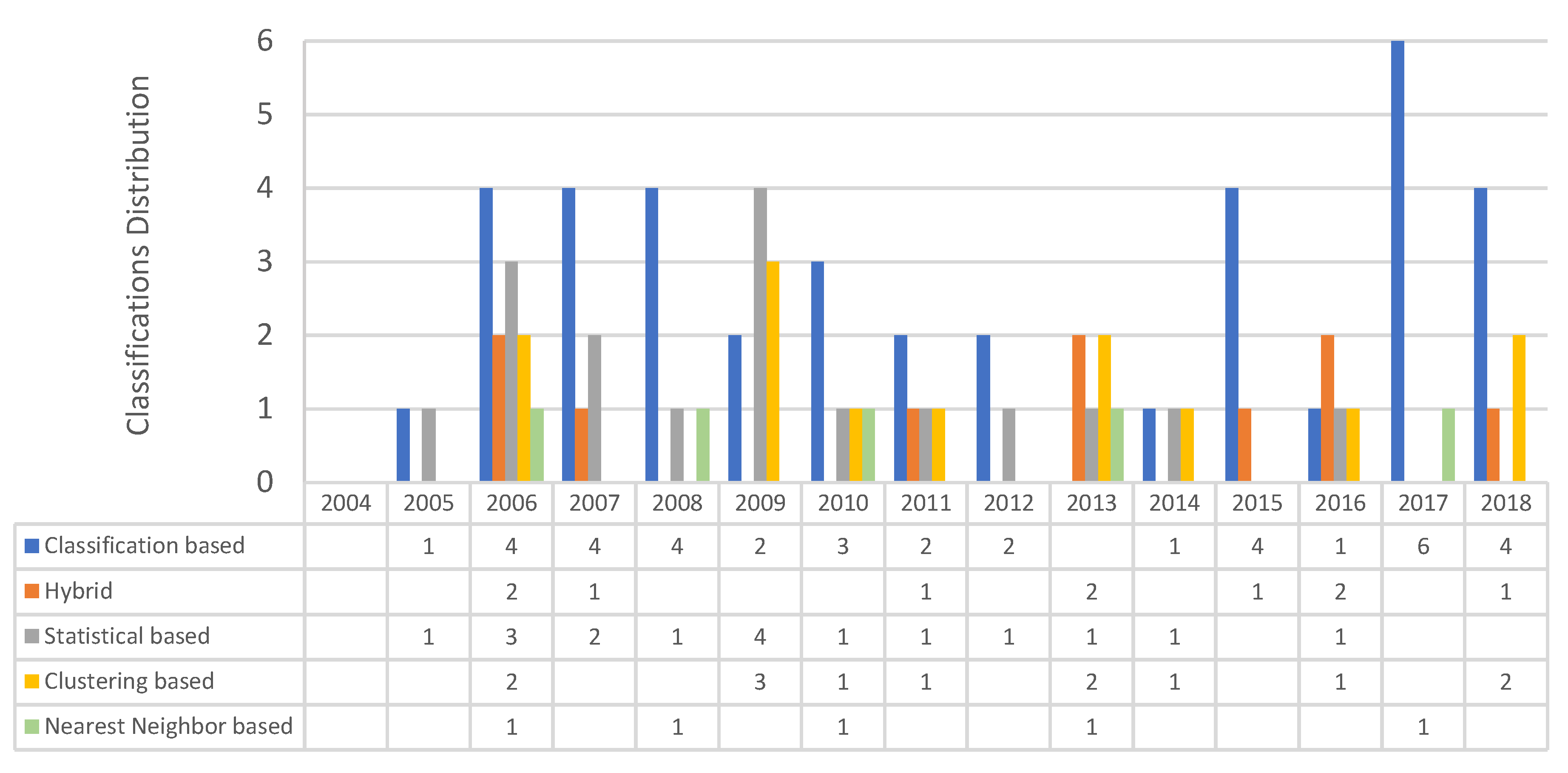
5.8. Classification of Outlier Detection Techniques Used in Previous Studies

The techniques for outlier detection in WSNs are presented in Figure 9: classification, nearest neighbor, statistical analysis, clustering, and spectral technique. A total of 38 studies use the classification approach, whereas 17 use statistical analysis, 13 use clustering, 10 use hybrid techniques, and 5 use nearest neighbor techniques.

6. RQ Results

The RQs of this study were addressed after extracting essential data from 117 selected research papers. Every study was mapped to the most relevant question and grouped based on similarity. The upcoming sections answer the RQs outlined in Section 4.2.

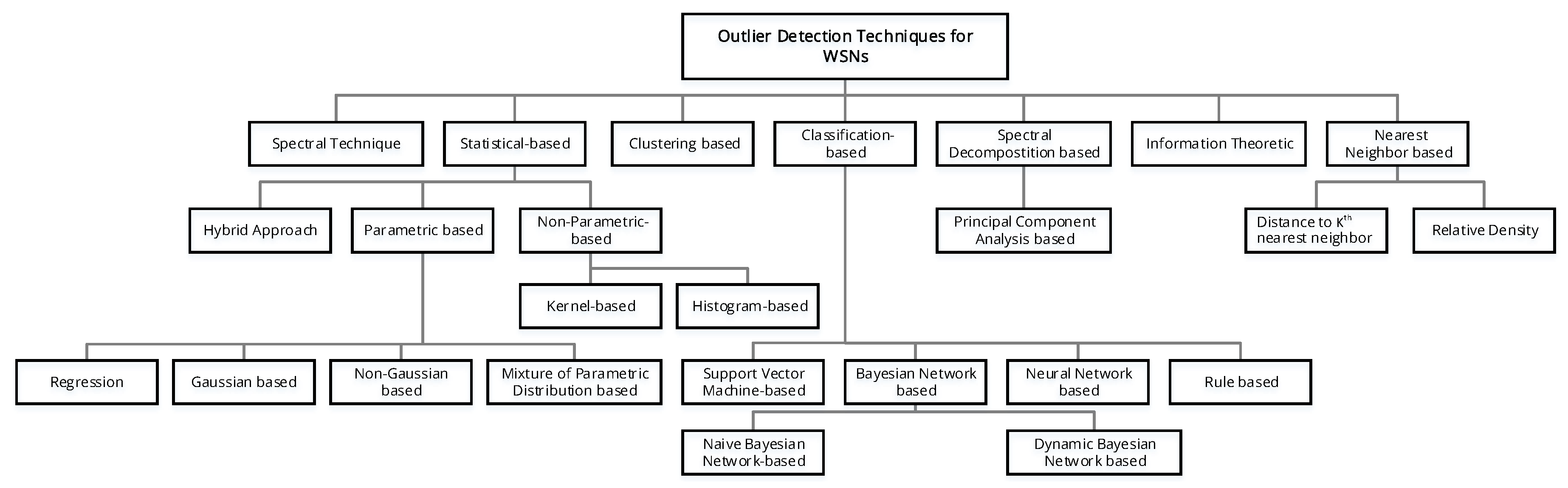
6.1. What is the Complete Taxonomy Framework for Outlier Detection Techniques for WSNs? (RQ1)

Lately, several studies have been employed for detecting outlier detection in WSNs. This highlights the need for a taxonomy to address all the techniques and requirements of WSNs. Figure 10 presents a taxonomy for detecting outlier detection techniques in WSN. For WSNs, outlier detection techniques can be classified into nearest neighbor-based, information-theoretic-based, statistical-based, clustering-based, spectral, classification-based, and spectral decomposition-based approaches. The statistics approach was divided into parametric, non-parametric, and hybrid methods based on the probability of the distribution model. Gaussian-based, regression-based, mixture-of-parametric-distribution-based, and non-Gaussian-based approaches are parametric approaches, whereas kernel-based and histogram-based approaches are non-parametric approaches. Furthermore, classification-based approaches are Bayesian network-based, support vector machine (SVM)-based, neural network-based, and rule-based approaches. The Bayesian network can be divided into naïve Bayesian network and dynamic Bayesian network (DBN) based on the degree of probability in dependencies among the variables. Spectral decomposition-based techniques apply principal component analysis (PCA) for outlier detection. The nearest neighbor-based methods employ distance to $K^{th}$ nearest neighbor and relative density for outlier detection. Therefore, in this study, we provide a comprehensive taxonomy framework and highlight the advantages and disadvantages of each class of outlier detection techniques under this taxonomy framework [6].

6.2. What Are the Outlier Detection Techniques that Have Been Used for WSNs? (RQ2)

Outlier detection methods for WSNs are classified in this section based on their respective disciplines. Figure 10 provides a description for each discipline.

6.2.1. Statistical-Based Approaches

Statistical-based approaches require a model for data distribution to detect outliers. A statistical model looks into data distribution and assesses the fit of data instances to the model. Data instances become outliers when the data probability produced by the model appears in distance measures. The methods are grouped into non-parametric and parametric. Parametric methods produce data from an acknowledged distribution that is presumed from data that are available based on either the Gaussian or non-Gaussian model. Meanwhile, non-parametric models dismiss data dispersion availability as a distance measure that is calculated with a statistical model and new data instances of other parameters to determine the outlier. Some of the statistical-based techniques that are considered in this paper are [11,36,37,38,39,40,41,42,44,45,51,67,75,123,142,144,153].

• Parametric-Based Approaches: These strategies consider the accessibility of information from the fundamental data distribution. It is followed by approximation of distribution limitations using the available data. Data distribution is classified as Gaussian-based models or non-Gaussian-based models. Gaussian models are characterized by a normal distribution of data.
  • Gaussian-Based Models: Outlying sensors and sensor networks’ event boundaries are identified by using two specific strategies described by [70]. These strategies depend on the spatial correspondence of the evaluation of adjacent sensor nodes to compare outlining sensors with the event boundary. The difference between readings of a node and the mean of the readings of its adjacent nodes is calculated by each node in the strategy employed for recognition of outlining sensors. This is followed by the regulation of every difference from the adjacent nodes. If the extent of variation of a reading of a node’s absolute value is considerably higher than the predetermined criteria, then the node is said to be an outlying node. The event boundary recognition strategy depends on the preceding outcomes of distant sensor recognition. In this case, the node is said to be an event node if there is a significant variation in the absolute value of the extent of divergence of the node in different geological areas. These strategies do not consider the temporal association of sensor readings, so their precision is not very high.
  • Non-Gaussian-Based Models: A mathematically supported strategy is proposed by [155], where the outliers in the shape of spontaneous noise are modeled using a symmetric $\alpha$- stable (${\mathrm{S}}_{\alpha }\mathrm{S}$) distribution. In this strategy, the time-space associations of sensor data are employed to recognize outliers. The anticipated data and sensing data are contrasted by every group node for identifying and correcting the temporal outliers. This corrected data from nodes are gathered by the cluster-head to identify spatial outliers that show significant divergence from regular data. There is a reduction in communication costs that can be attributed to local transfer. Moreover, costs incurred on calculation are minimized because a major part of computations is conducted by cluster-heads. However, it may not be appropriate to apply ${\mathrm{S}}_{\alpha }\mathrm{S}$ distribution to real sensor data. Powerful alterations of network topology may be experienced by the cluster-based model.
• Non-Parametric-Based Approaches: Accessibility of data distribution is not considered by non-parametric strategies. The space between new test cases and mathematical models is usually identified by these strategies. To identify whether the observation is an outlier or not, some criteria are applied to the measured space. Histograms and kernel density estimators are famous strategies in this regard. In histogram models, the rate of incidence of various data instances is determined by calculating the probable incidence of a data instance. Afterward, the test is contrasted with every type of histogram to determine the type to which it is associated. The probability distribution function (pdf) for regular instances is evaluated by kernel-density estimators and by employing the kernel functions. An outlier is found to be any new instance in a pdf that is found in a region characterized by a low probability.
  • Histogramming: Worldwide outliers in applications of sensor networks that are responsible for the collection of data are recognized by a strategy developed on the basis of a histogram proposed by [11]. This histogram is characterized by a minimization of the cost incurred for communication because it focuses on gathering histogram data instead of unprocessed data for further processing. Histogram information help to extract data distribution from the network and sort out non-outliers. Additional histogram data can be gathered from the network for recognizing outliers. Outliers are determined by a predetermined standard distance or by their position amongst the outliers. One shortcoming of this strategy is that communication expenses are increased because of the need to gather additional histogram data from the entire network. Moreover, merely single-dimensional data are considered by this strategy.
  • Kernel Functions: It is a strategy used for the detection of outliers online in transferring sensor data, it was recommended by [156]. It is based on kernels and is independent of the predetermined data distribution. The strategy uses the kernel density evaluator in order to estimate the fundamental distribution of sensor data. Thus, outliers are recognized by nodes in case of major divergence of value from the pre-set model of data distribution. An outlier is the value of a node whose adjacent node values do not meet the criteria set by the user. This strategy is also applicable to complex nodes for recognition of outliers overall. This strategy is highly dependent on pre-set criteria. This makes it problematic because it is very complicated to select suitable criteria. Moreover, identification of outliers in data with multiple variables may not be possible using a single criterion.
• Evaluation of Statistical-Based Techniques: These strategies have been proved mathematically to effectively recognize outliers when an accurate model of the probability distribution is given. Additionally, the basic information on which the model is constructed is not needed afterward. However, in reality, previous information on sensor stream distribution is usually unavailable. Hence, in the absence of a predetermined distribution to be followed by sensor data, parametric strategies are deemed to be ineffective. Non-parametric strategies are more efficient because they do not depend on distribution features. Histogram models are suitable for single variable data, but in the case of multiple variables, this model fails to consider the correlation between various aspects of data. For data with multiple variables, a kernel function is a better option, specifically in terms of computation cost.

6.2.2. Nearest Neighbor Based Techniques

These techniques are widely applied to analyze data instances based on the nearest neighbor via previous machine learning and data mining. Some acknowledged distances are employed to calculate the distance of data instances. If the data instance is positioned further from the neighbor, it is called an outlier. Univariate data prefer Euclidean distance, whereas multivariate data prefer Mahalanobis distance. Some examples of these methods are outlined in [43,46,47,48,60,149]. However, these methods are not popular and have several shortcomings, as depicted in the upcoming sections.

In cases where the distant positioned data instance is deemed to be an outlier, [157,158], many processes including categorization, clustering, and outlier identification are performed using this strategy. Data distribution is not considered by these strategies, but many mathematical strategies are simplified. An outlier identification strategy based on the closest node has a clear idea of closeness. Various clear distant notions are considered as a couple of data instances, a group of instances, or a series of instances. Euclidean distance is the optimum choice for both the univariate and multivariate constant features. The strategy for resolving the issue of uncontrolled worldwide outlier identification in a system of wireless sensors was recommended by [52]. Data similarity was the basis of this strategy. Distance correspondence is used by every node for the recognition of local outliers. These outliers are subsequently transmitted to adjacent nodes for rectification.

The process continues until every sensor node in the system finally corresponds to worldwide outliers. However, the cost of communication is increased because every node employs broadcast for facilitating communication between nodes in the system. Consequently, this algorithm is suitable for systems that evaluate outlier rating confidence by tuning the sliding window to the part where the precision of the algorithm is observed, a significant communication load is exerted, and significant power consumption is required. Moreover, [61] proposed an in-network strategy for outlier clean-up to be applied to sensor system data-gathering applications. Outlier correction based on wavelets and adjacent dynamic time warping distance based on the exclusion of outliers with respect to space-time related data that are used in this strategy. This ensures efficient clean-up of the sensor data by minimizing the transfer of outliers. Thus, many outliers are corrected or eliminated from broadcast in a maximum of two steps. However, this strategy is dependent on appropriate criteria that are difficult to determine. In 2007, a new uncontrolled strategy based on distance was given by [82] for identifying worldwide outliers in a snapshot and implementing a sensor system to handle queries. An arrangement similar to that of an aggregation tree is observed here when nodes gather data from their children and then forward the constructive data to their parents.

The sink is responsible for sorting the world’s leading outliers and forwarding these outliers to nodes in the system so that they can be checked. When a node does not correspond to worldwide outcomes determined by the sink, the process is performed again. Because only one dimension is considered, the cost of communication is minimized. The model of the sliding window is employed to conduct outlier queries. This identifies irregularities in the present window. To renew the addition or the removal of a present window, a single scan is conducted by the algorithm. Consequently, system efficacy is enhanced. The contribution of Angiulli et al. [50,95] was supported and broadened by Kontaki et al. [91]. They are known for their contribution to detecting universal outliers based on distance inflow of data, consequently resolve the issues of complication and use of memory. A new algorithm allowing the identification of outliers independently from the existing limitations was suggested by Yang et al. [57] proposed to calculate the ordered distance with a difference outlier factor. This strategy is based on the computation of a new outlier score for every point of data. This is done by considering the divergence between structured paces employed for the calculation of outlier scores.

The success of Local Outlier Factor (LOF) strategy and its recognition in high detection activity in dissimilar densities have proved that it is a significant strategy that can be modified in many ways. The precision of identification of LOF strategy is enhanced by some other strategies. Time complications are resolved to make the strategy precise by altering k-NNs or by conducting estimations [159]. Another strategy is to compare the efficiency of techniques based on mathematics and those based on the closest neighborhood to recognize outliers in the process of extraction of useful data. The comparison has revealed that the mathematical strategy of the histogram-based outlier score has more points of outliers compared to neighbor-based strategy, including LOF, class outlier factors, LOOP, and improving influenced outlierness. All these works showed only some outliers with severe divergence. An uncontrolled outlier identifier based on DNOD was recommended by [47], and it allowed to examine data collected by sensors for considering dimensions of outliers.

6.2.3. Clustering-Based Techniques

Clustering involves grouping data instances with similar attributes into clusters [160,161]. The algorithms of clustering can be distributed or centralized. The nodes transmit all data to the central node for clustering in the centralized algorithms, which is ineffective in communication. As for distributed algorithms, the nodes can cluster the data and send certain parameters to the gateway node to minimize overhead in communication. The distance measure is employed from the nearest cluster to determine the outlier [22,49,56,57,59,66,71,77,80,93,151]. Euclidean distance serves as a measurement of correspondence between two data instances, but the calculation of this correspondence in data with multiple variables is very costly. The strategy is based on clustering, and outliers are recognized on this basis. The data instances are deemed to be outliers if they have no relation to clusters or if their dimensions are smaller relatively to other clusters [6,19,162]. These strategies do not have former data regarding data distribution and can be applied to the incremental model. It is plagued by issues with determining the dimensions of the cluster.

Refs. [8,49,65] detail the benefits of clustering-based techniques. These partially controlled strategies are appropriate for the innovation’s identification [163], wherein regular data are used to create clusters signifying the normal form of data conduct [164,165]. Moreover, threats to the system are identified by K-means clustering, Self-Organising Maps (SOM), and expectation maximization. These methods employ clusters for categorizing test data. Similarly, a strategy has been proposed by Vinueza and Grudic [166] to detect local and universal outliers on the basis of the cluster. A data point is pronounced to be an outlier if it is located away from the clusters or if its class is located away from other points. Correspondingly, the clustering algorithm is used for the categorization of clustering-based strategies as an uncontrolled strategy. Afterward, data instances are evaluated on the basis of clusters.

In the clustering learning anomaly detectors algorithm employed by [167], an arbitrary sample was taken for calculating the mean distance between the nearest points to obtain data dimensions. The cluster was pronounced to be a local outlier if it had a density lower than that specified in the criteria, and the cluster was pronounced to be a universal outlier if it was located away from other clusters. A strategy was proposed by [168] that employed the recurrent point set mining for obtaining clusters by differentiating regular data from outliers and the COOLCAT strategy [169]. The strategy is called COOLCAT because it decreases the entropy of clusters and ultimately cools the clusters. Furthermore, a universal strategy was proposed by [22] for recognizing the offline dimensions of outliers in sensor nodes. A fixed-width algorithm for clustering is employed by every measured value of the sensor cluster. This is followed by the transmission of cluster conclusions to parent nodes. Outliers are recognized by the sink once the later receives the collected cluster statistics of the children clusters from the head cluster. An anomalous cluster is fixed in case the mean inter-distance of the clusters is more than one standard value of the group of inter-cluster distances.

The cost of communication is reduced, and energy-saving is ensured in such a way that the identification of irregularity is implemented only at the base station. However, one of the drawbacks of this strategy is that it does not apply to local and real-time decision-making. Moreover, a spatiotemporal strategy for the identification of outliers was proposed by [96]. This strategy is based on the concept of clustering known as the spatiotemporal density-based clustering in spatial databases (ST-DBSCAN), which is an extensive adaptation of the clustering strategy DBSCAN [170].

6.2.4. Classification-Based Techniques

Classification-based techniques can be supervised or unsupervised. The unsupervised methods learn the boundary (called sphere or quarter-sphere) during training and declare data instances outside the boundary as outliers. Nevertheless, classifiers need training for new datasets.

Classification methods are divided into SVM-based and Bayesian approaches [13,25,54,55,58,63,64,68,69,73,76,78,81,83,87,106,108,121,143,145,147,148,150,152].

Multi-class is the first group of categorization and includes neural networks and Bayesian networks. These strategies are based on the supposition that marked instances relating to multiple regular groups create the training data [171,172]. The discrimination between regular classes and other classes can only be pointed out if one has knowledge regarding classifiers. Classifiers get a confidence score from multi-category techniques. The instance is considered to be an outlier that is not belonging to any of the classifiers and this with taking into consideration that the test data are regular (i.e., none of the classifiers get a good score).

A probabilistic graphical model is employed by the strategies based on the Bayesian network for modification of a group of variables and their probable independence. Data are collected from various instances, and the probability of an instance is computed to be a part of the learned group. In 2004, a strategy was proposed by [173] to ensure structuring and learning mathematical data in WSNs. This was helpful for identifying local outliers and sorting defective sensors by applying the strategy to Bayesian model-based technique. The issues involved in understanding space-time correlations and limitations of the Bayesian classifier can be resolved by this strategy, which makes use of the classifier for probabilistic supposition. In the given model, the observed value for every sensor is controlled by the former reading of that particular sensor, and the whole values interval divides the subsequent readings in every class.

The next step is the prediction of the maximum probability class of the next reading. Here, a reading is pronounced to be an outlier if it has a lower probability in its own class as compared to other classes. A specific criterion is not needed for the recognition of outliers. This strategy can identify the lost readings in the system, but no consideration is given to multidimensional data. Bayesian networks are capable of telling if an observed value is related to class or not but do not consider provisional relation between the observed values of the sensory attributes. Similarly, a strategy based on BN was proposed for the recognition of local sensors in the flow of sensor data. BN is employed for understanding the spatiotemporal relations between various aspects and for evaluating the values that are lost from the flow of data emitting from the sensors. A year later, Ref. [135] came up with another strategy based on using DBNs along with a network topology. It developed over time to detect the local outliers in a sensor data flow. Inconsistent data can be recognized by two strategies, namely the Bayesian credible interval and the maximum posteriori measurement status. These strategies have the capacity to function in various data flows simultaneously. A Bayesian credible interval is structured for the latest dimensions and observations by hidden distributions, which are minimizing stepwise by a method known as Kalman filtering. In this method, the sensors provide the latest observed values. Outliers are the measured values that exceed the value of the anticipated interval. The second method involves more intricate DBN. This DBN identifies the outliers with the help of a couple of measured state variables. Moreover, another strategy has been proposed by experts: Hierarchical Bayesian Space-Time (HBST) [90]. In this strategy, the relations between time and space are only presumed and not computed. A tagging system is used for spotting data that do not meet the given criteria.

HBST is complicated, but it is accurate; its rate of fake identification is very low. It is much more appropriate for divergence models and unmodeled dynamics compared to linear auto-regression models. A Bayesian strategy for recognition of outliers within the data gathered using WSNs was recommended by [55]. This algorithm has many benefits: it enhances precision by resolving issues of categorization, time, and communication complications. It also makes relative improvements in the measure of latency period and uses energy in contrast to non-adaptive approaches. Various masses connected to the system are examined with the help of neural networks to create classifiers.

The neural network is a network of integrated nodes functioning similarly to the human brain. Every node is linked with adjacent nodes in closely located levels. The Replicator Neural Network (RNN) is a triple-layered network with three output and three input neurons. This neural network was used by [174] for data modeling. The input and output variables are the same in this network in order to form a clear and compact data model. The aim of this study was to measure distant data records in order to detect errors that are reforming from separate points of data. A graded score evaluator was employed to analyze the activity of the RNN. The efficiency of RNN in identifying outliers is demonstrated in two records that are accessible to the general public. This is similar to Smart Sifter [175], which creates models for recognizing outliers.

The difference lies in the technique of ranking the individuals, which is dependent on their extent of offense with the model. Sykacek [176] proposed another strategy to identify outliers using a multiple layer perception to serve as a regression model. Subsequently, outliers are perceived as data with their remaining parts located outside the error bars. WSNs models are also proposed based on RNNs for identifying outliers. Ref. [118] also proposed a general method for the identification of outliers. The purpose of this study is to recommend an algorithm allowing to identify irregularities. This method examines the identification of irregularity in sensor readings. For this purpose, SOM employing wavelet coefficients must be trained.

6.2.5. Information Theoretic

Various tools such as Kolmogorov complexity, entropy, and relative entropy are employed by data theoretic strategies for examining dataset components. Both physically organized data instances that are spatial and sequential data are considered. Data are simplified into simple components wherein component I is identified by the outlier recognition strategy. Component I has the utmost value of $C\left(D\right)-C(D-I)$. It is applicable to spatial, graphic, and sequential data. However, the determination of the most favorable dimension for components is the main concern regarding this strategy.

6.2.6. Spectral Decomposition-Based Approaches

PCA employs the strategies of spectral simplification [55] to reduce the volume of the data and develop patterns of regular data by proposing a model. An outlier is a data that is not capable of corresponding to the proposed model. However, PCA requires complex calculation activities to reduce the volume of data before recognizing outliers. Specifically, some main parts learn the data model, and, in the case of non-correspondence, that instance of data is regarded as an outlier. These spectral simplification strategies estimate data with characteristics ensuring the learning of inconsistencies in the data [8]. The key strategy for recognizing outliers is the determination of sub-spaces (for instance, embeddings and projections) that are appropriate for both controlled and uncontrolled circumstances.

Ref. [83] proposed a PCA-based technique to solve the data integrity and the accuracy problem caused by compromising or malfunctioning sensor nodes. This technique uses PCA to efficiently model spatiotemporal data correlations in a distributed manner and identify local outliers spanning through neighboring nodes. Each primary node that is offline builds a model of the normal condition by selecting appropriate principal components (PCs) and then obtaining sensor readings from other nodes in its group to conduct local real-time analysis. The readings that significantly vary from the modeled variation value under normal conditions are declared as outliers. The primary nodes eventually forward the information about the outlier data to the sink. The offline procedure for selecting appropriate PCs is computationally very expensive. PCA-based approaches tend to capture the normal pattern of the data using the subset of dimensions, and they can be applied to high-dimensional data. However, selecting suitable principal components, which is necessary to accurately estimate the correlation matrix of normal patterns, is computationally very expensive.

6.3. What Are the Challenges of Outlier Techniques in WSNs? (RQ3)

Extracting essential data from raw sensor data is vital [6]. Extracting sensor data embedded in networks designed to detect outliers is a difficult task. Common techniques are inappropriate to detect outliers in WSNs because of the following reasons:

• Resource limitations: Low-quality and cheap sensor nodes present several barriers, such as limited memory and energy, narrow communication bandwidth, and poor computational ability. Many common outlier detection techniques hesitate to probe into higher computational capabilities because of the high cost involved as well as the extensive storage and analysis that are needed. Thus, common sensors are inadequate to identify outliers in WSNs [6].
• High communication cost: A lot of energy in WSNs is channeled to radio communication, and the non-computation costs for communication in sensor nodes are higher than those for computation costs. Most common outlier detecting techniques employ centralized steps to analyze data, which causes higher energy use and communication overhead, decreasing network lifetime and blocking network traffic.
• Distributed streaming data: Sensor data that originate from varied channels may shift in a dynamic manner. Moreover, no model seems to spell out the distribution of these data. Additionally, calculating probabilities is a challenging task. Most techniques that identify outliers fail to satisfy the fixed criteria to process dispersion of stream data. Theoretical conceptions are unsuitable for sensor data and thus are inappropriate for WSNs.
• Heterogeneity and mobility of nodes, frequent communication failures, dynamic network topology: Sensor nodes placed in frenzy settings are deemed to fail because of dynamic network topology and frequent communication. Sensor nodes with varied capacities can move into different positions because each node may contain various kinds of sensors. Thus, the intricacy of generating a viable outlier detecting method for WSNs is heightened because of such dynamic and complex features.
• Large-scale deployment: The scale of WSNs may be massive and may thus require the higher task of detecting outliers, which cannot be performed by common sensors.
• Identifying outlier sources: A sensor network monitors activities and provides raw data. Nevertheless, it is difficult to determine outliers in complex and intricate WSNs. Common methods may not even be able to identify events from outliers. Hence, it is more challenging to identify outliers in WSNs from other normal events.

7. Advantages and Disadvantages of Existing Outlier Detection Techniques

This section compares outlier detection techniques used by previous studies and highlights the advantages and disadvantages of each algorithm.

7.1. Statistical-Based Techniques

Detection of outliers via the statistical method incorporates the production of observed profiles. The generated profile embeds several measures, such as activity intensity, audit record distribution, and ordinal measures (CPU usage). Two types of profiles are generated for the subjects: stored and current profiles. For the processing of network events (e.g., audit log records, incoming packets), the outlier detection system constantly updates the current system and outlier (degree of irregular activities). This is done after comparing the stored profile with the current one, that of current by employing the abnormality function of all related profile measures. When outliers exceed a particular aspect, the detection system signals an alert. Some benefits of outlier detection via statistical methods are listed in the following points:

• The systems, similar to many outlier detection systems, do not require prior knowledge of security flaws and attacks. Hence, the systems can detect ‘0 day’ or the latest attacks.
• The statistical techniques offer accurate alert regarding attacks for extended periods. Thus, they are excellent signals for forthcoming DoS attacks (e.g., port scan).

Some shortcomings of the statistical methods in WSNs are as follows:

• Skilled attackers can train a statistical outlier detection to accept abnormal behavior as normal.
• It is challenging to determine thresholds that balance the likelihood of false positives with that of false negatives.
• Statistical techniques demand accurate statistical distributions. However, not all behaviors can be modeled statistically. Most of the suggested outlier detection methods demand the assumption of a quasi-stationary process that cannot be estimated for most data [177].

7.2. Nearest-Neighbor-Based Techniques

The nearest neighbor-based outlier detection method demands distance/similarity measures based on dual data instances that can be calculated for various methods. Euclidean distance is the preferred choice for continuous features [178]. For multivariate data instances, distance/similarity is calculated for every feature and is later amalgamated [178]. In fact, numerous methods, including the clustering-based method, dismiss distance measure as a compulsory aspect. Although the measure has to be symmetric and positive, there is a need to meet the triangle disparity.

The two categories of the nearest neighbor-based outlier detection methods are: (1) methods that apply distance of data instance to its $k^{th}$ nearest neighbor as the outlier score; and (2) methods that calculate the relative density of every data instance to determine outlier score.

The benefits of nearest neighbor-based techniques are: (1) it is unsupervised and does not make any assumption about the underlying data distribution and (2) it is a straightforward method for varied types of data and requires appropriate distance measure for data [57].

7.3. Clustering-Based Techniques

The clustering technique is a popular choice in data mining to cluster data with similar traits [179,180]. In fact, clustering is a significant instrument for the analysis of outliers [181]. The primary presumption in many methods based on the clustering approach is that normal data are also linked to dense and huge clusters, whereas outliers are isolated or clustered in minute groups [179,181]. The benefits of clustering-based methods [6,8,49,57] are:

• Easy to adapt with incremental mode (after learning the clusters, new points can be inserted into the system and tested for outliers).
• Do not require supervision.
• Appropriate to detect outliers from temporal data.
• Have a rapid testing stage because the number of clusters that require comparisons is normally small.

Meanwhile, the drawbacks of these clustering-based techniques are:

• Rely highly on the efficiency of clustering algorithms to capture cluster structure in normal instances.
• Most methods that detect outliers are by-products of clustering and are thus non-optimized to detect outliers.
• Several clustering algorithms force every instance to be assigned to some clusters. This might result in anomalies getting assigned to a large cluster and being considered as normal instances by techniques that operate under the assumption that anomalies do not belong to any cluster.
• Some clustering algorithms insist on assigning each instance to a cluster. Thus, outliers may be linked to a large cluster and seen as a normal instance by methods that assume that outliers are always in isolation.
• Some clustering-based methods are effective only when outliers are not a part of essential clusters.
• There is bottleneck computation intricacy, particularly when O(N2d) clustering algorithm is applied.

7.4. Classification-Based Techniques

These methods can be supervised or unsupervised. The unsupervised methods learn the boundary (called sphere or quarter-sphere) at training and declare data instances outside the boundary as outliers. Nevertheless, classifiers need training for new datasets. The classification methods are divided into SVM-based and Bayesian approaches [13,25,54,55,58,63,64,68,69,73,76,78,81,83,87,106,108,121,143,145,147,148,150,152,182].

The benefits of the classification-based methods are as follows:

• Classification-based methods, particularly multi-class approaches, apply powerful algorithms that can differentiate instances from varied classes.
• The testing stage is rapid because the data instances are only compared with a pre-computed model.

The drawbacks of these classification-based methods are as follows:

• They rely on the availability of accurate labels for varied normal classes, which is difficult to obtain.
• Classification-based methods have a label for every test instance that turns into a drawback if an outlier score is desired for test instances. Several classification methods that gain probabilistic estimation scores from classifier outputs can be employed to overcome this issue [8].

7.5. Information Theoretic

These methods analyze information content from a dataset via information-theoretic measures such as Kolmogorov complexity, entropy, and relative entropy. Outliers in data generate irregularities in the information content of the dataset. Let $C\left(D\right)$ denote the intricacy of a given dataset, D. The fundamental information-theoretic method is elaborated as follows: given a dataset D, find the minimal subset of instances, I, such that $C\left(D\right)-C(D-I)$ is maximum. All the instances found in the subset are assumed to be outliers. The issue is overcome through this fundamental method of determining a Pareto-optimal solution that is not optimum, as other varied objectives require optimization. This method promotes dual optimization to reduce the size of the subset and to decrease dataset intricacy. The local search algorithm was employed by [183] to identify a subset in a linear manner by applying the entropy for intricate cases. Meanwhile, Ando proposed a method that applied the measure of information bottleneck [184]. Although the approximate methods have linear time intricacy, fundamental information-theoretic outlier detecting methods have exponential time intricacy [8]. The benefits of information-theoretic methods are as follows:

• Do not require supervision.
• Discard assumptions regarding underlying statistical data distribution.

The drawbacks of information-theoretic methods are as follows:

• High reliance on the selection of information-theoretic measures. These measures often identify outliers when they are present in large numbers.
• The information-theoretic methods used in spatial and sequence datasets depend on sub-structure size, which is challenging to determine.
• It is challenging to link test instances with outlier scores via the information-theoretic method.

7.6. Spectral Decomposition-Based Approaches

These methods seek the normal behavior of data via PCA [185]. PCA minimizes dimensionality prior to the detection of outliers. A technique that incorporates data derived from varied nodes in WSNs was developed by [149]. This technique amalgamates sensor data in a distributed manner to detect outliers from several neighboring nodes. A method that is based on PCA can address issues related to the integrity of data and accuracy due to malfunctioning nodes. This method has two phases: online and offline phases. The sub-space approach is used for the online phase [186] to segregate the data into two spaces: (1) contains normal data and reflects the modeled data trends, and (2) contains residual data. In the presence of an outlier, the residual domain has varied parameters, whereas the system can identify paths with outliers after choosing the parameters. The squared prediction error (SPE) [187] has been employed to detect abnormal settings. In the presence of an outlier, the SPE is greater than normal thresholds, whereas the system can detect nodes that have outliers. The selection of variables can vastly contribute to huge modifications in SPE. Moreover, multivariate data are weighed in for this technique, and spatiotemporal correlations are applied to identify outliers [89]. The benefits of spectral anomaly detection methods are as follows:

• Spectral methods can automatically minimize dimensionality and are thus adequate to handle datasets with high dimensions. They can be also applied as a pre-processing step, and they are followed by the use of existing outlier detection methods in the transformed space.
• Spectral methods do not require supervision.

The drawbacks of the spectral anomaly detection methods are as follows:

• Spectral methods are useful if both normal data and outliers are segregated for data at lower dimensions.
• The methods demand computation that is highly intricate.

Table 7. Comparison of anomaly detection in WSN based on the previous studies.

References	Detection Technique	Outlier Dimensional		Detection Mode		Detection Model
		Univariate	Multivariate	Online	Offline	Local	Global	Centralized
[104]	Clustering	x	✓	x	✓	x	✓	x
[57]	Hybrid	✓	x	x	✓	x	✓	x
[94]	Statistical	-	-	x	✓	✓	✓	x
[150]	Classification	x	✓	✓	x	✓	x	x
[38]	Statistical	✓	x	x	✓	-	-	-
[188]	Nearest neighbor	-	-	x	✓	x	✓	x
[100]	Nearest neighbor	-	-	x	✓	x	x	✓
[67]	Statistical	-	-	✓	x	x	✓	x
[47]	Nearest neighbor	-	-	x	✓	x	✓	x
[96]	Clustering	-	-	x	✓	✓	✓	x
[79]	Classification	x	✓	-	-	✓	x	x
[102]	Hybrid	x	✓	✓	x	-	-	-
[65]	Classification	-	-	✓	x	-	-	-
[55]	Classification	-	-	✓	x	-	-	-
[103]	Hybrid	✓	x	-	-	✓	✓	x
[80]	Clustering	x	-	x	✓	x	✓	x

reveals the common features of the current strategy for recognition of outliers. These strategies are specifically formulated for WSNs. Table 7 shows a comparative analysis of various strategies with respect to their dimension outlier (i.e., whether there are single or multiple variables involved), the status of recognition (i.e., online or offline), structural design, and space-time association. There are three main classifications of the current works according to Table 1: (1) Relation between sensor data of adjacent nodes, with respect to space, is employed by many strategies, but the problem lies in the selection of suitable adjacent ranges; (2) Relation between the sensor data, with respect to time, is considered by some strategies, but the appropriate selection of the sliding window dimension is an issue; (3) Some strategies consider space-time relation in the sensor data, completely ignoring the dependencies of various features of the sensor nodes on each other. These results have low precision in recognizing the outliers while they enhance the difficulty in calculations.

The formulation of an outlier recognition strategy that can be applied to diverse domains on the basis of various significant features is the main aim. These features include the flow of data and data involving multiple variables, the characteristics of the sensor node and its dependence on adjacent nodes, the determination of satisfactory and adaptable criteria for decision-making, and the power of renewal of sensor data and network topology. High-dimensional data and online approach for transfer of data with multiple variables ensure lower communication costs, and simplified computations can be managed by the outlier strategy of recognition under the specified criteria.

Additionally, for a better understanding of the WSN techniques, this study provides comparisons based on the algorithm, characteristics, and usability of these techniques, presented in

Table 8. Comparison of techniques for anomaly detection in WSNs.

References	Detection Technique	Characteristics	Usability/Limitations
[189]	kNN	The complexity of this technique is depending on the number of dimensions	Valuable, scalable, efficient, and human independent solution
[88,190]	Spectral	The detection performance is highly depending on the choices of features and distance measure	Robust to parameter perturbations and good performances with different anomaly scoring metrics
[117,191]	Gaussian	Use of the spatial correlation to determine outlying sensors and event boundaries	The accuracy is not relatively high due to the ignorance of the temporal correlation of sensor readings
[89,191]	Non-Gaussian	Use of the spatio-temporal correlations of data to locally detect outliers	Reduction of the communication cost (due to local transmission) and of the computational cost (due to the execution of tasks by the cluster-heads)
[138,191]	kernel	Use of kernel density estimator to approximate the underlying distribution of sensor data	High dependency on threshold definition (the choice of an appropriate threshold is quite difficult and a single threshold may also not be suitable for outlier detection in multi-dimensional data)
[20,191]	Histogram	Reduction of the communication cost by collecting histogram information rather than collecting raw data for centralized processing	The collection of more histogram information from the whole network will cause a communication overhead. In addition, this technique only considers one-dimensional data
[89,191]	Naïve Bayesian Network	Computation of the probabilities of each node locally	The spatial neighborhood under the dynamic change of network topology is not specified. In addition, this technique deals only with one-dimensional data
[89,191]	Bayesian Network (BN)	Use of BN to capture the spatio-temporal correlations that exist between the observations of sensor nodes and the conditional dependence between the observations of sensor attributes	Improvement of the accuracy in detecting outliers as it considers conditional dependencies between the attributes
[89,191]	Dynamic Bayesian Network	Identification of outliers by computing the posterior probability of the most recent data values in a sliding window	Possibility of operation on several data streams at once
[26,89,191]	Support vector machine	Mapping of the data into a higher dimensional feature space where it can be easily separated by a hyperplane	Identification of outliers from the data measurements collected after a long-time window and is not performed in real-time. In addition, this technique ignores the spatial correlation between neighboring nodes, which leads to inaccurate results of local outliers

. This table reveals how each defined technique can be applied for outlier detection in WSN based on their characteristics, usability, and drawbacks.

8. Evaluation of Outlier Detection Techniques

In this section, we provide an overview of used techniques for outlier detection techniques for WSNs and the requirements that an optimal outlier detection technique should meet.

Statistical-based approaches: They are more adapted when a small number of outliers exist in the WSN data. Statistical-based approaches work in an unsupervised way by building statistically-based models and applying descriptive statistics to detect outliers.

Parametric-based approaches: They are suitable for underlying WSN data that can be modeled by a probability distribution. Generally, parametric-based approaches can be used in Gaussian and non-Gaussian models. Gaussian models are used when the WSN data are compared with the neighbor in spatial correlation mode. In this case, Gaussian models need a pre-selected threshold to detect anomaly data. However, non-Gaussian models are used for local outlier detection. In this case, they use temporal correlation for outlier detection.

Non-parametric-based approaches: These approaches are interesting since no assumption about the distribution of WSNs data are required. Non-parametric-based approaches include histogram-based and kerned-based models. The first models involve determining the frequency of occurrence of different data instances. They can achieve excellent results for univariate WSNs data but less for multivariate data with interactions between the attributes. The second type, kerned-based models, uses kernel density to estimate the probability distribution function of sensor data. They can achieve excellent results with multivariate WSNs data with a good computational time.

Nearest Neighbor-based approaches: They are very convenient when the distance between two neighbor sensors is the key matter for the analysis of the WSN data. The nearest neighbor technique is one of the well-known techniques not only in WSN but also in data mining and machine learning. This technique requires the use of several distances between two sensor nodes. The goal of using nearest neighbor-based approaches is to assume that normal WSN data occur in dense neighborhoods, while outliers are far away from their closest neighbors.

Clustering-based approaches: They are used when similar WSN data instances are very important for data mining. These techniques provide WSN data in clusters with similar behavior. After that, points that are not within clusters can be considered as anomalies.

Classification-based approaches: They are divided into two types: supervised and unsupervised. Supervised techniques require labeling the WSN data and dividing it into training and testing parts. Unsupervised techniques do not require labeling the data; they determine the boundary of the normal instances and identify new instances existing outside this boundary as an outlier.

The SLR conducted in this work indicates an important need to design techniques related to outlier detection for WSN. The summary of the studied works can result in the following requirements that an optimal outlier detection technique should meet:

• High outlier detection rate.
• High scalability.
• High distinction between erroneous measurements and events.
• Low computational complexity and easy implementation.
• Consideration of correlation between attributes, spatial/spatiotemporal, and multivariate sensory data.
• Unsupervised techniques are preferred since the learning phase for WSN sensory data are a difficult task for supervised methods.
• Non-parametric methods are preferred for WSN sensory data due to the absence of knowledge about the data distribution.
• Energy-efficient and robust to communication failures.

9. Conclusions

The proposed study discussed outlier detection in WSNs. The study also provided information regarding WSN applications and definitions of outliers in previous studies. Moreover, different types of outlier sources in WSNs were discussed in detail. The study endeavored to provide a comprehensive report on outlier detection in the field of WSNs. The study used the systematic literature protocol and guidelines presented by Kitchenham. Data were collected from primary studies published from 2004 to October 2018 in the form of conference proceedings and journal articles. The study summarized and organized the existing literature related to outlier and anomaly detection in WSNs based on the defined keywords and RQs. A total of 117 primary studies were included based on the defined exclusion, inclusion, and quality criteria. The results of the proposed study presented the complete taxonomy framework for outlier detection techniques for WSNs. This study also introduced the key characteristics and brief explanations of existing outlier detection techniques, which were applied in the anticipated taxonomy framework. The study presented a list of techniques, and compared outlier detection techniques and their advantages and disadvantages used in each application domain. In addition, the challenges of outlier techniques in WSNs were explained.

Finally, the study provided a comparison of the defined techniques in terms of their characteristics, usability, and drawbacks for outlier detection in WSNs. The limitations of the existing techniques for WSNs call for new anomaly detection techniques that take into account multivariate data and the dependencies of attributes of the sensor node to offer reliable, real-time adaptive detection while considering the unique characteristics of WSNs. An interesting perspective of the proposed work would be to conduct a review of deep-learning-based methods [192] for outlier detection in WSNs.