Application of Fuzzy Analytic Hierarchy Process to Underground Mining Method Selection

Abstract

The paper proposes a problem-solving approach in the area of underground mining, related to the evaluation and selection of the optimal mining method, employing fuzzy multiple-criteria optimization. The application of fuzzy logic to decision-making in multiple-criteria optimization is particularly useful in cases where not enough information is available about a given system, and where expert knowledge and experience are an important aspect. With a straightforward objective, multiple-criteria decision-making is used to rank various mining methods relative to a set of criteria and to select the optimal solution. The considered mining methods represent possible alternatives. In addition, various criteria and subcriteria that influence the selection of the best available solution are defined and analyzed. The final decision concerning the selection of the optimal mining method is made based on mathematical optimization calculations. The paper demonstrates the proposed approach as applied in a case study.

1. Introduction

It is well-known that in most cases, a large number of criteria and subcriteria for decision-making matrices are uncertain and decision makers are unable to arrive at exact numerical values for comparing decisions. As such, mathematical methods are needed to effectively treat uncertainty, vagueness, and subjectivity. Viewed from that perspective, fuzzy logic is a scientifically based approach that relies on experience and intuition (or expert judgment). The fuzzy analytic hierarchy process (FAHP) enables the evaluation and analysis of criteria using fuzzified evaluation scales based on Saaty’s scale [1].

In recent years, scientists worldwide have introduced a number of new theories and procedures for selecting underground mining methods, which generally involve gray correlation and multiple-criteria decision-making (AHP, FAHP, TOPSIS, PROMETHEE, ELECTRE, and VIKOR). Multiple-criteria decision-making (MCDM) methods have been demonstrated as useful problem-solving tools in various fields of engineering [2,3,4]. FAHP is widely applied. Guo et al. [5] used FAHP to determine evaluation index weights when they assessed the stability of a worksite above an abandoned coalmine, which threatened the safety of a high-speed railroad line. Pipatprapa et al. [6] used structural equation modeling (SEM) and FAHP to investigate factors suitable for assessing the environmental performance of the food industry. Lee et al. [7] proposed an FAHP-based decision-making model for selecting the best location for a frontal solar facility, given that the electric power demand, fossil fuel depletion, and environmental awareness necessitate power supply from renewable sources. Chatterjee & Stević [8] used FAHP for supplier selection in supply chain management. Božanić et al. [9] compare the FAHP method to another method that uses the fuzzy approach in MCDM for ranking the locations for deep wading as a technique of crossing the river by the army tank units. Stanković et al. [10] used FAHP for determining the importance of the traffic accessibility criteria. Mallick et al. [11] applied FAHP in groundwater management of a semi-arid region.

An in-depth literature review revealed that much research has used MCDM techniques to define optimal mining methods for different ores. Özfırat [12] applied FAHP to assess the use of certain machinery in the Amasra coalmine, in order to boost production, downsize the workforce and, consequently, reduce the number of accidents. Chander et al. [13] propose a decision-making technique for the selection of the optimal underground bauxite mining method. Based on AHP and VIKOR multiple-criteria optimization techniques, their results show that the optimal mining method, in that case, was cut-and-fill. Balusa & Gorai [14] compare mining methods using five MCDM models (TOPSIS, VIKOR, ELECTRE, PROMETHEE II, and WPM). They employed AHP to determine the weights of effective criteria for the Tummalapalle uranium mine in India. The results indicate that the selected mining methods were not equally efficient. Balusa & Gorai [15] used FAHP to select suitable underground mining methods. Bogdanovic et al. [16] employed a combination of AHP and PROMETHEE to select the most suitable mining method for the Čoka Marin underground mine in Serbia: AHP to analyze the structure of the problem and determine criteria weights, and PROMETHEE for final ranking and sensitivity analysis. Alpay & Yavuz [17] developed a decision-making support system for the Karaburun underground chromite mine in Eskisehir, Turkey. They applied AHP to find acceptable alternatives. Yazdani-Chamzini et al. [18] proposed a selection model for the optimal mining method at the Angouran mine, one of the main producers of zinc in Iran. They developed the model based on FAHP and FTOPSIS. Then Asadi et al. [19] used a TOPSIS model to select the optimal mining method for the Tazareh coalmine in Iran. Javanshirgiv & Safari [20] applied fuzzy TOPSIS to select the optimal mining method for the Kamar Mahdi mine in Iran. Ataei et al. [21] also used TOPSIS to do the same for the Jajarm mine in Iran. For this mine, Naghadehi et al. [22] proposed a combination of FAHP and AHP: FAHP to determine criteria weights and AHP to rank the mining methods. On the other hand, some researchers have employed MCDM models to address mine dewatering, which is a parallel process in mining operations. Bajić et al. [23] describe the selection of the optimal groundwater control system for the open cast-mine Buvač (Bosnia and Herzegovina), using soft optimization and fuzzy optimization (VIKOR and FAHP) techniques. For the same case study, Polomčić et al. [24] performed mathematical optimization calculations applying fuzzy dynamic TOPSIS.

The present paper describes and tests a decision-making algorithm for the selection of the optimal underground mining method. The algorithm is applied in a real case study to the Borska Reka copper mine (Serbia). First, the relevant alternatives are identified and then the selection criteria are analyzed. This if followed by MCDM, to select the optimal mining method. Finally, the best choice is the method that maximizes the output of useful components and minimizes tailings. In addition, the optimal solution involves the shortest mining time and the lowest consumption of energy and materials, along with full safety at work and no adverse effect on mine development.

2. Case Study

The FAHP-based methodology for decision-making on the optimal underground mining method was applied in a real case study. The study area is the Borska Reka copper mine in eastern Serbia (Figure 1). In terms of regional metallogeny, the Bor ore field and Borska Reka copper mine belong the so-called Bor Zone, which coincides with the Timok igneous complex. In geologic terms, the sediments are composed of volcanites and volcanoclastic rocks, quartz-diorite porphyritic rocks, hydrothermally altered volcanic and volcanoclastic rocks, pelites with tuffs and tuffites, conglomerates, sandstones, Quaternary alluvial sediments, and technogenic deposits.

The mineral composition of the ore from Borska Reka includes chalcopyrite, covellite, chalcosine, rutile, hematite, magnetite, sphalerite, galenite, tetrahedrite, tennantite, digenite, cubanite, and native gold. The prevalent ore is pyrite, the dominant copper mineral is chalcopyrite, and there are covellite, chalcosine, and bornite to a lesser extent. On the other hand, enargite and molybdenite are very rare. However, this ratio of copper minerals is not uniform across the ore body. Certain parts have elevated concentrations of covellite, chalcosine and bornite, but they are rarely dominant. There are also frequent occurrences of rutile, magnetite and hematite, as well as sphalerite and galenite. Tetrahedrite tennantite, digenite, cubanite and native gold are very rare and occur sporadically.

Past exploration has revealed that the Borska Reka ore body is among very large deposits in the geometric sense, with elevated copper concentrations. The ore body is at an angle of 45°–55°. Its maximum length is ~1.410 m and maximum width 635 m. The ore body is deep; the average ultimate depth is ~920 m from the ground surface.

3. Methodology

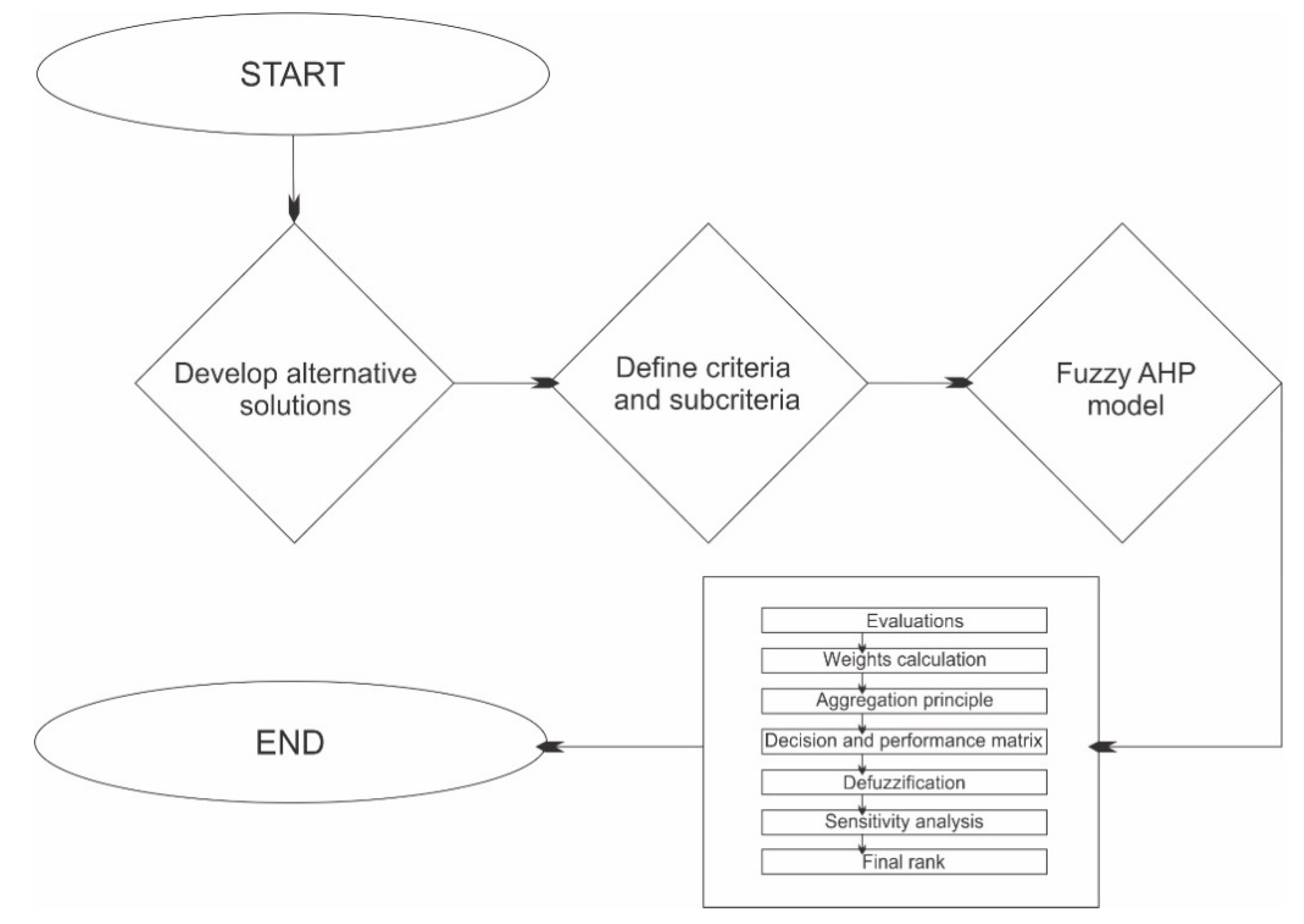
The underground mining decision-making algorithm is shown in Figure 2. FAHP is the optimization technique. In general, one of the limiting factors of conventional methods applied to select the optimal mining technology is often a lack of data. Mines are complex geologic systems and mining operations are dynamic as the size and depth of the mine constantly increase (in plain view and elevation). As such, mining requires continual adaptation to new conditions. The contribution to science of decision-making methods based on fuzzy logic is the ability to focus on overcoming uncertainties inherent in mining method selection.

On the other hand, compared to other methods that include the fuzzy approach, FAHP offers certain specific advantages in optimal underground mining method selection. Because of the depth of the ore deposit and imprecise data typical of such a geologic system, which make it impossible to accurately define all the physical, mechanical and geologic conditions, the entire mining process requires constant “learning” and gradual, hierarchical problem-solving, to achieve the set objective. FAHP involves a continual “learning process”, along with discussion among experts and prioritizing.

Consequently, the use of FAHP highlighted the quality of this technique based on expert judgment or, in other words, reflected the decision-makers’ knowledge and experience in evaluating information, to arrive at an optimal decision concerning multiple alternative underground mining methods.

FAHP is a combination of the conventional AHP method [1] and the fuzzy set theory [25]. It is implemented using triangular fuzzy numbers [26]. TFN (Figure 3) in set R is a triangular fuzzy number if its membership function ${\mu }_M\left(x\right):R\to \left[0,1\right]$ is defined as follows:

$${\mu }_{TFN}\left(x\right) = \{\begin{array}{c}\frac{x}{s-l}-\frac{l}{s-l}, x\in \left[l,s\right]\\ \frac{x}{s-d}-\frac{d}{s-d}, x\in \left[s,d\right]\\ 0, x\notin \left[l,d\right]\end{array}$$

where $l\le s\le d$.

The modification of AHP into FAHP is in that the relative importance of the optimality criteria is described by linguistic variables [27], determined by the expert, and modeled by triangular fuzzy numbers (TFN). In other words, fuzzy numbers describe the pairwise comparison matrices of the optimality criteria. The fuzzified Saaty scale, proposed by many authors [26,28,29,30] is used. One of them is shown in

Table 1. Fuzzified scale [26,30].

Linguistic Variable (Definition of Importance)	AHP Scale	FAHP Scale
		TFN $(0.5\le \mathit{\alpha }\le 2)$
Equal	1	(1, 1, 1 + α)
Weak	3	(3 − α, 3, 3 + α)
Strong	5	(5 − α, 5, 5 + α)
Proven dominance	7	(7 − α, 7, 7 + α)
Absolute dominance	9	(9 − α, 9, 9)
Intermediate values	2, 4, 6, 8	(x − 1, x, x + 1) x = 2, 4, 6,8

.

Chang [26] made the first development steps and Deng [30] modified the method. Also, Bajić et al. [23] applied fuzzy optimization to mine hydrogeology. Based on the above, the FAHP analysis was implemented in the following steps:

(a) First the problem relating to the selection of the underground mining method was examined and the alternatives and criteria/subcriteria that influence the selection of the optimal alternative were identified. This involved the selection of a team of experts and the “exploitation” of their knowledge and experience.

(b) Pairs of criteria (Equation (1)), subcriteria (Equation (2)) and alternatives (Equation (3)) were evaluated and compared using the FAHP scale (Table 1):

$$A = \left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1m}\\ a_{21}& a_{22}& \cdots & a_{2m}\\ \cdots & \cdots & \cdots & \cdots \\ a_{m1}& a_{m2}& \cdots & a_{mm}\end{array}\right]$$

(1)

where: $a_{ij}=1$ for every $i=j$, $\left(i,j=1,2,\dots ,m\right)$ and $a_{ij}=\frac{1}{a_{ji}}$

$$A_j = \left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1k_j}\\ a_{21}& a_{22}& \cdots & a_{2k_j}\\ \cdots & \cdots & \cdots & \cdots \\ a_{k_{j}1}& a_{k_{j}2}& \cdots & a_{k_j{k}_j}\end{array}\right]$$

(2)

where criterion $C_j$ is composed of $k_j$ subcriteria,

$$Y_k = \left[\begin{array}{cccc}{a}_{11}& a_{12}& \cdots & a_{1N}\\ a_{21}& a_{22}& \cdots & a_{2N}\\ \cdots & \cdots & \cdots & \cdots \\ a_{N1}& a_{N2}& \cdots & a_{NN}\end{array}\right]$$

(3)

where N is the number of alternatives relative to each of the K subcriteria; $k = 1,2,\dots ,K$.

(c) The weights of all three matrices from step b are determined gradually, using fuzzy extent analysis [26] or fuzzy arithmetic and the extension principle [31]. All the resulting weights are normalized:

$$w_i={\displaystyle \sum _{j=1}^m{a}_{ij}\otimes }{\left[{\displaystyle \sum _{k=1}^m{\displaystyle \sum _{l=1}^m{a}_{kl}}}\right]}^{-1}$$

(4)

where $i=1,2,\dots ,m$

$$w_j^{\prime }=\left({{\displaystyle \sum _{l=1}^{k_j}{a}_{il}\otimes \left[{\displaystyle \sum _{i=1}^{k_j}{\displaystyle \sum _{l=1}^{k_j}{a}_{il}}}\right]}}^{-1}\right)\otimes w_j$$

(5)

where $j=1,2,\dots ,m$; $p=1,2,\dots ,k_j$

$$W=\left(w_1^1,w_1^2,\dots ,w_1^{k_1};w_2^1,w_2^2\dots w_2^{k_2};\dots ;w_j^1,w_j^2,\dots ,w_j^{k_j};\dots ;w_m^1,w_m^2,\dots ,w_m^{k_m}\right)$$

(6)

where W are subcriteria weights, whose total “length” is K

$$W=\left(W_1,W_2,\dots ,W_K\right)$$

(7)

(d) The next step is the application of the aggregation principle, to reduce two hierarchy tiers (criteria and subcriteria) to a single tier:

$$K={\displaystyle \sum }_{j=1}^m{k}_j$$

(8)

where $C_1,C_2,\dots ,C_m$ is a set of m criteria, each with its subcriteria; $k_j$—number of subcriteria of the j-th criterion.

(e) The fuzzy decision matrix and fuzzy performance matrix are now calculated. The fuzzy decision matrix results from calculations of the fuzzy extent analysis from step c for the alternatives:

$$X = \left[\begin{array}{cccc}{x}_{11}& x_{12}& \cdots & x_{1K}\\ x_{21}& x_{22}& \cdots & x_{2K}\\ \cdots & \cdots & \cdots & \cdots \\ x_{N1}& x_{N2}& \cdots & x_{NK}\end{array}\right]$$

(9)

and the fuzzy performance matrix represents the overall performance of each alternative relative to all the subcriteria:

$$Z = \left[\begin{array}{cccc}{x}_{11}\otimes W_1& x_{12}\otimes W_2& \cdots & x_{1K}\otimes W_K\\ x_{21}\otimes W_1& x_{22}\otimes W_2& \cdots & x_{2K}\otimes W_K\\ \cdots & \cdots & \cdots & \cdots \\ x_{N1}\otimes W_1& x_{N2}\otimes W_2& \cdots & x_{NK}\otimes W_K\end{array}\right]$$

(10)

(f) The ultimate values of the alternatives are calculated in the form of triangular fuzzy numbers:

$$F_i = {\displaystyle \sum }_{j=1}^K{x}_{ij}\otimes W_j$$

(11)

(g) The final step includes defuzzification [32], ranking of alternatives and, in parallel, sensitivity analysis [33,34]. The optimal alternative is the one with the greatest weight. The sum of the weights of all the alternatives is equal to zero:

$$defuzzy\left(A\right)=\frac{\left(d-l\right)+\left(s-l\right)}{3}+l$$

(12)

The sensitivity analysis is performed by introducing the optimization index λ. The “total integral”—I is calculated, to express the expert’s risk assessment (0—pessimistic, 1—optimistic, and 0.5—moderate):

$$I = \frac{\left(d\lambda +s+\left(1-\lambda \right)l\right)}{2}, \lambda \in \left[0,1\right]$$

(13)

where: l, s and d are elements of the triangular fuzzy number.

A special-purpose application, Fuzzy-GWCS2 based on Microsoft Excel, was developed for the above mathematical optimization calculations. The objective was to provide clearer insight into the results and facilitate monitoring of changes in the final calculations during the sensitivity analysis.

4. Results and Discussion

FAHP-aided selection of underground mining methods enables efficient decision-making and facilitates solving of complex problems that involve vagueness and multiple uncertainties, like in the case of the Borska Reka copper mine. The first uncertainty was associated with the identification of all lithostratigraphic units. This copper deposit is highly specific, with occurrences of numerous minerals. On the other hand, there was a lack of information on its geometry and certain physical indicators and parameters pertaining to the ore and surrounding rocks.

Calculations were made using the MCDM model (or the algorithm shown in Figure 2), to determine the best mining alternative for the Borska Reka copper mine. The procedure was gradual, following the above steps a–g and using the specially developed Fuzzy-GWCS2 application.

The selection of a team of experts and “exploitation” of their knowledge and experience play a key role in decision- making and underground mining method selection. Teamwork ensures technically sustainable, economically viable and, above all, safe mining of copper ore.

Successful underground mining method selection requires substantial knowledge about the geology of the mineral ore deposit. In addition, the depth of the mine necessitates exploratory drilling experience. Because of the specific features of copper deposits, petrologists, mineralogists and geochemists contribute key knowledge and analysis of the minerals and their physical parameters. Hydrogeologists examine groundwater flow to the mine and ways of protecting the mine. Experts in economic geology and mine management assess the technoeconomic viability of mining. Geologists define the characteristics of the ore deposit. As a result, mining experts gain insight into applicable underground mining methods and develop alternative solutions. Engineers then synthesize the information and define and asses the criteria than affect the selection of the preferred underground mining method. The quality of the identification of mining conditions and the experts’ knowledge and experience directly influence the selection of the optimal method.

The given problem—selection of the optimal underground mining method—was examined in step a. Then the criteria and subcriteria that influence the selection were defined. Based on literature sources that address the selection of underground mining methods and the governing factors [18,35], the following three criteria were identified: technical, production, and economic.

The criteria were subdivided into subcriteria, in this case 18, as shown in

Table 2. Defining of criteria and subcriteria.

Criterion	Symbol	Subcriteria	Symbol
Technical	T	Depth of ore body	T1
		Thickness of ore body	T2
		Shape of ore body	T3
		Value of ore	T4
		Ore body slope (angle)	T5
		Rock hardness and stability	T6
		Form of ore body and contact with neighboring rocks	T7
		Mineral and chemical composition of ore	T8
Production	P	Mining method productivity and output	P1
		Safety at work	P2
		Adverse environmental impact	P3
		Ore dilution	P4
		Ore impoverishment	P5
		Ventilation	P6
		Hydrologic conditions	P7
Economic	E	Capital expenditure	E1
		Mining costs	E2
		Maintenance costs	E3

. Given the different types of essentially opposed criteria, the MCDM approach was a reasonable and justifiable choice.

In addition, five different alternatives (underground mining methods) were defined, including:

• Alternative 1—sublevel caving;
• Alternative 2—cut and fill;
• Alternative 3—shrinkage stoping;
• Alternative 4—block caving;
• Alternative 5—vertical crater retreat (VCR)

Mining methods depend on the shape, size and depth of the ore body, physical and mechanical properties of the ore and accompanying rocks, hydrologic conditions, sensitivity of ground surface to mining, mineral and chemical composition of the ore, mineral distribution, and value of ore. Consequently, all these characteristics are important and need to be taken into account when a decision is made about the optimal mining method.

In the case of ore bodies of irregular shape, such as that at Borska Reka, priority is usually given to a caving method. The ore body size is often the decisive factor, because it reflects ore reserves. In addition, the thickness of the ore body is important, as are its depth, angle, type of contact and tectonic circumstances. At large depths, the cut-and-fill method should be given priority over block caving.

In the present case study, the mineral and chemical composition was important because of the presence of pyrite and pyrrhotite. Copper pyrite ore, with more than 40% of sulfur, as well as other sulfide ores with elevated concentrations of pyrite and pyrrhotite, are susceptible to oxidation, self-ignition and sticking. If the ore is left in a crushed state for a long time, it becomes oxidized and warm in contact with air and humidity. This reduces the ore utilization rate. As such, if the ore contains large amounts of pyrite and pyrrhotite, cut-and-fill methods are given priority over shrinkage stoping or block caving methods. If the ore is highly valuable, often the method of choice is less effective but with a much higher ore utilization rate than vice-versa.

Ore impoverishment is the reduction in metal content of the produced ore, relative to that of the excavated block. Shrinkage stoping and caving methods typically lead to greater impoverishment. Also, even cut-and-fill methods, where the ore is loaded by means of mechanical devices (scrapers or shovels) directly from the fill, tend to result in a higher level of impoverishment. In general, however, cut-and-fill and block caving, compared to other methods, cause less impoverishment. In the case of the room-and-pillar methods, secondary cutting invariably leads to impoverishment because the ore is mixed with side or roof gangue.

Physical and mechanical characteristics are also taken into account. Rock hardness and stability tend to be the most important parameters because they affect the span and surface of the tunnels. With regard to hydrologic circumstances, the amount and properties of groundwater need to be known, particularly its effect on “plastic” rocks such as clays. The presence of water-bearing rocks and stagnant groundwater hinder the shrinkage stoping method. The preferred technologies are cut-and- fill (with hydraulic or paste backfill) or room-and-pillar mining methods. If the ore mineral distribution is not uniform, cut-and-fill methods are given priority.

Safety at work is an extremely important factor. The economic advantages of a given mining method should not threaten people’s lives, operations or the safety of mine installations. The selected mining method should not be capable of causing fire, inrush of groundwater or surface water, caving of underground or above-ground mine walls or other structural components, or endanger miners and mining. A healthy work environment requires good ventilation (fresh air supply and venting of harmful gases and dust), proper illumination and safe access to work stations, as well as machinery to relieve miners of heavy manual work and measures to ensure health protection. Certain underground mining methods degrade the environment by damaging the soil and potentially causing land subsidence. On the other hand, the productivity of the mining method is important in the technoeconomic assessment of a mine, given that a higher productivity leads to greater output. The productivity of a method is based on the rate of mining of blocks or parts of the ore body, and the capacity of the ore body depends on the ability to mine all active levels. The costs of mining are also examined, because spending is required before there can be a return on investment (such as for shafts or declines, mining equipment, crushers, transporters, and venting and dewatering systems). Also, there are costs associated with excavation (e.g., materials for tunneling and consumables such as ANFO explosives, detonators, drilling tools, diesel fuel, oil, lubricants, loader and transporter tires, steel, steel cables and cement, as well as the preparation and distribution of backfill paste, along with associated labor) and maintenance costs (of machinery and installations, as well as depreciation, overhead, etc.).

In view of the above facts and given that Borska Reka belongs to the group of ore bodies with relatively high copper concentrations, that the ore body is deep and that there are structures and facilities on the land surface, the research warranted the consideration of five high-productivity mining methods, which would ensure economically viable mining.

The criteria, subcriteria and alternatives were evaluated and the scores were input parameters for the MCDA model. Their weights determined in the form of fuzzy numbers per steps b and c. Equation (1) was used to evaluate the criteria, Equation (2) the subcriteria, and Equation (3) the alternatives. Evaluation was based on pairwise comparison (of criteria, subcriteria and alternatives), using linguistic variables and their numerical values from FAHP scales (Table 1).

Table 3. Evaluation of criteria.

	T			P			E
	TFN			TFN			TFN
T	1	1	1	0.33	0.5	1	1	2	3
P	1	2	3	1	1	1	1	2	3
E	0.33	0.5	1	0.33	0.5	1	1	1	1

shows the criteria scores in the form of triangular fuzzy numbers and their relative importance. Equations (4) through (7) were used to calculate weights by fuzzy extent analysis.

With regard to the selection of the most suitable underground mining method in the present case study, the technical and production criteria were given a slight advantage over the economic criterion. Then the subcriteria were evaluated. Given that each criterion was subdivided into a number of subcriteria (Table 2), this step involved the determination of the importance of all the subcriteria in a group, relative to each of the criteria.

Table 4. Evaluation of technical subcriteria.

	T1			T2			T3			T4
	TFN			TFN			TFN			TFN
T1	1	1	1	3	4	5	7	8	9	1	3	5
T2	0.2	0.25	0.33	1	1	1	7	9	9	1	2	3
T3	0.11	0.125	0.14	0.11	0.11	0.14	1	1	1	1	2	3
T4	0.2	0.33	1	0.33	0.5	1	0.33	0.5	1	1	1	1
T5	0.2	0.25	0.33	0.14	0.2	0.33	3	5	7	0.14	0.166	0.2
T6	0.33	0.5	1	0.2	0.33	1	7	8	9	0.11	0.14	0.2
T7	0.11	0.14	0.2	0.11	0.14	0.2	7	8	9	0.11	0.14	0.2
T8	0.14	0.2	0.33	0.33	0.5	1	3	5	7	0.2	0.33	1
	T5			T6			T7			T8
	TFN			TFN			TFN			TFN
T1	3	4	5	1	2	3	5	7	9	3	5	7
T2	3	5	7	1	3	5	5	7	9	1	2	3
T3	0.14	0.2	0.33	0.11	0.125	0.14	0.11	0.125	0.14	0.14	0.2	0.33
T4	5	6	7	5	7	9	5	7	9	1	3	5
T5	1	1	1	0.14	0.2	0.33	1	3	5	0.14	0.2	0.33
T6	3	5	7	1	1	1	7	9	9	1	2	3
T7	0.2	0.33	1	0.11	0.11	0.14	1	1	1	0.2	0.25	0.33
T8	3	5	7	0.33	0.5	1	3	4	5	1	1	1

shows the technical subcriteria scores. The relative weights of the technical subcriteria are presented in

Table A1. Weights of technical subcriteria.

Subcriteria	Weights (TFN)
T1	0.119	0.219	0.403
T2	0.095	0.188	0.342
T3	0.013	0.025	0.048
T4	0.088	0.163	0.312
T5	0.028	0.064	0.133
T6	0.097	0.167	0.286
T7	0.044	0.065	0.111
T8	0.054	0.106	0.214

(Appendix A).

Among the technical subcriteria, the most important were T₁—ore body depth and T₂—ore body thickness, which were given a slight advantage over the other subcriteria, per the FAHP scale.

Table 5. Evaluation of production criteria.

Cr.	P1			P2			P3			P4			P5			P6			P7
	TFN			TFN			TFN			TFN			TFN			TFN			TFN
P1	1	1	1	0.2	0.25	0.33	0.2	0.33	1	0.33	0.5	1	1	3	5	0.33	0.5	1	3	4	5
P2	3	4	5	1	1	1	3	4	5	3	5	7	1	3	5	1	2	3	3	4	5
P3	1	3	5	0.2	0.25	0.33	1	1	1	1	3	5	1	2	3	1	3	5	1	2	3
P4	1	2	3	0.14	0.2	0.33	0.2	0.33	1	1	1	1	0.2	0.33	1	0.2	0.25	0.33	1	2	3
P5	0.2	0.33	1	0.2	0.33	1	0.33	0.5	1	1	3	5	1	1	1	0.2	0.33	1	1	2	3
P6	1	2	3	0.33	0.5	1	0.2	0.33	1	3	4	5	1	3	5	1	1	1	1	3	5
P7	0.2	0.25	0.33	0.2	0.25	0.33	0.33	0.5	1	0.33	0.5	1	0.33	0.5	1	0.2	0.33	1	1	1	1

shows the relative scores of the production subcriteria. The relative weight of each subcriterion in the form of a fuzzy number is presented in

Table A2. Weights of production criteria.

Subcriteria	Weights (TFN)
P1	0.052	0.112	0.318
P2	0.128	0.300	0.688
P3	0.053	0.186	0.495
P4	0.032	0.079	0.214
P5	0.033	0.097	0.288
P6	0.064	0.180	0.466
P7	0.022	0.043	0.125

(Appendix A). Among the production subcriteria, a slight advantage, per the FAHP scale, was given to P₂—safety at work, P₃—environmental impact, and P₆—ventilation.

Table 6. Evaluation of economic subcriteria.

Cr.	E1			E2			E3
	TFN			TFN			TFN
E1	1	1	1	0.33	0.5	1	0.2	0.33	1
E2	1	2	3	1	1	1	1	3	5
E3	1	3	5	0.2	0.33	1	1	1	1

shows the relative scores of the economic subcriteria. The relative weight of each subcriterion in the form of a fuzzy number is presented in

Table A3. Weights of economic subcriteria.

Subcriteria	E1	E2	E3
	TFN	TFN	TFN
E1	0.080	0.150	0.446
E2	0.158	0.493	1.337
E3	0.116	0.356	1.040

(Appendix A).

The alternatives were evaluated in the next step, by pairwise comparison relative to each subcriterion. This involved 18 comparisons. The results are shown in

Table 7. Evaluation of alternatives relative to technical subcriteria.

T1	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.2	0.33	1	0.2	0.33	1	1	2	3	0.2	0.33	1
A2	1	3	5	1	1	1	1	2	3	7	9	9	3	4	5
A3	1	3	5	0.33	0.5	1	1	1	1	5	6	7	1	3	5
A4	0.33	0.5	1	0.11	0.11	0.14	0.14	0.166	0.2	1	1	1	0.14	0.2	0.33
A5	1	3	5	0.2	0.25	0.33	0.2	0.33	1	3	5	7	1	1	1
T2	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	7	9	9	3	4	5	1	3	5	1	2	3
A2	0.11	0.11	0.14	1	1	1	0.2	0.25	0.33	0.2	0.33	1	0.2	0.25	0.33
A3	0.2	0.25	0.33	3	4	5	1	1	1	1	3	5	0.2	0.25	0.33
A4	0.2	0.33	1	1	3	5	0.2	0.33	1	1	1	1	0.2	0.33	1
A5	0.33	0.5	1	3	4	5	3	4	5	1	3	5	1	1	1
T3	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	1	3	5	3	4	5	7	9	9	3	4	5
A2	0.2	0.33	1	1	1	1	1	3	5	3	5	7	1	3	5
A3	0.2	0.25	0.33	0.2	0.33	1	1	1	1	1	3	5	0.33	0.5	1
A4	0.11	0.11	0.14	0.14	0.2	0.33	0.2	0.33	1	1	1	1	0.2	0.25	0.33
A5	0.2	0.25	0.33	0.2	0.33	1	1	2	3	3	4	5	1	1	1
T4	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	3	5	7	1	3	5	3	4	5	0.33	0.5	1
A2	0.14	0.2	0.33	1	1	1	0.2	0.33	1	0.33	0.5	1	0.11	0.11	0.14
A3	0.2	0.33	1	1	3	5	1	1	1	1	3	5	0.2	0.25	0.33
A4	0.2	0.25	0.33	1	2	3	0.2	0.33	1	1	1	1	0.14	0.2	0.33
A5	1	2	3	7	9	9	3	4	5	3	5	7	1	1	1
T5	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	1	3	5	7	9	9	5	6	7	1	2	3
A2	0.2	0.33	1	1	1	1	3	4	5	1	3	5	1	3	5
A3	0.11	0.11	0.14	0.2	0.25	0.33	1	1	1	0.2	0.33	1	0.2	0.25	0.33
A4	0.14	0.166	0.2	0.2	0.33	1	1	3	5	1	1	1	0.2	0.25	0.33
A5	0.33	0.5	1	0.2	0.33	1	3	4	5	3	4	5	1	1	1
T6	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.2	0.33	1	1	3	5	3	4	5	0.2	0.33	1
A2	1	3	5	1	1	1	3	5	7	7	9	9	1	2	3
A3	0.2	0.33	1	0.14	0.2	0.33	1	1	1	1	3	5	0.2	0.25	0.33
A4	0.2	0.25	0.33	0.11	0.11	0.14	0.2	0.33	1	1	1	1	0.2	0.25	0.33
A5	1	3	5	0.33	0.5	1	3	4	5	3	4	5	1	1	1
T7	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.2	0.25	0.33	0.2	0.33	1	0.11	0.11	0.14	0.33	0.5	1
A2	3	4	5	1	1	1	1	2	3	0.33	0.5	1	3	4	5
A3	1	3	5	0.33	0.5	1	1	1	1	0.2	0.33	1	1	3	5
A4	7	9	9	1	2	3	1	3	5	1	1	1	3	5	7
A5	1	2	3	0.2	0.25	0.33	0.2	0.33	1	0.14	0.2	0.33	1	1	1
T8	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.14	0.166	0.2	1	3	5	0.2	0.25	0.33	0.2	0.33	1
A2	5	6	7	1	1	1	7	9	9	1	2	3	1	3	5
A3	0.2	0.33	1	0.11	0.11	0.14	1	1	1	0.2	0.25	0.33	0.2	0.25	0.33
A4	3	4	5	0.33	0.5	1	3	4	5	1	1	1	1	3	5
A5	1	3	5	0.2	0.33	1	3	4	5	0.2	0.33	1	1	1	1

,

Table 8. Evaluation of alternatives relative to production subcriteria.

P1	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	3	4	5	1	3	5	3	4	5	0.33	0.5	1
A2	0.2	0.25	0.33	1	1	1	0.2	0.25	0.33	0.33	0.5	1	0.11	0.11	0.14
A3	0.2	0.33	1	3	4	5	1	1	1	1	3	5	0.2	0.25	0.33
A4	0.2	0.25	0.33	1	2	3	0.2	0.33	1	1	1	1	0.14	0.2	0.33
A5	1	2	3	7	9	9	3	4	5	3	5	7	1	1	1
P2	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	1	3	5	3	5	7	5	6	7	0.2	0.33	1
A2	0.2	0.33	1	1	1	1	1	3	5	3	4	5	0.2	0.25	0.33
A3	0.14	0.2	0.33	0.2	0.33	1	1	1	1	1	2	3	0.14	0.166	0.2
A4	0.14	0.166	0.2	0.2	0.25	0.33	0.33	0.5	1	1	1	1	0.11	0.11	0.14
A5	1	3	5	3	4	5	5	6	7	7	9	9	1	1	1
P3	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.11	0.11	0.14	0.2	0.25	0.33	0.14	0.2	0.33	0.33	0.5	1
A2	7	9	9	1	1	1	3	4	5	1	2	3	5	6	7
A3	3	4	5	0.2	0.25	0.33	1	1	1	0.33	0.5	1	1	2	3
A4	3	5	7	0.33	0.5	1	1	2	3	1	1	1	3	4	5
A5	1	2	3	0.14	0.166	0.2	0.33	0.5	1	0.2	0.25	0.33	1	1	1
P4	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.14	0.166	0.2	0.2	0.33	1	0.33	0.5	1	0.2	0.33	1
A2	5	6	7	1	1	1	3	4	5	7	9	9	1	3	5
A3	1	3	5	0.2	0.25	0.33	1	1	1	3	4	5	0.2	0.33	1
A4	1	2	3	0.11	0.11	0.14	0.2	0.25	0.33	1	1	1	0.14	0.2	0.33
A5	1	3	5	0.2	0.33	1	1	3	5	3	5	7	1	1	1
P5	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.11	0.11	0.14	0.2	0.33	1	0.2	0.25	0.33	0.14	0.2	0.33
A2	7	9	9	1	1	1	5	6	7	1	3	5	1	2	3
A3	1	3	5	0.14	0.166	0.2	1	1	1	0.33	0.5	1	0.2	0.33	1
A4	3	4	5	0.2	0.33	1	1	2	3	1	1	1	0.2	0.33	1
A5	3	5	7	0.33	0.5	1	1	3	5	1	3	5	1	1	1
P6	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.2	0.25	0.33	0.11	0.11	0.14	0.14	0.2	0.33	0.33	0.5	1
A2	3	4	5	1	1	1	0.2	0.25	0.33	0.2	0.25	0.33	1	2	3
A3	7	9	9	3	4	5	1	1	1	1	3	5	5	6	7
A4	3	5	7	3	4	5	0.2	0.33	1	1	1	1	3	4	5
A5	1	2	3	0.33	0.5	1	0.14	0.166	0.2	0.2	0.25	0.33	1	1	1
P7	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	0.11	0.11	0.14	0.2	0.25	0.33	0.14	0.166	0.2	0.2	0.33	1
A2	7	9	9	1	1	1	3	4	5	1	3	5	5	6	7
A3	3	4	5	0.2	0.25	0.33	1	1	1	0.2	0.33	1	1	3	5
A4	5	6	7	0.2	0.33	1	1	3	5	1	1	1	3	4	5
A5	1	3	5	0.14	0.166	0.2	0.2	0.33	1	0.2	0.25	0.33	1	1	1

and

Table 9. Evaluation of alternatives relative to economic subcriteria.

E1	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	1	2	3	0.2	0.33	1	0.14	0.166	0.2	0.2	0.33	1
A2	0.33	0.5	1	1	1	1	0.2	0.25	0.33	0.11	0.11	0.14	0.2	0.25	0.33
A3	1	3	5	3	4	5	1	1	1	0.2	0.33	1	1	3	5
A4	5	6	7	7	9	9	1	3	5	1	1	1	3	4	5
A5	1	3	5	3	4	5	0.2	0.33	1	0.2	0.25	0.33	1	1	1
E2	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	3	4	5	1	3	5	1	3	5	0.2	0.33	1
A2	0.2	0.25	0.33	1	1	1	0.2	0.25	0.33	1	2	3	0.11	0.11	0.14
A3	0.2	0.33	1	3	4	5	1	1	1	1	2	3	0.2	0.25	0.33
A4	0.2	0.33	1	0.33	0.5	1	0.33	0.5	1	1	1	1	0.14	0.166	0.2
A5	1	3	5	7	9	9	3	4	5	5	6	7	1	1	1
E3	A1			A2			A3			A4			A5
	TFN			TFN			TFN			TFN			TFN
A1	1	1	1	7	9	9	3	4	5	5	6	7	1	2	3
A2	0.11	0.11	0.14	1	1	1	0.2	0.25	0.33	0.33	0.5	1	0.14	0.2	0.33
A3	0.2	0.25	0.33	3	4	5	1	1	1	1	3	5	0.2	0.33	1
A4	0.14	0.166	0.2	1	2	3	0.2	0.33	1	1	1	1	0.2	0.25	0.33
A5	0.33	0.5	1	3	5	7	1	3	5	3	4	5	1	1	1

. The respective calculated weight vectors are presented in

Table A4. Weights of alternatives relative to technical subcriteria.

T1	Weights (TFN)			T5	Weights (TFN)
A1	0.039	0.083	0.225	A1	0.229	0.430	0.758
A2	0.197	0.395	0.740	A2	0.095	0.232	0.515
A3	0.126	0.281	0.612	A3	0.026	0.039	0.085
A4	0.026	0.041	0.086	A4	0.039	0.097	0.228
A5	0.082	0.199	0.461	A5	0.115	0.201	0.394
T2	Weights (TFN)			T6	Weights (TFN)
A1	0.205	0.405	0.741	A1	0.082	0.181	0.419
A2	0.027	0.041	0.090	A2	0.198	0.417	0.807
A3	0.085	0.181	0.375	A3	0.039	0.099	0.247
A4	0.041	0.106	0.290	A4	0.026	0.040	0.090
A5	0.131	0.266	0.547	A5	0.127	0.261	0.548
T3	Weights (TFN)			T7	Weights (TFN)
A1	0.229	0.438	0.807	A1	0.029	0.048	0.118
A2	0.094	0.257	0.613	A2	0.134	0.254	0.513
A3	0.042	0.106	0.268	A3	0.057	0.173	0.444
A4	0.025	0.039	0.090	A4	0.209	0.441	0.855
A5	0.082	0.158	0.333	A5	0.041	0.083	0.193
T4	Weights (TFN)			T8	Weights (TFN)
A1	0.127	0.281	0.612	A1	0.039	0.097	0.228
A2	0.027	0.044	0.111	A2	0.229	0.430	0.758
A3	0.052	0.158	0.397	A3	0.026	0.039	0.085
A4	0.039	0.078	0.182	A4	0.127	0.256	0.515
A5	0.229	0.437	0.805	A5	0.082	0.177	0.394

,

Table A5. Weights of alternatives relative to production subcriteria.

P1	Weights (TFN)
A1	0.132	0.260	0.513
A2	0.029	0.044	0.084
A3	0.086	0.179	0.372
A4	0.040	0.078	0.171
A5	0.239	0.438	0.755
P2	Weights (TFN)
A1	0.149	0.291	0.569
A2	0.078	0.163	0.334
A3	0.036	0.070	0.150
A4	0.026	0.038	0.072
A5	0.248	0.437	0.732
P3	Weights (TFN)
A1	0.029	0.042	0.079
A2	0.280	0.456	0.708
A3	0.091	0.160	0.292
A4	0.137	0.259	0.481
A5	0.044	0.081	0.156
P4	Weights (TFN)
A1	0.028	0.046	0.127
A2	0.252	0.462	0.820
A3	0.080	0.172	0.374
A4	0.036	0.071	0.146
A5	0.092	0.247	0.577
P5	Weights (TFN)
A1	0.025	0.039	0.090
A2	0.227	0.437	0.805
A3	0.040	0.104	0.264
A4	0.082	0.159	0.354
A5	0.096	0.260	0.612
P6	Weights (TFN)
A1	0.028	0.040	0.075
A2	0.084	0.147	0.260
A3	0.265	0.452	0.728
A4	0.159	0.282	0.513
A5	0.042	0.077	0.149
P7	Weights (TFN)
A1	0.024	0.035	0.072
A2	0.248	0.438	0.734
A3	0.079	0.163	0.335
A4	0.149	0.273	0.516
A5	0.037	0.090	0.204

and

Table A6. Weights of alternatives relative to economic subcriteria.

E1	Weights (TFN)			E2	Weights (TFN)			E3	Weights (TFN)
A1	0.039	0.078	0.188	A1	0.098	0.236	0.513	A1	0.263	0.441	0.713
A2	0.028	0.043	0.085	A2	0.039	0.075	0.145	A2	0.027	0.041	0.080
A3	0.095	0.232	0.515	A3	0.085	0.158	0.312	A3	0.083	0.172	0.352
A4	0.260	0.471	0.818	A4	0.031	0.052	0.127	A4	0.039	0.075	0.157
A5	0.082	0.175	0.374	A5	0.268	0.479	0.815	A5	0.129	0.270	0.542

(Appendix A), based on the fuzzy extent analysis applying Equation (4) through (7).

Table A7. Ultimate weights of subcriteria.

Subcriterion	Symbol	Weights (TFN)
T1	W1	0.018	0.073	0.288
T2	W2	0.015	0.063	0.245
T3	W3	0.002	0.008	0.034
T4	W4	0.013	0.054	0.223
T5	W5	0.004	0.021	0.095
T6	W6	0.015	0.056	0.204
T7	W7	0.007	0.021	0.079
T8	W8	0.008	0.035	0.153
P1	W9	0.010	0.053	0.318
P2	W10	0.025	0.143	0.689
P3	W11	0.010	0.088	0.496
P4	W12	0.006	0.038	0.214
P5	W13	0.006	0.046	0.289
P6	W14	0.013	0.086	0.467
P7	W15	0.004	0.020	0.126
E1	W16	0.009	0.028	0.191
E2	W17	0.017	0.094	0.574
E3	W18	0.013	0.068	0.446

(Appendix A) shows (per step (d)) the ultimate weights of the subcriteria, calculated applying the aggregation principle according to Equation (8). The triangular fuzzy numbers of the criterion weights were multiplied by the weights of their subcriteria calculated in the previous step (c). Hence, one tier was eliminated from the criteria-subcriteria-alternatives hierarchy.

Then, using the equations described in step e, the fuzzy decision matrix was calculated for the five alternatives (Equation (5)), as was the fuzzy performance matrix (Equation (10)), which represented the overall performance of each alternative relative to all the subcriteria. It was a result of multiplying all the subcriteria weights by the elements of the decision matrix (

Table A8. Elements of the performance matrix.

Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W1	A1	0.000728	0.006069	0.065084	W10	A1	0.003817	0.041651	0.392601
	A2	0.003641	0.028898	0.213848		A2	0.002021	0.023312	0.230513
	A3	0.002333	0.020533	0.176657		A3	0.000928	0.010042	0.103385
	A4	0.000482	0.003005	0.024825		A4	0.000666	0.005505	0.049916
	A5	0.001512	0.014571	0.133237		A5	0.006362	0.062491	0.504773
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W2	A1	0.003029	0.025452	0.181489	W11	A1	0.000311	0.003785	0.039362
	A2	0.000398	0.002599	0.022094		A2	0.002971	0.040417	0.351445
	A3	0.001258	0.011386	0.092007		A3	0.000966	0.014238	0.145217
	A4	0.000606	0.006684	0.071018		A4	0.001456	0.022964	0.238982
	A5	0.001941	0.016745	0.134144		A5	0.000467	0.007194	0.07774
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W3	A1	0.00048	0.003662	0.027639	W12	A1	0.000178	0.001774	0.027396
	A2	0.000198	0.00215	0.021005		A2	0.001614	0.017546	0.176119
	A3	8.74E-05	0.000886	0.009209		A3	0.000513	0.006545	0.080428
	A4	5.28E-05	0.00033	0.003096		A4	0.000233	0.002716	0.03131
	A5	0.000173	0.001322	0.01142		A5	0.000589	0.009406	0.123936
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W4	A1	0.001751	0.015312	0.136508	W13	A1	0.000168	0.001832	0.026059
	A2	0.000374	0.002427	0.024931		A2	0.001527	0.020354	0.232674
	A3	0.000715	0.008597	0.088586		A3	0.000272	0.004842	0.076317
	A4	0.000534	0.004287	0.040665		A4	0.00055	0.007424	0.102377
	A5	0.003152	0.023818	0.179616		A5	0.000644	0.012116	0.176832
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W5	A1	0.001019	0.009255	0.072218	W14	A1	0.000358	0.003486	0.035279
	A2	0.000421	0.004993	0.049108		A2	0.001086	0.012693	0.121712
	A3	0.000116	0.000855	0.008088		A3	0.00342	0.038926	0.34019
	A4	0.000172	0.002092	0.021752		A4	0.002052	0.024253	0.239393
	A5	0.000511	0.004332	0.037553		A5	0.000537	0.006628	0.069676
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W6	A1	0.001248	0.010096	0.085902	W15	A1	0.000107	0.000732	0.009131
	A2	0.003004	0.023315	0.165196		A2	0.001098	0.009068	0.092337
	A3	0.000587	0.005572	0.050616		A3	0.000349	0.003383	0.042167
	A4	0.000395	0.002262	0.018502		A4	0.000659	0.00565	0.064978
	A5	0.001925	0.014572	0.112333		A5	0.000164	0.001871	0.025752
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W7	A1	0.000202	0.00105	0.009398	W16	A1	0.000346	0.002245	0.035966
	A2	0.000913	0.005516	0.040626		A2	0.000251	0.001238	0.016243
	A3	0.000387	0.003756	0.03521		A3	0.000846	0.006649	0.098616
	A4	0.001425	0.009593	0.067711		A4	0.002319	0.013498	0.156626
	A5	0.000278	0.001813	0.01533		A5	0.000737	0.005035	0.071526
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W8	A1	0.000329	0.003452	0.03495	W17	A1	0.001711	0.022177	0.294687
	A2	0.001945	0.015274	0.116035		A2	0.000693	0.007066	0.083206
	A3	0.000222	0.001411	0.012996		A3	0.00149	0.014837	0.179066
	A4	0.00108	0.009092	0.078904		A4	0.000552	0.004886	0.072805
	A5	0.0007	0.006299	0.060338		A5	0.004691	0.045019	0.468033
Weight	Alt.	Fuzzy Number			Weight	Alt.	Fuzzy Number
W9	A1	0.001375	0.013901	0.163554	W18	A1	0.003369	0.029912	0.318404
	A2	0.000304	0.002346	0.026938		A2	0.000353	0.002801	0.035661
	A3	0.000891	0.009541	0.118625		A3	0.00107	0.011666	0.157037
	A4	0.000419	0.004204	0.054454		A4	0.000503	0.005093	0.070431
	A5	0.002475	0.023353	0.240521		A5	0.001651	0.018355	0.241987

, Appendix A).

Per steps f and g,

Table 10. Ranking and optimal alternative.

TFN				Real Number	Ranking
A1	0.020	0.196	1.955	0.1978	3
A2	0.023	0.222	2.019	0.2048	2
A3	0.016	0.173	1.814	0.1833	4
A4	0.014	0.133	1.407	0.1421	5
A5	0.028	0.275	2.684	0.2717	1
Optimal alternative				A5

and

Table 11. Sensitivity analysis.

Alternatives	α = 0	α = 0.5	α = 1
A1	0.1962	0.1975	0.1977
A2	0.2220	0.2074	0.2059
A3	0.1724	0.1817	0.1826
A4	0.1339	0.1409	0.1416
A5	0.2752	0.2722	0.2719

show the ultimate scores of the five alternatives in the form of fuzzy numbers, obtained by adding the fuzzy numbers—elements of the fuzzy performance matrix, according to Equation (11). Then the ultimate weights of the alternatives are shown in the form of non-fuzzy numbers, after defuzzification employing Equation (12). The final ranking of the alternatives is based on the sensitivity analysis per Equation (13). 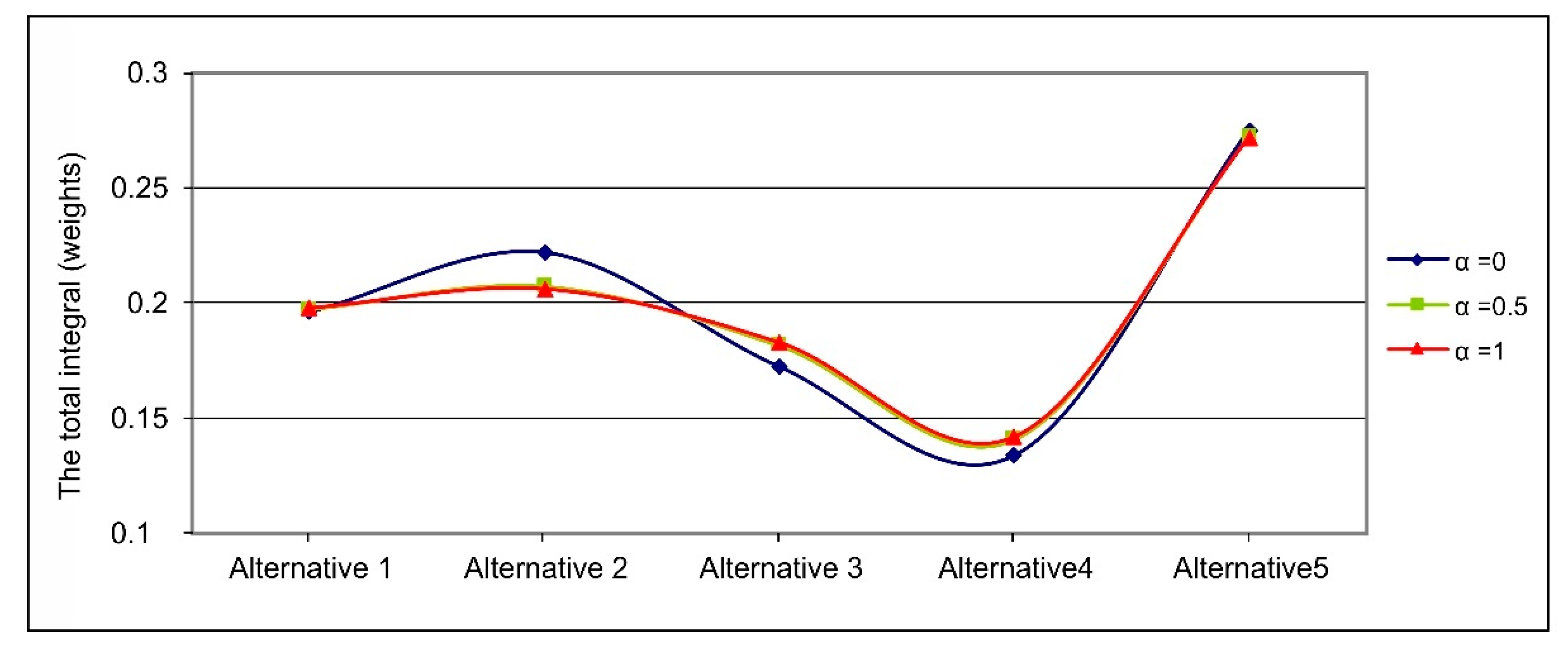Figure 4 shows the total integral value of moderate, pessimistic and optimistic experts’ risk assessments, or the weights of the alternatives relative to the optimization index parameters. If the decision-maker’s inclination is optimistic (α = 1), the weights of the alternatives vary over a very narrow range, compared to pessimistic (α = 0) and moderate (α = 0.5). Based on the sensitivity analysis, the average differences between the weights of the alternatives were in the 0.1–0.73% range for an optimization index of 0.5, and 0.75–7.8% for an optimization index of 0. Defuzzification yielded the weights of the alternatives in the form of “normal” or real numbers. The highest weight is the best score. Based on the results, alternative 5 is the optimal underground mining method, followed in descending order by Alternative 2, Alternative 1, Alternative 3 and Alternative 4.

According to the MCDA model, Alternative 5 (VCR) was proposed as the optimal underground mining method for the Borska Reka copper mine. This method does not require extensive preparations, its productivity is high and the costs of mining are relatively low. There are also other advantages, such as a high ore utilization rate, low ore impoverishment, and a high level of safety at work, which was one of the most important evaluation factors in the case study. For all these reasons, the method proposed for the given copper mine provides optimal mining conditions.

This procedure does not complete the analysis of the mining problem. Management support strategies are developed for the upcoming period of mining. Such strategies enable the management team to assume full professional responsibility for improving development plans. Additional future activities are defined to ensure mining efficiency and high productivity. This also includes the use of the latest technological achievements that help upgrade mining safety. On the one hand, the implementation of solutions and management team’s commitment contribute to sustainable development of the entire process of mining operations, while on the other hand, they contribute to long-term stable technical, economic, and production conditions.

5. Conclusions

The paper demonstrated that FAHP is an extremely useful technique in the mining industry, given that the criteria used in the case study were subjective and based on expert judgment (of mining engineers and geologists), which is an important consideration in underground mining.

The research indicated that an interdisciplinary approach connects underground mining with other areas of science. For example, it links mining with fuzzy logic (based on mathematics and psychology) and multiple-criteria decision-making.

The paper described and analyzed in detail the factors that influence the selection of the optimal underground mining method, including (i) technical (ore body depth, ore body thickness, ore body shape, value of ore, ore body slope, rock hardness and stability, type of ore body and contact with neighboring rocks, and the mineral and chemical composition of the ore), (ii) production (productivity, capacity, safety at work, environmental impact, ore dilution, ore impoverishment, ventilation and hydrologic conditions), and (iii) economic (capital expenditure, costs of mining and costs of maintenance). These criteria, along with their subcriteria, are deemed to be universal and applicable to other underground mines.

The practical importance of the proposed methodology was demonstrated in a case study that included the evaluation of criteria, subcriteria and alternatives applying FAHP, and decision-making/selection of the optimal underground mining method. This reflects the primary academic contribution and implications for further research.

In addition, the approach implemented fuzzy logic in multiple-criteria optimization related to underground mining. On the one hand, the objective of applying the fuzzy approach to decision-making and problem-solving in cases where there are several alternatives and analyzing the relevant factors is to arrive at the optimal solution. On the other hand, expert intuition and experience play an important role in the assessment of the ore system and underground mining methods, while fuzzy logic in mathematical calculations enables such a heuristic approach to problem solving. Such an interdisciplinary approach contributes to the quality and sustainable management of underground mining.