Abstract
In this paper, a hybrid neural network (HNN) that combines a convolutional neural network (CNN) and long short-term memory neural network (LSTM) is proposed to extract the high-level characteristics of materials for critical temperature (Tc) prediction of superconductors. Firstly, by obtaining 73,452 inorganic compounds from the Materials Project (MP) database and building an atomic environment matrix, we obtained a vector representation (atomic vector) of 87 atoms by singular value decomposition (SVD) of the atomic environment matrix. Then, the obtained atom vector was used to implement the coded representation of the superconductors in the order of the atoms in the chemical formula of the superconductor. The experimental results of the HNN model trained with 12,413 superconductors were compared with three benchmark neural network algorithms and multiple machine learning algorithms using two commonly used material characterization methods. The experimental results show that the HNN method proposed in this paper can effectively extract the characteristic relationships between the atoms of superconductors, and it has high accuracy in predicting the Tc.
1. Introduction
Following the discovery of superconductors more than a century ago, it became a focus of research [1]. The superconducting phenomenon [2] is an intrinsic quantum phenomenon caused by the limited attraction between paired electrons. It has unique properties such as zero direct current (DC) resistivity [2,3,4], as well as Meissner and Josephson effects [5,6,7], and its potential applications are increasing. There is even a deep connection between the superconducting state phenomenon and the Higgs mechanism in particle physics [8]. Superconductors can be roughly classified into cuprate-based, iron-based, and all other exotic superconductors. A large amount of research focuses on cuprates and iron-based compounds. Since the discovery of iron-based superconductors in 2008, various types of crystal-based iron-based superconductors were found. Their common feature is that they all have FeAs4/FeSe4 tetrahedral layers [9,10]. Experimental and theoretical studies found that FeAs4/FeSe4 tetrahedral layers in iron-based superconductors play a crucial role in superconductivity [9,10]. High-temperature superconductivity in copper oxides, first discovered 20 years ago [11], led researchers on a wide-ranging quest to understand and use this new state of matter. However, there are still many unresolved problems in superconducting research. For example, the transition temperature of superconductivity is quite different from the actual application. At the same time, the prediction of the Tc of superconductors, especially high-temperature superconductors, is not very accurate. The solution of these problems depends on the discovery of superconductors or similar materials and an understanding of the physical properties of these materials. Although this was the focus of research for the past 30 years, the prediction of Tc of superconductors is still very difficult.
Advances in computers, as well as the development and continuous improvement of first-principles computational quantum chemistry theories and statistical (or machine learning) methods, greatly influenced research activities related to material discovery and design [12]. Material design for high-throughput (HT) calculations made progress in determining the structure of thousands of inorganic solids [13,14]. Since 1970, density functional theory (DFT) is widely used in the calculation of solid-state physics. In most cases, compared with other methods for solving multi-body problems in quantum mechanics, DFT using local density approximation gives very satisfactory results, and solid-state computing is less expensive than experiments. DFT is the leading method for the calculation of electronic structures in various fields; however, these methods are currently not suitable for high-level calculations due to the high-cost calculation. When using standard exchanges and correlation functions such as Perdew-Berke-Ernzerhof (PBE) [15] which is currently the most widely used exchange-related functional form in the calculation of solid structures, there are cases where the system is underestimated compared to the experimental values.
In addition to prediction models based on physical principles/theories, the machine learning [16,17,18,19,20,21] approach for Tc prediction is a data-driven prediction model, which exploits the relationship between material composition similarity and Tc. The first step of such methods requires numerical characterization of the material, followed by applying various machine learning algorithms to practice the predictive model. Brgoch et al. [22] described each metal compound as a 136-dimensional vector based on the number, weight, radius, and the ordinal number of the constituent elements in the compound, and they used a support vector machine (SVM) algorithm to establish 3896 band-gap prediction models for each metal compound. Kitchin [23] used one-hot coding to represent each material as a vector based on the number of constituent elements in the compound and used the kernel ridge regression (KRR) algorithm to establish a prediction model of five attributes such as the total energy, density, and band gap of binary metal oxides. Xie [24], based on the element group number 9 attributes such as period number, electronegativity, and covalent electrons, used one-hot coding to represent each element as a 92-dimensional vector, using the 12 adjacent elements of each element in the crystal, where each crystal was represented as a three-dimensional matrix, and the band gaps, fermi energy, and shear modulus of the inorganic compound prediction model were established using CNN.
In the superconductor research field, the most comprehensive database is the Supercon database [25], which contains the compositions and the Tc of 30,057 metallic oxides or 514 organic superconductors as of April 17, 2019. In the past decade, these materials databases were applied to data-driven material informatics researches [26,27,28,29,30,31]. Indeed, these large data sources spurred researchers’ interest in applying advanced data-driven machine learning (ML) techniques to accelerate the discovery and design of new materials with selected engineering attributes [32,33,34]. Following this strategy, Stanev et al. [35] recently used Magpie [36] descriptors to characterize superconductors into 132-dimensional vectors and used the random forest (RF) algorithm to develop a Tc prediction model. Hamidieh et al. [37] used the same characterization method to establish a Tc prediction model for superconductors using 21,263 materials from SuperCon using a gradient boosting decision tree (GBDT). However, these methods of describing materials either only consider the type and number of constituent elements (One-hot), or only consider the attributes of constituent elements in isolation, and they do not consider the environment in which the constituent elements exist and the order dependency of the elements. The existence of the element’s environmental and order dependencies often greatly affects the properties of materials. Based on this, this paper proposes a method that uses atomic vectors [38,39] to describe materials and uses an HNN model that combines a convolutional neural network CNN and long short-term memory neural network (LSTM) to predict Tc. The HNN model uses CNN to extract the short-dependence feature relationships between atoms, and the LSTM extracts the long-dependence feature relationships between atoms. The contributions of this paper can be summarized as follows:
- (1)
- Extensive computational tests over three standard benchmark datasets demonstrate the advanced performance of our proposed HNN model.
- (2)
- The atomic vector characterization method used to represent superconductors, in addition to using Magpie, one-hot, and other methods, provides a better method for the characterization of superconductors, and this method can also be used to characterize other materials.
The structure of the article is as follows: firstly, we briefly introduce the generation process of the atomic vector, then introduce the source of the superconductor dataset used in this article, as well as the method of characterizing the data of the atomic vector and its model structure. Then, we compare the HNN model with the experimental results of CNN, LSTM, and fully connected neural networks (FNN), as well as the experimental results of multiple machine learning methods of traditional one-hot and Magpie material characterization methods.
2. Materials and Methods
2.1. Atomic Vector Generation Methods
The atomic vector (Atom2Vec) was first proposed by Quan et al. [38] of Stanford University. Below, we briefly describe the workflow of Atom2Vec. As shown in Figure 1, to capture the relationship between the atom and the environment, the first step is to generate an atom–environment pair for each compound in the material dataset. Before that, a clearer definition of the environment is needed. Atoms can be conveniently represented by chemical symbols. The environment includes two aspects: the number of target atoms in the compound and the number of different atoms in the residue. For example, we consider the compound Bi2Se3 from the miniature dataset of the seven samples given in Figure 1. Two atom–environment pairs are generated from Bi2Se3. For the atom Bi, the environment is expressed as “(2) Se3”; for the atom Se, the environment is expressed as “(3) Bi2.” Specifically, for the first pair, the “(2)” in (2) Se3 indicates the presence of two target atoms (here, a compound of Bi), and “Se3” indicates the presence of three Se atoms in the environment.
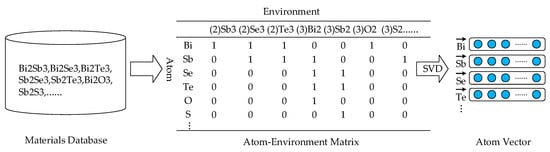
Figure 1.
Atomic vector generation method.
We obtained more than 73,452 binary, ternary, and quaternary inorganic compounds from the Materials Project database [40], and then generated a sparse atomic environment matrix. The SVD of the matrix was used to pair the columns, which were then compressed, and the singular vectors corresponding to the largest 20 singular values were taken, while each element was described as a 20-dimensional vector. Obviously, elements with similar properties would have similar row vectors in the atomic environment matrix, generating similar atomic vectors.
2.2. Dataset Selection and Material Characterization
The experimental data we selected came from the SuperCon database [25], which contains an exhaustive list of superconductors, all of which are from published papers. It contains two compounds, one is a metal oxide (metal-containing inorganic material, alloy compound, oxide, high-temperature superconductor, etc.), and the other is an organic superconductor. We obtained 12,413 kinds of metal oxide superconductors from this database, and the Tc of their superconductivity was 0.533 k–120 k (the distribution is shown in Figure 2a). Here, we consider the characteristics of the superconducting compound AxByCz, assuming that the atomic vectors of the elements A, B, and C are , and . The input compounds can be characterized as side-by-side atomic vectors, based on the effect of the number of atoms in a crystalline compound on the properties of the material. The corresponding number of atoms is added to the end of the atomic vector, and the compound is then characterized as follows:
where x, y, and z represent the number of corresponding elements in the superconducting compound.
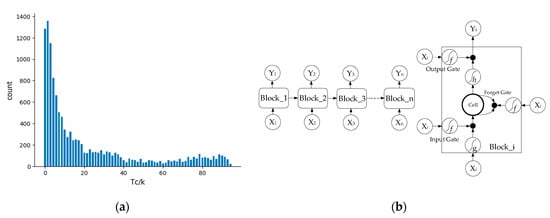
Figure 2.
(a) Tc distribution of superconductors; (b) long short-term memory neural network (LSTM) architecture.
After we counted superconductors obtained from the SuperCon database, we found that all materials contained no more than eight element types; thus, we characterized the superconductors as a matrix V (n × d) as described above, where n = 8 and d = 21. For those with fewer than eight atoms, we padded them with 0.
2.3. Atomic Hierarchical Feature Extraction Model
2.3.1. Inter-Atomic Short-Dependence Feature Extraction Method Based on CNN
CNN is a neural network specially used to process data with similar network structures. It was originally applied in the field of computer vision to extract local features [41,42]. CNN networks achieved significant results in tasks such as natural language processing, speech recognition, and face recognition [43,44,45], indicating that CNN has the ability to independently extract features. Due to the extremely complex crystal structure and the interdependence between atoms, it is often difficult to determine the interatomic dependencies from complex structures by relying on experts or prior knowledge. Therefore, this paper uses the CNN model (see Figure 3) to extract short-dependent feature relationships between atoms of crystals.
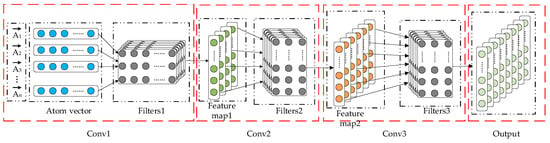
Figure 3.
Convolutional neural network (CNN) inter-atomic short-dependence feature extraction model.
As mentioned earlier, this article converts each compound into an atomic vector in parallel, and each element in the compound is a vector representation of the atom, which is used to obtain the attribute and environmental representation of the atom. In this way, the input compound can be represented as a matrix V ∈ R (n × d), where d is the dimension of the atomic vector plus 1, and n is the type of element in the crystal compound. After characterizing the input compound, a conventional layer is used to extract short-dependence features.
Specifically, the convolution layer extracts short-dependence features by continuously sliding window-shaped convolution kernels over the entire row of the matrix V, and the width l of the convolution kernel is the same as the width d of the atomic vector. The height h of the convolution kernel is multiple adjacent rows. Experimental results show that sliding three elements at a time can achieve good performance. The convolution kernel slides over matrix V and performs a convolution operation, where V [i:j] represents the sub-matrix of V from the i-th row to the j-th row, and Wi represents the i-th convolution kernel. Formally, the output of the convolution layer of the i-th convolution kernel is calculated as follows:
where is bitwise multiplication, ci is the feature learned by the i-th convolution kernel, b is the bias, and f is the activation function (such as sigmoid or tangent). In this study, the rectified linear unit (ReLU) was selected as the nonlinear activation function. For n convolution kernels, the generated n feature maps can be regarded as the input of the LSTM:Here, a comma indicates a column vector connection, and ci is a feature map generated using the i-th convolution kernel.
2.3.2. Inter-Atomic Long-Dependence Feature Extraction Method Based on LSTM
LSTM is a type of recurrent neutral network (RNN). LSTM achieved great success in many applications, such as unconstrained handwriting recognition [46], speech recognition [47], handwriting generation [35], machine translation [48], etc. Each step of the LSTM has a series of repeated neural network templates. In each step, a unit state (post hidden state , current step ) is controlled by a set of gates, including the forgotten gate , an input gate , and an output gate . These gates use the previously hidden state ht−1 and the current input xi together to decide how to update the current cell and the current hidden state ht (see Figure 2b). The LSTM conversion function is defined as follows:
where represents the sigmoid function f(x) = 1/(1 + e(−x)), and its output is [0, 1]. represents the hyperbolic tangent function, and ⊗ is a bitwise multiplication.
2.3.3. Architecture of HNN Model
Based on the above analysis, this paper proposes an HNN model based on CNN and LSTM. The architecture of the hierarchical feature extraction model is shown in Figure 4, and the algorithm is described below in detail.
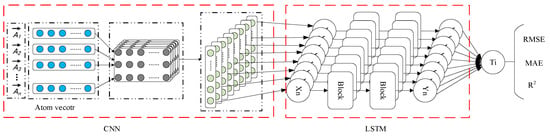
Figure 4.
The architecture of the HNN model.
Each superconductor is represented as a matrix V, whereby V is input into the first layer of a single CNN channel, with 32 convolution kernels; thus, the size of the convolution kernel is 3 × 21 × 1. The output of the first layer of convolution is input into the second layer convolution channel, with 32 channels and 64 convolution kernels; thus, the size of the convolution kernel is 3 × 1 × 32. The output of the second layer convolution channel is input into the third layer convolution channel. The number of channels is 64, and 128 convolution kernels are used; thus, the size of the convolution kernel is 3 × 1 × 64. After three layers of convolution operations, the CNN finally obtains a 2× 1 × 128 feature map. This feature map is input into a two-layer LSTM network with 256 forward-propagating LSTM neurons. In the first layer, we use the output of all hidden states to obtain the long-term dependency feature relationship between atoms. In the second layer, we only use the output of the last state to feed into the subsequent fully connected network for Tc prediction. After the LSTM network, each feature is mapped into a 1 × 1 × 256 matrix. The Tc of each superconductor is calculated using the last layer of the fully connected network. After each of the convolutional layers, a batch normalization layer [49] is used to improve the convergence speed of the model and reduce the influence of network weight initialization during the learning process. Except for the final output layer, a rectified linear unit (ReLu) [50] is used as the activation function for each layer of the neural network. The detailed parameters of each layer of the CNN model are shown in Table 1.

Table 1.
Parameters of the HNN model.
In order to ensure the stability and reliability of the computational experimental results, the HNN and all subsequent comparative computational experiments (RF, GBDT, etc.) were subjected to 10 iterations of 10-fold cross-validation to calculate the average performances. The whole model was developed based on Python 3.6. The neural network model used the Tensorflow14.0 [51] deep learning framework. The implementation of the baseline machine learning algorithms was based on Scikit-learn [52]. All the programs except the baseline machine learning algorithms were run on a Dell Server with a 3.6-GHz central processing unit (CPU) and NVIDIA GPU GTX1080Ti.
3. Results
In this section, to show that the neural network model proposed in this paper can extract short-dependence features and long-dependence features between atoms in superconductors, we firstly compare three benchmark methods, including CNN, LSTM, and a six-layer FNN model with 256, 128, 64, 32, and 1 hidden layer neurons, as well as the ReLu activation function. At the same time, to illustrate the advantages of this method over traditional material characterization methods combined with machine learning algorithms for material performance prediction, we also compared the use of one-hot and Magpie material characterization methods and used SVM, decision tree (DT), RF, GBDT, and KRR machine learning algorithms. SVM [53] was used to find the best separation hyperplane on the feature space to maximize the interval between positive and negative samples on the training set. After introducing the kernel method, SVM can be used to solve nonlinear problems. DT [54] is a tree structure in which each internal node represents a judgment on an attribute, each branch represents the output of a judgment result, and finally each leaf node represents a classification result. RF [55] is actually a special bagging [56] method that uses a decision tree as a model in bagging. GBDT [57] is also known as the multiple additive regression tree (MART), which learns to combine multiple weak learners effectively to build a strong learner with high prediction accuracy, which can reduce the variance and deviation of the prediction model. KRR [58] is the ridge regression (L2 regular linear regression [59]) using kernel techniques with the same learning form as SVM, but the loss function is different. To ensure the stability of the experimental results, each group of algorithms used the 10-fold cross-validation method for averaging during training.
In machine learning, the model can be thought of as a machine with many adjustable knobs, which are called hyperparameters. Adjusting the knobs can change the model’s performance. The search space for hyperparameters of neural networks mainly includes learning rate, optimization algorithms, and batch size; the search space for hyperparameters of SVM, RF, KRR, DT, and GBDT algorithms mainly includes the decision tree number, learning rate, sampling rate, and maximum depth of the decision tree. Among them, the learning rate is one of the most important hyperparameters of deep neural networks. We tried a learning rate from 0.1 to 1 × 10−6 (10-fold reduction each time).
For the regression model, we chose mean absolute error (MAE), root-mean-square error (RMSE), and R-squared (R2) as the evaluation indicators of the model. MAE is used to reflect the actual situation of the predicted value error, and RMSE is used to measure the deviation between the predicted value and the true value. R2 has a value in the range (0, 1), which is a statistic that measures the goodness of fit. The specific calculation formulas are shown below.
where m is the number of samples, and are the true and predicted values of the i-th sample label (Tc of the superconductors), and is the average of the true labels of m samples.
We set the initial values for all hyperparameters based on empirical intuition and then used a greedy algorithm to adjust each hyperparameter step by step instead of performing a grid search, which is not feasible due to computational cost. Finally, all the hyperparameters of the various models were determined, as shown in Table 2.

Table 2.
Hyperparameters of various model.
Figure 5a shows the changes in MAE values of all neural network models with the increase in the number of training epochs. Among them, the HNN model proposed in this paper obtained the minimum MAE value of 5.631 k after training 200 generations. At the same time, we can see that our model stabilized after about 80 generations, and the convergence rate was higher than that of the other three baseline models.
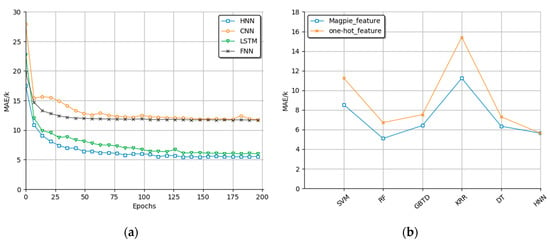
Figure 5.
(a) Prediction performance of each model described by atomic vectors. (b) Predicted results of various machine learning algorithms described by one-hot and Magpie.
In addition, Table 3 comprehensively evaluates the MAE, RMSE, and R2 values of the four models in the 200th generation. From the table, it can be seen that the HNN model was better than the three benchmark models from these three perspectives. Stanev et al. [35] used the Magpie feature combined with the RF method, and the result of R2 was 0.876, while the HNN could reach 0.899. Hamidieh et al. [37] changed RF to GBDT on the basis of Reference [35], and they used all the data in Supercon database; although the R2 could reach 0.920, the improvement of the results depended largely on the increase in the amount of data in the training model, and the generalization ability remains to be discussed. However, HNN had a better MAE than Reference [37] with less data. From Table 3, we can also see that the LSTM method alone could also achieve good results, indicating that considering the dependence of atoms in superconductors can help improve the prediction results.

Table 3.
RMSE (k), MAE (k), and R2 values of cross-validation results for each model described by atomic vectors.
Next, we compared the results using one-hot and Magpie material characterization methods to predict the Tc using multiple machine learning methods. It can be clearly seen from Figure 5b that the MAE values of the predicted results of various machine learning methods under the two material characterizations changed. In order to facilitate comparison, it is necessary to point out that the result of the HNN model in Figure 6 was obtained by using atomic vector characterization and the HNN method. In general, the prediction results described by Magpie were better than those described by one-hot, but the results of the HNN model proposed in this paper were still the best. Table 4 and Table 5 comprehensively evaluate the RMSE, MAE, and R2 results of various machine learning algorithms under the two material descriptions. It must not be noted here that the RF and gradients described by Magpie were used. Two models based on the integrated idea of the GBDT also achieved good results.
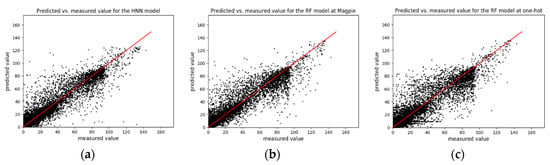
Figure 6.
Comparison of distributions of superconductors materials of different categories with (a) HNN; (b) RF (Magpie); (c) RF (one-hot).

Table 4.
RMSE (k), MAE (k), and R2 values of cross-validation results for various machine learning algorithms described by Magpie.

Table 5.
RMSE (k), MAE (k), and R2 values of cross-validation results of various machine learning algorithms described by one-hot.
At the same time, the results of these two methods were better than other conventional machine learning algorithms when using one-hot feature description. Figure 6 shows the predicted results of the three material description methods using the best model on the test set. The abscissa represents the measured value, and the ordinate represents the predicted value. Comparing Figure 6a–c, we find that the results in Figure 6c were the worst. The predicted value of the Tc between 60 k and 100 k using the Magpie feature and RF method was generally lower than the measured value. The HNN method in this temperature range was better than the RF method. However, the predicted value of superconductors using the atomic vector combined with the HNN method at a Tc of 40 k–60 k was more accurate than the RF method, and its predicted effect was not as good as that of the RF method.
The above two sets of experiments compared the predicted results of different machine learning algorithms under different network models with two traditional material representations described by the atomic vector. Among them, the prediction effect using the HNN model proposed in this paper was the best. This result shows that the atomic vector characterization of the material combined with the HNN model can adequately extract the inter-atomic characteristics of the superconductors. There are certain advantages.
4. Discussion
This paper proposed a prediction model for Tc of superconductors based on deep learning. System experiments and verifications showed that our HNN model has high prediction accuracy. Because deep learning has stronger generalization ability than machine learning models, we can use our proposed deep learning model to predict the Tc without using DFT, allowing us to find new superconductors. The first step in discovering new materials using deep learning methods is to establish an accurate material attribute prediction model, then construct an imaginary material space (such as AxByCz x + y + z < 10, where A, B, and C are different elements, and x, y, and z are subscripts of the corresponding elements), and finally build an accurate prediction model to screen for possible new materials in this space. For example, after using FNN to build an accurate prediction model of formation energy, Jha et al. [60] screened materials with low formation energy in the constructed material paradigm. After establishing a Tc prediction model using RF, Stanev et al. [35] screened the Inorganic Crystallographic Structure Database (ICSD) to find possible superconductors. Therefore, the model for predicting Tc proposed in this paper can be used to discover new superconductors.
Furthermore, the method of characterizing superconductors based on atomic vectors in this paper provides a new method in addition to Magpie and one-hot characterization methods, and this method can also be used for the characterization of other materials as inputs for a neural network in subsequent tasks.
5. Conclusions
This paper proposed a new model for predicting the material properties of compounds. It used the side-by-side arrangement of atomic vectors that can represent atomic properties and the environment in the compound as input. The architecture of LSTM stacked on the convolution layer was used. The short-dependence feature relationship between atoms was extracted, and the LSTM was used to extract the long-dependency feature relationship between atoms. To reflect the advantages of this model, we used the commonly used CNN, LSTM, and FNN as comparable models. The experimental results applied to the Tc prediction of superconducting materials showed that our proposed HNN model was superior to the three benchmark models from three angles of convergence speed, based on RMSE, MAE, and R2. The proposed HNN method can effectively extract the characteristic relationships between atoms of superconductors and predict the Tc.
Moreover, we used the one-hot and Magpie material characterization methods. The prediction results of various machine learning algorithms were compared with the experimental results of the HNN model. As a result, the prediction effect of this model was still good. At the same time, we also observed that, when using machine learning algorithms to predict material properties, Magpie features were generally better than one-hot features. In terms of algorithms, RF, GBTD, and other algorithms based on integrated ideas were generally better than other algorithms. The first step in discovering new materials using deep learning methods is to establish an accurate material attribute prediction model, then construct an imaginary material space, and finally build an accurate prediction model to screen for possible new materials in this space. Therefore, the model for predicting Tc proposed in this paper can be used to discover new superconductors.
Author Contributions
Conceptualization, J.H. and Y.D.; methodology, J.H., S.L., Y.D. and X.L.; software, Y.D. and X.L.; validation, X.L., T.H. and J.H.; investigation, R.D., Y.D., T.H., Z.C. and J.H.; writing—original draft preparation, Y.D., R.D. and J.H.; writing—review and editing, D.Y., J.H. and S.L.; supervision, J.H. and S.L.; project administration J.H.; funding acquisition J.H and S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was partially funded by the National Natural Science Foundation of China under Grant No. 51741101; S.L. is partially supported by the National Important Project under grant No. 2018AAA0101803 and by the Guizhou Province Science and Technology Project under grant No. [2015] 4011.
Acknowledgments
We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan X Pascal GPU used for this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Muller, K.A.; BEDNORZ, J.G. The Discovery of a Class of High-Temperature Superconductors. Science 1987, 237, 1133–1139. [Google Scholar] [CrossRef] [PubMed]
- Suhl, H.; Matthias, B.; Walker, L. Bardeen-Cooper-Schrieffer theory of superconductivity in the case of overlapping bands. Phys. Rev. Lett. 1959, 3, 552. [Google Scholar] [CrossRef]
- Cooper, J.; Chu, C.; Zhou, L.; Dunn, B.; Grüner, G. Determination of the magnetic field penetration depth in superconducting yttrium barium copper oxide: Deviations from the Bardeen-Cooper-Schrieffer laws. Phys. Rev. B 1988, 37, 638. [Google Scholar] [CrossRef] [PubMed]
- Amoretti, A.; Areán, D.; Goutéraux, B.; Musso, D. DC resistivity at holographic charge density wave quantum critical points. arXiv 2017, arXiv:1712.07994. [Google Scholar]
- Szeftel, J.; Sandeau, N.; Khater, A. Comparative Study of the Meissner and Skin Effects in Superconductors. Prog. Electromagn. Res. M 2018, 69, 69–76. [Google Scholar] [CrossRef]
- Goldman, A.M.; Kreisman, P. Meissner effect and vortex penetration in Josephson junctions. Phys. Rev. 1967, 164, 544. [Google Scholar] [CrossRef]
- Orignac, E.; Giamarchi, T. Meissner effect in a bosonic ladder. Phys. Rev. B 2001, 64, 144515. [Google Scholar] [CrossRef]
- Jing, W. Gravitational Higgs Mechanism in Inspiraling Scalarized NS-WD Binary. Int. J. Astron. Astrophys. 2017, 7, 202–212. [Google Scholar]
- Kamihara, Y.; Watanabe, T.; Hirano, M.; Hosono, H. Iron-based layered superconductor La [O1-x F x] FeAs (x = 0.05− 0.12) with T c = 26 K. J. Am. Chem. Soc. 2008, 130, 3296–3297. [Google Scholar] [CrossRef]
- Stewart, G. Superconductivity in iron compounds. Rev. Mod. Phys. 2011, 83, 1589. [Google Scholar] [CrossRef]
- Bonn, D. Are high-temperature superconductors exotic? Nat. Phys. 2006, 2, 159–168. [Google Scholar] [CrossRef]
- Kalidindi, S.R.; Graef, M.D. Materials Data Science: Current Status and Future Outlook. Ann. Rev. Mater. Sci. 2015, 45, 171–193. [Google Scholar] [CrossRef]
- Curtarolo, S.; Hart, G.L.W.; Nardelli, M.B.; Mingo, N.; Sanvito, S.; Levy, O. The high-throughput highway to computational materials design. Nat. Mater. 2013, 12, 191–201. [Google Scholar] [CrossRef] [PubMed]
- Setyawan, W.; Gaume, R.M.; Lam, S.; Feigelson, R.S.; Curtarolo, S. High-Throughput Combinatorial Database of Electronic Band Structures for Inorganic Scintillator Materials. ACS Comb. Sci. 2011, 13, 382–390. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Gao, Z.; Wang, Z.; Liu, W. Real-Time Recognition Method for 0.8 cm Darning Needles and KR22 Bearings Based on Convolution Neural Networks and Data Increase. Appl. Sci. 2018, 8, 1857. [Google Scholar] [CrossRef]
- Yang, J.; Li, S.; Wang, Z.; Yang, G. Real-time tiny part defect detection system in manufacturing using deep learning. IEEE Access 2019, 7, 89278–89291. [Google Scholar] [CrossRef]
- Dukenbayev, K.; Korolkov, I.V.; Tishkevich, D.I.; Kozlovskiy, A.L.; Trukhanov, S.V.; Gorin, Y.G.; Shumskaya, E.E.; Kaniukov, E.Y.; Vinnik, D.A.; Zdorovets, M.V. Fe3O4 Nanoparticles for Complex Targeted Delivery and Boron Neutron Capture Therapy. Nanomaterials 2019, 9, 494. [Google Scholar] [CrossRef]
- Tishkevich, D.I.; Grabchikov, S.S.; Lastovskii, S.B.; Trukhanov, S.V.; Zubar, T.I.; Vasin, D.S.; Trukhanov, A.V.; Kozlovskiy, A.L.; Zdorovets, M.M. Effect of the Synthesis Conditions and Microstructure for Highly Effective Electron Shields Production Based on Bi Coatings. Acs Appl. Energy Mater. 2018, 1, 1695–1702. [Google Scholar] [CrossRef]
- Yang, G.; Chen, Z.; Li, Y.; Su, Z. Rapid Relocation Method for Mobile Robot Based on Improved ORB-SLAM2 Algorithm. Remote Sens. 2019, 11, 149. [Google Scholar] [CrossRef]
- Li, X.; Dan, Y.; Dong, R.; Cao, Z.; Niu, C.; Song, Y.; Li, S.; Hu, J. Computational Screening of New Perovskite Materials Using Transfer Learning and Deep Learning. Appl. Sci. 2019, 9, 5510. [Google Scholar] [CrossRef]
- Zhuo, Y.; Mansouri Tehrani, A.; Brgoch, J. Predicting the Band Gaps of Inorganic Solids by Machine Learning. J. Phys. Chem. Lett. 2018, 9, 1668–1673. [Google Scholar] [CrossRef] [PubMed]
- Calfa, B.A.; Kitchin, J.R. Property prediction of crystalline solids from composition and crystal structure. Aiche J. 2016, 62, 2605–2613. [Google Scholar] [CrossRef]
- Xie, T.; Grossman, J.C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys. Rev. Lett. 2018, 120, 145301. [Google Scholar] [CrossRef] [PubMed]
- Mansouri Tehrani, A.; Oliynyk, A.O.; Parry, M.; Rizvi, Z.; Couper, S.; Lin, F.; Miyagi, L.; Sparks, T.D.; Brgoch, J. Machine learning directed search for ultraincompressible, superhard materials. J. Am. Chem. Soc. 2018, 140, 9844–9853. [Google Scholar] [CrossRef]
- Agrawal, A.; Choudhary, A. Perspective: Materials informatics and big data: Realization of the “fourth paradigm” of science in materials science. APL Mater. 2016, 4, 053208. [Google Scholar] [CrossRef]
- Hey, A.J.; Tansley, S.; Tolle, K.M. The Fourth Paradigm: Data-Intensive Scientific Discovery; Microsoft Research: Redmond, WA, USA, 2009; Volume 1. [Google Scholar]
- Rajan, K. Materials informatics: The materials “gene” and big data. Ann. Rev. Mater. Res. 2015, 45, 153–169. [Google Scholar] [CrossRef]
- Hill, J.; Mulholland, G.; Persson, K.; Seshadri, R.; Wolverton, C.; Meredig, B. Materials science with large-scale data and informatics: Unlocking new opportunities. MRS Bull. 2016, 41, 399–409. [Google Scholar] [CrossRef]
- Ward, L.; Wolverton, C. Atomistic calculations and materials informatics: A review. Curr. Opin. Solid State Mater. Sci. 2017, 21, 167–176. [Google Scholar] [CrossRef]
- Ramprasad, R.; Batra, R.; Pilania, G.; Mannodi-Kanakkithodi, A.; Kim, C. Machine learning in materials informatics: Recent applications and prospects. NPJ Comput. Mater. 2017, 3, 54. [Google Scholar] [CrossRef]
- Pozun, Z.D.; Hansen, K.; Sheppard, D.; Rupp, M.; Müller, K.-R.; Henkelman, G. Optimizing transition states via kernel-based machine learning. J. Chem. Phys. 2012, 136, 174101. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Rupp, M.; Gobre, V.; Vazquez-Mayagoitia, A.; Hansen, K.; Tkatchenko, A.; Müller, K.-R.; Von Lilienfeld, O.A. Machine learning of molecular electronic properties in chemical compound space. New J. Phys. 2013, 15, 095003. [Google Scholar] [CrossRef]
- Agrawal, A.; Deshpande, P.D.; Cecen, A.; Basavarsu, G.P.; Choudhary, A.N.; Kalidindi, S.R. Exploration of data science techniques to predict fatigue strength of steel from composition and processing parameters. Integr. Mater. Manuf. Innov. 2014, 3, 90–108. [Google Scholar] [CrossRef]
- Stanev, V.; Oses, C.; Kusne, A.G.; Rodriguez, E.; Paglione, J.; Curtarolo, S.; Takeuchi, I. Machine learning modeling of superconducting critical temperature. NPJ Comput. Mater. 2018, 4, 29. [Google Scholar] [CrossRef]
- Ward, L.; Agrawal, A.; Choudhary, A.; Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. NPJ Comput. Mater. 2016, 2, 16028. [Google Scholar] [CrossRef]
- Hamidieh, K. A data-driven statistical model for predicting the critical temperature of a superconductor. Comput. Mater. Sci. 2018, 154, 346–354. [Google Scholar] [CrossRef]
- Zhou, Q.; Tang, P.; Liu, S.; Pan, J.; Yan, Q.; Zhang, S.-C. Learning atoms for materials discovery. Proc. Natl. Acad. Sci. USA 2018, 115, E6411–E6417. [Google Scholar] [CrossRef]
- Lu, J.; Wang, C.; Zhang, Y.; Wang, C.; Zhang, Y. Predicting Molecular Energy Using Force-Field Optimized Geometries and Atomic Vector Representations Learned from an Improved Deep Tensor Neural Network. J. Chem. Theory Comput. 2019, 15, 4113–4121. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Wei, C.; Persson, K.A. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef]
- LeCun, Y.; Bengio, Y. Convolutional networks for images, speech, and time series. Handb. Brain Theory Neural Netw. 1995, 3361, 255–258. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Advances in Neural Information Processing Systems, Stateline, NV, USA, 3–8 December 2012; pp. 1097–1105. [Google Scholar]
- Su, Z.; Li, Y.; Yang, G. Dietary Composition Perception Algorithm Using Social Robot Audition for Mandarin Chinese. IEEE Access 2020, 8, 8768–8782. [Google Scholar] [CrossRef]
- Zhu, X.; Liu, H.; Lei, Z.; Shi, H.; Yang, F.; Yi, D.; Qi, G.; Li, S.Z. Large-scale bisample learning on id versus spot face recognition. Int. J. Comput. Vis. 2019, 127, 684–700. [Google Scholar] [CrossRef]
- Yu, Z.; Liu, F.; Liao, R.; Wang, Y.; Feng, H.; Zhu, X. Improvement of face recognition algorithm based on neural network. In Proceedings of the ICMTMA, Changsha, China, 10–11 February 2018; pp. 229–234. [Google Scholar]
- Yu, T.; Jin, H.; Nahrstedt, K. Mobile Devices based Eavesdropping of Handwriting. IEEE Trans. Mob. Comput. 2019, 1. [Google Scholar] [CrossRef]
- Tsai, R.T.-H.; Chen, C.-H.; Wu, C.-K.; Hsiao, Y.-C.; Lee, H.-y. Using Deep-Q Network to Select Candidates from N-best Speech Recognition Hypotheses for Enhancing Dialogue State Tracking. In Proceedings of the ICASSP 2019—2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hove, UK, 12–17 May 2019; pp. 7375–7379. [Google Scholar]
- Kim, Y.; Gao, Y.; Ney, H. Effective Cross-lingual Transfer of Neural Machine Translation Models without Shared Vocabularies. arXiv 2019, arXiv:1905.05475. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. arXiv 2015, arXiv:1502.03167. [Google Scholar]
- Li, Y.; Yuan, Y. Convergence analysis of two-layer neural networks with relu activation. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 597–607. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Corrado, G.S.; Davis, A.; Dean, J.; Devin, M. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv 2016, arXiv:1603.04467. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Suykens, J.A.; Vandewalle, J. Least squares support vector machine classifiers. Neural Process. Lett. 1999, 9, 293–300. [Google Scholar] [CrossRef]
- Quinlan, J.R. Simplifying decision trees. Int. J. Man Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- An, S.; Liu, W.; Venkatesh, S. Face recognition using kernel ridge regression. In Proceedings of the 2007 IEEE Conference on Computer Vision and Pattern Recognition, Minneapolis, MN, USA, 17–22 June 2007; pp. 1–7. [Google Scholar]
- Wagner, H.M. Linear programming techniques for regression analysis. J. Am. Stat. Assoc. 1959, 54, 206–212. [Google Scholar] [CrossRef]
- Jha, D.; Ward, L.; Paul, A.; Liao, W.-k.; Choudhary, A.; Wolverton, C.; Agrawal, A. Elemnet: Deep learning the chemistry of materials from only elemental composition. Sci. Rep. 2018, 8, 17593. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).