Thermal Abuse Behavior of the LIR2450 Micro Coin Cell Battery Having Capacity of 120 mAh with Internal Short Circuit by Penetrating Element
Abstract
1. Introduction
2. Experimental Study
3. Numerical Model
4. Results and Discussion
4.1. Validation
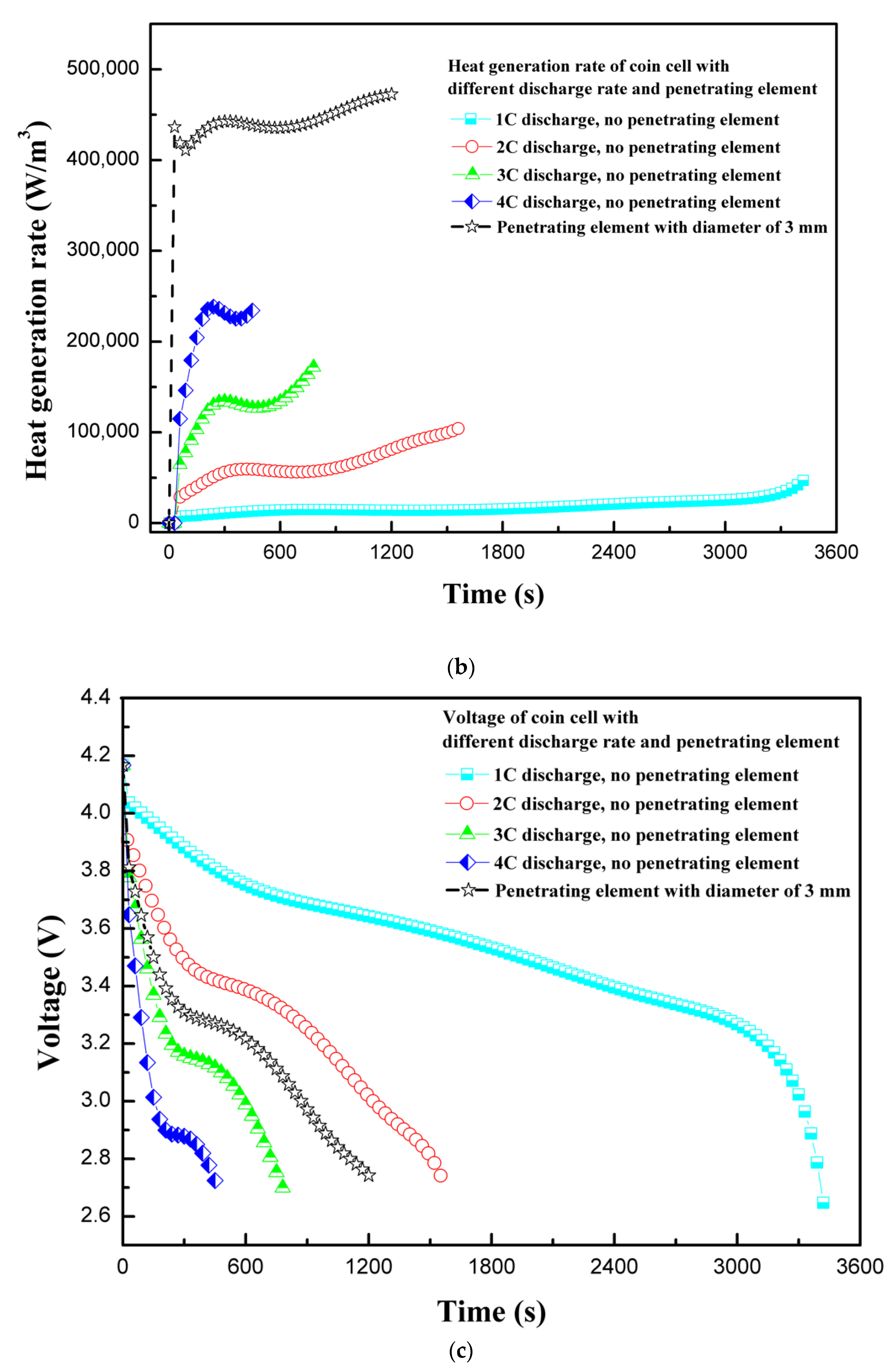
4.2. Effect of Discharge Rate
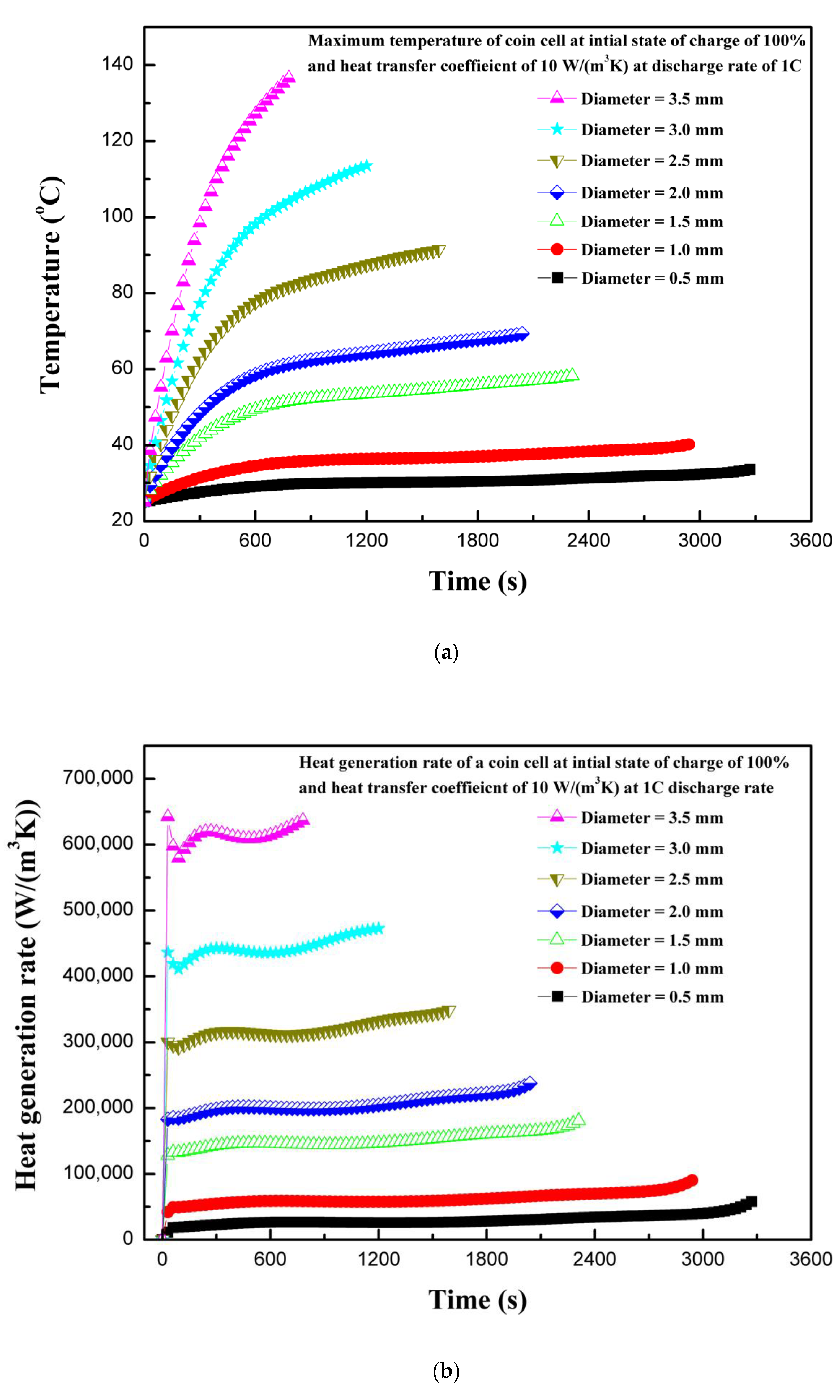
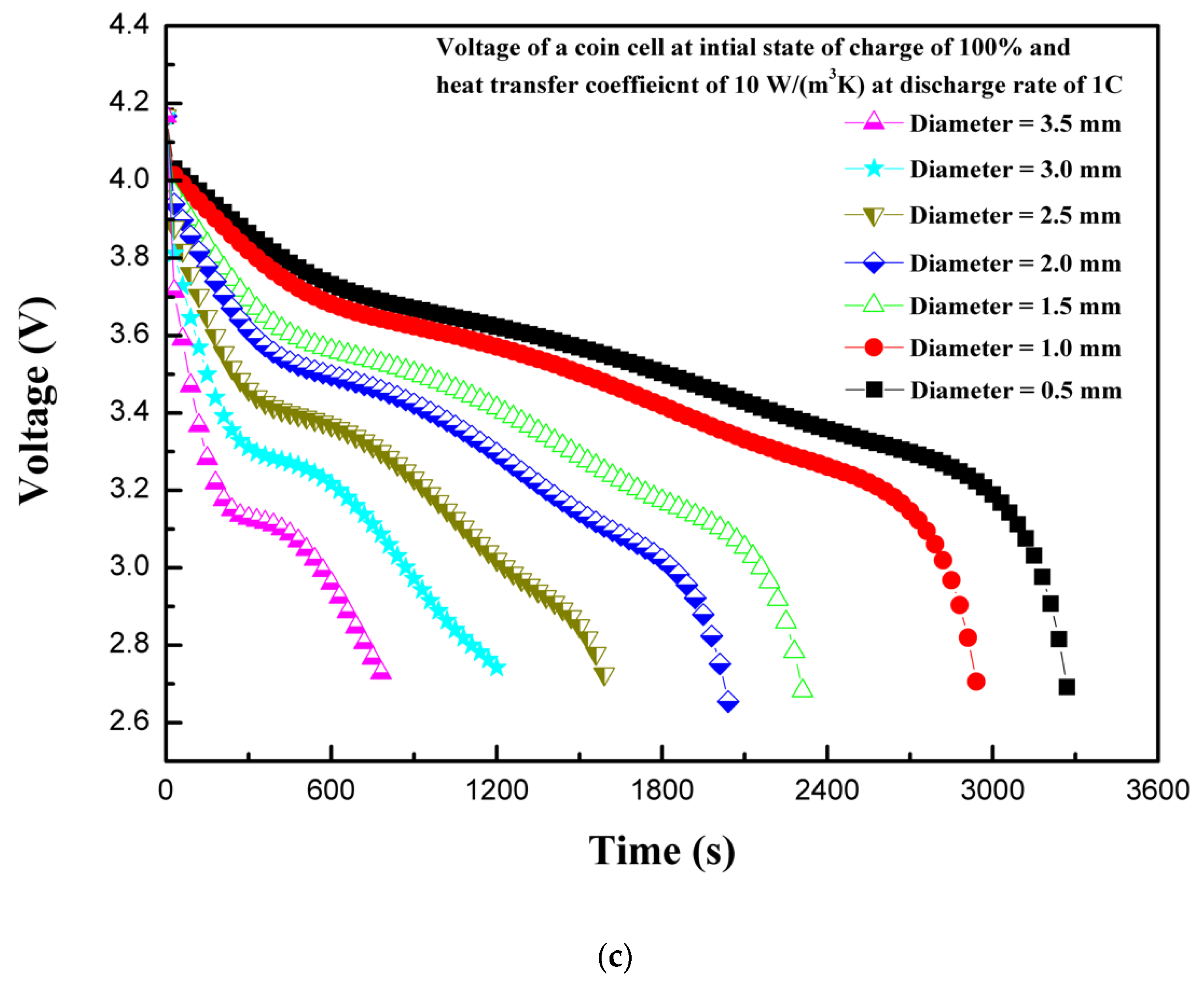
4.3. Effect of Penetarting Element Size
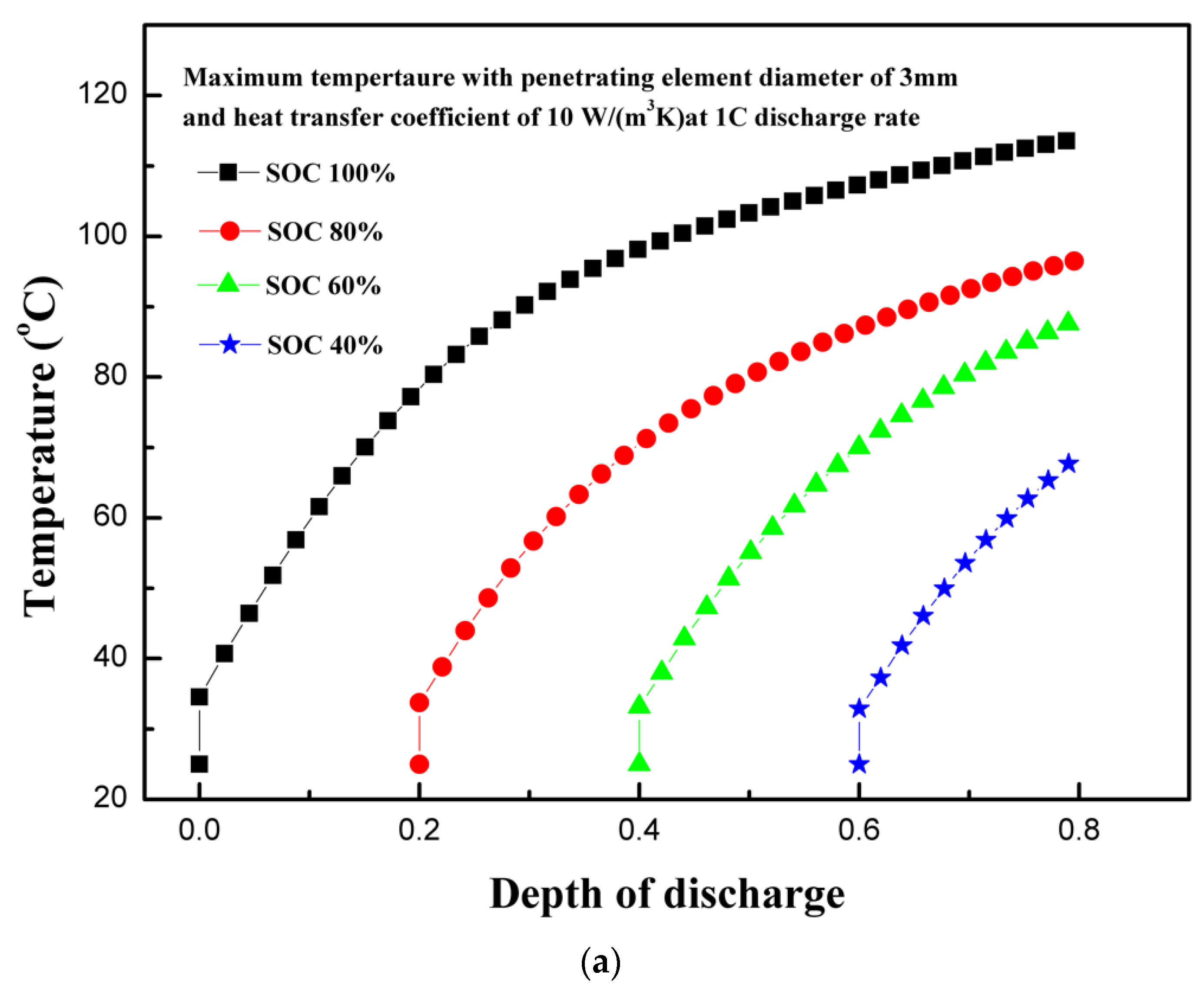
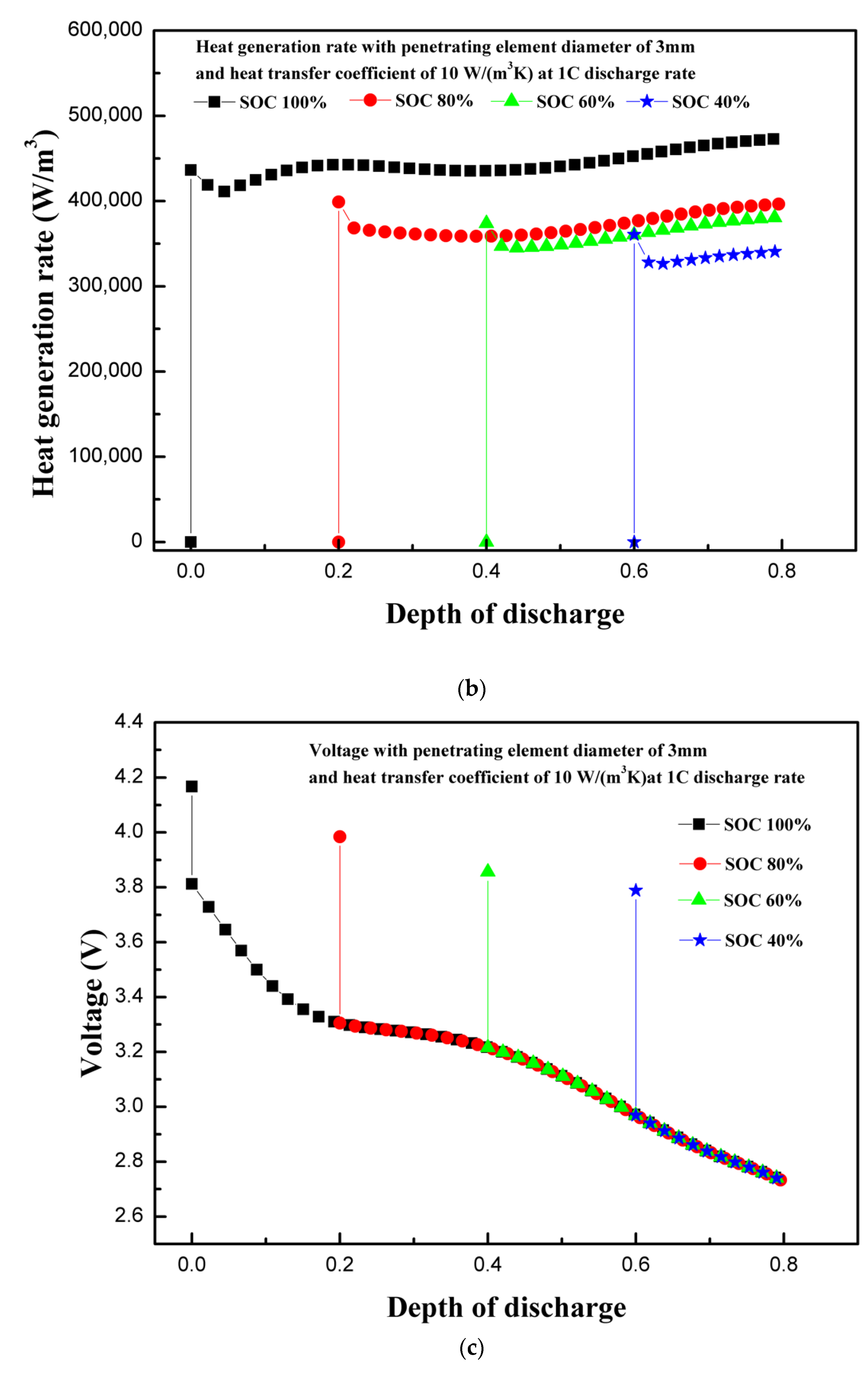
4.4. Effect of Initial State of Charge
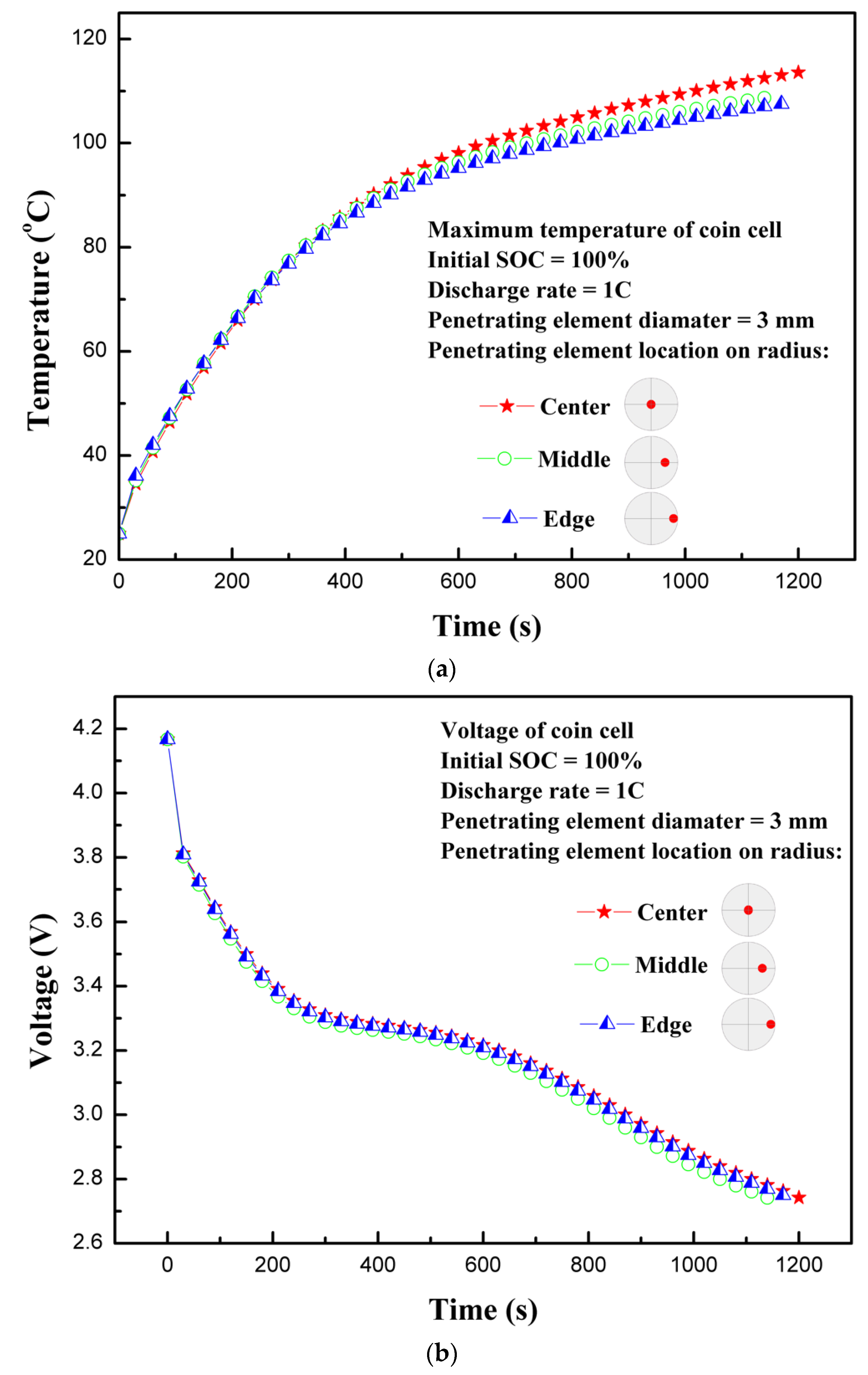
4.5. Effect of the Location of the Penetrating Element
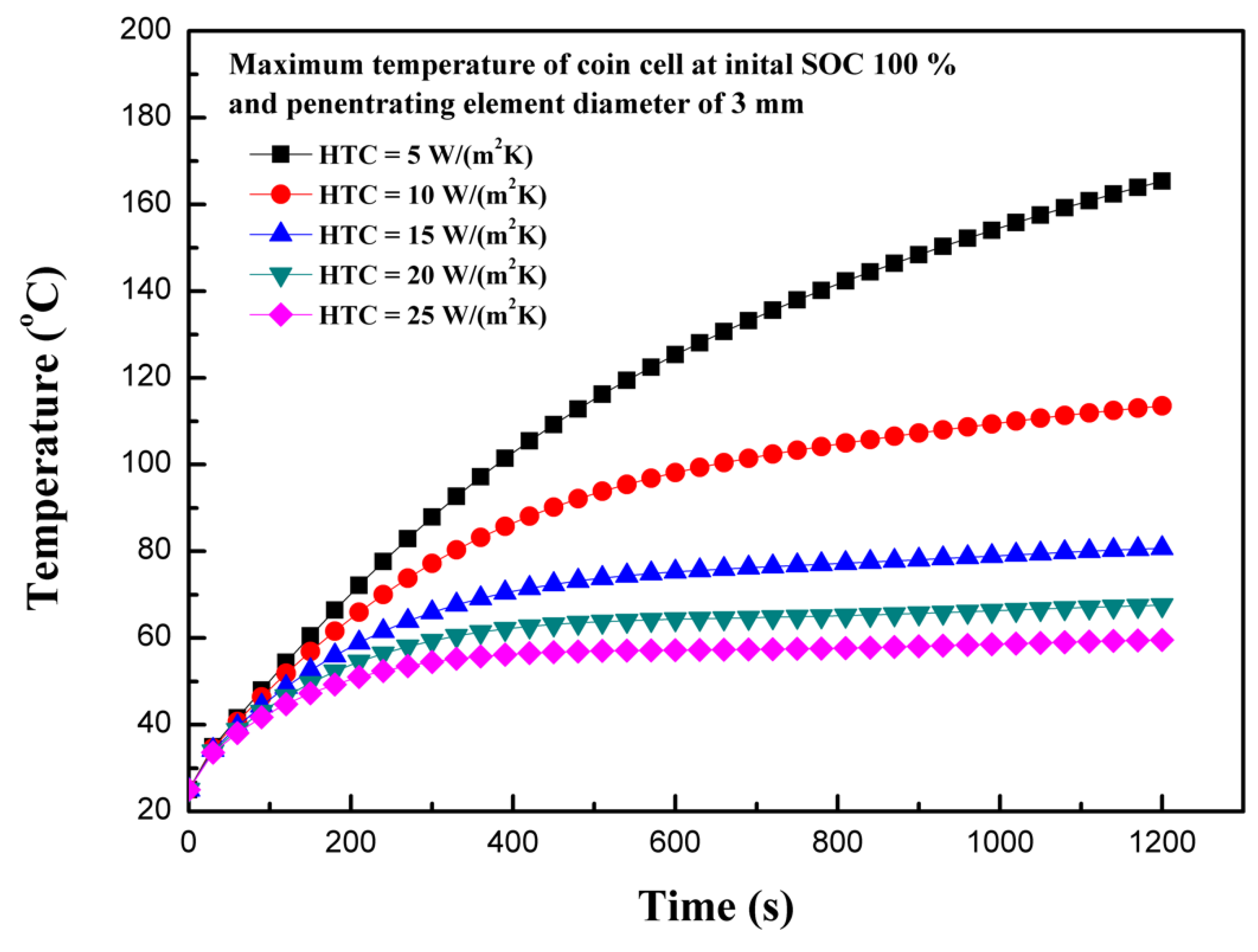
4.6. Effect of the Heat Transfer Coefficient
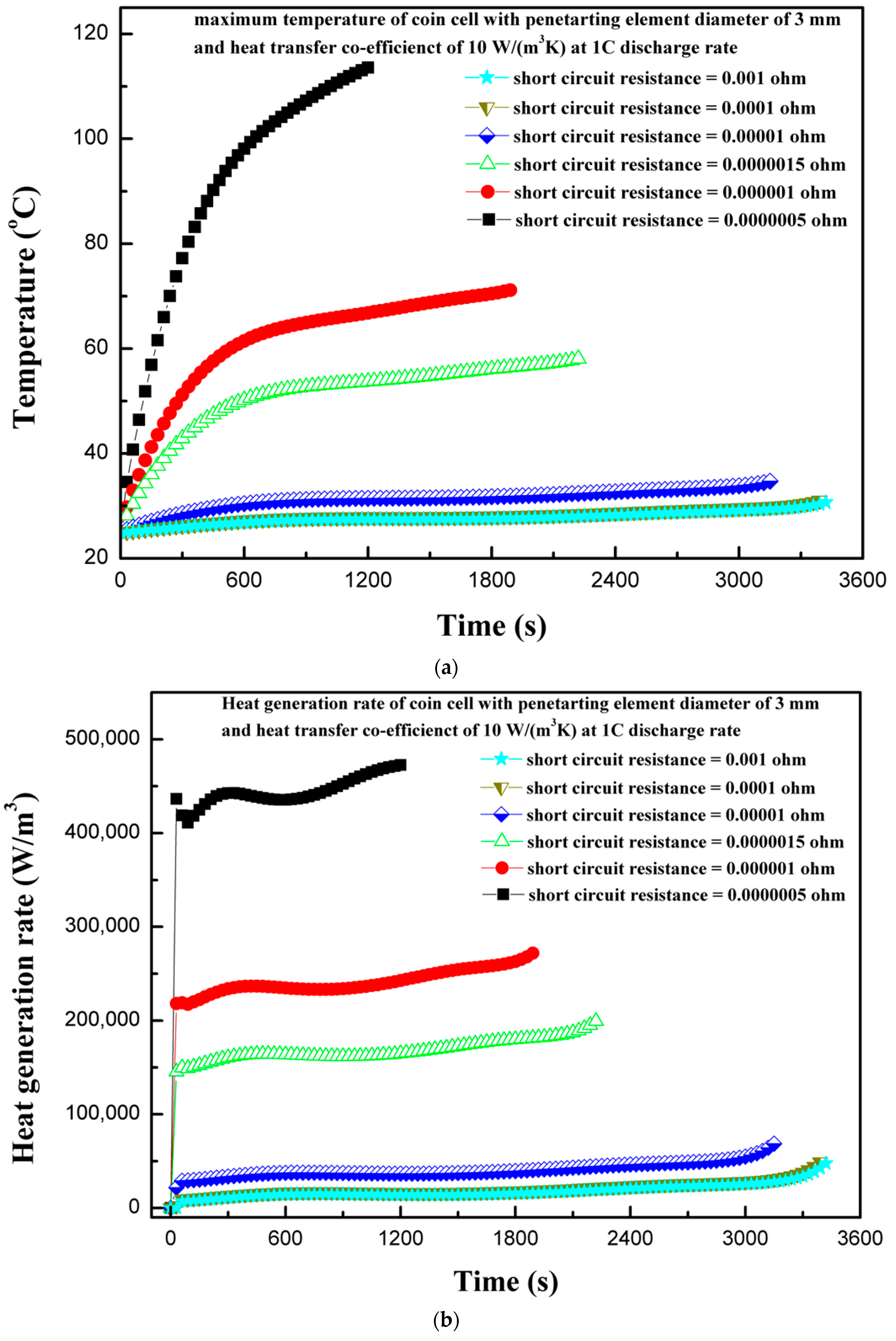
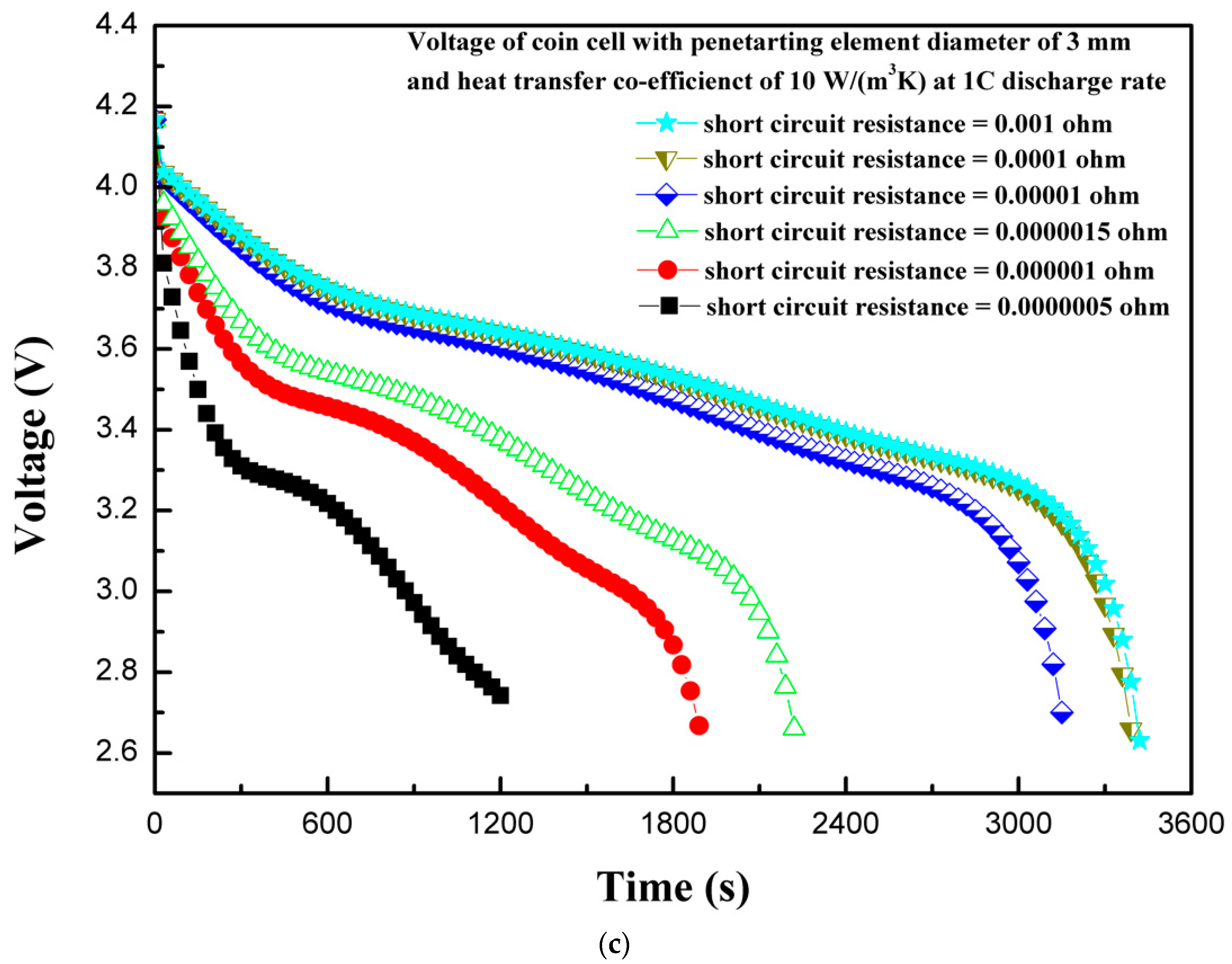
4.7. Effect of Short-Circuit Resistance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zubi, G.; López, R.D.; Carvalho, M.; Pasaoglu, G. The lithium-ion battery: State of the art and future perspectives. Renew. Sustain. Energy Rev. 2018, 89, 292–308. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, B.; Li, Q.; Cartmell, S.; Ferrara, S.; Deng, Z.D.; Xiao, J. Lithium and lithium ion batteries for applications in microelectronic devices: A review. J. Power Sources 2015, 286, 330–345. [Google Scholar] [CrossRef]
- Patil, M.S.; Panchal, S.; Kim, N.; Lee, M.-Y. Cooling Performance Characteristics of 20 Ah Lithium-Ion Pouch Cell with Cold Plates along Both Surfaces. Energies 2018, 11, 2550. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Lu, J.; Li, X. Temperature rise prediction of lithium-ion battery suffering external short circuit for all-climate electric vehicles application. Appl. Energy 2018, 213, 375–383. [Google Scholar] [CrossRef]
- Wang, Q.; Mao, B.; Stoliarov, S.I.; Sun, J. A review of lithium ion battery failure mechanisms and fire prevention strategies. Prog. Energy Combust. Sci. 2019, 73, 95–131. [Google Scholar] [CrossRef]
- Liu, B.; Yin, S.; Xu, J. Integrated computation model of lithium-ion battery subject to nail penetration. Appl. Energy 2016, 183, 278–289. [Google Scholar] [CrossRef]
- Liao, Z.; Zhang, S.; Li, K.; Zhao, M.; Qiu, Z.; Han, D.; Zhang, G.; Habetler, T.G. Hazard analysis of thermally abused lithium-ion batteries at different state of charges. J. Energy Storage 2020, 27, 101065. [Google Scholar] [CrossRef]
- Chen, M.; Liu, J.; He, Y.; Yuen, R.; Wang, J. Study of the fire hazards of lithium-ion batteries at different pressures. Appl. Therm. Eng. 2017, 125, 1061–1074. [Google Scholar] [CrossRef]
- Liu, B.; Jia, Y.; Yuan, C.; Wang, L.; Gao, X.; Yin, S.; Xu, J. Safety issues and mechanisms of lithium-ion battery cell upon mechanical abusive loading: A review. Energy Storage Mater. 2020, 24, 85–112. [Google Scholar] [CrossRef]
- Wang, Q.; Ping, P.; Zhao, X.; Chu, G.; Sun, J.; Chen, C. Thermal runaway caused fire and explosion of lithium ion battery. J. Power Sources 2012, 208, 210–224. [Google Scholar] [CrossRef]
- Williard, N.; He, W.; Hendricks, C.; Pecht, M. Lessons Learned from the 787 Dreamliner Issue on Lithium-Ion Battery Reliability. Energies 2013, 6, 4682–4695. [Google Scholar] [CrossRef]
- Qin, T.; Zeng, S.; Guo, J.; Skaf, Z. State of Health Estimation of Li-ion Batteries with Regeneration Phenomena: A Similar Rest Time-Based Prognostic Framework. Symmetry 2017, 9, 4. [Google Scholar] [CrossRef]
- Feng, X.; Sun, J.; Ouyang, M.; Wang, F.; He, X.; Lu, L.; Peng, H. Characterization of penetration induced thermal runaway propagation process within a large format lithium ion battery module. J. Power Sources 2015, 275, 261–273. [Google Scholar] [CrossRef]
- Ping, P.; Wang, Q.; Huang, P.; Sun, J.; Chen, C. Thermal behaviour analysis of lithium-ion battery at elevated temperature using deconvolution method. Appl. Energy 2014, 129, 261–273. [Google Scholar] [CrossRef]
- Xia, Y.; Chen, G.; Zhou, Q.; Shi, X.; Shi, F. Failure behaviours of 100% SOC lithium-ion battery modules under different impact loading conditions. Eng. Fail. Anal. 2017, 82, 149–160. [Google Scholar] [CrossRef]
- Yamanaka, T.; Takagishi, Y.; Tozuka, Y.; Yamaue, T. Modeling lithium ion battery nail penetration tests and quantitative evaluation of the degree of combustion risk. J. Power Sources 2019, 416, 132–140. [Google Scholar] [CrossRef]
- Chen, M.; Bai, F.; Song, W.; Lv, J.; Lin, S.; Feng, Z.; Li, Y.; Ding, Y. A multilayer electro-thermal model of pouch battery during normal discharge and internal short circuit process. Appl. Therm. Eng. 2017, 120, 506–516. [Google Scholar] [CrossRef]
- Shi, Y.; Noelle, D.J.; Wang, M.; Le, A.V.; Yoon, H.; Zhang, M.; Meng, Y.S.; Qiao, Y. Exothermic behaviors of mechanically abused lithium-ion batteries with dibenzylamine. J. Power Sources 2016, 326, 514–521. [Google Scholar] [CrossRef]
- Vyroubal, P.; Kazda, T. Finite element model of nail penetration into lithium ion battery. J. Energy Storage 2018, 20, 451–458. [Google Scholar] [CrossRef]
- Noelle, D.J. Investigating Internal Short Circuit Heating to Inform Novel Lithium-Ion Battery Safety Strategies. Ph.D. Thesis, University of California, San Diego, CA, USA, 2018. [Google Scholar]
- Fang, W.; Ramadass, P.; Zhang, Z. Study of internal short in a Li-ion cell-II. Numerical investigation using a 3D electrochemical-thermal model. J. Power Sources 2014, 248, 1090–1098. [Google Scholar] [CrossRef]
- Mao, B.; Chen, H.; Cui, Z.; Wu, T.; Wang, Q. Failure mechanism of the lithium ion battery during nail penetration. Int. J. Heat Mass Transf. 2018, 122, 1103–1115. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. Simulation and experimental study on lithium ion battery short circuit. Appl. Energy 2016, 173, 29–39. [Google Scholar] [CrossRef]
- Wang, M.; Le, A.V.; Noelle, D.J.; Shi, Y.; Meng, Y.S.; Qiao, Y. Internal-short-mitigating current collector for lithium-ion battery. J. Power Sources 2017, 349, 84–93. [Google Scholar] [CrossRef]
- Ansys Inc. “ANSYS Fluent theory guide 2019 release,” ANSYS, Inc., December 2019. [Online]. Available online: http://www.ansys.com (accessed on 1 December 2019).
- Kim, U.S.; Yi, J.; Shin, C.B.; Han, T.; Park, S. Modeling the Dependence of the Discharge Behavior of a Lithium-Ion Battery on the Environmental Temperature. J. Electrochem. Soc. 2011, 158, A611–A618. [Google Scholar]
- Gu, H. Mathematical Analysis of a Zn/NiOOH Cell. J. Electrochem. Soc. 1983, 130, 1459–1464. [Google Scholar] [CrossRef]
- Giel, H.; Henriques, D.; Bourne, G.; Markus, T. Investigation of the heat generation of a commercial 2032 (LiCoO2) coin cell with a novel differential scanning battery calorimeter. J. Power Sources 2018, 390, 116–126. [Google Scholar] [CrossRef]
- Kim, C.-S.; Yoo, J.-S.; Jeong, K.-M.; Kim, K.; Yi, C.-W. Investigation on internal short circuits of lithium polymer batteries with a ceramic-coated separator during nail penetration. J. Power Sources 2015, 289, 41–49. [Google Scholar] [CrossRef]
- Maleki, H.; Howard, J.N. Internal short circuit in Li-ion cells. J. Power Sources 2009, 191, 568–574. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, J.; Gu, J. A comprehensive study on Li-ion battery nail penetrations and the possible solutions. Energy 2017, 123, 392–401. [Google Scholar] [CrossRef]
- Cai, W.; Wang, H.; Maleki, H.; Howard, J.; Curzio, E.L. Experimental simulation of internal short circuit in Li-ion and Li-ion-polymer cells. J. Power Sources 2011, 196, 7779–7783. [Google Scholar] [CrossRef]
- Wang, Q.; Sun, J.; Yao, X.; Chen, C. Thermal Behavior of Lithiated Graphite with Electrolyte in Lithium-Ion Batteries. J. Electrochem. Soc. 2006, 153, A329–A333. [Google Scholar] [CrossRef]
- Maleki, H.; Deng, G.; Haller, I.K.; Anani, A.; Howard, J.N. Thermal Stability Studies of Binder Materials in Anodes for Lithium-Ion Batteries. J. Electrochem. Soc. 2000, 147, 4470–4475. [Google Scholar] [CrossRef]
- IATA. 2020 Lithium Battery Guidance Document. 2020. Available online: https://www.iata.org/contentassets/05e6d8742b0047259bf3a700bc9d42b9/lithium-battery-guidance-document-2020.pdf (accessed on 1 January 2020).
- Chiu, K.-C.; Lin, C.-H.; Yeh, S.-F.; Lin, Y.-H.; Chen, K.-C. An electrochemical modeling of lithium-ion battery nail penetration. J. Power Sources 2014, 251, 254–263. [Google Scholar] [CrossRef]
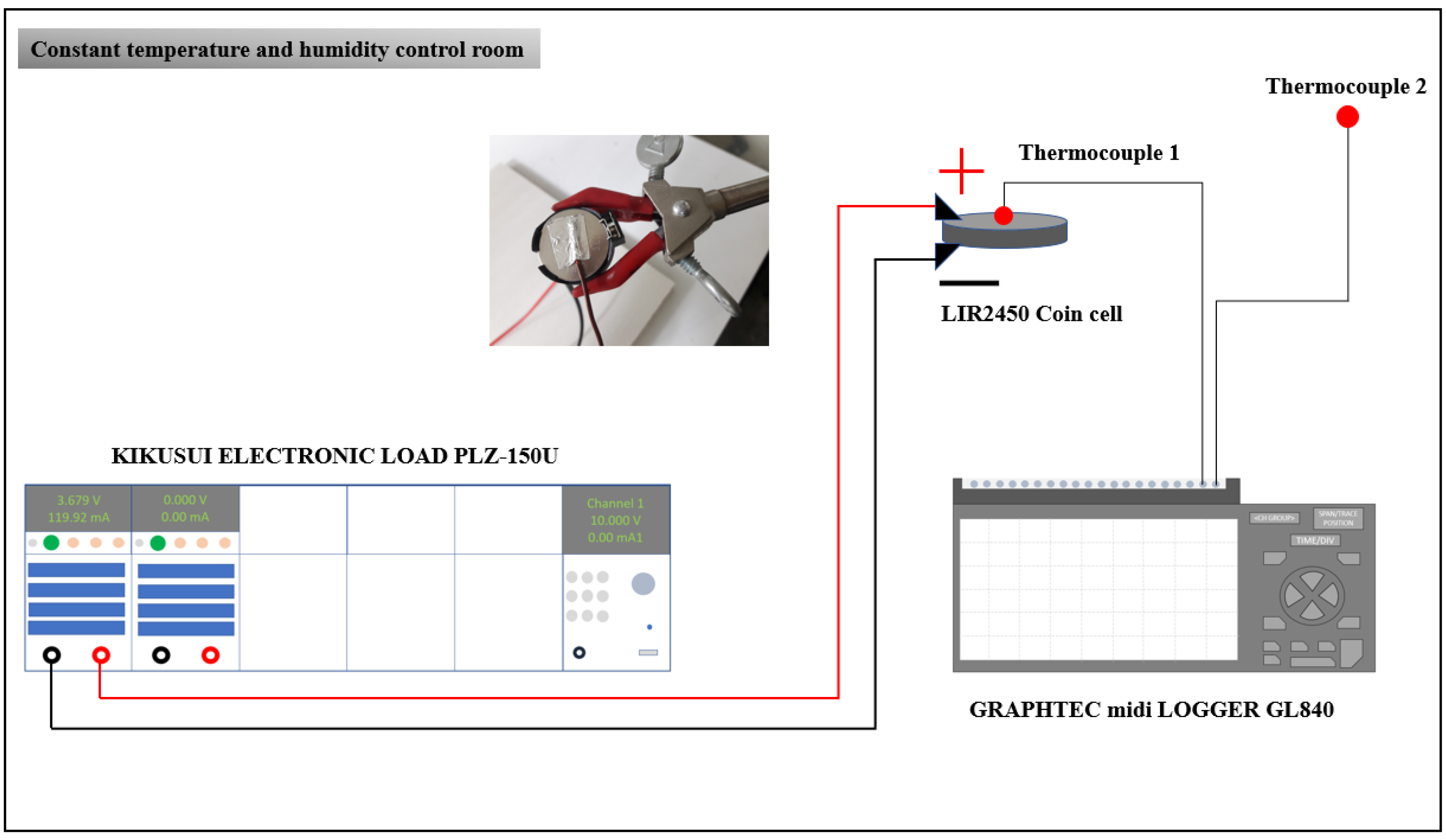
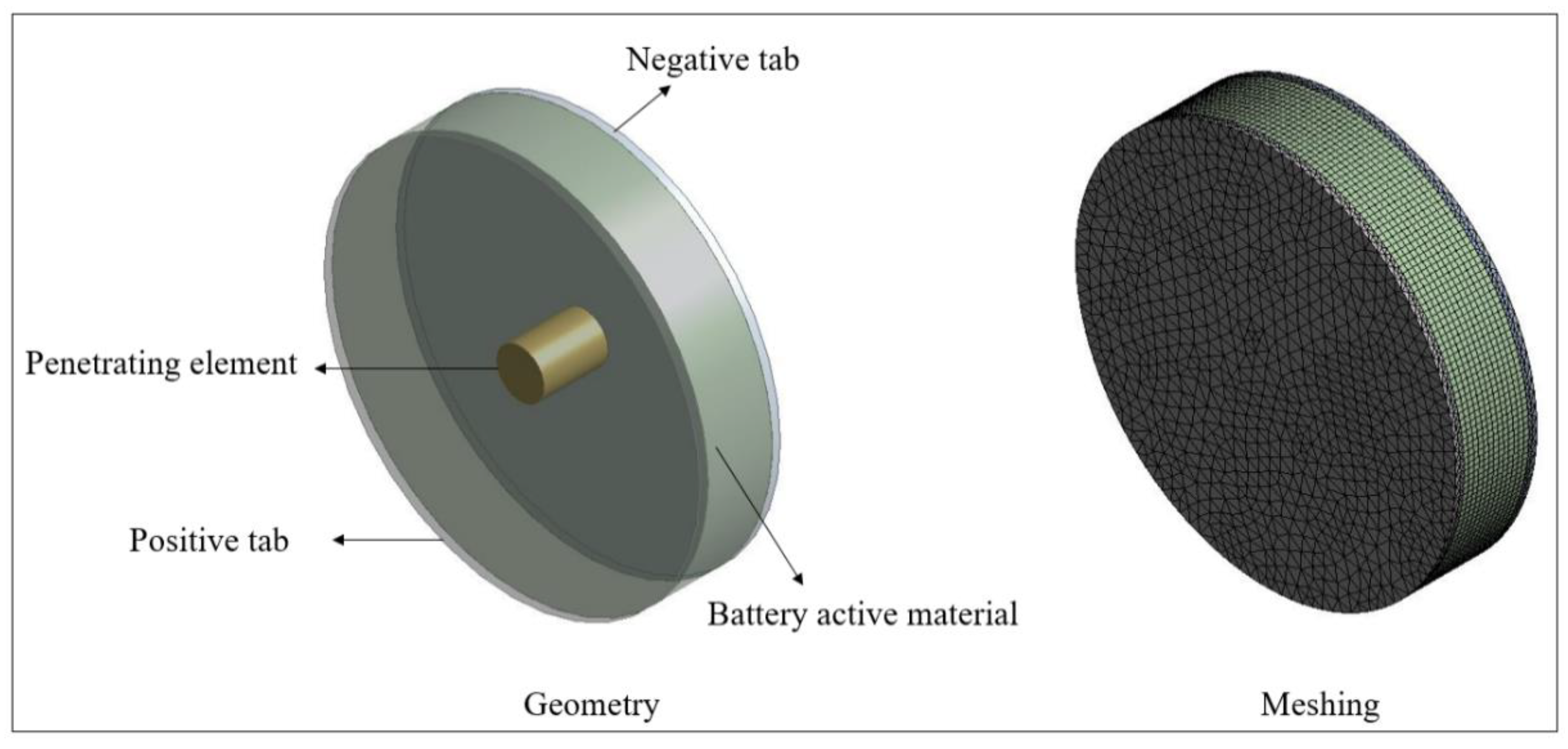
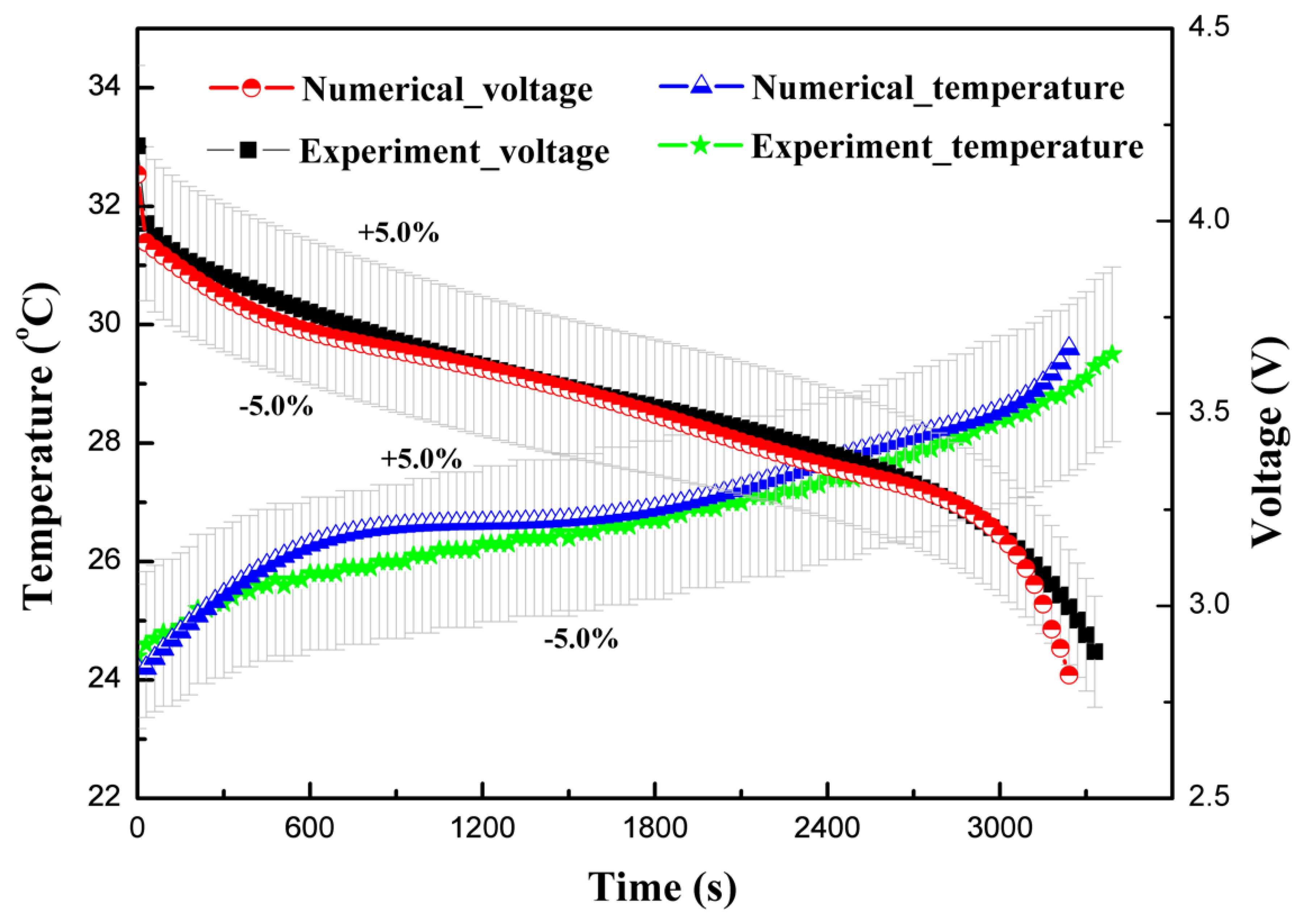
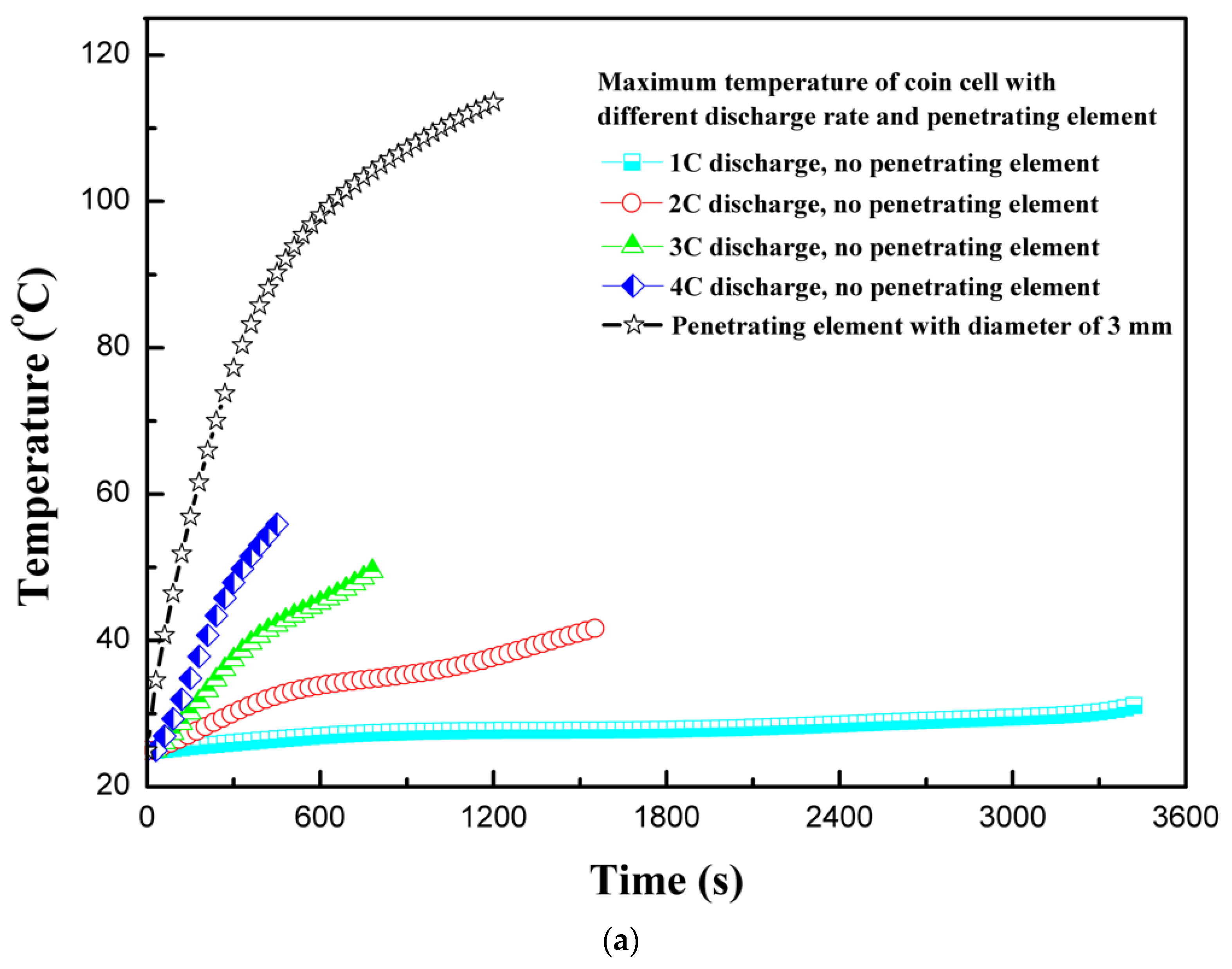

| Specifications | Values |
|---|---|
| Cathode material | LiCoO2 |
| Anode material | Graphite |
| Nominal capacity (mAh) | 120 |
| Mass (g) | 5 |
| Specific heat capacity (J/kg⋅K) | 1000 |
| Internal resistance (mΩ) | ≤400 |
| Density (kg/m3) | 1940 |
| Thermal conductivity (W/m-K) | 18.2 |
| Geometry specifications | |
| Diameter (mm) | 24.5 |
| Height (mm) | 5 |
| Equipment | Parameter | Specifications |
|---|---|---|
| KIKUSUI electronic load PLU-150 | Operating voltage | 1.5 to 150 V |
| Current range | 300 mA to 30 A | |
| Maximum power | 150 W | |
| GL820 Data logger | Operating range | −200 °C ≤ TS ≤ 400 °C |
| Constant temperature and humidity control room | Temperature range | −30 to 60 °C |
| Humidity range | 30% to 95% RH |
| Co-Efficient of U | Values | Co-Efficient of Y | Values |
|---|---|---|---|
| a0 | 4.167186 | b0 | 0.923942 |
| a1 | −1.12224 | b1 | −7.07927 |
| a2 | 1.522472 | b2 | 37.43602 |
| a3 | −3.46622 | b3 | −87.1731 |
| a4 | 5.954965 | b4 | 90.32512 |
| a5 | −3.55203 | b5 | −34.5455 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.-Y.; Kim, N.; Seo, J.-H.; Patil, M.S. Thermal Abuse Behavior of the LIR2450 Micro Coin Cell Battery Having Capacity of 120 mAh with Internal Short Circuit by Penetrating Element. Symmetry 2020, 12, 246. https://doi.org/10.3390/sym12020246
Lee M-Y, Kim N, Seo J-H, Patil MS. Thermal Abuse Behavior of the LIR2450 Micro Coin Cell Battery Having Capacity of 120 mAh with Internal Short Circuit by Penetrating Element. Symmetry. 2020; 12(2):246. https://doi.org/10.3390/sym12020246
Chicago/Turabian StyleLee, Moo-Yeon, Namwon Kim, Jae-Hyeong Seo, and Mahesh Suresh Patil. 2020. "Thermal Abuse Behavior of the LIR2450 Micro Coin Cell Battery Having Capacity of 120 mAh with Internal Short Circuit by Penetrating Element" Symmetry 12, no. 2: 246. https://doi.org/10.3390/sym12020246
APA StyleLee, M.-Y., Kim, N., Seo, J.-H., & Patil, M. S. (2020). Thermal Abuse Behavior of the LIR2450 Micro Coin Cell Battery Having Capacity of 120 mAh with Internal Short Circuit by Penetrating Element. Symmetry, 12(2), 246. https://doi.org/10.3390/sym12020246






