Towards Stochasticity through Joint Invariant Functions of Two Isomorphic Lie Algebras of SL(2R) Type
Abstract
1. Introduction
2. Short Reminder on the motion fractal theories in the Form of Scale Relativity
3. Dynamics in a Complex System in the Form of Schrödinger Type Fractal “Regimes”
4. Dynamic of Complex Systems in the Form of Hydrodynamic Type Fractal “Regimes”
5. Conclusions
- (i)
- In the fractal theory of motion in the form of scale relativity, it is shown that in the case of the nonrotational movements of the entities of a complex system, its dynamics are associated with the geodesics on a fractal manifold in the form of Schrödinger equations at different scale resolutions. In such a context:
- (i1)
- Explaining the dynamics of complex system entities in the form of one-dimensional stationary Schrödinger equations at various scale resolutions involves joint invariant functions at the action of two isomorphic groups of type (group of variables and parameters) as solutions of Stoka type equations. In such a context, special mechanisms for synchronizing the entities of a complex system become operable in the sense that not only the phases but the amplitudes of the complex system entities are homographically affected.
- (i2)
- The existence of a parallel transport of directions in the Levy–Civita sense, which specifies a certain amplitude-phase correlation for any entity of a complex system, explains a particular synchronization mechanism.
- (i3)
- (i4)
- A special synchronization through self-modulation in amplitudes between two entities of the same type of a complex systems is established. Such results are proved in the dynamic of laser ablation plasma (the synchronization on the oscillation modes between the Coulomb structure and thermal structure).
- (ii)
- In the fractal theory of motion in the form of scale relativity theory, it is shown that, in the general case, the dynamics in complex systems can be separated on the resolution scale (the differentiable and non-differentiable scales). Then, hydrodynamic type “regimes” to describe the dynamics become operational. In such a context:
- (ii1)
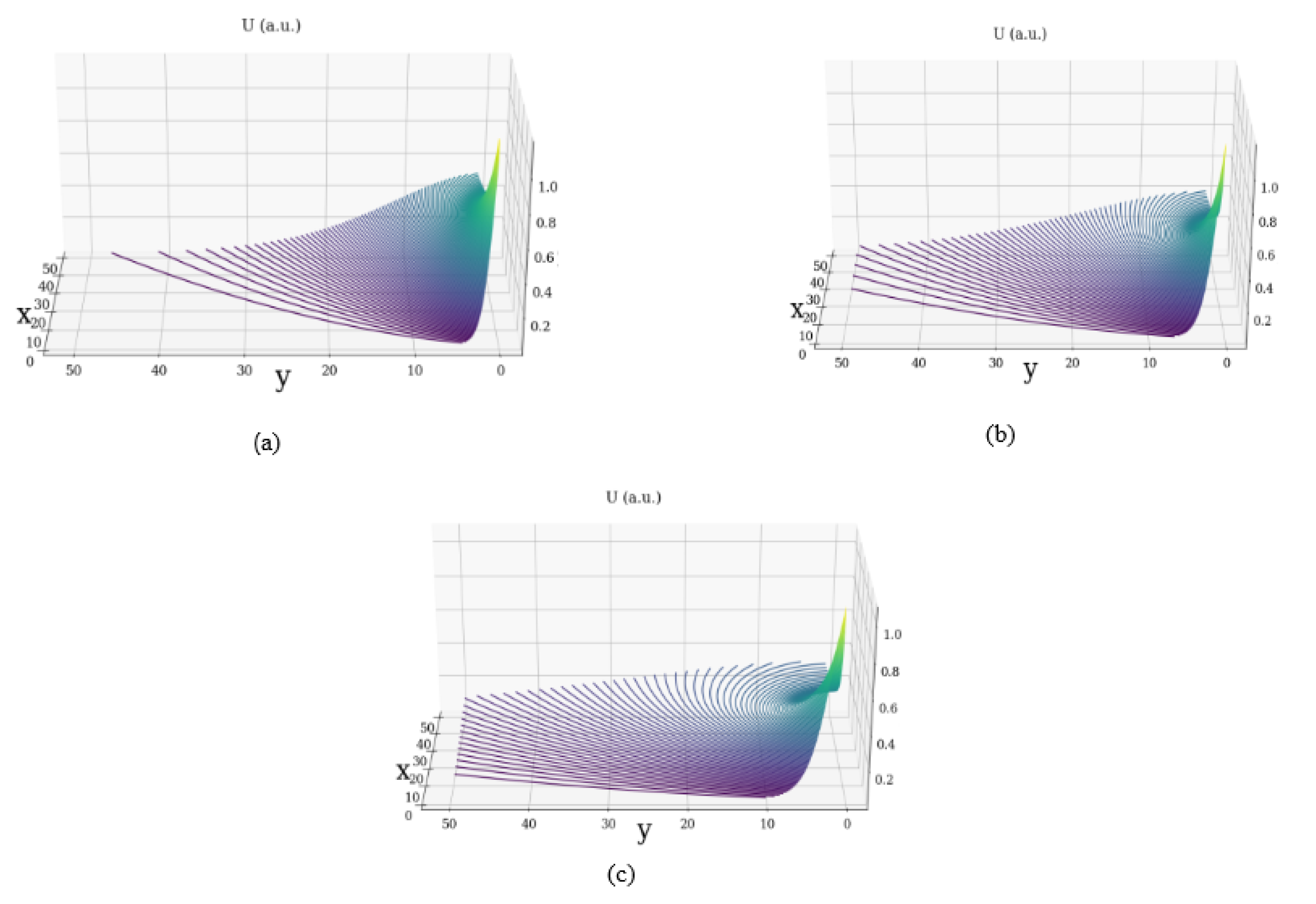
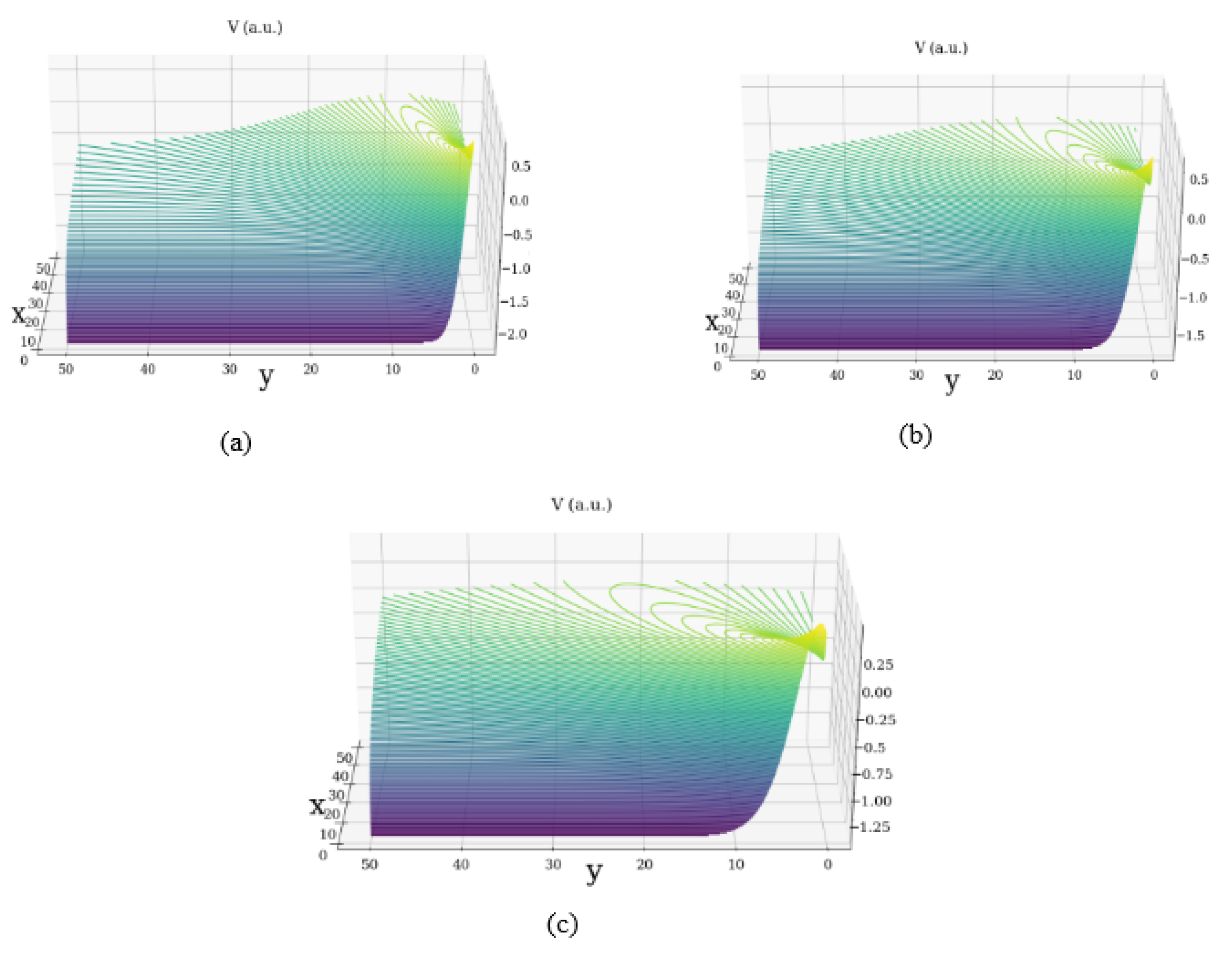
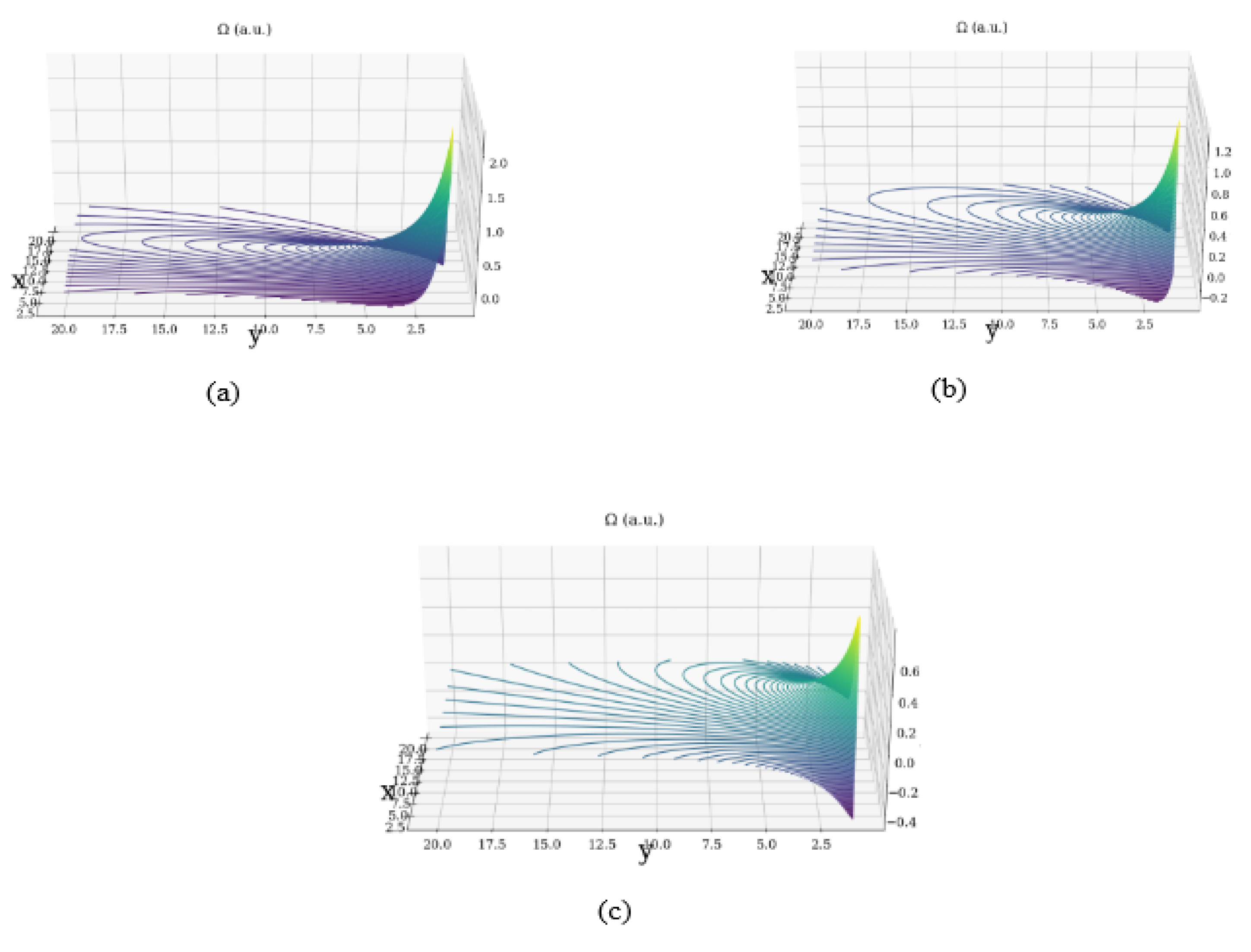
- In the static case of motions at a non-differentiable scale resolution, the velocity fields are given by means of nonlinear solutions of fractal soliton type and fractal soliton kink-type.
- (ii2)
- In the motion previous context, a fractal minimal vortex is generated. This case become the “source” of all turbulences in the dynamics of complex systems.
Author Contributions
Funding
Conflicts of Interest
Appendix A
- (i)
- (ii)
- The dynamics of complex systems structural units are described through fractal variables. Then, two derivatives of the variable field can be defined:
- (iii)
- The differential of the spatial coordinate field is given by the expression:
- (iv)
- (v)
- The differential time reflection invariance of any variable is recovered by means of the operator:
- (vi)
- Since the fractalization implies stochasticization [28], the whole statistic arsenal in the form of averages covariances, etc., becomes operational. Thus, let us choose for the average of the following functionality:with
- (vii)
- The complex system dynamics can be described through the scale covariant derivative given by the operator:where
References
- Cartan, E. La Théorie de Groupes Finis et Continus et la Géométrie Différentiele Traiteés par la Méthode du Répere Mobile; Gauthier-Villars: Paris, France, 1951. [Google Scholar]
- Postnikov, I. Groupes et Algebres de Lie; Édition Mir: Moscow, Russia, 1985. [Google Scholar]
- Simon, B. Representations of Finite and Compact Groups; American Mathematical Society: Providence, RI, USA, 1996. [Google Scholar]
- Stoka, M.I. Integral Geometry; Publishing House of the Academy: Bucharest, Romania, 1967. [Google Scholar]
- Stoka, M.I. Géométrie Intégrale; Memorial des Sciences Mathématiques; Gauthier Villars: Paris, France, 1968. [Google Scholar]
- Leuci, M.; Pastor, A.M. Families of Curves Measurable with Respect to the Affine Modular Group. Suppl. Ai Rend. Del Circ. Mat. Di Palermo 1994, 35, 171–201. [Google Scholar]
- Mazilu, N. The Stoka Theorem, a Side Story of Phisics in Gravitation Field. Suppl. Ai Rend. Del Circ. Mat. Di Palermo 2004, 77, 415–440. [Google Scholar]
- Mazilu, N.; Agop, M. At the Crossroads of Theories. Between Newton and Einstein—The Barbilian Universe; Ars Longa Publishing House: Iasi, Romania, 2010. (In Romanian) [Google Scholar]
- Mazilu, N.; Agop, M. Skyrmions: A Great Finishing Touch to Classical Newtonian Philosophy; World Philosophy Series; Nova: New York, NY, USA, 2012. [Google Scholar]
- Mercheş, I.; Agop, M. Differentiability and Fractality in Dynamics of Physical Systems; World Scientific: Singapore, 2016. [Google Scholar]
- Agop, M.; Mercheş, I. Operational Procedures Describing Physical Systems; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2019. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Jaynes, E.T. The Well-Posed Problem. Found. Phys. 1973, 3, 477–493. [Google Scholar] [CrossRef]
- Arnold, V.I. Mathematical Methods of Classical Mechanics; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Notalle, L. Scale Relativity and Fractal Space-Time. A New Approach to Unifying Relativity and Quantum Mechanics; Imperial College Press: London, UK, 2011. [Google Scholar]
- Bennett, C.H. How to Define Complexity in Physics and Why. In Complexity, Entropy, and the Physics of Information; Zurek, W.H., Ed.; Addison-Wesley Pub. Co.: Redwood City, CA, USA, 1990; pp. 137–148. [Google Scholar]
- Bar-Yam, Y. Dynamic of Complex System. The Advanced Book Program; Addison-Wesley: Reading, MA, USA, 1997. [Google Scholar]
- Badii, R.; Politi, A. Complexity: Hierarchical Structure and Scaling in Physics; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Mitchell, M. Complexity: A Guided Tour; Oxford University Press: Oxford, UK, 2009. [Google Scholar]
- Wójcik, D.; Białynicki-Birula, I.; Zyczkowski, K. Time Evolution of Quantum Fractals; PRL85, 5022; The American Physical Society: College Park, MD, USA, 2000. [Google Scholar]
- Aharony, A.; Feder, J. (Eds.) Fractals in Physics: Proceedings of the International Conference Honoring Benoit B. Mandelbrot on His 65th Birthday. Venice, France, Physica (Amsterdam) 38D, 1989; North-Holland: Amsterdam, The Netherlands, 1990. [Google Scholar]
- Meakin, P. Fractals, Scaling and Growth Far from Equilibrium; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- El-Nabulsi, R.A. Modifications at Large Distances from Fractional and Fractal Arguments. Fractals 2010, 18, 185–190. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on Fractal Subsets of Real LineI: Formulation. Fractals 2009, 17, 53–81. [Google Scholar] [CrossRef]
- Amir-Azizi, S.; Hey, A.J.; Morris, T.R. Quantum Fractals. Compl. Syst. 1987, 1, 923–938. [Google Scholar]
- Laskin, N. Fractional quantum mechanics and Lévy path integrals. Phys. Lett. A 2000, 268, 298–305. [Google Scholar] [CrossRef]
- Martins, J.; Ribeiro, H.V.; Evangelista, L.R.; da Silva, L.R.; Lenzi, E.K. Fractional Schrödinger equation with noninteger dimensions. Appl. Math. Comput. 2012, 219, 2313–2319. [Google Scholar] [CrossRef]
- Mandelbrot, B. The Fractal Theory of Nature; Freeman: San Francisco, CA, USA, 1982. [Google Scholar]
- Cresson, J.; Adda, F.B. Quantum Derivations and Schrödinger Equations. Chaos Solitons Fractals 2004, 19, 1323–1334. [Google Scholar]
- Mihaileanu, N. Complements of Projective and Differential Analytical Geometry (in Romanian); Didactic and Pedagogical Publishing House: Bucharest, Romania, 1971. [Google Scholar]
- Enescu, F.; Irimiciuc, S.A.; Cimpoesu, N.; Bedelean, H.; Bulai, G.; Gurlui, S.; Agop, M. Investigations of Laser Produced Plasmas Generated by Laser Ablation on Geomaterials. Experimental and Theoretical Aspects. Symmetry 2019, 11, 1391. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Bulai, G.; Gurlui, S.; Agop, M. On the separation of particle flow during pulse laser deposition of heterogeneous materials-A multi-fractal approach. Powder Technol. 2018, 339, 273–280. [Google Scholar] [CrossRef]
- Irimiciuc, S.A.; Bulai, G.; Agop, M.; Gurlui, S. Influence of laser-produced plasma parameters on the deposition process: In situ space-and time-resolved optical emission spectroscopy and fractal modeling approach. Appl. Phys. A 2018, 124, 615. [Google Scholar] [CrossRef]
- Schlichting, H. Boundary Layer Theory; McGraw-Hill: New York, NY, USA, 1970. [Google Scholar]
- Cristescu, C.C. Nonlinear Dynamics and Chaos: Theoretical Fundamentals and Applications; Romanian Academy Publishing House: Bucharest, Romania, 2008. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Agop, M.; Craus, M. Towards Stochasticity through Joint Invariant Functions of Two Isomorphic Lie Algebras of SL(2R) Type. Symmetry 2020, 12, 226. https://doi.org/10.3390/sym12020226
Agop M, Craus M. Towards Stochasticity through Joint Invariant Functions of Two Isomorphic Lie Algebras of SL(2R) Type. Symmetry. 2020; 12(2):226. https://doi.org/10.3390/sym12020226
Chicago/Turabian StyleAgop, Maricel, and Mitică Craus. 2020. "Towards Stochasticity through Joint Invariant Functions of Two Isomorphic Lie Algebras of SL(2R) Type" Symmetry 12, no. 2: 226. https://doi.org/10.3390/sym12020226
APA StyleAgop, M., & Craus, M. (2020). Towards Stochasticity through Joint Invariant Functions of Two Isomorphic Lie Algebras of SL(2R) Type. Symmetry, 12(2), 226. https://doi.org/10.3390/sym12020226





