Abstract
In this paper, we study the feasibility of performing fuzzy information retrieval by word embedding. We propose a fuzzy information retrieval approach to capture the relationships between words and query language, which combines some techniques of deep learning and fuzzy set theory. We try to leverage large scale data and the continuous-bag-of words model to find the relevant feature of words and obtain word embedding. To enhance retrieval effectiveness, we measure the relativity among words by word embedding, with the property of symmetry. Experimental results show that the recall ratio, precision ratio, and harmonic average of two ratios of the proposed method outperforms the ones of the traditional methods.
1. Introduction
Information retrieval has been a long-standing challenge for the computer science community. As is known to all, it originates from the reference work of the library [1], and the emergence of the computer relates it to other forms of content. Due to the rapid development of the internet in recent years, online search has become the preferred way for people to obtain information, besides, the advent and popularization of the internet causes the source of the information to be extensive. This explosion of information makes people face enormous challenges in effectively finding the information that they need. Consequently, the study of information retrieval is necessary.
So far, the models of information retrieval may be divided into four categories: boolean logic models, vector space models (VSM), probabilistic models, and fuzzy set models [2]. The traditional technology of information retrieval is based on boolean logic models. In the boolean logic model, we can propose any query which is in the form of a boolean expression of terms and the documents are converted into sets of words [3]. The document can be retrieved, when the query language is in sets of words. In other words, the boolean model demands that the query language must exactly match the document and the users must accurately input the query language [4]. In VSM, queries and documents are represented as multidimensional vectors. The similarity between the two vectors is utilized for measuring the correlation of queries and documents. However, vagueness is one of the inherent and vital characteristics of natural language. The information need of the users and the main theme of the documents can not be completely described by keywords. The situation is an important aspect that affects the effectiveness of information retrieval. To deal with such uncertainty, fuzzy set models are proposed, in which a fuzzy set for each query term is defined, correspondingly, each document has a degree of membership in the set.
A simple fact is that most information retrieval systems currently still utilize the boolean logic model. Since 1965, the fuzzy set theory proposed by Zadeh has been widely used to describe the uncertain and vague information [5]. Many researchers have adopted the fuzzy set theory in information retrieval [6]. The fuzzy information retrieval system plays an important role in the study of information retrieval. In [7], fuzzy indexing systems were applied in fuzzy information retrieval. Then, Lucarella used the fuzzy inference system to expand the query evaluation in [8]. To achieve the goal of enhancing the retrieval, the fuzzy associative mechanism was published. The fuzzy associative mechanisms exploited fuzzy thesauri, fuzzy pseudothesauri, and fuzzy clustering techniques to extend the set of the documents retrieval by a query with associated documents [9]. Compared with the associative retrieval mechanisms that the associations are crisp, the fuzzy associative retrieval is based on the concept of fuzzy associations [10]. In [11], Yasushi et al. presented a method that uses the keyword connection matrix to improve the fuzzy document retrieval system. The keyword connection matrix embodies similarities among keywords, as a thesaurus does. However, the keywords connection matrix only considers the relationship of the co-occurrence words in the document. In [12], Takenobu et al. attempted to construct a similarity thesaurus for replacing the keywords connection matrix to improve this problem. After that, Chen et al. pointed out that employing ontology to extend the user’s retrieval of words and index domain knowledge was also useful [13,14,15]. Sabour et al. presented a flexible fuzzy-based approach for querying relational databases [16].
It is known that information retrieval is concerned with the representation, storage, and access of a set of documents in the form of textual information items or records of variable length and format, such as books, journal articles, and technical reports [2,17]. The most popular indexing mechanism is based on term extraction and weighting, and its goal is to generate a formal representation of textual information items. While the previous researchers have enhanced the quality of fuzzy information retrieval to a certain degree, the index term weights of this research are according to the occurrences count of a term in the document. Although the way to use the occurrences count of terms is comparatively simple and easy to master, it requires a large number of training samples. Furthermore, two terms whose co-occurrences’ frequency is low may have a close relationship. The case is another aspect that influences the effectiveness of information retrieval.
In [18], Bengio et al. firstly introduced the neural network into the language model and proposed the concept of word embedding. Word embedding can use the information around the local context of words to obtain the vectors. Reference [18] used local gradient descent to adjust weights, but the use of the non-convex objective function could only get the local optimum. The multi-layer artificial neural network model has the ability of feature learning. Meanwhile, the layer-by-layer training method is capable of obtaining the optimum solution. Hinton et al. [19] put forward the multi-layer artificial neural network model and the layer-by-layer training method to address this question on the basis of the research of Bengio et al. Then, T. Mikolov et al. [20] found a relatively better and faster approach, which is called the continuous bag-of-words model to train word embedding. Meanwhile, T. Mikolov et al. proposed that word embedding can be used to measure the similarity among words. The word embedding that is trained by the continuous bag-of-words model has been broadly applied in many branches of natural language processing, such as text classification, document clustering, part of speech tagging, named entity recognition, and emotional analysis, and it has a good performance [21,22,23,24]. We consider that word embedding can extract features from the local context information of words. If two words are related to each other, the word embedding of the words is also similar. In this paper, we combine word embedding trained by the continuous bag-of-words model and fuzzy set theory to improve the result of fuzzy information retrieval.
The structure of the paper is as follows. In Section 2, we review the theory of fuzzy information retrieval models. In Section 3, the preliminary background for word embedding and a brief description of the continuous bag-of-words model are presented. An approach to fuzzy information retrieval based on word embedding is introduced in Section 4. With a series of experiments, we compare the fuzzy information retrieval performance of the proposed method with the traditional methods in Section 5. The conclusions are discussed in the final section.
2. Fuzzy Information Retrieval
The fuzzy information retrieval model is fuzzy generalizations of the boolean model. The fuzzy information retrieval model defines the fuzzy relationship between query language and the retrieved documents. The fuzzy information retrieval system assumes that a set of fuzzy documents is associated with each word in the query language. That is to say, each word in the query language defines a fuzzy set, and the elements in the sets are retrieved documents. Correspondingly, each document in the set has a degree of membership to correspond to each word in the query language. As a retrieval result, the fuzzy set reflects how well each document matches the query.
Indexing is the preliminary operation in the creation of the documents’ representation. In the procedure of defining an indexing, we should ensure that the indexing can present textual information not only accurately but also overall. An indexing function, as the membership function of the fuzzy set, is used to calculate the correlation between words. In other words, the results of the membership function are the weights between index item and words in retrieval documents. People can employ the function to achieve the goal that presents textual information properly. It presents as follows [6]:
in which is the membership function that computes the degree of correlation between each index term t and each retrieval document d, and T, D are the collection of each item in the query language and retrieval documents, respectively.
A commonly used definition of the membership function F is based on term frequency() and inverse document frequency() as the following [16]:
where
That is to say, is the frequency of index term t in document d, and is used to measure the importance and universality of the index term t. From Equation (3) and (4), we can find that the value of will be a little high if a term is high frequency for a given document and low frequency for the whole of the retrieved documents.
The other popular and efficient definition of the membership function F is as follows [11]:
where is the relevant value between index term t and word k. denotes the i-th document in the collection of retrieved documents, ⨁ is a fuzzy operator that proposed in [11] and defines as follow:
Then, Equation (5) becomes:
The definition of such functions is based on the statistical and quantitative analysis of the text which makes it possible to model the concept of importance of a word in describing the information carried by the document. At the same time, the work that models the concept of importance of a word becomes significant.
3. A Review of Continuous Bag-of-Word Model
Continuous bag of words model(CBOW) is a highly efficient shallow neural network algorithm. It is developed to generate vector representations of a language vocabulary so that the information of the words is encoded in the vector space structure [20]. Essentially, the continuous bag of words model is similar to the feedforward neural network language model (FFNNLM) [25]. FFNNLM is firstly proposed by Bengio et al., which applies the feedforward neural network (FFNN) into the language model and learns a distributed representation for words to solve the problem of high dimensionality. However, the non-linear hidden layer of the model is deleted and the projection layer of the model is applied for all words. That is to say, the continuous-bag-of words model is a simple neural network with three layers: input, projection, and output. The working principle of the model is shown in Figure 1.
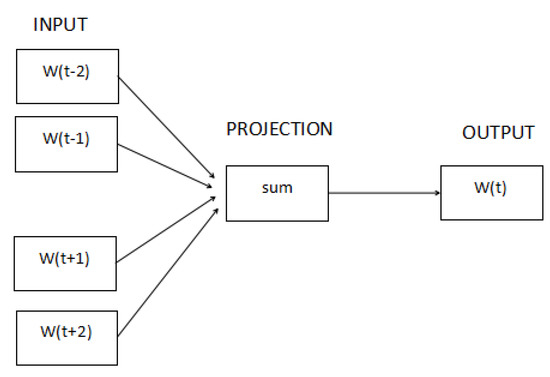
Figure 1.
CBOW Model.
We can see that the core thought of the continuous bag-of-words model predicts something about a vocabulary word from its context . In this way, we can take advantage of the maximum likelihood and set the objective function as follows [26]
where C denotes the corpus and context(w(t)) denotes the context of .
Although the hidden layer is removed in the continuous bag-of-words model, the active function in the output layer still uses the softmax function, which is expressed as
T. Mikolov et al. in [20] offer two methods that are separately called hierarchical softmax and negative sampling (NEG) to speed up the training process. Compared to hierarchical softmax, the training speed of negative sampling is faster and the training effect of negative sampling is better for common words and low latitude vectors. Hence, we employ negative sampling to make the process speedy and the word embedding credible. The negative sampling is simplified on the basis of the noise contrastive estimation. If the known word w is relative to the context of the word w, we call the word w the positive case and other irrelative word the negative case in the continuous bag-of-words model. To express the training label, the model defines the label of the positive case as 1 and the label of the negative case as 0:
Since the continuous bag-of-words model adopts the sigmoid function to be the activation function, the objective function is defined as follows [20]:
where is an untrained vector that the word u corresponds to. is the sum of the vectors of the context , is the subset of negative sampling and it demands . is the probability of the situation that the context is and the predictive center word u satisfies . Next, the continuous bag-of-words model utilizes the stochastic gradient ascent algorithm to optimize Equation (11). Hence, we can get the gradient of as follows:
the gradient of as follow:
From Equations (12) and (13), we can obtain:
where is the learning rate. In this way, the model achieves the goal of increasing the probability of positive samples, reducing the probability of negative samples, and training high-quality word embedding.
4. Fuzzy Information Retrieval Based on Word Embedding
It is important for a fuzzy information retrieval system to measure the relationship between words in the retrieval documents and words in the query language. The traditional methods of weighting the relationship are simple and easy to execute, but they will cause inaccuracy if the data set is sparse. The technology of word embedding can transform words into dense vectors. For similar words, the corresponding word vectors are similar. In addition, word embedding can improve the effects of data sparsity on natural language processing to a certain extent.
In this section, we use the continuous bag-of-words model to train word embedding, and we replace word frequency with word embedding to compute the relevance value between the word and each item of the query language. The modified cosine distance of word embedding is the tool of measuring the correlation degree between two words. The distance between two words satisfies the property of symmetry. Let , be the vectors of any two words in a retrieved document, the relevance value between and are defined as:
The detailed process of the model is as follows:
- Step 1
- Build a corpus. Then, the operations of word segment, part of speech tagging, and removal of the stop words are carried out. On this basis, the preprocessed corpus is trained by the continuous bag-of-words model. After that, the corresponding word embedding is obtained.
- Step 2
- Extract 20 keywords, these keywords can represent the meaning of the document in general, from each retrieved document. Set up the database with the names and keywords of each retrieved document.
- Step 3
- Input the query language. Do the same pretreatment as the trained corpus with the query.
- Step 4
- Calculate the modified vector cosine distance between keywords in each retrieved document and each word in the query language. Apply the fuzzy set theory and the membership function to get the degree of membership. The degree of membership expresses how much the retrieved documents belong to each word of the query language.
- Step 5
- Convert the query language into conjunctive normal form to obtain the membership value for each retrieved document that belongs to the query language.
- Step 6
- The documents whose membership values are greater than 0 are listed in descending order to make the fuzzy information retrieval system convenient for the user.
The Flow chart of the model is as follows in Figure 2:
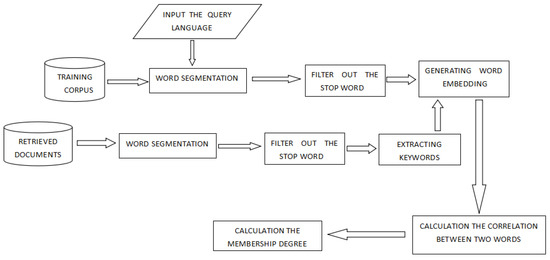
Figure 2.
Flow chart model.
5. Experiments
5.1. Evaluation Methods
We employ the recall ratio and the precision ratio to measure the performance of the fuzzy information retrieval system based on the continuous bag-of-words model. The precision ratio denotes how many of the retrieved documents are relevant, while the recall ratio expresses how many of the relevant documents are retrieved. The detailed definition of the two evaluation criterion as following [27]:
Since the relationship of mutual restraint exists between recall ratio and precision in the field of information retrieval, we add the harmonic mean of the two ratios to judge the result:
Under the principle that the ratios should be more accurate, we select 20 experimenters to determine the correlative retrieved documents for each of several queries.
5.2. Corpora and Training Details
We trained the word vectors on the data set which includes 3.3 GB of the Chinese Wikipedia corpus and 18,000 network news. The news is collected by web crawler technology and involves political, military, humanistic, historical, and other aspects. Then, we selected 150 documents from nine different topics. That is to say, we use 1350 documents that were chosen from various domains as retrieved data sets.
Simultaneously, we set the context window to 5, the dimension of the vector to 100, and the initial learning rate to 0.025. We ran 100 iterations for the words whose frequency was bigger than 1. Subsequently, we utilized the trained word embedding to compute the membership value. The retrieval threshold value was set to 0.6 and the results were compared with the fuzzy information retrieval system using the frequency of words and the keywords connection matrix.
5.3. Results
Table 1 and Table 2 are the degree of the relation that is computed by word embedding. We use the modified cosine distance between word embedding trained by the continuous bag-of-words model to calculate the relevance. Table 1 shows the distances between the related words. Table 2 shows the distances between unrelated words. From Table 1 and Table 2, we find that the word embedding can weight the relationship between two words accurately.

Table 1.
Sampling of trained word embedding.

Table 2.
Sampling of trained word embedding.
Next, we compared the different ways of computing the degree of association between words. The first one is based on the word frequency. It is shown as Equation (19) [11]:
where is the number of documents including both the i-th and the j-th words, is the number of documents including the i-th word and is the number of documents including the j-th word.
The second one is HowNet. HowNet is a detailed dictionary of semantic knowledge [28]. It adopts the method that is based on the world knowledge system to study semantic computation. HowNet holds that a word can be expressed by one or more primitives. Hence, it thinks that the work of computing word similarity can be directly transformed into the work of the calculation of primitive similarity. Equation (19) is the method to use the HowNet to calculate the degree of the relation [29]:
where and are the different words, and are one of the sememe of the word and , respectively. The method to compute the degree of primitive similarity is given as follow:
where and are different primitive, is path length of the semantic level system between and and is an adjustment parameter that usually takes 1.6. Here, we compare the degree of association between words by word frequency, HowNet and word embedding. The results are shown in Table 3. From Table 3, we can see that the Chinese words 镜子(mirror) and 化妆(make up) have a strong relationship in general. However, HowNet set 0.075074 as the weight of the two words. The Chinese word 周末(weekend) and 晴天(sunny day) can not be completely related. The weight calculated by word frequency is unaccepted. Evidently, the degree of association between words that are computed by word embedding is closer to real life.

Table 3.
Contrast results of different methods.
In the following, we use the modified cosine distance of word embedding, word frequency, and the keyword connection matrix to get the weights of words. Then, we employ, separately, term frequency, the inverse document frequency, and Equation (7) to be the membership functions to obtain the document sorting results that are calculated by three different weights of words. Concurrently, we compute their precision ratio, recall ratio, and the harmonic mean of the two ratios. In Figure 3, the harmonic mean of the precision ratio and recall ratio computed by word embedding is 48.68%, when we use Equation (2) as the membership function. In Figure 4, the harmonic mean of the precision ratio and recall ratio computed by word embedding is 62.23%, when we use Equation (7) as the membership function. We can see that the ratios that are computed by word embedding are radically better than the others.
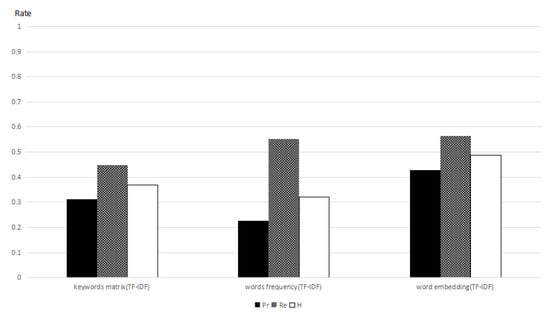
Figure 3.
Precision rate, recall rate, and the harmonic mean of the two ratio with respect to tf-idf.
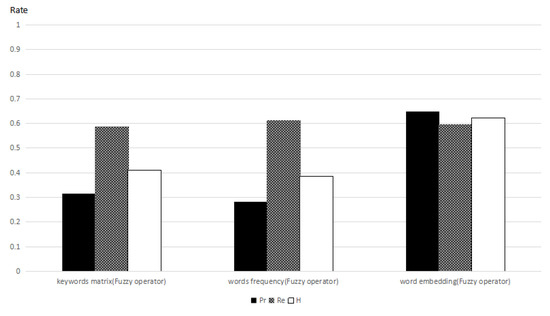
Figure 4.
Precision rate, recall rate, and the harmonic mean of the two ratio with respect to the fuzzy operation.
6. Conclusions
In this paper, we present an integrated approach to fuzzy information retrieval which combines word embedding and fuzzy set theory. Word embedding being trained by the continuous bag-of-words model is employed to calculate the cosine distance. The distance, having the property of symmetry, is treated as the tool of measuring the weights between words and the query language. We also use the fuzzy logic system to modify the query language in retrieval. A series of experiments was implemented to validate the method. The proposed fuzzy information retrieval method is proved to be better than the traditional methods. Although the experiments show a relatively good result, the method is not perfect. This is not surprising, we only discussed the ratios in the same retrieval threshold values. The data sets of the retrieved documents and the training corpus are also not varied enough. We will perform more extensive experiments on this in the near future and try to do the experiments under different thresholds.
Author Contributions
All authors contributed equally to the writing of this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by The National Natural Science Foundations of China (Grant No. 11671001 and No. 61876201).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pasi, G.; Bordogna, G. The Role of Fuzzy Sets in Information Retrieval. Stud. Fuzziness Soft Comput. 2013, 299, 525–532. [Google Scholar]
- Manning, C.D.; Raghavan, P.; Schetze, H. An Introduction to Information Retrieval. J. Am. Soc. Inf. Sci. 1993, 43, 824–825. [Google Scholar]
- Ponte, J.M.; Croft, W.B. A language modeling approach to information retrieval. In Proceedings of the 21st Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, Melbourne, Australia, 24–28 August 1998; pp. 275–281. [Google Scholar]
- Bordogna, G.; Pasi, G. A fuzzy linguistic approach generalizing Boolean Information Retrieval and Technology: A model and its evaluation. J. Assoc. Inf. Sci. 1993, 44, 70–82. [Google Scholar]
- Gupta, M.M. Fuzzy set theory and its applications. Fuzzy Sets Syst. 1992, 47, 396–397. [Google Scholar] [CrossRef]
- Kraft, D.H.; Bordogna, G.; Pasi, G. Fuzzy Set Techniques in Information Retrieval. In Fuzzy Sets in Approximate Reasoning and Information Systems; Springer: Boston, MA, USA, 1999; pp. 1029–1055. [Google Scholar]
- Miyamoto, S. Fuzzy Sets in Information Retrieval and Cluster Analysis; Springer: Dordrecht, The Netherlands, 1990. [Google Scholar]
- Lucarella, D. Uncertainty in information retrieval: An approach based on fuzzy sets. In Proceedings of the International Phoenix Conference on Computers and Communications, Scottsdale, AZ, USA, 21–23 March 1990; pp. 809–814. [Google Scholar]
- Miyamoto, S. Information retrieval based on fuzzy associations. Fuzzy Sets Syst. 1988, 38, 191–205. [Google Scholar] [CrossRef]
- Pasi, G. Fuzzy Sets in Information Retrieval: State of the Art and Research Trends. Stud. Fuzziness Soft Comput. 2008, 220, 517–535. [Google Scholar]
- Ogawa, Y.; Morita, T.; Kobayashi, K. A fuzzy document retrieval system using the keyword connection matrix and a learning method. Fuzzy Sets Syst. 1991, 39, 163–179. [Google Scholar] [CrossRef]
- Mandala, R.; Tokunaga, T.; Tanaka, H. Query expansion using heterogeneous thesauri. Inf. Process. Manag. 2000, 36, 361–378. [Google Scholar] [CrossRef]
- Chen, S.M.; Wang, J.Y. Document retrieval using knowledge-based fuzzy information retrieval techniques. IEEE Trans. Syst. Man Cybern. 1995, 25, 793–803. [Google Scholar] [CrossRef]
- Horng, Y.J.; Chen, S.M.; Chang, Y.C.; Lee, C.H. A new method for fuzzy information retrieval based on fuzzy hierarchical clustering and fuzzy inference techniques. IEEE Trans. Fuzzy Syst. 2005, 13, 216–228. [Google Scholar] [CrossRef]
- Kraft, D.H.; Chen, J.; Mikulcic, A. Combining fuzzy clustering and fuzzy inference in information retrieval. In Proceedings of the IEEE International Conference on Fuzzy Systems(FUZZ-IEEE’2000), San Antonio, TX, USA, 7–10 May 2000; Volume 1, pp. 375–380. [Google Scholar]
- Marrara, S.; Pasi, G. Fuzzy Approaches to Flexible Querying in XML Retrieval. Int. J. Comput. Intell. Syst. 2016, 9 (Suppl. 1), 95–103. [Google Scholar] [CrossRef]
- Sabour, A.A.; Gadallah, A.M.; Hefny, H.A. Flexible Querying of Relational Databases: Fuzzy Set Based Approach. Commun. Comput. Inf. Sci. 2014, 488, 446–455. [Google Scholar]
- Bengio, Y.; Ducharme, R.; Vincent, P.; Jauvin, C. A neural probabilistic language model. In Innovations in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006; pp. 137–186. [Google Scholar]
- Geoffrey, E.H.; Simon, O.; Yee-Whye, T. A fast learning algorithmfor deep belief nets. Read. Cogn. Sci. 2006, 323, 399–421. [Google Scholar]
- Mikolov, T.; Sutskever, I.; Chen, K.; Corrado, G.S.; Dean, J. Distributed Representations of Words and Phrases and their Compositionality. Adv. Neural Inf. Process. Syst. 2013, 26, 3111–3119. [Google Scholar]
- Zheng, X.; Chen, H.; Xu, T. Deep learning for Chinese word segmentation and POS tagging. In Proceedings of the Conference on Empirical Methods in Natural Language Processing, Seattle, WA, USA, 18–21 October 2013. [Google Scholar]
- Zhang, X.; Zhao, J.; Lecun, Y. Character-level convolutional networks for text classification. In International Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2015; pp. 649–657. [Google Scholar]
- Kusner, M.; Sun, Y.; Kolkin, N.; Weinberger, K. From word embeddings to document distances. In International Conference on International Conference on Machine Learning; JMLR.org: New York, NY, USA, 2015; pp. 957–966. [Google Scholar]
- Pathak, D.; Krahenbuhl, P.; Donahue, J.; Darrell, T.; Efros, A.A. Context encoders: Feature learning by inpainting. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 2536–2544. [Google Scholar]
- Bengio, Y.; Senecal, J.S. Quick Training of Probabilistic Neural Nets by Importance Sampling. In Proceedings of the AISTATS, Key West, FL, USA, 1–4 June 2003; pp. 1–9. [Google Scholar]
- Mikolov, T.; Chen, K.; Corrado, G.; Dean, J. Efficient Estimation of Word Representations in Vector Space. arXiv 2013, arXiv:1301.3781. [Google Scholar]
- Salton, G.; Mcgill, M.J. Introduction to Modern Information Retrieval; McGraw-Hill: New York, NY, USA, 1983; pp. 305–306. [Google Scholar]
- Wang, X.L.; Wang, D.; Yang, S.C.; Zhang, C. Word Semantic Similarity Algorithm Based on HowNet. Comput. Eng. 2014, 40, 177–181. [Google Scholar]
- Dong, Z.D.; Dong, Q. HowNet[EB/ OL]. 2013. Available online: http://www.keenage.com (accessed on 25 December 2019).
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).