Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches
Abstract
1. Introduction
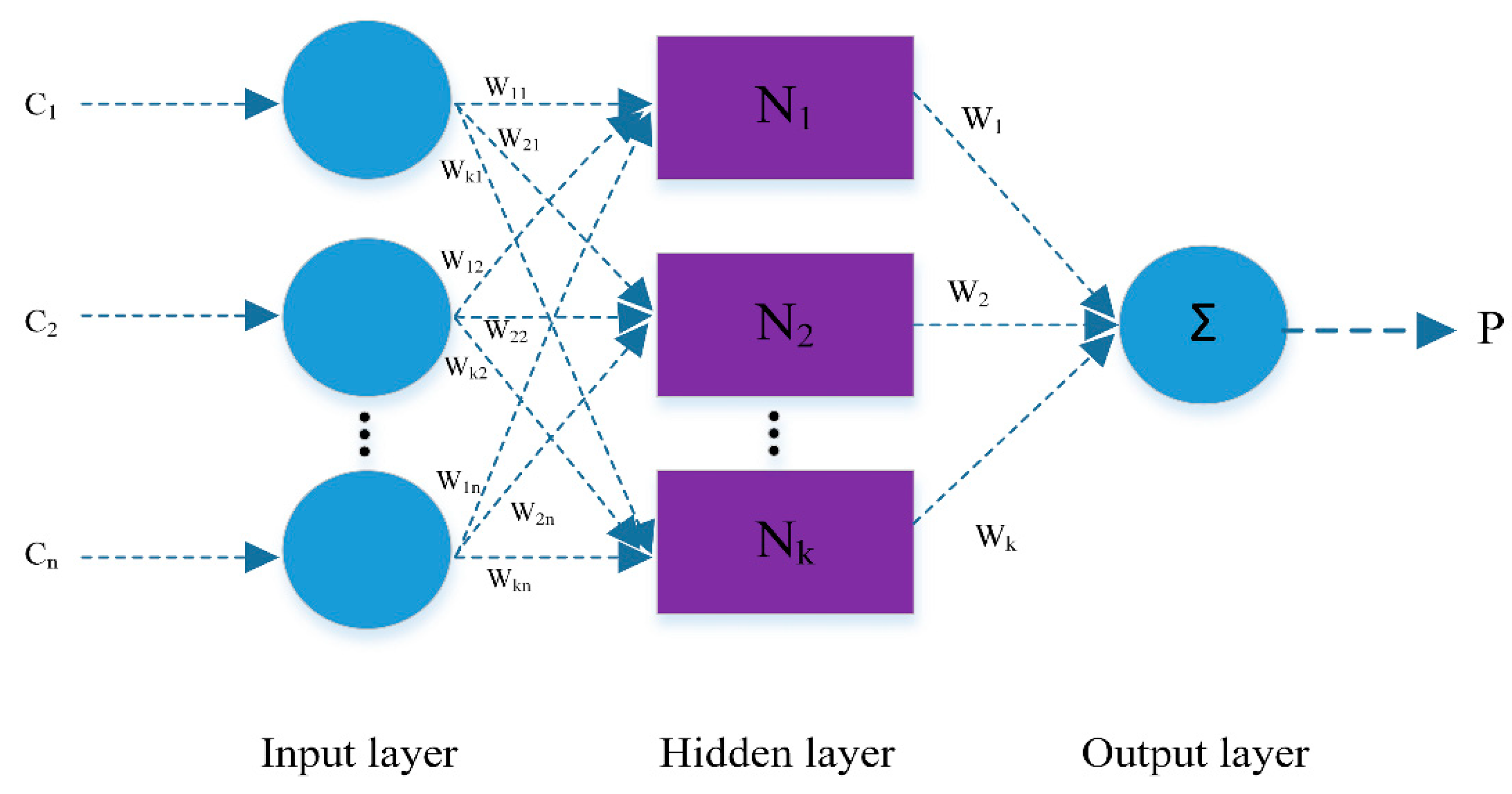
2. Methodology
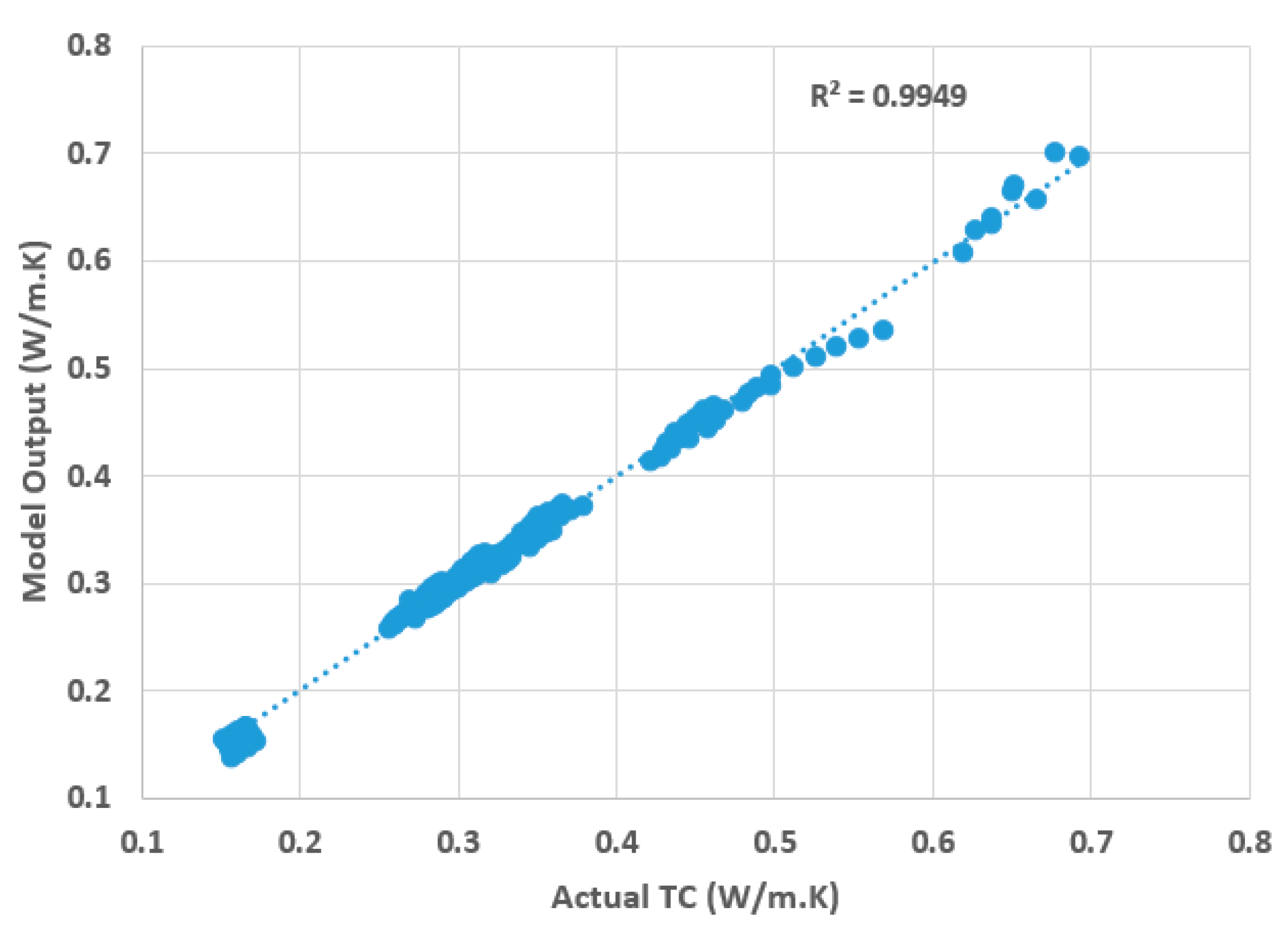
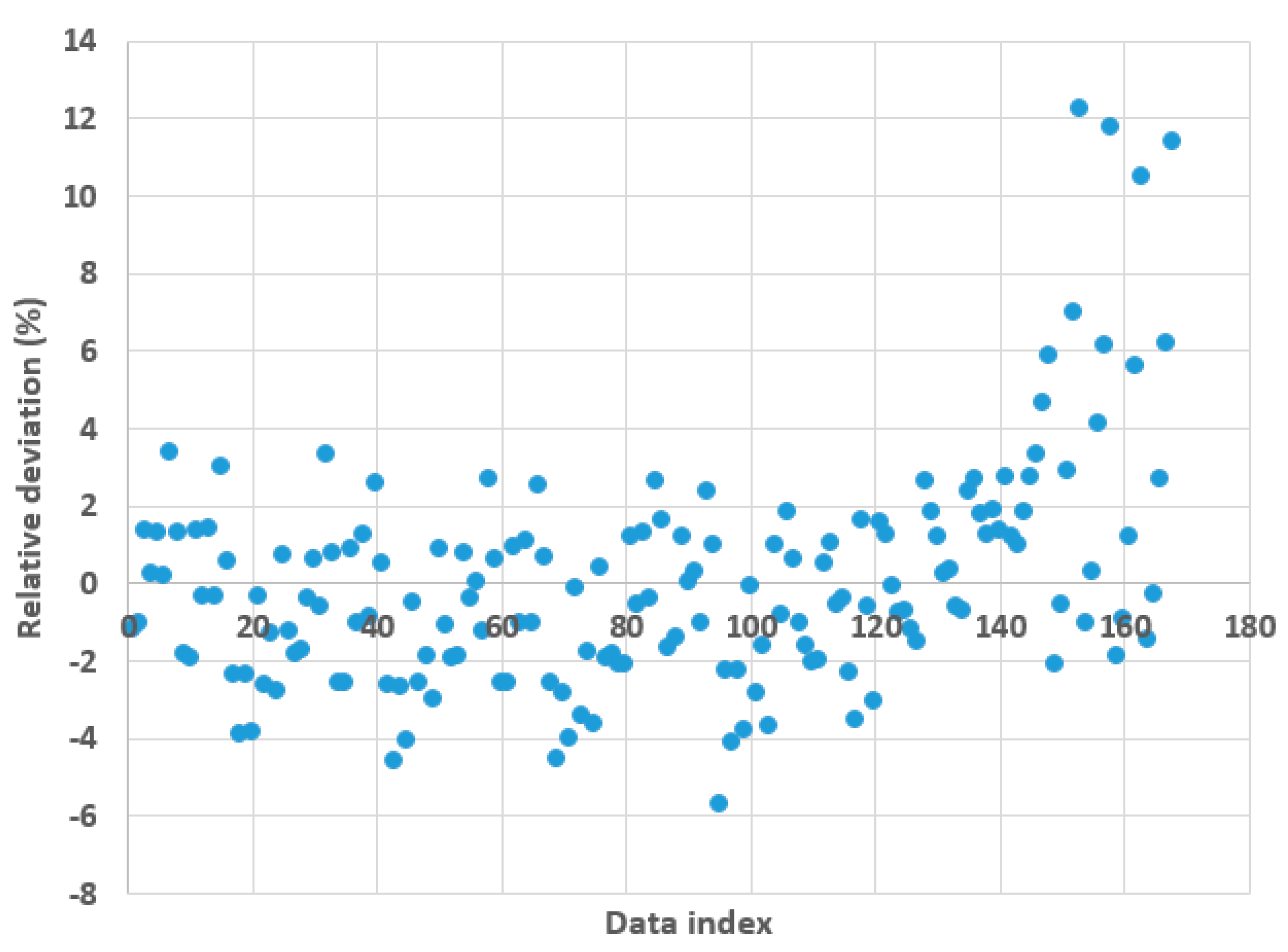
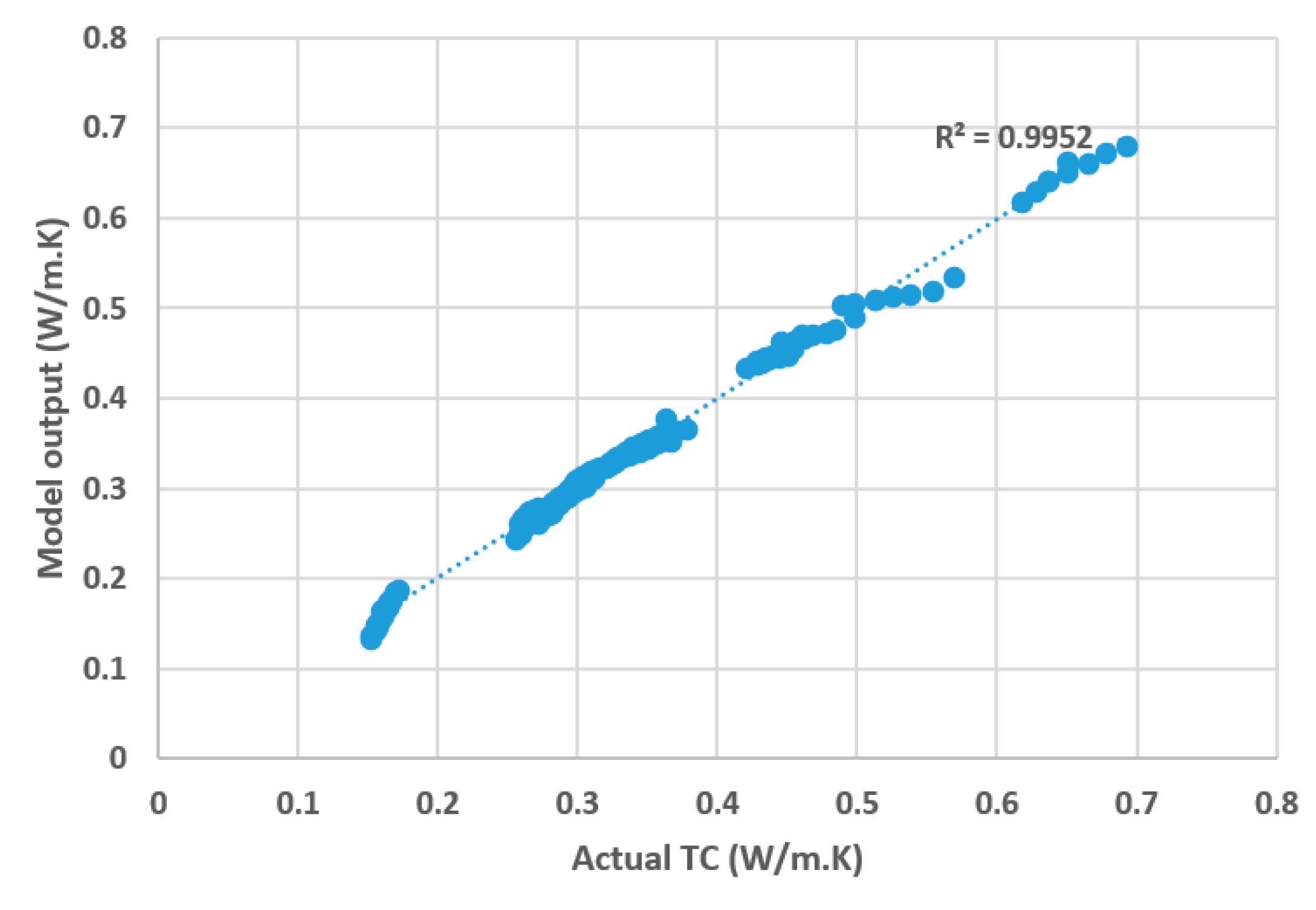
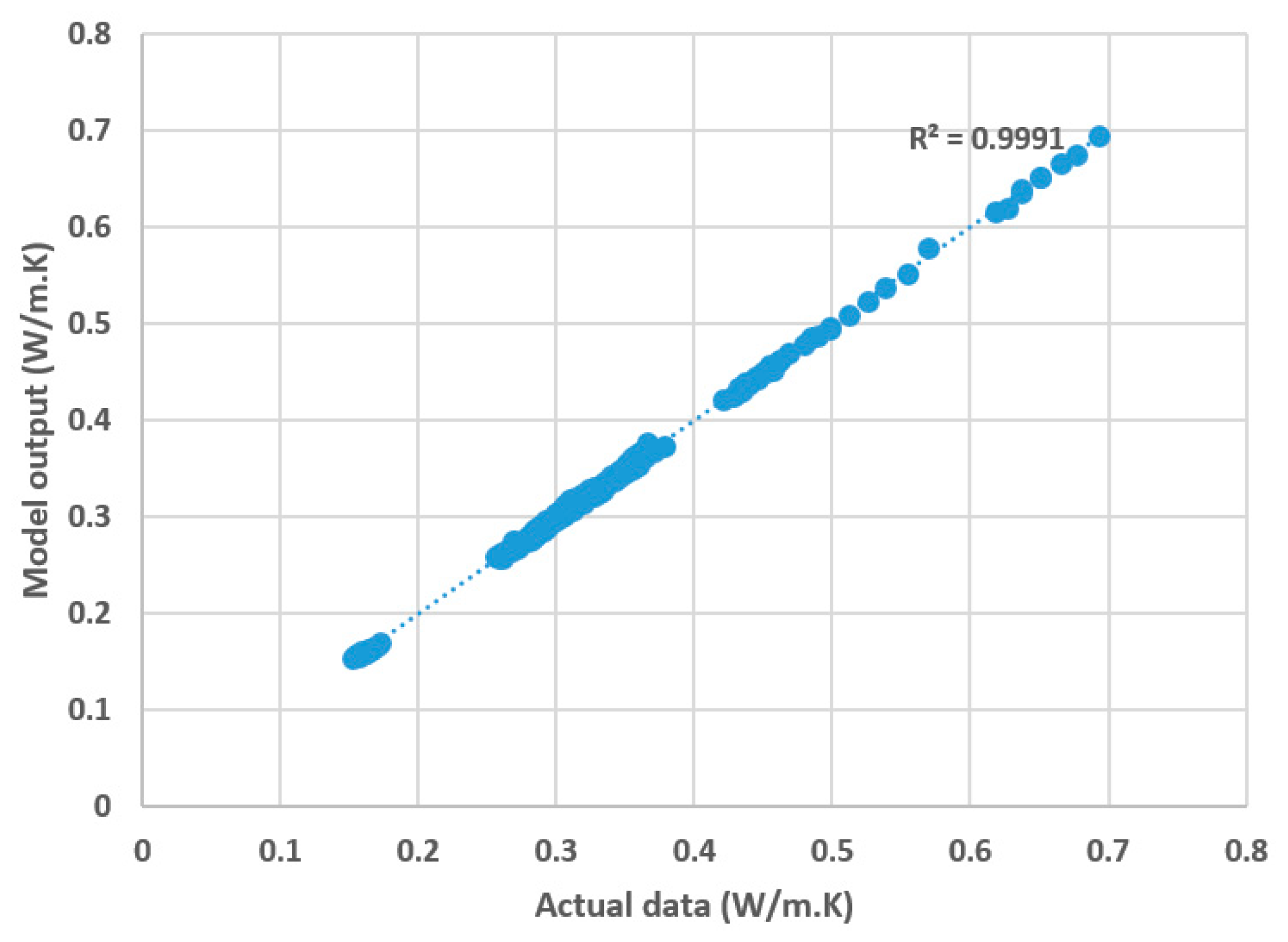
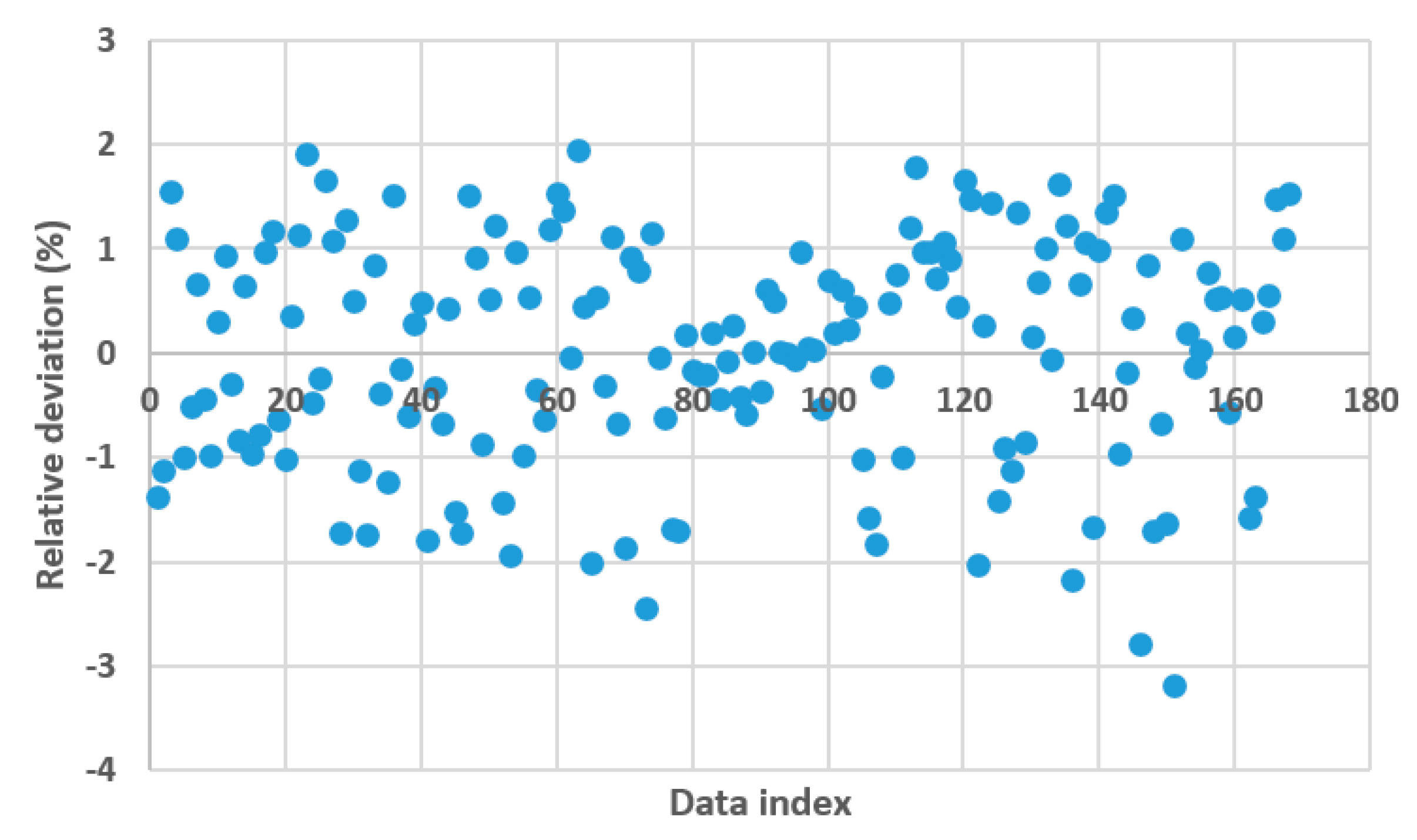
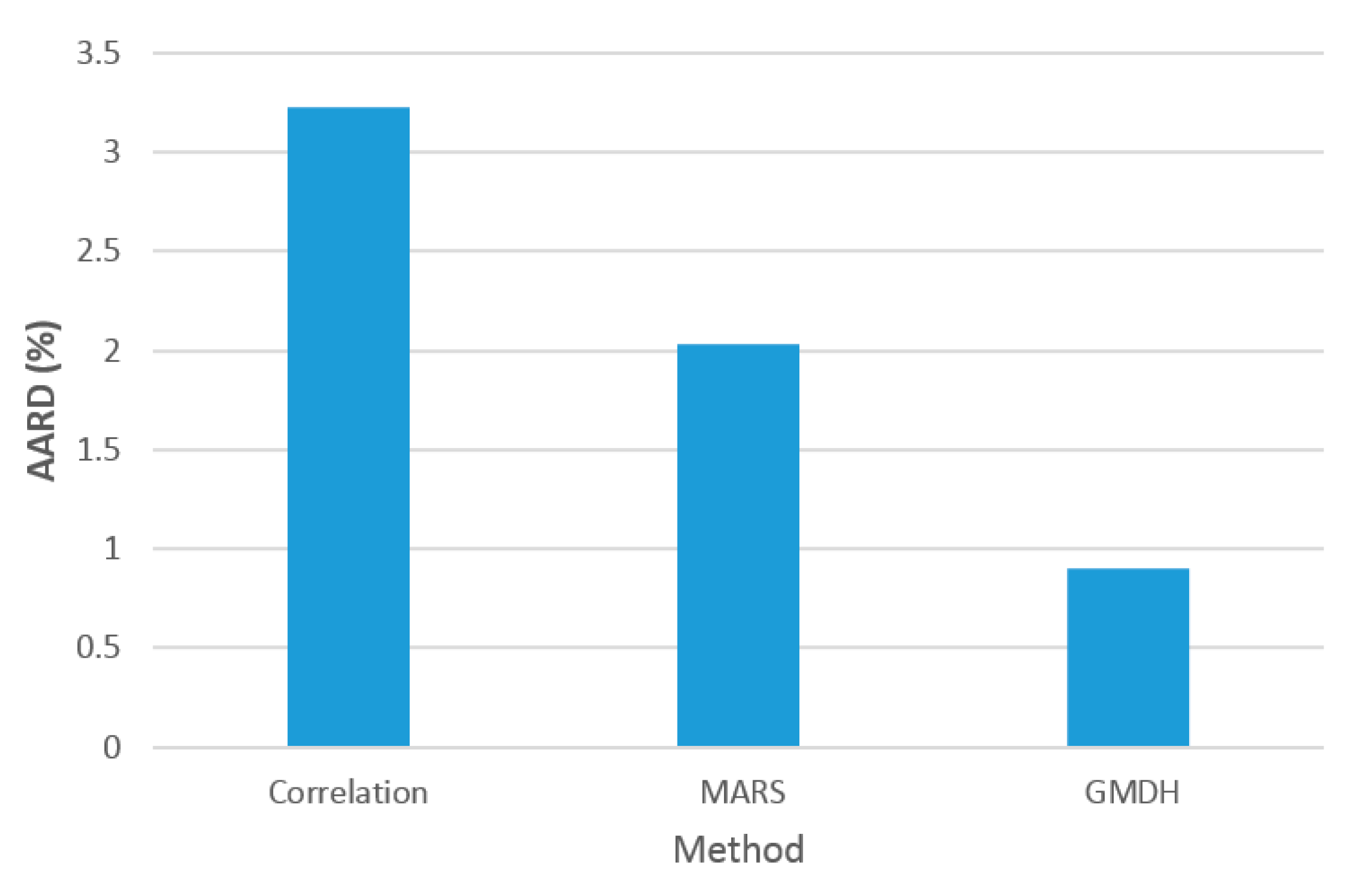
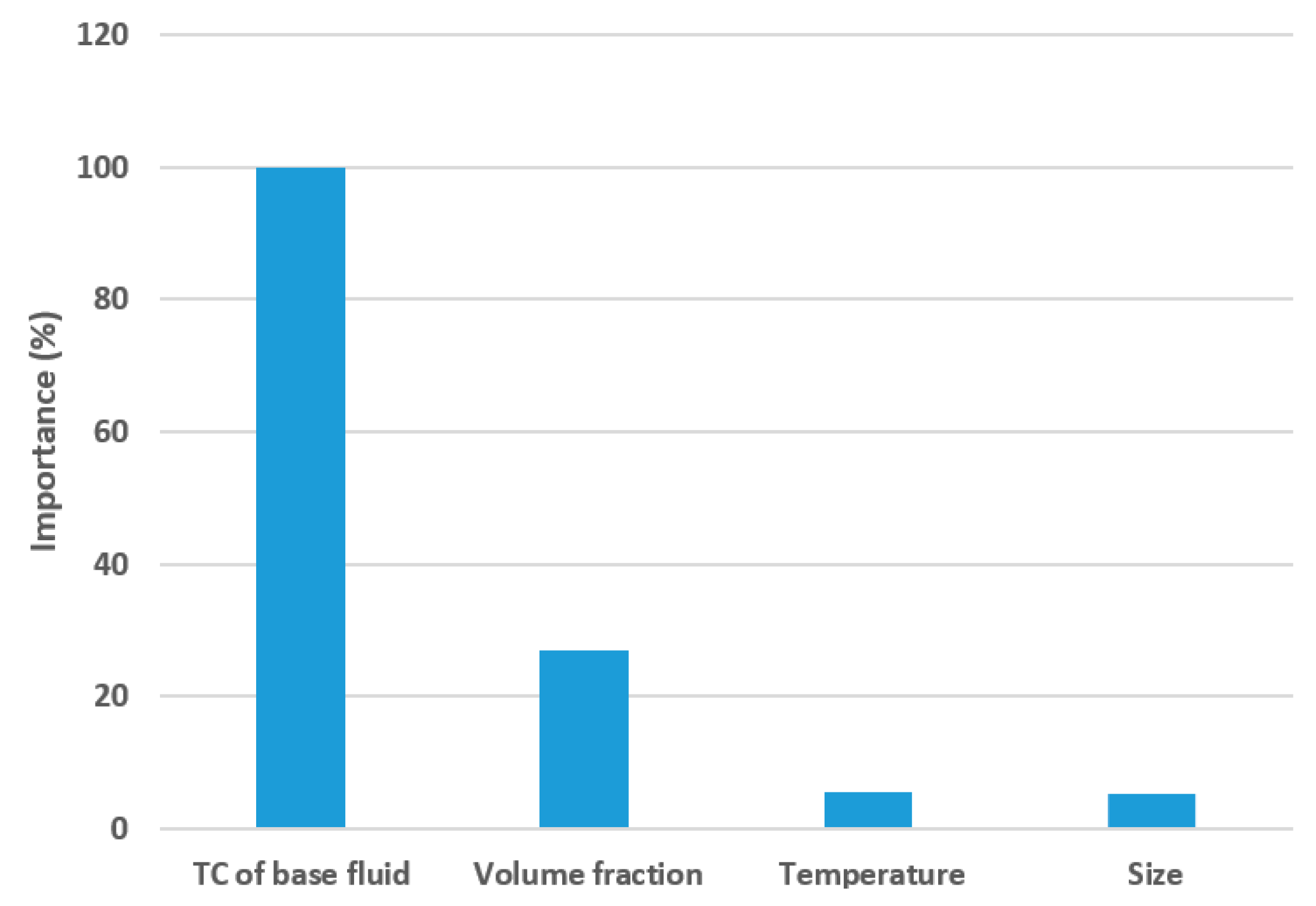
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Gan, Y.Y.; Ong, H.C.; Ling, T.C.; Zulkifli, N.W.M.; Wang, C.T.; Yang, Y.C. Thermal conductivity optimization and entropy generation analysis of titanium dioxide nanofluid in evacuated tube solar collector. Appl. Therm. Eng. 2018, 145, 155–164. [Google Scholar] [CrossRef]
- Jedi, A.; Razali, N.; Wan Mahmood, W.M.F.; Bakar, N.A.A. Statistical Criteria of Nanofluid Flows over a Stretching Sheet with the Effects of Magnetic Field and Viscous Dissipation. Symmetry 2019, 11, 1367. [Google Scholar] [CrossRef]
- Safaei, M.R.; Togun, H.; Vafai, K.; Kazi, S.N.; Badarudin, A. Investigation of Heat Transfer Enhancement in a Forward-Facing Contracting Channel Using FMWCNT Nanofluids. Numer. Heat Transf. Part A Appl. 2014, 66, 1321–1340. [Google Scholar] [CrossRef]
- Rafique, K.; Anwar, M.I.; Misiran, M.; Khan, I.; Seikh, A.H.; Sherif, E.-S.M.; Nisar, K.S. Numerical Analysis with Keller-Box Scheme for Stagnation Point Effect on Flow of Micropolar Nanofluid over an Inclined Surface. Symmetry 2019, 11, 1379. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rejvani, M.; Karimpour, R.; Abbasian Arani, A.A. Estimation of thermal conductivity of ethylene glycol-based nanofluid with hybrid suspensions of SWCNT–Al2O3 nanoparticles by correlation and ANN methods using experimental data. J. Therm. Anal. Calorim. 2017, 128, 1359–1371. [Google Scholar] [CrossRef]
- Arani, A.A.A.; Akbari, O.A.; Safaei, M.R.; Marzban, A.; Alrashed, A.A.A.A.; Ahmadi, G.R.; Nguyen, T.K. Heat transfer improvement of water/single-wall carbon nanotubes (SWCNT) nanofluid in a novel design of a truncated double-layered microchannel heat sink. Int. J. Heat Mass Transf. 2017, 113, 780–795. [Google Scholar] [CrossRef]
- Albojamal, A.; Hamzah, H.; Haghighi, A.; Vafai, K. Analysis of nanofluid transport through a wavy channel. Numer. Heat Transf. Part A Appl. 2017, 72, 869–890. [Google Scholar] [CrossRef]
- Irandoost Shahrestani, M.; Maleki, A.; Safdari Shadloo, M.; Tlili, I. Numerical Investigation of Forced Convective Heat Transfer and Performance Evaluation Criterion of Al2O3/Water Nanofluid Flow inside an Axisymmetric Microchannel. Symmetry 2020, 12, 120. [Google Scholar] [CrossRef]
- Shamaeil, M.; Firouzi, M.; Fakhar, A. The effects of temperature and volume fraction on the thermal conductivity of functionalized DWCNTs/ethylene glycol nanofluid. J. Therm. Anal. Calorim. 2016, 126, 1455–1462. [Google Scholar] [CrossRef]
- Guo, W.; Li, G.; Zheng, Y.; Dong, C. Measurement of the thermal conductivity of SiO2 nanofluids with an optimized transient hot wire method. Thermochim. Acta 2018, 661, 84–97. [Google Scholar] [CrossRef]
- Agarwal, R.; Verma, K.; Agrawal, N.K.; Singh, R. Sensitivity of thermal conductivity for Al2O3 nanofluids. Exp. Therm. Fluid Sci. 2017, 80, 19–26. [Google Scholar] [CrossRef]
- Bagheri, H.; Ahmadi Nadooshan, A. The effects of hybrid nano-powder of zinc oxide and multi walled carbon nanotubes on the thermal conductivity of an antifreeze. Phys. E Low-Dimens. Syst. Nanostructures 2018, 103, 361–366. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Gul, M.; Shehzad, S.A. Hall effects on peristalsis of boron nitride-ethylene glycol nanofluid with temperature dependent thermal conductivity. Phys. E Low-Dimens. Syst. Nanostructures 2018, 99, 275–284. [Google Scholar] [CrossRef]
- Jiang, H.; Zhang, Q.; Shi, L. Effective thermal conductivity of carbon nanotube-based nanofluid. J. Taiwan Inst. Chem. Eng. 2015, 55, 76–81. [Google Scholar] [CrossRef]
- Kumar, M.S.; Vasu, V.; Gopal, A.V. Thermal conductivity and rheological studies for Cu–Zn hybrid nanofluids with various basefluids. J. Taiwan Inst. Chem. Eng. 2016, 66, 321–327. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Mirlohi, A.; Alhuyi Nazari, M.; Ghasempour, R. A review of thermal conductivity of various nanofluids. J. Mol. Liq. 2018, 265, 181–188. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Abbasian Arani, A.A.; Shafiei Badi, R.; Rejvani, M. ANN modeling, cost performance and sensitivity analyzing of thermal conductivity of DWCNT–SiO2/EG hybrid nanofluid for higher heat transfer. J. Therm. Anal. Calorim. 2018, 131, 2381–2393. [Google Scholar] [CrossRef]
- Reddy, K.S.; Kamnapure, N.R.; Srivastava, S. Nanofluid and nanocomposite applications in solar energy conversion systems for performance enhancement: A review. Int. J. Low-Carbon Technol. 2016, 12, ctw007. [Google Scholar] [CrossRef]
- Gandomkar, A.; Saidi, M.H.; Shafii, M.B.; Vandadi, M.; Kalan, K. Visualization and comparative investigations of pulsating Ferro-fluid heat. Appl. Therm. Eng. 2017, 116, 56–65. [Google Scholar] [CrossRef]
- Leong, K.Y.; Saidur, R.; Mahlia, T.M.I.; Yau, Y.H. Performance investigation of nanofluids as working fluid in a thermosyphon air preheater. Int. Commun. Heat Mass Transf. 2012, 39, 523–529. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ramezanizadeh, M.; Nazari, M.A.; Lorenzini, G.; Kumar, R.; Jilte, R. Applications of nanofluids in geothermal: A review. Math. Model. Eng. Probl. 2018, 5, 281–285. [Google Scholar] [CrossRef]
- Akbari, O.A.; Safaei, M.R.; Goodarzi, M.; Akbar, N.S.; Zarringhalam, M.; Shabani, G.A.S.; Dahari, M. A modified two-phase mixture model of nanofluid flow and heat transfer in a 3-D curved microtube. Adv. Powder Technol. 2016, 27, 2175–2185. [Google Scholar] [CrossRef]
- Behnampour, A.; Akbari, O.A.; Safaei, M.R.; Ghavami, M.; Marzban, A.; Sheikh Shabani, G.A.; Zarringhalam, M.; Mashayekhi, R. Analysis of heat transfer and nanofluid fluid flow in microchannels with trapezoidal, rectangular and triangular shaped ribs. Phys. E Low-Dimens. Syst. Nanostructures 2017, 91, 15–31. [Google Scholar] [CrossRef]
- Abdollahzadeh Jamalabadi, M.; Ghasemi, M.; Alamian, R.; Wongwises, S.; Afrand, M.; Shadloo, M. Modeling of Subcooled Flow Boiling with Nanoparticles under the Influence of a Magnetic Field. Symmetry 2019, 11, 1275. [Google Scholar] [CrossRef]
- Elsayed, A.; Al-dadah, R.K.; Mahmoud, S.; Rezk, A. Numerical investigation of turbulent flow heat transfer and pressure drop of AL2O3/water nanofluid in helically coiled tubes. Int. J. Low-Carbon Technol. 2015, 10, 275–282. [Google Scholar] [CrossRef]
- Karana, D.R.; Sahoo, R.R. Effect on TEG performance for waste heat recovery of automobiles using MgO and ZnO nanofluid coolants. Case Stud. Therm. Eng. 2018, 12, 358–364. [Google Scholar] [CrossRef]
- Asadi, A.; Pourfattah, F. Heat transfer performance of two oil-based nanofluids containing ZnO and MgO nanoparticles; a comparative experimental investigation. Powder Technol. 2019, 343, 296–308. [Google Scholar] [CrossRef]
- Verma, S.K.; Tiwari, A.K.; Chauhan, D.S. Performance augmentation in flat plate solar collector using MgO/water nanofluid. Energy Convers. Manag. 2016, 124, 607–617. [Google Scholar] [CrossRef]
- Menlik, T.; Sözen, A.; Gürü, M.; Öztaş, S. Heat transfer enhancement using MgO/water nanofluid in heat pipe. J. Energy Inst. 2015, 88, 247–257. [Google Scholar] [CrossRef]
- Toghraie, D.; Sina, N.; Jolfaei, N.A.; Hajian, M.; Afrand, M. Designing an Artificial Neural Network (ANN) to predict the viscosity of Silver/Ethylene glycol nanofluid at different temperatures and volume fraction of nanoparticles. Phys. A Stat. Mech. Its Appl. 2019, 534, 122142. [Google Scholar] [CrossRef]
- Hemmat Esfe, M. Mathematical and artificial brain structure-based modeling of heat conductivity of water based nanofluid enriched by double wall carbon nanotubes. Phys. A Stat. Mech. Its Appl. 2019, 540, 120766. [Google Scholar] [CrossRef]
- Saeedi, A.H.; Akbari, M.; Toghraie, D. An experimental study on rheological behavior of a nanofluid containing oxide nanoparticle and proposing a new correlation. Phys. E Low-Dimens. Syst. Nanostructures 2018, 99, 285–293. [Google Scholar] [CrossRef]
- Ahmadi, M.-A.; Ahmadi, M.H.; Fahim Alavi, M.; Nazemzadegan, M.R.; Ghasempour, R.; Shamshirband, S. Determination of thermal conductivity ratio of CuO/ethylene glycol nanofluid by connectionist approach. J. Taiwan Inst. Chem. Eng. 2018, 91, 383–395. [Google Scholar] [CrossRef]
- Safaei, M.R.; Hajizadeh, A.; Afrand, M.; Qi, C.; Yarmand, H.; Zulkifli, N.W.B.M. Evaluating the effect of temperature and concentration on the thermal conductivity of ZnO-TiO2/EG hybrid nanofluid using artificial neural network and curve fitting on experimental data. Phys. A Stat. Mech. Its Appl. 2019, 519, 209–216. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; D’Orazio, A.; Karimipour, A.; Goodarzi, M.; Bach, Q.-V. A novel sensitivity analysis model of EANN for F-MWCNTs–Fe3O4/EG nanofluid thermal conductivity: Outputs predicted analytically instead of numerically to more accuracy and less costs. Phys. A Stat. Mech. Its Appl. 2019, 521, 406–415. [Google Scholar] [CrossRef]
- Alnaqi, A.A.; Sayyad Tavoos Hal, S.; Aghaei, A.; Soltanimehr, M.; Afrand, M.; Nguyen, T.K. Predicting the effect of functionalized multi-walled carbon nanotubes on thermal performance factor of water under various Reynolds number using artificial neural network. Phys. A Stat. Mech. Its Appl. 2019, 521, 493–500. [Google Scholar] [CrossRef]
- Komeilibirjandi, A.; Hossein, A.; Akbar, R. Thermal conductivity prediction of nanofluids containing CuO nanoparticles by using correlation and artificial neural network. J. Therm. Anal. Calorim. 2019. [Google Scholar] [CrossRef]
- Wu, H.; Al-Rashed, A.A.A.A.; Shahsavar, A.; Karimi, A.; Sardari, P.T. Curve-fitting on experimental thermal conductivity of motor oil under influence of hybrid nano additives containing multi-walled carbon nanotubes and zinc oxide. Phys. A Stat. Mech. Its Appl. 2019, 535, 122128. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Alhuyi Nazari, M.; Ahmadi, M.H.; Lorenzini, G.; Pop, I. A review on the applications of intelligence methods in predicting thermal conductivity of nanofluids. J. Therm. Anal. Calorim. 2019, 1–17. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Alhuyi Nazari, M.; Ghasempour, R.; Madah, H.; Shafii, M.B.; Ahmadi, M.A. Thermal conductivity ratio prediction of Al2O3/water nanofluid by applying connectionist methods. Colloids Surf. A Physicochem. Eng. Asp. 2018, 541, 154–164. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Ahmadi, M.A.; Nazari, M.A.; Mahian, O.; Ghasempour, R. A proposed model to predict thermal conductivity ratio of Al2O3/EG nanofluid by applying least squares support vector machine (LSSVM) and genetic algorithm as a connectionist approach. J. Therm. Anal. Calorim. 2019, 135, 271–281. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Baghban, A.; Sadeghzadeh, M.; Hadipoor, M.; Ghazvini, M. Evolving connectionist approaches to compute thermal conductivity of TiO2/water nanofluid. Phys. A Stat. Mech. Its Appl. 2019, 540, 122489. [Google Scholar] [CrossRef]
- Oduro, S.D.; Metia, S.; Duc, H.; Ha, Q.P. Predicting Carbon Monoxide Emissions with Multivariate Adaptive Regression Splines (MARS) and Artificial Neural Networks (ANNs). In Proceedings of the 32nd International Symposium on Automation and Robotics in Construction and Mining (ISARC 2015), Oulu, Finland, 15–18 June 2015. [Google Scholar]
- Put, R.; Xu, Q.S.; Massart, D.L.; Vander Heyden, Y. Multivariate adaptive regression splines (MARS) in chromatographic quantitative structure-retention relationship studies. J. Chromatogr. A 2004, 1055, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Xu, Q.-S.; Daszykowski, M.; Walczak, B.; Daeyaert, F.; de Jonge, M.R.; Heeres, J.; Koymans, L.M.H.; Lewi, P.J.; Vinkers, H.M.; Janssen, P.A.; et al. Multivariate adaptive regression splines—Studies of HIV reverse transcriptase inhibitors. Chemom. Intell. Lab. Syst. 2004, 72, 27–34. [Google Scholar] [CrossRef]
- Rounaghi, M.M.; Abbaszadeh, M.R.; Arashi, M. Stock price forecasting for companies listed on Tehran stock exchange using multivariate adaptive regression splines model and semi-parametric splines technique. Phys. A Stat. Mech. Its Appl. 2015, 438, 625–633. [Google Scholar] [CrossRef]
- Chao, K.-W.; Hu, N.-Z.; Chao, Y.-C.; Su, C.-K.; Chiu, W.-H. Implementation of Artificial Intelligence for Classification of Frogs in Bioacoustics. Symmetry 2019, 11, 1454. [Google Scholar] [CrossRef]
- Islam, K.T.; Raj, R.G.; Mujtaba, G. Recognition of Traffic Sign Based on Bag-of-Words and Artificial Neural Network. Symmetry 2017, 9, 138. [Google Scholar] [CrossRef]
- Yazdani-Chamzini, A.; Zavadskas, E.; Antucheviciene, J.; Bausys, R. A Model for Shovel Capital Cost Estimation, Using a Hybrid Model of Multivariate Regression and Neural Networks. Symmetry 2017, 9, 298. [Google Scholar] [CrossRef]
- Gholipour Khajeh, M.; Maleki, A.; Rosen, M.A.; Ahmadi, M.H. Electricity price forecasting using neural networks with an improved iterative training algorithm. Int. J. Ambient Energy 2018, 39, 147–158. [Google Scholar] [CrossRef]
- Zhang, W.; Maleki, A.; Rosen, M.A. A heuristic-based approach for optimizing a small independent solar and wind hybrid power scheme incorporating load forecasting. J. Clean. Prod. 2019, 241, 117920. [Google Scholar] [CrossRef]
- Ramezanizadeh, M.; Ahmadi, M.H.; Nazari, M.A.; Sadeghzadeh, M.; Chen, L. A review on the utilized machine learning approaches for modeling the dynamic viscosity of nanofluids. Renew. Sustain. Energy Rev. 2019, 114, 109345. [Google Scholar] [CrossRef]
- Mohamadian, F.; Eftekhar, L.; Haghighi Bardineh, Y. Applying GMDH artificial neural network to predict dynamic viscosity of an antimicrobial nanofluid. Mashhad Univ. Med. Sci. 2018, 5, 217–221. [Google Scholar]
- Pourkiaei, S.M.; Ahmadi, M.H.; Hasheminejad, S.M. Modeling and experimental verification of a 25W fabricated PEM fuel cell by parametric and GMDH-type neural network. Mech. Ind. 2016, 17, 105. [Google Scholar] [CrossRef]
- Jiang, Y.; Sulgani, M.T.; Ranjbarzadeh, R.; Karimipour, A.; Nguyen, T.K. Hybrid GMDH-type neural network to predict fluid surface tension, shear stress, dynamic viscosity & sensitivity analysis based on empirical data of iron(II) oxide nanoparticles in light crude oil mixture. Phys. A Stat. Mech. Its Appl. 2019, 526, 120948. [Google Scholar]
- Hemmat Esfe, M.; Afrand, M.; Karimipour, A.; Yan, W.-M.; Sina, N. An experimental study on thermal conductivity of MgO nanoparticles suspended in a binary mixture of water and ethylene glycol. Int. Commun. Heat Mass Transf. 2015, 67, 173–175. [Google Scholar] [CrossRef]
- Kim, S.H.; Choi, S.R.; Kim, D. Thermal Conductivity of Metal-Oxide Nanofluids: Particle Size Dependence and Effect of Laser Irradiation. J. Heat Transf. 2007, 129, 298. [Google Scholar] [CrossRef]
- Żyła, G. Viscosity and thermal conductivity of MgO–EG nanofluids. J. Therm. Anal. Calorim. 2017, 129, 171–180. [Google Scholar] [CrossRef]
- Xie, H.; Yu, W.; Chen, W. MgO nanofluids: Higher thermal conductivity and lower viscosity among ethylene glycol-based nanofluids containing oxide nanoparticles. J. Exp. Nanosci. 2010, 5, 463–472. [Google Scholar] [CrossRef]
- Hemmat Esfe, M.; Saedodin, S.; Bahiraei, M.; Toghraie, D.; Mahian, O.; Wongwises, S. Thermal conductivity modeling of MgO/EG nanofluids using experimental data and artificial neural network. J. Therm. Anal. Calorim. 2014, 118, 287–294. [Google Scholar] [CrossRef]

| a | b | c | d | e | f | g | h |
| 0.960011 | 0.002045 | 0.006512 | −0.00081 | −0.20459 | −0.000024 | 0.000235 | −0.00001 |
| i | j | k | l | m | n | o | |
| −0.00076 | 0.051041 | 0.007562 | −0.00014 | 0 | 0.00006 | −0.01792 |
| Basis Functions | |||||
| Relationship | |||||
| Basis Functions | |||||
| Relationship |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, N.; Maleki, A.; Alhuyi Nazari, M.; Tlili, I.; Safdari Shadloo, M. Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches. Symmetry 2020, 12, 206. https://doi.org/10.3390/sym12020206
Wang N, Maleki A, Alhuyi Nazari M, Tlili I, Safdari Shadloo M. Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches. Symmetry. 2020; 12(2):206. https://doi.org/10.3390/sym12020206
Chicago/Turabian StyleWang, Na, Akbar Maleki, Mohammad Alhuyi Nazari, Iskander Tlili, and Mostafa Safdari Shadloo. 2020. "Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches" Symmetry 12, no. 2: 206. https://doi.org/10.3390/sym12020206
APA StyleWang, N., Maleki, A., Alhuyi Nazari, M., Tlili, I., & Safdari Shadloo, M. (2020). Thermal Conductivity Modeling of Nanofluids Contain MgO Particles by Employing Different Approaches. Symmetry, 12(2), 206. https://doi.org/10.3390/sym12020206







