Abstract
This paper proposes a non-singular fast terminal sliding mode control strategy based on the self-organizing radial basis function neural network (RBFNN) approximation for the train key network system to realize the safe and reliable operation of the train. In order to improve the RBFNN approximation performance and speed, an improved multi-strategy particle swarm optimization (IMPSO) algorithm, which utilizes multi-strategy evolution ways with a nonlinear deceasing inertia weight to improve the global optimizing performance of particle swarm, is proposed to optimize the structure and parameters for better mapping the highly nonlinear characteristics of train traction braking. In addition, the IMPSO is also introduced into a non-singular fast terminal sliding mode (NFTSM) controller to obtain the most appropriate tuning parameters of the controller and suppresses the chattering phenomenon from sliding mode controller. The stability characteristic of the system under the proposed NFTSM controller is studied based on the Lyapunov theory. Further combined with effective delay prediction and delay compensation methods, the NFTSM high-precision control of the train key nonlinear network system is implemented. The simulation results show that the proposed method has more efficient and robust tracking performance and real-time performance compared with other control methods, which can provide effective means for realizing the symmetrical bus control by automatic train operation (ATO) at both ends of the train, with the safe operation of the train under every complex motion condition.
1. Introduction
Modern high-speed trains are using the train communication network (TCN) to realize train control and diagnosis. However, due to the existence of a large number of subsystems, the conversion of communication protocol and the changeable operating environment of the train network, the time delay is inevitably generated in the process of information transmission. If the time delay is too large, not only the stability of the control system will be affected, but also the safety of the passengers will be threatened. Therefore, it is critical to control the network delay in the train network systems [1].
TCN works in a particularly complex environment, and the traction and braking key systems of high-speed trains have obvious nonlinear characteristics, which bring difficulties to the research of train network control system [2]. In recent years, some scholars have studied the scheduling algorithm of the train network and the delay problem of composite Ethernet [3,4]. However, there are still few reports on the delay and control aspects of TCN networks.
At present, there are many nonlinear system control schemes and approaches proposed for reference. For the neural network control [5,6,7], He et al. [5] adopted the adaptive neural network to handle a robotic system with full-state constraints uncertainties and disturbances and employed the Moore–Penrose inverse term to prevent the violation of the full-state constraints, which guaranteed the control performance of the system. Wang et al. [6] considered the finite-time quantized feedback control for the first time compared with the existing researches, and a novel adaptive neural output-feedback control strategy was designed by proposing a new finite-time stability criterion and designing a state observer, which effectively solved the finite-time quantized feedback control problem for nonlinear functions. Hu et al. [7] proposed a neural network model composed of three networks for reinforcement learning to control a robotic manipulator with unknown parameters and dead zones, and the state of the robotic manipulator was predicted by the state network of the model, the action policy was learned by the action network, and the performance index of the action policy was estimated by a critic network. Further, the effectiveness and the stability of the model was demonstrated by applying on a simulated two-link robotic manipulator. In addition, dynamic optimization design of a neural network is an effective way to ensure that a neural network always works under the optimization of structure and combination parameters [8]. Therefore, the self-organizing learning method that simultaneously optimizes network structure and parameters has received widespread attention [9,10,11,12]. The optimization methods mainly include the genetic algorithm [9], the differential evolutionary algorithm [10], and the particle swarm optimization (PSO) algorithm [11,12]. Among them, the PSO algorithm is widely used in neural network learning due to its advantages of fast convergence speed and high optimization efficiency. Han et al. [11] designed a nonlinear regression function to adjust the inertia weight of PSO to enhance the searching ability of particles, and designed a unified criterion to obtain the parameters and network size of RBF neural network. Dong et al. [12] designed time-varying learning factors to balance the exploration and utilization ability of particles in the search space. Meanwhile, the local best information was added to the evolutionary process of particles for better population diversity. Further, the improved PSO algorithm was applied to train the RBF neural network for determining optimal network parameters, which effectively improved network generalization capability.
Among these control approaches, due to the intrinsic insensitivity of the sliding mode (SM) control to parameter variations and external disturbances, the SM control has been widely used in the designs of some train control systems [13,14,15]. Li et al. [13] designed a SM adaptive robust controller for automatic train operation (ATO) of high-speed trains with using the robust control to reduce all uncertainties of parameter variation caused by model errors, and achieved high precision tracking ability under different wind speeds. Li et al. [14] designed the distributed neural network SM control strategy to control the speed tracking of high-speed trains according to the dispersion characteristics of train model power or braking force input, and used the historical operation data of the train to compensate the current control law output to improve the control accuracy and practical stability. However, the conventional SM control suffers an obvious drawback, which is asymptotic error convergence of the closed loop system, due to the use of linear sliding surfaces [15]. Therefore, Venkataraman et al. [16] proposed a terminal sliding mode (TSM) control method with limited time, which had been widely concerned. However, TSM control in general has two limitations, one is the singular problem in the control process, and another is that the convergence rate of the system state is slow when the system state is far from the equilibrium point. In order to solve the singularity problem in the control process, Feng et al. [17] proposed a non-singular terminal sliding mode (NTSM) control method and verified the effectiveness of the method. On the other hand, to solve the problem of convergence rate, Yu et al. [18] proposed a fast terminal sliding mode (FTSM) control method, which could achieve faster convergence even when the system state was far away from the equilibrium point. Combining the advantages of the two control methods, the concept of the non-singular fast terminal sliding mode (NFTSM) control is proposed [19]. Followed along [19], Gao et al. [20] proposed a fast-integral terminal sliding mode control method for a cascaded nonlinear dynamical system with mismatched uncertainties, which not only avoided the singularity in the traditional terminal sliding mode, but also addressed the mismatched problems in the nonlinear control system. Yang et al. [21] proposed a time-specified nonsingular terminal sliding manifold consisting of pre-specified nonlinear functions for solving the problem of trajectory tracking for robotic airships, which can avoid the singularity problem and specify the convergence time of terminal sliding mode control. Yao et al. [22] proposed a novel nonlinear nonsingular terminal sliding manifold by considering that the unknown parameters needed to be estimated via the non-negative adaptive law. Meanwhile, the corresponding novel robust adaptive NTSM control strategy was designed to enable that the position tracking error and the velocity tracking error of the ATO system converge to zero finite time and eliminate the singularity caused by terminal sliding mode controller.
However, the nonlinear controlled objects of the above literatures are in some ways different from the train network control system, such as [14,15,22] were not concerned intensively with the train complex operating environment and the train communication network, which are the critical factors for the operation of the train. Thus, a suitable NFTSM control methodology guaranteeing robustness and other performances to the above factors must be developed to incorporate in the high-speed train network control system.
In this paper, a NFTSM control method based on the improved multi-strategy particle swarm optimization (IMPSO) algorithm and the RBF neural network (RBFNN) is proposed for the key nonlinear network control system. In order to improve the control accuracy, the multi-strategy evolution ways with a nonlinear deceasing inertia weight are adopted to improve global optimization characteristics of particle swarm, for quickly obtaining the most appropriate the tuning parameters of NFTSM controller with the elimination of sliding mode control chattering phenomenon. In addition, the IMPSO algorithm is also introduced into RBFNN to optimize the structure and parameters for better mapping the highly nonlinear characteristics of train traction braking, which ensures the safe and reliable operation of the train network control system, combined with effective delay prediction and delay compensation methods.
The rest of the paper is structured as follows: In Section 2, we design the NFTSM control strategy for a high-speed train network control system with train information transmission analysis. In Section 3, we build the multi point-mass with single-coordinate dynamic model, which describes the motion process of high-speed trains. In Section 4, we use the IMPSO algorithm with a nonlinear deceasing inertia weight to optimize the structure and parameters of RBFNN, so that the network better maps the highly nonlinear characteristics in the process of train traction braking. In Section 5, we design the NFTSM control law with proofing stability control system, and describe the flowchart of the proposed control strategy. In Section 6, we analyze the real-time performance of IMPSO-RBFNN and discuss the performance of the proposed control method compared with other control methods. Finally, conclusions and prospects are presented in Section 7.
In order to make the proposed method easier to describe and understand, we summarize the notation needed in our formulation in Appendix A.
2. The Design of the NFTSM Control Strategy for the High-Speed Train Network Control System
The operation environment of high-speed trains is complex and changeable, and there are many factors that affect the operation performance. Accurate control of the operation of trains is required to ensure smooth tracking under the desired speed of the train. The NFTSM control method has the advantages of high control accuracy, fast convergence speed, and strong robustness on the basis of ensuring the non-singular control. In order to ensure the safe and reliable operation of high-speed trains, we design a NFTSM network control system for high-speed trains, combining the optimization capability of the IMPSO algorithm and the approximation capability of RBFNN, as shown in Figure 1.
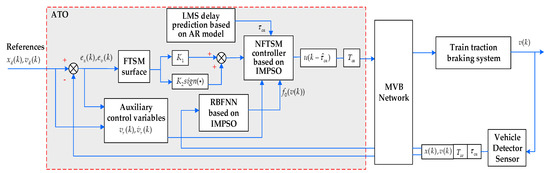
Figure 1.
Improved network control system of high-speed train based on Improved multi-strategy particle swarm optimization RBF neural network (IMPSO-RBFNN).
Figure 1 shows that all train information is transmitted through a multifunction vehicle bus (MVB). ATO is the core component of information transmission and processing calculation. ATO should not only calculate the effective control amount in time under the guidance of the designed control algorithm, but also reasonably arrange the control amount transmission sequence according to the accurate delay prediction method. Thus, the ATO sends the calculated control input and forward channel timestamp as a process data packet to the train traction braking system, which executes the latest control law and records the actual forward channel delay . The sensor periodically obtains the output according to the set sampling time and sends , timestamp , and as a process data packet back to ATO. Then, ATO will analyze the actual output of the current time through the timestamp, which combines with the current reference input signal () to calculate the control input of the next time, so as to realize the accurate tracking under the desired speed on the basis that the auto regressive (AR) model of the least mean square (LMS) algorithm accurately predicts the forward delay. Due to inconsistencies in the clocks of each subservice, clock correction is required at the same time the timestamp is received. If is the forward channel delay measured at different times, and is the sampling period, then it is defined as:
3. High-Speed Train Motion Model
The high-speed train motion model is a complex nonlinear system composed of multiple operating conditions. Therefore, it is extremely vital that the accurate motion model is built for the safe and reliable operation of the train. In order to fully reflect the changing laws of trains under different motion conditions, the multi point-mass with single-coordinate dynamic model [23] is adopted to describe the motion process of high-speed trains as:
where is the speed of the reference vehicle, is the acceleration coefficient, is the net force for the whole train, is the control force for the whole train, is the mutual influence of other vehicles on the reference vehicle, and is the resistance for the whole train composed of general resistance and additional resistance (ramp resistance , curve resistance , and tunnel resistance [24], which can be described as:
where , , and are the resistive coefficients for the vehicle, is the gradient angle of the rail for the vehicle, is the parameter obtained through test, is the radius of the curve for the vehicle passes, is the length of the tunnel for the vehicle, is the elastic-shaped variable in which tension or compression occurs in the elastic coupler of the vehicle, is the mass of the vehicle, and is the train rotary mass coefficient. By combining (2) and (3), the motion model of high-speed train can be given:
where is the nonlinear function of speed, which increases with the increase of train speed. Therefore, the train traction braking system has obvious multiple operating conditions and nonlinear characteristics at high speed. To guarantee the accuracy of the train running speed control, we will introduce the IMPSO algorithm and RBFNN into the NFTSM controller and utilize the global optimization characteristics of particle swarm to improve the approximation ability of RBFNN to the nonlinear disturbance in the process of train traction braking, and significantly reduce chattering caused by sliding mode control and the train running speed tracking error, which realizes the safe driving and parking precision.
4. IMPSO-RBF Neural Network
RBFNN is widely used in the control field because of its advantages such as fast learning speed, strong approximation ability, and difficulty in falling into local extremum [25]. However, the structure and parameter design of RBFNN directly affect its generalization ability with the increasing complexity of solving problems. In order to improve the learning efficiency of RBFNN, we use the IMPSO algorithm to optimize the structure and parameters of RBFNN so that the network has self-organizing learning ability and better maps the highly nonlinear characteristics in the process of train traction braking.
4.1. RBF Neural Network
Generally, an RBFNN consists of three layers: The input layer, the hidden layer, and the output layer [25]. For the input , the network output is as follows:
where is the output weight between the hidden neuron and the output neuron, is the output of the hidden neuron, and and are the center vector and width of the hidden neuron respectively, which can be described as:
where is the error function, is the learning rate, and is the momentum factor.
4.2. Particle Swarm Optimization Algorithm
PSO, as an optimization algorithm that utilizes the information exchange between the particles and the swarm to search cooperatively to obtain the global optimal solution, has the advantages of fast convergence speed and high optimization efficiency, and has been widely applied to optimization problems [26].
Generally, a swarm consists of a number of particles. Then, each particle carries dimensional information and has the memory ability to record the best previous position of each particle . Thus, the position and velocity of the particle in the iteration can be described as:
where with being the swarm size, is the position of the particle in the iteration, is the corresponding velocity, is the best position of the particle in the iteration, is the best position obtained by the swarm in the iteration, is the inertia weight, and are the acceleration constants, and is the random value uniformly distributed in (0,1). The dimensional information carried by each particle consists of the parameters to be optimized in the RBFNN and the NFTSM controller. To optimize the structure of RBFNN, the position update formula in (6) is represented in a discrete form as:
where with being the dimensionality of the searching space, is the position of the particle in the iteration and its value represents the number of neurons in the corresponding RBF neural network, and is the corresponding velocity; the sigmoid function can be described as:
4.3. Improved Multi-Strategy Particle Swarm Optimization Algorithm
The PSO algorithm easily falls into local optimum for solving complex multimodal optimization problems [27]. Considering the complexity of the controlled object in this paper, the adaptive multi-strategy evolutionary behavior with a nonlinear deceasing inertia weight is adopted to adjust the particle optimization velocity. In the optimization process, the evolutionary behavior of the particles is determined by calculating the immediate value, the future value, and the comprehensive value of different strategies, and the strategy behavioral mutation algorithm was proposed to avoid the algorithm falling into the local optimal solution.
4.3.1. Improved Multi-Strategy Evolutionary Behavior
The evolutionary behavior of learning based on individual optimal and globally optimal individual is as follows [27]:
where is the maximum inertia weight, is minimum inertia weight, is the current iteration times, and is the total number of iterations. It is noted that if the inertia weight is large enough, the algorithm has good global searching ability.
However, when is relatively small, the algorithm has good local searching performance [28]. Thus, the performance of PSO could be improved by setting the value of appropriately for a tradeoff between its local and global searching abilities. According to the problem in approach [27] that the linear deceasing in (10) easily leads to the algorithm falling into the local extremum at the beginning of the iteration process, we propose the strategy of the nonlinear deceasing for avoiding the algorithm falling into the local optimal solution to some extent, which can be described as:
where the decline rate of is relatively quick in the searching process, which is conducive to the particle swarm to explore the optimal solution at a relatively small velocity at the end of search and effectively avoids the algorithm falling into the local extremum.
The evolutionary behavior of learning based on group average knowledge is as follows [27]:
The evolutionary behavior of learning based on global optimal individual and other individuals’ knowledge is as follows [27]:
where and are different integers in , .
The evolutionary behavior of learning based on other individuals’ knowledge is as follows [27]:
where , , and are different integers in ,.
4.3.2. Multi-Strategy Value Comparison
In the process of individual evolution, the evolutionary strategy will directly affect the convergence of optimal algorithm, and the evolutionary strategy of the individual is determined by the selection probability of each strategy with calculating the immediate value, the future value, and the comprehensive value of each strategy in this paper, which can be described as [27]:
where , , and are the immediate value, the future value, and the comprehensive value of each evolutionary strategy, respectively; is the fitness in the iteration; is the fitness in the previous iteration; and are the number of success and total number of executions of the strategy used by individual before the iteration, respectively; and are the number of success and total number of execution of the strategy used by all the individual before the iteration, respectively; and are the constant; is the probability of each strategy adopted in the iteration; is the minimum selection probability of each strategy; and is the total number of strategy and 0 < < . The comprehensive value will comprehensively evaluate the influence of different strategies on the global optimal solution, which accelerates the convergence process.
4.3.3. Strategy Behavioral Mutation Algorithm
In order to avoid the algorithm falling into the local optimal solution, when the same strategy is always used in the evolutionary process and the optimization effect is poor, the mutation probability formula of strategy [27] should be used to adjust the selection probability of each evolutionary strategy.
where is the number of fitness before the iteration, is the fitness of the iteration, and is the mean value of fitness. If is less than a certain threshold , the selection probability of the strategy is set as .
5. Non-Singular Fast Terminal Sliding Mode Control
5.1. Control Law Design
Supposing that and are the desired position and speed of the train, respectively. Then, the position tracking error and the speed tracking error can be defined as:
Then, combining (2)−(4), the error system can be described as:
where represents the additional disturbance received by the train during operation.
In order to ensure that the , converges to the equilibrium point within finite-time and avoid the singular problem, the FTSM surface [29] is designed as:
where and are positive diagonal matrixes, and for , and . Comparing with the conventional TSM, the FTSM surface has faster convergence capability attributed to the additional nonlinear term .
Differentiating (19) with respect to time, yields
Taking use of (18) to substitute for , (20) can be rewritten as:
Then, we introduce the auxiliary variable , such that its time derivative . In terms (17) and (18), we have
By employing (22), we can rewrite (21) as:
where is the estimates of general resistance of train operation , and is the reconstruction error of the RBFNN.
Assumption 1.
The uncertain itemhas an upper bound as follows:, whereis the known positive constant [22,29].
In order to realize the fast tracking of a desired speed in a finite-time, in terms of the FTSM controller design procedure in approach [29], the control low with the estimates of RBFNN can be designed as:
where and are positive diagonal matrices to be designed. is to relieve the possible chattering phenomena and the control term is employed to suppress the external disturbance. In order to further improve the control effect, the above parameters are optimized by the IMPSO algorithm, which effectively enhances the effectiveness and robustness of the control algorithm.
However, regarding the controller in (24), we can find out that some singular phenomena occur when , due to the existence of singular item in . With the aim to settle the singular problem, referring to the approach [29], we design the saturation function to limit the singular item :
where , and is the positive constant to be designed.
As a consequence, the control law in (24) can be rewritten as:
where through defining .
5.2. Stability Analysis
Lemma 1
[30]. Consider a nonlinear system , , , , whereby the equilibrium point is built on the assumption that, as a continuous function, : is defined on an open neighborhood of the origin, such that the following conditions hold: (1) is positive definite; (2) there are real numbers and (0,1), such that
Then, the nonlinear system is locally finite-time stable. Furthermore, the given timesatisfiesfor allin a number of open neighborhoods of the origin. What is more, ifandis unbounded, the system is globally finite-time stable.
Lemma 2
[31]. Consider a vector , the following inequality holds:
Theorem 1.
Consider the network control system of high-speed train in (4). Then, the position and the speed tracking errors will converge to 0 in the finite-time, if the FTSM suface is given by (19), the control law is given by (26).
Proof.
Select the following Lyapunov function candidate:
The time derivative of is derived as:
Using (23), we obtain
By substituting for from (26) into (29), we can obtain that
Next, (30) can be simplified to
Considering the Assumption 1, we choose the and the gains to satisfy that is a little larger than the upper bound , such that
where (32) indicates that is bounded in accordance with Lyapunov theorem. In addition, considering that is defined with error vectors and , we can conclude that both and are bounded. Furthermore, and are set to be bounded such that and are bounded as well.
To demonstrate the finite-time stability of the network control system, we choose the and utilize Lemma 2, (31) can be rewritten as:
By setting , , and making use of Lemma 1, it is clear that the network control system is stable within finite-time when are in . For the convenience of proving, we separate the state space into two opposite areas, as follows:
If the error states are in , there are two different situations: ; . According to (18), we can conclude that when , will increase monotonically until getting and passing the boundary between and along a one-way path, while monotonically decreasing in the same way when .
On the basis of the analysis as mentioned above, the error states will pass from to in the finite-time instead of staying in all the time. Once the error states reach , the network control system will satisfy the condition of the finite-time stability given by (33). Therefore, whether the error states are in or , the position and the speed tracking errors will converge to the sliding mode surface and reach 0 in the finite-time. The proof is completed. □
5.3. Controller Preprocessing
The most important step in our control strategy is the controller preprocessing. Thus, the flowchart of the proposed control strategy is as shown in Figure 2.
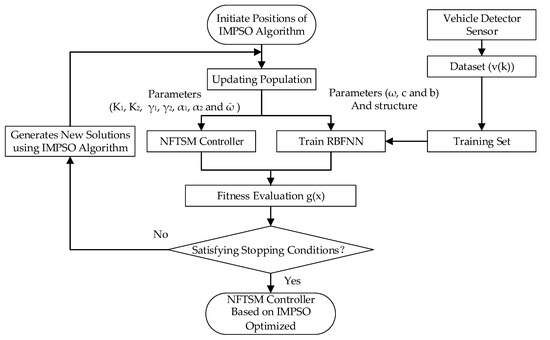
Figure 2.
Flowchart of the proposed control strategy.
In this strategy, the IMPSO algorithm is adopted to optimize the structure and parameters of RBFNN for better mapping the highly nonlinear characteristics of train traction braking. In addition, it is also introduced into the NFTSM controller to obtain the tuning parameters of the controller and suppresses the chattering phenomenon from the sliding mode controller. In the flowchart of the proposed control strategy, the fitness function is described as:
where is the train stopping time.
6. Simulation and Analysis
In order to verify the effectiveness of the above methods, we select the CRH3 (eight-section group) train [32] as the controlled object and the velocity range is 0 to 350 km/h. The desired speed curve includes all operating conditions of traction, braking, and inertia. The main parameters of CRH3 are shown in Table 1. The simulation ATO controller model is established in the central control unit (CCU). The IMPSO algorithm, RBFNN algorithm, and NFTSM control algorithm are implanted into it. According to the actual position and speed of the train obtained by the simulation sensor, the latest traction braking force values are calculated and then assigned to the traction braking simulation unit to perform corresponding actions, where the control input multistage saturation limit is described as:

Table 1.
The main parameters of CRH3.
The task execution period of each device is configured to be 50 ms, and all the modules of the data receiving and sending, algorithm, and model are executed in the same task to achieve synchronous calculation. In practical application, the characteristic period of each port is usually selected as a multiple of 64 ms. Therefore, the sampling period of 64 ms is selected here.
After the simulation test, the parameters of the IMPSO algorithm can be set as follows [27,33]: The total number of iterations is 80, the swarm size is 80, the maximum inertia weight is 0.9, the minimum inertia weight is 0.4, is 0.1, is 2, is 0.5, is 4, and is 1. The control system parameters optimized by the fitness function are shown in Table 2.

Table 2.
Control system parameters.
6.1. Real-Time Performance Analysis of the IMPSO-RBFNN
In order to verify the real-time performance of RBFNN after IMPSO optimization, the above algorithm is simulated in CCU, which works with the Intel(R) Core (TM) I5-7300HQ CPU@2.50 GHz processor and 8.00 GB memory, the real-time performance of IMPSO-RBFNN is shown in Table 3.

Table 3.
Real-time performance of RBFNN.
Table 3 shows that the training time slowly increases with the increase of hidden neurons. However, the approximation error changes obviously with the change of hidden neurons. Specially, the real-time performance of the RBFNN is the best when the number of neurons is 13, and its average training time is far less than the task period (50 ms), thus as long as the sampling time is chosen larger than 50 ms, on-line real-time control could be realized.
6.2. Delay Compensation Effect of Different Characteristic Periods
In order to analyze the delay compensation effect of different characteristic periods, the experiments compare the output effect of the proposed method with and without delay compensation. Setting the initial value of the control input and the speed output as 0. When the characteristic period is 64 ms, the speed response curve of tracking sine wave is shown in Figure 3a. Figure 3b is the characteristic period of 128 ms.
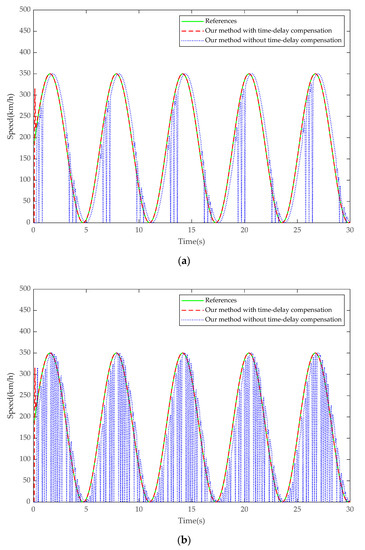
Figure 3.
Comparison of delay compensation effect of different characteristic periods: (a) Characteristic period 64 ms, (b) characteristic period 128 ms.
Figure 3 shows that our method can quickly and accurately track the speed response curve of various operating modes when time delay compensation is added; there is almost no-overshooting and the traction and braking effects are very ideal. Moreover, when the characteristic period is set as 128 ms, the forward and feedback channel delay continue to increase, adding up to more than 300 ms. If the delay control method is not added, the output will occasionally oscillate at different time points and become unstable. The reason for the oscillation is that the delay varies randomly and the time when the control quantity arrives at the actuator is not fixed, which leads to the failure of timely and effective control at many moments. The larger the characteristic period, the larger the delay and the more serious the oscillation. Therefore, it is very important to adopt effective methods for compensating the influence of delay, which is the key of fast and stable control of traction braking.
6.3. Compared with Other Control Methods
In order to verify the effectiveness and robustness of the proposed method under different reference signals, the RBFNN adaptive control method [5] with , , , , and ; the NFTSM control method [29] with , , , , , and , and ; and the sliding mode adaptive robust (SMAR) H∞ control method [13] with , , and are selected to be compared with the proposed method. The speed tracking effect of various control methods when the reference signal is a sine wave is shown in Figure 4. To simulate the real operating condition of the train, the control performances of various methods when the reference signal is a variety of operating modes were analyzed, as shown in Figure 5. In addition, the tracking error statistics are shown in Table 4.
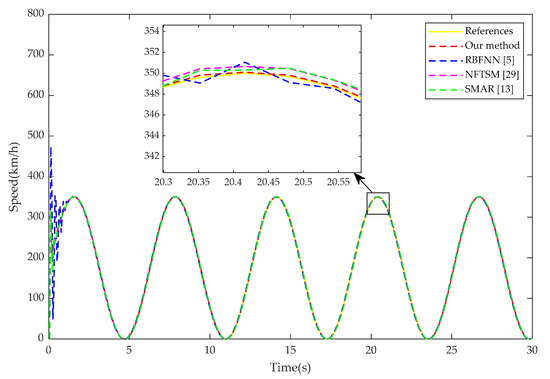
Figure 4.
Speed tracking under sine wave.

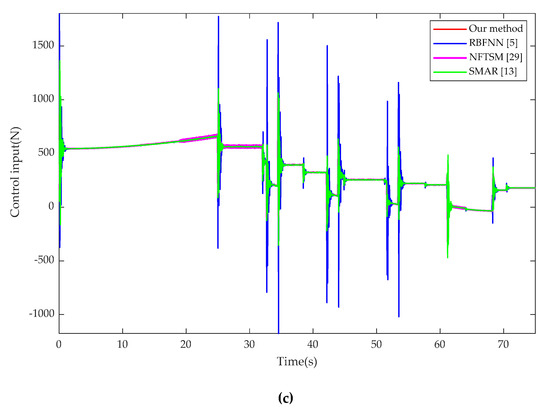
Figure 5.
Control performances of various methods under multiple operating modes: (a) Speed tracking under multiple operating modes; (b) position tracking under multiple operating modes; (c) control input under multiple operating modes.

Table 4.
Tracking error statistics.
Figure 4 shows that, under the frequently changing sine wave tracking trajectory, our method still maintains the advantages of accurate tracking and fast response, which has better control performances compared with other control methods. Figure 5 shows that the desired speed trajectory includes all operating conditions of traction, braking, and inertia. Compared with the RBFNN, NFTSM, and SMAR control methods, our method has better control performances in the whole acceleration and braking phase, and can achieve the smooth switching at different steady-state operating points, which fully meets the high precision tracking requirements of high-speed trains. Thus, it can be obviously seen that the NFTSM control method based on IMPSO-RBFNN optimization has a fast response speed and a good dynamic effect on the train nonlinear network control system, and can be applied to the complex nonlinearity-controlled object, which has ideal robustness and stability. Meanwhile, this method is simple in structure and easy to realize in train communication engineering.
Table 4 shows that, compared with the RBFNN, NFTSM, and SMAR control methods, our method has smaller speed and position tracking error, which has greater advantages in the control process.
6.4. Discussion
Our method utilizes the improved RBF neural network to obtain the real-time and accurate nonlinear characteristics of the train operation, and the control input is also adjusted quickly and effectively with this characteristic. In addition, owing to the introduction of nonlinear item on the sliding surface, the proposed control method can improve the finite-time convergence rate of system states. Meanwhile, the singular problem is settled via introducing a saturation function into the control input and the external disturbances are suppressed by designing robust control items. Thus, this control scheme can be applied to the complex nonlinearity-controlled object, which has ideal robustness and stability. Further, this method is simple in structure and easy to realize in train communication engineering.
In this paper, the TCN forward delay is compensated, and the actual impact of packet loss on the control system is not further considered. Experiments show that data transmission of MVB has a certain degree of packet loss, it needs to propose effective methods to suppress the effects of time delay and packet loss simultaneously. In addition, the influence of the strong wind and rainfall environment on the aerodynamic performance of the high-speed train was not studied. Thus, considering the above impact of multi-factors on control system, we will design a more efficient and robust train network control method for specific circumstances in the future.
7. Conclusions and Prospects
In this paper, we propose a non-singular fast terminal sliding mode control strategy for the train network key control system. The strategy utilizes RBF neural networks approximation and particle swarm optimization to design the NFTSM controller. The structure and parameters of RBFNN can be optimized and the ideal controller parameters of NFTSM can be obtained by an improved multi-strategy particle swarm optimization algorithm proposed in this paper, which not only approximates the nonlinear process of traction and braking quickly and accurately but also suppresses the chattering phenomenon of the controller effectively. The simulation results show that, compared with other control methods, the proposed method can quickly track the changes of reference signals and has better real-time performance, robustness, and stability. The research of this paper provides a reference for realizing the symmetrical bus control by ATO at both ends of the train and the optimal control of the train communication network, which has potential application prospects in further enhancing the economy, safety, and reliability of high-speed train operation.
Author Contributions
X.K. suggested the idea of the work and performed the experiments. T.Z. designed the experimental method. Both authors wrote and critically revised the paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Liaoning Province, grant number 20180551003
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| RBFNN | RBF Neural Network |
| IMPSO | Improved Multi-strategy Particle Swarm Optimization |
| NFTSM | Non-Singular Fast Terminal Sliding Mode |
| ATO MVB | Automatic Train Operation Multifunction Vehicle Bus |
| TCN | Train Communication Network |
| SM | Sliding Mode |
| PSO | Particle Swarm Optimization |
| TSM | Terminal Sliding Mode |
| NTSM | Non-Singular Terminal Sliding Mode |
| FTSM | Fast Terminal Sliding Mode |
| NFTSM AR LMS | Non-Singular Fast Terminal Sliding Mode Auto Regressive Least Mean Square |
| CCU | Central Control Unit |
| SMAR | Sliding Mode Adaptive Robust |
Appendix A
In this appendix, we list the symbols of notations in this paper, as shown in Table A1.

Table A1.
Symbols of notations.
Table A1.
Symbols of notations.
| Notation | Meaning |
|---|---|
| speed of the train | |
| position of the train | |
| the desired speed of the train | |
| the desired position of the train | |
| the net force for the train | |
| the control force for the train | |
| acceleration coefficient the train rotary mass coefficient | |
| the mutual influence of other vehicles on the reference vehicle | |
| the resistance for the train | |
| general resistance | |
| ramp resistance | |
| curve resistance | |
| tunnel resistance | |
| , and | the resistive coefficients for the vehicle |
| the gradient angle of the rail for the vehicle | |
| the parameter obtained through test | |
| the radius of the curve for the vehicle passes | |
| the length of the tunnel for the vehicle | |
| the shaped variable in the elastic coupler of the vehicle | |
| the mass of the vehicle | |
| the output weight between the hidden and output neuron | |
| the output of the hidden neuron | |
| the center vector of the hidden neuron | |
| the width of the hidden neuron | |
| the error function | |
| the learning rate | |
| the momentum factor | |
| the swarm size | |
| the position of the particle in the iteration | |
| the velocity of the particle in the iteration | |
| the best position of the particle in the iteration | |
| the best position obtained by the swarm in the iteration | |
| the inertia weight | |
| and | the acceleration constants |
| the random value uniformly distributed in (0,1) | |
| the sigmoid function | |
| the maximum inertia weight | |
| the minimum inertia weight | |
| the total number of iterations | |
| , and | the different integers in |
| the immediate value | |
| the future value | |
| the comprehensive value | |
| the fitness in the iteration | |
| the number of success of the strategy used by individual before the iteration | |
| the total number of executions of the strategy used by individual before the iteration | |
| the number of success of the strategy used by all the individual before the iteration | |
| the total number of executions of the strategy used by all the individual before the iteration | |
| the constant | |
| the constant | |
| the probability of each strategy adopted in the iteration | |
| the minimum selection probability of each strategy | |
| the total number of strategy | |
| the mean value of fitness | |
| threshold | |
| forward channel timestamp | |
| forward channel delay | |
| timestamp | |
| sampling period | |
| position tracking error | |
| speed tracking error | |
| additional disturbance | |
| FTSM surface | |
| and | positive diagonal matrixes |
| and | the constant |
| auxiliary variable | |
| the reconstruction error of the RBFNN | |
| known positive constant | |
| and | positive diagonal matrices |
| the singular item | |
| positive constant | |
| Lyapunov function | |
| fitness function | |
| the train stop time |
References
- Zhang, T. Real-Time Control Method for Communication Network of High-Speed EMU Based on T-S Fuzzy Model. China Railw. Sci. 2018, 39, 93–99. [Google Scholar]
- Fu, Y.T.; Yang, H. Speed Control of High-speed Electric Multiple Unit Using a Multiple Operating Condition ANFIS Model. J. China Railw. Soc. 2019, 41, 33–40. [Google Scholar]
- Zhou, J.; Wang, L. Scheduling Algorithm of PROFINET IRT Based on Train Communication Network. J. Beijing Jiaotong Univ. 2016, 40, 7–13. [Google Scholar]
- Wang, N.; Yu, Q.; Wan, H.; Song, X.; Zhao, X. Adaptive Scheduling for Multicluster Time-Triggered Train Communication Networks. IEEE Trans. Ind. Inf. 2018, 15, 1120–1130. [Google Scholar] [CrossRef]
- He, W.; Chen, Y.; Yin, Z. Adaptive Neural Network Control of an Uncertain Robot with Full-State Constraints. IEEE Trans. Cybern. 2017, 46, 620–629. [Google Scholar] [CrossRef]
- Wang, F.; Chen, B.; Lin, C.; Zhang, J.; Meng, X. Adaptive Neural Network Finite-Time Output Feedback Control of Quantized Nonlinear Systems. IEEE Trans. Cybern. 2018, 48, 1839–1848. [Google Scholar] [CrossRef]
- Hu, Y.; Si, B. A Reinforcement Learning Neural Network for Robotic Manipulator Control. Neural Comput. 2018, 30, 1983–2004. [Google Scholar] [CrossRef]
- Abedini, F.; Keyvanpour, M.R.; Menhaj, M.B. Neural Tensor Network Training Using Meta-Heuristic Algorithms for RDF Knowledge Bases Completion. Appl. Artif. Intell. 2019, 33, 656–667. [Google Scholar] [CrossRef]
- Jia, W.; Zhao, D.; Ding, L. An Optimized RBF Neural Network Algorithm Based on Partial Least Squares and Genetic Algorithm for Classification of Small Sample. Appl. Soft Comput. 2016, 48, 373–384. [Google Scholar] [CrossRef]
- Zhang, Q.; Gao, J.; Dong, H.; Mao, Y. WPD and DE/BBO-RBFNN for solution of rolling bearing fault diagnosis. Neurocomputing 2018, 312, 27–33. [Google Scholar] [CrossRef]
- Han, H.G.; Lu, W.; Hou, Y.; Qiao, J.F. An Adaptive-PSO-Based Self-Organizing RBF Neural Network. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 104–117. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Li, Y.J.; Wang, M. Fast Multi-Objective Antenna Optimization Based on RBF Neural Network Surrogate Model Optimized by Improved PSO Algorithm. Appl. Sci. 2019, 9, 2589. [Google Scholar] [CrossRef]
- Li, D.C.; Meng, J.J.; Xu, R.X.; Yin, M. Sliding Mode Adaptive Robust H∞ Control Method for High-speed Train under Strong Wind Conditions. J. China Railw. Soc. 2018, 40, 67–73. [Google Scholar]
- Li, Z.Q.; Jin, B.; Yang, H.; Tan, C.; Fu, Y.T. Distributed sliding mode control strategy for high-speed EMU strong coupling model. Acta Autom. Sin. 2019. [Google Scholar] [CrossRef]
- Yang, Y.N.; Yan, Y. Backstepping sliding mode control for uncertain strict-feedback nonlinear systems using neural-network-based adaptive gain scheduling. J. Syst. Eng. Electron. 2018, 29, 580–586. [Google Scholar]
- Venkataraman, S.T.; Gulati, S. Terminal sliding modes: A new approach to nonlinear control synthesis. In The 5th International Conference on Advanced Robotics; IEEE: Pisa, Italy, 1991; pp. 443–448. [Google Scholar]
- Feng, Y.; Yu, X.; Man, Z. Non-singular terminal sliding mode control of rigid manipulators. Automatica 2002, 38, 2159–2167. [Google Scholar] [CrossRef]
- Yu, X.H.; Man, Z.H. Fast terminal sliding-mode control design for nonlinear dynamical systems. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2002, 49, 261–264. [Google Scholar]
- Yang, L.; Yang, J. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems. Int. J. Robust Nonlinear Control 2011, 21, 1865–1879. [Google Scholar] [CrossRef]
- Guo, J.G.; Liu, Y.C.; Zhou, J. Integral terminal sliding mode control for nonlinear systems. J. Syst. Eng. Electron. 2018, 29, 571–579. [Google Scholar]
- Yang, Y.N. A time-specified nonsingular terminal sliding mode control approach for trajectory tracking of robotic airships. Nonlinear Dyn. 2018, 92, 1359–1367. [Google Scholar] [CrossRef]
- Yao, X.; Park, J.H.; Dong, H.; Guo, L.; Lin, X. Robust Adaptive Nonsingular Terminal Sliding Mode Control for Automatic Train Operation. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 2406–2415. [Google Scholar] [CrossRef]
- Song, Q. Robust Adaptive and Fault-tolerant Control of High Speed Trains. Beijing Jiaotong Univ. 2014. [Google Scholar]
- Wang, L.S. Predictive Control for Automatic Operation of High-speed Trains Based on Multi-point Model. Beijing Jiaotong Univ. 2016. [Google Scholar]
- Shallue, C.J.; Lee, J.; Antognini, J.; Sohl-Dickstein, J.; Frostig, R.; Dahl, G.E. Measuring the Effects of Data Parallelism on Neural Network Training. J. Mach. Learn. Res. 2019, 20, 1–49. [Google Scholar]
- Połap, D.; Woźniak, M.; Damaševičius, R.; Maskeliūnas, R. Bio-inspired voice evaluation mechanism. Appl. Soft Comput. 2019, 80, 342–357. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, P.C. An adaptive multi-strategy behavior particle swarm optimization algorithm. Control Decis. 2018. [Google Scholar] [CrossRef]
- Yang, B.W.; Qian, W.Y. Summary on improved inertia weight strategies for particle swarm optimization algorithm. J. Bohai Univ. (Nat. Sci. Ed.) 2019, 40, 274–288. [Google Scholar]
- Chen, Z.Y.; Yang, X.H.; Liu, X.P. RBFNN-based nonsingular fast terminal sliding mode control for robotic manipulators including actuator dynamics. Neurocomputing 2019, 362, 72–82. [Google Scholar] [CrossRef]
- Li, P.; Ma, J.; Zheng, Z.; Geng, L. Fast nonsingular integral terminal sliding mode control for nonlinear dynamical systems. In 2014 IEEE 53rd Annual Conference on Decision and Control (CDC); IEEE: Pisa, Italy, 2014; pp. 4739–4746. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1990; ISBN 0-521-30586-1. [Google Scholar]
- Zhong, L.S.; Li, B.; Gong, J.; Zhang, Y.X.; Zhu, Z.M. Maximum Likelihood Identification of Nonlinear Model for High-speed Train. Acta Autom. Sin. 2014, 40, 2950–2958. [Google Scholar]
- Yu, G.Q.; Li, L.D.; Yuan, Y.F. A Hybrid Particle Swarm Optimization Algorithm with Adaptive Inertia Weight. J. Harbin Univ. Sci. Technol. 2016, 21, 49–53. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).