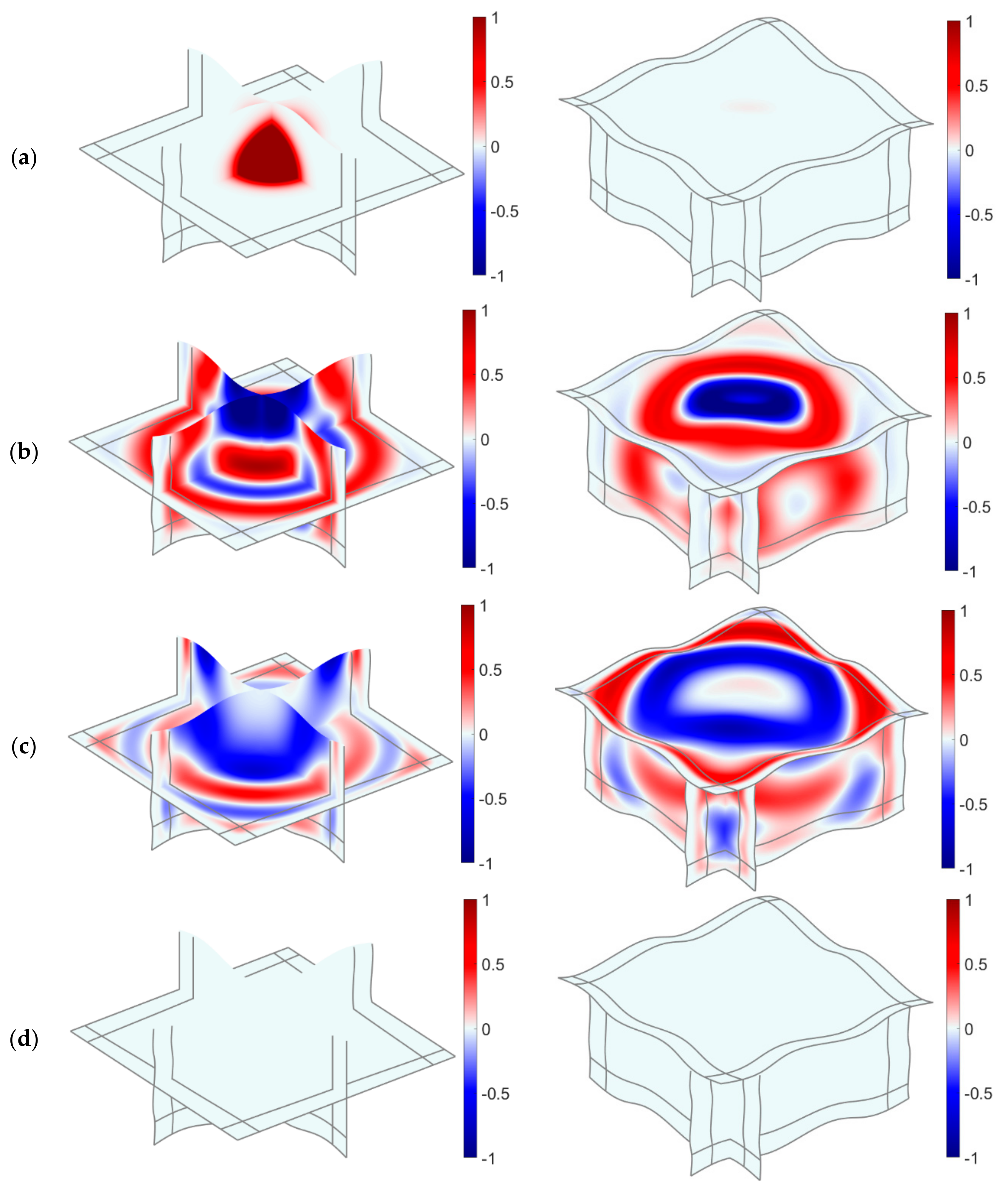
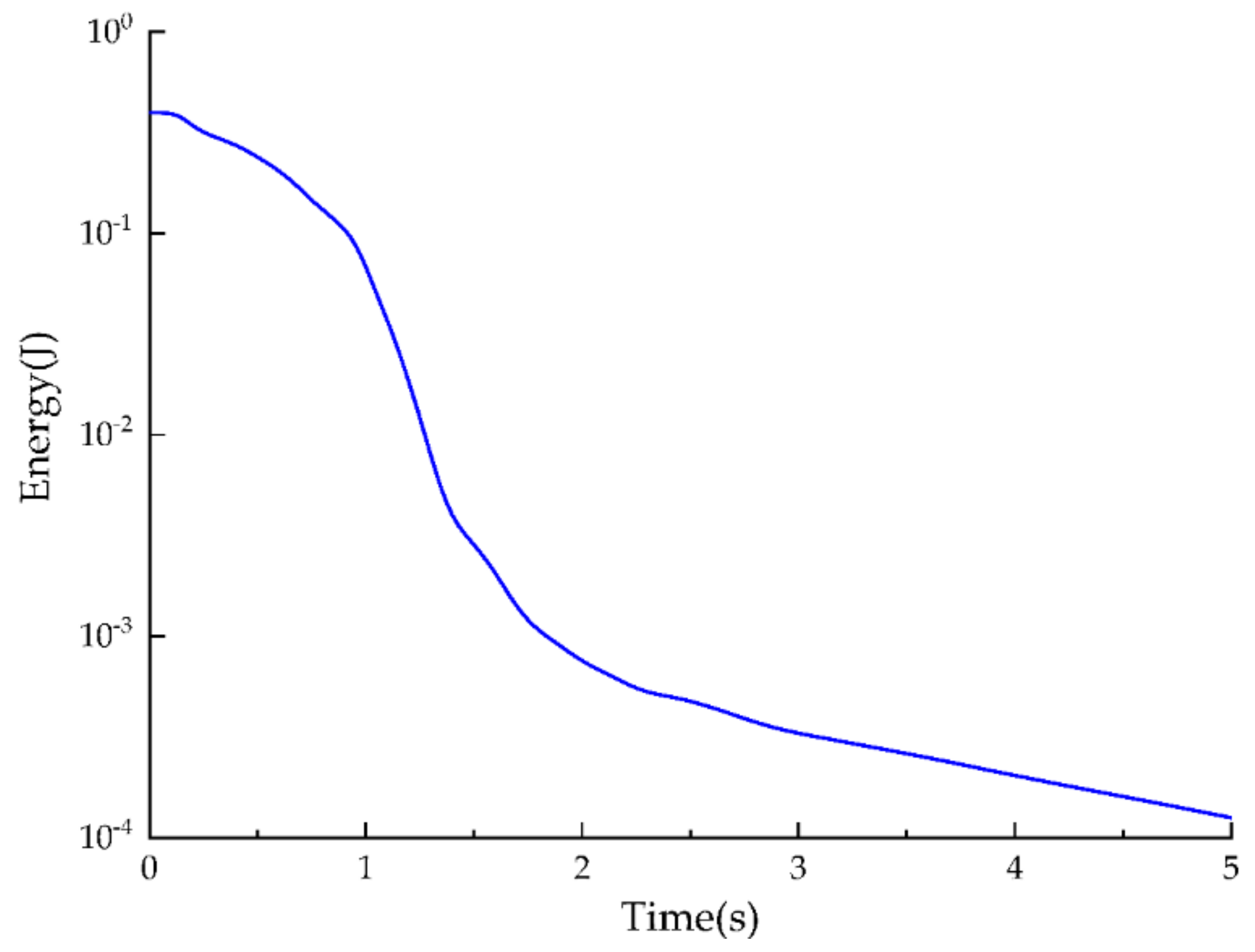
1. Introduction
In seismology, as well as in many other applications, such as acoustics, oceanography, and electromagnetics, a number of numerical methods to simulate elastic wave propagation have been developed. In general, the elastic wave equation can be discretized using various approaches, such as the finite difference method (FDM) [
1,
2,
3], finite element method (FEM) [
4,
5], spectral element method (SEM) [
6], boundary element method (BEM) [
7,
8], discontinuous Galerkin method (DGM) [
9], and others. Each of these methods has advantages, as well as drawbacks. FDM is successfully applied to solving the problems related to wave propagation and has been widely used in the field of seismic engineering, due to its high efficiency and ability to simulate complex media, such as layered ones. However, it is difficult to handle complex geometry, specifically with regard to the staggered grid method [
10]. In addition, several methods related to FDM have difficulties in ensuring long-time stability within the spatial and temporal domain [
11]. These drawbacks impose significant limitations to the simulation of large-scale, long-period, and undulating media. Therefore, a numerical method ensuring time and spatial stability is proposed.
Unlike the first- and second-order methods, higher-order FDMs (HOFDMs) can effectively reduce the degree of freedom required to simulate wave propagation. Therefore, HOFDMs are able to capture the wave-dominated phenomena, such as elastic wave propagation, more efficiently, as for a given error tolerance, the number of grid nodes can be reduced substantially and in several dimensions, and thereby, one may significantly decrease the computing time and memory required by orders of magnitude [
12]. However, one of the drawbacks of higher-order methods is their relative complexity, both in terms of derivation of formulas and programming implementation. Moreover, the larger amount of programming work is required during the simulation, meaning that a program has to perform more calculations, and more calls per grid node are required. It is deemed that such methods may become more broadly appealing and applied more widely if the associated complexity can be reduced.
The main purpose of the present study is to develop a stable HOFDM for the elastic wave equations both in 2D and 3D curve domains, and to facilitate an implementation procedure to be as simple as possible by establishing a generic framework under the premise. One of the appropriate HOFDMs combining the initial boundary value conditions is to apply summation-by-parts (SBP) [
13,
14,
15,
16,
17] operators to approximate derivatives of the spatial domain together with weak enforcement of boundary and interface conditions using the simultaneous-approximation-term (SAT) [
11,
18] method, or the projection method [
19,
20,
21]. The SBP-SAT methodology can be used to provide a strictly stable proof using the energy method that ensures the robustness within the spatial and temporal domain. Some review papers of SBP operators and examples of SBP-SAT can be found in References [
22,
23,
24,
25,
26].
The basic theory about the first-derivative SBP operators was proposed by Kreiss and Scherer [
13] seeking to transform the higher-order methods into a systematic means of proving stability through the energy method [
27]. The predominant concept of SBP operators is to mimic the integration-by-parts (IBP) property, so that stability of a discretization framework can be proved by using the energy method similarly to the case of the continuous problems. Initially introduced SBP operators principally have been developed in the context of HOFDMs, where the nodal distribution in a computational space is uniform. A matrix of SBP operators has periodically centered difference stencils in the interior grid nodes and specific one-sided ones near the boundary grid nodes to maintain the SBP property. SBP introduced above can be referred to as a classical SBP operator. Recently, the theory of classical SBP operators has been extended to a broader set of operators, for instance, upwind SBP operators [
28,
29], staggered and upwind SBP operators [
30], generalized SBP operators [
31,
32,
33], and multi-dimensional SBP operators [
34,
35]. Newly proposed SBP operators have new properties not presented in the classical SBP operators. A matrix of generalized SBP operators can use non-repeating difference stencils in the interior grid nodes that can be non-uniform depending on the distribution of grid nodes. Additionally, generalized SBP operators may exclude one or both boundary nodes. Multi-dimensional SBP operators can avoid dimension expansion in the form of tensor products. Upwind operators can naturally introduce artificial dissipation when combined with flux-splitting techniques for the hyperbolic system.
The SBP-SAT methodology has many useful properties, and one of them is to facilitate the derivation of higher-order spatial discretizations that are provably time-stable using a rather straightforward approach based on the energy method, in which the procedure is similar to the energy method in the continuous case. Another property is that the SBP-SAT methodology can handle the boundary condition in a flexible way, and the boundaries contain those of the computational domain and of interfaces between blocks, in which the blocks are obtained by dividing the computational domain [
36]. Referring to this property, an extremely large computational domain can be simulated by dividing the domain into several blocks of the suitable size. Then, simulation can proceed within blocks instead of in the whole computational domain, so that it can greatly alleviate the computer memory consumption. Additionally, an approximation of the derivative in each of the blocks is strictly determined by the solution in the particular block, and interfaces of blocks play the role of data transfer and assignment tools. Therefore, using the SBP-SAT methodology, wave propagation in a computational domain with special shapes can be simulated, which is difficult to achieve using the traditional FDMs, as it is shown in the conducted numerical simulation. Moreover, the interface does not have to be continuous, so that a geometric discontinuity can be simulated intentionally. More detailed contents on the SBP-SAT methodology can be found in Reference [
37].
Numerical methods require the domain of simulation to be divided into a finite number of nodes or elements, as it is difficult to simulate elastic wave propagation in a finite domain without employing boundaries to prevent spurious wave reflections back into the computational domain. In the elastodynamic simulation, a wide variety of absorbing layers and boundary conditions have been developed to truncate these domains and “absorb” the outgoing waves as much as possible to simulate the wave motion in finite computational domains (e.g., sponge zone [
38,
39], SMART layers [
40], paraxial conditions [
41,
42], continued fraction conditions [
43], transmitting boundary conditions [
44,
45], viscous boundary conditions [
46,
47], viscous-spring artificial boundary conditions [
48], optimized boundary conditions [
49], etc.). In addition, the perfectly matched layer (PML) [
50,
51,
52,
53], and high-order absorbing boundary conditions (ABCs) [
54,
55,
56] are now the most commonly used approaches to considerably limit spurious numerical reflections.
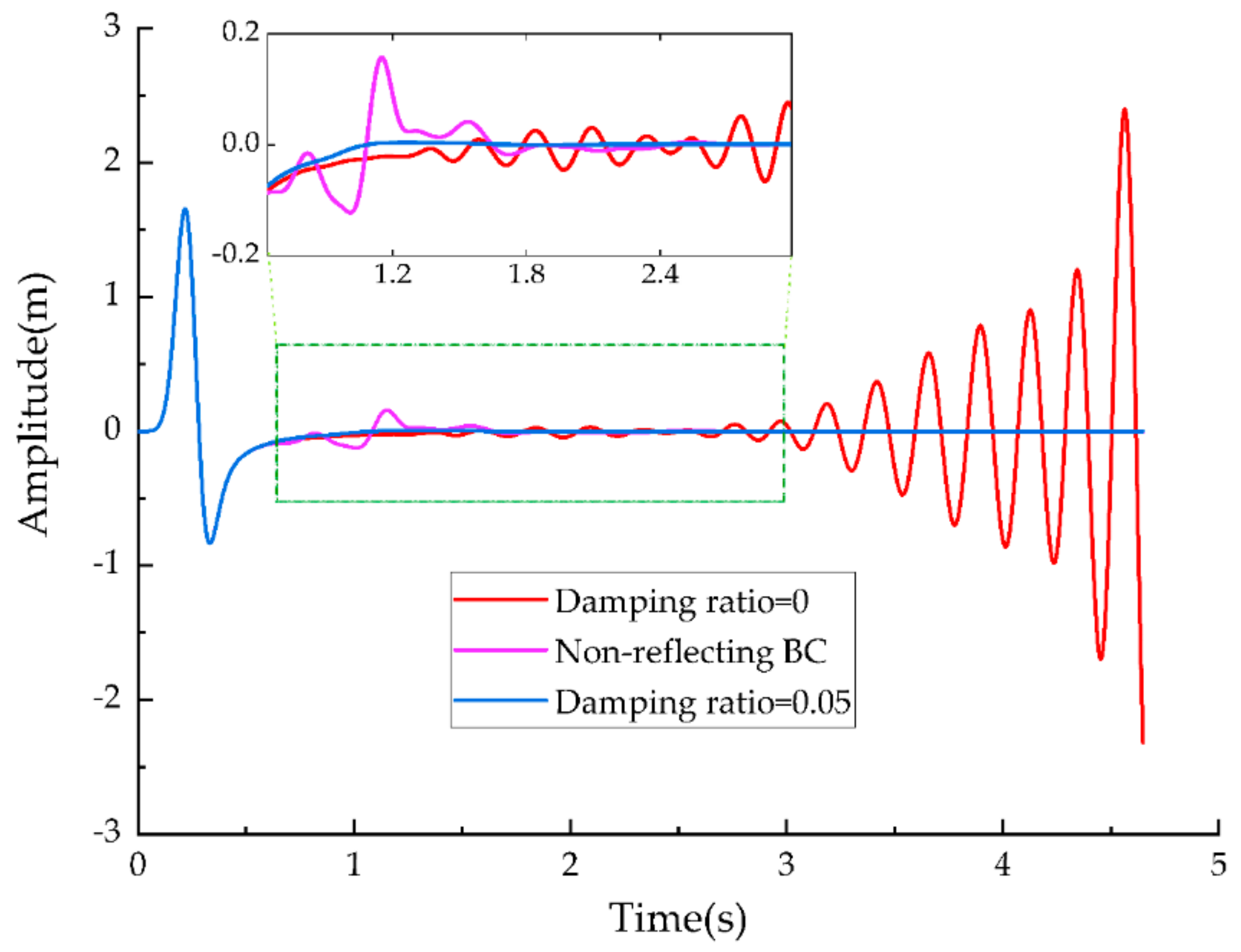
Considering a framework based on the SBP-SAT methodology, a suitable way to avoid artificial reflection is to impose characteristic BC expressed in terms of physical parameters of inflow and outflow, which represents a well-proven, first-order accurate non-reflecting BC. In this case, the energy method is still effective for the semi-approximation system leading to a well-proven approximation [
57,
58,
59,
60]. Even though the stability of this framework can be guaranteed in an acceptable manner, the reflected wave generated by the non-reflecting BC may cause continuous perturbations within the wavefield. Consequently, the wavefield may be distorted by the reflected wave in a large-scale or long-time simulation. This adverse effect can be corrected using PML. One of the advantages of PML is that it can control the attenuation effect of waves by changing the number of absorbing layers or damping functions in case of making waves attenuated as much as possible during the absorption. In the present paper, we combine PML and the SBP-SAT methodology to facilitate wave absorption at the boundaries. Description of frameworks utilizing SBP-SAT to discrete PML equations can be found in several papers [
61,
62,
63,
64].
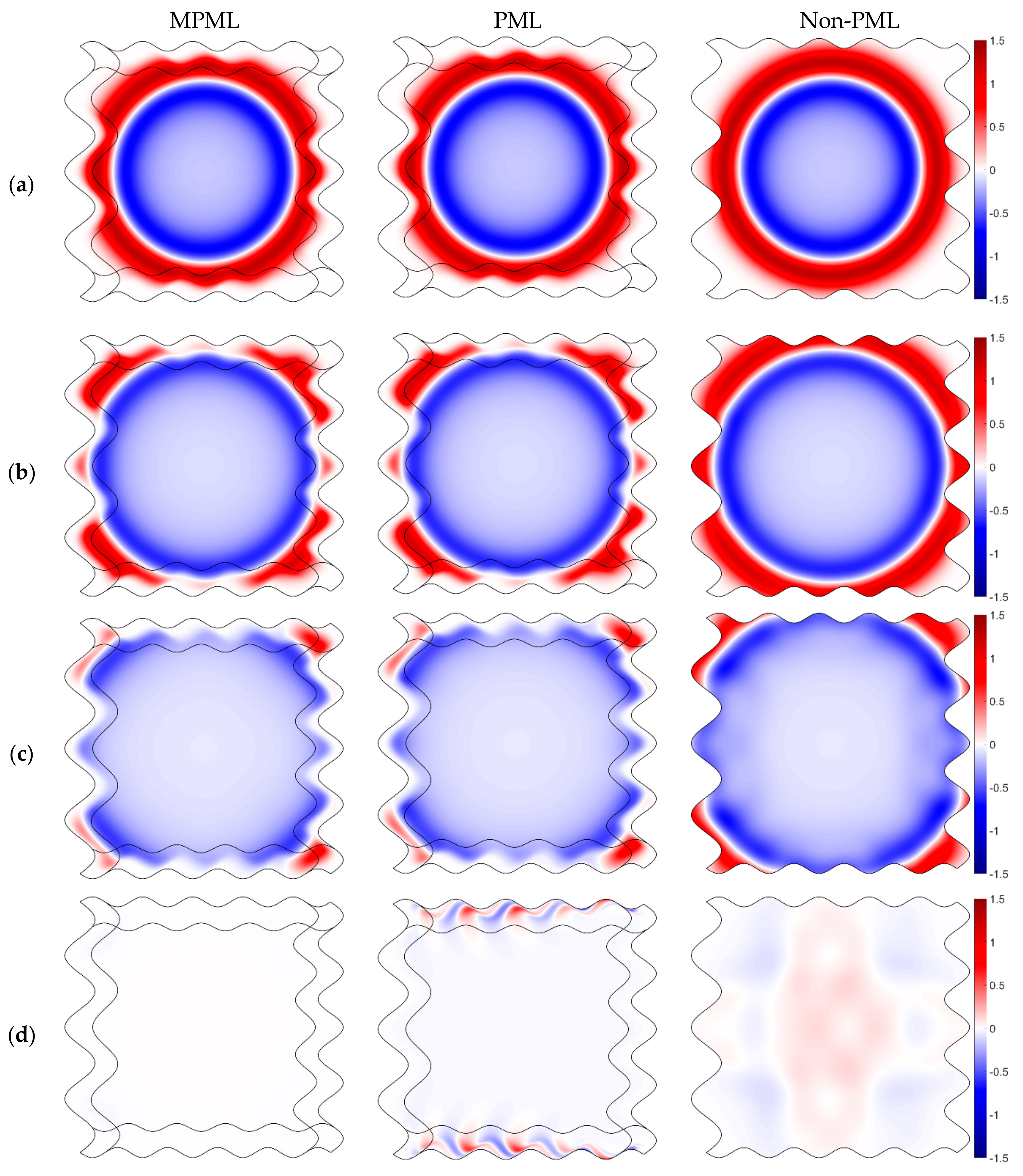
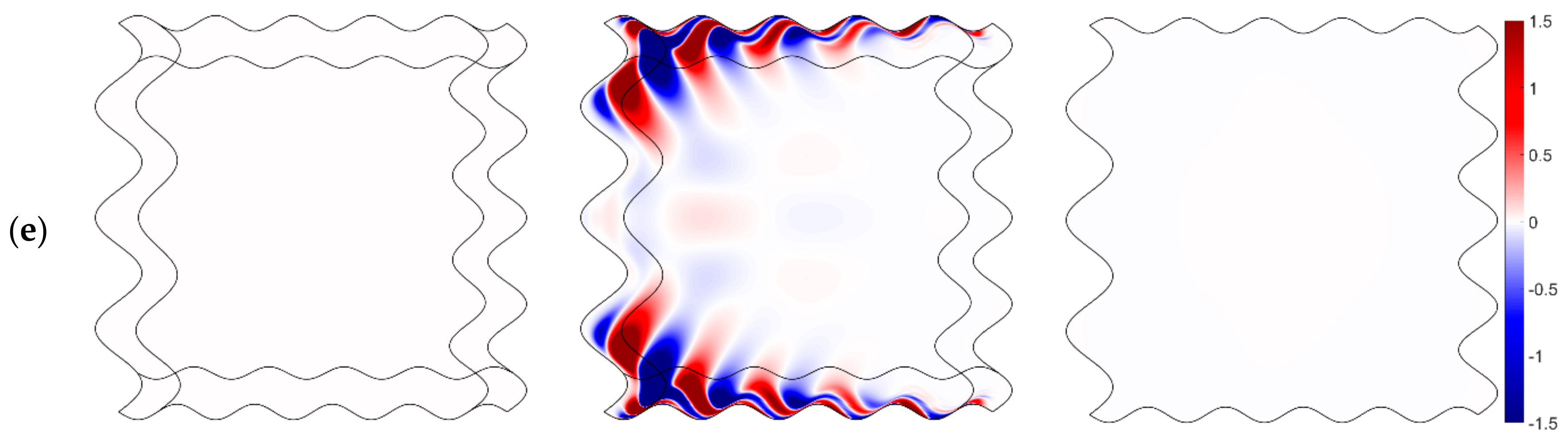
In most cases, PML has only one damping coefficient in the direction perpendicular to PML. Even though the simulations of modeling using PML provide a stable and satisfying result in the rectangular computational domains or isotropic medium, a well-known problem of PML and its variants/improvements is that the simulations of modeling using PML provide unstable results in certain kinds of the curve domains or anisotropic medium in terms of long-time wave propagation. The instability problems of PML were analyzed by Bécache et al. [
65] from a theoretical point of view and found that stability is related to the relative direction of the group velocity and wavenumber, which was defined as “slowness vector.” Meza-Fajardo and Papageorgiou [
66] explained the stability of PML referring to the eigenvalues of the coefficient matrix in the frequency domain, implying that a system is unstable when eigenvalues have positive real part roots. To mitigate this problem, they added appropriate non-zero damping coefficients to PML in the directions both parallel with and perpendicular to the PML/non-PML interfaces simultaneously. They also proposed the damping ratio defined as a ratio between the PML coefficients along with the directions parallel with and perpendicular to the PML/non-PML interfaces referred to as multi-axial PML (MPML). More details on MPML can be found in several related papers [
67,
68,
69,
70].
At present, a combination of the SBP-SAT methodology with PML is still mostly applied to the rectangular domain. However, several researchers combine the SBP-SAT methodology with MPML. In seismology, constructing a framework combining SBP-SAT and MPML is of great significance to simulate the propagation of the elastic wave in complex media and in models with complex geometric surfaces. Overall, the most applicable framework for the elastic wave equation is discretized in the form of full expansion. The discretization framework for the elastic wave equation in a different modal (SH, P-SV) or in different dimensions (2D, 3D) is rather different as it implies discrete each element of the elastic wave equation (every velocity and stress in the corresponding equation). The formula will be more complicated in the case of discretization in the curve domain for the Jacobian matrix, and the chain rules are introduced to reduce the generality of formula derivation and programming.
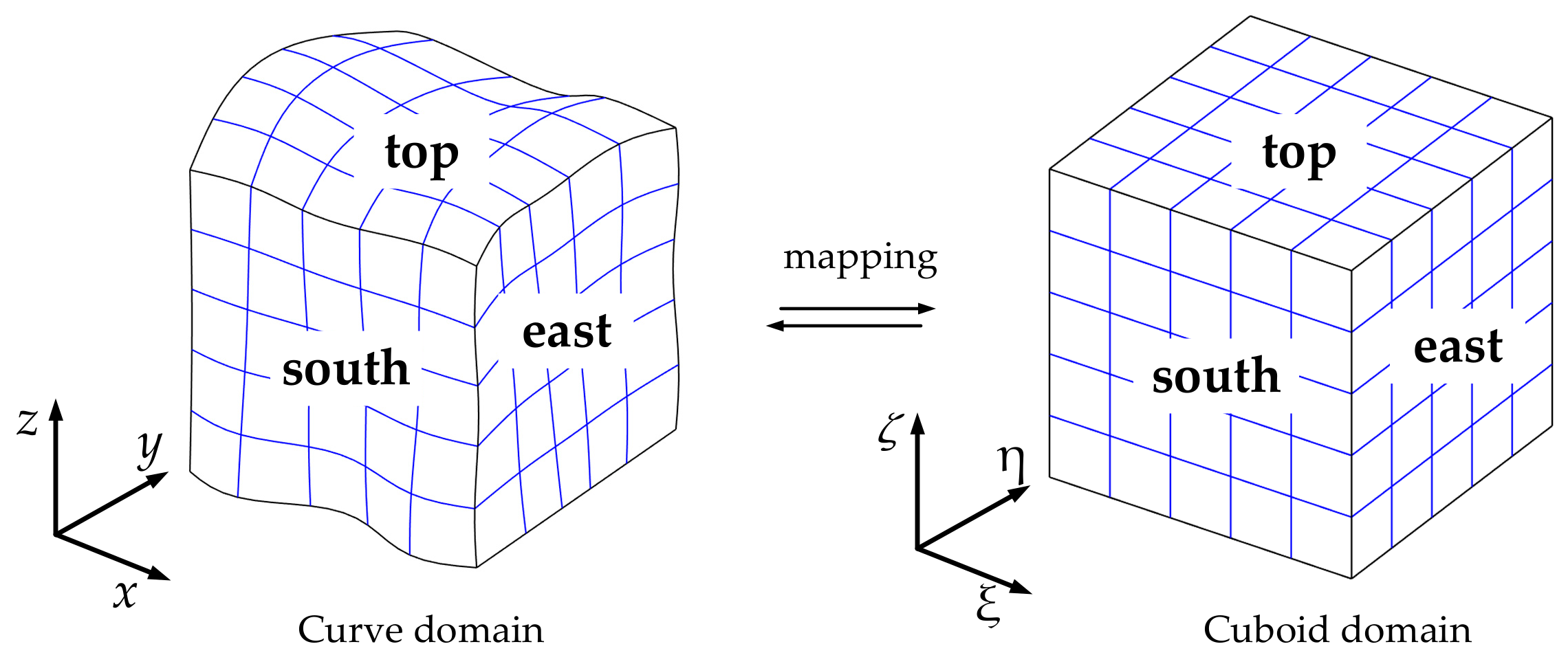
To address this situation, a generic representation of the elastic wave equation, referred to as symmetric matrix form (SMF), is introduced. Using SMF, a framework for the elastic wave equation is cast into the matrix form, and then the discretization can be treated in a generic system. Therefore, the expression of the SMF framework requires generic programming as well. Additionally, a generic stable discretization of SMF in the curve domain can be developed considering a similar framework in the regular domain, and this property has a positive effect on simplification of the formula derivation and program compilation, which can allow avoiding the introduction of direction vectors and the traction effect on the velocity and stress. The proposed framework is, therefore, applicable to a wide range of elastic wave equations.
The remainder of this paper is organized as follows. In
Section 2, the SMF of the elastic wave equation in 3D is formulated. It is shown that it can be further extended in the curve domain and then, the well-posed BCs of SMF of the elastic wave equations are established. Thereafter, in
Section 3, we propose applying MPML for SMF of the elastic wave equations and present the results of the stability analysis in continuous cases. A semi-discrete SBP-SAT methodology is presented in
Section 4. The results of the stability analysis within a discrete norm are discussed in
Section 5. It should be noted that the upwind SBP operators are used in this study. Numerical tests are presented in
Section 6. Subsequently, conclusions are drawn, and the future research directions are presented in
Section 7.
3. PML for SMF of the Elastic Wave Equations and Stability Analysis
To obtain a PML system for the corresponding wave equation, complex frequency-shifted (CFS) that introduces a coordinate transform,
, can be used, as equations inside the PML layer have exactly the same form as in the physical domain. The stripe of PML at the positive
-axis and the PML-non-PML interface starting at
are considered for convenience. Given a field variable
u, we obtain the following:
Consequently, the complex stretch function is defined as follows:
the Equation (29) can be rewritten as
From the relation Equation (30), we can transform the wave equation in the complex coordinate
into the Cartesian coordinate
, in which the analysis will be conducted. Then, employing the Fourier transform results in the following:
where
denotes the variable
U in the frequency domain. Equation (31) can be transformed into the time domain to obtain the PML equation suitable for the time-domain numerical method. The function of
has several forms, for standard PML, we obtain the following:
and for generalized PML (GPML), we have
for CFS-PML, the function is given by
In Equation (32) and Equation (34), is the damping function, is the complex frequency shift and is the scaling factor. is also the damping function similar to , and they are both used for damping the propagating wave exponentially inside PML. is the scaling parameter contributing to either stretching or compressing the coordinate. As the functions introduced above only depend on , we omit the variable for convenience. Equation (34) is adopted in the present study, and then the CFS-PML framework is implemented using auxiliary differential equation (ADE). Moreover, only has impact in PML, in the physical domain in terms of and .
Here, ADE CFS-PML is built through separating the
into two parts that has the form
Therefore, Equation (31) is equivalent to
where
is the auxiliary variable transformed into the frequency domain. Equation (36) is the unsplit-field CFS-PML framework in the frequency domain. The corresponding framework of Equation (36) in the time domain is given by,
Obviously, the PML framework is based on the original wave equations, so that it is easy to implement an existing code with minor necessary changes. Furthermore, SMF of the elastic wave equation can simplify the process of the problem analysis, as well as that of programming, as only
U and
A are modified to represent the different wave modal and wave dimensions. The PML framework presented above that has one damping function in the direction perpendicular to the stripe of PML is unstable in certain kinds of anisotropic medium or in the curve domain having curvilinear grids distribution. The MPML framework has a form similar to PML in which an additional damping function is implemented along the direction parallel with the stripe of PML. Therefore, the damping ratio defined as a ratio between the damping functions along with the directions parallel with and perpendicular to the stripe of PML, is introduced as follows:
Here, ADE CFS-PML is utilized in the main damping direction, and the standard PML is introduced in the additional damping directions, where
and
. For convenience, we present MPML located at the west of the physical domain as an example. Similar to Equation (37), the additional damping function in the direction parallel with PML is set to be proportional to the damping function in the direction perpendicular to PML, which can be expressed by the damping ratio.
We should note that all functions in square brackets only have an impact in the west stripe of PML, as well as ADE will be eliminated in the physical domain given that less memory usage is needed compared with split-MPL. MPML can be used to stabilize the numerical simulation for anisotropic medium or on curvilinear grids. The framework based on MPML does not differ significantly from the framework based on PML. Furthermore, SMF of the elastic wave equation has the same formulation both in the regular and curve domains. This property can allow simplifying considerably the derivation of the framework by hands, where more work can be done by computational means.
3.1. Energy Analysis of SMF Based on MPML in the Frequency Domain
In this section, the energy analysis is presented for SMF of the elastic wave equations combined with BC. It should be noted that the energy analysis of the SMF framework based on MPML and non-PML requires different procedures. The framework based on MPML cannot derive an analysis estimate in the time domain, while this can be done for the framework without MPML. Nevertheless, these two cases have a similar form in the corresponding domain. To begin with, we take the Fourier transform of (39) in time and remove the auxiliary equations that take the following form:
It should be noted that
and
are have impact to PML only in the west domain and are removed in the rest of the domain. Pre-multiplying
and adding the conjugate of the product, then integrating over the domain yields.
where
are bounary surfaces and the boundary terms are
Note that
is the inner product and Equation (42) represents non-reflecting boundaries in the cure domain. For the free-surface BC, take the top boundary surface, or other types of BC, as shown in Equation (27), yields
All boundary terms are non-positive, and . Therefore, .
3.2. Energy Analysis of SMF without PML in the Time Domain
The stability of SMF without PML can be proceeded in the time domain using the energy method. The derivation is similar to
Section 3.1. Multiplying Equation (23) by
, setting data to zero and adding its transpose, then integrating over the domain yields
Equation (44) is equivalent to
where the boundary terms in the time domain are similar to Equation (42), the bottom boundary as non-reflecting BC and the top boundary as free-surface BC or others are
Equations (46) non-positive so that Equations (45) satisfies the energy estimate. Using SMF, energy analysis can be greatly simplified as a generic system.