A New Bimodal Distribution for Modeling Asymmetric Bimodal Heavy-Tail Real Lifetime Data
Abstract
1. Introduction
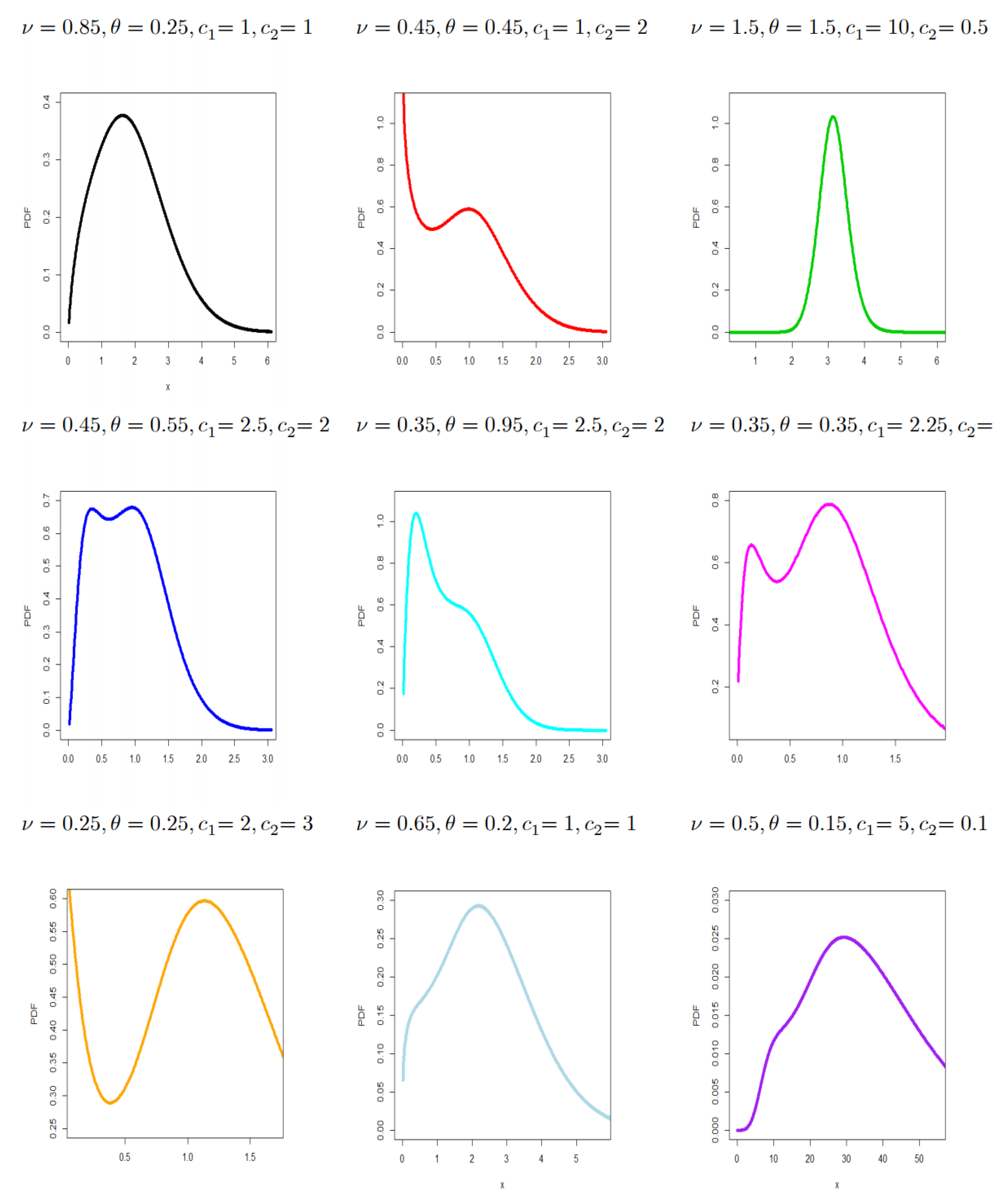
- The new density in (6) can be “unimodal and right-skewed,” “symmetric and unimodal,” and “bimodal density” with many useful shapes (see Figure 1).
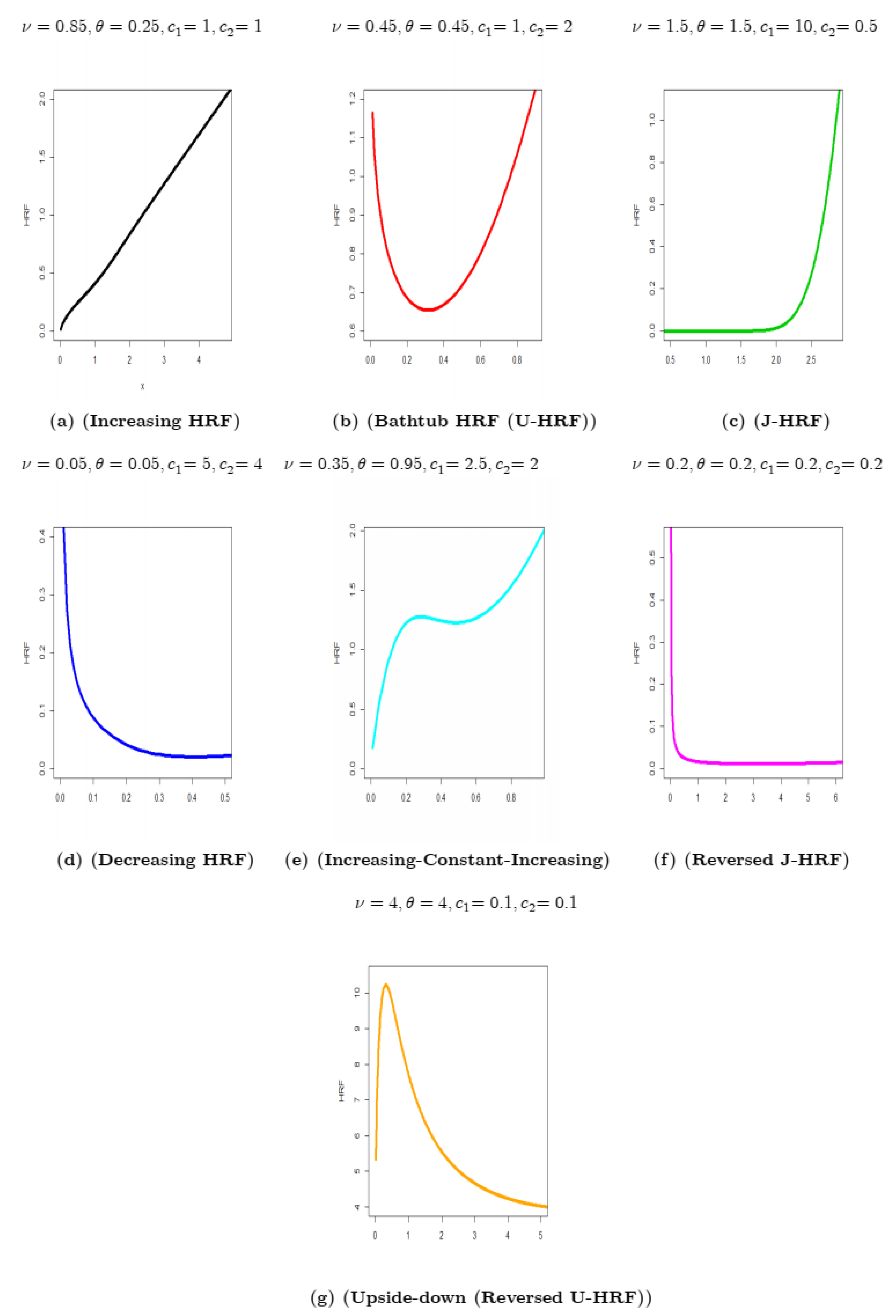
- The HRF of the new model can be “monotonically increasing,” “bathtub (U-HRF),” “J-shaped (J-HRF),” “monotonically decreasing,” “increasing-constant-increasing,” “reversed J-HRF,” and “upside-down (reversed U-HRF)” (see Figure 2).
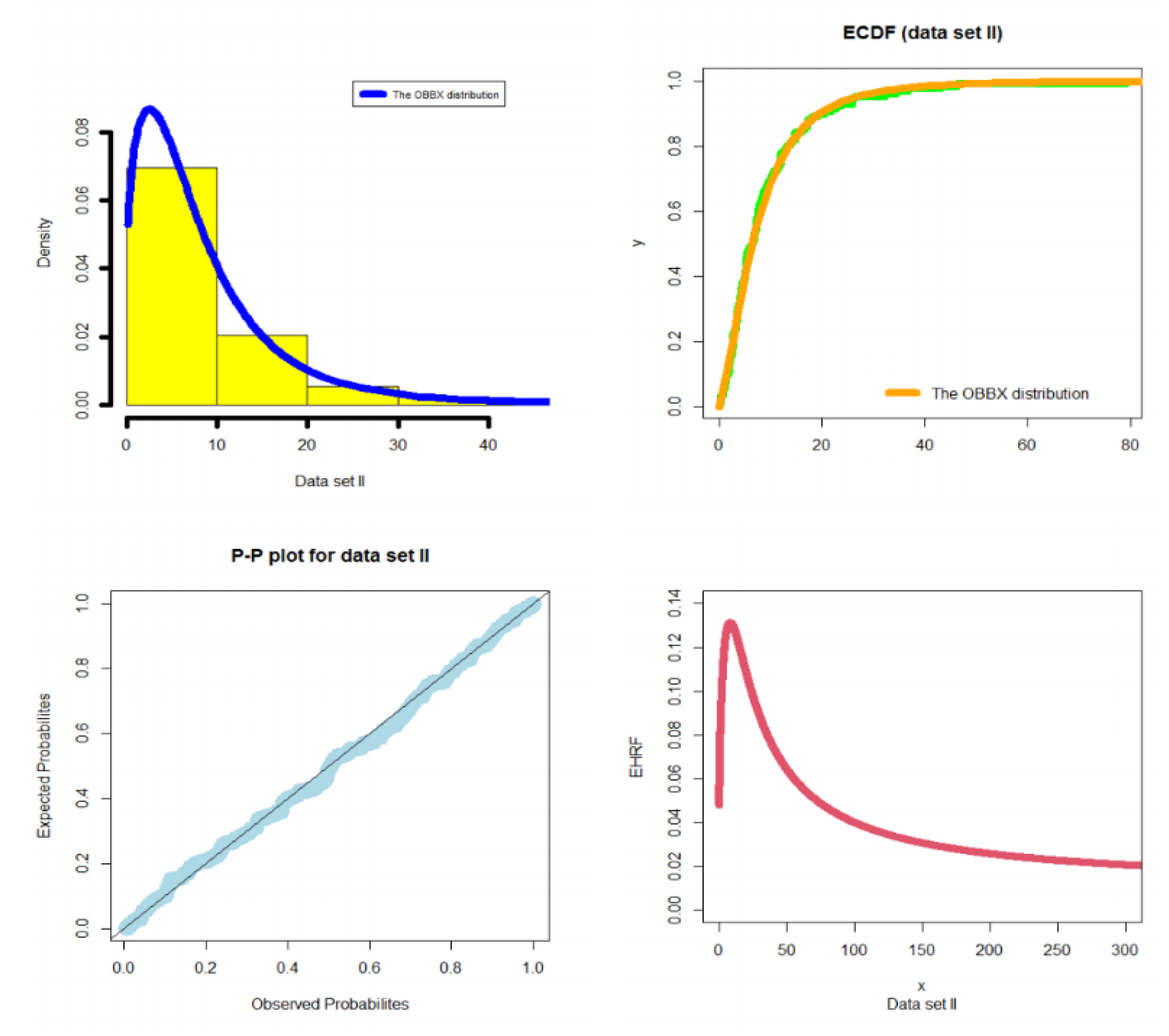
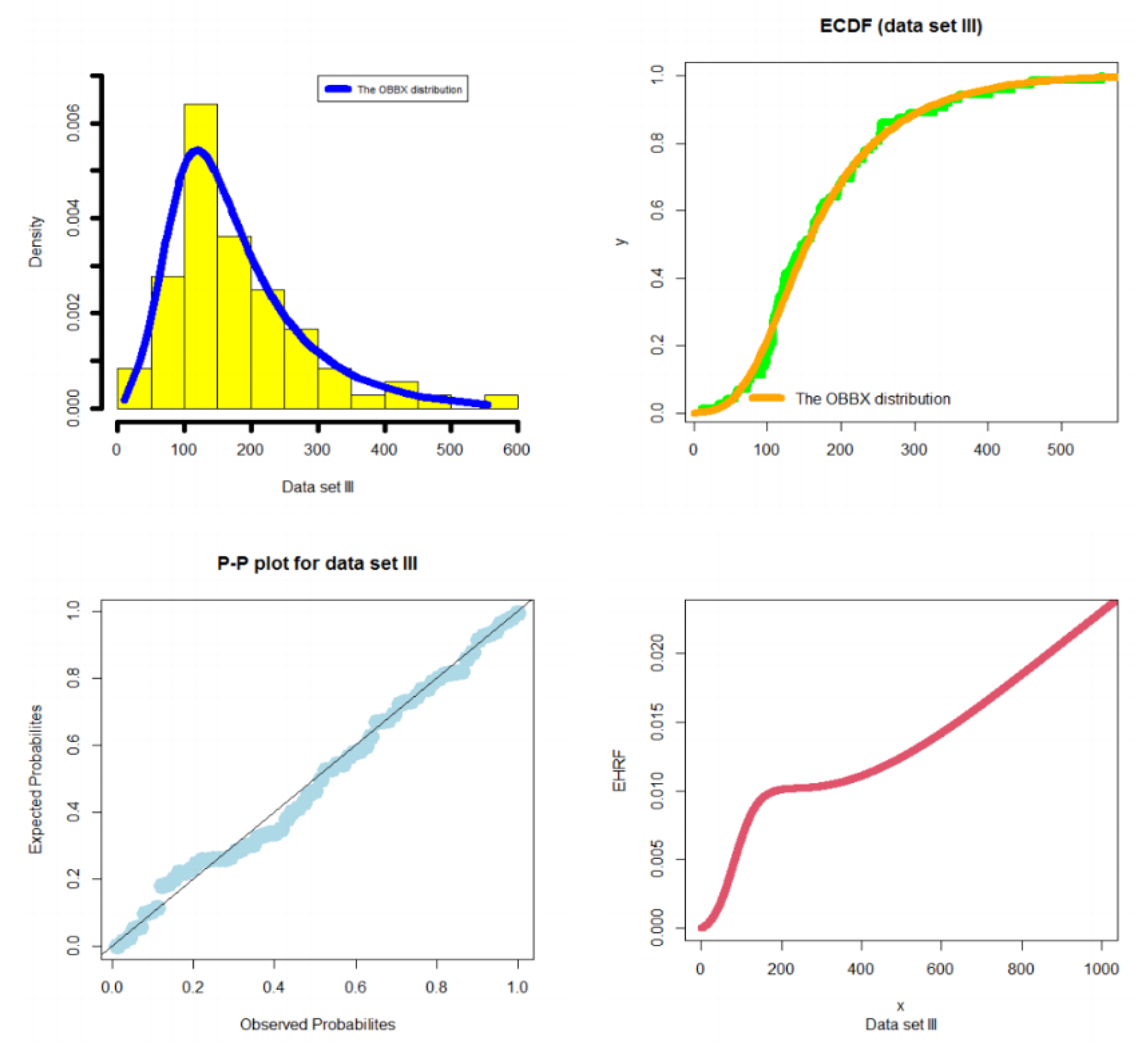
- In reliability analysis, the OBBX model could be chosen as the best model, especially in modeling asymmetric bimodal failure times data and the asymmetric bimodal right-skewed and heavy-tail survival times data as illustrated in Section 5.1 and Section 5.3, respectively.
- In medical fields, the OBBX model could be chosen as the best model, especially in modeling the bimodal right-skewed and heavy-tail cancer data, as illustrated in Section 5.2.
- In engineering, the OBBX model could be chosen as the best model, especially in modeling the asymmetric bimodal left-skewed and heavy-tail glass fibers data, as shown in Section 5.4.
2. Mathematical Properties
2.1. Useful Representations
2.2. Moments and Incomplete Moments
2.3. Moment Generating Function (MGF)
2.4. Residual Life and Reversed Residual Life Functions
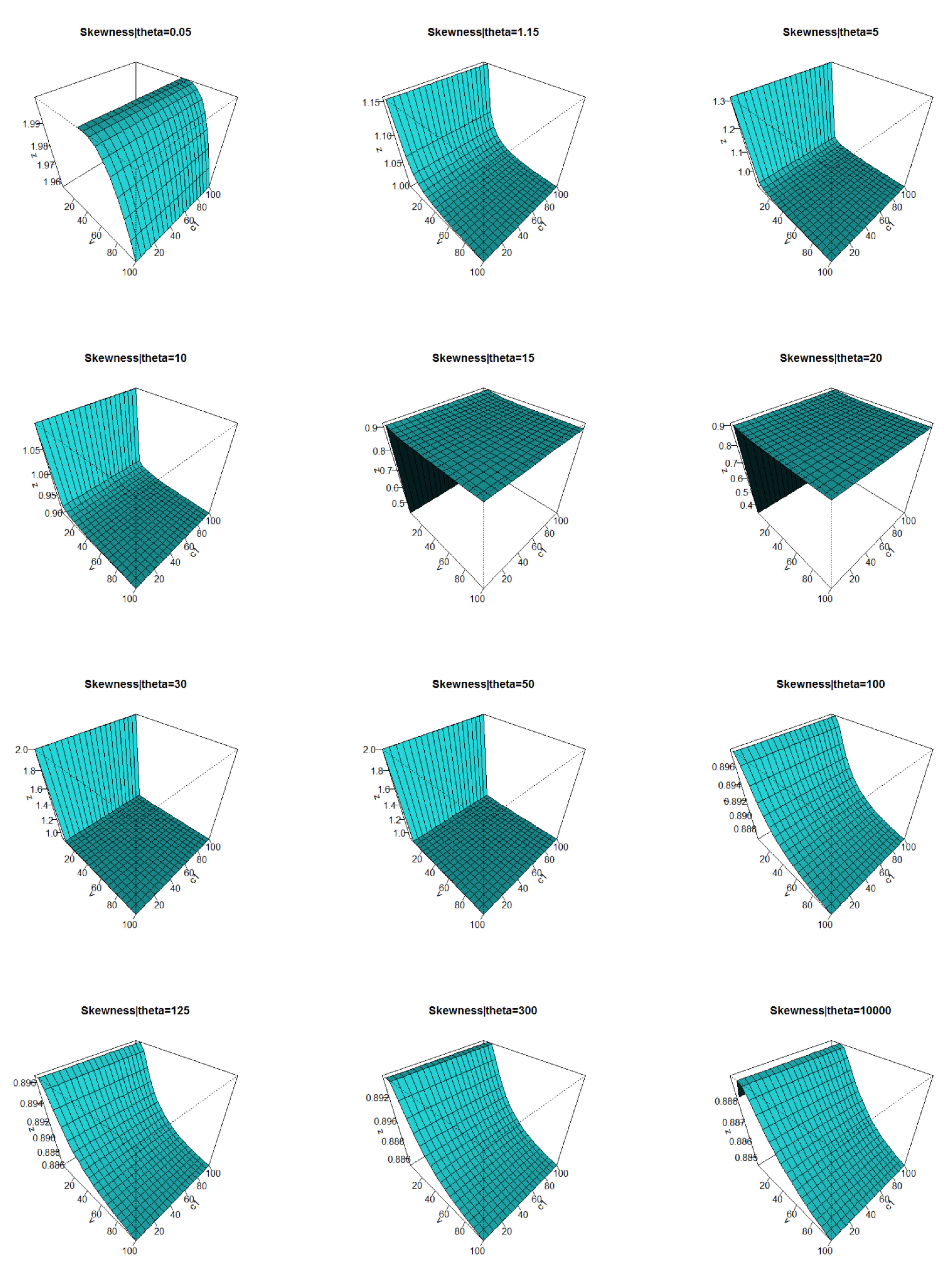
2.5. Numerical Analysis for the Mean, V, S, K, and DisIx
3. Maximum Likelihood Estimation
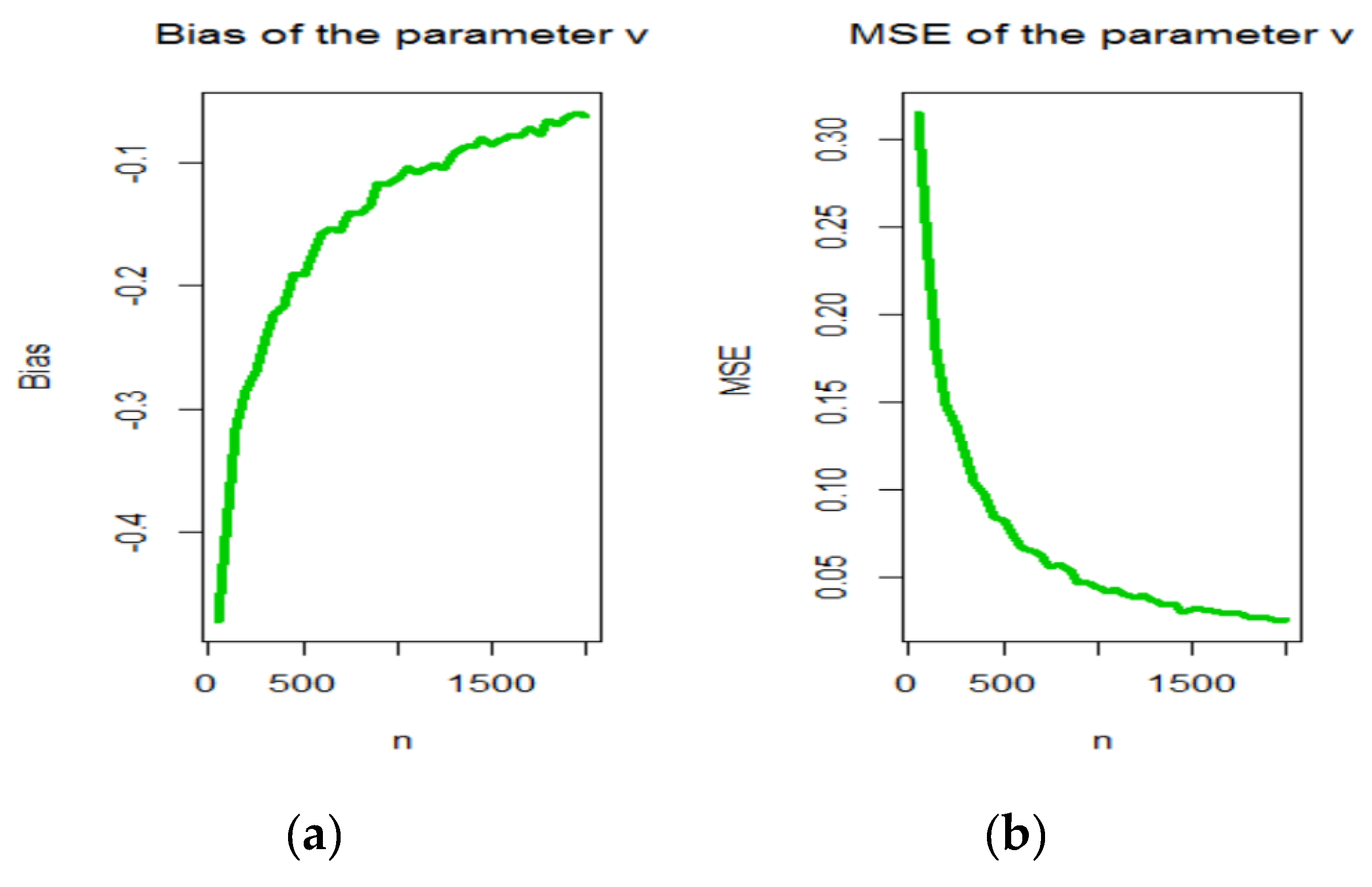
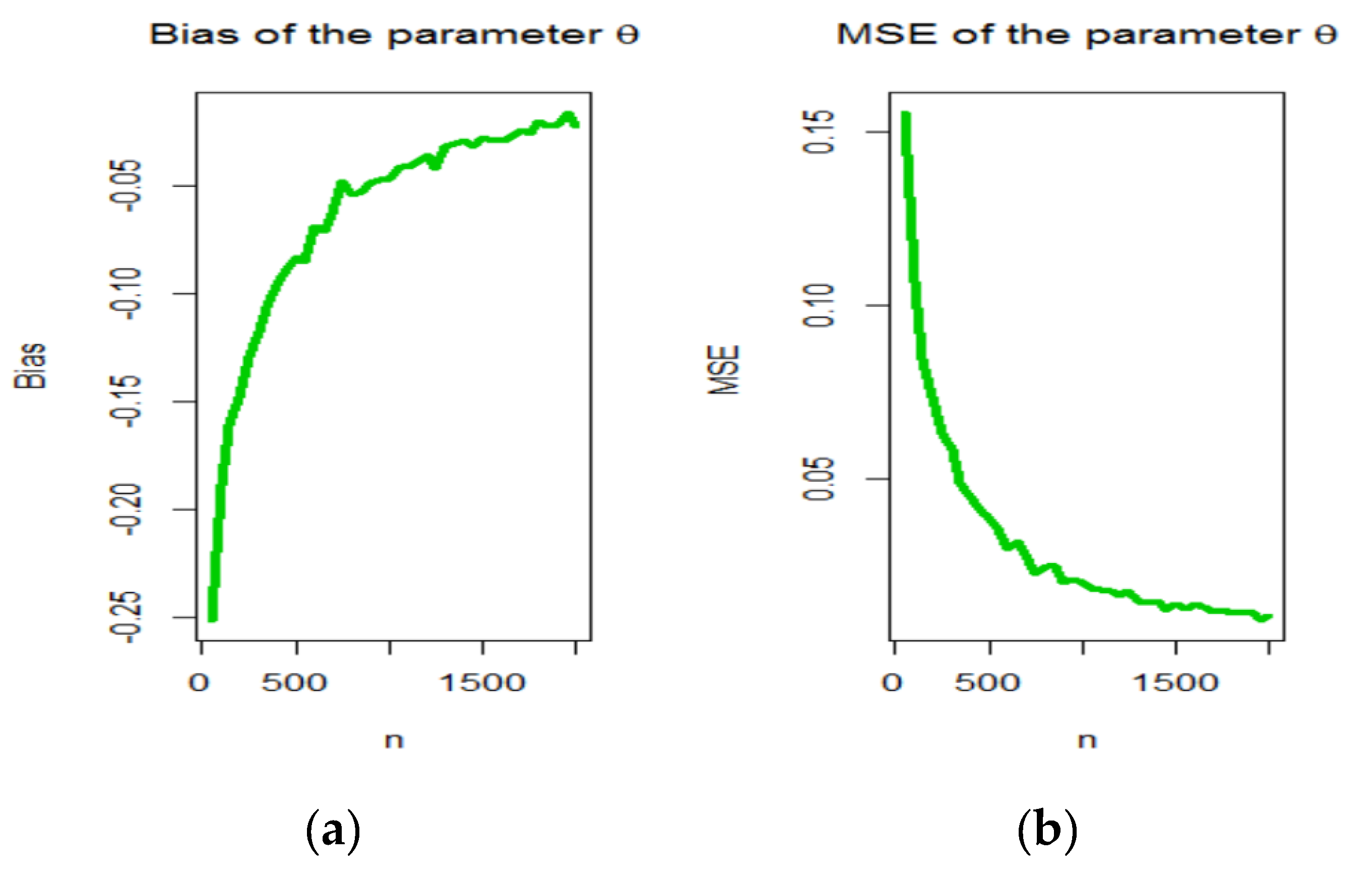
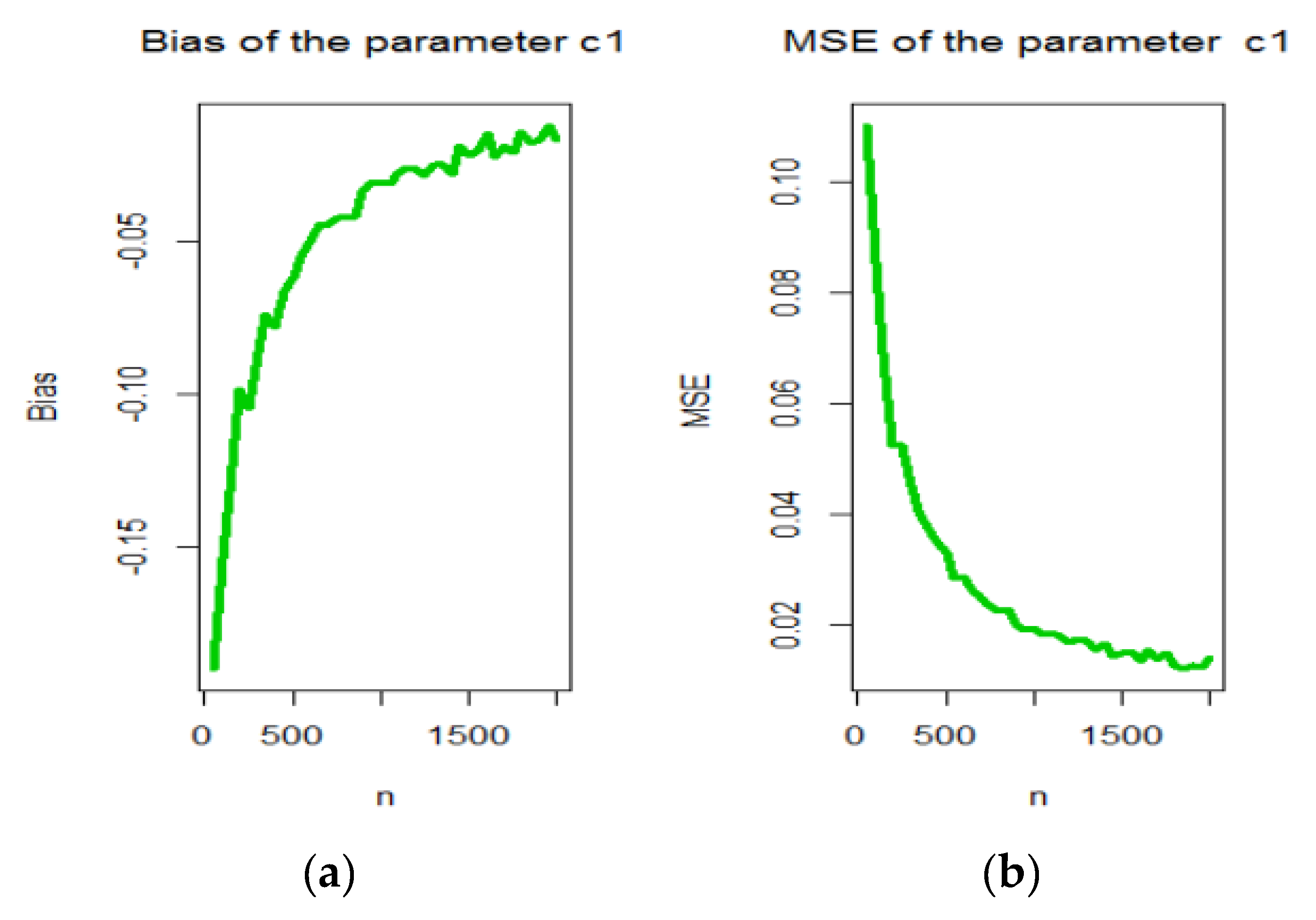
4. Graphical Assessment
- samples of size were generated from the OBBX distribution using (7);
- The MLEs for samples, say were computed.
- The SEs of the MLEs for the samples, say were computed by inverting the observed information matrix.
- The biases and mean squared errors given for . We repeated these steps for with , 2,…, 100 to compute the biases and mean squared errors () for and where and
5. Applications
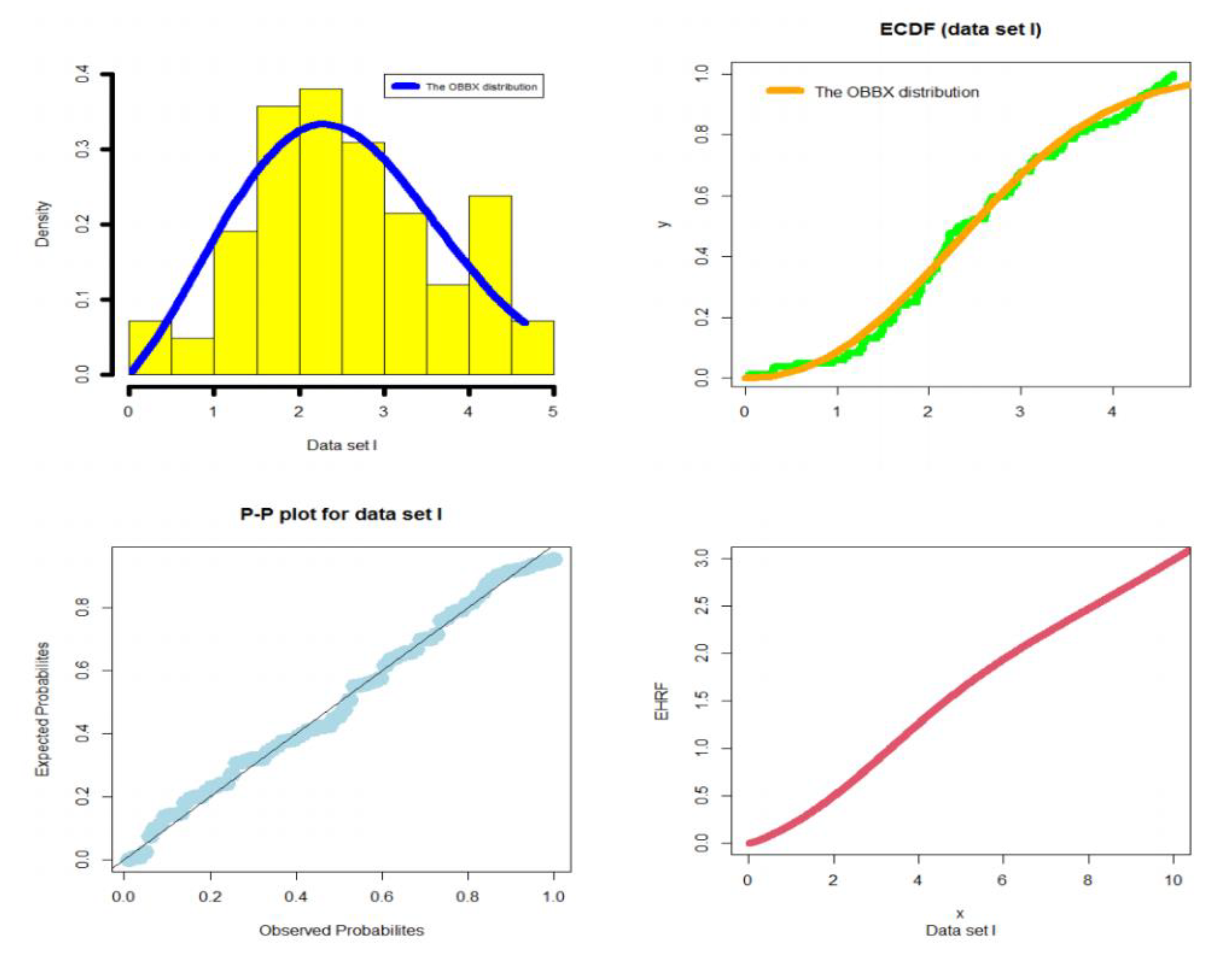
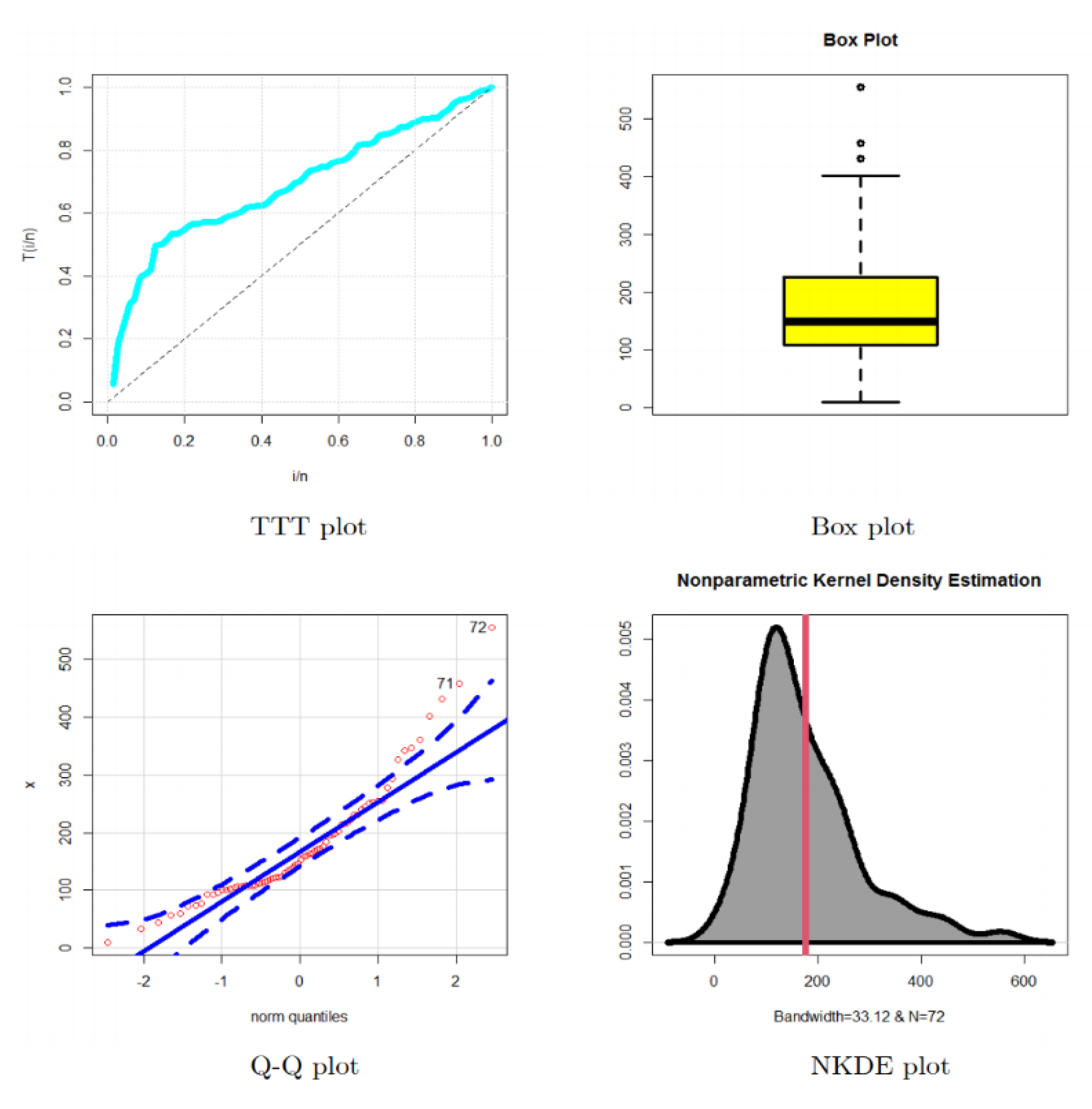
5.1. Modeling Failure Times
5.2. Modeling Cancer Data
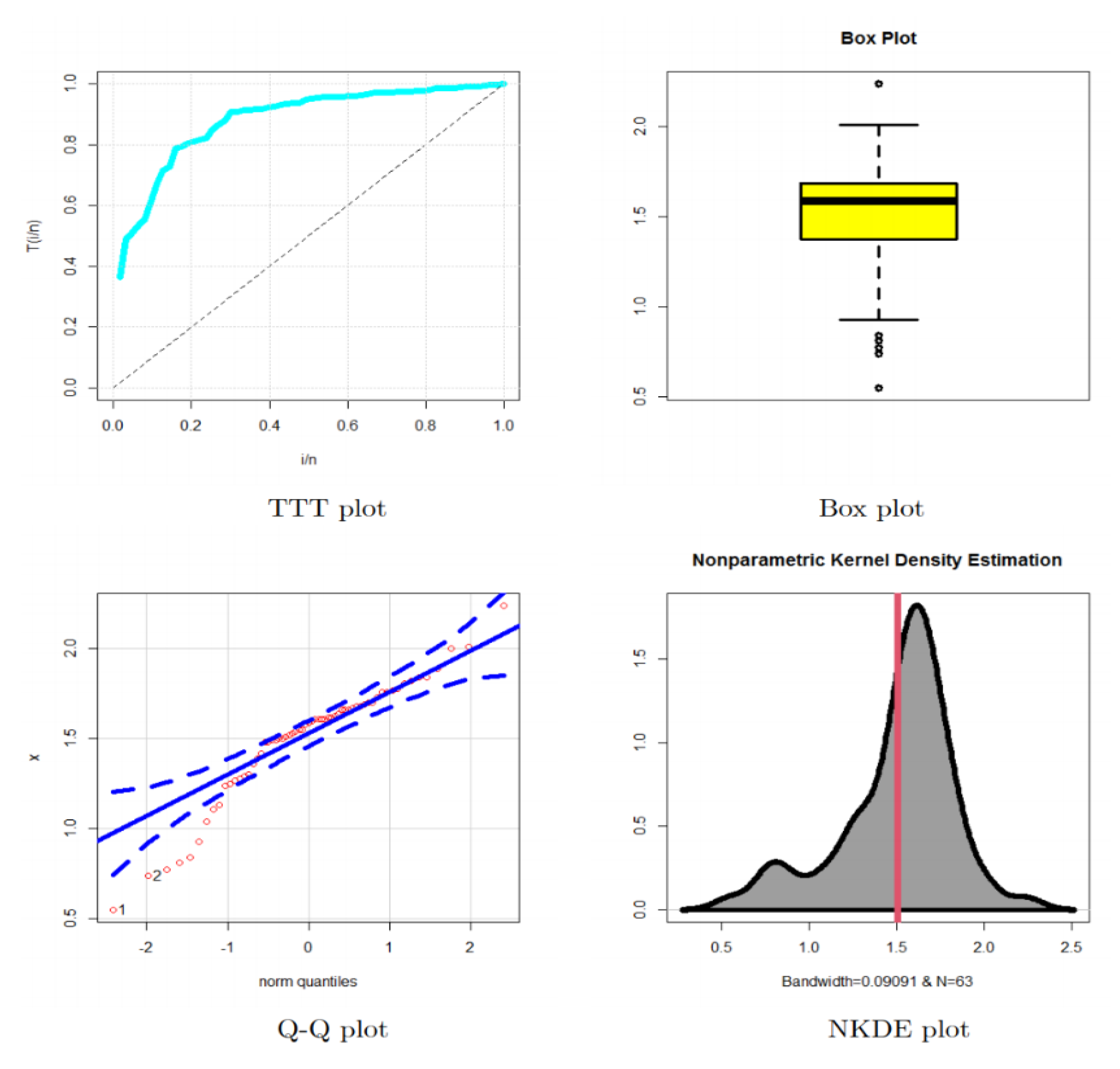
5.3. Modeling Survival Times
5.4. Glass Fibers Data
6. Concluding Remarks
- The new density can be “unimodal and right-skewed,” “symmetric and unimodal,” and “bimodal density” with many useful shapes.
- The HRF of the new model can be “monotonically increasing,” “bathtub (U-HRF),” “J-HRF,” “monotonically decreasing,” “increasing-constant-increasing,” “reversed J-HRF,” and “upside-down (reversed U-HRF).”
- In the reliability analysis, the OBBX model could be chosen as the best model, especially for modeling the asymmetric bimodal failure times data and the asymmetric bimodal right-skewed and heavy-tail survival times data.
- In medical fields, the OBBX model could be chosen as the best model, especially for modeling the bimodal right-skewed and heavy-tail cancer data.
- In engineering, the OBBX model could be chosen as the best model, especially for modeling the asymmetric bimodal left-skewed and heavy-tail glass fibers data.
- In modeling the failure times data, the OBBX model showed its superiority against the Burr type X, odd Lindley exponentiated Weibull, Burr X exponentiated Weibull, Poisson Topp Leone Weibull, Marshall Olkin extended Weibull, Gamma Weibull Kumaraswamy Weibull, beta Weibull, transmuted modified Weibull, modified beta Weibull, Mcdonald Weibull, and the transmuted exponentiated generalized Weibull distributions.
- In modeling the cancer data, the OBBX model showed its superiority against the Burr type X, Weibull, transmuted modified Weibull, modified beta Weibull, and transmuted additive Weibull distributions.
- In modeling the survival data, the OBBX model showed its superiority against the Burr type X, transmuted Burr type X, odd Lindley exponentiated Weibull, odd Weibull–Weibull, and gamma-exponentiated exponential distributions.
- In modeling the glass fibers data, the OBBX model showed its superiority against the Burr type X, transmuted Burr type X, odd Lindley Burr type X, odd Lindley exponentiated Weibull, exponentiated Weibull, transmuted Weibull, and odd log–logistic Weibull distributions.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Probability density function | |
| CDF | Cumulative distribution function |
| RF | Reliability function |
| MGF | Moment generating function |
| HRF | Hazard rate function |
| MLE | Maximum likelihood estimation |
| MSE | Mean square error |
| P-P | Probability–probability |
| TTT | Total time in test |
| RV | Random variable |
| BX | Burr type X |
| BXII | Burr type XII |
| O-G | Odd G family |
| OBG | Odd Burr-G family |
| OBBX | Odd Burr–Burr type X model |
| PRHR | Proportional reversed hazard rate family |
| O-BX | Odd Burr type X |
| PRHR-BX | Proportional reversed hazard rate Burr type X model |
| QF | Quantile function |
| DisIx | Dispersion index |
| V(W) | Variance |
| S(W) | Skewness |
| K(W) | Kurtosis |
| EPDF | Estimated probability density function |
| ECDF | Estimated cumulative distribution function |
| EHRF | Estimated hazard rate function |
| Q-Q | Quantile–quantile plot |
| NKDE | Nonparametric kernel density estimation plot |
Appendix A
- (c1)))^v))^theta))
- 2.
- #=======================================
- 3.
- (c1)))^v))^theta))
References
- Burr, I.W. Cumulative Frequency Functions. Ann. Math. Stat. 1942, 13, 215–232. [Google Scholar] [CrossRef]
- Ahmad, E.K.; Fakhry, M.E.; Jaheen, Z.F. Empirical Bayes estimation of P (Y < X) and characterizations of Burr-type X model. J. Stat. Plan. Inference 1997, 64, 297–308. [Google Scholar]
- Ali, M.M.; Yousof, H.M.; Ibrahim, M. A new version of the generalized Rayleigh distribution with copula, properties, applications and different methods of estimation. Optim. Decis. Mak. Oper. Res. Stat. Methodol. Appl. 2020, 1, 1–25. [Google Scholar]
- Ali, M.M.; Ibrahim, M.; Yousof, H.M. Expanding the Burr X model: Properties, copula, real data modeling and different methods of estimation. Optim. Decis. Mak. Oper. Res. Stat. Methodol. Appl. 2020, 1, 26–49. [Google Scholar]
- Nasir, M.A.; Korkmaz, M.C.; Jamal, F.; Yousof, H.M. On a new Weibull Burr XII distribution for lifetime data. Sohag J. Math. 2018, 5, 47–56. [Google Scholar] [CrossRef]
- Raqab, M.Z. Order statistics from the Burr type X model. Comput. Math. Appl. 1998, 36, 111–120. [Google Scholar] [CrossRef]
- Surles, J.; Padgett, W. Inference for P (Y < X) in the Burr type X model. J. Appl. Stat. Sci. 1998, 7, 225–238. [Google Scholar]
- Surles, J.G.; Padgett, W.J. Inference for Reliability and Stress-Strength for a Scaled Burr Type X Distribution. Lifetime Data Anal. 2001, 7, 187–200. [Google Scholar] [CrossRef]
- Sartawi, H.A.; Abu-Salih, M.S. Bayes prediction bounds for the Burr type X model. Commun. Stat. Theory Methods 1991, 20, 2307–2330. [Google Scholar] [CrossRef]
- Jaheen., Z.F. Bayesian approach to prediction with outliers from the Burr type X model. Microelectron. Reliab. 1995, 35, 45–47. [Google Scholar] [CrossRef]
- Jaheen., Z.F. Empirical Bayes estimation of the reliability and failure rate functions of the Burr type X failure model. J. Appl. Stat. Sci. 1996, 3, 281–288. [Google Scholar]
- Raqab, M.Z.; Kundu, D. Burr type X distribution: Revisited. J. Probab. Stat. Sci. 2006, 4, 179–193. [Google Scholar]
- Merovci, F.; Khaleel, M.A.; Ibrahim, N.A.; Shitan, M. The beta Burr type X distribution properties with application. SpringerPlus 2016, 5, 697. [Google Scholar] [CrossRef]
- Shayib, M.A.; Haghighi, A.M. An estimation of reliability: Case of one parameter Burr Type X distribution. Int. J. Stat. Econ. 2011, 6, 1–19. [Google Scholar]
- Yousof, H.M.; Afify, A.Z.; Hamedani, G.G.; Aryal, G. The Burr X Generator of Distributions for Lifetime Data. J. Stat. Theory Appl. 2017, 16, 288. [Google Scholar] [CrossRef]
- Abouelmagd, T.H.M.; Hamed, M.S.; Handique, L.; Goual, H.; Ali, M.M.; Yousof, H.M.; Korkma, M.C. A new class of distributions based on the zero truncated Poisson distribution with properties and applications. J. Non Linear Sci. Appl. 2019, 12, 152–164. [Google Scholar] [CrossRef]
- Mansour, M.; Rasekhi, M.; Ibrahim, M.; Aidi, K.; Yousof, H.M.; Elrazik, E.A. A New Parametric Life Distribution with Modified Bagdonavičius–Nikulin Goodness-of-Fit Test for Censored Validation, Properties, Applications, and Different Estimation Methods. Entropy 2020, 22, 592. [Google Scholar] [CrossRef]
- Mansour, M.M.; Butt, N.S.; Ansari, S.I.; Yousof, H.M.; Ali, M.M.; Ibrahim, M. A new exponentiated Weibull distribution’s extension: Copula, mathematical properties and applications. Contrib. Math. 2020, 57–66. [Google Scholar] [CrossRef]
- Mansour, M.; Korkmaz, M.Ç.; Ali, M.M.; Yousof, H.M.; Ansari, S.I.; Ibrahim, M. A generalization of the exponentiated Weibull model with properties, Copula and application. Eurasian Bull. Math. 2020, 3, 84–102. [Google Scholar]
- Alizadeh, M.; Cordeiro, G.M.; Nascimento, A.D.; Lima, M.D.C.S.; Ortega, E.M. Odd-Burr generalized family of distributions with some applications. J. Stat. Comput. Simul. 2017, 87, 367–389. [Google Scholar] [CrossRef]
- Yousof, H.M.; Jahanshahi, S.M.A.; Sharma, V.K. The Burr X Fréchet model for extreme values: Mathematical properties, classical Inference and Bayesian analysis. Pak. J. Stat. Oper. Res. 2019, 15, 797. [Google Scholar] [CrossRef]
- Khalil, M.G.; Hamedani, G.G.; Yousof, H.M. The Burr X exponentiated Weibull model: Characterizations, mathematical properties and applications to failure and survival times data. Pak. J. Stat. Oper. Res. 2019, 15, 141–160. [Google Scholar] [CrossRef]
- Elsayed, H.A.H.; Yousof, H.M. The Burr X Nadarajah Haghighi distribution: Statistical properties and application to the exceedances of flood peaks data. J. Math. Stat. 2019, 15, 146–157. [Google Scholar] [CrossRef]
- Gomes-Silva, F.S.; Percontini, A.; De Brito, E.; Ramos, M.W.; Venâncio, R.; Cordeiro, G.M. The odd Lindley-G family of distributions. Austrian J. Stat. 2017, 46, 65–87. [Google Scholar] [CrossRef]
- Merovci, F.; Yousof, H.; Hamedani, G.G. The Poisson Topp Leone Generator of Distributions for Lifetime Data: Theory, Characterizations and Applications. Pak. J. Stat. Oper. Res. 2020, 16, 343–355. [Google Scholar] [CrossRef]
- Ghitany, M.; Al-Hussaini, E.; Al-Jarallah, R. Marshall–Olkin extended Weibull distribution and its application to censored data. J. Appl. Stat. 2005, 32, 1025–1034. [Google Scholar] [CrossRef]
- Provost, S.B.; Saboor, A.; Ahmad, M. the gamma-weibull distribution. Pak. J. Statist. 2011, 27, 111–131. [Google Scholar]
- Cordeiro, G.M.; Ortega, E.M.M.; Nadarajah, S. The Kumaraswamy Weibull distribution with application to failure data. J. Frankl. Inst. 2010, 347, 1399–1429. [Google Scholar] [CrossRef]
- Lee, C.; Famoye, F.; Olumolade, O. Beta-Weibull Distribution: Some Properties and Applications to Censored Data. J. Mod. Appl. Stat. Methods 2007, 6, 173–186. [Google Scholar] [CrossRef]
- Khan, M.S.; King, R. Transmuted modified Weibull distribution: A generalization of the modified Weibull probability distribution. Eur. J. Pure Appl. Math. 2013, 6, 66–88. [Google Scholar]
- Khan, M.N. The modified beta Weibull distribution. Hacet. J. Math. Stat. 2015, 44, 1553–1568. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; Hashimoto, E.M.; Ortega, E.M.M. The McDonald Weibull model. Statistics 2014, 48, 256–278. [Google Scholar]
- Yousof, H.M.; Afify, A.Z.; Alizadeh, M.; Butt, N.S.; Hamedani, G. The Transmuted Exponentiated Generalized-G Family of Distributions. Pak. J. Stat. Oper. Res. 2015, 11, 441. [Google Scholar] [CrossRef]
- Elbatal, I.; Aryal, G. On the transmuted additiveWeibull distribution. Austrian J. Stat. 2013, 42, 117–132. [Google Scholar] [CrossRef]
- Yousof, H.M.; Afify, A.Z.; Cordeiro, G.M.; Alzaatreh, A.; Ahsanullah, M. A New Four-Parameter Weibull Model for Lifetime Data. J. Stat. Theory Appl. 2017, 16, 448. [Google Scholar]
- Cordeiro, G.M.; Yousof, H.M.; Ramires, T.G.; Ortega, E.M. The Burr XII System of densities: Properties, regression model and applications. J. Stat. Comput. Simul. 2018, 88, 432–456. [Google Scholar] [CrossRef]
- Yousof, H.M.; Alizadeh, M.; Jahanshahiand, S.M.A.; Ramires, T.G.; Ghosh, I.; Hamedani, G.G. The transmuted Topp-Leone G family of distributions: Theory, characterizations and applications. J. Data Sci. 2017, 15, 723–740. [Google Scholar]
- Yousof, H.M.; Rasekhi, M.; Afify, A.Z.; Ghosh, I.; Alizadeh, M.; Hamedani, G.G. The Beta Weibull-G family of distributions: Theory, characterizations and applications. Pak. J. Stat. 2017, 33, 95–116. [Google Scholar]
- Brito, E.; Cordeiro, G.M.; Yousof, H.M.; Alizadeh, M.; Silva, G.O. The Topp–Leone odd log-logistic family of distributions. J. Stat. Comput. 2017, 87, 3040–3058. [Google Scholar] [CrossRef]
- Aryal, G.R.; Yousof, H.M. The Exponentiated Generalized-G Poisson Family of Distributions. Stoch. Qual. Control 2017, 32, 7–23. [Google Scholar] [CrossRef]
- Korkmaz, M.C.; Yousof, H.M.; Hamedani, G.G. The Exponential Lindley Odd Log-Logistic-G Family: Properties, Characterizations and Applications. J. Stat. Theory Appl. 2018, 17, 554. [Google Scholar] [CrossRef]
- Yadav, A.S.; Goual, H.; Alotaibi, R.M.; Ali, M.M.; Yousof, H.M. Validation of the Topp-Leone-Lomax model via a modified Nikulin-Rao-Robson goodness-of-fit test with different methods of estimation. Symmetry 2020, 12, 57. [Google Scholar] [CrossRef]
- Al-babtain, A.A.; Elbatal, I.; Yousof, H.M. A New Flexible Three-Parameter Model: Properties, Clayton Copula, and Modeling Real Data. Symmetry 2020, 12, 440. [Google Scholar] [CrossRef]
- Lee, E.T.; Wang, J. Statistical Methods for Survival Data Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2003; Volume 476. [Google Scholar]
- Weibull, W. Wide applicability. J. Appl. Mech. 1951, 103, 293–297. [Google Scholar]
- Bjerkedal, T. Acquisition of resistance in guinea pigs infected with different doses of virulent tubercle bacilli1. Am. J. Epidemiol. 1960, 72, 130–148. [Google Scholar] [CrossRef] [PubMed]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar]
- Ristić, M.M.; Balakrishnan, N. The gamma-exponentiated exponential distribution. J. Stat. Comput. Simul. 2012, 82, 1191–1206. [Google Scholar]
- Smith, R.L.; Naylor, J. A comparison of maximum likelihood and Bayesian estimators for the three-parameter Weibull distribution. J. R. Stat. Soc. Ser. C 1987, 36, 358–369. [Google Scholar] [CrossRef]
- Hamedani, G.G.; Yousof, H.M.; Rasekhi, M.; Alizadeh, M.; Najibi, S.M. Type I general exponential class of distributions. Pak. J. Stat. Oper. Res. 2017, XIV, 39–55. [Google Scholar] [CrossRef][Green Version]
- Hamedani, G.G.; Altun, E.; Korkmaz, M.C.; Yousof, H.M.; Butt, N.S. A new extended G family of continuous distributions with mathematical properties, characterizations and regression modeling. Pak. J. Stat. Oper. Res. 2018, 14, 737–758. [Google Scholar] [CrossRef]
- Hamedani, G.G.; Rasekhi, M.; Najibi, S.M.; Yousof, H.M.; Alizadeh, M. Type II general exponential class of distributions. Pak. J. Stat. Oper. Res. 2019, XV, 503–523. [Google Scholar] [CrossRef]
- Jäntschi, L.; Bolboacă, S.D. Computation of probability associated with Anderson–Darling statistic. Mathematics 2018, 6, 88. [Google Scholar] [CrossRef]




| 1 | 2 | 1.5 | 0.5 | 1.3958 | 1.0652 | 1.0068 | 3.6312 | 0.7631 |
| 1 | 1.5769 | 0.4230 | 0.4614 | 3.1031 | 0.2682 | |||
| 5 | 1.8855 | 0.0271 | −0.3677 | 3.7912 | 0.0144 | |||
| 30 | 1.9753 | 0.0008 | −0.5491 | 4.2589 | 0.0004 | |||
| 50 | 1.9828 | 0.0003 | −0.5608 | 4.2901 | 0.0001 | |||
| 2 | 0.5 | 0.5 | 1.5 | 0.5220 | 0.0704 | 0.9528 | 4.2278 | 0.1348 |
| 1 | 0.3768 | 0.0305 | 0.7423 | 3.9547 | 0.0809 | |||
| 5 | 0.1930 | 0.0070 | 0.3053 | 2.8543 | 0.0365 | |||
| 50 | 0.0731 | 0.0012 | 0.3940 | 2.5613 | 0.0164 | |||
| 100 | 0.0535 | 0.0007 | 0.4433 | 2.8959 | 0.0126 | |||
| 200 | 0.0389 | 0.0004 | 0.4866 | 4.0305 | 0.0095 | |||
| 500 | 0.0252 | 0.0002 | 0.2288 | 1.8690 | 0.0064 | |||
| 1000 | 0.0181 | 8.4 × 10−5 | 1.8057 | 1.5059 | 0.0047 | |||
| 5 | 5 | 0.5 | 1.8 | 0.2391 | 0.0016 | −0.4656 | 3.4042 | 0.0069 |
| 1 | 0.4079 | 0.0018 | −0.6485 | 3.8647 | 0.0044 | |||
| 5 | 0.7632 | 0.0012 | −0.7280 | 4.1308 | 0.0015 | |||
| 50 | 1.1437 | 0.0006 | −0.8281 | 13.3165 | 0.0005 | |||
| 100 | 1.2381 | 0.0005 | −0.6902 | 4.0299 | 0.0004 | |||
| 500 | 1.4343 | 0.0004 | −0.6746 | 3.9872 | 0.0003 | |||
| 1000 | 1.5111 | 0.0004 | −0.6696 | 3.9739 | 0.0002 | |||
| 2000 | 1.5843 | 0.0003 | −0.6657 | 3.9787 | 0.0002 | |||
| 15 | 10 | 10 | 0.3 | 1.2 × 10−5 | 41.2151 | 1.0002 | 1.0005 | 3,376,320 |
| 0.5 | 3.2097 | 0.0013 | −0.9760 | 4.8669 | 0.0004 | |||
| 1 | 1.6049 | 0.0003 | −0.9812 | 5.3298 | 0.0002 | |||
| 2 | 0.8024 | 8.2 × 10−5 | −0.9760 | 4.8665 | 0.0001 | |||
| 3 | 0.5350 | 3.6 × 10−5 | −0.9760 | 4.8591 | 6.82 × 10−5 | |||
| 5 | 1.9 × 10−6 | 6.5 × 10−7 | 414.9644 | 172,196.5 | 0.3333 |
| Distribution | Estimates (SEs) | ||||
|---|---|---|---|---|---|
| BX(c1;c2) | 1.181876 | 0.377525 | |||
| (0.17060) | (0.02532) | ||||
| OLEW(θ;c1;c2) | 0.15935 | 0.7322 | 0.765 | ||
| (0.3712) | (1.778) | (0.041) | |||
| OLBX(θ;c1;c2) | 1.45406 | 0.7543 | 0.2379 | ||
| (0.9018) | (0.2530) | (0.0317) | |||
| BXEW(θ;c1;c2) | 0.63684 | 4.2622 | 0.5364 | ||
| (0.356) | (1.757) | (0.0997) | |||
| PTLW(θ;c1;c2) | −5.78175 | 4.22865 | 0.65801 | ||
| (1.395) | (1.167) | (0.039) | |||
| MOEW(θ;c1;c2) | 488.899 | 0.2832 | 1261.97 | ||
| (189.358) | (0.013) | (351.07) | |||
| GamW(θ;c1;c2) | 2.37697 | 0.84809 | 3.5344 | ||
| (0.378) | (0.00053) | (0.665) | |||
| OBBX(ν;θ;c1;c2) | 1.29102 | 3.1331 | 0.8448 | 0.1906 | |
| (0.544) | (2.3251) | (0.4961) | (0.084) | ||
| KumW(ν;θ;c1;c2) | 14.4331 | 0.2041 | 34.6599 | 81.8459 | |
| (27.095) | (0.042) | (17.527) | (52.014) | ||
| Beta-W(ν;θ;c1;c2) | 1.36 | 0.2981 | 34.1802 | 11.4956 | |
| (1.002) | (0.06) | (14.838) | (6.73) | ||
| TrMW(ν;θ;c1;c2) | 0.2722 | 1 | 4.6 × 10−6 | 0.4685 | |
| (0:014) | (5.2 × 10−5) | (1.9 × 10−4) | (0.165) | ||
| MBW(ν;θ;λ;c1;c2) | 10.1502 | 0.1632 | 57.4167 | 19.3859 | 2.0043 |
| (18.697) | (0.019) | (14.063) | (10.019) | (0.662) | |
| MacW(ν;θ;λ;c1;c2) | 1.9401 | 0.306 | 17.686 | 33.6388 | 16.7211 |
| (1.011) | (0.045) | (6.222) | (19.994) | (9.722) | |
| TrEGW(ν;θ;λ;c1;c2) | 4.2567 | 0.1532 | 0.0978 | 5.2313 | 1173.33 |
| (33.401) | (0.017) | (0.609) | (9.792) | (6.999) | |
| Distribution | CVM | AD | KS (p-Value) |
|---|---|---|---|
| OBBX | 0.0580 | 0.5777 | 0.05602 (0.9547) |
| OLEW | 0.0723 | 0.6086 | 0.87572 (<0.001) |
| OLBX | 0.0792 | 0.5910 | 0.37584 (<0.001) |
| BX | 0.0690 | 0.6916 | 0.07981 (0.6584) |
| BXEW | 0.0744 | 0.6420 | 0.06935 (0.8139) |
| PTLW | 0.1397 | 1.1939 | 0.11542 (0.8004) |
| MOEW | 0.3995 | 4.4477 | 0.06170 (0.9064) |
| GamW | 0.2553 | 1.9489 | 0.58482 (0.33119) |
| KumW | 0.1852 | 1.5059 | 0.23917 (0.43651) |
| Beta-W | 0.4652 | 3.2197 | 0.66032 (<0.001) |
| TrMW | 0.8065 | 11.2047 | 0.68989 (<0.001) |
| MBW | 0.4717 | 3.2656 | 0.33902 (<0.001) |
| MacW | 0.1986 | 1.5906 | 0.09243 (0.81193) |
| TrEGW | 1.0079 | 6.2332 | 0.22402 (<0.001) |
| Distribution | Estimates (SEs) | ||||
|---|---|---|---|---|---|
| BX(c1;c2) | 0.36413 | 0.04763 | |||
| (0.0373) | (0.0039) | ||||
| W(c1;c2) | 9.5593 | 1.0477 | |||
| (0.853) | (0.068) | ||||
| OBBX(ν;θ;c1;c2) | 5.6822 | 1.61069 | 0.0688 | 0.00067 | |
| (1.0574) | (0.7171) | (0.0066) | (<0.001) | ||
| TrMW(ν;θ;c1;c2) | 0.1208 | 0.8955 | 0.0002 | 0.2513 | |
| (0.024) | (0.626) | (0.011) | (0.407) | ||
| MBW(ν;θ;λ;c1;c2) | 0.1502 | 0.1632 | 57.4167 | 19.3859 | 2.0043 |
| (22.437) | (0.044) | (37.317) | (13.49) | (0.789) | |
| TrAW(ν;θ;λ;c1;c2) | 0.1139 | 0.9722 | 3.09 × 10−5 | 1.0065 | −0.163 |
| (0.032) | (0.125) | (6.12 × 10−3) | (0.035) | (0.28) |
| Distribution | CVM | AD | KS (p-Value) |
|---|---|---|---|
| OBBX | 0.0345 | 0.2038 | 0.04242 (0.9754) |
| W | 0.1055 | 0.6628 | 0.2665 (0.00662) |
| BX | 0.4747 | 2.7861 | 0.35516 (0.0042) |
| TrMW | 0.1251 | 0.7603 | 0.15875 (0.3969) |
| MBW | 0.1068 | 0.7207 | 0.25762 (0.3198) |
| TrAW | 0.1129 | 0.7033 | 0.16872 (0.3376) |
| Distribution | Estimates (SEs) | |||
|---|---|---|---|---|
| BX(c1;c2) | 0.93658 | 0.00478 | ||
| (0.1461) | (0.0004) | |||
| TrBX(θ;c1;c2) | 0.6328 | 1.03917 | 0.00417 | |
| (0.2453) | (0.1445) | (0.0005) | ||
| OLEW(ν;θ;c1;c2) | 0.0018 | 0.0716 | 0.2813 | |
| (0.0004) | (0.025) | (0.009) | ||
| OWW(θ;c1;c2) | 11.1576 | 0.0881 | 0.457 | |
| (4.5449) | (0.036) | (0.08) | ||
| GaEE(θ;c1;c2) | 2.1138 | 2.6006 | 0.0083 | |
| (1.3288) | (0.5597) | (0.005) | ||
| OBBX(ν;θ;c1;c2) | 3.24855 | 0.40541 | 0.2905 | 0.0029 |
| (0.8191) | (0.1563) | (0.039) | (0.0003) | |
| Distribution | CVM | AD | KS (p-Value) |
|---|---|---|---|
| OBBX | 0.0549 | 0.34601 | 0.06916 (0.8812) |
| BX | 0.1849 | 1.08578 | 0.096596 (0.5125) |
| TrBX | 0.1352 | 0.79259 | 0.085663 (0.6662) |
| OLEW | 0.2517 | 1.47502 | 0.999870 (<0.001) |
| OWW | 0.4494 | 2.47640 | 0.658701 (<0.001) |
| GaEE | 0.3150 | 1.72080 | 0.508710 (<0.001) |
| Distribution | Estimates (SEs) | |||
|---|---|---|---|---|
| BX(c1;c2) | 5.48597 | 0.9868 | ||
| (1.1853) | (0.0540) | |||
| TrBX(θ;c1;c2) | −0.65524 | 4.78605 | 1.04504 | |
| (0.19529) | (1.2831) | (0.0549) | ||
| OLBX(θ;c1;c2) | 0.65831 | 2.1019 | 0.8429 | |
| (0.5112) | (1.246) | (0.058) | ||
| OLEW(θ;c1;c2) | 0.50878 | 2.534 | 1.7122 | |
| (0.397) | (1.8298) | (0.0959) | ||
| EW(θ;c1;c2) | 0.67132 | 7.285 | 1.71811 | |
| (0.249) | (1.707) | (0.086) | ||
| TrW(θ;c1;c2) | −0.5010 | 5.1498 | 0.6458 | |
| (0.2741) | (0.6657) | (0.0235) | ||
| OLLW(θ;c1;c2) | 0.9439 | 6.0256 | 0.6159 | |
| (0.2689) | (1.3478) | (0.0164) | ||
| OBBX(ν;θ;c1;c2) | 5.8221 | 6.9739 | 0.3384 | 0.1739 |
| (6.1527) | (8.4085) | (0.449) | (0.2701) | |
| Distribution | CVM | AD | KS (p-Value) |
|---|---|---|---|
| OBBX | 0.2041 | 1.1216 | 0.14084 (0.1642) |
| OLBX | 0.2557 | 1.4154 | 0.62469 (<0.001) |
| TrBX | 0.4764 | 2.6163 | 0.19385 (0.01757) |
| OLEW | 0.2711 | 1.4965 | 0.66225 (<0.001) |
| BX | 0.5594 | 3.0722 | 0.21497 (0.00592 |
| EW | 0.6361 | 3.4842 | 0.15895 (<0.001) |
| TrW | 1.0358 | 0.1691 | 0.33359 (0.07651) |
| OLLW | 1.2364 | 0.2194 | 0.59001 (0.01543) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Butt, N.S.; Khalil, M.G. A New Bimodal Distribution for Modeling Asymmetric Bimodal Heavy-Tail Real Lifetime Data. Symmetry 2020, 12, 2058. https://doi.org/10.3390/sym12122058
Butt NS, Khalil MG. A New Bimodal Distribution for Modeling Asymmetric Bimodal Heavy-Tail Real Lifetime Data. Symmetry. 2020; 12(12):2058. https://doi.org/10.3390/sym12122058
Chicago/Turabian StyleButt, Nadeem S., and Mohamed G. Khalil. 2020. "A New Bimodal Distribution for Modeling Asymmetric Bimodal Heavy-Tail Real Lifetime Data" Symmetry 12, no. 12: 2058. https://doi.org/10.3390/sym12122058
APA StyleButt, N. S., & Khalil, M. G. (2020). A New Bimodal Distribution for Modeling Asymmetric Bimodal Heavy-Tail Real Lifetime Data. Symmetry, 12(12), 2058. https://doi.org/10.3390/sym12122058






