Critical Solutions of Scalarized Black Holes
Abstract
:1. Introduction
2. EMs Theory
3. Limit of Cold Black Holes
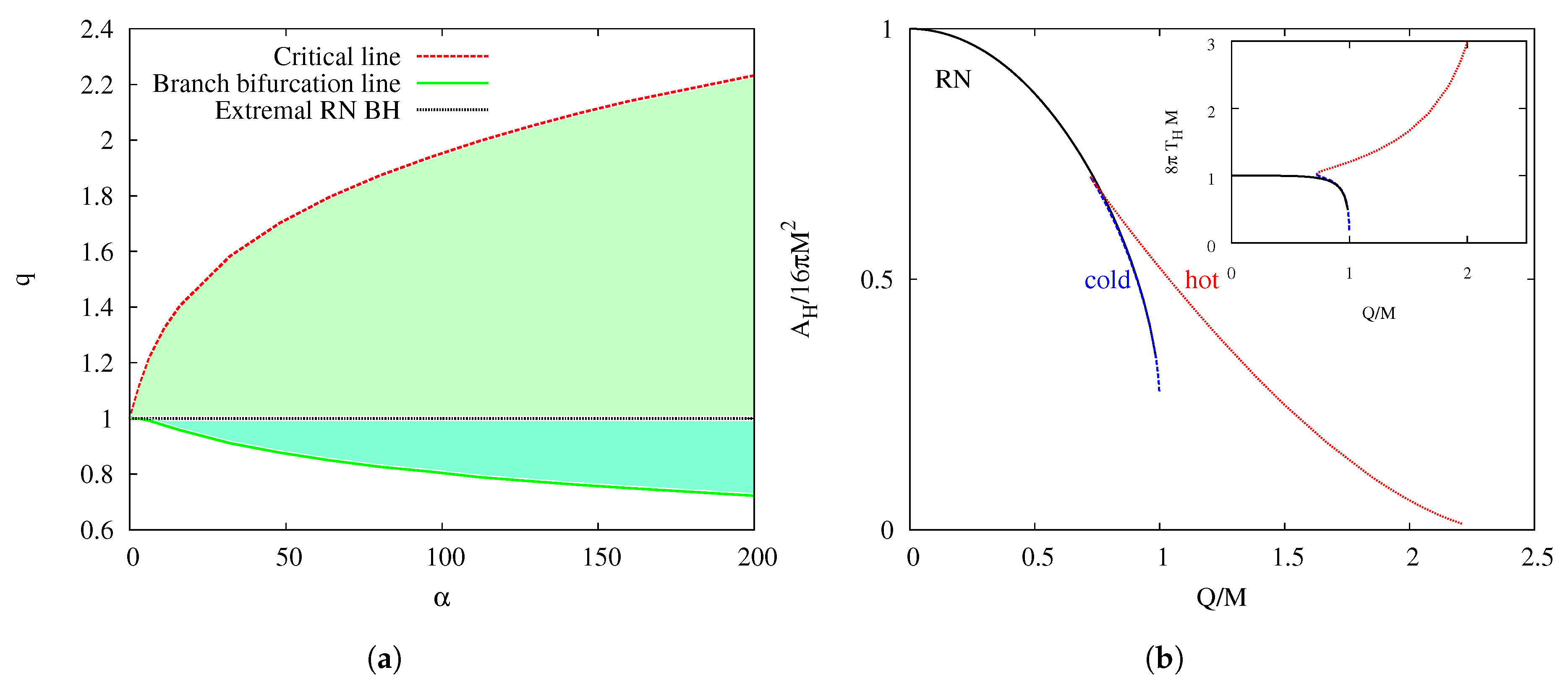
3.1. Branches of Black Holes
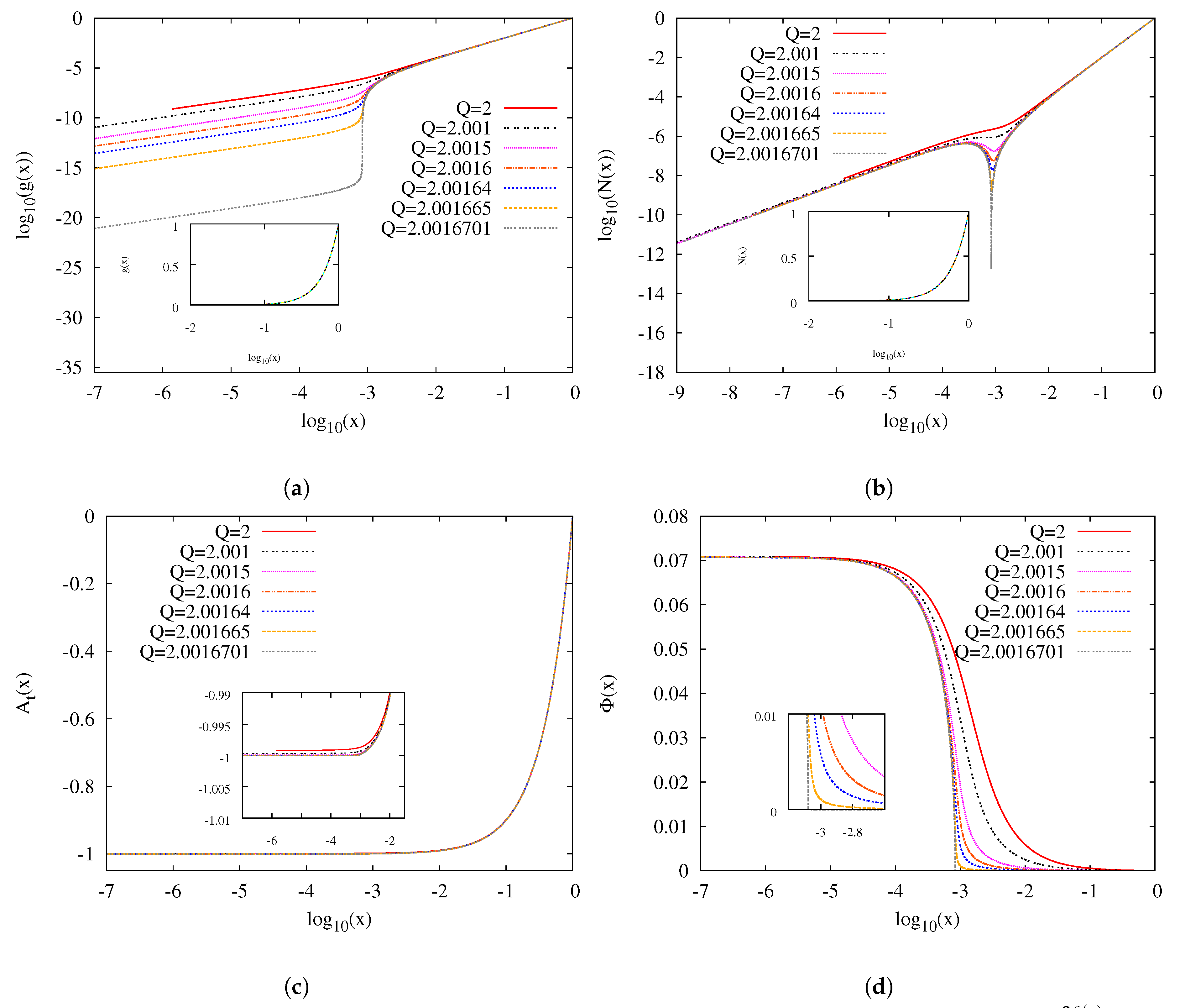
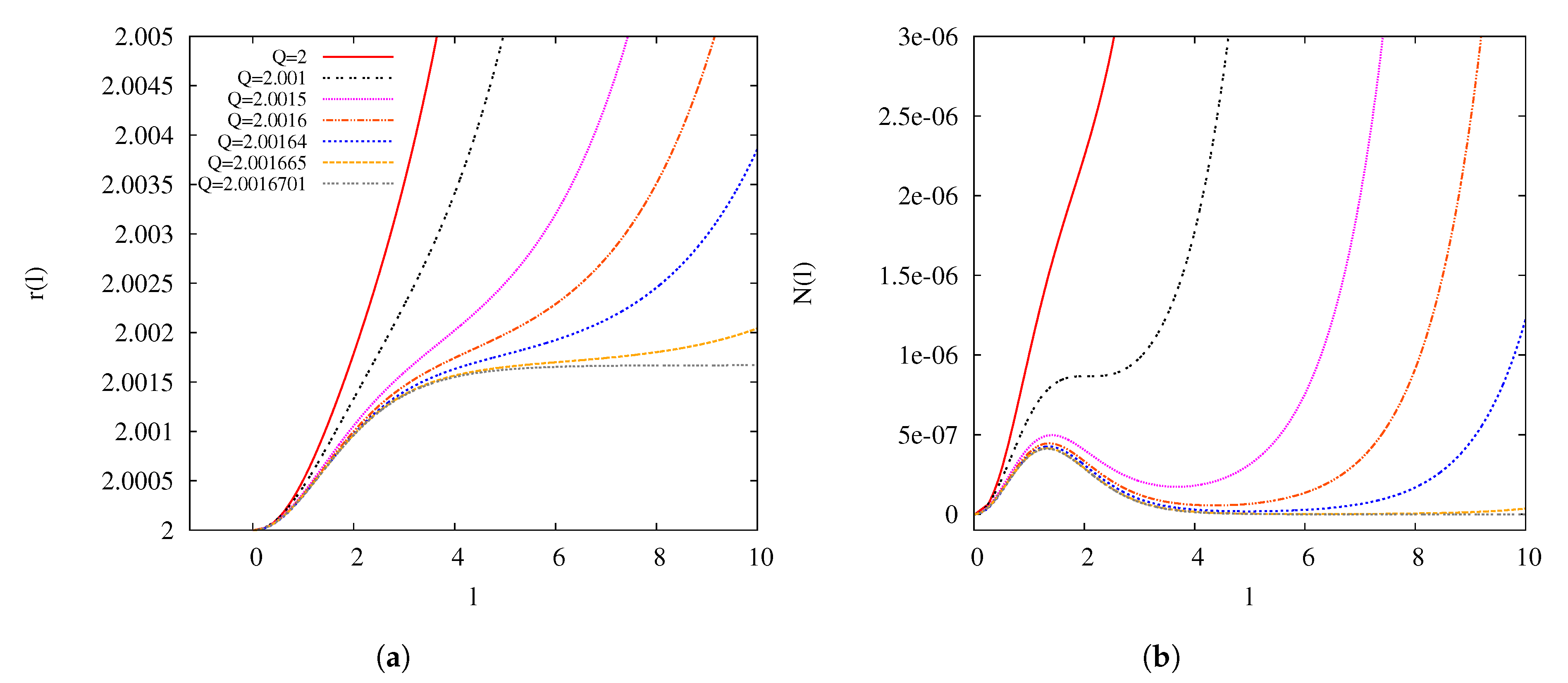
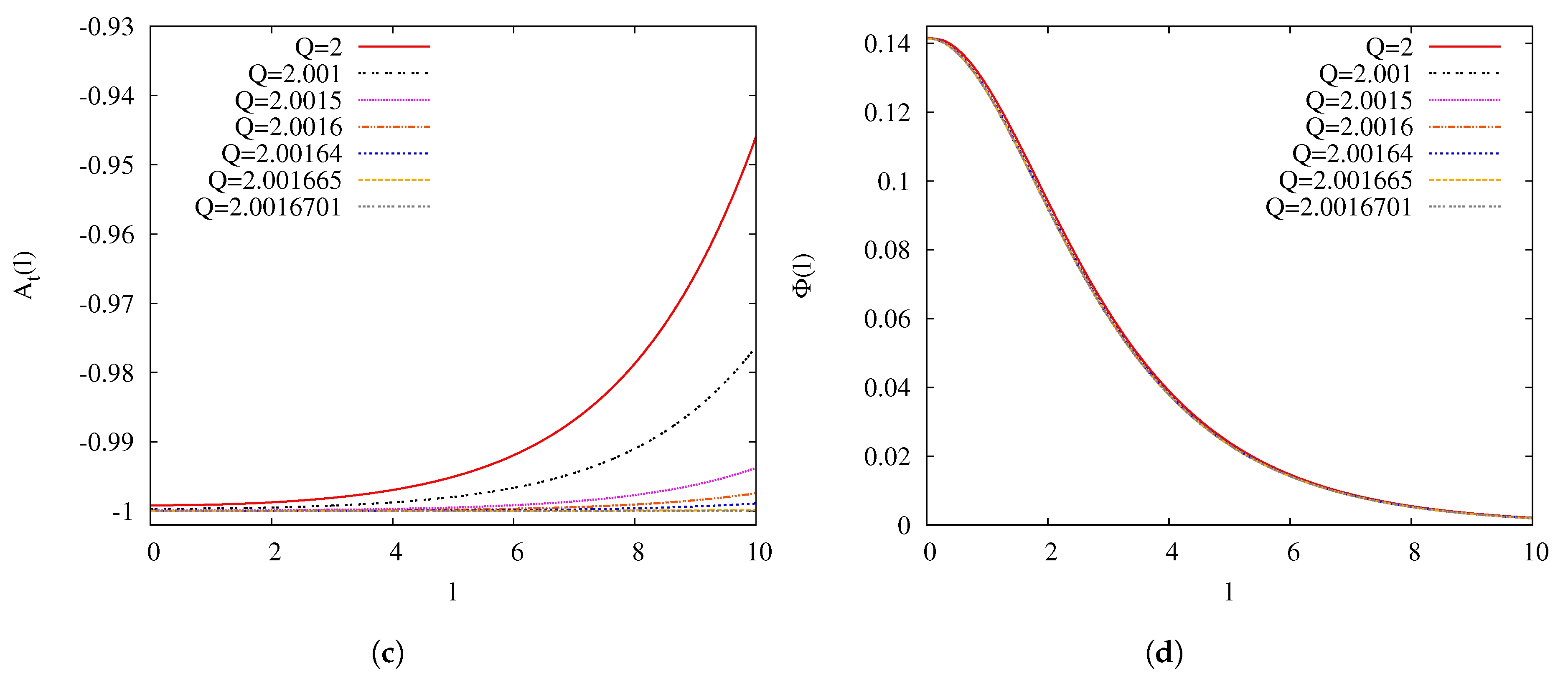
3.2. Approach to the Critical Solution for
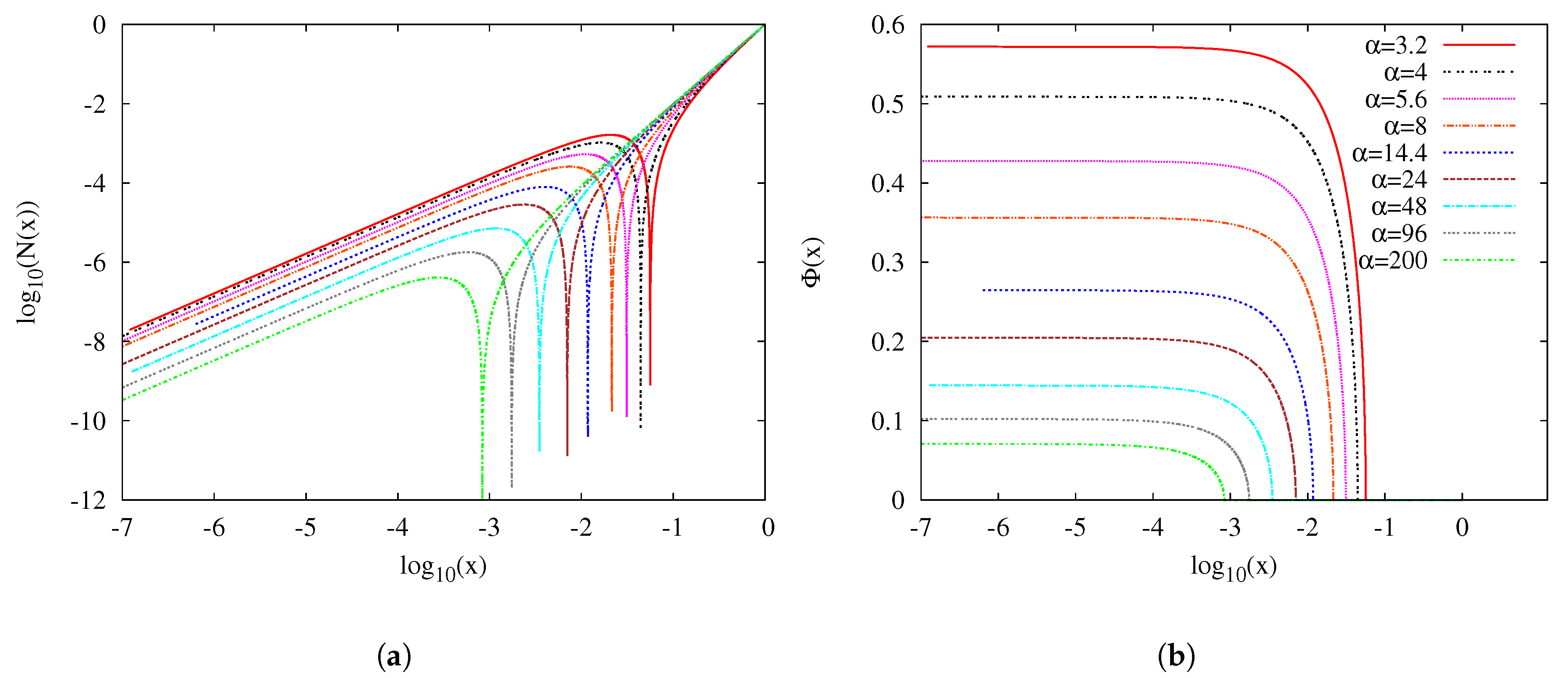
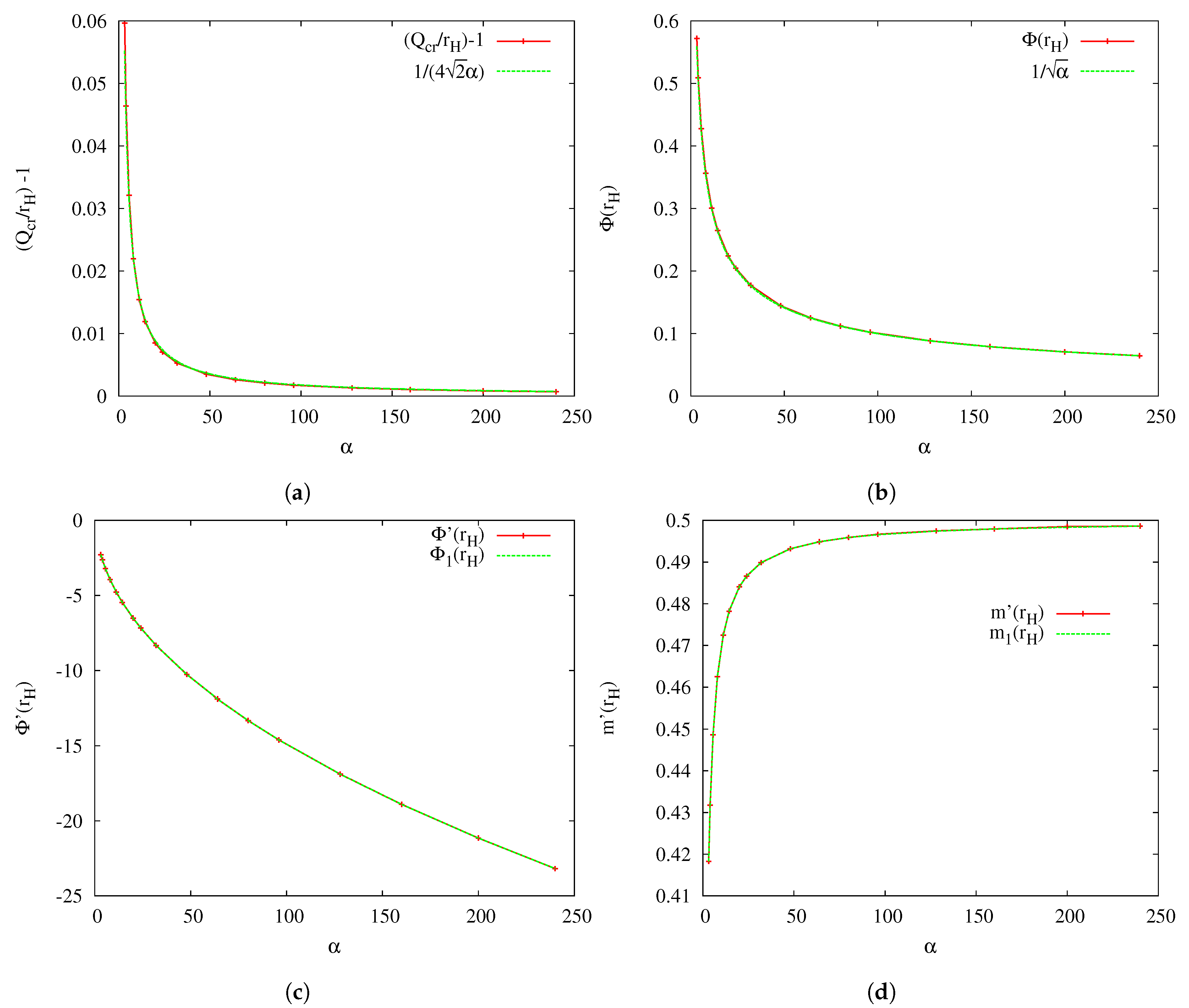
3.3. -Dependence of the Critical Solution
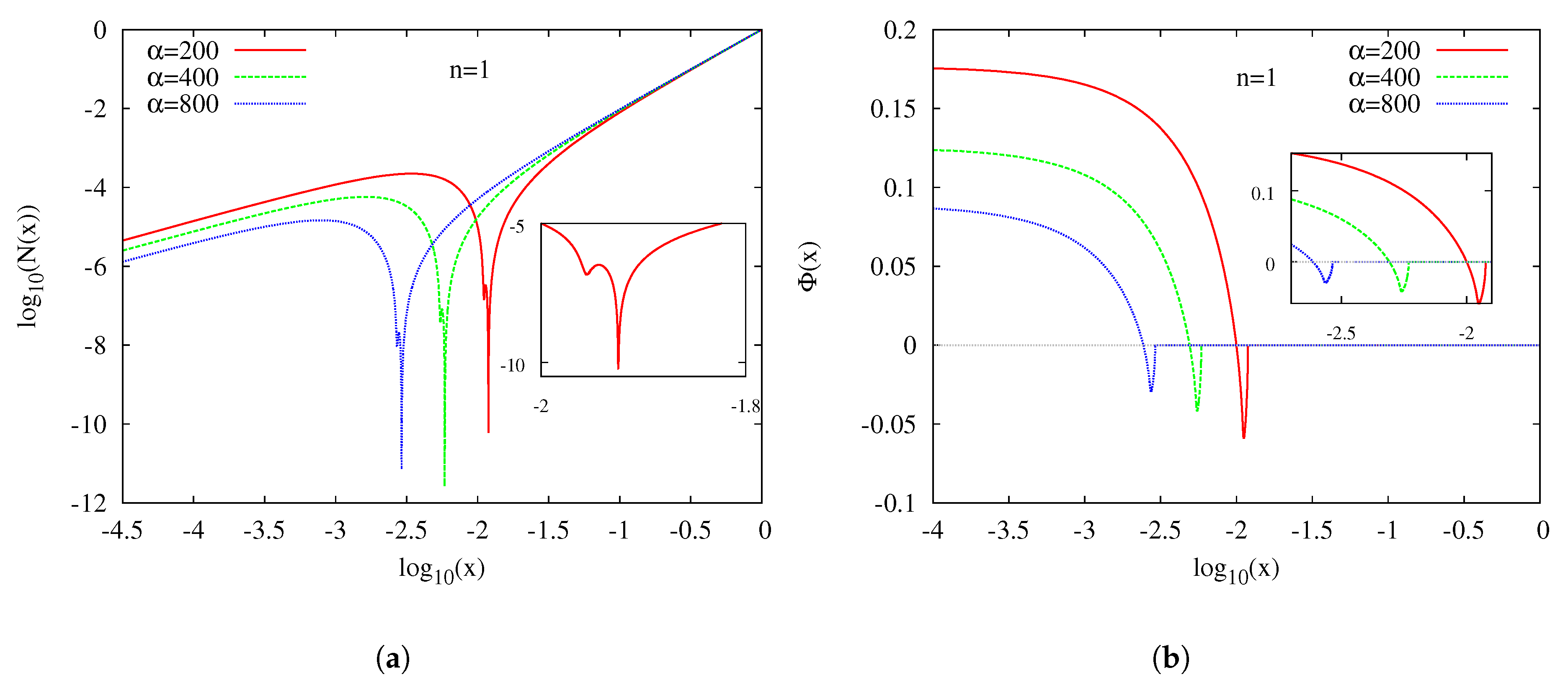
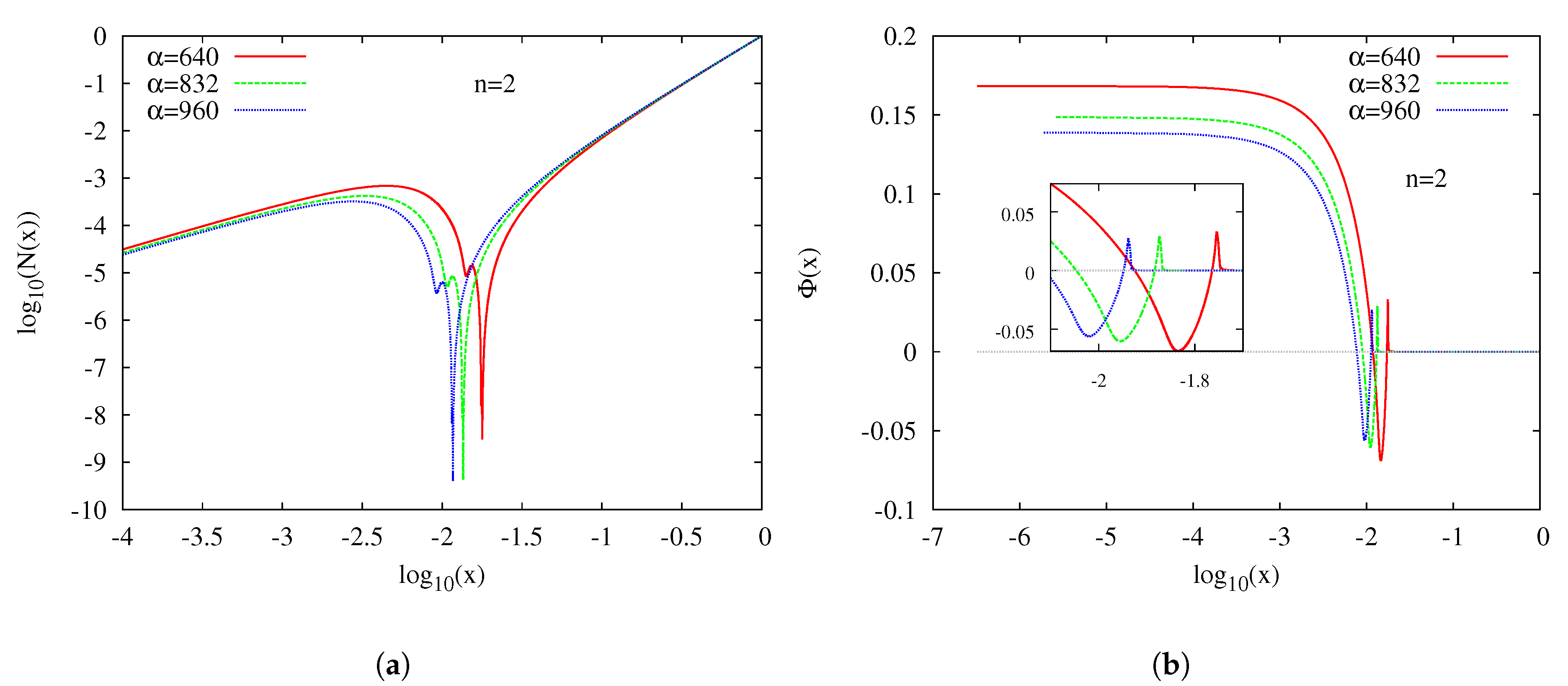
4. Excited Solutions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doneva, D.D.; Yazadjiev, S.S. New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar- Gauss-Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef] [Green Version]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss-Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef] [Green Version]
- Doneva, D.D.; Kiorpelidi, S.; Nedkova, P.G.; Papantonopoulos, E.; Yazadjiev, S.S. Charged Gauss-Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. D 2018, 98, 104056. [Google Scholar] [CrossRef] [Green Version]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef] [Green Version]
- Silva, H.O.; Macedo, C.F.; Sotiriou, T.P.; Gualtieri, L.; Sakstein, J.; Berti, E. Stability of scalarized black hole solutions in scalar-Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 064011. [Google Scholar] [CrossRef] [Green Version]
- Brihaye, Y.; Ducobu, L. Hairy black holes, boson stars and non-minimal coupling to curvature invariants. Phys. Lett. B 2019, 795, 135–143. [Google Scholar] [CrossRef]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S. Gauss-Bonnet black holes with a massive scalar field. Phys. Rev. D 2019, 99, 104045. [Google Scholar] [CrossRef] [Green Version]
- Myung, Y.S.; Zou, D.C. Black holes in Gauss–Bonnet and Chern–Simons-scalar theory. Int. J. Mod. Phys. D 2019, 28, 1950114. [Google Scholar] [CrossRef] [Green Version]
- Cunha, P.V.; Herdeiro, C.A.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor- Gauss-Bonnet Gravity. Phys. Rev. Lett. 2019, 123, 011101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Macedo, C.F.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef] [Green Version]
- Hod, S. Spontaneous scalarization of Gauss-Bonnet black holes: Analytic treatment in the linearized regime. Phys. Rev. D 2019, 100, 064039. [Google Scholar] [CrossRef] [Green Version]
- Collodel, L.G.; Kleihaus, B.; Kunz, J.; Berti, E. Spinning and excited black holes in Einstein-scalar- Gauss–Bonnet theory. Class. Quantum Gravity 2020, 37, 075018. [Google Scholar] [CrossRef] [Green Version]
- Bakopoulos, A.; Kanti, P.; Pappas, N. Large and ultracompact Gauss-Bonnet black holes with a self-interacting scalar field. Phys. Rev. D 2020, 101, 084059. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Axial perturbations of the scalarized Einstein-Gauss-Bonnet black holes. Phys. Rev. D 2020, 101, 104006. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Polar quasinormal modes of the scalarized Einstein-Gauss-Bonnet black holes. arXiv 2020, arXiv:2006.06006. [Google Scholar] [CrossRef]
- Dima, A.; Barausse, E.; Franchini, N.; Sotiriou, T.P. Spin-induced black hole spontaneous scalarization. arXiv 2020, arXiv:2006.03095. [Google Scholar]
- Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S. Black hole scalarization induced by the spin – 2+1 time evolution. Phys. Rev. D 2020, 102, 104027. [Google Scholar] [CrossRef]
- Berti, E.; Collodel, L.G.; Kleihaus, B.; Kunz, J. Spin-induced black-hole scalarization in Einstein-scalar-Gauss- Bonnet theory. arXiv 2020, arXiv:2009.03905. [Google Scholar]
- Herdeiro, C.A.; Radu, E.; Silva, H.O.; Sotiriou, T.P.; Yunes, N. Spin-induced scalarized black holes. arXiv 2020, arXiv:2009.03904. [Google Scholar]
- Herdeiro, C.A.; Radu, E.; Sanchis-Gual, N.; Font, J.A. Spontaneous Scalarization of Charged Black Holes. Phys. Rev. Lett. 2018, 121, 101102. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Myung, Y.S.; Zou, D.C. Instability of Reissner–Nordström black hole in Einstein–Maxwell–scalar theory. Eur. Phys. J. C 2019, 79, 273. [Google Scholar] [CrossRef]
- Boskovic, M.; Brito, R.; Cardoso, V.; Ikeda, T.; Witek, H. Axionic instabilities and new black hole solutions. Phys. Rev. D 2019, 99, 035006. [Google Scholar] [CrossRef] [Green Version]
- Myung, Y.S.; Zou, D.C. Quasinormal modes of scalarized black holes in the Einstein–Maxwell–Scalar theory. Phys. Lett. B 2019, 790, 400–407. [Google Scholar] [CrossRef]
- Fernandes, P.G.; Herdeiro, C.A.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Spontaneous Scalarisation of Charged Black Holes: Coupling Dependence and Dynamical Features. Class. Quantum Gravity 2020, 36, 134002, Erratum: Class. Quantum Gravity 2020, 37, 049501. [Google Scholar] [CrossRef] [Green Version]
- Brihaye, Y.; Hartmann, B. Spontaneous scalarization of charged black holes at the approach to extremality. Phys. Lett. B 2019, 792, 244–250. [Google Scholar] [CrossRef]
- Herdeiro, C.A.; Oliveira, J.M. On the inexistence of solitons in Einstein–Maxwell–scalar models. Class. Quantum Gravity 2019, 36, 105015. [Google Scholar] [CrossRef] [Green Version]
- Myung, Y.S.; Zou, D.C. Stability of scalarized charged black holes in the Einstein–Maxwell–scalar theory. Eur. Phys. J. C 2019, 79, 641. [Google Scholar] [CrossRef] [Green Version]
- Astefanesei, D.; Herdeiro, C.; Pombo, A.; Radu, E. Einstein–Maxwell–scalar black holes: Classes of solutions, dyons and extremality. JHEP 2019, 10, 078. [Google Scholar] [CrossRef] [Green Version]
- Konoplya, R.; Zhidenko, A. Analytical representation for metrics of scalarized Einstein-Maxwell black holes and their shadows. Phys. Rev. D 2019, 100, 044015. [Google Scholar] [CrossRef] [Green Version]
- Fernandes, P.G.; Herdeiro, C.A.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Charged black holes with axionic-type couplings: Classes of solutions and dynamical scalarization. Phys. Rev. D 2019, 100, 084045. [Google Scholar] [CrossRef] [Green Version]
- Herdeiro, C.A.; Oliveira, J.M. On the inexistence of self-gravitating solitons in generalised axion electrodynamics. Phys. Lett. B 2020, 800, 135076. [Google Scholar] [CrossRef]
- Zou, D.C.; Myung, Y.S. Scalarized charged black holes with scalar mass term. Phys. Rev. D 2019, 100, 124055. [Google Scholar] [CrossRef] [Green Version]
- Brihaye, Y.; Herdeiro, C.; Radu, E. Black Hole Spontaneous Scalarisation with a Positive Cosmological Constant. Phys. Lett. B 2020, 802, 135269. [Google Scholar] [CrossRef]
- Astefanesei, D.; Blázquez-Salcedo, J.L.; Herdeiro, C.; Radu, E.; Sanchis-Gual, N. Dynamically and thermodynamically stable black holes in Einstein-Maxwell-dilaton gravity. JHEP 2020, 7, 063. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.; Kunz, J.; Pombo, A.M.; Radu, E. Einstein–Maxwell–scalar black holes: The hot, the cold and the bald. Phys. Lett. B 2020, 806, 135493. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.; Kahlen, S.; Kunz, J.; Pombo, A.M.; Radu, E. Quasinormal modes of hot, cold and bald Einstein–Maxwell–scalar black holes. arXiv 2020, arXiv:2008.11744. [Google Scholar]
- Astefanesei, D.; Blázquez-Salcedo, J.L.; Gómez, F.; Rojas, R. Thermodynamically stable asymptotically flat hairy black holes with a dilaton potential: The general case. arXiv 2020, arXiv:2009.01854. [Google Scholar] [CrossRef] [Green Version]
- Gibbons, G.; Maeda, K.i. Black Holes and Membranes in Higher Dimensional Theories with Dilaton Fields. Nucl. Phys. B 1988, 298, 741–775. [Google Scholar] [CrossRef]
- Kanti, P.; Mavromatos, N.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 1996, 54, 5049–5058. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Volkov, M.S.; Gal’tsov, D.V. Gravitating nonAbelian solitons and black holes with Yang-Mills fields. Phys. Rep. 1999, 319, 1–83. [Google Scholar] [CrossRef] [Green Version]
- Gal’tsov, D. Gravitating lumps. In Proceedings of the 16th International Conference on General Relativity and Gravitation (GR16), Durban, South Africa, 15–21 July 2001; pp. 142–161. [Google Scholar] [CrossRef] [Green Version]
- Kleihaus, B.; Kunz, J.; Navarro-Lerida, F. Rotating black holes with non-Abelian hair. Class. Quantum Gravity 2016, 33, 234002. [Google Scholar] [CrossRef] [Green Version]
- Lee, K.M.; Nair, V.; Weinberg, E.J. Black holes in magnetic monopoles. Phys. Rev. D 1992, 45, 2751–2761. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions. Nucl. Phys. B 1992, 383, 357–376. [Google Scholar] [CrossRef] [Green Version]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions. 2. Nucl. Phys. B 1995, 442, 126–156. [Google Scholar] [CrossRef] [Green Version]
- Ridgway, S.; Weinberg, E.J. Instabilities of magnetically charged black holes. Phys. Rev. D 1995, 51, 638–646. [Google Scholar] [CrossRef] [Green Version]
- Brihaye, Y.; Hartmann, B.; Kunz, J. Gravitating dyons and dyonic black holes. Phys. Lett. B 1998, 441, 77–82. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, B.; Kleihaus, B.; Kunz, J. Gravitationally bound monopoles. Phys. Rev. Lett. 2001, 86, 1422–1425. [Google Scholar] [CrossRef] [Green Version]
- Hartmann, B.; Kleihaus, B.; Kunz, J. Axially symmetric monopoles and black holes in Einstein-Yang- Mills-Higgs theory. Phys. Rev. D 2002, 65, 024027. [Google Scholar] [CrossRef] [Green Version]
- Ascher, U.; Christiansen, J.; Russell, R. A Collocation Solver for Mixed Order Systems of Boundary Value Problems. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B. Strong gravity effects of charged Q-clouds and inflating black holes. arXiv 2020, arXiv:2009.08293. [Google Scholar]
- Brihaye, Y.; Cônsole, F.; Hartmann, B. Inflation inside non-topological defects and scalar black holes. arXiv 2020, arXiv:2010.15625. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Salcedo, J.L.; Kahlen, S.; Kunz, J. Critical Solutions of Scalarized Black Holes. Symmetry 2020, 12, 2057. https://doi.org/10.3390/sym12122057
Blázquez-Salcedo JL, Kahlen S, Kunz J. Critical Solutions of Scalarized Black Holes. Symmetry. 2020; 12(12):2057. https://doi.org/10.3390/sym12122057
Chicago/Turabian StyleBlázquez-Salcedo, Jose Luis, Sarah Kahlen, and Jutta Kunz. 2020. "Critical Solutions of Scalarized Black Holes" Symmetry 12, no. 12: 2057. https://doi.org/10.3390/sym12122057
APA StyleBlázquez-Salcedo, J. L., Kahlen, S., & Kunz, J. (2020). Critical Solutions of Scalarized Black Holes. Symmetry, 12(12), 2057. https://doi.org/10.3390/sym12122057




