Permutation Symmetry in Coherent Electrons Scattering by Disordered Media

Abstract

A non-Anderson weak localization of an electron beam scattered from disordered matter is considered with respect to the principle of electron indistinguishability. A weak localization of electrons of a new type is essentially associated with inelastic processing. The origin of inelasticity is not essential. We take into account the identity principle for electron beam and electrons of the atom of the scatterer with an open shell. In spite of isotropic scattering by each individual scatterer, the electron exchange contribution has a hidden parameters effect on the resulting angular dependence of the scattering cross-section. In this case, the electrons of the open shell of an atomic scatterer can be in the s-state, that is, the atomic shell remains spherically symmetric. The methods of an invariant time-dependent exchange perturbation theory and a Green functions with exchange were applied. An additional angular dependence of the scattering cross-section appears during the coherent scattering process. It is shown exactly for the helium scatterer that the role of exchange effects in the case of a singlet is negligible, while for the triplet state, it is decisive, especially for those values of the energy of incident electrons when de Broglie’s waves are commensurate with the atomic.

1. Introduction

The phenomenon of weak localization of conduction electrons, which manifests itself in the enhancement of backscattering of classical waves in disordered media, has attracted scientific interest in recent decades [1,2,3,4,5,6,7,8,9]. Weak localization manifests itself mainly in an increase in the probability of elastic backscattering in a narrow range of solid angles, of the order of $\lambda /l$, where $\lambda$ is the length of an electron or light wave, and $l$ is the mean free path of electrons and photons. Coherent phenomena associated with the scattering of external particles (such as electrons or neutrons) with fixed excitation energies of a disordered medium were studied in [10,11,12,13], where weak localization was observed for electron beams with energies from 10 to 1000 electron volts. Neutron beams were also the subject of this work [14]. According to these works, coherent phenomena can be observed in the enhancement of particle backscattering during elastic interaction with a disordered medium, despite the relatively high energies of the particle beams. The influence of inelastic processes on the conductivity under conditions of weak localization has been studied in many works [15,16,17,18]. In these cases, two basic assumptions are usually made. First, multiple scattering is represented as forward multiple scattering and single large-angle scattering [19]. Second, the scattering by each individual diffuser is considered to be isotropic. It was shown that the role of inelastic processes at weak localization is secondary and negative, since inelastic collisions violate phase relations, thereby reducing the probability of coherent processes. However, there are cases when inelastic processes do not lead to the loss of phase memory by the system. It was shown for the first time in [20]. In this case, in addition to the usual weak localization of the Anderson type, there is a weak localization of electrons of a new type or a new weak localization, which is essentially associated with inelastic processing. Moreover, the origin of inelasticity is not essential, for example, it can be a plasmon, photon, phonon, or exciton. Moreover, quantum coherence can exist even if the electron is exposed to an incoherent electromagnetic field. In these cases, the situation is considered when, in the case of an inelastic interaction, the particle loses a fixed energy and enters the inelastic channel, having an energy different from the initial value in the incident beam. In addition to inelastic collision, the particle can still participate in at least one elastic process, after which it leaves the medium and can be registered. This effect demonstrates itself in the scattering processes of high-energy electron beams, where electrons velocities are relativistic. The investigation of the process of the resonant spontaneous bremsstrahlung of ultrarelativistic electrons in the fields of a nucleus and a weak quasimonochromatic electromagnetic wave was done in [21,22]. There is a coherent scattering process of photons with inelastic interaction with ultrarelativistics electrons. In this case, a characteristic angular dependence with a frequency shift appears for photons. The process has been studied in a special kinematic region, where stimulated processes with correlated emission and absorption of photons of the first and second waves predominate (the effect of parametric interference). It is interesting that the described effect of a new type of weak localization for photons does not depend on the type of inelasticity, the creation of an electron-positron, or something else. The amount of energy loss is important. In this interference kinematics, correspondence is established between the emission angle and the energy of the final electron.

There are two ways to implement this process, so it can start or end with an inelastic collision. The interference of electron waves associated with these additional processes turns out to be constructive [23]. This manifests itself in an increase in the scattering of electrons at an angle other than π, and this difference can be significant. There are certain differences in the localization of electrons for different mechanisms of inelastic scattering, but it turns out that the general features of this phenomenon prevail. The most striking difference between localization of a new type in the case of inelastic scattering from ordinary weak localization is the difference in the characteristic scattering angles. The scattering probability here is maximal in the range of scattering angles close to $\pi /2$, and the effect manifests itself in a much wider range of angles than in the case of traditional localization, in which the beam enhancement is observed in forward or backward scattering at an angle of π. As already mentioned, the main difference between conventional and new weak localization is the typical electron scattering angle. The angular distribution of particles and radiation in the case of ordinary weak localization in a disordered medium is usually described using the maximum cross (or so-called “fan”) diagrams, which are used to calculate the electron radiation cross-section. Regular weak localization, in particular, can be described by a simple graphical method [24,25], which gives an idea of this phenomenon and explains why the angle pi is specific for regular weak localization. This method takes into account that an electron with momentum k is scattered through two complementary series of intermediate scattering states $k\to k_1\to k_2\to \dots \to k_{n-1}\to k_n=-k$ and $k\to k{\prime }_1=-k_{n-1}\to k{\prime }_2=-k_{n-2}\to \dots \to k{\prime }_{n-1}=-k_1\to k_n=-k$ to the state −k. Momentum changes: $q_1,q_2,\dots q_{n-1},q_n$ for the first scattering chain and $q_n,q_{n-1},\dots q_2,q_1$ for the second. The amplitudes in the final state −k are the same, and add up, and the waves in the forward and reverse directions are superimposed on each other constructively, reinforcing each other. This is due to the fact that the complementary scattering processes have the same changes in momentum, both in a straight line and in the opposite sequence. An explanation of why the coherent enhancement of electron scattering in the inelastic scattering channel occurs at angles other than π is proposed in [25]. A simple kinematic model is used to determine the basic properties of weak localization of electrons in the inelastic scattering channel. It easily reproduces the range of scattering angles characteristic of weak localization of electrons with energy loss. The results are consistent with the results based on the dynamic theory associated with the calculation of crossed and ladder diagrams. It is possible to trace the transition from a new type of weak localization to the usual weak localization with a decrease in energy losses. The new type of weak localization is consistent with regular weak localization if the energy losses are approximately equal to zero.

The range of angles in the elastic channel is of the order of $\lambda /l$, and in the inelastic channel is of the order $\gamma /\omega =\left(\lambda /l\right)\left(E/\hslash \omega \right)$, where γ is the electron collision frequency, E is its energy, and $\hslash \omega$ is the energy transferred to the medium. It is assumed that the energy of an electron incident on the medium is high enough to excite plasmons or atoms. However, this energy should not be too large so that the de Broglie wavelength of electrons was less but remained comparable to the distance between the centers of scattering, so that constructive interference of waves of scattered electrons inside condensed media could exist. The corresponding energy values for electron beams are in the range from hundreds of eV to keV. Moreover, the above statements remain valid both for the case of a small number of elastic collisions, and for a sufficiently large number; the main thing in this case is only one inelastic collision [23]. The main reason for the difficulty of fixing the indicated effect in a solid is that the very phenomenon of the new weak localization and all possible measurable parameters have been considered and calculated for an infinite three-dimensional medium, while the role of surface effects at a boundary of a condensed medium is large.

Taking into account the principle of indistinguishability of electrons in a beam and a medium, as was shown for a neutral atomic medium [26], but also takes place in a solid, this shifts the scattering enhancement to the parameters of an ordinary weak localization. As it is shown in [26], the scattering intensity includes the electron exchange terms varying directly as cosχ, where χ is a scattering angle. The expression for intensity contains two main terms, the first one is specific for the new weak localization, and the exchange interaction here contributes as an increasing pre-factor. The second term is entirely produced by electron exchange and is proportional to cosχ. Despite the obtained interesting exchange effect in a new type of weak localization for hydrogen scatterers, there was no systematic method allowing the principle of indistinguishability and permutation symmetry to be taken into account when describing scattering processes in the general case. The exchange effect considered in [24] is a good example of the importance of developing a general formalism that makes it possible to take into account the permutation symmetry of a many-electron system in the scattering problem in general and for weak localization, in particular.

In the presented work, we discuss how exchange affects the scattering of electrons in a disordered medium in a general case. We will take into account the identity of the incident electrons and electrons belonging to multielectron scatterer atoms. An invariant exchange perturbation theory method [27,28] is applied for the development of the cross-section for the weak localization scattering process while taking into account exchange effects. It is shown that, in spite of isotropic scattering by each individual scatterer, the number of electrons and their spin state in the open shell of the atom radically affect the resulting angular dependence of the scattering cross-section of incident electrons. In this case, the electrons themselves of the open shell of the scattering atom can be in the s-state, that is, the shell of the atom remains spherically symmetric. An additional angular dependence of the scattering cross-section appears, which is proportional to cosχ and does not depend on the number and state of the spin of electrons with an open or closed shell. The main difference, depending on the number of electrons and their spin states, is the coefficient in front of cosχ.

2. Probability of Plasmon Emission with Atom Excitation and Electron Exchange

We consider the interaction of electrons with a medium, accompanying the excitation of atoms when electrons are scattered by them, by the same way as in [20] by using the interaction operator in the form of the sum of two contributions:

$$V=V_{at}+V_{pl},$$

(1)

where the operator $V_{at}$ describes electron interaction with atoms of medium, numbered by indexes l:

$$V_{at}={{\displaystyle \sum }}_{l}V\left(r-R_l\right),$$

(2)

and $V_{pl}$ describes the interaction of the moving electron with the electric polarization field of the medium electrons, which arises under this action. Then, let the process of inelastic scattering of an electron be associated with the loss of energy on the plasmon:

$$V_{pl}={\displaystyle \int }dr\widehat{\rho }\left(\mathrm{r}\right)\widehat{\varphi }\left(r\right),$$

(3)

where $\widehat{\varphi }\left(r\right)$ is the operator of the electric field potential due to plasma oscillation and $\widehat{\rho }\left(r\right)$ is the charge density operator.

The initial state of the system corresponding to an incident electron and an atom of the medium (for example, a Zi-Ni alloy doped with Ca, Mg, or hydrogen or He) is described by the wave vector $|n,p\rangle$, antisymmetric taking into account the electronic permutations between the atom and the incident electron. Here, n is the set of quantum numbers of atoms in the initial state, and p is the momentum of the incident electron. Regarding the exchange perturbation theory method [27,28], the final state of the whole system can be described by the non-symmetric wave function $|m,p-Q)=|m\rangle \cdot |p-Q\rangle$, which is a simple product of the atomic function $|m\rangle$, antisymmetrized with internal electron permutations, and a free electron function $|p-Q\rangle$, where Q is the total momentum transferred to the medium. It should be underlined that the operator (2) describing electron interaction with atoms has a non-symmetric form regarding the interatomic electron permutations (the exchange of numbered atomic electrons with the free electron of incident):

$$\left[\widehat{A}{V}_{at}\right]\ne 0,$$

(4)

where $\widehat{A}$ is the antisymmetrization operator [27,28]. Acting on a non-symmetric wave function, operator $\widehat{A}$ performs antisymmetrization:

$$|n,p\rangle =\widehat{A}|n,p)=\frac{1}{f_{np}}{{\displaystyle \sum }}_{\nu }{\left(-1\right)}^{g_{\nu }}{|n,p)}_{\nu },$$

(5)

where $g_{\nu }$ is the parity of the $\nu -th$ permutation, $(n,p|n,p\rangle =1,$ $f_{np}={{\displaystyle \sum }}_{\nu }{\left(-1\right)}^{g_{\nu }}(n,p{|n,p)}_{\nu }$ are the normalization condition and a normalization factor, $|n,p)=|n\rangle \cdot |p\rangle \equiv {|n,p)}_0$ is the wave vector of the zeroth permutation with the initial arrangement of the electrons, and the subindex shows that the number of the permutation is ν = 0. Here, we deal with the antisymmetric non-orthogonal basis, while $0<(m,p\prime |n,p\rangle <1,$ is the same as for $0<\langle m,p\prime |n,p\rangle <1$, but this set meet a completeness property:

$${{\displaystyle \sum }}_{n,p}|n,p\rangle \frac{f_{np}}{{\rm N}}(n,p|=\widehat{1},$$

(6)

where ${\rm N}$ is the total number of electron permutations. The proof of completeness property (6) is described in detail in Appendix A. Generally speaking, both the “zero” Hamiltonian ${\widehat{H}}_0$ describing a multicentre many-electron system without interatomic interaction, and the perturbation operator $\widehat{V}$ describing this interatomic interaction are not invariant to the operation of antisymmetrization, taking into account the rearrangement of electrons between the two subsystems: $[\widehat{A}{\widehat{H}}_0]\ne 0,[\widehat{A}V]\ne 0$. At the same time, the complete Hamiltonian of the system $\widehat{H}={\widehat{H}}_0+\widehat{V}$ retains its invariance: $\left[\widehat{A}\widehat{H}\right]=0$. This discrepancy means a serious problem related to the fact that the zero-order wave function, antisymmetrized with respect to center-to-center electron permutations, is not an eigenfunction of the non-invariant Hamiltonian ${\widehat{H}}_0$ [27], and the corrections are obtained by applying an asymmetric operator of interactions containing non-physical contributions. In [27,28], a special symmetric form of the perturbation operator and zeroth Hamiltonian were developed. It allows corrections of the wave functions, properly antisymmetrised, and the energy corrections to be obtained by using the correct antisymmetric basis of the wavefunctions:

$$\begin{array}{l}{\widehat{H}}_0=\left({\displaystyle {\displaystyle \sum }_{\nu =0}^{\nu ={\rm N}}}{H}_{\nu }^0{\Lambda }^{\nu }\right)={\displaystyle {\displaystyle \sum }_{\nu =0}^{{\rm N}}}{H}_{\nu }^0{\displaystyle \sum }_n\frac{|{n,p)}_{\nu }({p,n|}_{\nu }}{f_{np}},\\ {\widehat{V}}_{at}=\left({{\displaystyle \sum }}_{\nu =0}^{\nu ={\rm N}}{V}_{\nu }{\Lambda }^{\nu }\right)={{\displaystyle \sum }}_{\nu =0}^{{\rm N}}{V}_{\nu }{{\displaystyle \sum }}_n\frac{|{n,p)}_{\nu }({p,n|}_{\nu }}{f_{np}},\end{array}$$

where ${\Lambda }^{\nu }$ denotes a projector onto an asymmetric state, corresponding to the $\nu -th$ permutation ${\Lambda }^{\nu }={\displaystyle \sum }_n\frac{|{n,p)}_{\nu }({p,n|}_{\nu }}{f_n^{{\rm N}}},$ and ${\Lambda }^{\nu }|n,p\rangle ={\left(-1\right)}^{g_{\nu }}|n,p)$, and ${\rm N}$, as mentioned before, is the total number of permutations. In this case, the Hamiltonian ${\widehat{H}}_0$ describing a system without the interaction of two subsystems has an eigenvector, which has an antisymmetric form taking into account the electronic permutations between these subsystems:

$${\widehat{H}}_0|n,p\rangle =\left(E_n+p^2/2m\right)|n,p\rangle .$$

(7)

In our case, the second term of the perturbation operator (1) $V_{pl}$ has a symmetric form with respect to the permutations of electrons. It is important to emphasize that after obtaining all the corrections to the energy and the wave vector in all orders of the perturbation theory in the general formalism, all matrix elements containing the complex symmetric form (6) of the perturbation operator can be analytically reduced to a simple form. This is a symmetry-adapted form that includes the usual asymmetric perturbation operator corresponding to the initial zero permutation of electrons. Such a form is more convenient for practical applications. We transform all matrix elements in the following way:

$$\begin{array}{l}(k,p\prime |\widehat{V}|n,p\rangle =(k,p\prime |{\displaystyle {\displaystyle \sum }_{\nu =0}^{{\rm N}}}{V}_{\nu }{\Lambda }^{\nu }|n,p\rangle =(k,p\prime |{\displaystyle {\displaystyle \sum }_{\nu =0}^{{\rm N}}}\frac{{\left(-1\right)}^{g_{\nu }}}{f_{np}}{V}_{\nu }|{n,p)}_{\nu }=\\ {\displaystyle {\displaystyle \sum }_{\nu =0}^{{\rm N}}}\frac{{\left(-1\right)}^{g_{\nu }}}{f_{kp}}{(k,p\prime |}_{\nu }{V}_{p=0}|{n,p)}_{\nu =0}=\frac{f_{np}}{f_{kp}}k,p\prime |V_{\nu =0}|n,p).\end{array}$$

(8)

The probability of a transition of the system in unit time from one state to another with transfer of momentum Q from the incident electron to the medium and with transition of the medium from state n to state m has the form obtained in [27,28], taking into account electron exchange

$$w_{mn,Q}=\frac{2\pi }{\hslash }\delta \left(E_n-E_m+E_p-E_{p-Q}\right){\left|\langle m,p-Q|\widehat{T}|n,p)\right|}^2,$$

(9)

where operator $\widehat{T}$ is the operator of transition on the energy surface [27,28,29], the general operator equation for which with taking into account electron permutations between subsystems is:

$$\begin{gathered} \widehat{T}=V^{\mathbb{N}}+V^{\mathbb{N}}{\left(E_i-H_0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{{\rm N}}\right)}^{-1}\widehat{T}, \\ {V}^{\mathbb{N}}=V\left(\frac{\widehat{f}}{{\rm N}}\right),\_\_\_\_\widehat{f}|n,p\rangle =f_{np}|n,p\rangle , \end{gathered}$$

(10)

where η is the relaxation frequency in the general case. We rewrite it as a series:

$$\begin{gathered} \widehat{T}=V^{\mathbb{N}}+V^{\mathbb{N}}{\left(E_i-H_0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{{\rm N}}\right)}^{-1}{V}^{\mathbb{N}}+ \\ {V}^{\mathbb{N}}{\left(E_i-H_{p=0}^0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{{\rm N}}\right)}^{-1}{V}^{\mathbb{N}}{\left(E_i-H_{p=0}^0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{{\rm N}}\right)}^{-1}{V}^{\mathbb{N}}+\dots \end{gathered}$$

(11)

In the matrix element $\langle m,p-Q|\widehat{T}|n,p)$ in Equation (9), the bra-vector has an antisymmetric form with respect to electronic permutations, and the ket-vector has a simple non-symmetric form. Then, a transition amplitude will be:

$$\begin{array}{l}\langle m,p-Q|\widehat{T}|n,p)=\langle m,p-Q|{(V_{at}+V_{pl})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(V_{at}+\underset{\_}{V_{pl}})}^{\mathbb{N}}{\widehat{G}}_0^{\mathbb{N}}{(\underset{\_}{V_{at}}+V_{pl})}^{\mathbb{N}}|n,p)+\\ \langle m,p-Q|{(V_{at}+\underset{\_}{V_{pl}})}^{\mathbb{N}}{\widehat{G}}_0^{\mathbb{N}}{(\underset{\_}{V_{at}}+V_{pl})}^{\mathbb{N}}{\widehat{G}}_0^{\mathbb{N}}{(\underset{\_}{V_{at}}+V_{pl})}^{\mathbb{N}}|n,p)+\dots =\langle m,p-Q|{(\underset{\_}{V_{pl}})}^{\mathbb{N}}{\widehat{G}}_a^{\mathbb{N}}{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\\ \langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a^{\mathbb{N}}{(\underset{\_}{V_{pl}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(V_{at})}^{\mathbb{N}}{\widehat{G}}_a^{\mathbb{N}}{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)\dots ,\end{array}$$

(12)

where we denote the normalized (indexed $N$) resolvent operator ${\widehat{G}}_0^{\mathbb{N}}$ (or the Green’s function for the coordinate representation) and the operator equation taking into account an antisymmetric nonorthogonal basis:

$$\begin{gathered} {\widehat{G}}_0^{\mathbb{N}}={\left(E_i-H_0+i\eta \right)}^{-1}{\left(\frac{\widehat{f}}{{\rm N}}\right)}^{-1} \\ {\widehat{G}}_a^{\mathbb{N}}={\widehat{G}}_0^{\mathbb{N}}+{\widehat{G}}_0^{\mathbb{N}}{V}_{at}^{\mathbb{N}}{\widehat{G}}_a^{\mathbb{N}}. \end{gathered}$$

(13)

Since the plasmon excitation is small, we can consider this process in the Born approximation. We do not fix our attention on the features of plasmon excitation in different situations, as it was done in detail in [22,30], where the excitation and propagation of bulk and surface plasma waves by incident electrons were analyzed. The motion of electrons was considered both in vacuum when approaching the surface of the metal, and inside the metal, the boundary of which elastically and specularly reflected the internal nonequilibrium electrons. The effect of electron boundary scattering parameters on the structure of bulk and surface plasmon resonances was analyzed in [31]. The probability of transition radiation of bulk plasmon by an electron moving in vacuum was examined.

We leave only the first two terms in Equation (12), where the scattering process begins or ends with plasmon excitation, and omit all other terms where the inelastic process with a plasmon occurs between the processes of elastic scattering by atoms. This is because we are not interested in small-angle scattering by the medium as a whole. The mentioned two terms we shall write out in the form:

$$\begin{array}{l}\langle m,p-Q|\widehat{T}|{\Psi }_p^{+})=\{\langle m,p-Q|\left(\underset{\_}{V_{pl}}\right)|m,p-Q+q)\left[\langle m,p-Q+q|{\delta }_{Qq}|n,p)+\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)\right]+\\ \left[\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)+\langle m,p-Q|{\delta }_{Qq}|n,p-q)\right]\langle n,p-q|\underset{\_}{V_{pl}}|n,p)\}=\\ \langle m,p-q|n,p-q)\langle n,p-q|V_{pl}|n,p)+\langle m,p-q|V_{pl}|m,p)\langle m,p|n,p)+\\ \{\langle m,p-Q|\left(\underset{\_}{V_{pl}}\right)|m,p-Q+q)\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)\langle n,p-q|\underset{\_}{V_{pl}}|n,p)\},\end{array}$$

(14)

where the first two matrix elements describe the process of plasmon excitation without atomic scattering. However, the exchange coefficients:

$$S_{mnp-q}=\langle m,p-q|n,p-q) \mathrm{and} S_{mnp}=\langle m,p|n,p),$$

(15)

mean the exchange density due to the entanglement of electronic states. The third term of Equation (14) corresponds to a process that begins with scattering by atoms and ends with excitation of plasmons. The fourth term corresponds to the process in which the events occur in the opposite order. Since we are not interested in small-angle scattering by the medium as a whole, as mentioned earlier, we can omit the first two terms.

Dividing the result of Equation (9) by the flux density of incident particles ($j_p=\hslash k_p/m_e$, where $k_p$ is the wavevector of the relative movement of the incident electrons and m_e is their mass), we obtain an expression for the cross-section of scattering events and reactions. Then, we multiply this expression for the cross-section by the number of final states in the volume per unit energy interval for scattering along the unit vector $n_f$ into a solid angle element dΩ, $d\rho \left(E_f\right)=\frac{m{k}_f}{{\left(2\pi \right)}^3{\hslash }^2}d\Omega$, because the final state is within the continuous spectrum. Then, for the differential cross-section summed over the final states of the medium, it has the form:

$$\begin{array}{l}d{\sigma }_{fi}=\frac{m_e^2{k}_f}{{\left(2\pi {\hslash }^2\right)}^2{k}_p}{\left|\langle m,p-Q|\widehat{T}|{\Psi }_{n,p}^{+})\right|}^{2}d\Omega d\left(\hslash \omega \right)\to \\ {\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}{{\displaystyle \sum }}_q{\left|\langle m,p-Q|\widehat{T}|{\Psi }_{n,p}^{+})\right|}^{2}d{\Omega }_{Q}d\omega .\end{array}$$

(16)

For electrons, we take into account the disorder of the medium, and for the plasmon electric field, we assume that the medium is completely homogeneous. Therefore, we can assume that the matrix elements in Equation (14) are approximately equal to each other:

$$\langle n,p-q|V_{pl}|n,p)\approx \langle m,p-q|V_{pl}|m,p)\approx \langle m,p-Q|\left(\underset{\_}{V_{pl}}\right)|m,p-Q+q)$$

and the exchange coefficients $S_{mnp-q}$ and $S_{mnp}$ have the same order and are proportional to $\frac{1}{{[1+{(p/\hslash )}^2{a}_B^2]}^2}=\frac{1}{{\left[1+{\left(a_B/{ƛ}_p\right)}^2\right]}^2}$, then we can rewrite Equation (16) in the form:

$$\begin{gathered} d{\sigma }_{fi}={\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}\times \\ {{\displaystyle \sum }}_q{\left|\langle m,p-Q|\left(\underset{\_}{V_{pl}}\right)|m,p-Q+q)\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)\langle n,p-q|\underset{\_}{V_{pl}}|n,p)\right|}^{2}d{\Omega }_{Q}d\omega , \end{gathered}$$

(17)

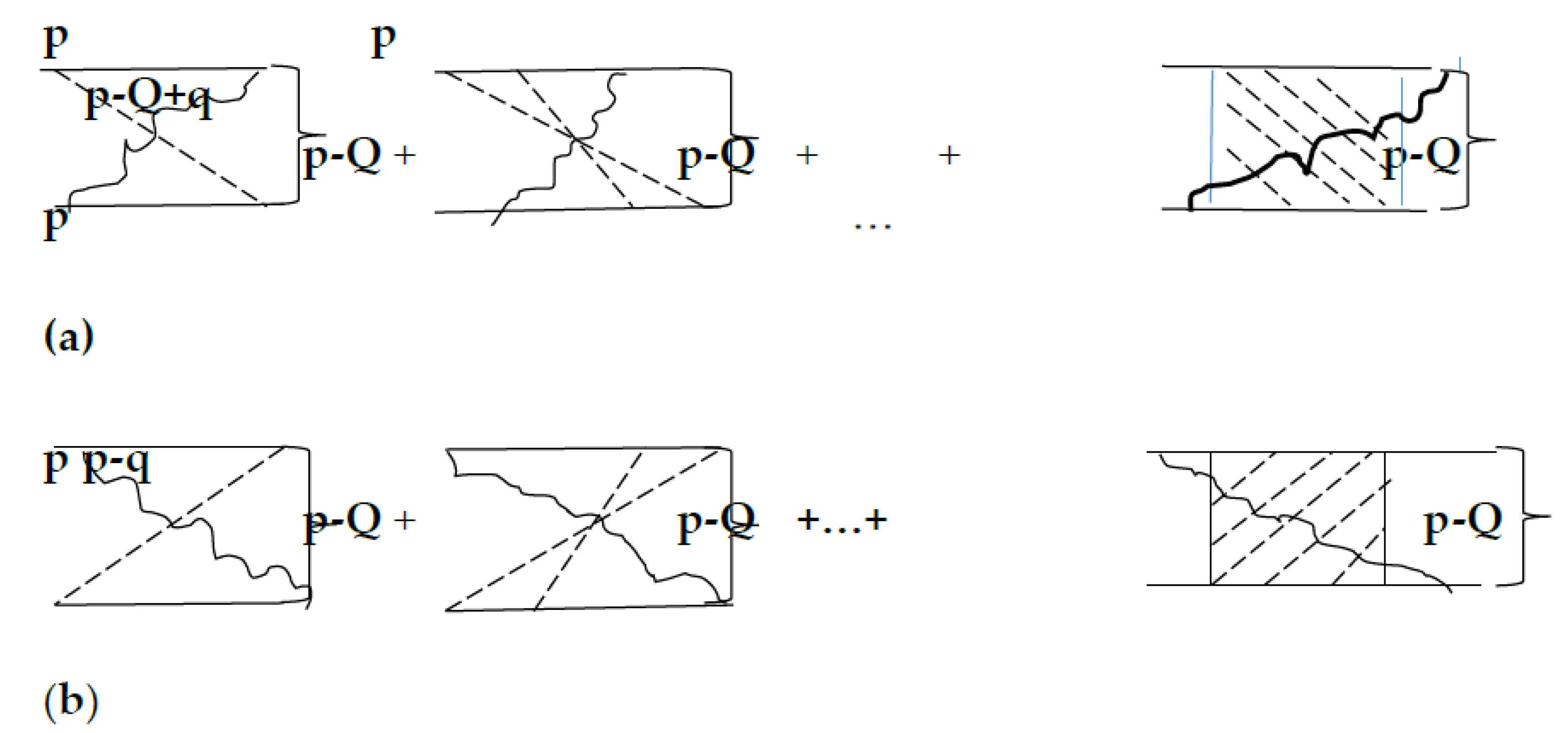
which is illustrated in Figure 1 by the set of so-called fan diagrams determining the effect of new angle dependence of the effective cross-section.

As usual, in the diagrams that match Equation (17), we will use the dotted line to connect two vertices belonging to the same atom. The lower parts of the diagrams correspond to the analytic expression, which is the complex conjugation of the expression equivalent to the upper parts. The wavy line corresponds to the plasmon. The set of ladder diagrams, correspondent to the terms contributed to the cross-section (17), are independent of the electron-scattering angle. The relation of the crossed diagram contributions and ladder diagrams determine a so-called coherency degree [25]:

$$\begin{array}{l}\frac{d{\sigma }_{fi}}{d{\Omega }_Q}={\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}\times \\ {\displaystyle {\displaystyle \sum }_q}{w}_{mnQ}{\left|\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)\right|}^{2}d\omega \\ where,\\ w_{mnQ}={\left|\langle m,p-q|n,p-q)\langle n,p-q|V_{pl}|n,p)\right|}^2\sim \\ {\left|\langle m,p-q|V_{pl}|m,p)\langle m,p|n,p)\right|}^2\sim {\left|\langle m,p-Q|\left(\underset{\_}{V_{pl}}\right)|m,p-Q+q)\right|}^2.\end{array}$$

(18)

Neglecting exchange effects, in the resulting expression (17), both bra- and ket- vectors become non symmetric, and we obtain the well-known result obtained in [25,26,27]. In contrast to the usual weak localization, one of the crossed lines in the new type of weak localization corresponds to inelastic scattering, while the others correspond to elastic interaction with randomly distributed power centers. According to formula (18), crossed diagrams together with the corresponding ladder diagrams contribute to the scattering probability factor $\Im \left(\omega ,\chi \right)$ [20]:

$$\begin{array}{l}{{\displaystyle \int }}^{ }d{\Omega }_Q{\displaystyle {\displaystyle \sum }_q}{w}_{mnQ}\left(q,\hslash \omega \right){\left|\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)\right|}^{2}d\omega \to \\ {\displaystyle {\displaystyle \sum }_q}{w}_{mnQ}\left(q,\hslash \omega \right)d\omega {\left|m,p-Q+q{V}_{at}|n,p)\right|}^2\times \\ {{\displaystyle \int }}^{ }d{\Omega }_Q{\left|p-Q+q{\widehat{G}}_{a}p-Q+q)+|m,p-Q{\widehat{G}}_{a}m,p-Q)\right|}^{2}d\omega ,\\ \Im \left(\omega ,\chi \right)=\frac{{\hslash }^2}{{\left(2\pi \hslash \right)}^3}{{\displaystyle \int }}_0^{\infty }qdq{w}_{mn}\left(q,\hslash \omega \right){{\displaystyle \int }}^{ }{\left|G\left(p-Q+q,E_p\right)+G\left(p-q,E_p-\hslash \omega \right)\right|}^{2}d{\Omega }_Q.\end{array}$$

(19)

It was shown in [24,25,26] that the angular dependence characteristic of a new weak localization arises due to the term in the integrand, which describes the contribution of the interference of two electron waves propagating along the same path in opposite directions:

$$\begin{array}{l}{G}^{*}\left(p-Q+q,E_p\right)G\left(p-q,E_p-\hslash \omega \right)+G\left(p-Q+q,E_p\right)G^{*}\left(p-q,E_p-\hslash \omega \right)=\\ \frac{1}{E_p-E_{p-Q+q}+i\gamma }\cdot \frac{1}{E_p-E_{p-q}-\hslash \omega -i\gamma }+\frac{1}{E_p-E_{p-Q+q}-i\gamma }\cdot \frac{1}{E_p-E_{p-q}-\hslash \omega +i\gamma },\end{array}$$

(20)

where γ is the electron collision frequency.

This means that weak localization occurs due to such collisions of electrons in which each subsequent scattering begins earlier than the end of the previous one. Thus, a new weak localization is realized when two conditions are met simultaneously:

$$\{\begin{array}{c}|E_p-E_{p-Q+q}=0,\\ |E_p-E_{p-q}-\hslash \omega =0\end{array}.$$

(21)

If we denote $p\prime =p-Q$, then a simple kinematic approach explains the range of the scattering angle $\chi ={cos}^{-1}\frac{p\cdot p\prime }{p\cdot p\prime }$ typical for the new type of weak localization:

$$cos\chi =-\frac{p^2+p{\prime }^2}{2pp\prime }+\frac{2{\left(m\hslash \omega \right)}^2}{pp\prime q^2},.$$

(22)

For more details, [24,25], where it is explained why the ang1es typical of the new type of weak localization differ from π, and by using the simple kinematic approach, these angles can be estimated very accurately.

Considering Equation (18) taking into account the exchange contributions, we can write the following:

$$\begin{array}{c}{\sigma }_{fi}\left(\chi ,\omega \right)={\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}\times \\ {{\displaystyle \int }}^{ }d{\Omega }_Q{\displaystyle {\displaystyle \sum }_q}{w}_{mnQ}\left(q,\hslash \omega \right){\left|\langle m,p-Q+q|{\widehat{G}}_a{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)+\langle m,p-Q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}{\widehat{G}}_a|n,p-q)\right|}^2=\\ {\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}{\displaystyle {\displaystyle \sum }_q}{w}_{mnQ}\left(q,\hslash \omega \right){\left|\langle m,p-Q+q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)\right|}^2\times \\ {{\displaystyle \int }}^{ }d{\Omega }_Q{\left|\langle m,p-Q+q|{\widehat{G}}_a|m,p-Q+q)+\langle n,p-q|{\widehat{G}}_a|n,p-q)\right|}^2.\end{array}$$

(23)

In the case of an antisymmetric basis, the calculation of matrix elements $\langle n,p-q|{\widehat{G}}_a|n,p-q)$ requires additional comments. Instead of the resolvent operator ${\widehat{G}}_a$, we will use a one-electron Green function $G_a^{ex}\left(r,r\prime \right)$ taking into account that exchange contributions influence the one-particle system:

$$G_a^{ex}\left(r,r\prime ,R\right)=\langle n,p-q|{\widehat{G}}_a{|n,p-q)}_{rr\prime }=\frac{{{\displaystyle \sum }}_{lp}{f}_{nl}\left(r,R\right)f{\ast }_{ln}\left(r\prime ,R\right)}{E_p-E_{p-q}-\hslash \omega +i\gamma },$$

(24)

where:

$$\begin{gathered} f_{nl}\left(r,R\right)={{\displaystyle \int }}^{ }d{r}_{1}d{r}_2\dots r_n\left({\displaystyle \sum }_{\nu }^{{\rm N}}{\left(-1\right)}^{g_{\nu }}{\Psi }_n{}^{*}\left(r_1-R,r_2-R,\dots {\left(r-R\right)}_{\nu }\dots r_k-R\right)\psi {*}_{p-q}\left(r_{\nu }\right)\right)\times \\ \sqrt{\frac{f_{lp}}{{\rm N}}}{\Psi }_l\left(r_1-R,r_2-R,\dots r_{\nu }-R\dots r_k-R\right){\psi }_{p-q}\left(r\right), \end{gathered}$$

(25)

$$\begin{gathered} f_{ln}\left(r\prime ,R\right)={{\displaystyle \int }}^{ }d{r}_{1}d{r}_2\dots r_n\left({\displaystyle \sum }_{\nu }^{{\rm N}}{\left(-1\right)}^{g_{\nu }}{\Psi }_l{}^{*}\left(r_1-R,r_2-R,\dots {\left(r\prime -R\right)}_{\nu }\dots r_k-R\right)\psi {*}_{p-q}\left(r_{\nu }\right)\right)\times \\ \sqrt{\frac{f_{lp}}{{\rm N}}}{\Psi }_n\left(r_1-R,r_2-R,\dots r_{\nu }-R\dots r_k-R\right){\psi }_{p-q}\left(r\prime \right). \end{gathered}$$

(26)

Integration over the conductor volume V means averaging over randomly distributed scatterers. Here, we used the completeness property (6). In the same way, we rewrite the matrix element of another resolvent operator:

$$\begin{gathered} G_{a\left(p-Q+q\right)}^{ex}\left(r,r\prime \right)=\langle m,p-Q+q|{\widehat{G}}_a|{m,p-Q+q)}_{r,r\prime }=\frac{{{\displaystyle \sum }}_{lp}{\overline{f_{ml}\left(r,R\right)f_{lm}\left(r\prime ,R\right)}}_R}{E_p-E_{p-Q+q}+i\gamma }, \\ {\overline{f_{ml}\left(r,R\right)f_{lm}\left(r\prime ,R\right)}}_R=\frac{1}{V}{{\displaystyle \int }}_V{f}_{ml}\left(r,R\right)f_{lm}\left(r\prime ,R\right)dR. \end{gathered}$$

(27)

The spectral density ${\sigma }_{fi}\left(\chi ,\omega \right)$ of the cross-section (23) of the process of inelastic scattering of electrons on disordered media consisting of atomic defects in a metal alloy (metal alloy doped with di- or trivalent atoms), taking into account exchange effects, has the form:

$$\begin{gathered} {\sigma }_{fi}\left(\chi ,\omega \right)={\left(\frac{m_e}{2{\hslash }^2}\right)}^{3/2}\frac{{\left(p^2-2m_e\hslash \omega \right)}^{1/2}}{2{\pi }^{2}p}{\displaystyle \sum }_q{w}_{mnQ}\left(q,\hslash \omega \right){\left|\langle m,p-Q+q|{(\underset{\_}{V_{at}})}^{\mathbb{N}}|n,p)\right|}^2\times \\ {{\displaystyle \int }}^{ }d{\Omega }_Q{\left|\frac{{{\displaystyle \sum }}_{lp}{\overline{f_{ml}\left(r,R\right)f_{lm}\left(r\prime ,R\right)}}_R}{E_p-E_{p-Q+q}+i\gamma }+\frac{{{\displaystyle \sum }}_{lp}{\overline{f_{nl}\left(r,R\right)f_{ln}\left(r\prime ,R\right)}}_R}{E_p-E_{p-q}-\hslash \omega +i\gamma }\right|}^2. \end{gathered}$$

(28)

Using the obtained general expression for the cross-section (18) for the case considered in [24], the alloy doped by hydrogen atoms as disordered centers, we obtain the same expression for the Green functions and for the scattering probability. It proves a limit transition of the obtained general expression (18) for the cross-section to the known case described in [24].

3. The Electron Identity Principle in Quantum Interference for Multielectron Scatterers

In our consideration, we take into account the identity of the beam electrons and the electrons belonging to the atoms of the scatterer. Firstly, we use a scatterer as a helium-like atom in the ground state (1s², ¹S) and in the excited state (1s¹2s¹, ³S).

3.1. Helium-Like Scatterer ¹S

The wave functions of the ground state of a helium-like atom and a free (incident) electron are:

$$\begin{gathered} {\Phi }_{He}\left(R-{r_1}_1,R-{r_2}_2;{{\xi }_1}_1,{{\xi }_2}_2\right)=\left({\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right)\right)\cdot \frac{1}{\sqrt{2}}\left(\alpha 1\beta 2-\beta 1\alpha 2\right), \\ {\psi }_p\left(r\right)=e^{i\frac{p\cdot r}{\hslash }}, \end{gathered}$$

(29)

where ${\phi }_{1s}\left(R-r_i\right)=\left({\alpha }^3/\pi {)}^{1/2}exp(-\alpha \left|R-r_i\right|\right),$ $\alpha =27/16$.

The vector of the initial state, corresponding to the permutation ν = 0, but antisymmetrized only accounting for the internal permutations in the helium atom, see Equation (29), has the form:

$$|{\Phi }_i^{\nu =0})={\Phi }_{He}\left(r_1,r_2\right){{\rm X}}_{He}\left({\xi }_1{\xi }_2\right){\psi }_e\left(r\right){\chi }_e\left(\xi \right)=|n=0,p).$$

(30)

We obtain the antisymmetric wave function by applying the normalized Young operator [29,32] to the wave function of the free electron–helium system as follows: Antisymmetrization of the atomic wavefunction given by Equation (30) over interatomic electrons permutations performed using the four independent Young’s operators: ${\omega }_{11}^{\left[21\right]};{\omega }_{12}^{\left[21\right]};{\omega }_{21}^{\left[21\right]};{\omega }_{22}^{\left[21\right]}$ (see Appendix A), where:

$$\Psi =\frac{1}{f_0}\left({\Psi }_{11}\left(r_1,r_2,r\right){{\rm X}}_{22}\left({\xi }_1,{\xi }_2,\xi \right)+{\Psi }_{12}\left(r_1,r_2,r\right){{\rm X}}_{21}\left({\xi }_1,{\xi }_2,\xi \right)\right),$$

$$\begin{array}{l}{\Psi }_{11}\left(r_1,r_2,r\right)={\omega }_{11}^{\left[21\right]}{\Phi }_{He}\left(r_1,r_2\right){\psi }_p\left(r\right)=\frac{1}{\sqrt{3}}\left(2{\Phi }_{He}\left(r_1,r_2\right){\psi }_p\left(r\right)-{\Phi }_{He}\left(r_1,r\right){\psi }_p\left(r_2\right)-{\Phi }_{He}\left(r,r_2\right){\psi }_p\left(r_1\right)\right)\\ {\Psi }_{12}\left(r_1,r_2,r\right)={\omega }_{12}^{\left[21\right]}{\Phi }_{He}\left(r_1,r_2\right){\psi }_p\left(r\right)=\left({\Phi }_{He}\left(r_1,r\right){\psi }_p\left(r_2\right)-{\Phi }_{He}\left(r,r_2\right){\psi }_p\left(r_1\right)\right)\\ {{\rm X}}_{21}\left({\xi }_1,{\xi }_2,\xi \right)={\omega }_{21}^{\left[21\right]}{{\rm X}}_{He}\left({\xi }_1{\xi }_2\right){\chi }_e\left(\xi \right)={\omega }_{21}^{\left[21\right]}\frac{1}{\sqrt{2}}\left({\alpha }_1{\beta }_2-{\beta }_1{\alpha }_2\right){\chi }_e\left(\xi \right)=\\ \frac{1}{\sqrt{2}}\left[\left({\alpha }_1\beta -{\beta }_1\alpha \right){\chi }_2\left(\xi \right)-\left(\alpha {\beta }_2-\beta {\alpha }_2\right){\chi }_1\left(\xi \right)\right]\\ {{\rm X}}_{22}\left({\xi }_1,{\xi }_2,\xi \right)={\omega }_{22}^{\left[21\right]}{{\rm X}}_{He}\left({\xi }_1{\xi }_2\right){\chi }_e\left(\xi \right)=\\ \frac{1}{\sqrt{3}}\frac{1}{\sqrt{2}}\left[2\left({\alpha }_1{\beta }_2-{\beta }_1{\alpha }_2\right){\chi }_e\left(\xi \right)+\left({\alpha }_1\beta -{\beta }_1\alpha \right){\chi }_2\left(\xi \right)+\left(\alpha {\beta }_2-\beta {\alpha }_2\right){\chi }_1\left(\xi \right)\right],\end{array}$$

(31)

where $f_0$ is the normalized factor, determined by:

$$\begin{gathered} {\overline{\langle \left({\Psi }_{11}\left(r_1,r_2,r\right){{\rm X}}_{22}\left({\xi }_1,{\xi }_2,\xi \right)+{\Psi }_{12}\left(r_1,r_2,r\right){{\rm X}}_{21}\left({\xi }_1,{\xi }_2,\xi \right)\right)|{\Phi }_{He}\left(R-r_1,R-r_2,{\xi }_1,{\xi }_2\right){\psi }_p\left(r\right)\chi \left(\xi \right))}}_R= \\ {f}_0=\frac{4\pi n}{3}{\left(\frac{2\pi \hslash }{p}\right)}^3\left(1-\frac{\left(2p/\hslash \alpha \right)}{1+\left(p/\hslash \alpha \right)}\right). \end{gathered}$$

(32)

For this case, Equations (25) and (26) will have the forms:

$$\begin{array}{l}{f}_{nl}\left(r,R\right)\to f_{00}\left(r,R\right)=\\ {{\displaystyle \int }}^{ }d{r}_{1}d{r}_2\frac{1}{\sqrt{3}}\{2{\phi }_{1s}\left(r_1-R\right){\phi }_{1s}\left(r_2-R\right)\psi {*}_{p-q}\left(r\right)-\\ {\phi }_{1s}\left(r_1-R\right){\phi }_{1s}\left(r-R\right)\psi {*}_{p-q}\left(r_2\right)-{\phi }_{1s}\left(r_2-R\right){\phi }_{1s}\left(r-R\right)\psi {*}_{p-q}\left(r_1\right)\}\times \\ \sqrt{\frac{f_0}{6}}\left({\phi }_{1s}\left(R-r_1\right){\phi }_{1s}\left(R-r_2\right)\right){\psi }_{p-q}\left(r″\right)\frac{2}{\sqrt{3}}=\\ \frac{4}{3}\sqrt{\frac{f_0}{6}}\left\{e^{i\frac{\left(p-q\right)\left(r″-r\right)}{\hslash }}-\frac{8}{{\left(1+{\frac{{\left|p-q\right|}^2}{{\alpha }^2\hslash }}^2\right)}^2}exp\left(i\frac{\left(p-q\right)r″}{\hslash }-\alpha \left|r-R\right|\right)\right\}.\end{array}$$

(33)

That is, the Green’s function (28), averaged over randomly distributed centers, can be written as:

$$\begin{array}{l}{G}_{\left(p-Q+q\right)}^{ex}\left(r,r\prime \right)=\frac{1}{V}{{\displaystyle \int }}_{V}dR{G}_{a\left(p-Q+q\right)}^{ex}\left(r,r\prime ,R\right)\to \frac{1}{V}{{\displaystyle \int }}_{V}dR\frac{{{\displaystyle \sum }}_p{f}_{00}\left(r\right)f{*}_{00}\left(r\prime \right)}{E_p-E_{p-Q+q}+i\gamma }=\\ {\left(\frac{4}{3}\right)}^2\frac{f_0}{6}\frac{1}{V}{{\displaystyle \int }}_{V}dR{\displaystyle {\displaystyle \sum }_p}\{\frac{exp\left(-i\frac{p\left(r-r\prime \right)}{\hslash }\right)}{E_p-E_{p-Q+q}+i\gamma }\left[1+\frac{8^2}{{\left(1+{\frac{{\left|p\right|}^2}{{\alpha }^2\hslash }}^2\right)}^4}\right]-\\ \frac{8}{{\left(1+{\frac{{\left|p\right|}^2}{{\alpha }^2\hslash }}^2\right)}^2}\frac{exp\left(i\frac{p\left(R+r\prime -r\right)}{\hslash }-\alpha \left|r-R\right|\right)+exp\left(-i\frac{p\left(R-r\prime +r\right)}{\hslash }-\alpha \left|r\prime -R\right|\right)}{E_p-E_{p-Q+q}+i\gamma }+\\ \frac{8^2}{{\left(1+{\frac{{\left|p\right|}^2}{{\alpha }^2\hslash }}^2\right)}^4}\frac{exp\left(-\alpha \left|r-R\right|-\alpha \left|r\prime -R\right|\right)}{E_p-E_{p-Q+q}+i\gamma }\}=\\ G_{0\left(p-Q+q\right)}^{ex}\left(r,r\prime \right)-G_{1\left(p-Q+q\right)}^{ex}\left(r,r\prime \right)+G_{a\left(p-Q+q\right)}^{ex}\left(r,r\prime \right),\end{array}$$

(34)

which has the same construction as in [26] but with a well-defined sign in front of the second term.

Here, $G_0^{ex}\left(r,r\prime \right)$ is the ordinary Green’s function, previously considered in [22,24,26], making it the main contribution to the new weak localization, corrected only by adding a normalization factor due to exchange effects. The specific exchange contribution has the form:

$$G_{1p-Q+q)}^{ex}\left(r,r\prime \right)={\left(\frac{4}{3}\right)}^2\frac{f_0}{6V{\alpha }^3}2\pi {{\displaystyle \sum }}_p\frac{8^2}{{\left(1+{\frac{p^2}{{\alpha }^2\hslash }}^2\right)}^4}\frac{\left(1+\frac{ip\left(r-r\prime \right)}{2\hslash }\right)e^{-i\frac{p\left(r-r\prime \right)}{\hslash }}}{E_p-E_{p-Q+q}+i\gamma },.$$

(35)

Since we are interested in the correlation length $\left|\mathit{r}-\mathit{r}\prime \right|\le {\lambda }_p$, we can neglect the higher-order terms of the parameter $\frac{\mathit{p}\left(\mathit{r}-\mathit{r}\prime \right)}{\hslash }$. Then, this term in the p-representation after the Fourier transform and an ordinary Green function in the p-representation have the following form:

$$\begin{gathered} G_1^{ex}\left(p-Q+q\right)=G_1^{ex}\left(p\prime +q\right)=\frac{2^{10}}{3^4}\left(1-\frac{{\left(\frac{2p}{\hslash \alpha }\right)}^3}{{\left(1+{\left(\frac{p}{\hslash \alpha }\right)}^2\right)}^4}\right)\frac{{\left(\frac{\hslash }{\alpha p}\right)}^3}{{\left(1+{\frac{p^2}{{\alpha }^2\hslash }}^2\right)}^4}\frac{{(2\pi )}^2{n}^2}{E_p-E_{p-Q+q}+i\gamma }, \\ {G}_0\left(p\prime +q\right)=\frac{1}{E_p-E_{p-Q+q}+i\gamma }.. \end{gathered}$$

(36)

The third term $G_a^{ex}\left(r,r\prime \right)$ describes a process that begins and ends at the same atom; therefore, it does not contribute to the quantum transfer of electrons.

Now, consider the main pre-factor $\Xi$ in the cross-section (28):

$$\begin{gathered} \Xi ={\displaystyle \int }d{\Omega }_Q{\left|\frac{{{\displaystyle \sum }}_{lp}{\overline{f_{ml}\left(r,R\right)f_{lm}\left(r\prime ,R\right)}}_R}{E_p-E_{p-Q+q}+i\gamma }+\frac{{{\displaystyle \sum }}_{lp}{\overline{f_{nl}\left(r\right)f_{ln}\left(r\prime \right)}}_R}{E_p-E_{p-q}-\hslash \omega +i\gamma }\right|}^2= \\ {\displaystyle \int }d{\Omega }_Q{\left|G^{ex}\left(p-Q+q\right)+G^{ex}\left(p-q\right)\right|}^2, \end{gathered}$$

(37)

where we denoted the Green’s function (34) in the p-representation as $G^{ex}\left(p-Q+q\right)=G_0^{ex}\left(p\prime +q\right)-G_1^{ex}\left(p\prime +q\right),$ taking into account $p-Q=p\prime$, and in exactly the same way the Green’s function of the second term in the same representation as $G^{ex}\left(p-q\right)=G_0^{ex}\left(p-q\right)-G_1^{ex}\left(p-q\right)$. Then, the factor $\Xi$ consists of three contributions, background, “the simple new weak localization”, and the exchange term:

$$\Xi ={\Xi }_{bg}+{\Xi }_0-{\Xi }_{exc}.$$

(38)

The background term has the following form:

$$\begin{array}{l}{\Xi }_{bg}={{\displaystyle \int }}^{ }d{\Omega }_Q\left\{{\left|G_0^{ex}\left(p\prime +q\right)-G_1^{ex}\left(p\prime +q\right)\right|}^2+{\left|G_0^{ex}\left(p-q\right)-G_1^{ex}\left(p-q\right)\right|}^2\right\}=\\ {{\displaystyle \int }}^{ }d{\Omega }_Q{\{\left|G_0^{ex}\left(p\prime +q\right)\right|}^2+{\left|G_1^{ex}\left(p\prime +q\right)\right|}^2+{\left|G_0^{ex}\left(p-q\right)\right|}^2+{\left|G_1^{ex}\left(p-q\right)\right|}^2-\\ \left[G_0^{ex*}\left(p\prime +q\right)G_1^{ex}\left(p\prime +q\right)+G_1^{ex*}\left(p\prime +q\right)G_0^{ex}\left(p\prime +q\right)+G_0^{ex*}\left(p-q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p-q\right)G_0^{ex}\left(p-q\right)\}\right].\end{array}$$

(39)

Substituting Expression (36), we obtain:

$$\begin{array}{l}{\Xi }_{bg}=\left(1-\frac{\pi }{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^6}\frac{2^{10}{(\pi n)}^2}{3{\alpha }^6}\right)\times \\ [5\left(\frac{1}{{\left(v\prime q\right)}^2}ln\left(\frac{{(v\prime q-\hslash \omega )}^2+{(\hslash \gamma )}^2}{{(v\prime q+\hslash \omega )}^2+{(\hslash \gamma )}^2}\right)-\frac{1}{{\left(vq\right)}^2}ln\left(\frac{{(vq-\hslash \omega )}^2+{(\hslash \gamma )}^2}{{(vq+\hslash \omega )}^2+{(\hslash \gamma )}^2}\right)\right)-\\ \left(4-\frac{25}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^2}\right)\frac{{\Gamma }^2\left(5\right){(vq)}^2}{{\left(\frac{{\hslash }^2{\alpha }^2}{2m}\right)}^4{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^4}].\end{array}$$

(40)

“The ordinary new weak localization” contribution has the form:

$$\begin{array}{l}{\Xi }_0={{\displaystyle \int }}^{ }d{\Omega }_{\mathit{Q}}\left\{G_0^{ex*}\left(p\prime +q\right)G_0^{ex}\left(p-q\right)+G_0^{ex*}\left(p-q\right)G_0^{ex}{(p\prime +q)}^2\right\}=\\ \frac{4\pi }{\left(qv\right)\hslash \gamma }\cdot \left[arctg\left(\frac{qv+\hslash {\omega }_p}{\hslash \gamma }\right)+arctg\left(\frac{qv-\hslash {\omega }_p}{\hslash \gamma }\right)-\frac{\gamma }{\sqrt{2{\omega }_p^2\left(1-cos\chi \right)-\frac{q^2{v}^2}{{\hslash }^2}{sin}^2\chi }}\right]\times \\ ln\left(\frac{{\hslash }^2{\omega }_p^2-q^2{v}^{2}cos\chi +qv\sqrt{2{\hslash }^2{\omega }_p^2\left(1-cos\chi \right)-q^2{v}^2{sin}^2\chi }}{{\hslash }^2{\omega }_p^2-q^2{v}^{2}cos\chi -qv\sqrt{2{\hslash }^2{\omega }_p^2\left(1-cos\chi \right)-q^2{v}^2{sin}^2\chi }}\right).\end{array}$$

(41)

This expression was first obtained in [20] and used in [26]. The Langmuir frequency is denoted as ω_p, and γ is the collision frequency. The specific exchange contribution in the cross-section is:

$$\begin{array}{l}{\Xi }_{exc}={{\displaystyle \int }}^{ }d{\Omega }_Q\{G_0^{ex*}\left(p+q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p\prime +q\right)G_0^{ex}\left(p-q\right)+G_0^{ex*}\left(p-q\right)G_1^{ex}\left(p\prime +q\right)+G_1^{ex*}\left(p-q\right)G_0^{ex}\left(p\prime +q\right)-\\ \left(G_1^{ex*}\left(p\prime +q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p-q\right)G_1^{ex}\left(p\prime +q\right)\right)\}=\\ \frac{2^8\frac{n\pi }{{\alpha }^3}}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^3}\{{\Xi }_0\left(1-\frac{2^5\frac{n\pi }{{\alpha }^3}}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^5}\right)-cos\chi \left(4+\frac{\hslash {\omega }_L}{vq}ln\left(\frac{{(vq-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(vq+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\right)\frac{{(2m)}^2\cdot 4\pi }{{(\hslash \alpha )}^4{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^2}\left(1-\frac{2^5\frac{n\pi }{{\alpha }^3}{\Gamma }^2\left(5\right)}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^5}\right)\},\end{array}$$

(42)

where $\Gamma \left(5\right)=4!$ is a Γ-function. Then, taking into account Equations (39)–(42), the main factor determining the angular dependence of the scattering cross-section is:

$$\begin{array}{l}\Xi \left(\chi \right)={\Xi }_{bg}+{\Xi }_0\left(1-\frac{2^8\frac{n\pi }{{\alpha }^3}}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^3}+\frac{2^{13}{\left(\frac{n\pi }{{\alpha }^3}\right)}^2}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^8}\right)+\\ \frac{2^8\frac{n\pi }{{\alpha }^3}}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^3}cos\chi \left(4+\frac{\hslash {\omega }_L}{vq}ln\left(\frac{{(vq-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(vq+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\right)\frac{{(2m)}^2\cdot 4\pi }{{(\hslash \alpha )}^4{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^2}\left(1-\frac{2^5\frac{n\pi }{{\alpha }^3}{\Gamma }^2\left(5\right)}{{(1+\frac{p^2}{{(\hslash \alpha )}^2})}^5}\right)=\\ {\Xi }_{bg}+{\Xi }_{0exc}+{\Xi }_{1exc}.\end{array}$$

(43)

Thus, the cross-section ${\sigma }_{fi}\left(\chi ,\omega \right)\propto \Xi \left(\chi \right)$. is proportional to the factor $\Xi \left(\chi \right)$ determined by Equation (43), which contains the total dependence on the scattering angle.

3.2. Helium-Like Scatterer ³S

The wave functions of the excited state helium-like atom and a free (incident) electron are:

$${\Phi }_{He}\left(R-{r_1}_1,R-{r_2}_2;{\xi }_1,{\xi }_2\right)=\frac{1}{\sqrt{2}}\left({\phi }_{1s}\left(R-r_1\right){\phi }_{2s}\left(R-r_2\right)-{\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_1\right)\right)\cdot {\rm X}\left(\alpha 1\alpha 2\right),$$

(44)

where:

$$\begin{array}{l}{\phi }_{2s}\left(R-r_i\right)={({\alpha }^3/2^3\pi )}^{1/2}\left(1-\frac{\alpha \left|R-r_i\right|}{2}\right)exp\left(-\frac{\alpha \left|R-r_i\right|}{2}\right),\\ \alpha =27/16.\end{array}$$

(45)

The vector of the initial state, corresponding to the permutation ν = 0, but antisymmetrized only accounting for the internal permutations in the helium atom, see Equation (44), has the form: $|{\Phi }_i^{\nu =0})={\Phi }_{He}\left(r_1,r_2\right){{\rm X}}_{He}\left({\xi }_1{\xi }_2\right){\psi }_e\left(\mathit{r}\right){\chi }_e\left(\xi \right)=|n=1\ast ,p)$.

The antisymmetrized vector of the final state is:

$$\begin{array}{l}\Psi \left(r_1,r_2,r_3{\alpha }_1{\alpha }_2{\alpha }_3\right)=\frac{\left(\alpha 1\alpha 2\alpha 3\right)}{f_1\sqrt{3!}}\left|\begin{array}{ccc}{\varphi }_{1s}\left(R-r_1\right)& {\varphi }_{2s}\left(R-r_1\right)& {\psi }_p\left(r_1\right)\\ {\varphi }_{1s}\left(R-r_2\right)& {\varphi }_{2s}\left(R-r_2\right)& {\psi }_p\left(r_2\right)\\ {\varphi }_{1s\alpha }\left(R-r_3\right)& {\varphi }_{2s}\left(R-r_3\right)& {\psi }_p\left(r_3\right)\end{array}\right|=\\ \frac{\left(\alpha 1\alpha 2\alpha 3\right)}{f_1\sqrt{3}}(\frac{1}{\sqrt{2}}\left[{\varphi }_{1s}\left(R-r_1\right){\varphi }_{2s}\left(R-r_2\right)-{\varphi }_{1s}\left(R-r_2\right){\varphi }_{2s}\left(R-r_1\right)\right]\cdot {\psi }_p\left(r_3\right)-\\ \left[{\varphi }_{1s}\left(R-r_1\right){\varphi }_{2s}\left(R-r_3\right)-{\varphi }_{2s}\left(R-r_1\right){\varphi }_{1s}\left(R-r_3\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_2\right)+\\ \left[{\varphi }_{1s}\left(R-r_2\right){\varphi }_{2s}\left(R-r_3\right)-{\varphi }_{1s}\left(R-r_3\right){\varphi }_{2s}\left(R-r_2\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_1\right)).\end{array}$$

(46)

Then, an exchange normalization factor:

$$\begin{array}{l}{f}_1={{\displaystyle \iiint }}^{ }d{r}_{1}d{r}_{2}d{r}_3\frac{1}{\sqrt{2}}\overline{\left(\phi {*}_{1s}\left(R-r_1\right)\phi {*}_{2s}\left(R-r_2\right)-\phi {*}_{1s}\left(R-r_2\right)\phi {*}_{2s}\left(R-r_1\right)\right){\psi }_p\left(r_3\right)}\times \\ \frac{1}{\sqrt{3}}\overline{(\frac{1}{\sqrt{2}}\left[{\varphi }_{1s}\left(R-r_1\right){\varphi }_{2s}\left(R-r_2\right)-{\varphi }_{1s}\left(R-r_2\right){\varphi }_{2s}\left(R-r_1\right)\right]\cdot {\psi }_p\left(r_3\right)-\left[{\varphi }_{1s}\left(R-r_1\right){\varphi }_{2s}\left(R-r_3\right)-{\varphi }_{2s}\left(R-r_1\right){\varphi }_{1s}\left(R-r_3\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_2\right)}+\\ {\overline{\left[{\varphi }_{1s}\left(R-r_2\right){\varphi }_{2s}\left(R-r_3\right)-{\varphi }_{1s}\left(R-r_3\right){\varphi }_{2s}\left(R-r_2\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_1\right))}}_R=\\ \frac{1}{\sqrt{3}}{\overline{\left\{1-\left[{\left|\langle {\varphi }_{2s}|{\psi }_p\rangle \right|}^2+{\left|\langle {\varphi }_{1s}|{\psi }_p\rangle \right|}^2\right]\right\}}}_R=\\ \frac{4\pi n}{3}{{\left(\frac{2\pi \hslash }{p}\right)}^3}^3\frac{1}{\sqrt{3}}\left\{1-2^6\left[{\left(\frac{{\left(\frac{2p}{\hslash }\alpha \right)}^4+7\cdot 2{\left(\frac{2p}{\hslash }\alpha \right)}^2-11}{{\left(1+{\left(\frac{2p}{\hslash }\alpha \right)}^2\right)}^4}\right)}^2+\frac{4}{{\left(4+{\left(\frac{2p}{\alpha \hslash }\right)}^2\right)}^4}\right]\right\}.\end{array}$$

A one-electron amplitude with respect to the electron permutations has the form:

$$\begin{array}{l}{f}_{11}\left(r,R\right)=\frac{\left(\alpha 1\alpha 2\alpha 3\right)}{f_1\sqrt{3}}{{\displaystyle \int }}^{ }d{r}_{1}d{r}_2(\frac{1}{\sqrt{2}}\left[{\phi }_{1s}\left(R-r_1\right){\phi }_{2s}\left(R-r_2\right)-{\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r_1\right)\right]\cdot {\psi }_p\left(r\right)-\\ \left[{\phi }_{1s}\left(R-r_1\right){\phi }_{2s}\left(R-r\right)-{\phi }_{2s}\left(R-r_1\right){\phi }_{1s}\left(R-r\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_2\right)+\\ \left[{\phi }_{1s}\left(R-r_2\right){\phi }_{2s}\left(R-r\right)-{\phi }_{1s}\left(R-r\right){\phi }_{2s}\left(R-r_2\right)\right]\cdot \frac{1}{\sqrt{2}}{\psi }_p\left(r_1\right))\times \\ \sqrt{\frac{f_1}{6}}\frac{1}{\sqrt{2}}\left(\phi {*}_{1s}\left(R-r_1\right)\phi {*}_{2s}\left(R-r_2\right)-\phi {*}_{1s}\left(R-r_2\right)\phi {*}_{2s}\left(R-r_1\right)\right)\psi {*}_p\left(r\prime \prime \right)=\\ \frac{1}{\sqrt{6f_1}\sqrt{3}}(e^{ip\left(r-r\prime \prime \right)/\hslash }-{({\alpha }^3/\pi )}^{1/2}exp\left(-\frac{\alpha \left|R-r\right|}{2}-\frac{ipr\prime \prime }{\hslash }\right)\times \\ [-2^{-3/2}\left(1-\frac{\alpha \left|R-r\right|}{2}\right)\frac{4\pi \Gamma \left(5\right){\left(\alpha /2\right)}^3\left({\left(\alpha /2\right)}^2-{\left(p/\hslash \right)}^2\right)}{{\left({\left(\alpha /2\right)}^2+{\left(p/\hslash \right)}^2\right)}^4}+\\ \left(2^{-3/2}\left(1-\frac{\alpha \left|R-r\right|}{2}\right)+exp(-\frac{\alpha \left|R-r\right|}{2}\right)\frac{8\pi \left(\alpha /2\right)}{{\left({\left(\alpha /2\right)}^2+{\left(p/\hslash \right)}^2\right)}^2}]).\end{array}$$

(47)

These amplitudes determine a one-electron Green function while accounting for the exchange contributions:

$$\begin{array}{l}G\left(\mathit{r},\mathit{r}\prime \right)=\frac{1}{18f_1}{\displaystyle {\displaystyle \sum }_p}\frac{1}{E_p-E_{\mathit{p}-\mathit{Q}+\mathit{q}}+i\gamma }\left(e^{i\mathit{p}\left(\mathit{r}-\mathit{r}\prime \right)/\hslash }-{({\alpha }^3/\pi )}^{1/2}{e}^{i\mathit{p}\left(\mathit{r}-\mathit{r}\prime \right)/\hslash }\left(e^{-\frac{i\mathit{p}\mathit{r}}{\hslash }}+e^{\frac{i\mathit{p}\mathit{r}\prime }{\hslash }}\right)\frac{8\pi }{{\left(\alpha /2\right)}^3}\right)\times \\ \left[2^{-3/2}\left(\frac{\Gamma \left(5\right){\left(\alpha /2\right)}^3\left({\left(\alpha /2\right)}^2-{\left(p/\hslash \right)}^2\right)}{{\left({\left(\alpha /2\right)}^2+{\left(p/\hslash \right)}^2\right)}^4}-2\right)+\frac{\left(\alpha /2\right)}{8{\left({\left(\alpha /2\right)}^2+{\left(p/\hslash \right)}^2\right)}^2}\right])+G_{aa}\left(\mathit{r},\mathit{r}\prime \right)=\\ \frac{1}{18f_1}{\displaystyle {\displaystyle \sum }_p}\frac{e^{ip\left(r-r\prime \right)/\hslash }}{E_p-E_{p-Q+q}+i\gamma }-\frac{1}{18f_1}\left({\displaystyle {\displaystyle \sum }_p}\frac{e^{ip\left(r-r\prime \right)/\hslash }}{E_p-E_{p-Q+q}+i\gamma }\left(2-\frac{ip\left(r-r\prime \right)}{\hslash }\right)8^{2}n{\left(\alpha /2\right)}^{-3}\right)\times \\ \left[\left(\frac{\Gamma \left(5\right)\left(1-{\left(2p/\hslash \alpha \right)}^2\right)}{{\left(1+{\left(2p/\hslash \alpha \right)}^2\right)}^4}-2\right)+\frac{1}{8{\left(1+{\left(2p/\hslash \alpha \right)}^2\right)}^2}\right])+G_{aa}\left(r,r\prime \right)=\\ \frac{1}{18f_1}\left(G_0\left(r,r\prime \right)-G_1^{exc}\left(r,r\prime \right)+G_{aa}\right).\\ G_1^{exc}\left(r,r\prime \right)={\displaystyle {\displaystyle \sum }_p}\frac{e^{ip\left(r-r\prime \right)/\hslash }}{E_p-E_{p-Q+q}+i\gamma }\left(2-\frac{ip\left(r-r\prime \right)}{\hslash }\right)8^{2}n{\left(\alpha /2\right)}^{-3}\left[\left(\frac{\Gamma \left(5\right)\left(1-{\left(2p/\hslash \alpha \right)}^2\right)}{{\left(1+{\left(2p/\hslash \alpha \right)}^2\right)}^4}-2\right)+\frac{1}{8{\left(1+{\left(2p/\hslash \alpha \right)}^2\right)}^2}\right].\end{array}$$

(48)

The mentioned Green function in p-representation is:

$$\begin{array}{l}G\left(p-Q+q\right)=G\left(p\prime +q\right)=\frac{n{\alpha }^{-3}}{18f_1}{G}_0\left(p\prime +q\right)\left(1+2^{11}\pi \right)-\frac{2^{10}\pi n{\alpha }^{-3}}{18f_1}{G}_1^{exc}\left(p\prime +q\right)=\\ \frac{n{\alpha }^{-3}}{18f_1}{G}_0(\left(p\prime +q\right)\left(1+2^{11}\pi \right)-\\ \frac{2^{10}\pi n{\alpha }^{-3}}{18f_1}\frac{1}{E_p-E_{\mathit{p}-\mathit{Q}+\mathit{q}}+i\gamma }\cdot \left[\frac{1}{8{\left(1+{\left(2\left|\mathit{p}\prime +\mathit{q}\right|/\hslash \alpha \right)}^2\right)}^2}-\frac{24}{{\left(1+{\left(2\left|\mathit{p}\prime +\mathit{q}\right|/\hslash \alpha \right)}^2\right)}^3}+\frac{24}{{\left(1+{\left(2\left|\mathit{p}\prime +\mathit{q}\right|/\hslash \alpha \right)}^2\right)}^4}\right]).\end{array}$$

(49)

where the general $G_0\left(p\prime +q\right)$ and the exchange $G_1^{exc}\left(p\prime +q\right)$ contributions are:

$$\begin{array}{c}{G}_0\left(p\prime +q\right)=\frac{1}{E_p-E_{p-Q+q}+i\gamma }\\ G_1^{exc}\left(p\prime +q\right)=\\ \frac{1}{E_p-E_{p-Q+q}+i\gamma }\cdot \left[\frac{1}{8{\left(1+{\left(2\left|p\prime +q\right|/\hslash \alpha \right)}^2\right)}^2}-\frac{24}{{\left(1+{\left(2\left|p\prime +q\right|/\hslash \alpha \right)}^2\right)}^3}+\frac{24}{{\left(1+{\left(2\left|p\prime +q\right|/\hslash \alpha \right)}^2\right)}^4}\right].\end{array}$$

(50)

The contribution $\Xi$ in the cross-section (28) in the form (38) for our case of the excited helium atom has the same structure as Equation (40), where the background contribution is:

$$\begin{gathered} {\Xi }_{bg}={\left(\frac{2^{10}\pi n{\alpha }^{-3}}{18f_1}\right)}^2{{\displaystyle \int }}^{ }d{\Omega }_Q\{4\left({\left|G_0^{ex}\left(p\prime +q\right)\right|}^2+{\left|G_0^{ex}\left(p-q\right)\right|}^2\right)+\left({\left|G_1^{ex}\left(p\prime +q\right)\right|}^2+{\left|G_1^{ex}\left(p-q\right)\right|}^2\right)- \\ 2\left[G_0^{ex*}\left(p\prime +q\right)G_1^{ex}\left(p\prime +q\right)+G_1^{ex*}\left(p\prime +q\right)G_0^{ex}\left(p\prime +q\right)+G_0^{ex*}\left(p-q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p-q\right)G_0^{ex}\left(p-q\right)\}\right]. \end{gathered}$$

(51)

The exchange contribution (42) in this case has the form:

$$\begin{gathered} {\Xi }_{exc}={{\displaystyle \int }}^{ }d{\Omega }_Q\{G_0^{ex*}\left(p\prime +q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p\prime +q\right)G_0^{ex}\left(p-q\right)+G_0^{ex*}\left(p-q\right)G_1^{ex}\left(p\prime +q\right)+ \\ {G}_1^{ex*}\left(p-q\right)G_0^{ex}\left(p\prime +q\right)-\left(G_1^{ex*}\left(p\prime +q\right)G_1^{ex}\left(p-q\right)+G_1^{ex*}\left(p-q\right)G_1^{ex}\left(p\prime +q\right)\right)\}. \end{gathered}$$

(52)

The explicit form is presented in Appendix A (see Equations (A3) and (A4)). In this expression, we neglected by the second order small terms proportional to $q^2$, while the inelastic momentum loss is $q\ll p$. Thus, the exchange contribution to the cross-section has the form:

$$\begin{array}{l}{\Xi }_{exc}=-{\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\{\frac{1}{8}\frac{\partial }{\partial ℝ}+12\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)\frac{{\partial }^2}{\partial {ℝ}^2}+4{\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\frac{{\partial }^3}{\partial {ℝ}^3}\}\left[\frac{1}{\left(ℝ-\hslash \omega -i\gamma \right)}+c.c.\right]\left(J_0+J_2\right)-\\ {\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\times \left\{\frac{1}{8}\frac{\partial }{\partial {ℝ}^{\prime }}+12\frac{{\left(\hslash \alpha \right)}^2}{8m}\frac{{\partial }^2}{\partial {{ℝ}^{\prime }}^2}+4{\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\frac{{\partial }^3}{\partial {{ℝ}^{\prime }}^3}\right\}\left[\frac{1}{{ℝ}^{\prime }+\hslash \omega +i\gamma }+c.c.\right]\left(J_0+J_1\right)-\\ {\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^4\left[\frac{1}{8}\frac{\partial }{\partial {ℝ}^{\prime }}+12\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)\frac{{\partial }^2}{\partial {ℝ}^{\prime 2}}+4{\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\frac{{\partial }^3}{\partial {ℝ}^{\prime 3}}\right]\times \\ \left[\frac{1}{8}\frac{\partial }{\partial ℝ}+12\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)\frac{{\partial }^2}{\partial {ℝ}^2}+4{\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}\right)}^2\frac{{\partial }^3}{\partial {ℝ}^3}\right]\times \\ \frac{1}{ℝ-i\gamma }\frac{1}{{ℝ}^{\prime }-i\gamma }\left\{J_0+J_1+J_2+J_3\right\}.,\end{array}$$

(53)

where the contribution $J_0={\Xi }_0$ is determined by Equation (41), c.c. is denoted by a complex conjugate expression. Here:

$$\begin{gathered} ℝ=\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}+E_p\right) \\ {ℝ}^{\prime }=ℝ-\hslash \omega =\left(\frac{{\left(\hslash \alpha \right)}^2}{8m}+E_p-\hslash \omega \right). \end{gathered}$$

(54)

The total exchange contribution consists of four terms:

$${\Xi }_{exc}={\Xi }_{exc0}+{\Xi }_{exc1}+{\Xi }_{exc2}+{\Xi }_{exc3},$$

(55)

where each term is determined in detail in Appendix A, and the results of the calculations for each term are the following:

(1)

The usual term “new weak localization” ${\Xi }_{exc0}$, which retains the angular dependence of the kinematic model with a factor depending on the exchange contributions:

$$\begin{array}{l}{\Xi }_{exc\_0}=\{\frac{1}{2^6}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2\frac{1}{{(ℝ)}^2}\left[\frac{{(ℝ)}^2}{{\left(ℝ-\hslash \omega \right)}^2}+1\right]-12{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^3\frac{1}{{(ℝ)}^3}\left[\frac{{(ℝ)}^3}{{\left(ℝ-\hslash \omega \right)}^3}+1\right]+\\ 3{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^4\frac{1}{{(ℝ)}^4}\left[\frac{{(ℝ)}^4}{{\left(ℝ-\hslash \omega \right)}^4}+1\right]-\frac{1}{2^{14}}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^4\frac{1}{{\left(ℝ-\hslash \omega \right)}^2{(ℝ)}^2}+\\ \frac{3}{2^{10}}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^5\frac{1}{{(ℝ)}^5}\left(\frac{{(ℝ)}^2}{{\left(ℝ-\hslash \omega \right)}^2}+\frac{{(ℝ)}^3}{{\left(ℝ-\hslash \omega \right)}^3}\right)-\frac{9\cdot }{2^6}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^6\frac{1}{{(ℝ)}^6}\frac{{(ℝ)}^3}{{\left(ℝ-\hslash \omega \right)}^3}-\\ \frac{3}{2^{13}}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^6\frac{1}{{(ℝ)}^6}\left(\frac{{(ℝ)}^2}{{\left(ℝ-\hslash \omega \right)}^2}+\frac{{(ℝ)}^4}{{\left(ℝ-\hslash \omega \right)}^4}\right)+\\ \frac{9}{2^9}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^7\frac{1}{{(ℝ)}^7}\left(\frac{{(ℝ)}^4}{{\left(ℝ-\hslash \omega \right)}^4}+\frac{{(ℝ)}^3}{{\left(ℝ-\hslash \omega \right)}^3}\right)-\frac{9}{2^{12}}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^8\frac{1}{{\left(ℝ-\hslash \omega \right)}^4{(ℝ)}^4}\}{J}_0.\end{array}$$

(56)

(2)

There are three typical exchange contributions, which differ from each other, each of which contains, in addition to the background exchange terms, a term proportional to cosχ

$$\begin{array}{l}{\Xi }_{exc1}=\frac{1}{8}\frac{\pi }{{ℝ}^4}{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2\left\{1+\frac{1}{2^5}\left[\frac{1}{8}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{\left(ℝ-\hslash \omega \right)}^2}-6\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^3}{{\left(ℝ-\hslash \omega \right)}^3}+\frac{3}{4}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^4}{{\left(ℝ-\hslash \omega \right)}^4}\right]\right\}\times \\ \{\frac{ℝ}{vq}ln\left(\frac{{(vq-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(vq+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\left[\frac{1}{8}\left(2+\frac{3\hslash \omega }{ℝ}\right)-3\frac{{\left(\hslash \alpha \right)}^2}{2m}\left(\frac{6}{ℝ}+\frac{12\hslash \omega }{{ℝ}^2}\right)+{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2\left(\frac{6}{{ℝ}^2}+\frac{15\hslash \omega }{{ℝ}^3}\right)\right]+\\ 3\frac{v\text{'}}{v}cos\chi \left(2+\frac{\hslash \omega }{2v\cdot q}ln\left(\frac{{(vq-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(vq+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\right)\left[\frac{1}{4}-24\frac{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}{ℝ}+10\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{ℝ}^2}\right]\}.\end{array}$$

(57)

$$\begin{array}{l}{\Xi }_{exc2}=\frac{1}{8}\left(\frac{\pi }{{ℝ}^4}\right){\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2\left\{1+\frac{1}{2^5}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{\left(ℝ-\hslash \omega \right)}^2}\left[\frac{1}{8}-6\frac{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}{\left(ℝ-\hslash \omega \right)}+\frac{3}{4}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{\left(ℝ-\hslash \omega \right)}^2}\right]\right\}\times \\ \{\frac{2ℝ}{v\prime q}ln\left(\frac{{(v\prime q-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(v\prime q+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\left[\frac{1}{8}-9\frac{\frac{{\left(\hslash \alpha \right)}^2}{2m}}{ℝ}+3\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{ℝ}^2}\right]+\\ +3\frac{v}{v\prime }cos\chi \left(2+\frac{\hslash \omega +i\gamma }{2v\cdot q}ln\left(\frac{{(v\prime q-\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}{{(v\prime q+\hslash {\omega }_p)}^2+{(\hslash \gamma )}^2}\right)\right)\left[\frac{1}{4}-\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)\frac{24}{ℝ}+{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2\frac{10}{{ℝ}^2}\right]\}.\end{array}$$

(58)

$$\begin{array}{l}{\Xi }_{exc3}=-\pi \cdot cos\chi \frac{1}{{\left(ℝ-\hslash \omega \right)}^2}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^4}{{\left(4ℝ\right)}^4}\left[-\frac{1}{2}+24\frac{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}{\left(ℝ-\hslash \omega \right)}+3\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{\left(ℝ-\hslash \omega \right)}^2}\right]\times \\ \{\left[-\frac{1}{8}\left(3+\frac{4\hslash \omega }{ℝ}\right)+\frac{5}{3}\frac{\left(vq\right)\left(v\prime q\right)}{{ℝ}^2}\right]+6\frac{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}{ℝ}\left[\left(6+\frac{10\hslash \omega }{ℝ}\right)-5\frac{\left(vq\right)\left(v\prime q\right)}{{ℝ}^2}\right]+\\ \frac{5}{2}\frac{{\left(\frac{{\left(\hslash \alpha \right)}^2}{2m}\right)}^2}{{ℝ}^2}\left[-6\left(1+\frac{2\hslash \omega }{ℝ}\right)+7\frac{\left(vq\right)\left(v\prime q\right)}{{ℝ}^2}\right]\}.\end{array}$$

(59)

These three exchange terms (57)–(59) depend on the initial atomic states of the scatterers, the number of electrons, and their multiplicity, but this dependence is expressed in the value of the background contribution and the value of the factor in front of cosχ. Variance in the number of electrons for different scatterers and their states does not lead to a new angular dependence in the scattering cross-section under conditions of a new weak localization.

In our work, we consider the identity of the incident electrons and electrons on helium-like scatterers. Helium-doped Zi-Ni alloys were used as a disordered medium. Doping the samples with helium increases disorder and enhances quantum interference. For our estimates, we take ${\omega }_p\sim {10}^{15}$, then the energy losses due to inelastic scattering will be ~1 eV, then the contribution from the usual weak localization of a new type, determined by Equation (42), to the factor in the cross-section is shown in Figure 2a. It is easy to see the fluctuations of the factor with increasing energy of the incident electron (the value determined by Equation (52)) and the singularity at an angle of 2.9 rad, which corresponds to 166 angular degrees. This angle is in a good agreement with the results of the kinematic model Equation (22):

$$cos\chi =-\frac{E_p+\left(E_p-\hslash \omega \right)}{2\sqrt{E_p\left(E_p-\hslash \omega \right)}}+2\frac{{\left(\hslash \omega \right)}^2}{vv\prime q^2}\approx 0.98,\Rightarrow \chi \approx 2,94,$$

(60)

where it was taken $\frac{\hslash \omega }{vq}\approx 0.1,$ and $\frac{\hslash \omega }{E_p}\approx 0.05$. Taking into account the identity of incident electrons with atomic electrons increases the contribution ${\Xi }_{exc0}$ in Equation (57) by 3–15 times dependently from the incident electron energy and does not change the singularity angle (see Figure 2b). True, it should be noted that a special contribution of exchange effects occurs at low energies, of the order of E_p ~2 (a.u.) atomic energy units, which is natural, since the de Broglie wavelength of an incident electron becomes comparable to the wavelength of an atomic electron. Under such conditions, exchange effects become dominant. Both exchange eigenvalues ${\Xi }_{exc1},$ ${\Xi }_{exc2}$, proportional to cosχ, give the same contribution as shown in Figure 2c. Naturally, it makes the main contribution, only at low energies of incident electrons, less than 3 eV. The third exchange term also proportional to cosχ makes the main exchange contribution in this effect. It is shown in Figure 2d. Then, the total angle factor in the scattering cross-section has the form shown in Figure 2e. Figure 2f,h show the shape of the peak for the incident electron energy ~2 a.u. for the intrinsic contribution J₀ (41), and its increasing exchange effects and for the total factor in the cross-section taking into account the exchange terms. It can be argued that the exchange effects do not change the shape and angular position of this peak. The peak size depends on the energy of the incident electrons due to the exchange effects associated with the ratio of the de Broglie wavelength to the size of the atom, as mentioned above. Figure 3 shows all contributions to the angle factor of the cross-section for the singlet state of the helium atom. Here, the intrinsic contribution J₀ (41) is the same, but the exchange coefficient differs from that shown in Figure 2b and is determined by the exchange effects from the overlap of the wave function of freely falling electrons with the singlet state of the helium atom. The exchange factor of the singlet state is shown in Figure 3a, and it is 1.5 times less then the triplet’s exchange factor. The eigent exchange contribution ${\Xi }_{exc1}$, proportional to cosχ, presented by Equation (44), is shown in Figure 3b, and it has the same shape as the ${\Xi }_{exc3}$ of the triplet state but is five times less compared with the last. The total angle factor to the cross-section, including the exchange effects from the singlet state, is shown in Figure 3c.

4. Discussion

Investigation of the influence of exchange effects on the process of coherent backscattering of electrons by disordered media is a very important task both for weak localization of the Anderson type and for a new type of weak localization with an inelastic process. For a new type of weak localization, this problem stood and was solved theoretically only for the case of hydrogen-like scatterers in metal alloys [26], where an additional angular dependence was mentioned, proportional to cosχ in the cross-section. It is now clear that this new dependence is not clearly visible, in contrast to the angular dependence of the new weak localization, explained by the kinematic consideration. The latter has a sharper peak and remains invariable even in the range of beam energies, where exchange effects are strong. In this work, we investigated the exchange effects from the first principle consideration for general case. We used the formulas for the S-matrix and scattering cross-section developed generally [27] while taking into account the exchange contributions. We developed the Green function (13), taking into account the wave function overlapping due to permutation symmetry. After analyzing all exchange contributions in the example of helium-like scatterers in metallic alloys, we come to the conclusion that exchange effects do not change the angle dependence in the new weak localization but could change the size of the peak very dramatically. A detailed comparison of the influence of exchange effects on the new weak localization for the singlet and triplet states of the helium atom shows exactly that the role of exchange effects in the case of a singlet is negligible. While, for the triplet state, it is decisive, especially for those values of the energy of incident electrons when de Broglie’s waves are commensurate with the atomic.

5. Conclusions

In our work, we focused on two aspects of the theoretical description of non-Anderson weak localization of electrons in disordered media. First, we made an attempt to create a general method for taking into account the exchange of electrons between the incident beam and the belonging of electrons to atomic scatterers, using the formalism of the invariant exchange perturbation theory. We applied the general expressions for the scattering amplitude and scattering probability with the allowance for permutation symmetry obtained in [27,28] to the problem of the process of electron scattering by disordered media under new weak localization. The result of this development of the theory is expressed by Equations (27) and (28). Second, we applied the developed general equations to a specific system: a scattering electron beam on disordered helium-like scatterers in Zi-Ni alloys doped with helium. We performed a detailed analytical calculation of the angle factor in the scattering cross-section for this system. We showed that the exchange contribution in the angle dependence of the electrons’ cross-section under the “new weak localization” condition appears in two apostasies, in the additional angle dependence, proportional to cosχ, and in the exchange factor to the “kinematic” angle dependence. In our opinion, such consideration would also be useful for the so-called anti-Anderson localization considered experimentally and theoretically in the works [33,34,35,36] for the different disordered systems.