Exploring Finite-Sized Scale Invariance in Stochastic Variability with Toy Models: The Ornstein–Uhlenbeck Model
Abstract
:1. Introduction
2. Stochastic Processes: Ornstein–Uhlenbeck Model for Transport
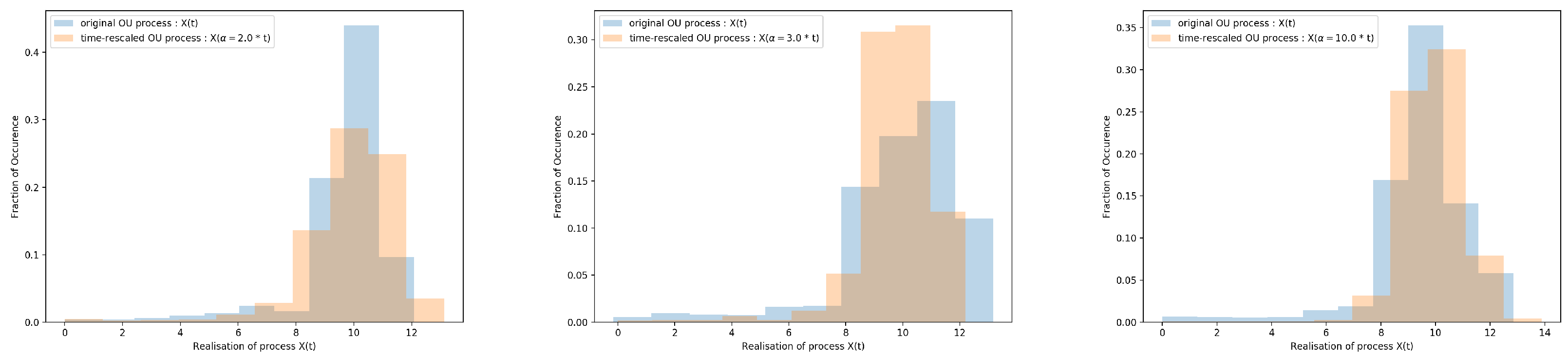
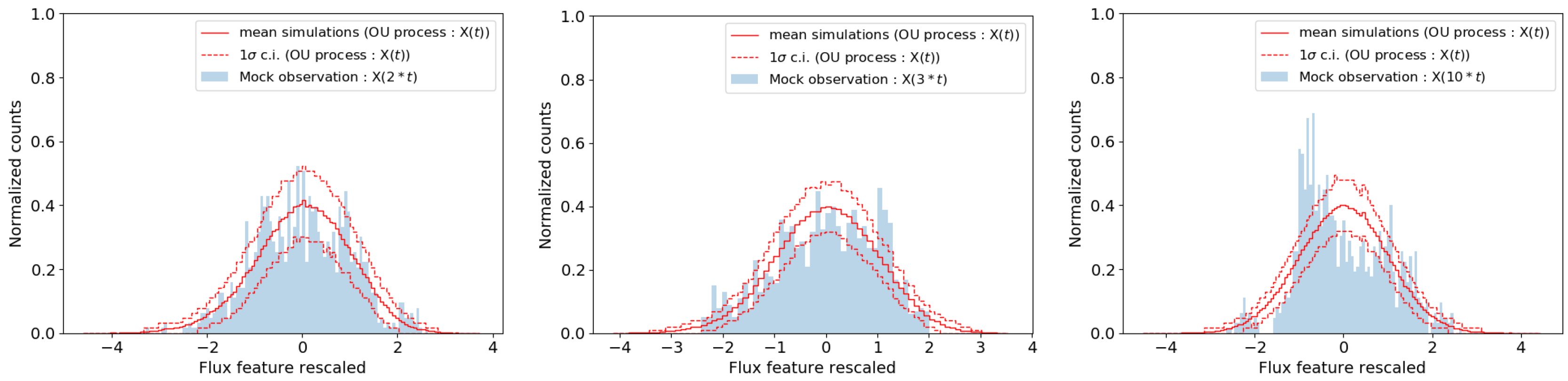
3. Testing Stochastic Properties with OU Simulations
4. Discussions and Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Lyubarskii, Y.E. Flicker noise in accretion discs. Mon. Not. R. Astron. Soc. 1997, 292, 679–685. [Google Scholar] [CrossRef] [Green Version]
- Uttley, P.; McHardy, I.M.; Vaughan, S. Non-linear X-ray variability in X-ray binaries and active galaxies. Mon. Not. R. Astron. Soc. 2005, 359, 345–362. [Google Scholar] [CrossRef] [Green Version]
- Kelly, B.C.; Bechtold, J.; Siemiginowska, A. Are the Variations in Quasar Optical Flux Driven by Thermal Fluctuations? Astrophys. J. 2009, 698, 895–910. [Google Scholar] [CrossRef]
- Sobolewska, M.A.; Siemiginowska, A.; Kelly, B.C.; Nalewajko, K. Stochastic Modeling of the Fermi/LAT γ-Ray Blazar Variability. Astrophys. J. 2014, 786, 143. [Google Scholar] [CrossRef] [Green Version]
- Vaughan, S.; Uttley, P. Studying accreting black holes and neutron stars with time series: Beyond the power spectrum. arXiv 2008, arXiv:0802.0391. [Google Scholar]
- Vaughan, S.; Edelson, R.; Warwick, R.S.; Uttley, P. On characterizing the variability properties of X-ray light curves from active galaxies. Mon. Not. R. Astron. Soc. 2003, 345, 1271–1284. [Google Scholar] [CrossRef]
- Scargle, J.D. Studies in astronomical time series analysis. I—Modeling random processes in the time domain. Astrophys. J. Suppl. Ser. 1981, 45, 1–71. [Google Scholar] [CrossRef]
- Bhatt, N.; Bhattacharyya, S. Time evolution of the probability density function of a gamma-ray burst: A possible indication of the turbulent origin of gamma-ray bursts. Mon. Not. R. Astron. Soc. 2012, 420, 1706–1713. [Google Scholar] [CrossRef]
- Bhattacharyya, S.; Ghosh, R.; Chatterjee, R.; Das, N. Blazar Variability: A Study of Nonstationarity and the Flux-Rms Relation. Astrophys. J. 2020, 897, 25. [Google Scholar] [CrossRef]
- Budai, A.; Raffai, P.; Borgulya, B.; Dawes, B.A.; Szeifert, G.; Varga, V. A statistical method to detect non-stationarities of gamma-ray burst jets. Mon. Not. R. Astron. Soc. 2020, 491, 1391–1397. [Google Scholar] [CrossRef]
- McHardy, I.; Czerny, B. Fractal X-ray time variability and spectral invariance of the Seyfert galaxy NGC5506. Nature 1987, 325, 696–698. [Google Scholar] [CrossRef]
- Georganopoulos, M.; Marscher, A.P. Self-Similarity and Observed Properties in Blazars. In Proceedings of the Astronomical Society of the Pacific Conference Series, Turku, Finland, 22–26 June 1999; p. 359. [Google Scholar]
- An, T.; Baan, W.A. The Dynamic Evolution of Young Extragalactic Radio Sources. Astrophys. J. 2012, 760, 77. [Google Scholar] [CrossRef] [Green Version]
- Marscher, A.P. Turbulent, Extreme Multi-zone Model for Simulating Flux and Polarization Variability in Blazars. Astrophys. J. 2014, 780, 87. [Google Scholar] [CrossRef]
- Blandford, R.D.; McKee, C.F. Fluid dynamics of relativistic blast waves. Phys. Fluids 1976, 19, 1130–1138. [Google Scholar] [CrossRef]
- Falle, S.A.E.G. Self-similar jets. Mon. Not. R. Astron. Soc. 1991, 250, 581–596. [Google Scholar] [CrossRef]
- Riordan, M.O.; Pe’er, A.; McKinney, J.C. Blazar Variability from Turbulence in Jets Launched by Magnetically Arrested Accretion Flows. Astrophys. J. 2017, 843, 81. [Google Scholar] [CrossRef] [Green Version]
- Klewicki, J.C. Self-similar mean dynamics in turbulent wall flows. J. Fluid Mech. 2013, 718, 596–621. [Google Scholar] [CrossRef]
- Tudor, C. Analysis of Variations for Self-Similar Processes: A Stochastic Calculus Approach; Springer: Cham, Switzerland, 2013. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Zrake, J. Inverse Cascade of Nonhelical Magnetic Turbulence in a Relativistic Fluid. Astrophys. J. Lett. 2014, 794, L26. [Google Scholar] [CrossRef] [Green Version]
- Manneville, P. Intermittency, self-similarity and 1/f spectrum in dissipative dynamical systems. J. Phys. 1980, 41, 1235–1243. [Google Scholar] [CrossRef]
- Alston, W.N. Non-stationary variability in accreting compact objects. Mon. Not. R. Astron. Soc. 2019, 485, 260–265. [Google Scholar] [CrossRef]
- Takata, T.; Mukuta, Y.; Mizumoto, Y. Modeling the Variability of Active Galactic Nuclei by an Infinite Mixture of Ornstein–Uhlenbeck (OU) Processes. Astrophys. J. 2018, 869, 178. [Google Scholar] [CrossRef] [Green Version]
- Amblard, P.O.; Borgnat, P.; Flandrin, P. Stochastic processes with finite size scale invariance. In Proceedings of the Noise in Complex Systems and Stochastic Dynamics, Santa Fe, NM, USA, 2–4 June 2003. [Google Scholar] [CrossRef]
- Chiaberge, M.; Ghisellini, G. Rapid variability in the synchrotron self-Compton model for blazars. Mon. Not. R. Astron. Soc. 1999, 306, 551–560. [Google Scholar] [CrossRef] [Green Version]
- Böttcher, M.; Chiang, J. X-Ray Spectral Variability Signatures of Flares in BL Lacertae Objects. Astrophys. J. 2002, 581, 127–142. [Google Scholar] [CrossRef]
- Finke, J.D.; Becker, P.A. Fourier Analysis of Blazar Variability. Astrophys. J. 2014, 791, 21. [Google Scholar] [CrossRef] [Green Version]
- Gao, J.B.; Cao, Y.; Lee, J.M. Principal component analysis of 1/ fα noise. Phys. Lett. 2003, 314, 392–400. [Google Scholar] [CrossRef]
- Serinaldi, F. Use and misuse of some Hurst parameter estimators applied to stationary and non-stationary financial time series. Phys. Stat. Mech. Its Appl. 2010, 389, 2770–2781. [Google Scholar] [CrossRef]
- Romoli, C.; Chakraborty, N.; Dorner, D.; Taylor, A.; Blank, M. Flux Distribution of Gamma-Ray Emission in Blazars: The Example of Mrk 501. Galaxies 2018, 6, 135. [Google Scholar] [CrossRef] [Green Version]
- Chakraborty, N. Investigating Multiwavelength Lognormality with Simulations—Case of Mrk 421. Galaxies 2020, 8, 7. [Google Scholar] [CrossRef] [Green Version]
- Tarnopolski, M.; Żywucka, N.; Marchenko, V.; Pascual-Granado, J. A Comprehensive Power Spectral Density Analysis of Astronomical Time Series. I. The Fermi-LAT Gamma-Ray Light Curves of Selected Blazars. Astrophys. J. Suppl. Ser. 2020, 250, 1. [Google Scholar] [CrossRef]
- Boffetta, G.; Carbone, V.; Giuliani, P.; Veltri, P.; Vulpiani, A. Power Laws in Solar Flares: Self-Organized Criticality or Turbulence? Phys. Rev. Lett. 1999, 83, 4662–4665. [Google Scholar] [CrossRef] [Green Version]
- Cafiero, G.; Vassilicos, J.C. Non-equilibrium turbulence scalings and self-similarity in turbulent planar jets. Proc. R. Soc. Math. Phys. Eng. Sci. 2019, 475, 20190038. [Google Scholar] [CrossRef] [Green Version]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chakraborty, N. Exploring Finite-Sized Scale Invariance in Stochastic Variability with Toy Models: The Ornstein–Uhlenbeck Model. Symmetry 2020, 12, 1927. https://doi.org/10.3390/sym12111927
Chakraborty N. Exploring Finite-Sized Scale Invariance in Stochastic Variability with Toy Models: The Ornstein–Uhlenbeck Model. Symmetry. 2020; 12(11):1927. https://doi.org/10.3390/sym12111927
Chicago/Turabian StyleChakraborty, Nachiketa. 2020. "Exploring Finite-Sized Scale Invariance in Stochastic Variability with Toy Models: The Ornstein–Uhlenbeck Model" Symmetry 12, no. 11: 1927. https://doi.org/10.3390/sym12111927
APA StyleChakraborty, N. (2020). Exploring Finite-Sized Scale Invariance in Stochastic Variability with Toy Models: The Ornstein–Uhlenbeck Model. Symmetry, 12(11), 1927. https://doi.org/10.3390/sym12111927




