Pricing Various Types of Power Options under Stochastic Volatility
Abstract
1. Introduction
2. Model Specification and Pricing Formula for Power Options
3. Application to Various Power Payoffs
3.1. Symmetric Power Option
3.2. Polynomial Options
3.3. Soft Strike Options
4. Numerical Experiments
4.1. The General Case
4.2. The Symmetric Case
5. Conclusions and Discussion
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tompkins, R.G. Power options: Hedging nonlinear risks. J. Risk 1999, 2, 29–45. [Google Scholar] [CrossRef]
- Esser, A. General variation Principles for Arbitrary payoffs and applications to power options under stochastic volatility. Financ. Mark. Portf. Manag. 2003, 17, 351–372. [Google Scholar] [CrossRef]
- Heynen, R.C.; Kat, H.M. Pricing and hedging power options. Financ. Eng. Jpn. Mark. 1996, 3, 253–261. [Google Scholar] [CrossRef]
- Wilmott, P. Derivatives: The Theory and Practice of Financial Engineering; Wiley: New York, NY, USA, 1998. [Google Scholar]
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Heston, S.L. A closed-form solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Hull, J.; White, A. The pricing of options on assets with stochastic volatilities. J. Financ. 1987, 42, 281–300. [Google Scholar] [CrossRef]
- Schöbel, R.; Zhu, J. Stochastic volatility with an Ornstein-Uhlenbeck process: An extension. Eur. Financ. Rev. 1999, 3, 23–46. [Google Scholar] [CrossRef]
- Stein, E.M.; Stein, J.C. Stock price distributions with stochastic volatility: An analytic approach. Rev. Financ. Stud. 1991, 4, 727–752. [Google Scholar] [CrossRef]
- Bakshi, G.; Madan, D. Spanning and derivative-security valuation. J. Financ. Econ. 2000, 55, 205–238. [Google Scholar] [CrossRef]
- Scott, L. Pricing stock options in a jump-diffusion model with stochastic volatility and interest rates: Applications of Fourier inversion methods. Math. Financ. 1997, 7, 413–424. [Google Scholar] [CrossRef]
- Kim, J.; Kim, B.; Moon, K.-S.; Wee, I.-S. Valuation of power options under Heston’s stochastic volatility model. J. Econ. Dyn. Control 2012, 36, 1796–1813. [Google Scholar] [CrossRef]
- Ibrahim, S.N.I.; O’Hara, J.G.; Constantinou, N. Pricing power options under the Heston dynamics using the FFT. New Trends Math. Sci. 2013, 1, 1–9. [Google Scholar]
- Macovschi, S.; Quittard-Pinon, F. On the pricing of power and other polynomial options. J. Deriv. 2006, 13, 61–71. [Google Scholar] [CrossRef]
- Hart, I.; Ross, M. Striking continuity. Risk 1994, 7, 51–56. [Google Scholar]
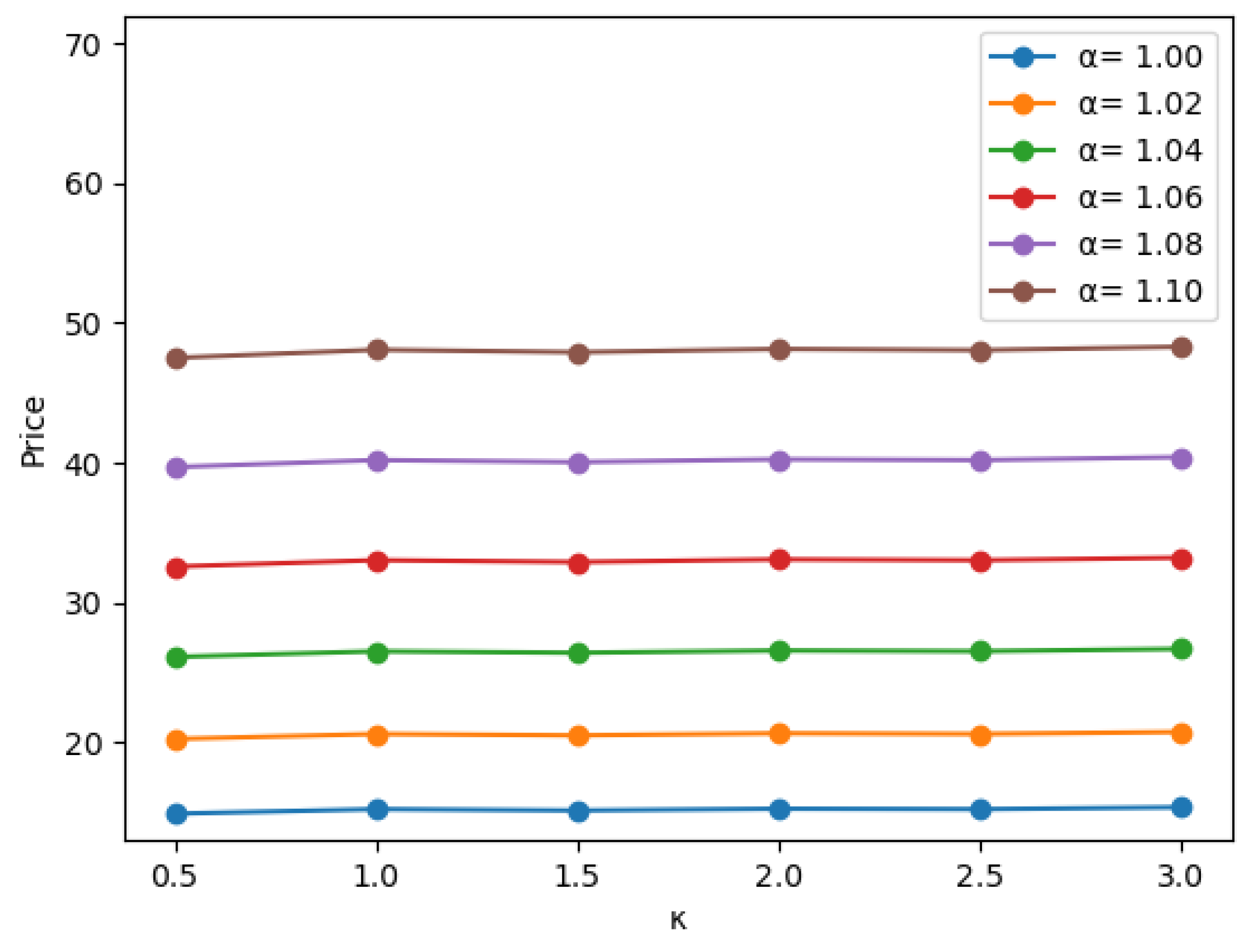
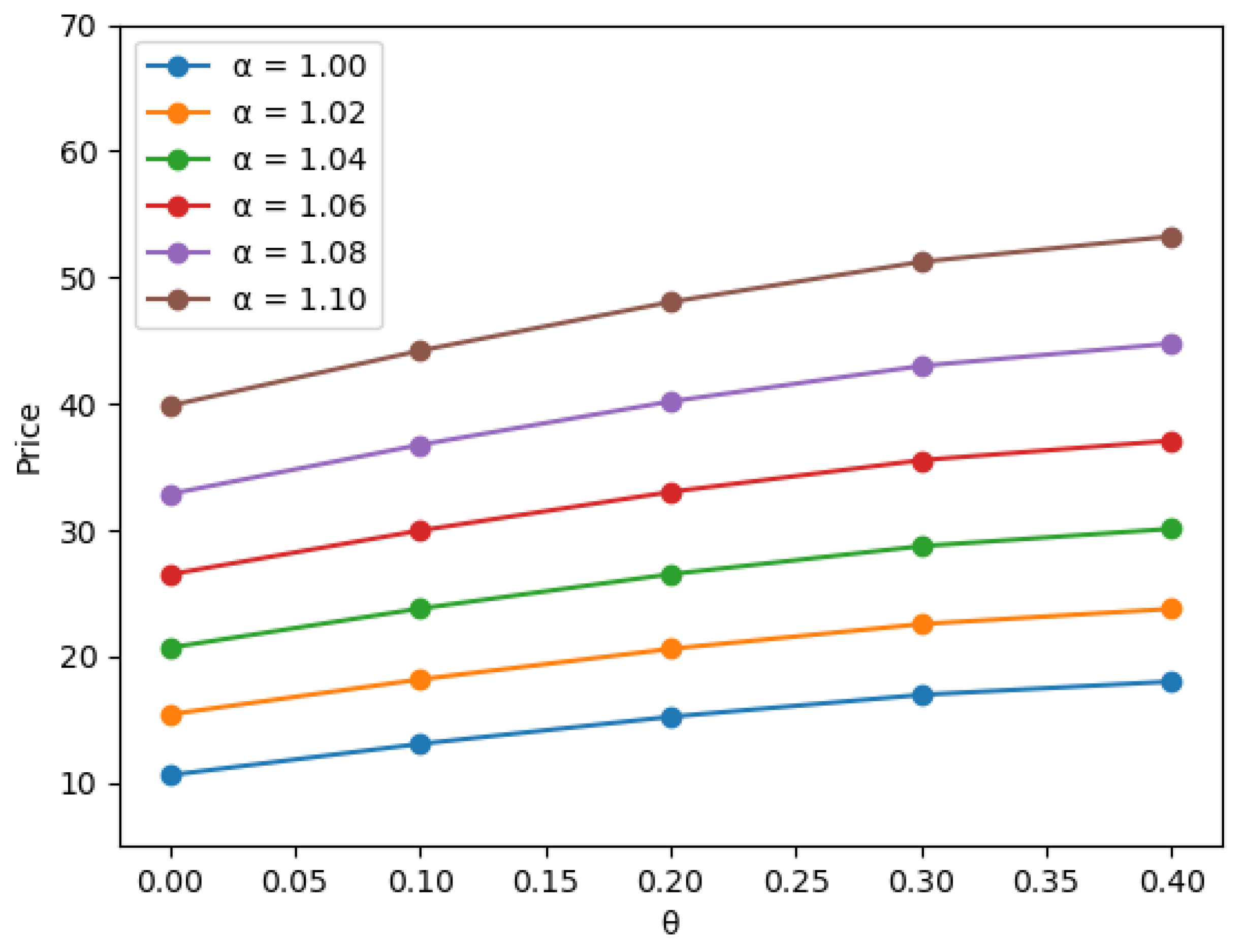


| Prices |
| Prices |
| Prices |
| Prices |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, Y.; Kim, Y.; Lee, J. Pricing Various Types of Power Options under Stochastic Volatility. Symmetry 2020, 12, 1911. https://doi.org/10.3390/sym12111911
Lee Y, Kim Y, Lee J. Pricing Various Types of Power Options under Stochastic Volatility. Symmetry. 2020; 12(11):1911. https://doi.org/10.3390/sym12111911
Chicago/Turabian StyleLee, Youngrok, Yehun Kim, and Jaesung Lee. 2020. "Pricing Various Types of Power Options under Stochastic Volatility" Symmetry 12, no. 11: 1911. https://doi.org/10.3390/sym12111911
APA StyleLee, Y., Kim, Y., & Lee, J. (2020). Pricing Various Types of Power Options under Stochastic Volatility. Symmetry, 12(11), 1911. https://doi.org/10.3390/sym12111911





