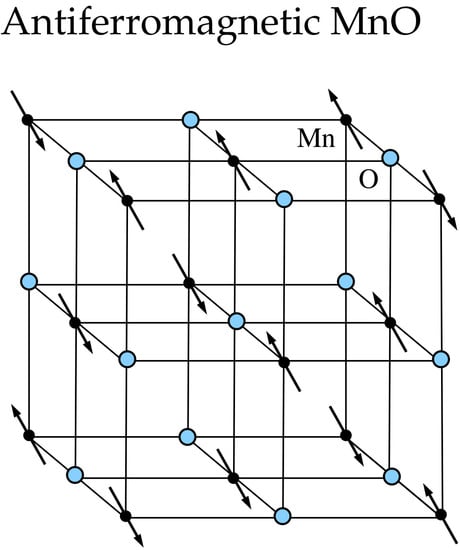
Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO
Abstract
1. Introduction
1.1. Problem Statement
1.2. Organization of the Paper
2. Magnetic Group of the Antiferromagnetic State
3. Rhombohedral-Like Distortion
4. Interpretation of the Experimental Findings of Goodwin et al.
- (i)
- The significant shifts of the Mn atoms in the direction realize the magnetic group and stabilize in this way the antiferromagnetic structure; see Section 2.
- (ii)
- The observed displacements of the Mn atoms in Equation (10) are greatest in the direction; they are even 12 times greater than in the direction. This corroborates my supposition [5] that the mutual attraction between Mn atoms with opposite shifts in the direction is mainly responsible for the rhombohedral-like deformation of the crystal. The displacements are maximal in the direction since in this direction, they are parallel to the plane and, thus, do not destroy the magnetic group , as illustrated by the red line in Figure 1.
5. Conventional Band Structure
6. Symmetry-Adapted and Optimally Localized Wannier Functions in MnO
6.1. Optimally Localized Wannier Functions Symmetry-Adapted to the Paramagnetic fcc Structure
- (i)
- (ii)
- (iii)
- The point group of the positions [19] of the Mn atoms is equal to the full cubic point group . The Wannier functions belong to the representation of included below the atom.
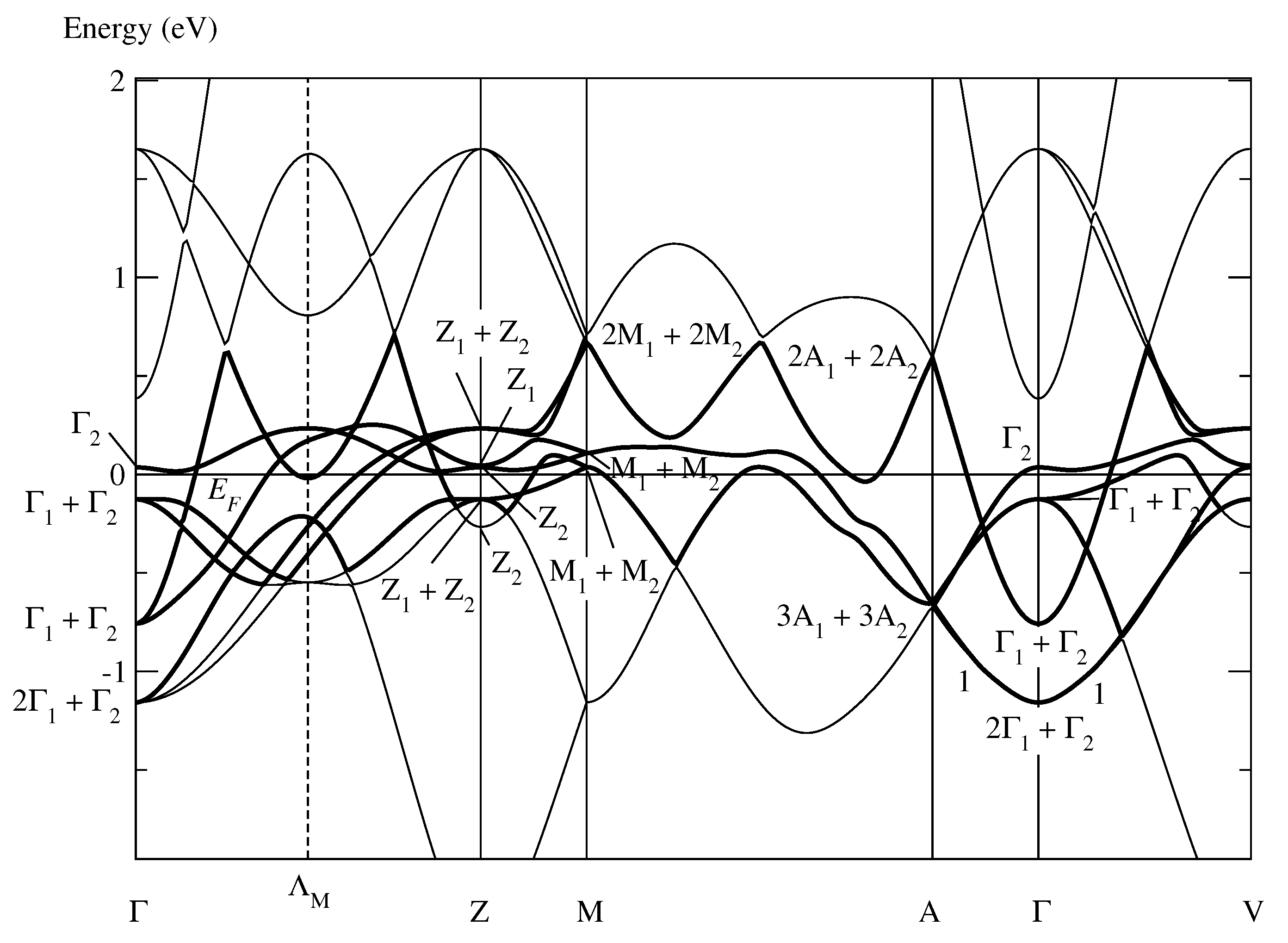
6.2. Optimally Localized Wannier Functions Symmetry-Adapted to the Antiferromagnetic Structure
- (i)
- (ii)
- The bands are determined by means of Theorem 5 of [19].
- (iii)
- The point groups and of the positions [19] of the Mn respective O atoms contain, in each case, only the identity operation:Thus, the Wannier functions at the Mn or O atoms belong to the simple representation:
of and .1 - (iv)
- (v)
- The entry “OK” indicates that the Wannier functions follow not only Theorem 5, but also Theorem 7 of [19]. Consequently, they may not only be chosen symmetry-adapted to the space group , but also to the complete magnetic group .
7. Results
- (i)
- The insulating ground state of both paramagnetic and antiferromagnetic MnO,
- (ii)
- the stability of the antiferromagnetic state,
- (iii)
- the rhombohedral-like deformation in the antiferromagnetic phase,
- The antiferromagnetic state in MnO is evidently stabilized by strongly correlated atomic-like electrons in a magnetic band. The magnetic band in MnO is even a magnetic super band because it comprises all the electrons at the Fermi level. Thus, the special atomic-like motion in this band qualifies antiferromagnetic MnO to be a Mott insulator.
- The Bloch functions of a (roughly) half filled energy band in the paramagnetic band structure of MnO can be unitarily transformed into optimally localized Wannier functions symmetry-adapted to the fcc symmetry of the paramagnetic phase. These Wannier functions are situated at the Mn atoms, have d symmetry, and comprise all the electrons at the Fermi level. Thus, the atomic-like motion represented by these Wannier functions qualifies also paramagnetic MnO to be a Mott insulator.
- The magnetic structure is stabilized by a shift of the Mn atoms in the direction. These shifts evidently produce the rhombohedral-like deformation of the crystal because the attraction between the Mn atoms increases slightly when the Mn atoms are shifted in opposite directions. This concept presented in [5] was corroborated by the experimental observations of Goodwin et al. [15].
- The rhombohedral-like distortion does not possess a rhombohedral (trigonal) space group, but is an inner distortion of the base-centered monoclinic magnetic group in Equation (4). The group , on the other hand, must not be broken because it stabilizes the antiferromagnetic structure.
8. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| NHM | Nonadiabatic Heisenberg model |
| E | Identity operation |
| I | Inversion |
| Rotation through , as indicated in Figure 1 | |
| Reflection | |
| K | Anti-unitary operator of time inversion |
References
- Rooksby, H. A note on the structure of nickel oxide at subnormal AND elevated temperatures. Acta Crystallogr. 1948, 1, 226. [Google Scholar] [CrossRef]
- Shull, C.G.; Strauser, W.A.; Wollan, E.O. Neutron Diffraction by Paramagnetic and Antiferromagnetic Substances. Phys. Rev. 1951, 83, 333–345. [Google Scholar] [CrossRef]
- Roth, W.L. Magnetic Structures of MnO, FeO, CoO, and NiO. Phys. Rev. 1958, 110, 1333–1341. [Google Scholar] [CrossRef]
- Cracknell, A.P.; Joshua, S.J. The space group corepresentations of antiferromagnetic NiO. Math. Proc. Camb. Philos. Soc. 1969, 66, 493–504. [Google Scholar] [CrossRef]
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Insulating Ground State of NiO. Symmetry 2019, 12, 56. [Google Scholar] [CrossRef]
- Austin, I.G.; Mott, N.F. Metallic and Nonmetallic Behavior in Transition Metal Oxides. Science 1970, 168, 71–77. [Google Scholar] [CrossRef]
- Mott, N.F. On the transition to metallic conduction in semiconductors. Can. J. Phys. 1956, 34, 1356–1368. [Google Scholar] [CrossRef]
- Mott, N.F. The transition to the metallic state. Philos. Mag. 1961, 6, 287–309. [Google Scholar] [CrossRef]
- Mott, N.F. The Basis of the Electron Theory of Metals, with Special Reference to the Transition Metals. Proc. Phys. Soc. Sect. 1949, 62, 416–422. [Google Scholar] [CrossRef]
- Gavriliuk, A.G.; Trojan, I.A.; Struzhkin, V.V. Insulator-Metal Transition in Highly Compressed NiO. Phys. Rev. Lett. 2012, 109, 086402. [Google Scholar] [CrossRef]
- Trimarchi, G.; Wang, Z.; Zunger, A. Polymorphous band structure model of gapping in the antiferromagnetic and paramagnetic phases of the Mott insulators MnO, FeO, CoO, and NiO. Phys. Rev. B 2018, 97, 035107. [Google Scholar] [CrossRef]
- Lu, L.; Song, M.; Liu, W.; Reyes, A.P.; Kuhns, P.; Lee, H.O.; Fisher, I.R.; Mitrović, V.F. Magnetism and local symmetry breaking in a Mott insulator with strong spin orbit interactions. Nat. Commun. 2017, 8, 14407. [Google Scholar] [CrossRef] [PubMed]
- Krüger, E. Nonadiabatic extension of the Heisenberg model. Phys. Rev. B 2001, 63. [Google Scholar] [CrossRef]
- Krüger, E. Wannier States of FCC Symmetry Qualifying Paramagnetic NiO to Be a Mott Insulator. Symmetry 2020, 12, 687. [Google Scholar] [CrossRef]
- Goodwin, A.L.; Tucker, M.G.; Dove, M.T.; Keen, D.A. Magnetic Structure of MnO at 10 K from Total Neutron Scattering Data. Phys. Rev. Lett. 2006, 96, 047209. [Google Scholar] [CrossRef]
- Blum, V.; Gehrke, R.; Hanke, F.; Havu, P.; Havu, V.; Ren, X.; Reuter, K.; Scheffler, M. Ab initio molecular simulations with numeric atom-centered orbitals. Comput. Phys. Commun. 2009, 180, 2175–2196. [Google Scholar] [CrossRef]
- Havu, V.; Blum, V.; Havu, P.; Scheffler, M. Efficient O(N)O(N) integration for all-electron electronic structure calculation using numeric basis functions. Comput. Phys. Commun. 2009, 228, 8367–8379. [Google Scholar] [CrossRef]
- Bradley, C.; Cracknell, A.P. The Mathematical Theory of Symmetry in Solids; Claredon: Oxford, UK, 1972. [Google Scholar]
- Krüger, E.; Strunk, H.P. Group Theory of Wannier Functions Providing the Basis for a Deeper Understanding of Magnetism and Superconductivity. Symmetry 2015, 7, 561–598. [Google Scholar] [CrossRef]
- Krüger, E. Modified BCS Mechanism of Cooper Pair Formation in Narrow Energy Bands of Special Symmetry I. Band Structure of Niobium. J. Supercond. 2001, 14, 469–489. [Google Scholar] [CrossRef]
- Krüger, E. Stability and symmetry of the spin-density-wave-state in chromium. Phys. Rev. B 1989, 40, 11090–11103. [Google Scholar] [CrossRef]
- Krüger, E. Energy band with Wannier functions of ferromagnetic symmetry as the cause of ferromagnetism in iron. Phys. Rev. B 1999, 59, 13795–13805. [Google Scholar] [CrossRef]
- Krüger, E. Structural Distortion Stabilizing the Antiferromagnetic and Semiconducting Ground State of BaMn2As2. Symmetry 2016, 8, 99. [Google Scholar] [CrossRef]

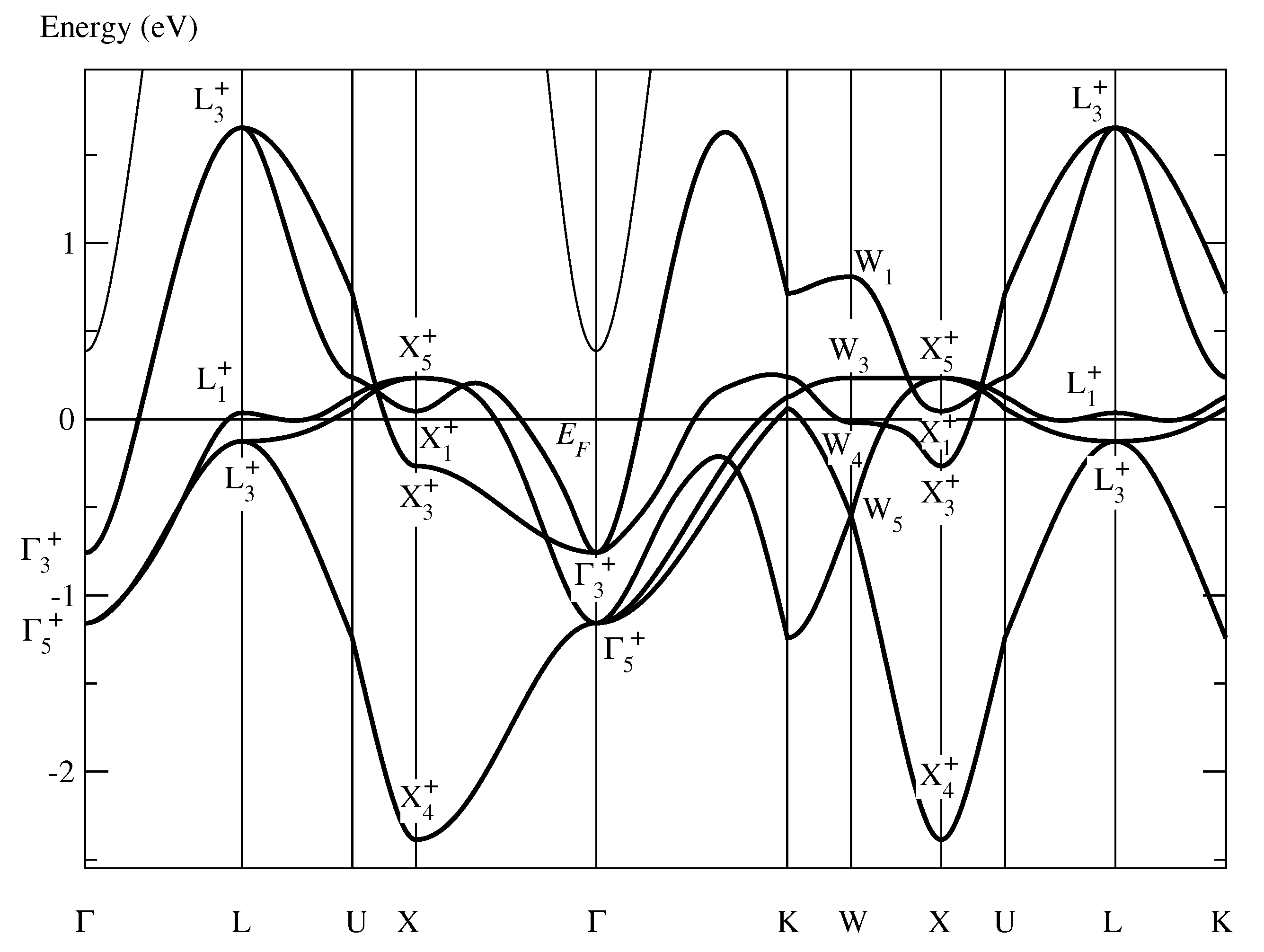
| Mn (000) | X | L | W | ||
|---|---|---|---|---|---|
| Band 5 | + | + | |||
| Band 8 | + | + | + |
| (a) Mn | Mn (000) | Mn | A | Z | M | L | V | ||
|---|---|---|---|---|---|---|---|---|---|
| Band 1 | OK | + | + | + | + | 2 | 2 | ||
| (b) O | O | O | A | Z | M | L | V | ||
| Band 1 | OK | + | + | + | + | 2 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krüger, E. Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO. Symmetry 2020, 12, 1913. https://doi.org/10.3390/sym12111913
Krüger E. Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO. Symmetry. 2020; 12(11):1913. https://doi.org/10.3390/sym12111913
Chicago/Turabian StyleKrüger, Ekkehard. 2020. "Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO" Symmetry 12, no. 11: 1913. https://doi.org/10.3390/sym12111913
APA StyleKrüger, E. (2020). Nonadiabatic Atomic-Like State Stabilizing Antiferromagnetism and Mott Insulation in MnO. Symmetry, 12(11), 1913. https://doi.org/10.3390/sym12111913