1. Introduction
A new physical theory—dozy-chaos mechanics or quantum-classical mechanics [
1,
2,
3,
4]—is designed to describe elementary physico-chemical processes, taking into account the chaotic dynamics of their transient state. The simplest version of quantum-classical mechanics is the quantum-classical mechanics of elementary electron transfers in condensed media [
5,
6]. This theory arose about twenty years ago [
5,
6] and proved its efficiency in explaining the optical spectra of polymethine dyes and their aggregates [
3,
4,
5,
6,
7,
8,
9,
10,
11] and other physico-chemical phenomena [
2,
12,
13,
14]. The very first attempts to create it [
15,
16,
17,
18], which later turned out to be its particular cases [
2,
4,
5,
7,
8,
9], were undertaken more than thirty years ago. Quantum-classical mechanics can be considered as a kind of “generalization” of quantum mechanics, in which a new property of the electron is revealed [
1,
2,
19]. This new property arises for an electron when it forms chemical bonds between atoms and consists in the appearance as a result of this ability to provoke chaos in the vibrational motion of nuclei in the process of molecular quantum transitions. The theoretical discovery of this unique ability of the electron made it possible to find out the reason for the reorganization of the structure of the nuclear subsystem of the molecule and molecular systems as a result of electronic transitions in them. In other words, the discovery of the ability of an electron to create chaos in the motion of nuclei in a transient molecular state made it possible to explain how a light electron manages to shift the equilibrium positions of vibrations of very heavy nuclei, which occurs as a result of the redistribution of the electron charge during molecular “quantum” transitions. This chaos is called dozy chaos [
7,
8,
20], since it occurs only in a transient molecular state and is absent in the initial and final adiabatic molecular states. As a result of the appearance of dozy chaos, the energy spectrum of electrons and nuclei in the transient state becomes continuous, which indicates the classical nature of the motion of electrons and nuclei in this state, while the initial and final states are quantum states that differ sharply from each other in the electronic and nuclear structure. For this reason, dozy-chaos mechanics can also be called quantum-classical mechanics [
1,
2,
3,
19], and the electron itself, which creates chaos in the transient state, can be called a quantum-classical electron [
19]. Consequently, the molecular “quantum” transition can be called the quantum-classical molecular transition.
Formally, dozy chaos arises, in theory, as a result of replacing the infinitesimal imaginary addition
(
) in the energy denominator of the spectral representation of the full Green’s function of an electron-nuclear system with a finite value [
5,
6,
7,
8,
20]. This procedure of changing the quantity
is forced and is associated with the elimination of an essential singularity that exists in the rates of molecular transitions if their dynamics are considered beyond the Born–Oppenheimer adiabatic approximation and the Franck–Condon principle [
21,
22,
23,
24,
25,
26]. The quantity
can be considered as the width of the electron-nuclear energy levels in the transient molecular state, which ensures the exchange of energy and motion between electrons and nuclei in the transient state. However, as the comparison of theoretical results with experimental data on the optical spectra of polymethine dyes and their aggregates shows, the value of
turns out to be much larger than the value of the vibrational quantum
of nuclei:
[
1,
2,
3,
4,
5,
6,
7,
8,
9,
19,
20]. This circumstance points to the fact that the exchange of energy and motion between electrons and nuclei is so intense that it leads to chaos in their joint motion in a transient state. This chaos is the dozy chaos that we discussed above, and the quantity
is called dozy-chaos energy [
7,
8,
20].
Note that the well-known imaginary, damping gamma terms in the standard theory of radiation–matter interactions [
27,
28] are related to removing resonance singularities in perturbation theory. In quantum-classical mechanics, we are talking about the elimination of an essential singularity in the rates of electron-nuclear(-vibrational) transitions, which arises when taking into account the full-fledged electron-nuclear motion in the transient state, that is, when considering the electron-nuclear motion beyond the Born–Oppenheimer adiabatic approximation and the Franck–Condon principle. This motion is singular due to the incommensurability of the masses of light electrons and heavy nuclei and regardless of whether it is resonant or non-resonant. This is the fundamental novelty of our problem and our approach to its solution, where it becomes necessary to damp the singular dynamics in molecular systems, in comparison with the standard theory of radiation–matter interactions, where it becomes necessary to damp only resonances in atomic systems. Moreover, our imaginary gamma term already exists in the energy denominator of the total electron-nuclear(-vibrational) Green’s function, by definition, as an infinitely small quantity. To eliminate the singularity in the rates of molecular transitions, which, as indicated above, exists within the framework of quantum mechanics, this gamma-term is simply assumed not to be infinitely small but finite, and thus becomes the dozy-chaos energy
. For details of the discussion of this issue, see [
2,
3,
4,
7,
8].
Dozy chaos is a mix of chaotic motions of the electronic charge, nuclear reorganization, and the electromagnetic field (dozy-chaos radiation) via which electrons and nuclei interact in the transient state. Apparently, the main mechanism for the occurrence of dozy chaos is associated with the interaction of an electron with optical phonons (see more details in Section 3 in [
1]).
The emergence of chaos in dynamical systems is usually associated with the presence of any nonlinear interactions in them. In quantum-classical mechanics [
2], the electron–phonon interaction in the original Hamiltonian is assumed to be linear (see term
in Equation (1),
Section 2) and has the same form as in the standard theory of many-phonon transitions [
29], on the basis of which it was built. The condition
arising in the complete Green’s function of the system (see above) leads to its modification and, therefore, takes the whole theory beyond the scope of quantum mechanics. Therefore, it presents a challenge to solve the inverse problem, namely, using the modified Green’s function or/and the general result for the rate constant of quantum-classical transitions (see
Section 3), to find the form of the original non-Hermitian Hamiltonian [
1] that corresponds to such a modified Green function or/and our overall result for the rate constant. In this non-Hermitian Hamiltonian obtained from the solution of the inverse problem, the electron–phonon interaction can turn out to be nonlinear [
1]. Thus, the successful solution of the inverse problem will make it possible to clarify, in more detail, the nature of dozy chaos. On the other hand, it is also a challenge to register dozy chaos in an experiment, for example, using X-ray free-electron lasers [
2,
20].
The quantum-classical electron that provokes dozy chaos can be considered as some organizing physical principle in nature [
19], and quantum-classical mechanics itself, and in this particular case, the quantum-classical mechanics of elementary electron transfers in condensed media, can be considered as the physical theory in which this organizing principle was discovered in science.
In any fundamental physical theory, as a rule, some kind of symmetry laws arises. Dozy-chaos mechanics, or in other words, quantum-classical mechanics, is no exception. The purpose of this concept review of the dozy-chaos mechanics of elementary charged particle (electron or proton) transfers in condensed media is to draw attention to a certain set of symmetries that arise in theory and are associated with various features and modes of charge-transfer dynamics. We call this set of symmetries dynamic symmetry in dozy-chaos mechanics.
2. On Dozy-Chaos Mechanics of Elementary Electron Transfers
The Hamiltonian for describing the elementary electron transfers in condensed media has the form [
1,
2,
3,
4,
5,
6,
7,
8,
9]:
where 1 and 2 are the indices of the electron donor and acceptor, respectively;
is the effective mass of the electron;
is the electron’s radius vector;
are the real normal phonon coordinates;
are the eigenfrequencies of normal vibrations;
is the phonon index;
is the electron–phonon coupling term. In comparison with the Hamiltonian in the standard theory of many-phonon transitions (see [
29]), in the theory of elementary electron transfers, the Hamiltonian is complicated merely by an extra electron potential well
set apart from the original well
by the distance
[
5,
6]. The nuclear reorganization energy
associated with the reorganization of the structure of the nuclear subsystem of the molecular system during electronic transitions in it (see
Section 1), in this case, during elementary electron transfers in condensed matter, is defined as follows [
2,
3,
4]
where
are the shifts of the normal phonon coordinates
, which correspond to the shifts in the equilibrium positions of the nuclei, caused by the presence of an electron in the medium on the donor 1 or on the acceptor 2.
The solution to the problem is sought by Green’s function method:
where
are the eigenfunctions of the total Hamiltonian
of the system—in our case, the Hamiltonian (1);
is the set of all electronic and nuclear (phonon) coordinates;
are the eigenvalues of
and
is the exact value of the total energy of the system;
(
) is the standard, infinitesimally small imaginary additive—the energy denominator vanishes when
; the aforementioned singularity in the rates of “quantum” transitions is eliminated by replacing
in the energy denominator of Green’s function (3) with a finite quantity [
2,
3,
4,
5,
6,
7,
8,
9]. The general formula for the rate constant of electron photo-transfers is obtained using the technique first described by Egorov [
15,
16], which generalizes the generating polynomial technique of Krivoglaz and Pekar [
30,
31] in the theory of many-phonon processes [
29]; see the review article [
2] for details.
3. General Formula for the Rate Constant of Electron Photo-Transfers
The general result for the rate constant (optical absorption)
is expressed in terms of Green’s function of the elementary electron-charge transfers and two generating functions (see [
2,
5]):
where the contours encircle the points
,
, and
, correspondingly. Green’s function of the elementary electron-charge transfers
and the generating functions
and
can be found in [
2,
5], where
(Planck’s distribution function) is as follows
The energy
of the absorbed photon and the heat energy
are related by the law of conservation of energy:
is the electron binding energy on the donor 1 and
is the electron-binding energy on the acceptor 2. The heat energy
corresponds to the inverse processes relative to optical absorption, i.e., to luminescence [
3,
29] (see
Section 10). The wavelength λ, indicated on the
x-axis in the figures below, corresponds to the frequency
in Equation (6) by the standard formula
(
and
are the speed of light in vacuum and the refractive index, respectively). The conservation law (Equation (6)) corresponds to the entire shape of the optical band as a whole: by varying the heat energy
, we vary the frequency of light
and determine one or another part of the absorption band [
2,
3,
4,
5,
6,
7,
8,
9,
29].
4. The Analytical Result for Optical Absorption Band Shapes and Its Invariance with Respect to the Change in the Sign of Dozy-Chaos Energy γ
From the general result of dozy-chaos mechanics of elementary electron transfers, Equation (4), the expression for the light absorption factor
(the optical extinction coefficient
[
2,
3,
4,
5,
6,
7,
8,
9,
29] is proportional to
), has been obtained. The obtained expression for
K in the framework of the Einstein model of nuclear vibrations in the framework of the Einstein model of nuclear vibrations (
), although it is rather complex, is fully expressed in elementary functions and has the following form [
2,
5,
6]:
where
,
Here, we use the notation
and where we finally have
The factor
becomes
where
and
Inequalities (9) and (11) are not any significant restrictions on the parameters of the system and associated with items of routine approximations made in the calculations (see [
2]). The time scales
,
, and
, given by Equation (13), control the dynamics of elementary electron-transfer processes. They are discussed in
Section 9. The time scale
(see Equation (13)) together with the law of conservation of energy (6) and the other parameters of a donor–acceptor system control the dynamics of producing the shape of optical bands [
2,
4].
Let us consider further the issues related to the change in the sign of the dozy-chaos energy . On the one hand, in standard quantum mechanics, where the value of is infinitesimal and where this value is introduced formally in order to avoid zero in the energy denominator of the spectral representation of Green’s function (see Equation (3)), the sign of can be either positive or negative. On the other hand, in quantum-classical mechanics, although the value of becomes a finite value, the choice of its sign turns out to be insignificant here too. It is easy to show, for example, that our result for the light absorption factor , given by Equations (6)–(26), is an even function of . For this, it is sufficient to consider those equations that include the dimensionless quantity (see Equation (12)), in which the reorganization energy is positive by definition (see Equation (2)). So, it is easy to see that the quantity (see Equation (10)) is an even function of : in the nontrivial term , the cofactors and are even functions of , and the cofactors and are odd functions of . Further, the factor (see Equation (24)) is obviously an even function of .
The invariance with respect to the change in the sign of the dozy-chaos energy
is consistent with the physical case that both the virtual acts of transformation of electron movements and energies into nuclear reorganization movements and energies and the reverse acts occur in the transient dozy-chaos state [
4,
7,
8,
9]. For definiteness, we set
here, there, and everywhere.
5. Potential Box with a Movable Wall. Optical Absorption Band Shapes as Dependent on the Dozy-Chaos Energy γ: From Symmetry to Asymmetry
The reason for the appearance of a singularity in the rates of molecular “quantum” transitions can be seen already from the example of a one-dimensional potential box with a movable wall [
1]. The movable wall corresponds to the reorganization of the nuclear subsystem of the molecular system. As indicated above (
Section 1), within the framework of quantum mechanics, due to the incommensurability of the masses of electrons and nuclei, the dynamics of nuclear reorganization is singular. Accordingly, if the movable wall of the potential box moves without friction, then this corresponds to an infinitely fast expansion of the potential box during the transition of an electron from the ground state to the first excited state, which leads to a singular “collapse” of their energy levels.
The singularity can be eliminated by assuming that the wall moves with friction [
1]. In the exact theory, this assumption corresponds to the introduction of transient chaos into the dynamics of reorganization of the electron-nuclear motion, that is, the introduction of dozy chaos.
In
Figure 1, optical absorption band shapes (for
), as dependent on the dozy-chaos energy
, are computed from Equations (6)–(26). At high energies
, the band shape is close to symmetric and is Gaussian-like (see
Section 6). With a decrease in the value of
, in the red region of the spectrum, a peak appears against the background of a Gaussian-like band, which, with decreasing
, shifts more and more to the red region of the spectrum and becomes more and more pronounced. Thus, with a decrease in the value of the dozy-chaos energy
, the band shape transforms from symmetric to asymmetric.
6. Passage to the Limit to the Standard Theory of Many-Phonon Transitions and the Symmetry of the Standard Result. The Reason for the Asymmetry of the Optical Absorption Band Shape in Dozy-Chaos Mechanics
The limit passage from expressions (6)–(26) for the optical absorption
to the standard result in the theory of many-phonon transitions [
29] can be realized by letting the dozy-chaos energy
tend to infinity (
according to Equation (12)) in Equation (10) for
(see Figure 3 in [
2]) and to zero (
) in Equation (24) for
(see Equation (162) in [
2]). An equation of the standard type for the optical absorption
(for
) is thus obtained [
2,
5]:
where
and
. A formula of this type was obtained by Markus in his electron-transfer model [
32,
33,
34,
35,
36,
37] and is often called the Marcus formula, and the energy
is called the reorganization energy of Marcus. Similar and more general formulas were previously obtained in the theory of many-phonon transitions (see [
29,
38]) for optical transitions by Huang and Rhys [
39] and Pekar [
40,
41,
42] (see also Lax [
43] and Krivoglaz and Pekar [
30]), and for nonradiative transitions, by Huang and Rhys [
39] and Krivoglaz [
31].
The result in the standard theory of many-phonon transitions, given by Equation (27) and corresponding to high (i.e., room) temperatures, is a symmetric Gaussian function for the shape of the optical absorption band. It completely neglects the dynamics of the transient molecular state. This result corresponds to the high values of the dozy-chaos energy
in dozy-chaos mechanics (see
Figure 1). Physically, large values of
in dozy-chaos mechanics correspond to a pronounced chaos in the transient state and, hence, a weak organization of the quantum-classical molecular transition (see
Section 1). With a decrease in the dozy-chaos energy
, the transient state becomes less chaotic and the organization of the quantum-classical transition increases, which is manifested in the appearance of a narrow optical absorption peak in the red spectral region and a strong asymmetry of the absorption band shape (see
Figure 1).
We also note that the half-width of the Gaussian function for the shape of the optical absorption band (Equation (27))
is determined both by the individual properties of the “donor-acceptor + medium” system, which are expressed in the reorganization energy
, and by the properties of an ensemble of these systems, which are expressed in temperature
. In other words, even within the framework of the well-known standard theory of many-phonon transitions [
29,
38], the effects of homogeneous and inhomogeneous broadening in the optical band cannot be separated. The introduction into the theory of a new “homogeneous effect” in the form of the dozy-chaos energy
in Green’s function of the system (Equation (3)) further confuses homogeneous and inhomogeneous effects in the shape of an optical band, greatly complicating the analytical result for it (cf. Equation (27) and Equations (6)–(26)). A discussion of the physical meaning of each of the terms included in this complex analytical result (Equations (6)–(26)) can be found in [
2,
4]. Our complex result gives a greater variety of optical band shapes (see, e.g.,
Figure 1) compared to the two band shapes, Lorentzian and Gaussian, which are the result of homogeneous and inhomogeneous effects known from the standard quantum theory of spectral line broadening. These two differences can only be understood in an open quantum system framework where the quantum system is coupled to an external classical bath. In contrast to the standard quantum theory, where the dynamics of quantum transitions are not considered, in quantum-classical mechanics, this bath, which is already quantum here, enters the entire closed quantum “donor-acceptor + medium” system (see the last, phonon term in the Hamiltonian (1)) and becomes classical only in a dynamic (chaotic) transient state (see Green’s function (3) with
).
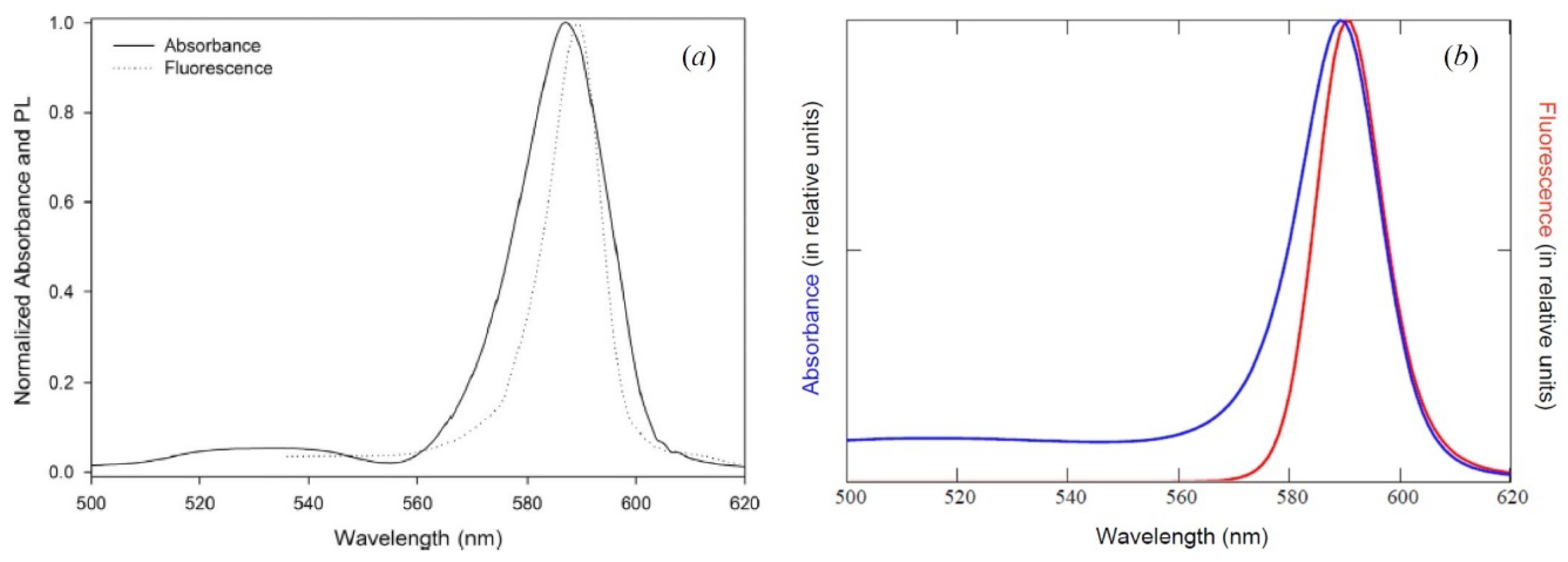
8. Implementation of the Egorov Resonance in the Quasi-Symmetric Serious of Optical Band Shapes of a Representative Polymethine Dye
Experimentally, the dynamic electron-nuclear-reorganization resonance (the Egorov resonance, see
Section 7) manifests itself, for example, in polymethine dyes [
3,
4,
5,
6,
7,
8,
9], namely, in the resonance nature of the dependence of the shape of the optical absorption band on the length of the polymethine chain
(see
Figure 2). The optical band with
corresponds to the Egorov resonance or is close to it.
To fit the theoretical result for the optical bands, which is given by Equations (6)–(26) to the corresponding experimental data (
Figure 2a), we need estimated numerical values for the ground-state energies of the dye monomers,
, and also for the energy gaps between their ground and excited states,
. These estimates follow from literature data [
5,
46,
47,
48,
49]:
and
. In addition, we need estimated numerical values for the reorganization energy of the nuclear environment of dye monomers,
. The estimate of
is found from the Egorov resonance (see Equations (29)–(31)) from the length of the optical chromophore [
5,
6]:
, where
is the length of the optical chromophore of the dye monomers (
,
nm; see the caption to
Figure 2).
Under resonance conditions (Equation (29)), the motion of the reorganization of the nuclei of the medium significantly contributes to the electronic transition in the optical
-electron chromophore—the polymethine chain with
as compared to the electronic transition in the optical
-electron chromophores of polymethine dyes with
. As can be seen from the numerical data in the caption to
Figure 2, the series of the dozy-chaos energies
has a minimum at
. Therefore, the appearance of the resonant band corresponding to
can also be interpreted as the transfer of chaos (dozy chaos) from the peak of a band into its wing(s) by a chaotic motion of the quantum-classical
-electronic state of the polymethine chain embedded in the medium as a result of the transition from “non-resonant” chains with
to the “resonant” chain with
.
Thus, the presence of symmetry in the shape of an optical band at high (room) temperatures is associated with a primitive, Franck–Condon picture of the dynamics of molecular “quantum” transitions. The loss of this symmetry and the appearance of a peak against the background of a wide band wing are related, as already noted in
Section 6, to the effect of self-organization of transition dynamics in dozy-chaos mechanics, which is expressed, in particular, in the “pumping” of dozy chaos from one part of the optical band to another part (from the peak region to the wing). Therefore, the series for the shape of the optical bands of a representative polymethine dye, thiapolymethinecyanine, depending on the length of its polymethine chain, has a quasi-symmetric character with respect to the Egorov resonance (see
Figure 2), which corresponds to the most organized quantum-classical transition.
9. The Egorov Resonance and Its “Antisymmetric Twin”
The five principal parameters of the problem, viz. electron mass
, electron-donor binding energy
, distance between the donor and the acceptor
, environmental reorganization energy
E, and dozy-chaos energy
, may be combined into three quantities:
having a time dimension (cf. Equations (13)) and representing two physically meaningful resonances [
6]:
The former resonance is between the extended electron motion and the ordered constituent of the environmental nuclear reorganization motion, i.e., it is the Egorov resonance (cf. Equations (29)–(31)). The latter is between the electron motion and, conversely, the chaotic constituent of nuclear reorganization. Since the dozy-chaos energy
can be considered, in a sense, as the imaginary part of a complex reorganization energy in which the reorganization energy
is its real part [
9], then this second resonance can be considered as some antisymmetric twin with respect to the Egorov resonance. Both of these resonances can be regarded as the simplest dynamic invariants for the transient state. The dynamic resonance-invariants are alternatives to the Born–Oppenheimer adiabatic invariants (potential energy surfaces). In other words, these two resonances are the simplest manifestation of the relationship between electron and nuclear movements in the transient state.
Details of the transient-state-dynamics interpretation based on the Heisenberg uncertainty relation can be found in [
6,
7,
8]. In particular, according to this interpretation, in the simplest cases, elementary electron transfers can be considered as a motion of a free electron–phonon quasiparticle, the so-called transferon, corresponding to the Egorov resonance, or, alternatively, as a motion of a free electron–phonon antiquasiparticle, the so-called dissipon, corresponding to the antisymmetric twin of the Egorov resonance.
11. A Simplified Version of Dozy-Chaos Mechanics—Nonradiative Transitions
All of the results of the optical spectra match, generally, weak dozy chaos (
). Strong dozy chaos (
) leads to the elucidation of important patterns in the reactions of proton transfers [
12,
51] and comparatively fresh temperature-dependent effects on electron transfers in Langmuir–Blodgett films [
13,
52]. In the case of strong dozy chaos, the dynamics of quantum-classical transitions become weakly dependent on dozy chaos, and the electronic component of the complete electron-nuclear amplitude of transitions can be fitted by the Gamow tunnel exponential, dependent on the transient phonon environment. This elementary method permit us to evade the consideration of the imaginary additive
in the spectral representation of the complete Green’s function and to word the physical nature of the transient state, not in the concept of dozy chaos but in the concept of a large number of tunnel and over-barrier energy states providing the “quantum” transition of an elementary charged particle. This method was worked out [
16] long before the development of quantum-classical (dozy-chaos) mechanics [
2,
3,
4,
5,
6,
7,
8,
9], and now we can say that the concept of a large number of tunnel and over-barrier states is a simplified version of the concept of dozy chaos.
The general result for the rate constant in the simplified version of dozy-chaos mechanics
is expressed in terms of the the Gamow tunnel exponential, dependent on the transient phonon-environment-energy
and one generating function [
15,
16]:
where the contours encircle the points
,
, and
, correspondingly (cf. Equation (4)). The Gamow tunnel exponential is
where the function
is given by the following formula:
(here, there, and everywhere,
). The generating function is as follows:
The result (34) applies to both optical and nonradiative processes. In the case of optical processes, the heat energy
is determined from the law of conservation of energy (6) (
—absorption and
—luminescence), where the frequency
in the cases of nonradiative endothermic and exothermic processes:
and
From the general result for the rate constant in the simplified version of dozy-chaos mechanics, Equations (34)–(39), in the framework of the Einstein model of nuclear vibrations (
), the simple expression for the rate constant
has been obtained [
16]:
(cf. Equations (7) and (8)), where
is the Gamow exponential (cf. Equation (27)) and
(cf. Equations (10) and (13)). If, as in the case of the complete theory for optical processes (
Section 2,
Section 3 and
Section 4), we assume that the expression for the rate constant of the reverse process
is obtained by changing the sign in the heat energy
and in the donor–acceptor distance
(see
Section 10.1 and
Section 10.3) in corresponding expression for the rate constant of the direct process
in the considered simplified version of dozy-chaos mechanics, then, applying this position to Equation (40), we obtain
where
is the equilibrium constant of charged-particle-transfer reactions in the simplified version of dozy-chaos mechanics. In the limit
, we obtain from Equation (42) the well-known detailed balance relationship in statistical physics and in the standard theory of many-phonon transitions [
29,
31].
12. The Simplified Version of Dozy-Chaos Mechanics: Proton-Transfer Reactions. On Symmetry in the Brönsted Relationship
Grounded on the simplified version of dozy-chaos mechanics [
16] (
Section 11), in 1990, a theoretical description of the basic experimental patterns in the Brönsted relationship [
51] for the reactions of proton transfer (acid-base catalysis) was given [
12]. The Brönsted relationship was found by Brönsted and Pedersen in 1924 (see [
51]). The theory in [
16] is immediately appropriate to the explanation of electron transfers. To explain the reactions of transfers of heavy charged particles (proton transfers), the result of thermic fluctuations of the potential barrier transparence must be considered because of fluctuations in the barrier width. In contrast to the elementary proton transfer, the electron-transfer process is insensitive to small fluctuations in the barrier width due to the large size of the electronic wave function in the initial and final states. The analytical formulas for the proton-transfer rate constants are obtained. In acid catalysis, the empirical Brönsted relationship is
where
is the rate constant,
is the empirical equilibrium constant, and
and
are constants. In base catalysis, the empirical Brönsted relationship is
The theoretically-obtained Brönsted coefficients
and
(the Einstein model of nuclear vibrations
) for direct (acid catalysis) and inverse (base catalysis) reactions [
12]
and
(
is given by Equation (41) and
is barrier rigidity) are symmetric relative to
and meet the generally known empirical equality [
53,
54]
(which directly follows from the Brӧnsted relationships (43) and (44)).
13. The Simplified Version of Dozy-Chaos Mechanics: Symmetrization of the Amplitude and Rate Constant of the Transition for the Case of Different Electron–Phonon Interactions on the Donor and Acceptor
Until now, both in the case of the complete theory for optical processes (
Section 2,
Section 3 and
Section 4) and in the case of its simplified version for nonradiative processes (
Section 11), we have considered the case of the same electron–phonon interaction when a light charged particle, in particular an electron, is localized on the donor or on the acceptor. In other words, it was assumed that the reorganization energy
(Equation (2)). For example, “quantum” transitions and the corresponding shapes of optical bands in polymethine dyes are well described by the case of the same value of the electron–phonon interaction on the donor and on the acceptor, because charge alternation occurs in the polymethine chain upon optical excitation [
1,
3,
4,
5,
6]. In this section, we will briefly consider the case of different electron–phonon interactions when an electron is localized on a donor or acceptor. This corresponds to different magnitude shifts of the normal phonon coordinates
and
(in the case of the same interaction,
[
2]) and an obvious redefinition of the reorganization energy
(Equation (2)):
where
. For example, in the case of nonradiative processes, the change in sign in the heat energy
(Equations (38) and (39)) and in the donor–acceptor distance
(Equation (1)) is associated with the permutation of indices 1 and 2 in the reverse order. The assumption
leads to asymmetry with respect to the permutation of indices 1 and 2 in the expression for the rate constant of transitions and the loss of connection between forward and reverse processes, expressed in Equation (42). To restore this connection, it is necessary to symmetrize the expression for the amplitude and rate constant of electron transfers with respect to different values of the electron–phonon interaction at the donor and at the acceptor, which leads to the case of reorganization energies
.
The symmetrization method proposed in [
14,
17,
18] consists of the fact that, in addition to the transition amplitude [
2,
3,
4]
which, in view of taking the wave function
in the Born–Oppenheimer adiabatic approximation
and taking into account the entire dynamics of the transition only in the wave function
(
is Green’s function of the Hamiltonian
,
[
2,
3,
4]), can be called the amplitude of the transition on the acceptor
, we introduce into the theory also the amplitude
in which, on the contrary, the wave function
is taken in the adiabatic approximation
, and the entire dynamics of the transition are taken into account only in the wave function
. This new amplitude
can be called the amplitude of the transition on the donor. Then, the half-sum of these two amplitudes is taken as the total transition amplitude:
Since the symmetrization is carried out only with respect to the electron–phonon interaction, in Equation (51), the permutation of indices 1 and 2 in the quantity is not performed and the sign of does not change.
Using Equation (51), for the case of different electron–phonon interactions on the donor and acceptor in the framework of the Einstein model of nuclear vibrations (
), the simple analytical expression for the rate constant has been obtained [
17,
18]:
where
. Substituting
into Equation (52), we obtain Equation (40) for the rate constant in the case of the same electron–phonon interaction on the donor and acceptor. It is easy to see that Equation (52) satisfies the relationship of detailed balance in the simplified version of dozy-chaos mechanics (Equation (42)).
14. Conclusions
In this final section, we will list all kinds of symmetries in dozy-chaos mechanics of elementary electron transfers considered in the article and discuss their physical meaning.
First of all, one should note the symmetry associated with the invariance of the expression for the rate constant of elementary electron transfers with respect to sign reversal in the dozy-chaos energy
(
Section 4). This invariance is consistent with the physical case that both the virtual acts of transformation of electron movements and energies into nuclear reorganization movements and energies and the reverse acts occur in the transient dozy-chaos state [
4,
7,
8,
9].
The result in the standard theory of many-phonon transitions [
29], corresponding to high (that is, room) temperatures, is a symmetric Gaussian function for the shape of the optical absorption band. It completely neglects the dynamics of the transient molecular state. This result corresponds to the high values of the dozy-chaos energy
in dozy-chaos mechanics (see
Figure 1). Physically, the high values of
in dozy-chaos mechanics correspond to the weak organization of the quantum-classical molecular transition (
Section 1). With a decrease in the dozy-chaos energy
, the organization of the quantum-classical transition increases, which is manifested in the appearance of a narrow optical absorption peak in the red region of the spectrum and strong asymmetry of the absorption band (
Section 5,
Figure 1). In other words, the presence of symmetry in the shape of an optical band at high (room) temperatures is associated with a primitive, Franck–Condon picture of molecular “quantum” transitions. The loss of this symmetry is associated with taking into account the effect of self-organization of the dynamics of transitions in dozy-chaos mechanics, which is expressed, in particular, in the “pumping” of dozy chaos from one part of the optical band (narrow peak) to another part (wide wing).
A series for the shape of optical absorption bands in polymethine dyes, depending on the length of the polymethine chain, has a quasi-symmetric and resonant character, where a certain “average” chain length corresponds to the resonance (
Section 8,
Figure 2). In theory, this resonance—the “center of symmetry” of the series—is the Egorov resonance (
Section 7).
An important illustration of the dynamics of the transient state for the Egorov resonance (Equations (29)–(31)) is a qualitative picture of the dynamics based on the use of the Heisenberg uncertainty relation [
6,
7,
8] (
Section 9). In this picture, a quasiparticle called transferon corresponds to the Egorov resonance. This quasiparticle has an antisymmetric twin—an antiquasiparticle called dissipon (Equation (33)). The transferon is depicted by a narrow optical band and the dissipon by a broad one. Strictly speaking, the dissipon is a certain broad resonance rather than (narrow) resonance proper.
Dozy-chaos mechanics, where the transition from absorption spectra to luminescence spectra is carried out by changing only the sign in the heat energy
, as in the standard theory of many-phonon transitions [
29], gives a mirror-symmetric picture of the shapes of absorption and luminescence bands (
Section 10.1). However, the need to take into account the dynamics of the “quantum” transition in the theory leads to the need to change the sign in the donor–acceptor distance
as well. This, in turn, leads to the appearance of mirror asymmetry in the pattern of absorption and luminescence band shapes (
Section 10.3): transitions with light emission give narrower bands in comparison with absorption bands. Physically, this means that, as a result of taking into account the chaotic dynamics of “quantum” transitions in dozy-chaos mechanics, transitions with emission of photons show themselves to be more organized in comparison with transitions with absorption of photons.
Nonradiative transitions are considered within the framework of a simplified version of dozy-chaos mechanics, in which the electronic component of the complete electron-nuclear amplitude of transitions is fitted by the Gamow tunnel exponential, dependent on the transient phonon environment (
Section 11). As in dozy-chaos mechanics for optical processes in its full formulation, this simplified version of dozy-chaos mechanics is considered for the case of the same electron–phonon interactions on the donor and acceptor. Direct and reverse processes turn out to be related not by the standard detailed balance relationship known from statistical physics but by a new, more complex, detailed balance relationship, which, in addition to the standard equilibrium constant, includes an exponential factor with the donor–acceptor distance in the exponent (Equation (42)).
Within the framework of the simplified version of dozy-chaos mechanics and the Einstein model of nuclear vibrations, the previously obtained [
12] expressions for the Brӧnsted coefficients
and
for proton-transfer reactions (
Section 12), which satisfy the well-known symmetric relation (Equation (47)), are given.
A simplified version of dozy-chaos mechanics is also considered for the case of electron–phonon interactions on the donor and acceptor of different magnitudes (
Section 13), where a special procedure for the symmetrization of the total amplitude of the quantum-classical transition (Equation (51)) and the corresponding rate constant is performed. The analytical result obtained earlier [
17,
18] for the rate constant of nonradiative transitions (Equation (52)), which satisfies the new detailed balance relationship (Equation (42)), is presented.
In conclusion, we note that it is of interest to generalize dozy-chaos mechanics for optical processes in its full formulation (
Section 2,
Section 3 and
Section 4) for the case of different electron–phonon interactions on the donor and acceptor, as well as to construct a theory of nonradiative dozy-chaos processes in its full version. An important point in the formulation of the problem in the theory of nonradiative dozy-chaos processes is the determination of the perturbation operator in the amplitude of the transition which causes the nonradiative transition. In the standard theory of many-phonon transitions [
29], the well-known operator of nonadiabaticity [
29,
31] is taken as such an operator (see [
2]). It is also of interest to generalize dozy-chaos mechanics to the case of nonlinear optics [
1,
10,
19].