1. Introduction
A prosthesis is a (usually removable) artificial replacement of missing body parts; the term can also describe an additional part that helps with manipulations [
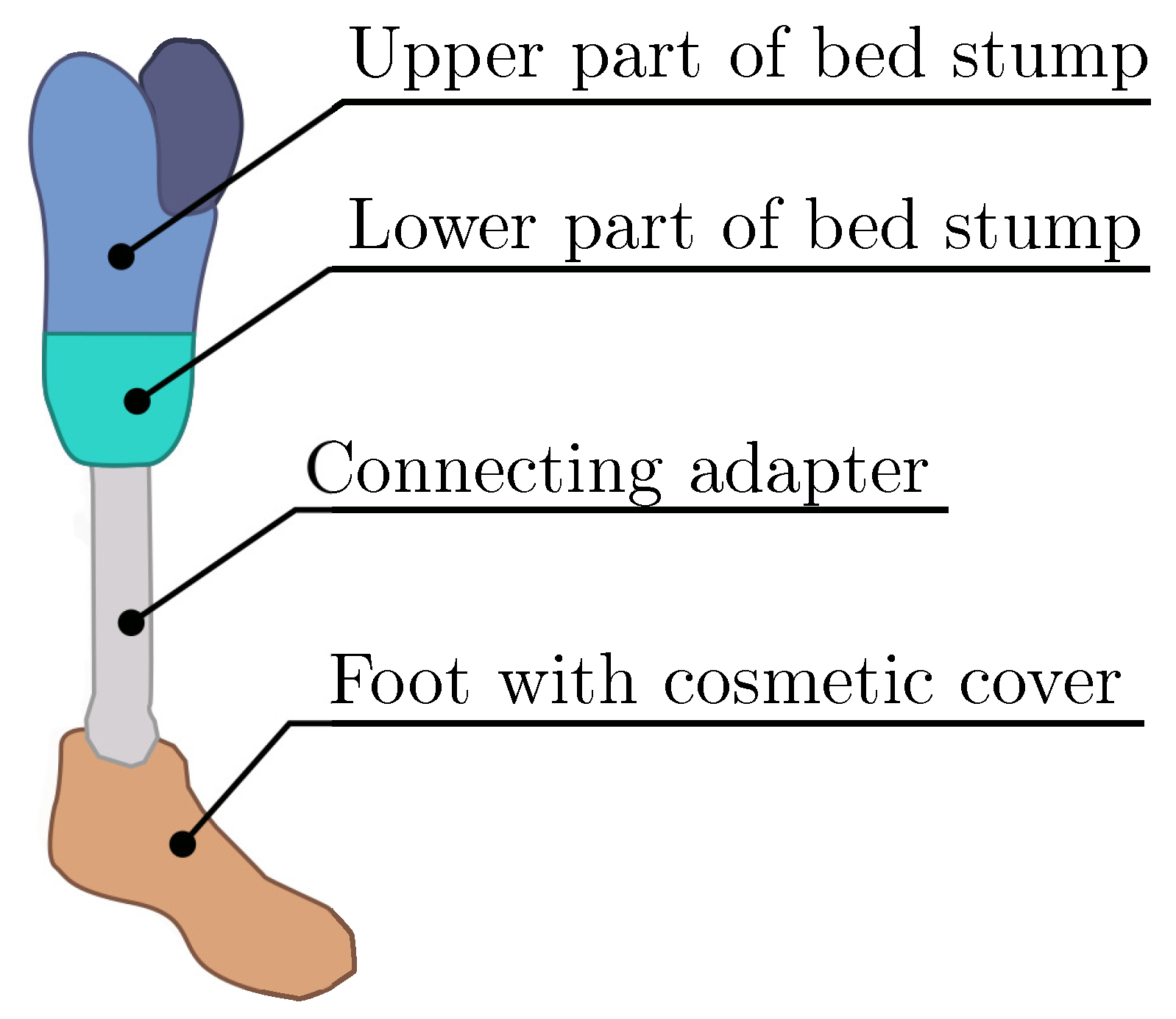
1]. Below the knee, or transtibial, amputation ]1causes asymmetry of the patient. The transtibial prosthesis (TRP) is a prosthetic aid used as a replacement of the lower limb amputated below the knee, see
Figure 1. This prosthesis helps with maintaining body symmetry and with load distribution. Prosthetic aids allow for patients to return to activities they had before the amputation [
2]. TRP consists of many catalog parts (such as the connecting adapter and the foot), which can be selected based on the levels of amputation. The only non-standard part is the bed stump (BST), also called a transtibial socket, which must be adapted to the patient.
The design of BST mainly depends on the shape and length of the stump, the weight of the patient, and their movement requirements. BST is individually produced for each patient and it contains the highest volume of material of the entire TRP [
3]. Appropriate physical properties of the BST, such as weight, stiffness, and inertia, facilitate patient’s getting accustomed to the prosthesis. However, due to the relatively high weight and often excessive amounts of material where it is not needed, a typical BST does not allow ideal patient movement. The common procedure for the production of BST includes the preparation of a cast of the stump [
4], according to which the bed is made. The cast is subsequently hand-shaped to only transmit pressure to certain load-bearing areas of the patient’s stump, thus preventing painful stimuli. This process is demanding, time-consuming, and requires considerable experience on the side of the prosthetic technician.
The aim of our study was to offer an alternative to the conservative manufacturing of prostheses by using modern methods of additive manufacturing (AM). In conservative manufacturing, direct involvement of a technician or a doctor is necessary, which makes the process time-consuming. The proposed procedure facilitates the automation of this process. Currently, AM has already become a manufacturing tool, but the used procedures are rather simple, since the production typically uses universal designs of the lower part (with lattice infilling) of the BST and only the upper part of the BST is custom-made. The new procedure that is proposed in this paper provides a basis for the customization even of the lower part of the BST according to the patient’s weight and center of gravity.
This paper aims to investigate the weight reduction of the lower part of the bed stump from the perspectives of the stiffness and load-bearing capacity, as well as the patient’s needs. Topology optimization (TOP) can be used as a tool for mass reduction, since it can be tasked with an equivalent objective. In our study, the main objective was to maximize the stiffness (minimize the compliance) with respect to the volume fraction. Volume fraction is the percentage of volume remaining after optimization. It should be noted that the goal of this optimization is not improving the stress distribution, but rather achieving the optimal tradeoff between the stiffness of the BST and weight reduction. Hence, the shape (material distribution) of the BST is very important, since it determines the amount of used material.
The use of a 3D printing method, such as the Selective Laser Sintering technology (SLS), in the production of the stump bed was described by Faustini et al. [
5]. SLS is based on gradual sintering of powder layers while using a laser beam and it is capable of achieving high accuracy, even with complex shapes [
6]. One advantage of SLS is that both the base plate and work chamber are heated, which prevents the printed part from warping or shrinking during printing. Another advantage of this method is the possibility to print without support [
7], which is crucial, since it reduces the necessary post-production time. Another commonly used AM method is multi-jet fusion (MJF), which is similar to SLS. More about AM can found, for example, in the paper by Ligon et al. [
8], who described various types of AM, materials that are suitable for each method, and showcased some applications, including medical ones. BSTs can also be produced by other methods than SLS or MJF; however, the other methods would most likely require supports during printing, which do not add anything to the structural stiffness. Mostly, they need to be removed, which, in turn, prolongs the time of manufacturing. In some cases, the part even has to be split in order to facilitate the removal of the support and then glued back together. Nevertheless, such an approach compromises the homogeneity of the part, which would negatively affect the strength of the BST.
Faustini et al. [
5] suggested a framework for individualized BST production while using a combination of computer-aided design (CAD) model and finite element method (FEM). In their paper, the bed was designed using a CAD system that was based on the scan of the patient’s stump. In the areas of contact of the bed with the sensitive sites of the distal end of the tibia and the head of the fibula, the thickness of the bed wall was reduced in order to minimize the transmitted pressure. They also recommend the use of the SLS method, since it can print complex models without losing quality.
In a more recent paper, Hsu et al. [
9] deals with a similar topic, i.e., rapid prototyping of the prosthetic socket. They highlighted that, although researchers have shown the potential of rapid prototyping in the development of prosthetic aids, the industry has not adopted it. The uncertain quality (and strength) of the prosthesis and the costs of the technology are considered the principal barriers in the way of a wider deployment of these methods, along with the absence of available suitable CAD software. The latter objection has been recently, to a large degree, removed thanks to the development of open-source and freeware software (such as Blender, FreeCAD, etc.); however, an additional software facilitating structural analysis is still necessary.
The paper by Marsalek et al. [
10] demonstrated the capability of the SLS method for the production of flexible structures with complex geometries while using the PA12 (Polyamide 12) material. Other examples of printing complex geometries using TOP have been published by Jancar et al. [
11,
12]. However, these papers use a different printing method, namely Selective laser melting (SLM)—a method that is similar to SLS, which, however, prints metal alloys and requires supports.
To consider an AM part equal to conservatively manufactured parts, it is necessary to evaluate its material properties. It is a well-known fact that 3D-printed materials may act anisotropically. Lammens et al. [
13] evaluated dogbone models 3D-printed with different orientations (flatwise, edgewise, and upright) while using the SLS method and the PA12 material. Their results suggest that the orientation greatly impacts the ultimate strength of the material, but it does not affect the Young’s modulus and Poisson’s ration. Therefore, the 3D prints produced using their method can be viewed as isotropic materials (i.e., independent of print orientation).
The presented paper describes a novel procedure for the individualized design of the lower part of a BST. A lattice-filled STL (standard triangle language) model of the BST was acquired and used as a basis for further optimization aiming to design a stiff, but lightweight, BST with filled geometry. Lattice infilling is sometimes used to reduce the BST weight. Campbell et al. studied the ultimate strength of BST printed by Fused Deposition Modeling (FDM) while using PLA (polylactic acid) and the weights of their tested samples (a typical approximate weight of a BST is 300 g) [
14]. However, lattice infilling does not provide an ideal distribution of the inner BST material, as the stiffness of lattice infilling throughout the BST is uniform; however, walking causes the bending of BST and some areas should have higher stiffness to resist this bending. New possibilities of computer modeling methods, such as topology optimization, appear promising for designing achieve optimal material distribution.
For the purposes of this study, the lower part of the STL model of the BST was filled (
Figure 2). The upper part of the BST is not optimized in this paper, since a guideline for that part is available in the review by Stevens et al. [
15], who prepared six recommendations. For example, they recommend the use of viscoelastic interface liners in order to improve load distribution, reduce pain, and increase comfort. It is not uncommon that patients have a painful experience with the TRP, more can be found for example in the study by Dillingham et al. [
16]. Typical pain and skin irritation can be reduced if the BST is directly attached to the bone, which is, however, associated with other problems. Most commonly, a metal implant is attached to the bone of the stump and, as metals tend to corrode, this can have undesired health effects, as reviewed by Chin et al. [
17].
2. Materials and Methods
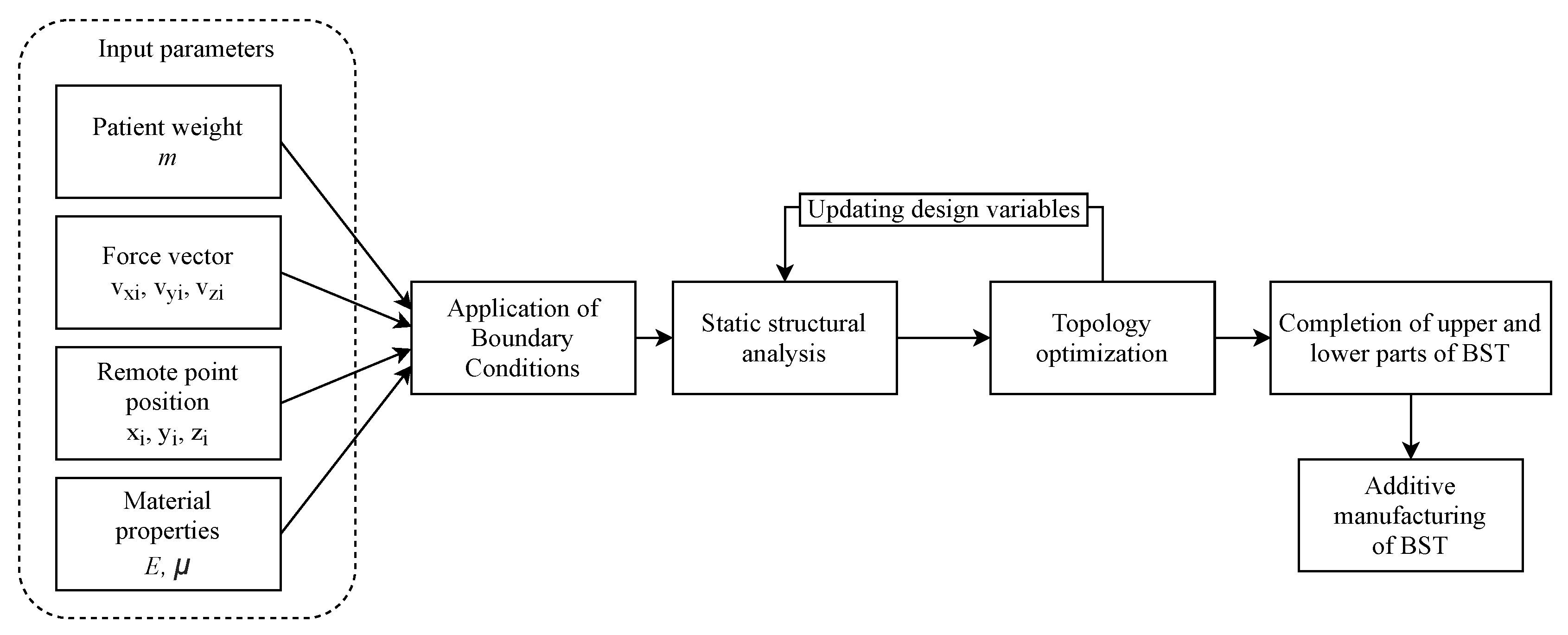
The new procedure begins when the patient after amputation undergoes an orthopedic examination. The orthopedist prepares input parameters for modeling, such as the weight
m and position of the center of gravity. Subsequently, boundary conditions (i.e., external forces acting on the prosthesis) are calculated while using weight. The calculated forces are then used as the input for the computational model using FEM. We assumed that the FEM analysis can be used to perform static structural analysis of BST within each individual stage of the gait, applying forces as boundary conditions describing the static load on the BST. We also assume that BST material can be described by linear elastic behavior, which only requires two input parameters, Young’s modulus
E and Poisson’s ratio
. The assembled model is then optimized through the topology optimization method (TOP). It should be noted that the static structural analysis combined with TOP creates a loop with termination criteria. After finding an optimal distribution of the material in the lower part of the BST, the lower part is combined with the mapped upper part of the BST. Once the shape of the entire BST is defined, it is ready to be produced by additive manufacturing (AM) offering high geometrical freedom when compared to traditional manufacturing. Once produced, the prosthesis is ready to use. The procedure is depicted in a diagram, see
Figure 3.
The following paragraphs describe the newly designed three-stage procedure in detail. In the first stage, the gait is analyzed to set the boundary conditions for the computational model. The second stage describes the preparation of the computational model while using FEM. The third stage is then devoted to topology optimization. The whole procedure can be performed in commercial software solutions; however, in our case, it is programmed in the MATLAB language, which offers greater control over the optimization and is future-proof (the analysis can be extended by additional modules).
2.1. Description of Walking Stages
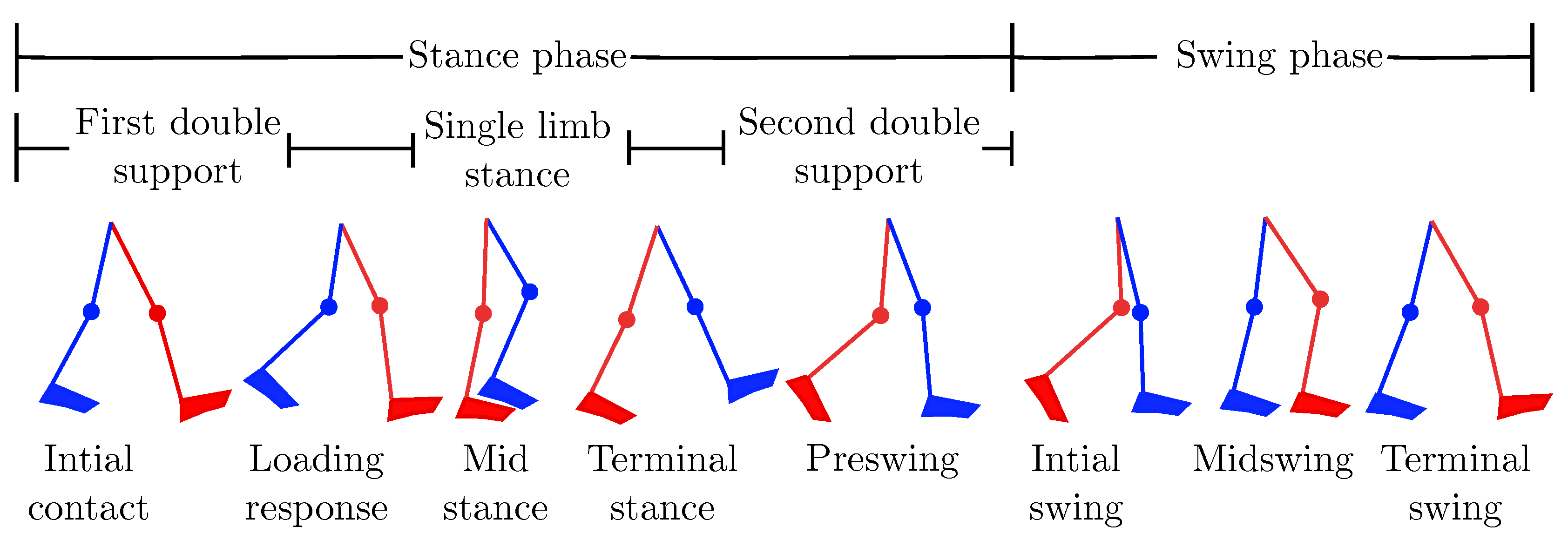
Walking is one of the basic forms of human movement. This complex process consists of consequent steps, see
Figure 4 and article by Kibushi et al. [
18]. A step is defined as a movement of the leg between the time points when the foot leaves the surface and touches it again. During this motion, one leg does not move and it can be called static. In the first part of the step, the foot of the dynamic leg leaves the surface and the static leg holds the full body weight. Next, the heel of the dynamic leg touches the surface in order to prevent falling, followed by the toes ensuring the overall balance. In the following step, the roles of legs switch. Even this simplest explanation of walking shows us possible boundary conditions, such as the force from the heel (when the dynamic leg touches the surface) and forces from the toe (when the static leg holds the full weight). Other types of movement (such as fast walk, running, climbing, etc.) depend on the frequency, speed of the process, and angle of the surface. The TOP of the lower part of the BST takes into account two main load cases that occur during walking, i.e., the heel and toe touches. These two cases are the most critical, since every other mentioned case could be viewed as their combination. One could argue that standing still could be also considered to be an important load state; it is, however, already included in the previous cases (i.e., the load while standing is much lower than that present during movement). The forces acting during these two cases cause the bending moment and bending stress in the BST, which has to automatically sustain the stationary body weight. Additionally, during standing, forces would be split evenly between both legs. It should be noted that, in this paper, we assume that walking on an infinite plane without tilting.
2.2. BST Material
BST is principally a multi-material part. It combines rigid parts, which have to withhold bending that results from the loads and forces in action, and soft parts absorbing energy, which help to ease pain in the residual limb [
19]. This means that the whole BST part should be rigid with a soft interface inside the upper part of the BST. Quintero-Quiroz et al. [
19] performed a review of the materials that were used for lower limb prosthetic and orthotic interface and sockets, and associated skin problems. They pointed out that commonly used materials are polymers-based, such as polyethylene, polypropylene, and nylon. Some prostheses can be manufactured from composites. Fibers considerably increase the mechanical properties of the BST. The soft interface should be made of foam or silicone thermoplastic elastomers. Silicone is a very suitable material due to its viscoelastic nature [
15].
Currently, materials used in AM vary greatly, depending on the type of AM technology. 3D printing technologies commonly used in medical fields include FDM, SLS, and MJF [
20]. PLA is a popular material for the FDM method that is usable for BST [
14]. Popular materials for SLS and MJF methods include PA12 and PA11 [
5].
Nylon–Polyamide 12 (PA12), a thermoplastic material with good chemical and wear resistance and high toughness, was selected as the material considered in this study. It has a great strength-to-weight ratio. It can be also recycled, with the maximal ratio for safe quality three-dimensional (3D) printing being 80% new and 20% recycled material [
21]. It is also an appropriate material for contact with human skin and, moreover, is self-supporting if SLS and MJF methods are used. The linear elastic material model of PA12 was used for the description of the behavior of the 3D printing material.
Table 1 lists the material properties and characteristics of PA12 reported by Faes et al. [
22].
2.3. Design of Computational Model
The computational model is made using FEM. The principle of FEM is to break the geometry into simple elements connected with nodes. This process is called discretization and the connected elements are called “mesh” (
Figure 5). In structural analysis, these finite elements are described by the stiffness matrix. In this work, 3D finite elements are used. The stiffness matrix of each element is calculated as the volume integral
where
is the strain-displacement matrix and
represents the stress-strain matrix. The integral is solved numerically. To be able to calculate the primary variable, i.e, the displacement, it is necessary to assemble global stiffness matrices; in other words, all of the element stiffness matrices
are assembled into a global stiffness matrix
. After assembling the
, the static equilibrium equation is solved
where
is the force vector and
is the displacement vector. After finding the primary variable (the displacement), secondary variables are calculated (such as the strain or stress of the part). This is a fundamental description of FEM in structural analysis. The procedure of creating stiffness matrices for used elements can be found in books by Bhatti [
23,
24]. In these books, fundamental topics (from basic principles shown on simple elements, such as truss and beam element to simulating plane stress elements) and advanced topics (from the analysis of elastic solids to nonlinear analysis) in FEM are described, as well as the procedure to create a stiffness matrix of linear and quadratic elements. These books also offer MATLAB scripts for preparing linear solid elements. These scripts were slightly changed in our study in order to improve calculation times. Further practical advice on the use of FEM in other industrial applications can be found e.g., in papers by the group of Horyl and Marsalek [
25,
26].
The first step of the assembly of the computational model of the lower part of the BST was to create the mesh. In this step, the ANSYS2019R3 software was used as the mesh generator (mesher). The designed geometry of the lower part of the BST is complex in shape; as a result, the easiest way to create the mesh is to use tetrahedron elements. However, this comes with disadvantages, such as the “forced” usage of the quadratic approximation for achieving decent results. On the other hand, the advantage of the linear tetrahedron elements is a mesh with fewer nodes and, therefore, fewer degrees of freedom. However, to achieve results that were comparable to those achievable using a hexahedral mesh, the tetrahedral mesh has to be finer, which negates the above-mentioned advantage. A hybrid mesh with both tetra- and hexahedral elements has, unfortunately, similar properties and results as the tetrahedral mesh. This type of mesh is not evaluated in this paper. The uniform hexahedral mesh delivers a better shape and allows us to use more filtering schemes (which is an important process in topology optimization, see
Section 2.5) than non-uniform mesh. Uniform computational models support the use of linear hexahedral elements. One of the methods that can be used for providing uniform elements, the Cartesian method, comes with the advantage of fitting to the geometry of the desired model. A disadvantage of this method rests, however, in shape differences, mainly in the round edges. Another disadvantage of the Cartesian method is that it does not support flexibility in minor changes of the mesh. For example, a change of the element size from 2 mm to 2.1 mm will not provide a different mesh.
For the purposes of this work, four different meshes were tested.
Table 2 lists the mesh statistics. The first mesh was made of tetrahedral elements and the last three were made using the Cartesian method with coarser, normal, and fine hexahedral meshes.
Figure 5 shows the difference between a tetrahedral and hexahedral mesh.
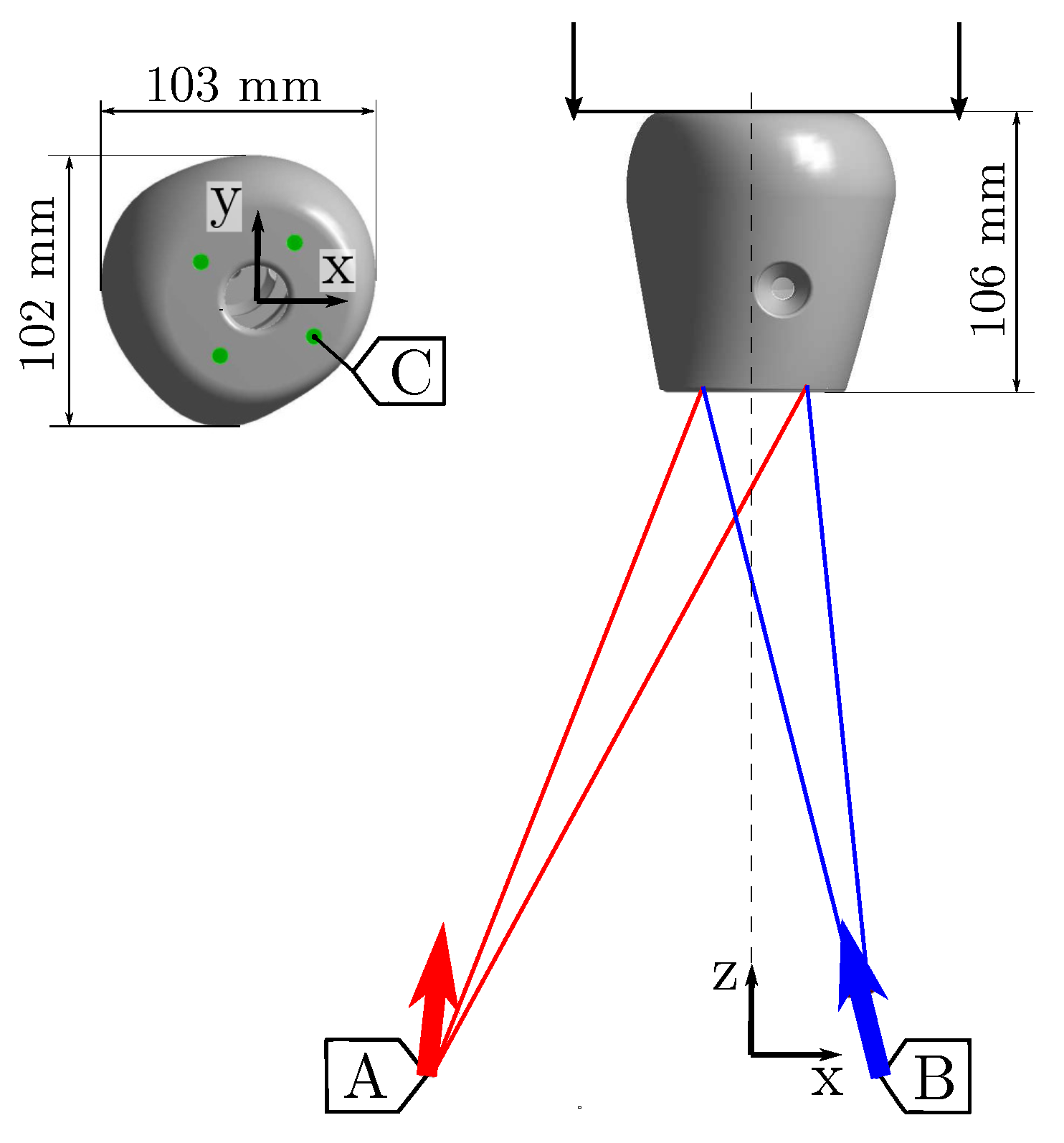
The computational model aims to simulate the course of walking while using TRP. Another important factor influencing the optimization results is the correct description of the boundary conditions in the presented computational model. The simulation of bolted connections, including connected parts, is a very complex process [
27]. To simplify the model and speed up the proposed procedure, one-dimensional truss elements were used in order to replace the connecting adapter and foot including bolted connections (
Figure 1). The stiffness matrix assembly of truss elements
can be found in the book by Bathe et al. [
28], the practical application of truss elements was showcased in an article by Klemenc et al. [
29]. High Young’s modulus value simulates an almost rigid connecting adapter. The behavior of the proposed boundary conditions was derived from a laboratory experiment, in which the test equipment is on both ends connected to the lower part of the BST using bolts (considered rigid). The test equipment acts as a lever simulating the force from the toe and the heel. The global stiffness matrix consists of
where
is the stiffness matrix of BST and
is the stiffness matrix of truss elements.
The location matrix approach [
30] was chosen for creating the global stiffness matrix and global force vector. In the first step, the location matrix containing information about nodes (and their degree of freedom) was assembled. Additionally, the local stiffness matrices were combined into a single vector (array) and then added to the corresponding location matrix. This approach ensured low memory usage since it was not necessary to prepare a “full” matrix, just its sparse version (which was sufficient since most stiffness matrices are sparse). Hughes [
30] suggested using the loop cycle for creating a matrix, but it is faster to assemble a global matrix using the MATLAB function “sparse”. The function automatically adds up stiffness values if they are in the same position in the global matrix. The scheme of a simplified computational model is depicted in
Figure 6. Subsequently, loading forces with corresponding vectors and remote points positions were calculated, which was an important part of the bed stump customization. In this paper, three patients’ weights were examined:
m = 98 kg, representing the mean weight of the 95th percentile human model,
m = 78 kg, representing the mean weight of the 50th percentile human model [
31], and
m = 120 kg representing a weight extreme. In the table below,
Table 3, the position of the remote point, corresponding force vector (related to the original coordinate system), and values of the force multiplied by safety factors are presented (dynamic factor
= 2.00 and general safety factor
= 1.50).
2.4. Topology Optimization of Designed Model
The process of optimization is an important part of the newly designed procedure. The main goal is to modify the lower part of the BST, minimize the weight, while maximizing the stiffness. This goal can be formulated as an objective function [
32]. Many tools can help us to solve objective functions. In our case, topology optimization was chosen as an optimization tool. This tool is being increasingly used in recent years, especially thanks to the advancements in computer performance and in new manufacturing technologies (in particular, the above-mentioned AM, 3D printing) [
33]. Topology optimization is, in principle, a calculation of the structural distribution of the material without defining a precise initial or final shape. The principle is to find black and white distribution, i.e., places where there are solids and where there are voids. Because we are solving on a supporting structure, the optimization can find new innovative and effective structural layout.
In our case, the objective of topology optimization was to solve the minimum compliance problem. As walking is a complex process, the objective was divided into multiple objectives that corresponded to multiple load cases. The used principle is called a weighted sum method [
34], in which the multi-objective function is defined as the sum of objective functions
with weights
. The objective function represents potential deformation energy of the m-th load case
where
is the force array of the m-th load case and
is the displacement array of the m-th load case.The array of displacement is solved while using the equilibrium equation
where [K] is the global stiffness matrix. The volume constraint
depends on the size of the volume fraction
, where
is the array with element volumes. The design variable range is
where
is also labeled as filtered density. If we substitute the equilibrium equation into an objective function and apply the material model, we obtain
where
is the displacement vector of the element and [k
] is the stiffness matrix of each solid element. The material model is a power law, which is called Solid Isotropic Material with Penalization (SIMP) [
35]. The value of the penalization factor
p is set to
. SIMP is described by the equation
where
is Young’s modulus of the original material (PA12). It is also recommended for the constraints to have minimal allowed design variables to ensure the displacement is solvable, which reduces the possibility of the global stiffness matrix being singular. The recommended minimal value is
=
. Alternatively, the Young’s modulus of void
can be added to the model
The value of Young’s modulus of void should be
MPa. In this paper, the value is set to
MPa [
36]. It is recommended to prepare local stiffness matrices of elements before the optimization. In the static linear analysis, Young’s modulus is scalar and it can be factored out. The equation for the local stiffness matrix is
where [k
] is the stiffness matrix with unit Young’s modulus. This approach drastically reduces the computing time, because the numerical integration of each element is computed only once.
For solving the optimization, it is necessary to find an appropriate method, such as Karush–Kuhn–Tucker (KKT) conditions [
32]. KKT conditions are used in many algorithms dealing with minimizing problems (in particular, the minimizing compliance problem). The algorithm used in this paper is called the Optimality criterion. It was obtained and adapted from the paper by Liu et al. [
36] in order to fulfill the mentioned objective functions.
It should be noted that TOP has two termination criteria. The first criterion is achieving the maximal number of iterations. In this work, the maximal recommended value is 200. The second criterion is achieving the minimum change of design variables from the previous iteration [
37]
where
are design variables of the current iteration,
are the design variables of the previous iteration and
is the tolerance value (in this case
).
The advantage of multiple load cases lies in creating a stable and robust design. Additionally, the process of preparing an additional load case is uncomplicated—since the global stiffness matrix is already prepared for the first load case, it can be used for any subsequent load case. However, a considerable disadvantage is represented by the computing time. It is increasing linearly with each case and solving a matrix with two load cases takes, therefore, about two times longer.
2.5. Filtering Method
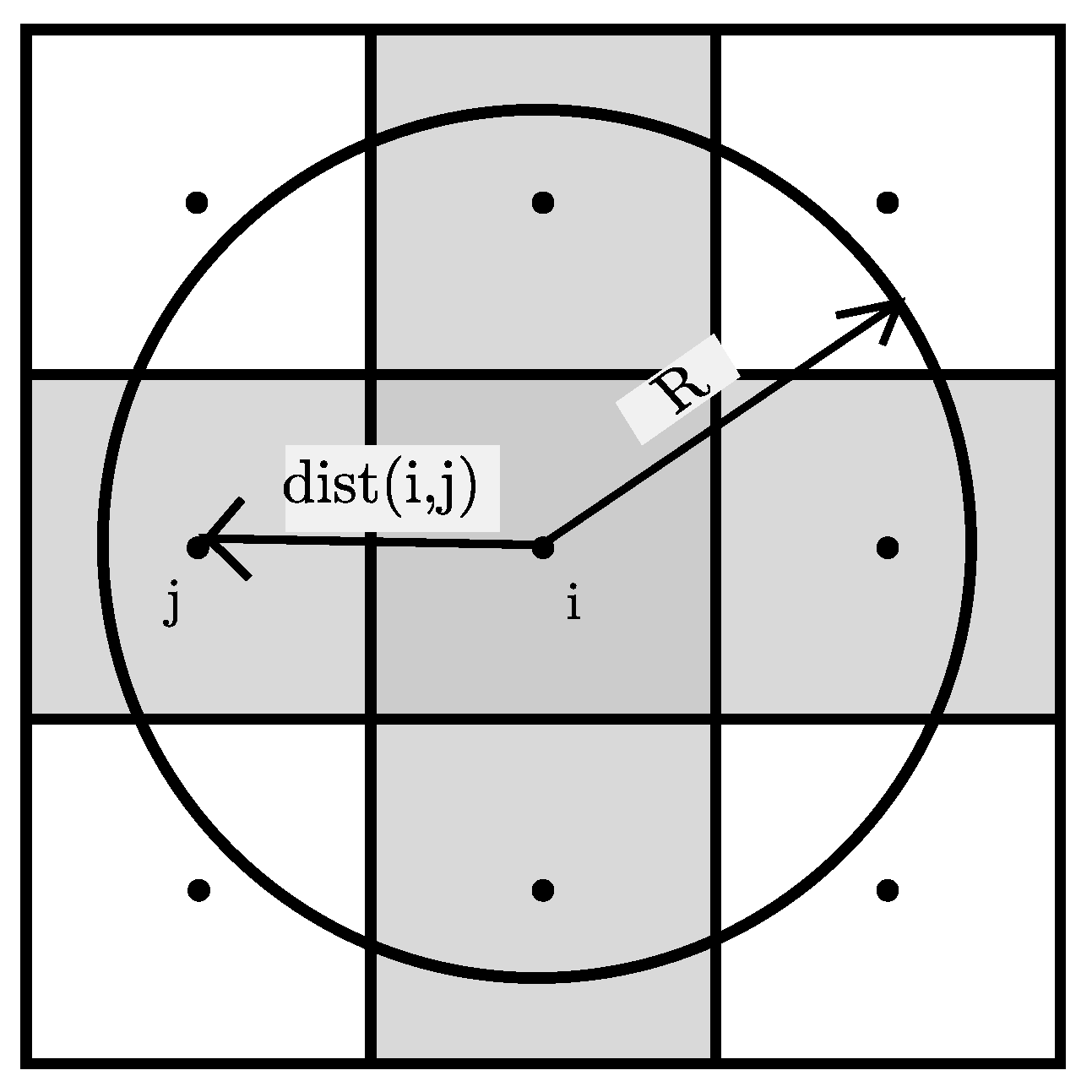
The deployment of the filtering method is one of the possible approaches for resolving TOP-associated problems [
38]. The method does not ensure the existence of the solution, but numerous numerical experiments proved that the results were mesh-independent [
37]. Filters usually have a common parameter, called the weight factor (or the matrix of the weight factor)
where
R is the radius of the filter and
is the operator calculating the distance between the
i-th and
j-th elements. This means that, if the distance is greater than the radius, then the weight factor is zero. If the distance is zero, the weight factor has a value of the radius. In a two-dimensional (2D) problem, the radius forms a circle, see
Figure 7 and in a 3D problem, it creates a sphere.
The Grayscale filter [
39] with a density filter is an appropriate choice of the filter for the presented procedure. The principle of the density filter approach lies in averaging the design variables of elements to its neighborhood. This method should ensure smoothing of the stiffness. This filtered density is used in the static analysis. Generally, the density is calculated as 0 or 1. After applying the filter, the areas with intermediate density are penalized by the SIMP model. The deformation energy (objection function) is also averaged. The principle of the Grayscale filter is also to penalize the volume constraint [
40]. Based on the penalization, the filter underestimates the intermediate density, which gradually leads to a reduction of the value down to 0 (void). Underestimation also takes place in the inner iteration of the used algorithm. This leads to fewer iterations needed for finding the solution. The solution has fewer "light-grey" areas. It should be noted that the Grayscale filter does not ensure a checkerboard-free design and it has to be used with an additional filter (in this case, with the density filter).
3. Results
The lower part of the BST was optimized based on the use of the newly designed procedure. The following figures display finite elements with their design variables
. There are two color schemes: a discrete scheme (Gray–Brown–Red) and a continuous gradient scheme (from yellow to blue). The classic black&white gradient scheme does not provide acceptable figures.
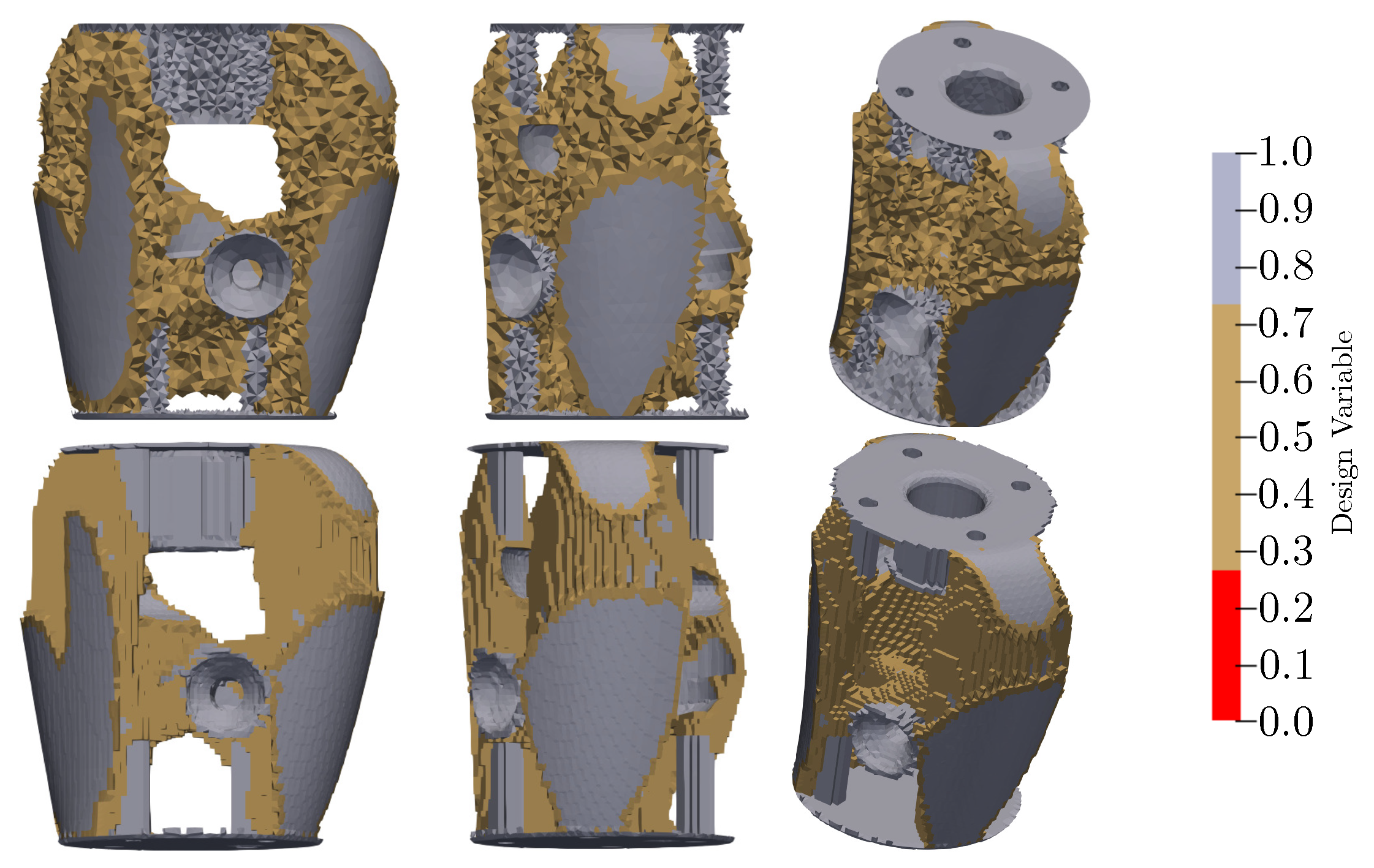
Figure 8 shows the final optimized shapes with tetrahedral and with hexahedral elements. The grey color indicates areas that have to be preserved (these elements carry the structure).
Elements in brown do not fully participate in the stiffness (partially at best). The number of these elements can be controlled by the designer. A fine line between the value of the objective function and the constraint function has to be established (lower number of elements leads to the volume minimization, but the structure can become compliant). The third color (red) is not present in
Figure 8 because the limit of the design variable was set to 0.30. Anyway, these elements should be removed since they do not help carry the structure. The settings were the same for all analyses (unless otherwise stated). In the first analysis, the used mesh was the only difference. The results look similar, which means that results from the proposed design procedure (processed using MATLAB code) are not dependent on the mesh.
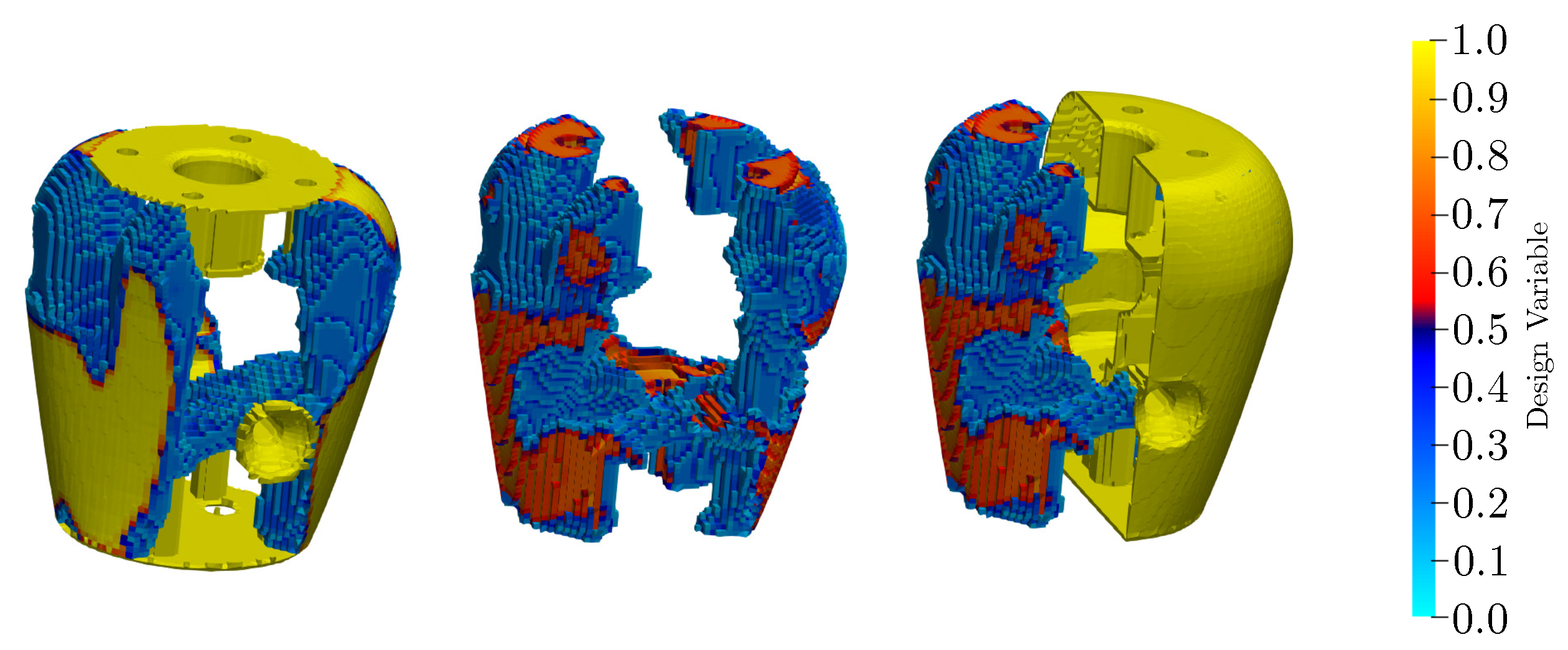
Figure 9 shows a comparison of the result with and without preserved exterior s]1urfaces. The yellow color on the scale indicates elements that must be preserved and the blue color indicates those that can be removed.
It is obvious that the shapes are similar, almost the same. However, the model without preserved exterior surfaces is not as appealing as the model with preserved surfaces. The middle figure shows the BST core if outside surfaces are preserved. Two penalization factors are chosen (
p = 3 and
p = 4). In
Figure 10, both results for the normal hexahedral mesh are presented (section by a plane). At the first sight, these shapes seem identical, but it should be noted that non-yellow elements are more penalized when
. This modification helps to control intermediate density. Exterior surfaces are preserved due to the functions of these surfaces and appearance.
Table 4 describes the weights of full geometry, geometry with infilling, and shape optimized using TOP. The results are divided into the robust and lightweight designs. The robust design means that every element with the design variable below the limit of 0.01 is removed. In the lightweight design, the limit is set to 0.30, which leads to removing more elements from the BST. The table also contains the values of the objective functions. You can notice that the compliance of the lightweight design (
) is approximately 50% higher while it weighs less than half of the original.
The results for different loads are detailed in
Table 5. The relative error in the norm form is less than 10%. It is a result of the used approach and the utilization of linear analysis for model evaluation.
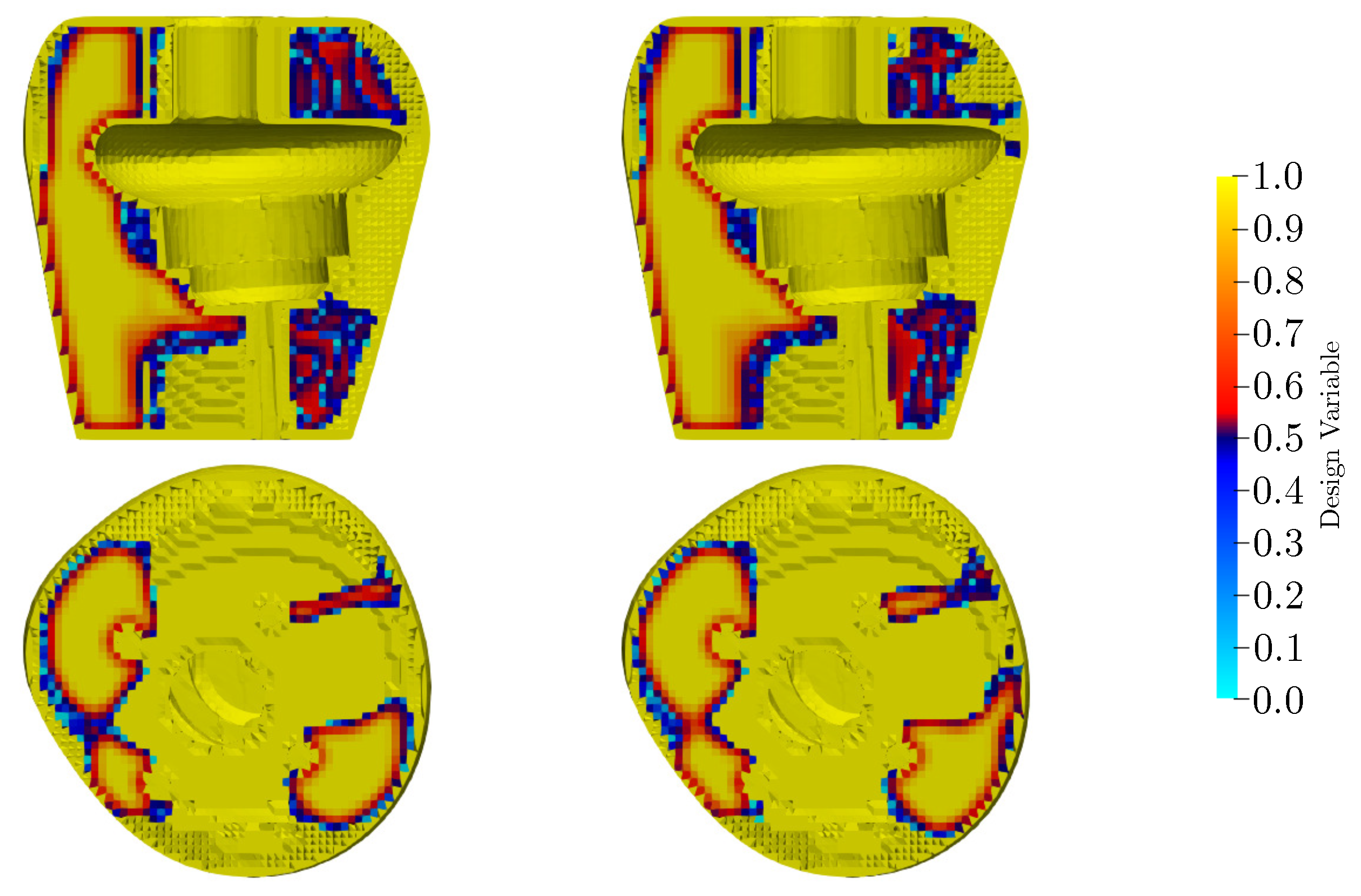
Figure 11 shows the BST core for different patient weights using a hexahedral normal mesh. Only small differences are visible (circled in the figure); the overall cores of BST, however, seem the same. Nevertheless, the use of a tetrahedral mesh shows literally no difference in the shape, regardless of the load (
Figure 12). This also showcases how poorly linear tetrahedral elements perform in structural analysis. Only the extreme weight (120 kg) resulted in a different value of the norm objective function.
4. Discussion
The presented paper describes the new design procedure of the transtibial prosthesis bed stump while using topology optimization. The new procedure starts with measuring the patient weight, which determines forces acting upon the prosthesis. These forces are subsequently inputted into the computational model using FEM for solving static structural analyses. Subsequently, the computational model is optimized through a topology optimization algorithm with input from a static structural problem (namely displacement and stiffness matrices). Termination criteria decide the end of the loop of the topology optimization. The optimized shape is ready to be produced by AM, with the SLS method being well-suited for this application.
Three important stages of the procedure are described. The first stage is studying gait stages. The second stage describes the preparation of the computational model. The model is then constructed while using finite elements. As the BST geometry is complex, only a few types of mesh can be created.
In the third stage, topology optimization is used on the computational model. In this paper, the necessary theoretical background of topology optimization was also explained. It should be noted that, during topology optimization, active elements can be forced, which leads to preserving important parts of the BST geometry (such as exterior surfaces).
The obtained results are evaluated based on the presented stages; in addition, four prepared discretizations of the lower part of the BST while using tetrahedral and hexahedral elements are analyzed. The results from topology optimization varied with inputs and output evaluation. In the first part of the evaluation, the mesh-independence was investigated (results are mesh-independent, see
Figure 8). In the second part, we tested whether the preservation of the exterior faces works (it works, see
Figure 9). The third part compared results obtained with different penalization and cut off-limits. In the last part, the effects of different loads on the hexahedral and tetrahedral meshes were evaluated.
This procedure is based on the assumption that loads can be used in static structural analysis. Optimization provides material distribution for the static stiffness. However, forces caused by walking have a harmonic character. Therefore, it would be recommended to invest time in the optimization of dynamic stiffness. The optimization of dynamic stiffness can be formulated as maximizing the natural frequencies—a type of objective function. Used material could also act nonlinearly; it would be, therefore, appropriate to prepare a nonlinear solver for large deflection (deformation), which would help to prevent the structure from being prone to buckling.
The optimization problem that we tackled in this study can also be solved in commercial software (e.g., ANSYS Workbench 2019R1). In view of this, the importance of investing time into preparing MATLAB scripts might not be apparent at the first glance. One could argue that, if the results are comparable, why should anyone develop scripts? However, fine-tuning optimization is difficult in commercial software solutions since the software limits the inputs (for example, one cannot define the element’s neighborhood, since it is already defined by the software). Commercial software might also be limited by the used analysis, potentially offering only static structural and modal optimization. However, the methods of TOP are still developing and it might be necessary to perform a complex optimization. Scripting also provides the user with freedom in expanding its optimization (for example, adding modules, as mentioned above). We assume that, for full deployment of this procedure in production, it is necessary to have all of the parameters of the design under control.
The paper only focuses on the modeling of the BST but to prove the usefulness of the procedure, additional experiments are necessary. These experiments should evaluate the critical failure force and fatigue, especially the high cycle fatigue life since patients are using their prosthesis on a daily basis. After that, the mathematical models should be extended to help predict fatigue. Further experiments should also provide more information on whether AM is a suitable technology for prosthesis production.
5. Conclusions
In this paper, a pilot study of the new procedure using topology optimization is showcased. The procedure offers designers a new innovative solution for complex geometry. This innovative solution cannot be used in conjunction with conservative manufacturing methods; instead, it is recommended to use AM (the SLS method). Because this is only a pilot study, the procedure will be tested and improved on a higher number of patients with different “levels” of amputation.
When compared to the uniform lattice infilling, this procedure offers a better weight reduction without making the BST too compliant. The reduction of the weight achieved by the lattice infilling design is approximately 16%, while the procedure that is described in this paper provides us with 36% to 58% reduction. The deformation energy of the proposed designs has increased by at most 70% when compared to that calculated with full geometry. This means that we managed to create a design with significantly reduced weight without making the BST too compliant. Therefore, the objective of this study was met.
Although the weight of the designed part was significantly reduced, we cannot consider it to be a generally valid optimal solution. We have to point out that it is an optimal result for the two load cases analyzed in our study, but walking is a complex action, which does not only depend on the toe and heel. The recommendation is as follows: for optimization, it is suggested to add at least two more load cases. Forces should act at a plane that is perpendicular to the current one (plane made with toe and heel). Other forces could cause torsion of the BST We also assumed walking on a level plane but the forces can act differently when walking uphill or downhill; the same can be said if walking is not even. If we would like to describe walking completely, we would need over 20 load cases, which would, however, be associated with an immense increase of the computing time. For example, the computing time for the finer hexahedral mesh (approximately 0.6 million degrees of freedom) is 2.6 h (30 iterations) on a modern machine (workstation Intel i5-10600K 12 cores, 32 GB RAM, SSD). Approximately 5 min. is needed for each iteration. If two additional forces are present, time would be multiplied by 2 (i.e., 10 min. per iteration). At that point, it would be recommended to invest resources in finding parallel solvers. The paper by Makropoulos et al. [
41] dealt with solving elastic (and mainly elastoplasticity) problems while using parallel solvers (solving tens of millions of unknowns).
The difference between the modeled patient weights was negligible, because the model was solved by linear analysis. A plastic material is not as stiff as steel, which means that major deformations can occur. The recommendation is to invest time in creating a solver with large deformations, for example, using the Arc-Length algorithm. Again, however, this addition will increase the computing time and it would be beneficial to find a parallel solver.
The paper also recommends the use of a filtering method. Using a combination of the Grayscale filter and the density filter is great for practical application, since it provides a robust design with fewer iterations. The only disadvantage is the presence of “grey” regions (intermediate design variable), which could be hard to assess without prior experience.
There are 12 variants of results that vary in the element size, analysis settings, and post-processing. The mesh should be as uniform as possible and, hence, the Cartesian method is recommended. However, it comes with some disadvantages, such as differences in the shape resulting from geometry (e.g., problems associated with round edges). Smaller elements are also likely to provide better results (offering greater freedom within optimization). However, it should be noted that, even the state-of-the-art methods of additive manufacturing can have limitations in printable sizes (and their tolerances). It is also recommended to continue post-processing in the form of shape smoothing, because the results usually have many sharp edges and corners. Ultimately, the results can be viewed as estimated results, which are able to help the designer to appropriately remove the unnecessary material creating new geometry.