Multivariate Control Chart Based on Kernel PCA for Monitoring Mixed Variable and Attribute Quality Characteristics
Abstract
1. Introduction
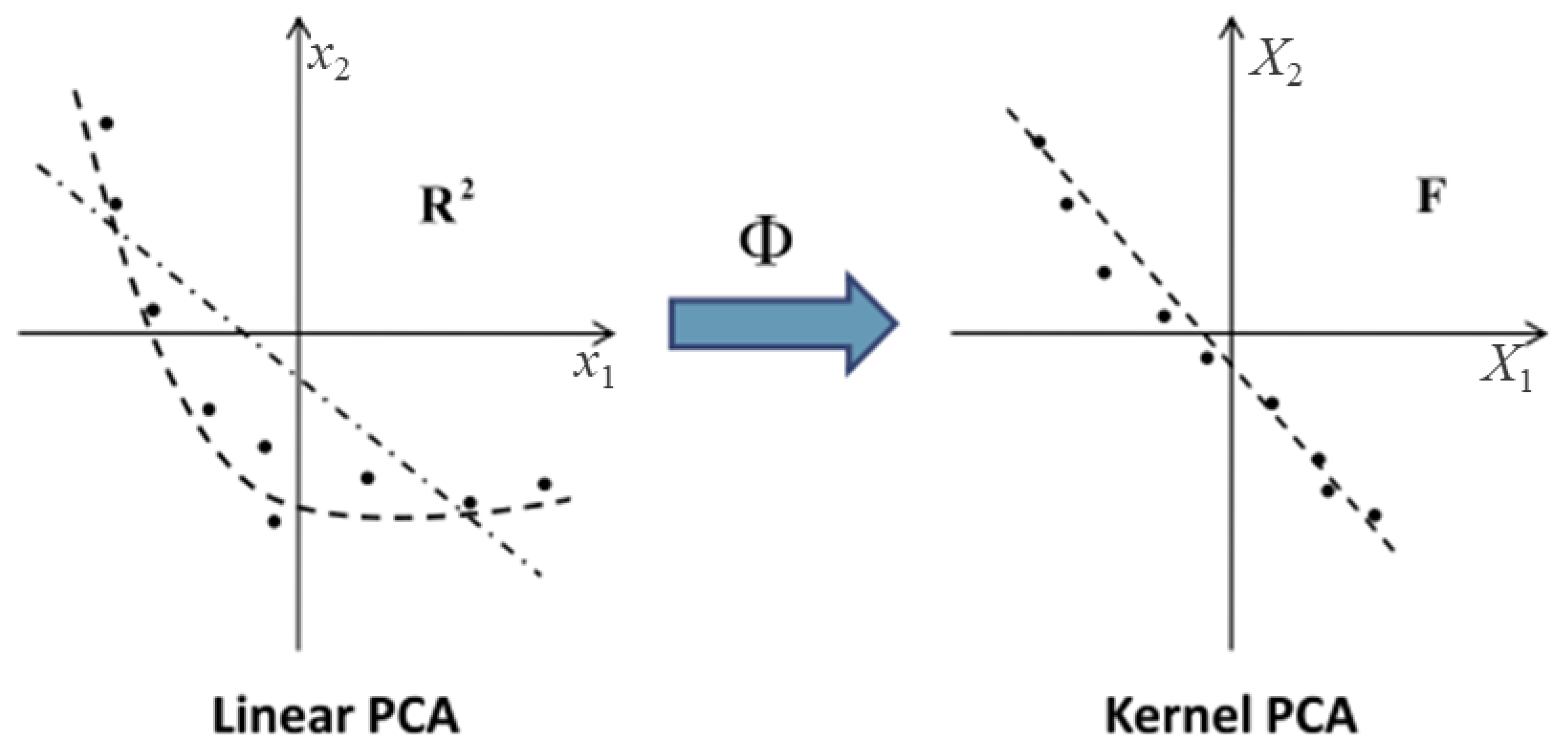
2. Kernel PCA Mix Control Chart
2.1. Kernel PCA
2.2. Kernel PCA Mix Control Chart Procedures
- Form matrix sized where:
- sized is centered on a matrix which is contained the metric data.
- sized is centered on a matrix which is contained binary coding from every level of nonmetric data . For example, has three categories such as “no defect”, “minor defect”, and “major defect” represented as 1, 2, and 3, respectivelywhere the dummy variable for “no defect” symbolized as 1 is 1 0 0, the dummy variable for “minor defect” symbolized as 2 is 0 1 0, and the dummy variable for “major defect” represented as 3 is 0 0 1.
- Calculate
- Choose the kernel function.
- Calculate the matrix kernel
- Calculate principal component score t as follows:
- From the first l principal component t, calculate the T2 statistics using the following equation:where , and eigenvalues that correspond to v-th PCs.
3. KDE Control Limit
- Linear Kernel K(xi,xj) = 〈xi,xj〉.
- Polynomial Kernel K(x,y) = (〈x,y〉 + 1)d.
- Radial Basis Function (RBF) Kernel
- (balanced case),
- (imbalanced case),
- (extreme imbalanced case).
3.1. Linear Kernel
3.2. Polynomial Kernel
3.3. RBF Kernel
4. Performance of the Proposed Chart
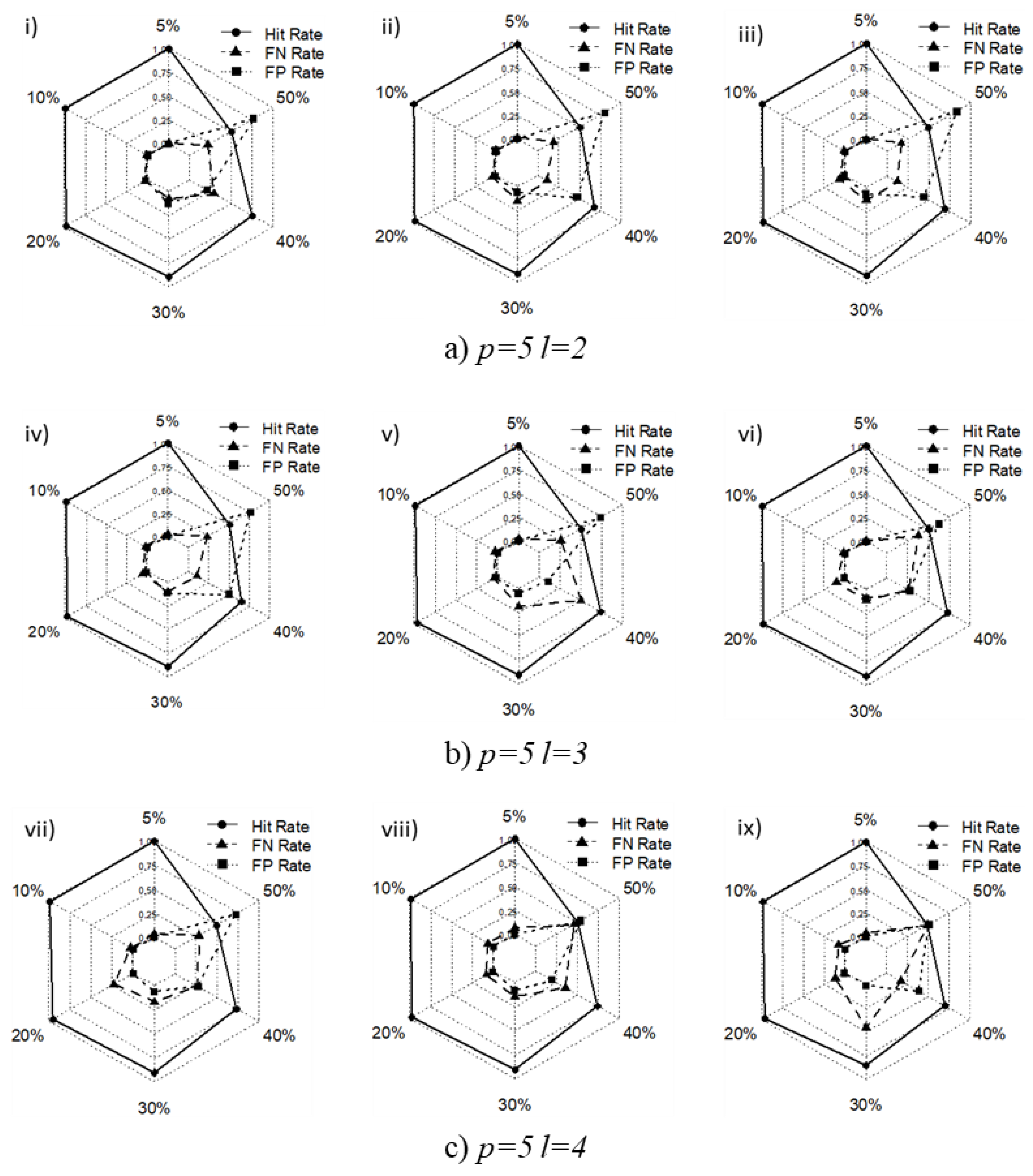
4.1. Detecting Outlier
4.1.1. Simulation Setup
4.1.2. Simulation Results
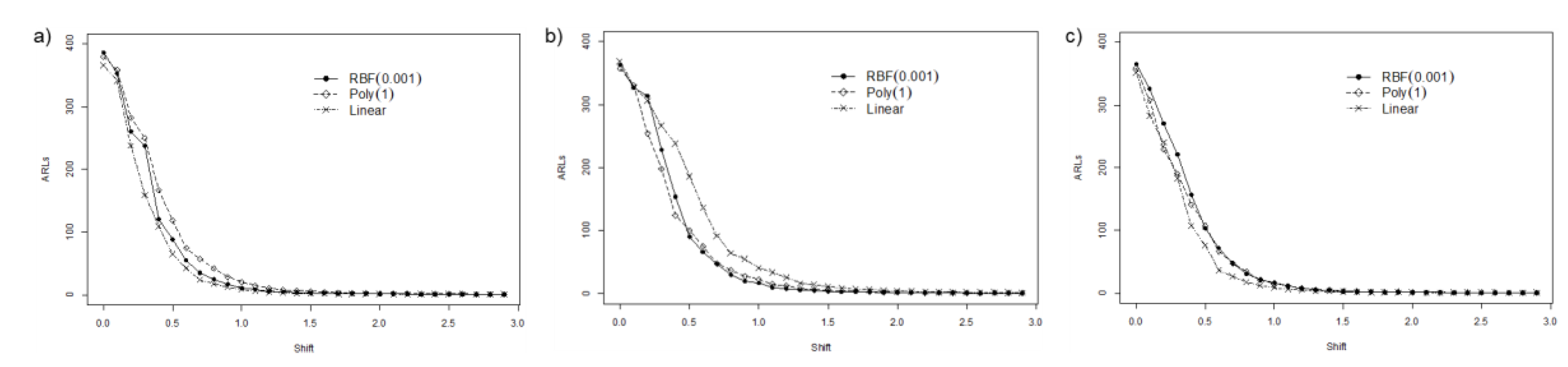
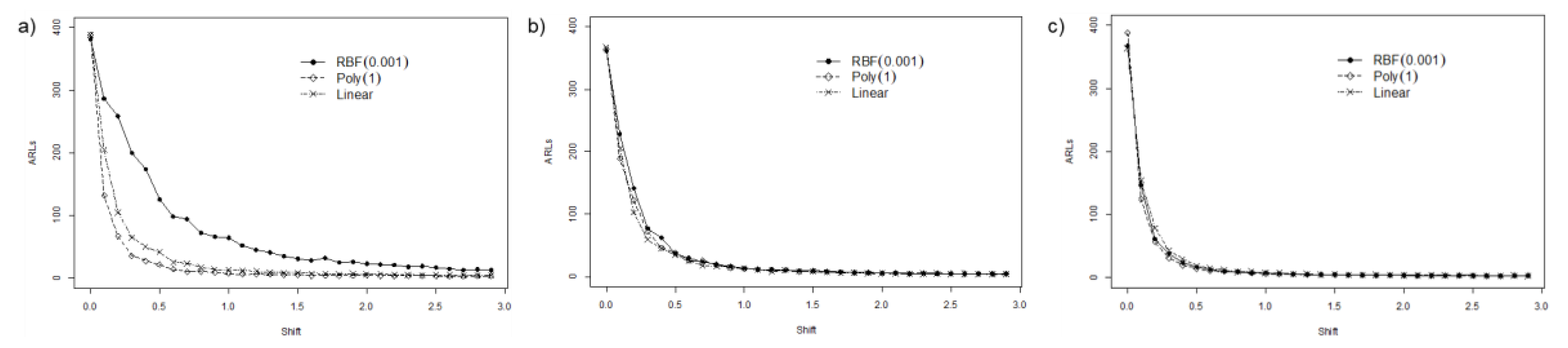
4.2. Detecting Shift in the Process
4.2.1. Extreme Imbalanced
4.2.2. Imbalanced
4.2.3. Balanced
4.3. Summary and Discussion
5. Applications
5.1. Simulated Data
5.2. Real Data
6. Managerial Implication
7. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9990 | 0.0082 | 0.0006 | 0.9968 | 0.0126 | 0.0022 |
| ii | 0.9989 | 0.0108 | 0.0005 | 0.9949 | 0.0072 | 0.0048 |
| iii | 0.9980 | 0.0034 | 0.0019 | 0.9972 | 0.0120 | 0.0018 |
| iv | 0.9985 | 0.0232 | 0.0004 | 0.9961 | 0.0197 | 0.0021 |
| v | 0.9985 | 0.0204 | 0.0005 | 0.9960 | 0.0295 | 0.0012 |
| vi | 0.9983 | 0.0078 | 0.0013 | 0.9961 | 0.0208 | 0.0020 |
| vii | 0.9981 | 0.0340 | 0.0002 | 0.9953 | 0.0286 | 0.0021 |
| viii | 0.9963 | 0.0722 | 0.0001 | 0.9932 | 0.0627 | 0.0006 |
| ix | 0.9978 | 0.0402 | 0.0002 | 0.9913 | 0.0834 | 0.0004 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9762 | 0.0316 | 0.0219 | 0.8892 | 0.0734 | 0.1269 |
| ii | 0.9784 | 0.0414 | 0.0166 | 0.9127 | 0.1515 | 0.0597 |
| iii | 0.9802 | 0.0679 | 0.0078 | 0.9105 | 0.1313 | 0.0716 |
| iv | 0.9761 | 0.0537 | 0.0164 | 0.8920 | 0.0974 | 0.1125 |
| v | 0.9733 | 0.0420 | 0.0229 | 0.9080 | 0.1916 | 0.0494 |
| vi | 0.9738 | 0.1040 | 0.0068 | 0.8993 | 0.1173 | 0.0936 |
| vii | 0.9521 | 0.2320 | 0.0019 | 0.9021 | 0.1719 | 0.0661 |
| viii | 0.9737 | 0.0873 | 0.0110 | 0.8993 | 0.1448 | 0.0818 |
| ix | 0.9705 | 0.1144 | 0.0083 | 0.8563 | 0.4560 | 0.0099 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.7491 | 0.2988 | 0.2190 | 0.5001 | 0.2254 | 0.7745 |
| ii | 0.6728 | 0.1134 | 0.4698 | 0.5013 | 0.1903 | 0.8070 |
| iii | 0.6852 | 0.1269 | 0.4401 | 0.4985 | 0.1686 | 0.8345 |
| iv | 0.6569 | 0.1056 | 0.5015 | 0.5002 | 0.2320 | 0.7677 |
| v | 0.7377 | 0.5011 | 0.1032 | 0.5009 | 0.2608 | 0.7374 |
| vi | 0.7320 | 0.2549 | 0.2768 | 0.5012 | 0.3773 | 0.6203 |
| vii | 0.7293 | 0.2701 | 0.2712 | 0.4969 | 0.2847 | 0.7215 |
| viii | 0.7405 | 0.3587 | 0.1935 | 0.5000 | 0.4616 | 0.5385 |
| ix | 0.6984 | 0.1764 | 0.3851 | 0.4993 | 0.4956 | 0.5057 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9989 | 0.0168 | 0.0003 | 0.9970 | 0.0156 | 0.0016 |
| ii | 0.9991 | 0.0118 | 0.0004 | 0.9969 | 0.0131 | 0.0019 |
| iii | 0.9990 | 0.0094 | 0.0006 | 0.9964 | 0.0323 | 0.0005 |
| iv | 0.9985 | 0.0140 | 0.0008 | 0.9948 | 0.0471 | 0.0006 |
| v | 0.9987 | 0.0124 | 0.0008 | 0.9958 | 0.0329 | 0.0011 |
| vi | 0.9984 | 0.0184 | 0.0008 | 0.9953 | 0.0118 | 0.0039 |
| vii | 0.9964 | 0.0714 | 0.0001 | 0.9948 | 0.0374 | 0.0016 |
| viii | 0.9981 | 0.0250 | 0.0007 | 0.9933 | 0.0621 | 0.0005 |
| ix | 0.9968 | 0.0614 | 0.0001 | 0.9948 | 0.0388 | 0.0015 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9775 | 0.0338 | 0.0197 | 0.9109 | 0.1282 | 0.0724 |
| ii | 0.9805 | 0.0531 | 0.0110 | 0.9012 | 0.1002 | 0.0982 |
| iii | 0.9791 | 0.0405 | 0.0160 | 0.8878 | 0.0735 | 0.1287 |
| iv | 0.9728 | 0.1147 | 0.0053 | 0.9061 | 0.1607 | 0.0652 |
| v | 0.9751 | 0.0462 | 0.0195 | 0.9006 | 0.1217 | 0.0898 |
| vi | 0.9758 | 0.0459 | 0.0188 | 0.9002 | 0.2621 | 0.0302 |
| vii | 0.9718 | 0.0489 | 0.0230 | 0.8961 | 0.1312 | 0.0922 |
| viii | 0.9721 | 0.0539 | 0.0214 | 0.8999 | 0.2430 | 0.0389 |
| ix | 0.9719 | 0.1062 | 0.0086 | 0.8850 | 0.1042 | 0.1196 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.7061 | 0.1532 | 0.3877 | 0.5009 | 0.2100 | 0.7882 |
| Ii | 0.7352 | 0.2314 | 0.2870 | 0.4996 | 0.2009 | 0.8000 |
| Iii | 0.7137 | 0.1764 | 0.3595 | 0.5001 | 0.2589 | 0.7410 |
| Iv | 0.6933 | 0.1531 | 0.4091 | 0.4985 | 0.3272 | 0.6759 |
| V | 0.7368 | 0.2681 | 0.2598 | 0.4986 | 0.2994 | 0.7034 |
| vi | 0.7231 | 0.2207 | 0.3143 | 0.4988 | 0.3352 | 0.6671 |
| vii | 0.7159 | 0.2166 | 0.3291 | 0.4999 | 0.2743 | 0.7258 |
| viii | 0.7226 | 0.2461 | 0.2982 | 0.4999 | 0.2245 | 0.7757 |
| ix | 0.7330 | 0.2971 | 0.2469 | 0.4997 | 0.3320 | 0.6686 |
| Scenario | ||||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9991 | 0.0094 | 0.0005 | 0.9976 | 0.0152 | 0.0010 |
| ii | 0.9993 | 0.0086 | 0.0003 | 0.9977 | 0.0153 | 0.0009 |
| iii | 0.9989 | 0.0060 | 0.0008 | 0.9972 | 0.0211 | 0.0008 |
| iv | 0.9987 | 0.0123 | 0.0007 | 0.9959 | 0.0301 | 0.0012 |
| v | 0.9986 | 0.0109 | 0.0009 | 0.9956 | 0.0340 | 0.0011 |
| vi | 0.9987 | 0.0198 | 0.0004 | 0.9959 | 0.0275 | 0.0015 |
| vii | 0.9979 | 0.0124 | 0.0016 | 0.9952 | 0.0308 | 0.0019 |
| viii | 0.9975 | 0.0462 | 0.0001 | 0.9955 | 0.0317 | 0.0014 |
| ix | 0.9984 | 0.0184 | 0.0007 | 0.9949 | 0.0426 | 0.0009 |
| Scenario | ε = 20% | ε = 30% | ||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.9801 | 0.0337 | 0.0165 | 0.8822 | 0.0590 | 0.1429 |
| ii | 0.9778 | 0.0291 | 0.0204 | 0.9154 | 0.1205 | 0.0692 |
| iii | 0.9824 | 0.0508 | 0.0093 | 0.9099 | 0.2463 | 0.0231 |
| iv | 0.9728 | 0.0387 | 0.0244 | 0.9007 | 0.1158 | 0.0923 |
| v | 0.9660 | 0.0265 | 0.0359 | 0.9045 | 0.1338 | 0.0791 |
| vi | 0.9745 | 0.0440 | 0.0209 | 0.8812 | 0.0776 | 0.1365 |
| vii | 0.9648 | 0.1655 | 0.0026 | 0.9017 | 0.1300 | 0.0848 |
| viii | 0.9750 | 0.0538 | 0.0177 | 0.9082 | 0.1758 | 0.0558 |
| ix | 0.9700 | 0.1341 | 0.0040 | 0.9072 | 0.1675 | 0.0608 |
| Scenario | ε = 40% | ε = 50% | ||||
| Hit Rate | FN Rate | FP Rate | Hit Rate | FN Rate | FP Rate | |
| i | 0.7361 | 0.2238 | 0.2906 | 0.4996 | 0.2591 | 0.7416 |
| ii | 0.7349 | 0.2098 | 0.3019 | 0.5006 | 0.4056 | 0.5933 |
| iii | 0.7350 | 0.2118 | 0.3004 | 0.4982 | 0.2819 | 0.7217 |
| iv | 0.7202 | 0.2077 | 0.3279 | 0.5014 | 0.2229 | 0.7744 |
| v | 0.7070 | 0.1784 | 0.3694 | 0.5005 | 0.6262 | 0.3728 |
| vi | 0.7000 | 0.1662 | 0.3892 | 0.5019 | 0.2490 | 0.7472 |
| vii | 0.7189 | 0.2161 | 0.3244 | 0.5001 | 0.3647 | 0.6351 |
| viii | 0.7359 | 0.2788 | 0.2544 | 0.4991 | 0.3117 | 0.6902 |
| ix | 0.7325 | 0.2540 | 0.2764 | 0.5004 | 0.2676 | 0.7316 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 386.221 | 379.075 | 365.194 |
| 0.1 | 0.0025 | 353.105 | 358.055 | 341.855 |
| 0.2 | 0.0050 | 260.201 | 282.095 | 237.335 |
| 0.3 | 0.0075 | 236.995 | 249.421 | 159.401 |
| 0.4 | 0.0100 | 119.915 | 166.745 | 109.505 |
| 0.5 | 0.0125 | 88.045 | 117.945 | 65.1308 |
| 0.6 | 0.0150 | 54.982 | 74.185 | 42.411 |
| 0.7 | 0.0175 | 35.195 | 57.105 | 24.155 |
| 0.8 | 0.0200 | 25.005 | 42.295 | 17.541 |
| 0.9 | 0.0225 | 16.545 | 28.530 | 12.075 |
| 1.0 | 0.0250 | 10.751 | 20.582 | 9.195 |
| 1.1 | 0.0275 | 8.307 | 14.291 | 6.815 |
| 1.2 | 0.0300 | 5.895 | 10.425 | 4.335 |
| 1.3 | 0.0325 | 4.615 | 8.222 | 3.441 |
| 1.4 | 0.0350 | 4.164 | 6.685 | 2.593 |
| 1.5 | 0.0375 | 2.811 | 5.565 | 2.445 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 362.455 | 357.21 | 368.175 |
| 0.1 | 0.0025 | 326.510 | 330.370 | 328.430 |
| 0.2 | 0.0050 | 314.055 | 253.810 | 305.860 |
| 0.3 | 0.0075 | 227.840 | 197.685 | 266.260 |
| 0.4 | 0.0100 | 153.770 | 124.415 | 238.035 |
| 0.5 | 0.0125 | 90.460 | 99.950 | 185.685 |
| 0.6 | 0.0150 | 66.235 | 75.310 | 136.395 |
| 0.7 | 0.0175 | 47.225 | 47.925 | 91.755 |
| 0.8 | 0.0200 | 30.040 | 36.930 | 64.465 |
| 0.9 | 0.0225 | 20.005 | 27.735 | 55.045 |
| 1.0 | 0.0250 | 16.620 | 22.370 | 40.715 |
| 1.1 | 0.0275 | 9.930 | 15.050 | 34.060 |
| 1.2 | 0.0300 | 7.560 | 12.555 | 25.985 |
| 1.3 | 0.0325 | 5.780 | 7.225 | 16.330 |
| 1.4 | 0.0350 | 4.480 | 6.640 | 14.010 |
| 1.5 | 0.0375 | 3.925 | 5.225 | 10.945 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 364.425 | 359.040 | 351.510 |
| 0.1 | 0.0025 | 325.890 | 307.205 | 282.950 |
| 0.2 | 0.0050 | 270.730 | 229.495 | 240.455 |
| 0.3 | 0.0075 | 220.725 | 190.665 | 182.670 |
| 0.4 | 0.0100 | 157.060 | 141.245 | 107.775 |
| 0.5 | 0.0125 | 103.130 | 107.685 | 76.505 |
| 0.6 | 0.0150 | 71.660 | 66.605 | 37.040 |
| 0.7 | 0.0175 | 47.840 | 47.645 | 26.845 |
| 0.8 | 0.0200 | 31.330 | 34.700 | 17.955 |
| 0.9 | 0.0225 | 21.765 | 20.820 | 12.165 |
| 1.0 | 0.0250 | 16.580 | 15.775 | 8.985 |
| 1.1 | 0.0275 | 11.385 | 11.305 | 6.610 |
| 1.2 | 0.0300 | 8.025 | 7.890 | 5.160 |
| 1.3 | 0.0325 | 5.815 | 5.665 | 3.545 |
| 1.4 | 0.0350 | 4.875 | 4.840 | 2.995 |
| 1.5 | 0.0375 | 3.655 | 3.115 | 2.515 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 384.025 | 362.975 | 378.955 |
| 0.1 | 0.0025 | 201.185 | 112.091 | 110.12 |
| 0.2 | 0.0050 | 105.521 | 51.482 | 48.485 |
| 0.3 | 0.0075 | 58.972 | 28.981 | 29.690 |
| 0.4 | 0.0100 | 46.851 | 21.675 | 17.275 |
| 0.5 | 0.0125 | 36.065 | 14.685 | 13.241 |
| 0.6 | 0.0150 | 25.685 | 12.135 | 11.015 |
| 0.7 | 0.0175 | 20.352 | 9.515 | 8.195 |
| 0.8 | 0.0200 | 16.151 | 8.755 | 7.760 |
| 0.9 | 0.0225 | 14.222 | 6.542 | 5.775 |
| 1.0 | 0.0250 | 12.701 | 6.163 | 5.631 |
| 1.1 | 0.0275 | 10.141 | 5.621 | 5.352 |
| 1.2 | 0.0300 | 10.111 | 5.210 | 4.605 |
| 1.3 | 0.0325 | 9.370 | 5.005 | 4.825 |
| 1.4 | 0.0350 | 8.001 | 4.655 | 3.362 |
| 1.5 | 0.0375 | 8.025 | 3.855 | 4.265 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 369.025 | 380.04 | 365.145 |
| 0.1 | 0.0025 | 196.880 | 120.265 | 121.500 |
| 0.2 | 0.0050 | 104.580 | 54.185 | 64.130 |
| 0.3 | 0.0075 | 52.845 | 33.930 | 34.475 |
| 0.4 | 0.0100 | 40.210 | 20.265 | 23.995 |
| 0.5 | 0.0125 | 25.925 | 15.600 | 14.590 |
| 0.6 | 0.0150 | 20.940 | 12.755 | 14.920 |
| 0.7 | 0.0175 | 17.880 | 8.760 | 11.355 |
| 0.8 | 0.0200 | 13.400 | 8.225 | 9.655 |
| 0.9 | 0.0225 | 12.105 | 7.480 | 7.850 |
| 1.0 | 0.0250 | 10.355 | 5.605 | 7.360 |
| 1.1 | 0.0275 | 8.620 | 6.270 | 6.935 |
| 1.2 | 0.0300 | 7.725 | 5.050 | 5.860 |
| 1.3 | 0.0325 | 7.920 | 5.080 | 5.810 |
| 1.4 | 0.0350 | 6.870 | 4.870 | 4.960 |
| 1.5 | 0.0375 | 6.020 | 4.180 | 4.745 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 366.170 | 356.350 | 360.710 |
| 0.1 | 0.0025 | 189.895 | 135.420 | 141.050 |
| 0.2 | 0.0050 | 82.905 | 58.890 | 62.395 |
| 0.3 | 0.0075 | 44.645 | 40.855 | 36.430 |
| 0.4 | 0.0100 | 31.450 | 21.180 | 24.260 |
| 0.5 | 0.0125 | 24.900 | 16.725 | 16.325 |
| 0.6 | 0.0150 | 17.610 | 13.455 | 12.685 |
| 0.7 | 0.0175 | 14.075 | 10.630 | 9.945 |
| 0.8 | 0.0200 | 10.665 | 7.650 | 9.210 |
| 0.9 | 0.0225 | 10.065 | 8.325 | 7.005 |
| 1.0 | 0.0250 | 9.725 | 6.200 | 7.590 |
| 1.1 | 0.0275 | 7.095 | 6.420 | 6.990 |
| 1.2 | 0.0300 | 7.165 | 5.600 | 6.210 |
| 1.3 | 0.0325 | 6.390 | 5.310 | 5.510 |
| 1.4 | 0.0350 | 6.035 | 4.740 | 4.360 |
| 1.5 | 0.0375 | 5.060 | 4.515 | 4.570 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 380.765 | 388.43 | 388.155 |
| 0.1 | 0.0025 | 286.715 | 131.855 | 205.025 |
| 0.2 | 0.0050 | 258.211 | 66.763 | 104.961 |
| 0.3 | 0.0075 | 199.535 | 35.440 | 64.611 |
| 0.4 | 0.0100 | 174.015 | 27.561 | 50.075 |
| 0.5 | 0.0125 | 125.242 | 20.835 | 41.332 |
| 0.6 | 0.0150 | 98.741 | 13.985 | 25.425 |
| 0.7 | 0.0175 | 94.721 | 10.721 | 23.351 |
| 0.8 | 0.0200 | 72.552 | 10.385 | 17.281 |
| 0.9 | 0.0225 | 66.411 | 8.961 | 14.015 |
| 1.0 | 0.0250 | 64.092 | 6.990 | 13.272 |
| 1.1 | 0.0275 | 51.721 | 6.205 | 12.245 |
| 1.2 | 0.0300 | 44.495 | 6.695 | 11.131 |
| 1.3 | 0.0325 | 41.312 | 6.081 | 8.565 |
| 1.4 | 0.0350 | 35.025 | 5.622 | 8.465 |
| 1.5 | 0.0375 | 31.112 | 5.361 | 8.425 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 360.92 | 364.295 | 366.095 |
| 0.1 | 0.0025 | 228.395 | 189.135 | 205.490 |
| 0.2 | 0.0050 | 141.870 | 121.995 | 102.540 |
| 0.3 | 0.0075 | 77.115 | 71.655 | 59.360 |
| 0.4 | 0.0100 | 61.580 | 46.030 | 45.345 |
| 0.5 | 0.0125 | 36.800 | 38.575 | 34.255 |
| 0.6 | 0.0150 | 29.860 | 26.030 | 25.575 |
| 0.7 | 0.0175 | 23.410 | 26.030 | 17.965 |
| 0.8 | 0.0200 | 19.785 | 19.700 | 16.910 |
| 0.9 | 0.0225 | 16.905 | 14.245 | 15.370 |
| 1.0 | 0.0250 | 13.835 | 12.510 | 13.815 |
| 1.1 | 0.0275 | 11.890 | 11.980 | 11.430 |
| 1.2 | 0.0300 | 11.705 | 10.165 | 8795 |
| 1.3 | 0.0325 | 9.845 | 11.230 | 10.145 |
| 1.4 | 0.0350 | 9.350 | 8.155 | 8.335 |
| 1.5 | 0.0375 | 9.485 | 9.370 | 8.080 |
| Shift | Kernel | |||
|---|---|---|---|---|
| δμ | δθ | RBF (0.001) | Poly (1) | Linear |
| 0 | 0 | 367.040 | 388.005 | 363.535 |
| 0.1 | 0.0025 | 146.845 | 124.230 | 153.925 |
| 0.2 | 0.0050 | 61.075 | 56.070 | 78.945 |
| 0.3 | 0.0075 | 37.595 | 30.505 | 43.010 |
| 0.4 | 0.0100 | 24.050 | 19.800 | 29.545 |
| 0.5 | 0.0125 | 16.650 | 14.650 | 18.340 |
| 0.6 | 0.0150 | 12.310 | 10.640 | 15.205 |
| 0.7 | 0.0175 | 9.255 | 10.055 | 12.315 |
| 0.8 | 0.0200 | 8.790 | 9.055 | 9.130 |
| 0.9 | 0.0225 | 7.825 | 6.900 | 9.840 |
| 1.0 | 0.0250 | 7.550 | 6.095 | 6.970 |
| 1.1 | 0.0275 | 6.245 | 5.545 | 7.615 |
| 1.2 | 0.0300 | 5.815 | 5.490 | 5.315 |
| 1.3 | 0.0325 | 4.900 | 5.025 | 5.975 |
| 1.4 | 0.0350 | 4.920 | 4.720 | 4.730 |
| 1.5 | 0.0375 | 4.665 | 4.525 | 5.150 |
References
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: New York, NY, USA, 2009; ISBN 0470169923. [Google Scholar]
- Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D.D. Intrusion Detection System using Multivariate Control Chart Hotelling’s T2 based on PCA. Int. J. Adv. Sci. Eng. Inf. Technol. 2018, 8, 1905–1911. [Google Scholar] [CrossRef]
- Maleki, F.; Mehri, S.; Aghaie, A.; Shahriari, H. Robust T2 control chart using median-based estimators. Qual. Reliab. Eng. Int. 2020, 36, 2187–2201. [Google Scholar] [CrossRef]
- Ahsan, M.; Mashuri, M.; Lee, M.H.; Kuswanto, H.; Prastyo, D.D. Robust adaptive multivariate Hotelling’s T2 control chart based on kernel density estimation for intrusion detection system. Expert Syst. Appl. 2020, 145, 113105. [Google Scholar] [CrossRef]
- Salmasnia, A.; Kaveie, M.; Namdar, M. An integrated production and maintenance planning model under VP-T2 Hotelling chart. Comput. Ind. Eng. 2018, 118, 89–103. [Google Scholar] [CrossRef]
- Chong, N.L.; Khoo, M.B.C.; Haq, A.; Castagliola, P. Hotelling’s T2 control charts with fixed and variable sample sizes for monitoring short production runs. Qual. Reliab. Eng. Int. 2019, 35, 14–29. [Google Scholar] [CrossRef]
- Haq, A.; Khoo, M.B.C. An adaptive multivariate EWMA chart. Comput. Ind. Eng. 2019, 127, 549–557. [Google Scholar] [CrossRef]
- Haq, A. One-sided and two one-sided MEWMA charts for monitoring process mean. J. Stat. Comput. Simul. 2020, 90, 699–718. [Google Scholar] [CrossRef]
- Haq, A.; Munir, T.; Khoo, M.B.C. Dual multivariate CUSUM mean charts. Comput. Ind. Eng. 2019, 137, 106028. [Google Scholar] [CrossRef]
- Khusna, H.; Mashuri, M.; Suhartono; Prastyo, D.D.; Lee, M.H.; Ahsan, M. Residual-based maximum MCUSUM control chart for joint monitoring the mean and variability of multivariate autocorrelated processes. Prod. Manuf. Res. 2019, 7, 364–394. [Google Scholar] [CrossRef]
- Zaman, B.; Lee, M.H.; Riaz, M.; Abujiya, M.R. An improved process monitoring by mixed multivariate memory control charts: An application in wind turbine field. Comput. Ind. Eng. 2020, 142, 106343. [Google Scholar] [CrossRef]
- Aldosari, M.S.; Aslam, M.; Srinivasa Rao, G.; Jun, C.-H. An attribute control chart for multivariate Poisson distribution using multiple dependent state repetitive sampling. Qual. Reliab. Eng. Int. 2019, 35, 627–643. [Google Scholar] [CrossRef]
- Mashuri, M.; Wibawati; Purhadi; Irhamah. A Fuzzy Bivariate Poisson Control Chart. Symmetry 2020, 12, 573. [Google Scholar]
- Lee, J.; Peng, Y.; Wang, N.; Reynolds, M.R., Jr. A GLR control chart for monitoring a multinomial process. Qual. Reliab. Eng. Int. 2017, 33, 1773–1782. [Google Scholar] [CrossRef]
- Pu, X.; Li, Y.; Xiang, D. Mixed variables-attributes test plans for single and double acceptance sampling under exponential distribution. Math. Probl. Eng. 2011, 2011, 1–15. [Google Scholar] [CrossRef]
- Aslam, M.; Azam, M.; Khan, N.; Jun, C.H. A mixed control chart to monitor the process. Int. J. Prod. Res. 2015, 53, 4684–4693. [Google Scholar] [CrossRef]
- Aslam, M.; Khan, N.; Aldosari, M.S.; Jun, C.H. Mixed Control Charts Using EWMA Statistics. IEEE Access 2016, 4, 8286–8293. [Google Scholar] [CrossRef]
- Wang, J.; Su, Q.; Fang, Y.; Zhang, P. A multivariate sign chart for monitoring dependence among mixed-type data. Comput. Ind. Eng. 2018, 126, 625–636. [Google Scholar] [CrossRef]
- Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D.D.; Khusna, H. Multivariate Control Chart based on PCA Mix for Variable and Attribute Quality Characteristics. Prod. Manuf. Res. 2018, 6, 364–384. [Google Scholar] [CrossRef]
- Ahsan, M.; Mashuri, M.; Kuswanto, H.; Prastyo, D.D.; Khusna, H. Outlier detection using PCA mix based T2 control chart for continuous and categorical data. Commun. Stat.-Simul. Comput. 2019, 1–28. [Google Scholar] [CrossRef]
- Phaladiganon, P.; Kim, S.B.; Chen, V.C.P.; Jiang, W. Principal component analysis-based control charts for multivariate nonnormal distributions. Expert Syst. Appl. 2013, 40, 3044–3054. [Google Scholar] [CrossRef]
- Schölkopf, B.; Smola, A.; Müller, K.-R. Kernel principal component analysis. Artif. Neural Netw.-ICANN 1997, 97, 583–588. [Google Scholar] [CrossRef]
- Ma, X.; Zabaras, N. Kernel principal component analysis for stochastic input model generation. J. Comput. Phys. 2011, 230, 7311–7331. [Google Scholar] [CrossRef]
- Lee, J.-M.; Yoo, C.; Choi, S.W.; Vanrolleghem, P.A.; Lee, I.-B. Nonlinear process monitoring using kernel principal component analysis. Chem. Eng. Sci. 2004, 59, 223–234. [Google Scholar] [CrossRef]
- Stefatos, G.; Hamza, A. Ben Statistical process control using kernel PCA. In Proceedings of the 2007 Mediterranean Conference on Control & Automation, Athens, Greece, 27–29 June 2007; pp. 1–6. [Google Scholar]
- Dong, D.; McAvoy, T.J. Nonlinear principal component analysis—Based on principal curves and neural networks. Comput. Chem. Eng. 1996, 20, 65–78. [Google Scholar] [CrossRef]
- Boser, B.E.; Guyon, I.M.; Vapnik, V.N. A Training Algorithm for Optimal Margin Classifiers. In Proceedings of the 5th Annual Acm Workshop on Computational Learning Theory, Pittsburgh, PA, USA, 27–29 July 1992; pp. 144–152. [Google Scholar]
- Khusna, H.; Mashuri, M.; Ahsan, M.; Suhartono, S.; Prastyo, D.D. Bootstrap Based Maximum Multivariate CUSUM Control Chart. Qual. Technol. Quant. Manag. 2018, 17, 52–74. [Google Scholar] [CrossRef]
- Khediri, I.B.; Limam, M.; Weihs, C. Variable window adaptive Kernel Principal Component Analysis for nonlinear nonstationary process monitoring. Comput. Ind. Eng. 2011, 61, 437–446. [Google Scholar] [CrossRef]







| p = 5, l = 2 | 10,170.30 | 11,267.65 | 11,217.93 |
| 375.01 | 387.40 | 365.19 | |
| p = 5, l = 3 | 13,292.86 | 13,567.33 | 13,582.07 |
| 376.94 | 385.82 | 379.60 | |
| p = 5, l = 4 | 16,007.85 | 15,845.09 | 15,942.24 |
| 361.19 | 356.42 | 376.72 |
| d | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| p = 5, l = 2 | 10,115.98 | 32,409.33 | 71,318.15 |
| 355.84 | 804.52 | 844.36 | |
| p = 5, l = 3 | 13,129.43 | 39,586.61 | 83,200.83 |
| 358.20 | 774.80 | 815.38 | |
| p = 5, l = 4 | 15,708.87 | 48,741.28 | 90,609.87 |
| 386.68 | 812.37 | 696.31 | |
| d | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| p = 5, l = 2 | 10,665.10 | 19,383.63 | 57,755.22 |
| 371.39 | 487.68 | 755.76 | |
| p = 5, l = 3 | 13,316.01 | 24,878.64 | 71,965.38 |
| 385.64 | 717.66 | 699.74 | |
| p = 5, l = 4 | 15,864.00 | 29,099.03 | 81,079.33 |
| 351.55 | 656.43 | 620.34 | |
| d | |||
|---|---|---|---|
| 1 | 2 | 3 | |
| p = 5, l = 2 | 11,293.83 | 16,354.36 | 48,299.77 |
| 379.08 | 542.78 | 668.36 | |
| p = 5, l = 3 | 13,476.47 | 22,357.91 | 119,229.20 |
| 354.44 | 787.47 | 957.12 | |
| p = 5, l = 4 | 15,820.29 | 26,376.10 | 77,170.29 |
| 351.76 | 830.91 | 631.40 | |
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | |
|---|---|---|---|---|---|
| p = 5, l = 2 | 10,490.03 | 9974.92 | 9358.18 | 6338.11 | 5570.16 |
| 388.28 | 381.70 | 418.82 | 404.65 | 512.10 | |
| p = 5, l = 3 | 12,854.18 | 12,165.33 | 11,727.51 | 7129.09 | 6302.07 |
| 367.22 | 394.55 | 390.09 | 900.73 | 1000.00 | |
| p = 5, l = 4 | 16,197.98 | 14,669.40 | 13,256.48 | 7799.56 | 6556.82 |
| 361.66 | 355.83 | 418.54 | 1000.00 | 904.12 | |
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | |
|---|---|---|---|---|---|
| p = 5, l = 2 | 10,464.28 | 9642.60 | 9939.38 | 6487.39 | 5731.99 |
| 369.76 | 366.09 | 468.92 | 477.56 | 584.15 | |
| p = 5, l = 3 | 12,714.55 | 13,059.87 | 11,763.30 | 7276.46 | 6496.19 |
| 360.03 | 385.56 | 444.63 | 962.98 | 1000.00 | |
| p = 5, l = 4 | 16,821.44 | 14,567.58 | 13,399.80 | 7999.69 | 6759.66 |
| 386.13 | 359.66 | 406.92 | 1000.00 | 1000.00 | |
| 0.001 | 0.005 | 0.01 | 0.05 | 0.1 | |
|---|---|---|---|---|---|
| p = 5, l = 2 | 11,379.40 | 10,474.76 | 9693.14 | 6445.41 | 5714.85 |
| 386.22 | 385.89 | 358.27 | 463.50 | 687.76 | |
| p = 5, l = 3 | 13,524.98 | 12,872.44 | 11,690.72 | 7353.56 | 6392.95 |
| 361.81 | 443.36 | 436.45 | 1000.00 | 1000.00 | |
| p = 5, l = 4 | 15,611.95 | 14,734.50 | 14,882.03 | 7874.67 | 6690.34 |
| 354.36 | 397.19 | 437.90 | 1000.00 | 1000.00 | |
| Scenario | Nonmetric Parameter | p | l |
|---|---|---|---|
| i | 5 | 2 | |
| ii | 5 | 2 | |
| iii | 5 | 2 | |
| iv | 5 | 3 | |
| v | 5 | 3 | |
| vi | 5 | 3 | |
| vii | 5 | 4 | |
| viii | 5 | 4 | |
| ix | 5 | 4 |
| Parameter of Nonmetric Data | l | Kernel Function | ||
|---|---|---|---|---|
| RBF | Polynomial | Linear | ||
| Balanced | 2 | ⁂● | ||
| 3 | ⁂● | ⁂● | ||
| 4 | ⁂● | ⁂● | ||
| Imbalanced | 2 | ⁂● | ||
| 3 | ⁂● | ⁂● | ||
| 4 | ⁂● | ⁂● | ||
| Extreme Imbalanced | 2 | ● | ● | |
| 3 | ● | ● | ||
| 4 | ● | |||
| Scenario | p | l | In Control Mean Process μ | Shifted Mean Process | |||
|---|---|---|---|---|---|---|---|
| 1 | 0.30 | 0.30 | 0.40 | 5 | 4 | 0 | 2 |
| 2 | 0.10 | 0.10 | 0.80 | 5 | 4 | 0 | 2 |
| 3 | 0.05 | 0.05 | 0.90 | 5 | 4 | 0 | 2 |
| Criteria | Number of Observations | |
|---|---|---|
| PCA Mix Chart [19] | Proposed Chart with RBF Kernel [This Study] | |
| In-control observations | 247 | 247 |
| Out of control observations | 3 | 3 |
| Success detection of in-control observations | 247 | 246 |
| Success detection of out-of-control observations | 2 | 3 |
| Misdetection of in-control observations | 0 | 1 |
| Misdetection of out-of-control observations | 1 | 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahsan, M.; Mashuri, M.; Wibawati; Khusna, H.; Lee, M.H. Multivariate Control Chart Based on Kernel PCA for Monitoring Mixed Variable and Attribute Quality Characteristics. Symmetry 2020, 12, 1838. https://doi.org/10.3390/sym12111838
Ahsan M, Mashuri M, Wibawati, Khusna H, Lee MH. Multivariate Control Chart Based on Kernel PCA for Monitoring Mixed Variable and Attribute Quality Characteristics. Symmetry. 2020; 12(11):1838. https://doi.org/10.3390/sym12111838
Chicago/Turabian StyleAhsan, Muhammad, Muhammad Mashuri, Wibawati, Hidayatul Khusna, and Muhammad Hisyam Lee. 2020. "Multivariate Control Chart Based on Kernel PCA for Monitoring Mixed Variable and Attribute Quality Characteristics" Symmetry 12, no. 11: 1838. https://doi.org/10.3390/sym12111838
APA StyleAhsan, M., Mashuri, M., Wibawati, Khusna, H., & Lee, M. H. (2020). Multivariate Control Chart Based on Kernel PCA for Monitoring Mixed Variable and Attribute Quality Characteristics. Symmetry, 12(11), 1838. https://doi.org/10.3390/sym12111838





