A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems
Abstract
1. Introduction
2. The Basic Butterfly Optimization Algorithm (BOA)
3. The Basic Particle Swarm Optimization (PSO) Model
4. The Proposed Algorithm
4.1. Cubic Map
4.2. Nonlinear Parameter Control Strategy
4.3. Hybrid BOA with PSO
| Algorithm 1. Pseudo-code of hybrid PSO with BOA (PSOBOA) |
| 1. Generate the initialize population of the butterflies Xi (i = 1, 2, …, n) randomly |
| 2. Initialize the parameter r1, r2, C1 and C2 |
| 3. Define senser modality c, power exponent a and switch probability p |
| 4. Calculate the fitness value of each butterflies |
| 5. While t = 1: the max iterations |
| 6. For each search agent |
| 7. Update the fragrance of current search agent by Equation (1) |
| 8. End for 9. Find the best f |
| 10. For each search agent |
| 11. Set a random number r in [0,1] |
| 12. If r < p then |
| 13. Move towards best position by Equation (13) |
| 14. Else |
| 15. Move randomly by Equation (14) |
| 16. End if |
| 17. End for |
| 18. Update the velocity using Equation (11) |
| 19. Calculate the new fitness value of each butterflies |
| 20. If < best f |
| 21. Update the position of best f using Equation (12) |
| 22. End if |
| 23. Update the value of power exponent a |
| 24. t = t + 1 |
| 25. End while |
| 26. Return the best solution and its fitness value |
4.4. The Proposed HPSOBOA
| Algorithm 2. Pseudo-code of novel HPSOBOA |
| 1. Generate the initialize population of the butterflies Xi (i = 1, 2, …, n) using cubic map |
| 2. Initialize the parameter r1, r2, C1 and C2 and switch probability p |
| 3. Define senser modality c and the initial value of power exponent a |
| 4. Calculate the fitness value of each butterflies |
| 5. While t = 1: the max iterations |
| 6. For each search agent |
| 7. Update the fragrance of current search agent by Equation (1) |
| 8. End for 9. Find the best f |
| 10. For each search agent |
| 11. Set a random number r in [0,1] |
| 12. If r < p then |
| 13. Move towards best position by Equation (13) |
| 14. Else |
| 15. Move randomly by Equation (14) |
| 16. End if |
| 17. End for |
| 18. Update the velocity using Equation (11) |
| 19. Calculate the new fitness value of each butterflies |
| 20. If < best f |
| 21. Update the position of best f using Equation (12) |
| 22. End if |
| 23. Update the value of power exponent a using Equation (10) |
| 24. t = t + 1 |
| 25. End while |
| 26. Output the best solution |
5. Experiments and Comparison Results
5.1. Numerical Optimization Funtions and Experiments
5.1.1. The 26 Test Functions
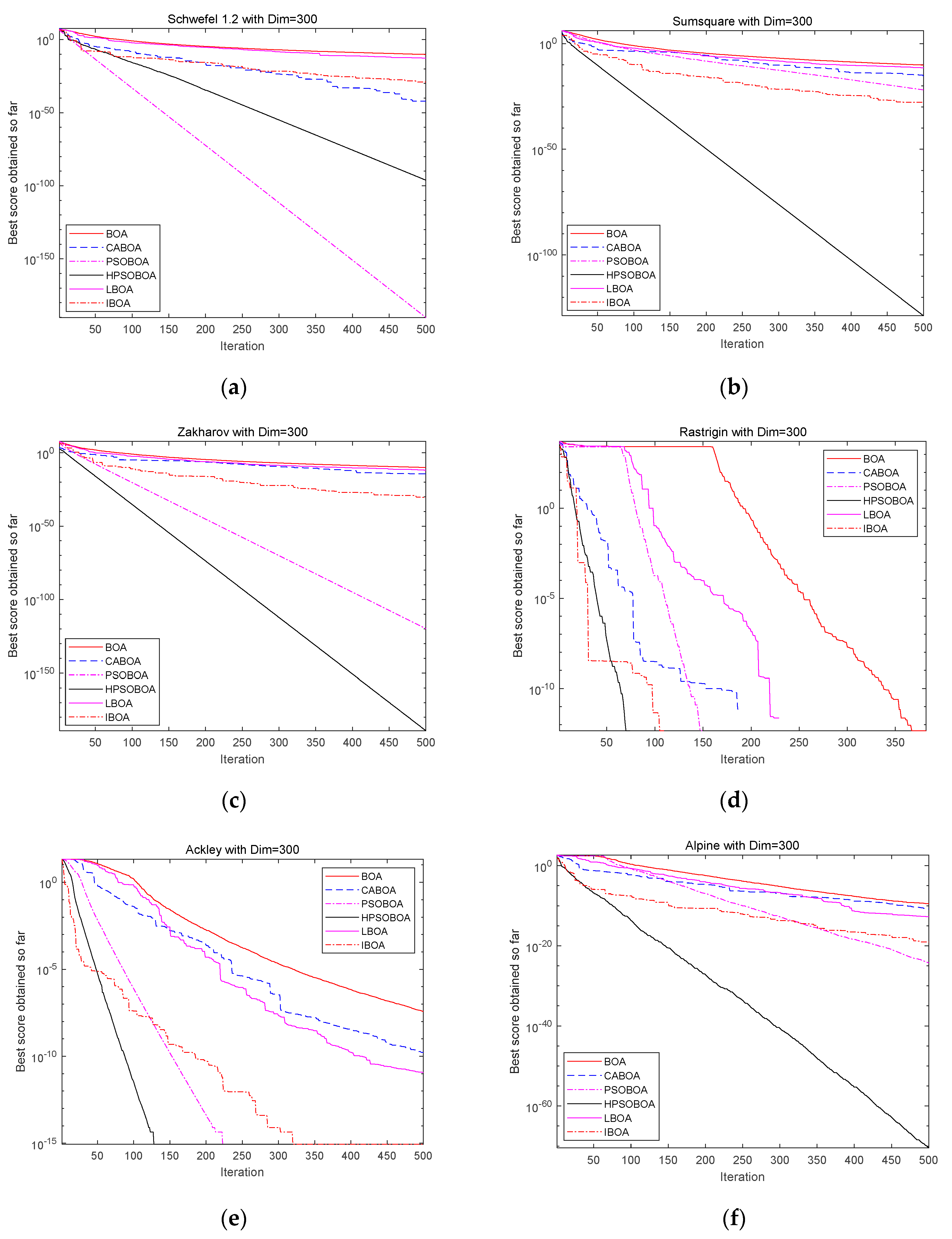
5.1.2. Experiment 1: Comparison with BOA, CBOA, PSOBOA, HPSOBOA, LBOA, and IBOA
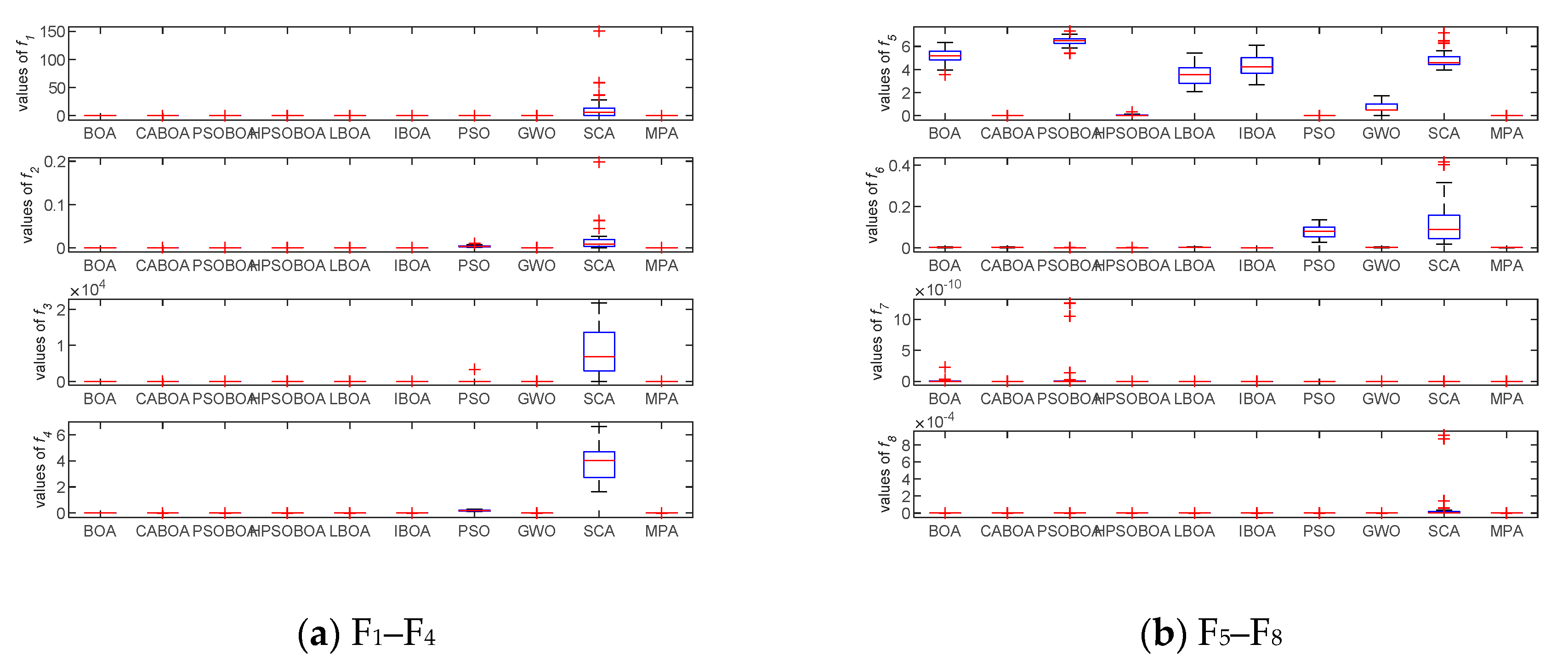
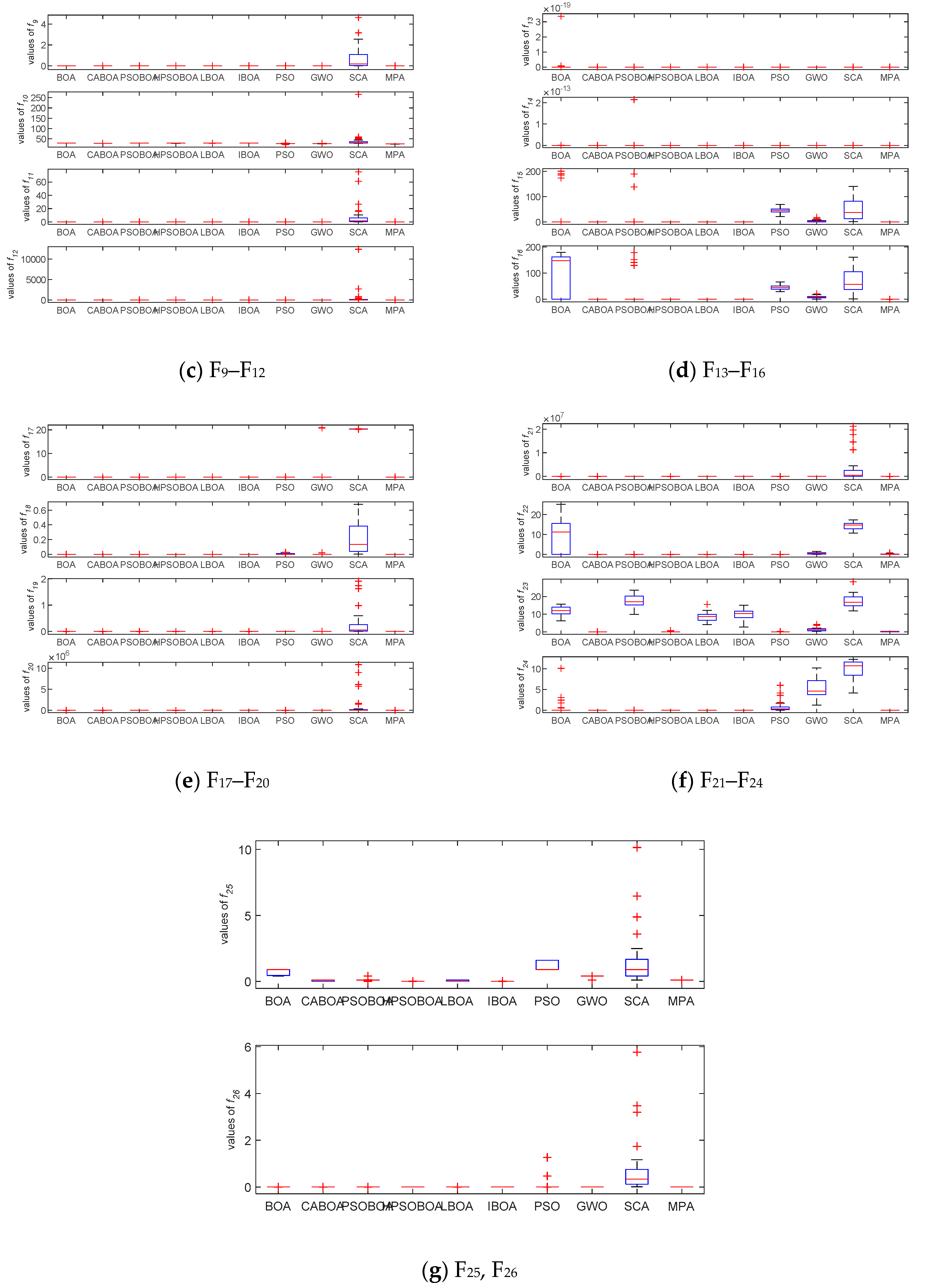
5.1.3. Experiment 2: Comparison with Other Swarm Algorithms
5.1.4. Performance Measures
5.2. Comparison of the Parameter Settings of Ten Algorithms
5.3. Results of Experiment 1
5.4. Results of Experiment 2
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Arora, S.; Singh, S. Butterfly optimization algorithm: A novel approach for global optimization. Soft Comput. 2019, 23, 715–734. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Butterfly Algorithm with Lévy Flights for Global Optimization. In Proceedings of the 2015 International Conference on Signal Processing, Computing and Control (2015 ISPCC), Waknaghat, India, 24–26 September 2015; pp. 220–224. [Google Scholar]
- Arora, S.; Singh, S. An improved butterfly optimization algorithm with chaos. J. Intell. Fuzzy Syst. 2017, 32, 1079–1088. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. An Effective Hybrid Butterfly Optimization Algorithm with Artificial Bee Colony for Numerical Optimization. Int. J. Interact. Multimed. Artif. Intell. 2017, 4, 14–21. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S. Node Localization in Wireless Sensor Networks Using Butterfly Optimization Algorithm. Arab. J. Sci. Eng. 2017, 42, 3325–3335. [Google Scholar] [CrossRef]
- Arora, S.; Singh, S.; Yetilmezsoy, K. A modified butterfly optimization algorithm for mechanical design optimization problems. J. Braz. Soc. Mech. Sci. 2018, 40, 1–17. [Google Scholar] [CrossRef]
- Singh, B.; Anand, P. A novel adaptive butterfly optimization algorithm. Int. J. Comput. Mater. Sci. Eng. 2019, 7, 1850026. [Google Scholar] [CrossRef]
- Sharma, S.; Saha, A.K. m-MBOA: A novel butterfly optimization algorithm enhanced with mutualism scheme. Soft Comput. 2019, 24, 4809–4827. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, W.; Wang, H.; Khodaei, H. Improved Butterfly Optimization Algorithm for CCHP Driven by PEMFC. Appl. Therm. Eng. 2019, 173, 114766. [Google Scholar]
- Li, G.; Shuang, F.; Zhao, P.; Le, C. An Improved Butterfly Optimization Algorithm for Engineering Design Problems Using the Cross-Entropy Method. Symmetry 2019, 11, 1049. [Google Scholar] [CrossRef]
- Wen, L.; Cao, Y. A hybrid intelligent predicting model for exploring household CO2 emissions mitigation strategies derived from butterfly optimization algorithm. Sci. Total Environ. 2020, 727, 138572. [Google Scholar] [CrossRef]
- Tan, L.S.; Zainuddin, Z.; Ong, P. Wavelet neural networks based solutions for elliptic partial differential equations with improved butterfly optimization algorithm training. Appl. Soft Comput. 2020, 95, 106518. [Google Scholar] [CrossRef]
- Malisetti, N.R.; Pamula, V.K. Performance of Quasi Oppositional Butterfly Optimization Algorithm for Cluster Head Selection in WSNs. Procedia Comput. Sci. 2020, 171, 1953–1960. [Google Scholar] [CrossRef]
- Sharma, T.K.; Kumar Sahoo, A.; Goyal, P. Bidirectional butterfly optimization algorithm and engineering applications. Mater. Today Proc. 2020, in press. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- McCall, J. Genetic algorithms for modelling and optimisation. J. Comput. Appl. Math. 2005, 184, 205–222. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential Evolution—A Simple and Efficient Heuristic for global Optimization over Continuous Spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Dorigo, M.; Di Car, G. Ant Colony Optimization: A New Meta-Heuristic. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; pp. 1470–1477. [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Rashedi, E.; Nezamabadi-pour, H.; Saryazdi, S. GSA: A Gravitational Search Algorithm. Inf. Sci. 2009, 179, 2232–2248. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Based Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- Hashim, F.A.; Houssein, E.H.; Mabrouk, M.S.; Al-Atabany, W.; Mirjalili, S. Henry gas solubility optimization: A novel physics-based algorithm. Future Gener. Comput. Syst. 2019, 101, 646–667. [Google Scholar] [CrossRef]
- Yang, X. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization; Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Pan, W. A new Fruit Fly Optimization Algorithm: Taking the financial distress model as an example. Knowl. Based Syst. 2012, 26, 69–74. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Mirjalili, S. Moth-flame optimization algorithm: A novel nature-inspired heuristic paradigm. Knowl. Based Syst. 2015, 89, 228–249. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H.; Mirjalili, S.Z.; Saremi, S.; Faris, H.; Mirjalili, S.M. Salp Swarm Algorithm: A bio-inspired optimizer for engineering design problems. Adv. Eng. Softw. 2017, 114, 163–191. [Google Scholar] [CrossRef]
- Saremi, S.; Mirjalili, S.; Lewis, A. Grasshopper Optimisation Algorithm: Theory and application. Adv. Eng. Softw. 2017, 105, 30–47. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Mirjalili, S.; Gandomi, A.H. Marine Predators Algorithm: A nature-inspired metaheuristic. Expert Syst. Appl. 2020, 152, 113377. [Google Scholar] [CrossRef]
- Li, M.D.; Zhao, H.; Weng, X.W.; Han, T. A novel nature-inspired algorithm for optimization: Virus colony search. Adv. Eng. Softw. 2016, 92, 65–88. [Google Scholar] [CrossRef]
- Mirjalili, S.; Gandomi, A.H. Chaotic gravitational constants for the gravitational search algorithm. Appl. Soft Comput. 2017, 53, 407–419. [Google Scholar] [CrossRef]
- Faramarzi, A.; Heidarinejad, M.; Stephens, B.; Mirjalili, S. Equilibrium optimizer: A novel optimization algorithm. Knowl. Based Syst. 2020, 191, 105190. [Google Scholar] [CrossRef]
- Zhen, Z.; Wang, Z.; Gu, Z.; Liu, Y. A Novel Memetic Algorithm for Global Optimization Based on PSO and SFLA. Lecture Notes Comput. Sci. 2007, 4683, 127–136. [Google Scholar]
- Niu, B.; Li, L. A Novel PSO-DE-Based Hybrid Algorithm for Global Optimization. Lecture Notes Comput. Sci. 2008, 5227, 156–163. [Google Scholar]
- Lai, X.; Zhang, M. An efficient ensemble of GA and PSO for real function optimization. In Proceedings of the 2009 2nd IEEE International Conference on Computer Science and Information Technology, Beijing, China, 8–11 August 2009; pp. 651–655. [Google Scholar]
- Mirjalili, S.; Hashim, S.Z.M. A new hybrid PSOGSA algorithm for function optimization. In Proceedings of the International Conference on Computer and Information Application (ICCIA 2010), Tianjin, China, 3–5 December 2010; pp. 374–377. [Google Scholar]
- Wang, G.; Gandomi, A.H.; Alavi, A.H.; Deb, S. A hybrid method based on krill herd and quantum-behaved particle swarm optimization. Neural Comput. Appl. 2016, 27, 989–1006. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, R.H.; Totlani, R. A Novel Hybrid PSO-DA Algorithm for Global Numerical Optimization. In Networking Communication and Data Knowledge Engineering; Springer: Singapore, 2017; pp. 287–298. [Google Scholar] [CrossRef]
- Trivedi, I.N.; Jangir, P.; Kumar, A.; Jangir, N.; Totlani, A.R. A Novel Hybrid PSO–WOA Algorithm for Global Numerical Functions Optimization. In Advances in Computer and Computational Sciences; Springer: Singapore, 2017; pp. 53–60. [Google Scholar] [CrossRef]
- Laskar, N.M.; Guha, K.; Chatterjee, I.; Chanda, S.; Baishnab, K.L.; Paul, P.K. HWPSO: A new hybrid whale-particle swarm optimization algorithm and its application in electronic design optimization problems. Appl. Intell. 2019, 49, 265–291. [Google Scholar] [CrossRef]
- Yu, P.; Chen, G. Hopf bifurcation control using nonlinear feedback with polynomial functions. Int. J. Bifurcat. Chaos 2004, 14, 1683–1704. [Google Scholar] [CrossRef]
- Xu, F.; Yu, P.; Liao, X. Global analysis on n-scroll chaotic attractors of modified Chua’s circuit. Int. J. Bifurcat. Chaos 2009, 19, 135–157. [Google Scholar] [CrossRef]
- Yu, P.; Lü, J. Bifurcation control for a class of Lorenz-like systems. Int. J. Bifurcat. Chaos 2011, 21, 2647–2664. [Google Scholar] [CrossRef]
- Xu, F.; Yu, P.; Liao, X. Synchronization and stabilization of multi-scroll integer and fractional order chaotic attractors generated using trigonometric functions. Int. J. Bifurcat. Chaos 2013, 23, 1350145. [Google Scholar] [CrossRef]
- Wang, G.; Guo, L.; Gandomi, A.H.; Hao, G.; Wang, H. Chaotic Krill Herd algorithm. Inf. Sci. 2014, 274, 17–34. [Google Scholar] [CrossRef]
- Yousri, D.; AbdelAty, A.M.; Said, L.A.; Elwakil, A.S.; Maundy, B.; Radwan, A.G. Chaotic Flower Pollination and Grey Wolf Algorithms for parameter extraction of bio-impedance models. Appl. Soft Comput. 2019, 75, 750–774. [Google Scholar] [CrossRef]
- Palacios, A. Cycling chaos in one-dimensional coupled iterated maps. Int. J. Bifurcat. Chaos 2002, 12, 1859–1868. [Google Scholar] [CrossRef]
- Meddis, R. Unified analysis of variance by ranks. Br. J. Math. Stat. Psychol. 1980, 33, 84–98. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual Comparisons by Ranking Methods. Biometr. Bull. 1945, 1, 80–83. [Google Scholar] [CrossRef]
- Caruso, G.; Di Battista, T.; Gattone, S.A. A Micro-level Analysis of Regional Economic Activity through a PCA Approach. Adv. Intell. Syst. Comput. 2020, 1009, 227–234. [Google Scholar]




| Name | Formula of Functions | Dim | Range | Type | fmin |
|---|---|---|---|---|---|
| Sphere | 30 | [−100,100] | U | 0 | |
| Schwefel 2.22 | 30 | [−10,10] | U | 0 | |
| Schwefel 1.2 | 30 | [−100,100] | U | 0 | |
| Schwefel 2.21 | 30 | [−10,10] | U | 0 | |
| Step | 30 | [−10,10] | U | 0 | |
| Quartic | 30 | [−1.28,1.28] | U | 0 | |
| Exponential | 30 | [−10,10] | U | 0 | |
| Sum power | 30 | [−1,1] | U | 0 | |
| Sum square | 30 | [−10,10] | U | 0 | |
| Rosenbrock | 30 | [−5,10] | U | 0 | |
| Zakharov | 30 | [−5,10] | U | 0 | |
| Trid | 30 | [−10,10] | U | 0 | |
| Elliptic | 30 | [−100,100] | U | 0 | |
| Cigar | 30 | [−100,100] | U | 0 | |
| Rastrigin | 30 | [−5.12,5.12] | M | 0 | |
| NCRastrigin | 30 | [−5.12,5.12] | M | 0 | |
| Ackley | 30 | [−50,50] | M | 0 | |
| Griewank | 30 | [−600,600] | M | 0 | |
| Alpine | 30 | [−10,10] | M | 0 | |
| Penalized 1 | 30 | [−100,100] | M | 0 | |
| Penalized 2 | 30 | [−100,100] | M | 0 | |
| Schwefel | 30 | [−100,100] | M | 0 | |
| Levy | 30 | [−10,10] | M | 0 | |
| Weierstrass | 30 | [−1,1] | M | 0 | |
| Solomon | 30 | [−100,100] | M | 0 | |
| Bohachevsky | 30 | [−10,10] | M | 0 |
| NO. | Algorithms | Population Size | Parameter Settings |
|---|---|---|---|
| 1 | Butterfly Optimization Algorithm (BOA) | 30 | a = 0.1, c(0) = 0.01, p = 0.6 |
| 2 | Butterfly Optimization Algorithm with Cubic map (CBOA) | 30 | afirst = 0.1, afinal = 0.3, c(0) = 0.01, p = 0.6, x(0) = 0.315, ρ = 0.295 |
| 3 | PSOBOA | 30 | a = 0.1, c(0) = 0.01, p = 0.6, c1 = c2 = 0.5 |
| 4 | Hybrid PSO with BOA and Cubic map (HPSOBOA) | 30 | afirst = 0.1, afinal = 0.3, c(0) = 0.01, p = 0.6, x(0) = 0.315, ρ = 0.295, c1 = c2 = 0.5 |
| 5 | Butterfly Optimization Algorithm with Lévy flights (LBOA) | 30 | a = 0.1, c(0) = 0.01, p = 0.6, λ = 1.5 |
| 6 | Improved Butterfly Optimization Algorithm (IBOA) | 30 | a(0) = 0.1, c(0) = 0.01, p = 0.6, r(0) = 0.33, μ = 4 |
| 7 | Particle Swarm Optimization (PSO) | 30 | c1 = c2 = 2, Vmax = 1, Vmin = −1, ωmax = 0.9, ωmin = 0.2 |
| 8 | Grey Wolf Optimizer (GWO) | 30 | afirst = 2, afinal = 0 |
| 9 | Sine Cosine Algorithm (SCA) | 30 | a = 2, r1(0) = 2 |
| 10 | Marine Predators Algorithm (MPA) | 30 | a = 0.1, c(0) = 0.01, p = 0.6 |
| Functions | BOA | CABOA | PSOBOA | HBOAPSO | LBOA | IBOA | BOA | CABOA | PSOBOA | HBOAPSO | LBOA | IBOA | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dim = 100 | Dim = 300 | ||||||||||||
| Schwefel 1.2 | Worst | 8.23 × 10−11 | 3.16 × 10−18 | 6.40 × 10−9 | 2.89 × 10−207 | 1.67 × 10−11 | 9.22 × 10−29 | 9.21 × 10−11 | 3.95 × 10−27 | 4.06 × 10−9 | 2.65 × 10−76 | 2.56 × 10−11 | 4.53 × 10−29 |
| Best | 5.68 × 10−11 | 1.48 × 10−30 | 4.03 × 10−287 | 7.12 × 10−218 | 6.56 × 10−14 | 9.39 × 10−34 | 6.14 × 10−11 | 6.44 × 10−41 | 4.93 × 10−285 | 4.57 × 10−274 | 3.27 × 10−13 | 2.82 × 10−32 | |
| Avg | 6.95 × 10−11 | 1.12 × 10−19 | 2.13 × 10−10 | 2.32 × 10−207 | 4.43 × 10−12 | 4.34 × 10−30 | 7.49 × 10−11 | 1.32 × 10−28 | 1.35 × 10−10 | 8.85 × 10−78 | 3.46 × 10−12 | 2.73 × 10−30 | |
| Std | 6.15 × 10−12 | 5.76 × 10−19 | 1.17 × 10−9 | 0.00 × 100 | 4.29 × 10−12 | 1.68 × 10−29 | 7.44 × 10−12 | 7.20 × 10−28 | 7.41 × 10−10 | 4.85 × 10−77 | 4.86 × 10−12 | 8.16 × 10−30 | |
| rank | 5.97 | 3.97 | 1.97 | 1.17 | 4.97 | 2.97 | 5.97 | 2.80 | 1.87 | 1.63 | 4.97 | 3.77 | |
| SR/% | 0.00 | 100.00 | 96.67 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 | 96.67 | 100.00 | 0.00 | 100.00 | |
| Sumsquare | Worst | 1.07 × 10−10 | 2.33 × 10−12 | 2.98 × 10−9 | 5.82 × 10−20 | 1.16 × 10−11 | 1.35 × 10−29 | 1.06 × 10−10 | 2.50 × 10−12 | 5.21 × 10−9 | 8.92 × 10−24 | 1.18 × 10−11 | 4.98 × 10−30 |
| Best | 6.71 × 10−11 | 4.45 × 10−19 | 3.42 × 10−294 | 3.47 × 10−294 | 1.34 × 10−14 | 9.55 × 10−34 | 7.33 × 10−11 | 1.00 × 10−16 | 9.50 × 10−272 | 1.35 × 10−292 | 2.87 × 10−15 | 5.72 × 10−33 | |
| Avg | 8.63 × 10−11 | 2.14 × 10−13 | 1.01 × 10−10 | 1.94 × 10−21 | 3.20 × 10−12 | 1.35 × 10−30 | 8.95 × 10−11 | 1.93 × 10−13 | 1.98 × 10−10 | 2.97 × 10−25 | 3.03 × 10−12 | 1.01 × 10−30 | |
| Std | 8.78 × 10−12 | 4.62 × 10−13 | 5.43 × 10−10 | 1.06 × 10−20 | 2.80 × 10−12 | 2.71 × 10−30 | 8.84 × 10−12 | 4.82 × 10−13 | 9.56 × 10−10 | 1.63 × 10−24 | 3.64 × 10−12 | 1.20 × 10−30 | |
| rank | 5.97 | 3.93 | 1.90 | 1.43 | 4.93 | 2.83 | 5.93 | 3.90 | 1.70 | 1.77 | 4.90 | 2.80 | |
| SR/% | 0.00 | 43.33 | 93.33 | 100.00 | 0.00 | 100.00 | 0.00 | 46.67 | 90.00 | 100.00 | 3.33 | 100.00 | |
| Zakharov | Worst | 1.11 × 10−10 | 5.43 × 10−12 | 2.38 × 10−5 | 2.28 × 10−71 | 1.95 × 10−11 | 2.64 × 10−29 | 1.03 × 10−10 | 6.45 × 10−13 | 2.45 × 10−7 | 2.74 × 10−72 | 2.04 × 10−11 | 2.84 × 10−29 |
| Best | 5.70 × 10−11 | 3.06 × 10−17 | 2.14 × 10−294 | 4.25 × 10−289 | 7.01 × 10−15 | 4.38 × 10−33 | 6.88 × 10−11 | 4.94 × 10−16 | 7.09 × 10−293 | 4.43 × 10−287 | 4.80 × 10−14 | 8.50 × 10−33 | |
| Avg | 8.18 × 10−11 | 5.01 × 10−13 | 7.95 × 10−7 | 7.59 × 10−73 | 4.42 × 10−12 | 1.57 × 10−30 | 8.41 × 10−11 | 9.96 × 10−14 | 1.60 × 10−8 | 9.12 × 10−74 | 4.75 × 10−12 | 3.43 × 10−30 | |
| Std | 1.13 × 10−11 | 1.21 × 10−12 | 4.35 × 10−6 | 4.16 × 10−72 | 4.89 × 10−12 | 4.85 × 10−30 | 8.57 × 10−12 | 1.61 × 10−13 | 6.11 × 10−8 | 5.00 × 10−73 | 5.45 × 10−12 | 6.09 × 10−30 | |
| rank | 5.97 | 3.93 | 2.30 | 1.07 | 4.93 | 2.80 | 5.93 | 3.93 | 2.07 | 1.47 | 4.93 | 2.67 | |
| SR/% | 0.00 | 43.33 | 86.67 | 100.00 | 3.33 | 100.00 | 0.00 | 36.67 | 86.67 | 100.00 | 0.00 | 100.00 | |
| Rastrigin | Worst | 4.44 × 10−7 | 0.00 × 100 | 1.39 × 10−9 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 2.36 × 10−7 | 0.00 × 100 | 3.65 × 10−9 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 |
| Best | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| Avg | 1.48 × 10−8 | 0.00 × 100 | 4.65 × 10−11 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 7.88 × 10−9 | 0.00 × 100 | 1.22 × 10−10 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| Std | 8.11 × 10−8 | 0.00 × 100 | 2.55 × 10−10 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 4.32 × 10−8 | 0.00 × 100 | 6.67 × 10−10 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | |
| rank | 3.92 | 3.40 | 3.48 | 3.40 | 3.40 | 3.40 | 3.58 | 3.47 | 3.55 | 3.47 | 3.47 | 3.47 | |
| SR/% | 83.33 | 100.00 | 96.67 | 100.00 | 100.00 | 100.00 | 96.67 | 100.00 | 96.67 | 100.00 | 100.00 | 100.00 | |
| Ackley | Worst | 3.23 × 10−8 | 1.62 × 10−8 | 1.58 × 10−6 | 1.85 × 10−8 | 5.46 × 10−10 | 8.88 × 10−16 | 4.86 × 10−8 | 6.44 × 10−9 | 2.67 × 10−9 | 2.51 × 10−12 | 7.15 × 10−9 | 8.88 × 10−16 |
| Best | 1.59 × 10−9 | 3.02 × 10−10 | 8.88 × 10−16 | 8.88 × 10−16 | 4.44 × 10−15 | 8.88 × 10−16 | 2.30 × 10−8 | 1.80 × 10−10 | 8.88 × 10−16 | 8.88 × 10−16 | 4.49 × 10−13 | 8.88 × 10−16 | |
| Avg | 1.34 × 10−8 | 3.17 × 10−9 | 5.26 × 10−8 | 6.38 × 10−10 | 4.02 × 10−11 | 8.88 × 10−16 | 3.38 × 10−8 | 2.09 × 10−9 | 1.75 × 10−10 | 1.33 × 10−13 | 5.19 × 10−10 | 8.88 × 10−16 | |
| Std | 8.14 × 10−9 | 3.96 × 10−9 | 2.88 × 10−7 | 3.38 × 10−9 | 1.20 × 10−10 | 0.00 × 100 | 5.63 × 10−9 | 1.97 × 10−9 | 6.66 × 10−10 | 5.21 × 10−13 | 1.33 × 10−9 | 0.00 × 100 | |
| rank | 5.97 | 4.93 | 2.10 | 2.20 | 3.90 | 1.90 | 6.00 | 4.97 | 2.08 | 2.05 | 4.00 | 1.90 | |
| SR/% | 0.00 | 0.00 | 96.67 | 86.67 | 13.33 | 100.00 | 0.00 | 0.00 | 90.00 | 93.33 | 0.00 | 100.00 | |
| Alpine | Worst | 1.30 × 10−10 | 6.56 × 10−7 | 1.80 × 10−12 | 9.13 × 10−41 | 9.60 × 10−12 | 4.41 × 10−19 | 7.31 × 10−10 | 1.80 × 10−6 | 1.04 × 10−11 | 8.54 × 10−23 | 6.14 × 10−11 | 4.97 × 10−19 |
| Best | 2.31 × 10−11 | 3.36 × 10−11 | 3.11 × 10−146 | 9.85 × 10−136 | 2.17 × 10−17 | 3.81 × 10−21 | 5.21 × 10−11 | 5.68 × 10−12 | 8.46 × 10−147 | 3.37 × 10−131 | 9.80 × 10−18 | 4.96 × 10−21 | |
| Avg | 6.94 × 10−11 | 2.57 × 10−8 | 6.01 × 10−14 | 3.18 × 10−42 | 9.82 × 10−13 | 7.90 × 10−20 | 2.67 × 10−10 | 6.34 × 10−8 | 3.46 × 10−13 | 3.00 × 10−24 | 7.53 × 10−12 | 1.33 × 10−19 | |
| Std | 3.01 × 10−11 | 1.20 × 10−7 | 3.29 × 10−13 | 1.67 × 10−41 | 2.21 × 10−12 | 9.09 × 10−20 | 1.76 × 10−10 | 3.28 × 10−7 | 1.89 × 10−12 | 1.56 × 10−23 | 1.22 × 10−11 | 1.48 × 10−19 | |
| rank | 5.00 | 6.00 | 1.73 | 1.37 | 4.00 | 2.90 | 5.77 | 5.23 | 1.43 | 1.73 | 4.00 | 2.83 | |
| SR/% | 0.00 | 0.00 | 96.67 | 100.00 | 43.33 | 100.00 | 0.00 | 0.00 | 96.67 | 100.00 | 10.00 | 100.00 | |
| Avg.rank | 5.464 | 4.361 | 2.247 | 1.772 | 4.356 | 2.800 | 5.531 | 4.050 | 2.117 | 2.019 | 4.378 | 2.906 | |
| Final rank | 6 | 5 | 2 | 1 | 4 | 3 | 6 | 4 | 2 | 1 | 5 | 3 | |
| Functions | BOA | CABOA | PSOBOA | HBOAPSO | LBOA | IBOA | PSO | GWO | SCA | MPA | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| F1 | Avg | 7.78 × 10−11 | 1.01 × 10−13 | 1.68 × 10−10 | 3.74 × 10−104 | 3.92 × 10−12 | 1.61 × 10−30 | 1.11 × 10−5 | 6.20 × 10−28 | 1.39 × 101 | 4.93 × 10−23 |
| Std | 7.67 × 10−12 | 2.11 × 10−13 | 9.17 × 10−10 | 2.05 × 10−103 | 4.46 × 10−12 | 3.90 × 10−30 | 2.12 × 10−5 | 7.68 × 10−28 | 2.88 × 101 | 7.29 × 10−23 | |
| F2 | Avg | 2.23 × 10−8 | 1.25 × 10−14 | 4.14 × 10−10 | 2.63 × 10−22 | 1.38 × 10−9 | 5.11 × 10−19 | 3.35 × 10−3 | 1.04 × 10−16 | 1.87 × 10−2 | 2.99 × 10−13 |
| Std | 7.12 × 10−9 | 2.15 × 10−14 | 2.27 × 10−9 | 1.44 × 10−21 | 2.08 × 10−9 | 1.73 × 10−18 | 2.18 × 10−3 | 8.66 × 10−17 | 3.66 × 10−2 | 2.56 × 10−13 | |
| F3 | Avg | 6.34 × 10−11 | 6.30 × 10−13 | 8.05 × 10−17 | 3.04 × 10−71 | 2.74 × 10−12 | 6.15 × 10−31 | 1.23 × 102 | 7.24 × 10−6 | 8.03 × 103 | 1.52 × 10−4 |
| Std | 5.70 × 10−12 | 1.37 × 10−12 | 4.41 × 10−16 | 1.67 × 10−70 | 2.44 × 10−12 | 1.16 × 10−30 | 5.98 × 102 | 1.51 × 10−5 | 6.30 × 103 | 3.15 × 10−4 | |
| F4 | Avg | 2.59 × 10−8 | 2.77 × 10−10 | 9.39 × 10−8 | 3.61 × 10−46 | 2.30 × 10−9 | 1.36 × 10−19 | 1.85 × 10−1 | 8.57 × 10−8 | 3.77 × 100 | 3.29 × 10−10 |
| Std | 2.58 × 10−9 | 2.96 × 10−10 | 5.14 × 10−7 | 1.97 × 10−45 | 2.36 × 10−9 | 1.97 × 10−19 | 4.62 × 10−2 | 8.56 × 10−8 | 1.30 × 100 | 2.23 × 10−10 | |
| F5 | Avg | 5.17 × 100 | 8.50 × 10−6 | 6.47 × 100 | 4.17 × 10−2 | 3.52 × 100 | 4.44 × 100 | 3.69 × 10−6 | 6.84 × 10−1 | 4.85 × 100 | 1.25 × 10−7 |
| Std | 6.09 × 10−1 | 1.06 × 10−5 | 3.90 × 10−1 | 6.41 × 10−2 | 8.50 × 10−1 | 8.70 × 10−1 | 4.74 × 10−6 | 4.38 × 10−1 | 7.32 × 10−1 | 4.78 × 10−7 | |
| F6 | Avg | 2.03 × 10−3 | 2.00 × 10−3 | 2.53 × 10−4 | 2.55 × 10−4 | 2.10 × 10−3 | 1.22 × 10−4 | 7.98 × 10−2 | 1.69 × 10−3 | 1.19 × 10−1 | 1.31 × 10−3 |
| Std | 8.70 × 10−4 | 7.89 × 10−4 | 3.21 × 10−4 | 4.00 × 10−4 | 9.63 × 10−4 | 8.06 × 10−5 | 3.14 × 10−2 | 8.21 × 10−4 | 1.04 × 10−1 | 5.47 × 10−4 | |
| F7 | Avg | 1.05 × 10−11 | 1.48 × 10−62 | 8.41 × 10−11 | 1.48 × 10−62 | 5.23 × 10−20 | 1.19 × 10−19 | 0.00 × 100 | 5.10 × 10−58 | 1.38 × 10−40 | 7.18 × 10−66 |
| Std | 4.21 × 10−11 | 6.67 × 10−63 | 2.94 × 10−10 | 6.70 × 10−63 | 1.41 × 10−19 | 5.94 × 10−19 | 0.00 × 100 | 1.71 × 10−57 | 7.24 × 10−40 | 7.74 × 10−70 | |
| F8 | Avg | 6.33 × 10−14 | 6.58 × 10−15 | 1.42 × 10−17 | 3.19 × 10−118 | 7.51 × 10−16 | 1.32 × 10−36 | 1.37 × 10−14 | 2.21 × 10−95 | 7.27 × 10−5 | 1.41 × 10−60 |
| Std | 3.60 × 10−14 | 1.19 × 10−14 | 7.78 × 10−17 | 1.68 × 10−117 | 9.49 × 10−16 | 4.59 × 10−36 | 4.69 × 10−14 | 1.20 × 10−94 | 2.25 × 10−4 | 5.28 × 10−60 | |
| F9 | Avg | 7.01 × 10−11 | 2.91 × 10−13 | 1.87 × 10−16 | 2.72 × 10−99 | 2.36 × 10−12 | 5.60 × 10−31 | 1.67 × 10−4 | 1.50 × 10−28 | 7.67 × 10−1 | 1.07 × 10−23 |
| Std | 7.91 × 10−12 | 7.08 × 10−13 | 1.02 × 10−15 | 1.31 × 10−98 | 2.76 × 10−12 | 1.87 × 10−30 | 3.97 × 10−4 | 1.96 × 10−28 | 1.13 × 100 | 1.36 × 10−23 | |
| F10 | Avg | 2.89 × 101 | 2.87 × 101 | 2.90 × 101 | 2.89 × 101 | 2.88 × 101 | 2.89 × 101 | 2.67 × 101 | 2.68 × 101 | 4.19 × 101 | 2.53 × 101 |
| Std | 2.54 × 10−2 | 1.39 × 10−5 | 2.16 × 10−2 | 8.18 × 10−2 | 3.18 × 10−2 | 3.40 × 10−2 | 1.34 × 100 | 7.02 × 10−1 | 4.32 × 101 | 3.86 × 10−1 | |
| F11 | Avg | 6.72 × 10−11 | 2.37 × 10−14 | 1.32 × 10−8 | 3.64 × 10−78 | 2.78 × 10−12 | 1.10 × 10−30 | 9.02 × 10−5 | 2.24 × 10−28 | 8.79 × 100 | 1.09 × 10−23 |
| Std | 6.90 × 10−12 | 4.24 × 10−14 | 6.84 × 10−8 | 1.99 × 10−77 | 2.63 × 10−12 | 2.90 × 10−30 | 1.05 × 10−4 | 3.10 × 10−28 | 1.74 × 101 | 2.38 × 10−23 | |
| F12 | Avg | 9.72 × 10−1 | 4.77 × 10−1 | 9.91 × 10−1 | 9.75 × 10−1 | 9.34 × 10−1 | 9.71 × 10−1 | 7.66 × 10−1 | 6.67 × 10−1 | 5.86 × 102 | 6.67 × 10−1 |
| Std | 1.14 × 10−2 | 3.45 × 10−1 | 5.24 × 10−3 | 8.45 × 10−2 | 2.11 × 10−2 | 7.36 × 10−3 | 3.39 × 10−1 | 2.62 × 10−6 | 2.29 × 103 | 5.38 × 10−8 | |
| F13 | Avg | 1.16 × 10−20 | 4.17 × 10−30 | 6.44 × 10−24 | 5.73 × 10−92 | 1.20 × 10−24 | 3.03 × 10−35 | 7.70 × 10−77 | 0.00 × 100 | 2.43 × 10−96 | 1.97 × 10−162 |
| Std | 6.14 × 10−20 | 2.18 × 10−29 | 3.00 × 10−23 | 3.14 × 10−91 | 5.29 × 10−24 | 6.42 × 10−35 | 3.27 × 10−76 | 0.00 × 100 | 1.31 × 10−95 | 1.09 × 10−161 | |
| F14 | Avg | 6.51 × 10−17 | 2.24 × 10−23 | 7.15 × 10−15 | 1.28 × 10−63 | 4.71 × 10−18 | 8.45 × 10−31 | 7.38 × 10−61 | 8.59 × 10−201 | 6.47 × 10−67 | 1.07 × 10−63 |
| Std | 1.39 × 10−16 | 7.51 × 10−23 | 3.92 × 10−14 | 7.04 × 10−63 | 7.50 × 10−18 | 2.52 × 10−30 | 3.81 × 10−60 | 0.00 × 100 | 3.37 × 10−66 | 5.84 × 10−63 | |
| F15 | Avg | 2.51 × 101 | 0.00 × 100 | 1.10 × 101 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 4.56 × 101 | 3.36 × 100 | 4.42 × 101 | 0.00 × 100 |
| Std | 6.52 × 101 | 0.00 × 100 | 4.22 × 101 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 1.11 × 101 | 4.42 × 100 | 3.71 × 101 | 0.00 × 100 | |
| F16 | Avg | 9.36 × 101 | 0.00 × 100 | 2.00 × 101 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 4.48 × 101 | 8.20 × 100 | 7.08 × 101 | 1.01 × 10−8 |
| Std | 8.04 × 101 | 0.00 × 100 | 5.23 × 101 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 9.04 × 100 | 5.18 × 100 | 4.45 × 101 | 4.72 × 10−8 | |
| F17 | Avg | 1.09 × 10−9 | 1.84 × 10−9 | 5.63 × 10−8 | 8.96 × 10−11 | 2.34 × 10−12 | 8.88 × 10−16 | 1.69 × 10−3 | 2.79 × 100 | 2.03 × 101 | 1.06 × 10−3 |
| Std | 8.16 × 10−10 | 1.76 × 10−9 | 3.06 × 10−7 | 4.73 × 10−10 | 7.87 × 10−12 | 0.00 × 100 | 1.32 × 10−3 | 7.22 × 100 | 5.27 × 10−2 | 5.83 × 10−3 | |
| F18 | Avg | 7.64 × 10−12 | 1.70 × 10−14 | 2.61 × 10−8 | 0.00 × 100 | 3.48 × 10−13 | 0.00 × 100 | 5.33 × 10−3 | 1.31 × 10−3 | 2.17 × 10−1 | 0.00 × 100 |
| Std | 6.94 × 10−12 | 1.82 × 10−14 | 1.35 × 10−7 | 0.00 × 100 | 8.78 × 10−13 | 0.00 × 100 | 7.48 × 10−3 | 4.99 × 10−3 | 2.13 × 10−1 | 0.00 × 100 | |
| F19 | Avg | 1.90 × 10−10 | 6.76 × 10−6 | 4.77 × 10−7 | 2.54 × 10−45 | 6.32 × 10−14 | 8.93 × 10−20 | 1.15 × 10−3 | 5.15 × 10−4 | 3.02 × 10−1 | 2.12 × 10−14 |
| Std | 1.00 × 10−10 | 3.13 × 10−5 | 1.78 × 10−6 | 1.39 × 10−44 | 1.73 × 10−13 | 1.19 × 10−19 | 9.36 × 10−4 | 7.29 × 10−4 | 5.38 × 10−1 | 1.52 × 10−14 | |
| F20 | Avg | 5.56 × 10−1 | 1.90 × 10−4 | 8.75 × 10−1 | 2.84 × 10−3 | 3.06 × 10−1 | 4.97 × 10−1 | 4.44 × 100 | 4.74 × 10−2 | 1.17 × 106 | 5.79 × 10−5 |
| Std | 1.40 × 10−1 | 4.90 × 10−4 | 2.11 × 10−1 | 3.79 × 10−3 | 9.96 × 10−2 | 1.37 × 10−1 | 2.62 × 100 | 2.27 × 10−2 | 2.83 × 106 | 3.17 × 10−4 | |
| F21 | Avg | 3.52 × 100 | 1.36 × 10−2 | 4.42 × 100 | 3.93 × 10−2 | 2.41 × 100 | 3.15 × 100 | 1.89 × 10−6 | 9.27 × 10−1 | 3.48 × 106 | 1.38 × 10−2 |
| Std | 5.92 × 10−1 | 4.57 × 10−2 | 7.32 × 10−1 | 4.57 × 10−2 | 5.15 × 10−1 | 4.40 × 10−1 | 3.64 × 10−6 | 2.80 × 10−1 | 6.37 × 106 | 3.69 × 10−2 | |
| F22 | Avg | 9.76 × 100 | 5.52 × 10−16 | 3.42 × 10−7 | 8.38 × 10−77 | 1.56 × 10−3 | 3.56 × 10−26 | 6.71 × 10−4 | 5.34 × 10−1 | 1.42 × 101 | 1.11 × 10−1 |
| Std | 7.84 × 100 | 4.56 × 10−16 | 1.88 × 10−6 | 4.30 × 10−76 | 8.54 × 10−3 | 7.84 × 10−26 | 2.74 × 10−3 | 4.25 × 10−1 | 1.87 × 100 | 1.72 × 10−1 | |
| F23 | Avg | 1.17 × 101 | 4.35 × 10−4 | 1.75 × 101 | 7.28 × 10−2 | 8.42 × 100 | 9.83 × 100 | 4.77 × 10−2 | 1.42 × 100 | 1.74 × 101 | 1.35 × 10−1 |
| Std | 2.66 × 100 | 4.66 × 10−4 | 3.79 × 100 | 1.87 × 10−1 | 2.56 × 100 | 2.47 × 100 | 6.58 × 10−2 | 1.13 × 100 | 3.58 × 100 | 1.13 × 10−1 | |
| F24 | Avg | 6.21 × 10−1 | 0.00 × 100 | 3.36 × 10−11 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 9.15 × 10−1 | 5.05 × 100 | 9.91 × 100 | 0.00 × 100 |
| Std | 1.95 × 100 | 0.00 × 100 | 1.84 × 10−10 | 0.00 × 100 | 0.00 × 100 | 0.00 × 100 | 1.40 × 100 | 2.35 × 100 | 2.00 × 100 | 0.00 × 100 | |
| F25 | Avg | 7.65 × 10−1 | 7.30 × 10−2 | 1.41 × 10−1 | 2.53 × 10−8 | 3.65 × 10−2 | 2.25 × 10−32 | 1.15 × 100 | 3.48 × 10−1 | 1.66 × 100 | 9.95 × 10−2 |
| Std | 2.21 × 10−1 | 4.47 × 10−2 | 1.21 × 10−1 | 1.38 × 10−7 | 4.88 × 10−2 | 5.88 × 10−32 | 3.41 × 10−1 | 1.13 × 10−1 | 2.15 × 100 | 8.20 × 10−17 | |
| F26 | Avg | 7.96 × 10−11 | 6.54 × 10−15 | 6.50 × 10−12 | 0.00 × 100 | 3.22 × 10−12 | 0.00 × 100 | 1.00 × 10−1 | 0.00 × 100 | 7.60 × 10−1 | 0.00 × 100 |
| Std | 8.77 × 10−12 | 1.52 × 10−14 | 3.54 × 10−11 | 0.00 × 100 | 2.68 × 10−12 | 0.00 × 100 | 3.29 × 10−1 | 0.00 × 100 | 1.27 × 100 | 0.00 × 100 | |
| Functions | BOA | CABOA | PSOBOA | HBOAPSO | LBOA | IBOA | PSO | GWO | SCA | MPA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 0.00 | 43.33 | 93.33 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 |
| F2 | 0.00 | 76.67 | 86.67 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 | 0.00 |
| F3 | 0.00 | 30.00 | 100.00 | 100.00 | 3.33 | 100.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F4 | 0.00 | 0.00 | 90.00 | 100.00 | 0.00 | 100.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F5 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F6 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F7 | 0.00 | 100.00 | 56.67 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| F8 | 0.00 | 80.00 | 100.00 | 100.00 | 100.00 | 100.00 | 80.00 | 100.00 | 0.00 | 100.00 |
| F9 | 0.00 | 56.67 | 100.00 | 100.00 | 3.33 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 |
| F10 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F11 | 0.00 | 63.33 | 90.00 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 |
| F12 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F13 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| F14 | 100.00 | 100.00 | 96.67 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| F15 | 50.00 | 100.00 | 86.67 | 100.00 | 100.00 | 100.00 | 0.00 | 0.00 | 0.00 | 100.00 |
| F16 | 3.33 | 100.00 | 90.00 | 100.00 | 100.00 | 100.00 | 0.00 | 0.00 | 0.00 | 50.00 |
| F17 | 0.00 | 0.00 | 83.33 | 93.33 | 30.00 | 100.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F18 | 0.00 | 46.67 | 93.33 | 100.00 | 23.33 | 100.00 | 0.00 | 93.33 | 0.00 | 100.00 |
| F19 | 0.00 | 0.00 | 86.67 | 100.00 | 56.67 | 100.00 | 0.00 | 33.33 | 0.00 | 23.33 |
| F20 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F21 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F22 | 16.67 | 100.00 | 90.00 | 100.00 | 96.67 | 100.00 | 0.00 | 0.00 | 0.00 | 13.33 |
| F23 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F24 | 23.33 | 100.00 | 96.67 | 100.00 | 100.00 | 100.00 | 0.00 | 0.00 | 0.00 | 100.00 |
| F25 | 0.00 | 0.00 | 10.00 | 100.00 | 30.00 | 100.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| F26 | 0.00 | 86.67 | 93.33 | 100.00 | 3.33 | 100.00 | 0.00 | 100.00 | 0.00 | 100.00 |
| times | 2 | 7 | 4 | 18 | 7 | 19 | 3 | 9 | 3 | 11 |
| SR rank | 8 | 5 | 6 | 2 | 5 | 1 | 7 | 4 | 7 | 3 |
| Rank | BOA | CABOA | PSOBOA | HBOAPSO | LBOA | IBOA | PSO | GWO | SCA | MPA |
|---|---|---|---|---|---|---|---|---|---|---|
| F1 | 7.97 | 5.93 | 2.10 | 1.53 | 6.97 | 2.83 | 9.00 | 3.83 | 10.00 | 4.83 |
| F2 | 8.00 | 4.87 | 1.93 | 1.63 | 6.97 | 2.83 | 9.03 | 3.87 | 9.97 | 5.90 |
| F3 | 6.00 | 4.00 | 1.70 | 1.33 | 5.00 | 2.97 | 9.00 | 7.03 | 10.00 | 7.97 |
| F4 | 7.17 | 4.07 | 1.83 | 1.47 | 5.97 | 2.87 | 9.00 | 7.77 | 10.00 | 4.87 |
| F5 | 8.83 | 2.93 | 10.00 | 4.07 | 6.00 | 7.13 | 2.07 | 4.93 | 8.03 | 1.00 |
| F6 | 6.87 | 6.67 | 2.43 | 1.77 | 7.07 | 1.80 | 9.47 | 5.27 | 9.53 | 4.13 |
| F7 | 9.53 | 3.68 | 9.43 | 3.65 | 8.00 | 7.03 | 1.00 | 4.53 | 6.00 | 2.13 |
| F8 | 8.97 | 6.97 | 1.90 | 1.60 | 6.20 | 4.93 | 7.87 | 2.73 | 10.00 | 3.83 |
| F9 | 8.00 | 6.00 | 1.90 | 1.30 | 7.00 | 2.93 | 9.00 | 3.93 | 10.00 | 4.93 |
| F10 | 7.70 | 3.90 | 9.13 | 6.97 | 5.30 | 6.30 | 2.97 | 2.63 | 9.07 | 1.03 |
| F11 | 7.90 | 5.90 | 2.67 | 1.03 | 6.90 | 2.87 | 9.00 | 3.87 | 10.00 | 4.87 |
| F12 | 6.23 | 2.97 | 7.83 | 8.60 | 4.70 | 6.17 | 4.00 | 2.77 | 10.00 | 1.73 |
| F13 | 10.00 | 7.20 | 5.03 | 3.13 | 8.93 | 7.40 | 5.70 | 1.00 | 4.57 | 2.03 |
| F14 | 9.97 | 7.57 | 3.83 | 2.07 | 8.97 | 7.30 | 5.67 | 1.50 | 4.33 | 3.80 |
| F15 | 5.90 | 3.68 | 4.28 | 3.68 | 3.68 | 3.68 | 9.47 | 7.80 | 9.13 | 3.68 |
| F16 | 8.90 | 3.18 | 4.02 | 3.18 | 3.18 | 3.18 | 8.53 | 7.13 | 9.07 | 4.62 |
| F17 | 6.60 | 7.57 | 2.47 | 2.12 | 3.57 | 1.98 | 8.83 | 6.10 | 9.87 | 5.90 |
| F18 | 7.87 | 5.82 | 3.30 | 2.97 | 6.75 | 2.97 | 9.00 | 3.37 | 10.00 | 2.97 |
| F19 | 6.33 | 7.33 | 2.23 | 1.37 | 4.17 | 2.80 | 9.00 | 6.77 | 10.00 | 5.00 |
| F20 | 7.03 | 2.00 | 8.03 | 3.00 | 5.03 | 6.03 | 8.87 | 4.00 | 10.00 | 1.00 |
| F21 | 8.00 | 2.83 | 9.00 | 3.97 | 6.00 | 7.00 | 1.50 | 5.00 | 10.00 | 1.70 |
| F22 | 8.40 | 4.93 | 2.30 | 1.03 | 4.03 | 2.87 | 6.53 | 8.33 | 9.73 | 6.83 |
| F23 | 8.00 | 1.10 | 9.70 | 2.27 | 6.07 | 6.93 | 2.80 | 4.97 | 9.30 | 3.87 |
| F24 | 6.43 | 3.58 | 3.68 | 3.58 | 3.58 | 3.58 | 7.97 | 9.00 | 10.00 | 3.58 |
| F25 | 8.77 | 4.80 | 5.90 | 1.07 | 3.47 | 2.00 | 9.03 | 6.77 | 9.20 | 4.00 |
| F26 | 7.97 | 4.60 | 3.53 | 3.23 | 6.97 | 3.23 | 9.00 | 3.23 | 10.00 | 3.23 |
| Avg-rank | 7.82 | 4.77 | 4.62 | 2.75 | 5.79 | 4.29 | 7.05 | 4.93 | 9.15 | 3.83 |
| Final rank | 9 | 5 | 4 | 1 | 7 | 3 | 8 | 6 | 10 | 2 |
| Ranksum | BOA | CABOA | PSOBOA | LBOA | IBOA | PSO | GWO | SCA | MPA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 3.02 × 10−11 | 3.02 × 10−11 | 0.035137 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F2 | 3.02 × 10−11 | 3.02 × 10−11 | 0.325527 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F3 | 3.02 × 10−11 | 3.02 × 10−11 | 0.001597 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F4 | 3.02 × 10−11 | 3.02 × 10−11 | 0.014412 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F5 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.31 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 |
| F6 | 4.20 × 10−10 | 2.15 × 10−10 | 0.200949 | 1.33 × 10−10 | 0.520145 | 3.02 × 10−11 | 7.38 × 10−10 | 3.02 × 10−11 | 2.44 × 10−9 |
| F7 | 5.18 × 10−12 | 1.00 × 100 | 5.18 × 10−12 | 5.18 × 10−12 | 5.16 × 10−12 | 1.19 × 10−13 | 0.009689 | 5.18 × 10−12 | 9.85 × 10−11 |
| F8 | 3.02 × 10−11 | 3.02 × 10−11 | 0.122353 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F9 | 3.02 × 10−11 | 3.02 × 10−11 | 0.001302 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F10 | 0.340288 | 3.02 × 10−11 | 3.16 × 10−5 | 0.003671 | 0.200949 | 2.20 × 10−7 | 4.50 × 10−11 | 1.34 × 10−5 | 3.02 × 10−11 |
| F11 | 0.340288 | 3.02 × 10−11 | 3.16 × 10−5 | 0.003671 | 0.200949 | 2.20 × 10−7 | 4.50 × 10−11 | 1.34 × 10−5 | 3.02 × 10−11 |
| F12 | 8.48 × 10−9 | 4.69 × 10−8 | 4.12 × 10−6 | 8.48 × 10−9 | 8.48 × 10−9 | 1.43 × 10−8 | 5.57 × 10−10 | 3.02 × 10−11 | 5.57 × 10−10 |
| F13 | 3.02 × 10−11 | 3.02 × 10−11 | 0.00557 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.21 × 10−12 | 1.29 × 10−9 | 2.53 × 10−4 |
| F14 | 3.02 × 10−11 | 3.02 × 10−11 | 0.001953 | 3.02 × 10−11 | 3.02 × 10−11 | 4.62 × 10−10 | 0.09049 | 7.69 × 10−8 | 9.06 × 10−8 |
| F15 | 1.27 × 10−5 | NaN | 0.041926 | NaN | NaN | 1.21 × 10−12 | 1.19 × 10−12 | 1.21 × 10−12 | NaN |
| F16 | 1.21 × 10−12 | NaN | 0.041926 | NaN | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | 1.27 × 10−5 |
| F17 | 6.03 × 10−11 | 2.89 × 10−11 | 0.248673 | 5.93 × 10−7 | 0.160802 | 2.37 × 10−12 | 2.80 × 10−10 | 2.37 × 10−12 | 6.24 × 10−10 |
| F18 | 1.21 × 10−12 | 4.57 × 10−12 | 0.160802 | 4.57 × 10−12 | NaN | 1.21 × 10−12 | 0.160802 | 1.21 × 10−12 | NaN |
| F19 | 3.02 × 10−11 | 3.02 × 10−11 | 0.003671 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F20 | 3.02 × 10−11 | 3.08 × 10−8 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.34 × 10−11 | 3.02 × 10−11 | 1.09 × 10−10 |
| F21 | 3.02 × 10−11 | 9.51 × 10−6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 4.12 × 10−6 |
| F22 | 3.02 × 10−11 | 3.02 × 10−11 | 1.58 × 10−4 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 |
| F23 | 3.02 × 10−11 | 1.39 × 10−6 | 3.02 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.11 × 10−4 | 2.37 × 10−10 | 3.02 × 10−11 | 1.86 × 10−6 |
| F24 | 1.95 × 10−9 | NaN | 0.333711 | NaN | NaN | 1.21 × 10−12 | 1.21 × 10−12 | 1.21 × 10−12 | NaN |
| F25 | 3.02 × 10−11 | 5.49 × 10−11 | 1.09 × 10−10 | 8.89 × 10−10 | 8.48 × 10−9 | 1.90 × 10−11 | 3.02 × 10−11 | 3.02 × 10−11 | 1.55 × 10−11 |
| F26 | 1.21 × 10−12 | 2.93 × 10−5 | 0.160802 | 1.21 × 10−12 | NaN | 1.21 × 10−12 | NaN | 1.21 × 10−12 | NaN |
| H | BOA | CABOA | PSOBOA | LBOA | IBOA | PSO | GWO | SCA | MPA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F2 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| F3 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F4 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F5 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| F6 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| F7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F8 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| F9 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F10 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| F11 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 |
| F12 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F13 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F14 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 |
| F15 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| F16 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| F17 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| F18 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| F19 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F20 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F21 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F22 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F23 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F24 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| F25 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| F26 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| t-tset | BOA | CABOA | PSOBOA | LBOA | IBOA | PSO | GWO | SCA | MPA |
|---|---|---|---|---|---|---|---|---|---|
| F1 | 6.6456 | 6.6456 | 2.1068 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F2 | 6.6456 | 6.6456 | 0.9832 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F3 | 6.6456 | 6.6456 | 3.1565 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F4 | 6.6456 | 6.6456 | 2.4468 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F5 | 6.6456 | −6.6456 | 6.6456 | 6.6456 | 6.6456 | −6.6456 | 5.6846 | 6.6456 | −6.6456 |
| F6 | 6.2464 | 6.3499 | 1.2789 | 6.4238 | 0.6431 | 6.6456 | 6.1577 | 6.6456 | 5.9655 |
| F7 | 6.9005 | 0.0000 | 6.9005 | 6.9005 | 6.9010 | −7.4180 | 2.5867 | 6.9005 | −6.4692 |
| F8 | 6.6456 | 6.6456 | 1.5450 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F9 | 6.6456 | 6.6456 | 3.2156 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F10 | 0.9536 | −6.6456 | 4.1618 | −2.9051 | −1.2789 | −5.1819 | −6.5865 | 4.3540 | −6.6456 |
| F11 | 6.6456 | 6.6456 | 3.7183 | 6.6456 | 6.6456 | 6.6456 | −6.5865 | 6.6456 | 6.6456 |
| F12 | −5.7585 | −5.4628 | −4.6053 | −5.7585 | −5.7585 | −5.6698 | −6.2021 | 6.6456 | −6.2021 |
| F13 | 6.6456 | 6.6456 | 2.7721 | 6.6456 | 6.6456 | 6.6456 | −7.1040 | 6.0690 | −3.6591 |
| F14 | 6.6456 | 6.6456 | 3.0973 | 6.6456 | 6.6456 | 6.2316 | −1.6928 | 5.3741 | 5.3446 |
| F15 | 4.3649 | NaN | 2.0343 | NaN | NaN | 7.1040 | 7.1063 | 7.1040 | NaN |
| F16 | 7.1040 | NaN | 2.0343 | NaN | NaN | 7.1040 | 7.1040 | 7.1040 | 4.3650 |
| F17 | 6.5431 | 6.6523 | 1.1536 | 4.9936 | −1.4024 | 7.0110 | 6.3094 | 7.0110 | 6.1844 |
| F18 | 7.1040 | 6.9183 | 1.4024 | 6.9182 | NaN | 7.1040 | 1.4024 | 7.1040 | NaN |
| F19 | 6.6456 | 6.6456 | 2.9051 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F20 | 6.6456 | −5.5368 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6308 | 6.6456 | −6.4534 |
| F21 | 6.6456 | −4.4279 | 6.6456 | 6.6456 | 6.6456 | −6.6456 | 6.6456 | 6.6456 | −4.6053 |
| F22 | 6.6456 | 6.6456 | 3.7774 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 | 6.6456 |
| F23 | 6.6456 | −4.8271 | 6.6456 | 6.6456 | 6.6456 | 3.8661 | 6.3351 | 6.6456 | 4.7680 |
| F24 | 6.0023 | NaN | 0.9667 | NaN | NaN | 7.1040 | 7.1040 | 7.1040 | NaN |
| F25 | 6.6456 | 6.5569 | 6.4534 | 6.1281 | 5.7585 | 6.7136 | 6.6456 | 6.6456 | 6.7434 |
| F26 | 7.1040 | 4.1785 | 1.4024 | 7.1040 | NaN | 7.1040 | NaN | 7.1040 | NaN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Long, D.; Qin, T.; Yang, J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry 2020, 12, 1800. https://doi.org/10.3390/sym12111800
Zhang M, Long D, Qin T, Yang J. A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry. 2020; 12(11):1800. https://doi.org/10.3390/sym12111800
Chicago/Turabian StyleZhang, Mengjian, Daoyin Long, Tao Qin, and Jing Yang. 2020. "A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems" Symmetry 12, no. 11: 1800. https://doi.org/10.3390/sym12111800
APA StyleZhang, M., Long, D., Qin, T., & Yang, J. (2020). A Chaotic Hybrid Butterfly Optimization Algorithm with Particle Swarm Optimization for High-Dimensional Optimization Problems. Symmetry, 12(11), 1800. https://doi.org/10.3390/sym12111800




